Abstract
Proteins from the kinesin-8 family promote microtubule (MT) depolymerization, a process thought to be important for the control of microtubule length in living cells. In addition to this MT shortening activity, kinesin 8s are motors that show plus-end directed motility on MTs. Here we describe a simple model that incorporates directional motion and destabilization of the MT plus-end by kinesin 8. Our model quantitatively reproduces the key features of length-versus-time traces for stabilized MTs in the presence of purified kinesin 8, including length-dependent depolymerization. Comparison of model predictions with experiments suggests that kinesin 8 depolymerizes processively, i.e., one motor can remove multiple tubulin dimers from a stabilized MT. Fluctuations in MT length as a function of time are related to depolymerization processivity. We have also determined the parameter regime in which the rate of MT depolymerization is length dependent: length-dependent depolymerization occurs only when MTs are sufficiently short; this crossover is sensitive to the bulk motor concentration.
Introduction
Regulation of microtubule (MT) length is an important cellular process. Abnormal MT lengths can mislocalize the nucleus or mitotic spindle and cause defects in polarized cell growth or mitosis. Although MT length regulation is not fully understood, several mechanisms have been proposed, including chemical gradients in the mitotic spindle (1), cortical interactions (2), trafficking of proteins that bind to MT-ends (3), and a balance between proteins that promote MT polymerization and depolymerization (4,5).
Kinesin-8 proteins appear to help regulate MT length in vivo. Deletion of kinesin-8 genes leads to longer interphase and spindle MTs and defects in mitosis (6–12), suggesting that kinesin 8s promote MT depolymerization. In addition, kinesin-8 motors show processive, plus-end directed motility on MTs in vivo (12,13). Recent work has shown that kinesin-8 proteins are important in chromosome oscillations and MT length fluctuations (7,13,14).
Biochemical experiments with some purified kinesin 8s have reproduced many of the observations made in vivo: kinesin 8 moves processively toward the MT plus-end (15) and the MTs then depolymerize, even when stabilized with taxol or GMPCPP (8,12,15). Kinesin 8s are thus thought to be able to remove the GTP-tubulin cap that stabilizes growing MTs in vivo. Varga et al. recently proposed that the processive motility of kinesin 8s preferentially increases their concentration at the ends of longer MTs (15), thereby more rapidly depolymerizing longer MTs. They proposed that this length-dependent activity serves to regulate MT length. Howard and Hyman proposed that a constant MT growth rate coupled with length-dependent depolymerization would result in a tighter distribution of MT lengths than that set by dynamic instability (4). In particular, MT dynamic instability gives an exponential distribution of MT lengths (16,17), while a coupling between MT growth and length-dependent depolymerization could give a tighter distribution (18). The in vitro experiments are consistent with the in vivo observation of longer MTs when the kinesin 8 is deleted, but the reasons why kinesin-8 depletion and overexpression alter mitotic oscillations are less clear.
Given that not all of the in vivo results can be simply understood in terms of the in vitro observations, we sought to determine if a detailed theory of the in vitro experiments could lead to insights into the behavior of kinesin 8s in cells. We have developed a simple mathematical model that quantitatively captures the length-versus-time traces of stabilized MTs in the presence of purified kinesin 8. The results are consistent with processive MT depolymerization by kinesin 8, i.e., multiple tubulin dimers can be sequentially removed by a single motor. We explored a consequence of this processive depolymerization: altered fluctuations in MT length during depolymerization. In addition, we studied the distribution of motors along the MT and find that length-dependent MT depolymerization occurs only for sufficiently short MTs, i.e., those below a crossover length, which depends strongly on the bulk motor concentration and model parameters.
Our work builds on previous physical theory that considered the motion of multiple motors on a one-dimensional track: Parmeggiani et al. studied a model similar to ours but disallowed changes in the length of the track (19). Nowak et al. extended this work to allow track lengthening catalyzed by motors (20). Other theoretical articles have focused specifically on MT depolymerization by kinesins. For example, the coupling between motor motion and MT depolymerization is thought to be important for kinesin-13 proteins, which also depolymerize GMPCPP- and taxol-stabilized MTs (21). An important difference from this work is that the kinesin-13 protein MCAK moves on MTs by diffusion along the MT lattice, not through motor activity, and it accumulates at the MT-ends through a binding preference for this part of the MT. A previously developed theory of MT shortening by MCAK focused on the dynamic accumulation of motors at the MT-end (22). Both the experiments and theory on MCAK found evidence for processive depolymerization. Finally, a model of MT shortening catalyzed by either kinesin-8 or -13 motors was recently introduced (18).
Our work extends previous theories of motor motion and depolymerization in important ways. The mathematical model we consider is similar to that of Govindan et al. (18). The key differences are that Govindan et al. neglected motor crowding effects and analyzed the steady state of the model, while here we include crowding effects and non-steady-state dynamics. An important theoretical challenge arises because the rate at which motors accumulate at the MT-end and the rate of MT length change are similar (as observed in experiments, see (12,15)). A steady-state analysis, while mathematically more tractable, may therefore miss dynamic behavior present in the experiments. In this article, we first consider a kinetic Monte-Carlo simulation of the full model. Then we develop a mean-field model that explicitly considers non-steady-state effects by describing the coupling between the dynamics of the MT-end and the motor occupancy at the end. The depolymerization rates we obtain in the mean-field model agree well with Monte-Carlo simulations of the full model. We compare the results of the model, including non-steady-state effects, to the experimental data obtained by Varga et al. (15) on length-dependent depolymerization of MTs by Kip3p (see Fig. 11 below).
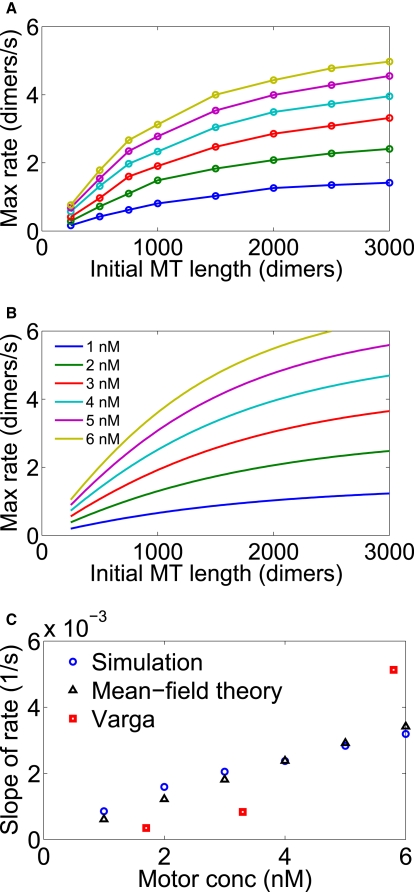
Figure 11.
Variation of the maximum depolymerization rate with initial MT length, showing predictions of (A) the simulations and (B) the mean-field model under conditions of transient shortening. (C) To compare to the results of Varga et al., we fit a straight line to the first 1000 dimers of each curve in panels A and B, and determined the slope as a function of bulk motor concentration. The data of Varga et al. (15) are shown for comparison.
A Mathematical Model of Kinesin-8 Action on mts Quantitatively Reproduces Experiments
Our theoretical model of kinesin-8 motors includes biased motor motion toward MT plus-ends and motor-catalyzed depolymerization of MT plus-ends. A schematic of the model is shown in Fig. 1 A. The position x, in units of tubulin dimers, is measured from the MT minus-end (x = 0). We assume motors track individual protofilaments and step from one tubulin dimer to the next (a length of 8 nm) toward the MT plus-end at rate v. We assume the motors do not step backward (k− = 0), as kinesin-8 motors have shown highly biased motion (15).
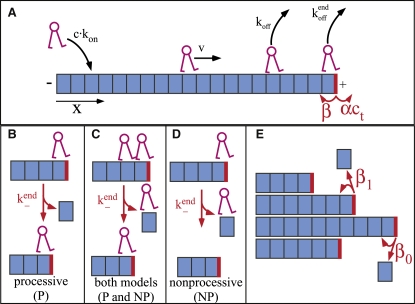
Figure 1.
Model of kinesin-8 motor protein's interaction with a MT protofilament showing the key rates. Rates in black affect only the motor, while those in red affect the MT plus-end. The plus-end of the MT protofilament is indicated by a thick vertical (red) line, and the dimers are indicated by (blue) boxes. Note that depolymerization (at rate k−end) affects both the motor and the MT plus-end. (A) A motor binds to a dimer of the MT with on rate konc and unbinds with rate koff. The motor steps forward at rate v; backward motion is not considered, due to the biased motion of kinesin 8s. MT dynamics are represented by allowing dimers to add to a MT-end at rate αct (where ct is the bulk concentration of tubulin dimers) and dissociate at rate β. (B–D) Depolymerization models. (B) If the motor depolymerizes processively, it removes a MT dimer as it steps backward (with rate k−end), thereby shortening the MT. (C) If the dimer behind the MT-end is occupied, the motor falls off the MT in either model. (D) In the nonprocessive depolymerization model, the motor removes a single tubulin dimer and falls off the MT. (E) Lateral interactions help stabilize MTs. We incorporated this into our model by allowing the depolymerization rate to depend on the number of neighboring protofilaments (i.e., 0, 1, or 2). In this case, the rate at which a terminal tubulin dimer unbinds from a protofilament is given by β0 if the dimer has no lateral neighbors; β1 if the dimer has one lateral neighbor; and β2 if the dimer has two lateral neighbors.
Motors can bind to and unbind from the MT. The on-rate is konc, where c is the bulk concentration of motors (typically assumed to be constant). The off-rate is koff, unless the motor is bound at the end of the MT. Motors dissociate from the plus-end of the MT at rate koffend. We neglect any special affinity that the motors may have for the MT minus-end, since their plus-end directed motility makes their occupancy at the minus-end negligible. We also assume that motors have a negligible affinity for soluble tubulin dimers. Although the binding affinity of kinesin-8 motors for soluble tubulin is currently unknown (12), when we allowed motor binding to free tubulin with an affinity as large as the affinity for MT dimers, there was little change in the results (see below, and other data not shown). Therefore, the precise value of the affinity is not important for our results.
We considered two distinct depolymerization mechanisms: one assumes processive depolymerization (P), and the other assumes purely nonprocessive depolymerization (NP).
In the first case (P), motors processively depolymerize protofilaments by removing one dimer and stepping backward at rate k−end. If there is another motor bound behind the depolymerizing motor, the motor at the end is assumed to unbind. This assumption is motivated by live-cell imaging of fluorescent Kip3p, which showed that a clump of motors accumulates at the MT plus-end during MT growth, but the clump fluorescence greatly decreases during MT shrinkage (12,15). Since protofilaments are straight in the bulk of the MT and protofilament curvature is associated with depolymerization (23), our picture of processive depolymerization is consistent with a structural mechanism in which the motor has a higher affinity for a straight protofilament than a curved region of the protofilament. Our picture of processive depolymerization is also consistent with individual motors inducing catastrophe (in dynamic MTs) and thereby removing large numbers of tubulin dimers. In the absence of crowding effects (if motors fall off before reaching another motor), then the number of dimers removed per motor is a = k−end/koffend. Since motor crowding reduces the depolymerization processivity, the value a will only be observed for sufficiently low motor concentration. Note that this picture of depolymerization can apply either to a motor that directly catalyzes depolymerization, or a motor that recruits to the MT-end another protein that promotes depolymerization.
In the second depolymerization mechanism (NP), motors are assumed to remove a single dimer and fall off with that dimer. In this case, each motor removes at most one dimer (a motor could unbind before removing a dimer).
Our idealized MTs consist of 13 protofilaments arranged cylindrically (we neglect helical arrangement of protofilaments, an assumption that has little effect on our results since we primarily consider independent protofilaments). In all modeling, we further assume that dimer removal by motors is noncooperative, both within and between protofilaments. If each motor acts independently (the case of noncooperative motors), then the rate of depolymerization is, on average, proportional to the density of motors at the end of the MT. (Note that we do consider the possibility of protofilament interactions in tubulin depolymerization; see below.)
Typically, we consider motor-induced depolymerization of stable MTs, so that the MT has no intrinsic dynamics. However, in some cases we use a simple model of MT dynamics: dimers add to a MT-end at rate αct (where ct is the bulk concentration of tubulin dimers) and dissociate at rate β (Fig. 1). In one set of simulations, we allowed the depolymerization rate β to depend on the number of lateral interactions between protofilaments (24,25). In this case, the rate at which a terminal tubulin dimer unbinds from a protofilament is given by β0 if the dimer has no lateral neighbors; β1 if the dimer has one lateral neighbor; and β2 if the dimer has two lateral neighbors.
We developed a kinetic Monte Carlo simulation of the full model, and studied analytic approximations to the model.
Depolymerization of stabilized MTs
In the minimal model of stabilized MTs (Fig. 1, A–D), there are five independent parameters. Three parameters can be derived directly from the data of Varga et al. on the budding yeast kinesin-8 motor Kip3p (15). (See Table 1 for a summary of estimated parameter values.) For these estimates, we assumed that each motor and protofilament behaves independently: we neglected effects of protofilament interactions, motor crowding, and motor depolymerization cooperativity. The measured motor velocity was 3.6 μm min−1, which gives v = 7.5 dimers s−1. The average run length of a motor was 12 μm, which gives ℓ = 1500 dimers. (Note that this run length is likely a lower bound, since the experiments ignored motors that reach the MT-end when determining the run length.) Since ℓ = v/koff, this implies koff = 5 × 10−3 s−1. The typical residence time of a motor at the end of the microtubule was half a minute, so koffend = 3.3 × 10−2 s−1.
Table 1.
| Quantity | Symbol | Typical value(s) |
|---|---|---|
| Position along MT | x | 0–2500 dimers |
| MT length | L | 0–2500 dimers |
| Motor velocity | v | 7.5 dimers s−1 |
| Motor on rate constant | kon | 3 × 10−6 site−1 nM−1 s−1 |
| Motor off rate | koff | 5 × 10−3s−1 |
| Equilibrium constant for motor binding to MT | K = koff/kon | 1.67 μM |
| Motor run length | ℓ = v/koff | 1500 dimers |
| Motor off rate at MT-end | koffend | 3.3 × 10−2 s−1 |
| Rate of motor-catalyzed MT depolymerization | k−end | 13 dimers s−1 |
| Motor depolymerization processivity (upper bound) | a = k−end/koffend | 1–400 dimers |
| Bulk motor concentration | c | 1–200 nM |
| Motor occupancy per tubulin dimer | ρ(x) | 0–1 |
| Steady-state motor occupancy away from MT-ends | ρ0 = konc/(konc + koff) | 6 × 10−4 − 6 × 10−2 |
| Motor occupancy at MT plus-end | ρe | 0–1 |
| Motor occupancy boundary length | λ = v/(konc + koff) | 1400–1500 dimers |
| Timescale of approach to steady-state motor occupancy | τ = 1/(konc + koff) | 185–200 s |
| Length of crossover to length-dependent depolymerization | d | 0–2400 dimers |
| Bulk tubulin concentration | ct | 10–100 nM |
| MT polymerization rate constant | α | 5.4 dimers μM−1 s−1 |
| MT depolymerization rate | β | 0.1 dimers s−1 |
The two parameters k−end and kon were not directly measured for Kip3p, but we can estimate their values from the experimental data. The maximum depolymerization velocity observed was ∼2 μm min−1. This suggests k−end ≥ 4 dimers s−1. However, by comparing our simulations with the data of Varga et al. (15), we found a better fit using the value k−end = 13 dimers s−1 (see below). We estimated the motor binding rate from the kymograph of Fig. 3 D from Varga et al., which shows nine binding events in 6 min on a MT 12 μm in length, for an unspecified bulk motor concentration (of order ∼1 nM). This gives a microscopic rate constant of ∼10−6 site−1 nM−1 s−1. We determined the value kon = 3 × 10−6 site−1 nM−1 s−1 by comparing simulations to the experimental data. In our model, the parameter with the greatest uncertainty is kon. We discuss most results using our best-fit value and discuss below the consequences of varying this value.
Figure 3.
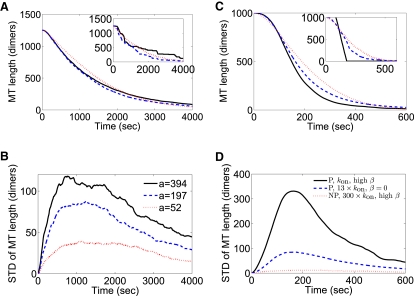
Effects of depolymerization processivity on MT length fluctuations. We chose model parameters that led to similar overall behavior of MT length versus time (A and C) but had different motor-induced depolymerization rates and motor on-rates. All simulations of model P used the experimentally derived value koffend = 3.3 × 10−2 s−1. The maximum processivity (the maximum number of dimers removed per motor) is a = k−end/koffend. (A) We first considered completely stable MTs, those with β0, 1, 2 = 0, and varied kon and k−end to obtain curves, which all have a similar average shape. The trace with a = 394 uses c = 1 nM and the best-fit parameters found when comparing to experiments: kon = 3 × 10−6 site−1 nM−1 s−1 and k−end = 13 dimers s−1. The curve with a = 197 has the on-rate constant doubled to 6 × 10−6 site−1 nM−1 s−1 and the maximum depolymerization rate halved to 6.5 dimers s−1. The curve with a = 52 has the on-rate constant increased by a factor of 8 to kon = 24 × 10−6 site−1 nM−1 s−1 and k−end = 1.7 dimers s−1. Curves in the main panel show averages of 500 simulations, each of a MT with 13 independent protofilaments. Curves in the inset panel show results of individual simulations; the roughness of the MT length versus time behavior decreases as a is decreased. (B) The standard deviation of MT length as a function of time for the simulations shown in panel A. Simulations with higher a show larger standard deviation. (C) Allowing protofilaments without two neighbors to spontaneously depolymerize (P, kon, high β) gives a similar average curve to a simulation with fully stable MTs, but kon increased by a factor of 13. A similar average curve can also be obtained in the nonprocessive case, but only if protofilaments without two neighbors spontaneously depolymerize and kon is increased by a factor of 300 (NP, 300 × kon, high β). (D) The standard deviation of MT length for the simulations shown in panel C.
We first simulated intrinsically stable MTs. The simulations started with bare MTs (no motors bound), and motor binding was begun at t = 0. Using the values of k−end = 13 s−1 and kon = 3 × 10−6 site−1 nM−1 s−1, we found good qualitative agreement with experiments. The depolymerization rate in the simulations increased as the motor occupancy along the MT increased. The time required for equilibration of the motor occupancy was approximately the typical time a motor stayed bound, 1/koff (see further discussion of occupancy equilibration below in Motor Occupancy Profile). The depolymerization rate later decreased once the MT shortened sufficiently.
Our simulations of stabilized MTs did not exhibit the long-time behavior observed in the experiments of Varga et al. (15). In these experiments, kinesin-8 motors were not able to fully depolymerize GMPCPP-stabilized MTs: the depolymerization rate slowed and dropped to zero over several minutes, leading to a long-time tail in the plot of MT length as a function of time. This could have occurred for several reasons:
-
1.
The motor activity may have decreased, e.g., due to depletion of ATP.
-
2.
The motors may have bound to free tubulin dimers or the cover glass, effects that would deplete the concentration of free motors (12,15).
-
3.
Motors may depolymerize cooperatively, so that the decrease in motor concentration at the end of a MT due to shortening had a nonlinear effect on the depolymerization velocity.
-
4.
The slow polymerization activity of GMPCPP tubulin (26) may have prevented full MT depolymerization, because tubulin dimers could add to the end of the MT, increasing its length.
We found that motor binding to free tubulin is not likely to explain the long-time tails. We simulated binding of motors to free tubulin dimers with varying binding affinity. Even when the affinity is large—as large as the affinity for tubulin in the MT lattice—we found only a small change in the depolymerization dynamics (data not shown).
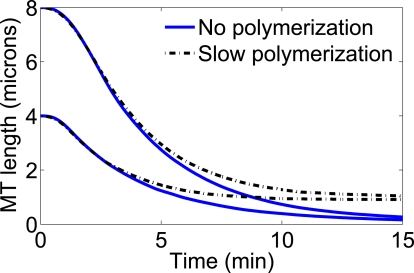
We then modeled polymerization and depolymerization of the MTs with nonzero values of the rate constants α and β (Fig. 1). The intrinsic dynamics of the MT plus-end could have two effects on the motors at the MT-end: 1), the motors could remain attached to the tubulin dimer that is removed; or 2), the motor could be displaced backward and remain on the MT. We found that the former led to significantly decreased MT depolymerization rates (the intrinsic MT dynamics lead to the unbinding of many motors), while the latter gave quantitative agreement with the in vitro experiments. In particular, we estimated that the total tubulin concentration in the experiments of Varga et al. is ∼100 nM. Therefore, we included in the model the measured rates α = 5.4 dimers μM−1 s−1 and β = 0.1 dimers s−1 (26) and found quantitative agreement between the simulation traces and the experiments (see Fig. 2). In this case, the free tubulin concentration becomes high enough that polymerization is large enough to balance motor-induced depolymerization and the MTs approach a constant, time-independent length. Thus, we conclude that the accumulation of free tubulin within the flow chambers, and the subsequent slow polymerization of the MTs, can account for the long-time tails observed in the experiments of Varga et al. (15).
Figure 2.
The slow polymerization of GMPCPP MTs in the presence of free tubulin accounts for the long-time tails observed in Varga et al. (15). In that work, Kip3p was unable to fully depolymerize the MTs over the course of a single experiment. In our simulations, adding previously measured MT polymerization and depolymerization rates for GMPCPP stabilized MTs (26) reproduced the observed behavior. The solid traces were made assuming that the only MT dynamics were those caused by the motors, while the dashed traces were made including intrinsic MT polymerization and depolymerization.
After showing that including the slow polymerization activity of GMPCPP tubulin in the model is sufficient to resolve this qualitative disagreement between experiments and theory, we fit the experimental data to determine the unknown parameters. With processive depolymerization (model P), the only free parameters were k−end, kon, and β0,1. Fig. 3 shows similar MT length versus time curves for different values of these parameters. In model P with independent protofilaments (β0, 1 = 0), a lower depolymerization processivity could (within some range) be offset by a higher on-rate (Fig. 3 A). In addition, decreasing the stability of neighborless protofilaments has similar effects to increasing the MT depolymerization processivity (Fig. 3 C). With nonprocessive depolymerization (model NP), only very high β0, 1 give MT depolymerization time courses that match the experimental results (see below, where nonprocessive depolymerization is discussed in more detail). The best-fit experimental traces were obtained with k−end = 13 s−1 and kon = 3 × 10−6 site−1 nM−1 s−1.
Evidence for processive depolymerization by kinesin-8 motors
Processive depolymerization of MTs by motors is more consistent with the parameters measured by Varga et al. than nonprocessive depolymerization. In particular, they found that an individual motor is resident at the MT-end for ∼30 s (at low motor density), and the depolymerization velocity they observed had a maximum of 2 μm min−1 (at higher motor density). This suggests that (if residence times are similar over a range of motor densities) ∼125 tubulin dimers could be depolymerized during the binding time of a single motor at the MT-end (15). Our best fits to the experimental data gave a higher maximum depolymerization rate for individual motors. We found the best fit with k−end = 13 dimers s−1. This would imply a maximum number of dimers removed per motor a = k−end/koffend ∼400 dimers. (Note that our simulations assumed no interactions between protofilaments or motors, each of which could alter the apparent number of dimers removed per motor.)
We performed simulations to determine whether nonprocessive depolymerization is consistent with the experiments of Varga et al. In this model (NP), we assumed that each motor could remove only one tubulin dimer. We tried but failed to match the experimentally observed traces assuming completely stable MTs. Increases in the motor on-rate by up to a factor of 1000 still produced simulations in which depolymerization occurred much more slowly than seen in experiments (data not shown).
Nonprocessive depolymerization by itself is insufficient to account for the experimental results. However, combining model NP with intrinsically unstable MTs is partially consistent with experiments. The apparent motor processivity increases if protofilaments are not completely stable. We altered the protofilament depolymerization rate β to depend on the number of neighbors the terminal tubulin dimer has. This modeling choice mimics the stabilizing lateral bonds thought to be present between protofilaments (24,25). We note that our simple model does not attempt to fully describe MT dynamics, and we considered only the limiting case of strong lateral interactions: those protofilaments missing at least one neighbor had a very high intrinsic depolymerization rate β0, 1 = 13 s−1. In this case, model NP produced similar behavior to that seen in experiments only with an on-rate a full 20-fold higher than our estimate. The maximum depolymerization rate was then 2 dimers s−1 or 1 μm min−1.
From this analysis, we conclude that if kinesin-8 motors depolymerize MTs nonprocessively, GMPCPP-stabilized MTs must show some intrinsic instability. Specifically, protofilament interactions must cause at least one full row of dimers to be destabilized by the removal of a single dimer. Based on current experimental results, we cannot unambiguously distinguish this case from a processive motor and stable protofilaments. However, we note that the averaged length-versus-time traces are not identical between these two cases. There is less time variation in the MT depolymerization rate in model NP than in model P.
The apparent motor processivity may be due to the inherent instability of MT protofilaments lacking neighbors. However, our results indicate that Kip3p likely depolymerizes MTs processively. We note that our analysis assumes independent motors and neglects effects of motor cooperativity. Including motor cooperativity could lead to different conclusions about motor processivity. Thus, it would be interesting to consider effects of motor cooperativity in future work.
Fluctuations during processive depolymerization
Our results so far have focused on averaged MT behavior. However, fluctuations of MT length about the average are sensitive to kinesin-8 motor depolymerization processivity. To illustrate this effect, we chose parameters that give similar average length versus time dynamics by keeping the product of the microscopic depolymerization rate k−end and the on-rate constant kon approximately fixed while varying the maximum depolymerization processivity, a (Fig. 3). When a is increased, the dynamics of MT length as a function of time become more rough (Fig. 3 A, inset). Motivated by the work of Shaevitz et al., who considered the variance of stepping behavior for conventional kinesin and showed that the variance increased as the step size increased (27), we quantified the fluctuations in MT length as a function of time by determining the standard deviation of MT length in our simulations (Fig. 3 B). For independent protofilaments, we found that the standard deviation increases with a. As expected, the maximum standard deviation scales as a1/2. For these simulations in particular, the maximum standard deviation of MT length ≈ 6a1/2.
Thus, we propose that experimental measurement of the variance in MT length as a function of time can be used to assess depolymerization processivity. One experimental technique to measure the fluctuations is to start with MTs of a certain average length, measure the MT length again after a fixed time, and determine changes in the width of the MT length distribution. Suppose the experimental parameters correspond to those used in Fig. 3, A and B. Our idealized simulation started with 10-μm long MTs; we then determined the length distribution of MTs after ∼1000 s of depolymerization, when the variance is largest. The standard deviation of MT lengths in the simulations was ∼320 nm for a = 52, 700 nm for a = 197, and 950 nm for a = 394, a difference that could be measurable by high-resolution light microscopy. A real experiment would begin with a distribution of MT lengths, but would still observe broadening of the MT length distribution.
Our ability to predict the precise magnitude of MT length fluctuations is limited by several uncertainties. In our model, the fluctuations in depolymerization are primarily controlled by variation in the arrival time of motors to the end of the MT. Particularly when the density of motors on the MT is low, the time between motor arrivals can be long (seconds). Alterations in the fluctuations due to effects we have neglected—such as motor backward stepping or complex ATP hydrolysis kinetics—would alter the behavior of the motors on short timescales, but should have a relatively small effect on the longer timescale behavior we discuss here. The greatest improvement in our ability to predict MT length fluctuations would result from improved measurement of parameters such as the motor binding rate. Finally, the magnitude of the fluctuations depends on the strength of lateral bonds between protofilaments in the MT. We considered simulations both with and without strong lateral interactions (β0, 1 = 13 s−1), as shown in Fig. 3, C and D.
Mean-Field Model of Motor-Mt Dynamics
The Monte Carlo simulations accurately represent the full model, but the equations are complex and analysis requires running many simulations. We therefore developed simpler mean-field models that describe the average occupancy of motors along the MT and the position of the MT-end. A mean-field model considers averaged values of variables such as motor occupancy and depolymerization rate, and therefore neglects stochastic fluctuations. While these models are approximations to the full model, they are useful for a simpler, approximate analysis and for understanding the importance of fluctuations (which are absent in the mean-field models).
We analyzed two classes of mean-field model: 1), a description of the motor occupancy profile, which characterizes the distribution of motors along the MT; and 2), a description of the MT-end, which uses the results of the motor occupancy studies to develop a simple model of the MT depolymerization dynamics.
Motor occupancy profile
To develop and analyze this model, we neglect MT dynamics. (Recall that in the in vitro experiments, the MT intrinsic dynamics primarily affect the long time behavior, i.e., when the tubulin concentration in the flow chamber is sufficiently high to cause significant polymerization.) The average fractional occupancy of motors along the MT, ρ, is described by (19)
| (1) |
On the right-hand side, the first term represents the rate of change of motor concentration due to biased motion of the motors with velocity v, the second term represents the binding of motors to unoccupied sites at rate konc, and the third term represents unbinding of motors from occupied sites at rate koff. The bulk motor concentration c is assumed constant. This equation treats motor crowding effects in a mean-field approximation: the rate of binding of motors to the MT is assumed proportional to (1 − ρ), decreasing in proportion to the average occupancy of a particular site. We neglect crowding effects in the transport term , which, if considered, make the density equation nonlinear (19).
The steady-state density distribution away from either of the MT-ends is given by the constant solution to this equation:
| (2) |
Note that if the on-rate is sufficiently small, that is, konc ≪ koff, then ρ0 ≈ konc/koff = c/K. In other words, the average motor occupancy on the MT is approximately the bulk motor concentration divided by the equilibrium constant for motor binding to the MT.
Away from either of the MT-ends, the density approaches the constant value ρ0. If we consider a spatially constant occupancy, which is not equal to ρ0, the time dependence of Eq. 1 has exponential solutions. If, at time t = 0, motors are introduced to the system, the density far from the MT-ends will change in time according to
| (3) |
The characteristic timescale is
| (4) |
As shown in Fig. 4, this expression agrees well with the simulation results, giving a value of the occupancy within 10% of the value from simulations for the region away from the plus-end of the MT.
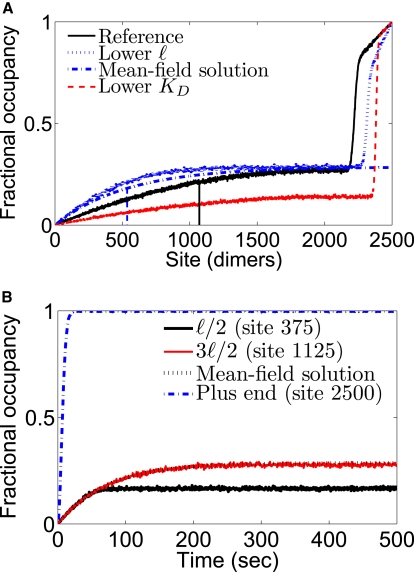
Figure 4.
(A) Examples of motor occupancy profiles. For this figure, we assumed a much higher on-rate than found in experiments to make occupancy changes visible. The reference parameter set has konc = 0.002 dimer−1 s−1 (which would correspond to a bulk motor concentration of 667 nM at the typical on-rate constant of kon = 3 × 10−6 dimer−1 s−1 nM−1), koff = 0.005 s−1, and koffend = 0.02 s−1 (black solid line). Therefore ℓ = 1071 dimers (black vertical line). The curve with decreased ℓ (blue dotted line) has konc and koff both doubled to halve ℓ to 536 dimers (blue vertical dashed-dotted line) while keeping KD unchanged. For these parameters, the mean-field expression for the occupancy from Eq. 5 is the blue dashed/dotted line. The curve with decreased KD has konc halved (red dashed line). (B) Average motor density as a function of time for the lower ℓ parameter set at three positions along the MT: ℓ/2 (black solid line), 3ℓ2 (red solid line) with the mean-field analytic expression of Eq. 3 superimposed (black dotted line), and the MT plus-end (blue dashed-dotted line). All plots are averages of 500 simulated MTs.
Near the MT-ends there is a boundary layer where transport effects and boundary conditions change the motor density away from ρ0 (18–20). Near the minus-end (small x), the boundary layer has low motor density; this occurs because the number of motors that have moved out of a region near the minus-end is not balanced by motors moving into that region from the minus-end. At x = 0, the motor density is exactly zero. In the linear mean-field approximation described by equation (2), the steady-state density is then
| (5) |
where λ = v/(koff + konc) = vτ is the length scale that characterizes the boundary layer of the density distribution near the minus-end. In Fig. 4, we show that the steady-state simulation results are well represented by this occupancy profile.
For small on-rate (konc ≪ koff), this length scale is λ ≈ v/koff = ℓ, the motor-run length. For x ≪ λ, the motor occupancy increases linearly with x, with slope ρ0/λ = konc/v.
Motor occupancy profiles consistent with this result have been observed both in vitro and in vivo. Varga et al. observed a linear increase in Kip3p motor occupancy with position in vitro (15). (We note that if the slope of this linear increase could be measured it would provide a direct measure of the motor on rate kon.) Stumpff et al. imaged human kinesin-8 fluorescence along MTs in fixed cells and observed a gradient in fluorescence that is qualitatively consistent with the model predictions (13); similar gradients in motor fluorescence were seen in yeast cells by Varga et al. (15) and Gupta et al. (12).
Mean-Field Model of Plus-End Dynamics
The dynamics of the microtubule are controlled by the density of motors at the MT-end. Here we formulate and analyze a mean-field description of the motor occupancy at the MT-end and the MT length. Because motors promote MT shortening, the density at the MT plus-end is constantly changing, making the dynamics here typically non-steady state.
We define ρe(t) to be the average motor occupancy at the last site on the MT-end. In this model, we do not consider protofilament interactions, so we are effectively considering a single-protofilament MT. The MT length is represented by L(t) and its rate of change is dL/dt, which is negative during depolymerization. The coupled dynamics of the end occupancy and MT-end change according to
| (6) |
| (7) |
The first term on the right side of Eq. 6 represents the arrival of motors from the region adjacent to the end, where the density is ρ(L − ɛ, t) and ɛ is a small parameter. Solving for the full time dependence of ρ(L − ɛ, t) is, in general, difficult; one would have to solve for the time-varying density near a moving boundary. However, we have assumed that a motor falls off while depolymerizing if the dimer directly adjacent is occupied (Fig. 1 C). Thus, if a transient clump of motors developed at the MT plus-end, it would be quickly removed at rate k−end = 13 s−1, faster than other processes in the model. Thus, we can approximate ρ(L − ɛ, t) ≈ ρ(L − ɛ) ≈ ρ(L), where ρ(x) is the motor occupancy for a region far from the MT plus-end. This density ρ(x) may vary in time or be a steady-state value, but we assume that ρ(x) is controlled by dynamics away from the MT-end. The second term on the right side of Eq. 6 describes unbinding of the motor at the end. In Eq. 7, we assume that the rate of MT shortening is proportional to the depolymerization rate and the motor density at the end. Note that if ρe is constant in time, then according to Eq. 7 the MT shortens at a constant rate.
These equations can be combined to write
| (8) |
Equation 8 can be numerically integrated or studied analytically within certain limits. Below we first determine analytically the constant depolymerization rate of very long MTs, where ρ(L) ≈ ρ0 as determined from Eq. 2. We then compare this predicted constant depolymerization rate with simulations on long MTs.
Then we will consider how long it takes to approach this constant depolymerization rate, and find a typical timescale of tens of seconds. This rapid approach to constant depolymerization led us to consider quasistatic depolymerization. We will assume that even when the motor density away from the MT-end varies spatially, the motor occupancy at the MT plus-end rapidly tracks these changes.
Constant depolymerization of long MTs
We will consider first the limit of long MTs with a constant motor density, so that ρ(L) = ρ0, independent of MT length. In this limit, the constant depolymerization velocity of the MT is determined by the steady-state value of ρe. In this case, Eq. 8 simplifies to one with no L dependence:
| (9) |
| (10) |
This equation has steady-state solutions determined by the quadratic equation
| (11) |
Defining g = (v − k−end)ρ0 + koffend, we can write the solutions as
| (12) |
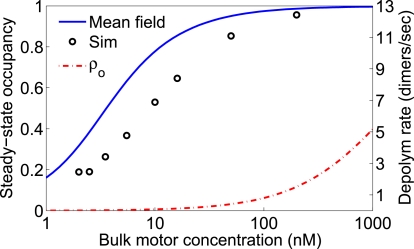
The physically relevant solution (with 0 ≤ ρe ≤ 1) is the negative root. When the end occupancy is constant, the depolymerization rate is |dL/dt| = k−endρe. In Fig. 5, we show the predicted steady-state occupancy at the MT-end, the resulting shortening rate, and comparison with simulations. (For details of the simulations, see Length-Dependent Depolymerization, below.)
Figure 5.
Steady-state motor occupancy and depolymerization rate of long MTs. Left axis shows steady-state motor occupancy at the MT plus-end (solid blue line, black circles) or away from the end (red dashed-dotted line) as a function of bulk motor concentration. The mean-field model (solid blue line) is the prediction of Eq. 12 for the steady-state occupancy of the MT plus-end. Right axis shows the resulting steady depolymerization rate in the mean-field model (solid blue line) and simulations (black circles). The simulation results were determined from the simulations shown in Fig. 8.
The effect of fluctuations is to decrease the depolymerization rate, relative to mean-field predictions. This is intuitively reasonable, because when a fluctuation leads to a higher-than-average density, the motor at the MT-end is then rapidly knocked off (see Fig. 1), which leads to a decrease in the density at the end. Therefore, fluctuations, which decrease the motor density at the end, decrease the depolymerization rate more than fluctuations that increase the motor density at the end increase the depolymerization rate. Despite this small error, the mean-field theory predicts the shape of the curve correctly and determines the depolymerization rate to within 50%.
Approach to steady state
We note that these predictions assume that the MTs start with an initial length long enough that the steady-state motor occupancy at the end can be reached. This assumption may not apply in experiments (see below). We therefore determine the approach of solutions of Eq. 10 to steady state. This equation is a Ricatti equation with constant coefficients, of the form , which can be transformed into a linear, second-order ODE using the substitution . The function u(t) then has two exponential solutions with inverse time constants
| (13) |
The resulting time-dependent solution for the density, given ρe(t = 0) = ρi, is
| (14) |
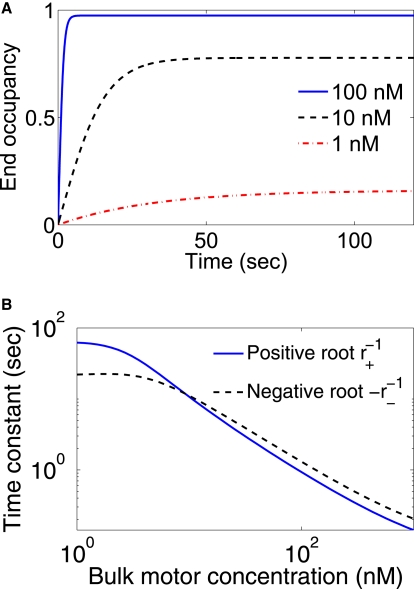
Typical values of parameters give h < 0 and therefore r+ > 0 and r− < 0, so the dynamics will be controlled by the r+ terms for long times. The decay times r±−1 are approximately seconds to tens of seconds, with slower times for lower concentrations. See Fig. 6 for the values of the time constants and a typical time trace determined by Eq. 14.
Figure 6.
Approach to steady-state end occupancy in the mean-field model. (A) End occupancy, beginning from ρe(t = 0) = 0, for representative values of the bulk motor concentration. (B) Values of the time constants r±−1 as a function of bulk motor concentration.
Note that this equation assumes that the motor density outside the end of the MT has reached the steady-state value ρ0. As shown in Fig. 4, it can take several minutes for the density (away from the MT-end) to equilibrate. Therefore, the dynamics of the MT-end are limited by the dynamics of motors away from the end more than by the processes at the end.
Quasistatic depolymerization of MTs
Outside the regime of constant depolymerization, we can still make a simple approximation to the depolymerization rate by assuming that the plus-end of the MT has a motor density determined by the instantaneous solution of the steady-state equation, but with a varying density away from the end. In other words, we assume that the time for motor density at the MT plus-end to reach steady state is short compared to other timescales in the problem. This is a reasonable approximation, given that the dynamics at the end of the MT reach steady state in seconds to tens of seconds (Fig. 6) while MT shortening typically takes minutes.
In the quasistatic approximation, we solve
| (15) |
| (16) |
The solutions here are similar to those of Eq. 12, but with the varying density ρ(L) apparent in the solution:
| (17) |
Defining g(L) = (v − k−end)ρ(L) + koffend, the physically relevant solution is
| (18) |
This quasistatic density at the end of the MT then determines the depolymerization rate via Eq. 16. We will study the accuracy of this quasistatic approximation below in the phase diagram of Length-Dependent Depolymerization.
Length-Dependent Depolymerization
A key feature of the results of Varga et al. is the observation of length-dependent MT depolymerization (15), where the depolymerization rate decreases as the MT length decreases. Since the depolymerization rate cannot increase indefinitely with MT length, a long MT (L ≫ ℓ) will not show length-dependent depolymerization until it becomes sufficiently short. The crossover length d is the length at which length-dependent depolymerization begins; for MT lengths L > d, the depolymerization rate is constant, whereas for L < d, the depolymerization rate decreases as L decreases. Here we determine the crossover length d as a function of motor parameters and experimental conditions.
Motors accumulate at the MT plus-end for several reasons. First, motors have different residence times at the MT-end than away from the end. Away from the ends of the MT, a motor moves away from a dimer at rate v. The off-rate for a motor from the last dimer along the MT is koffend. This will increase the motor occupancy by a factor of v/koffend ∼200 (although note that the average motor occupancy per site cannot be >1; see Fig. 5). Second, depolymerization moves the MT-end closer to motors away from the end; in the frame of the MT-end, motors approach at a rate v − dL/dt, where dL/dt is the rate of change of MT length. Third, motors could accumulate at the MT-end due to direct binding of motors to the end. The latter effect is neglected here.
To characterize length-dependent depolymerization and to understand its role in vivo, we estimated the crossover length d analytically and compared it to simulations. We consider length-dependent depolymerization in two limits: first, we consider the case most independent of initial conditions, which corresponds to starting with very long MTs or preequilibrated motor occupancy along the MT. Second, we consider the case where the initial motor occupancy on the MT is zero; this case is more relevant to an experiment started with the addition of motors to previously unoccupied MTs. See Fig. 7 for a comparison of depolymerization of preequilibrated MTs to depolymerization with an initial transient.
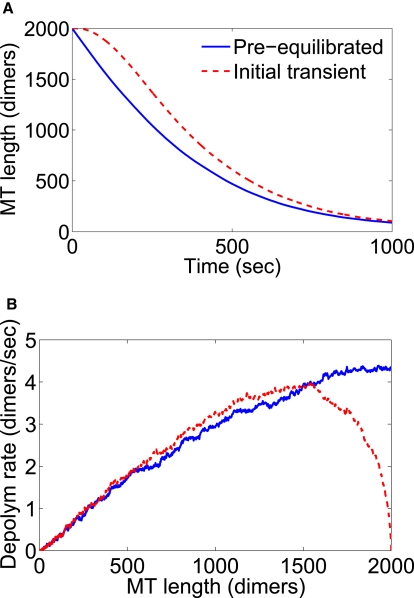
Figure 7.
Steady-state versus transient depolymerization. The transient condition (when motors are added at t = 0, red dashed line) gives dynamics with an initial lag when compared to the condition with preequilibrated motors (blue solid line). Results shown are from simulations (average of 500 runs) with bulk motor concentration of 5.5 nM. (A) MT length as a function of time. (B) Depolymerization rate as a function of MT length.
Length-dependent depolymerization independent of initial conditions
Here we characterize length-dependent depolymerization in a regime that is, as much as possible, independent of the initial conditions or the starting time of an experiment. Such a limit would be reached in experiments (or in cellular conditions) if one either 1), started the experiment with very long MTs or 2), equilibrated the motor density on the MTs before the start of depolymerization.
To approach this limit in the simulations, we implemented both long initial MTs and motor preequilibration. We started with MTs 4000 dimers long (32 μm) and ran the simulations for 1000 s with motor binding, unbinding, and motion allowed but depolymerization turned off. This starting point was then used for simulations of MT shortening. Averaged simulation results are shown in Fig. 8. By examining the depolymerization rate versus MT length (Fig. 8 B), we can see that initially the depolymerization rate is high, but it drops quickly as the clump of motors at the MT plus-end is removed during depolymerization. Then the depolymerization rate reaches a constant value that holds over a range of MT lengths. (This constant rate is compared to the predictions of the mean-field model in Fig. 5.) Once the MT is sufficiently short, the depolymerization rate drops below the steady-state value. Eventually the depolymerization rate drops to zero for an MT of length zero.
Figure 8.
Depolymerization of long MTs. Each curve is the average of 500 independent simulations. Each simulation was started from a preequilibrated MT: the simulation was run for 1000 s with no filament depolymerization, to allow the motor density on the MT to reach steady state. (A) Length versus time. (B) Depolymerization rate versus MT length. Black squares indicate the crossover to length-dependent depolymerization. (C) Standard deviation of MT length versus MT length. (D) Length of crossover to length-dependent depolymerization in the simulations (red circles) and the mean-field model (blue solid line).
We also determined the fluctuations in MT length about the average: Fig. 8 C shows the standard deviation in MT length as a function of MT length during shortening. Lower motor concentration leads to a significantly larger standard deviation in MT length, indicating that larger fluctuations about the average occur when fewer motors are present.
The length where the depolymerization rate drops below the steady-state value is the crossover length d where length-dependent depolymerization sets in (Fig. 8 D). We defined the crossover length d as the MT length where the depolymerization rate first decreased by 20% from the steady-state value. The results from simulations are shown in Fig. 8 D. We calculated d in the mean-field model by rewriting Eq. 8 using L rather than t as the independent variable:
| (19) |
| (20) |
We then numerically integrated Eq. 20 with L0 = 2 × 105 dimers and determined the crossover length d where the depolymerization rate decreases by 20% below the steady-state rate. These results are the solid curve in Fig. 8 D. The predictions of the mean-field model agree tolerably well with the simulations.
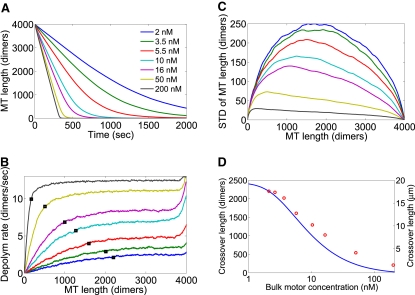
For these results, we find that the crossover length d is 10 μm or longer for bulk motor concentrations of 10 nM or lower. However, for high bulk motor concentration of 50 nM or more, the crossover length decreases to 4 μm or less. This suggests that length-dependent depolymerization is only prominent for sufficiently low motor concentration. This difference may partially explain why Varga et al. observed length-dependent depolymerization but Gupta et al. (12) did not. The Varga experiments used lower bulk motor concentrations (15).
To further understand the behavior of length-dependent depolymerization, we examined how the crossover length d changes when two key parameters are varied. We changed the bulk motor concentration and the motor off-rate at the MT-end and determined d. We studied this crossover using the mean-field model in two limits: first, we numerically integrated Eq. 20 to determine the crossover length in the full mean-field model. Second, we determined the crossover length in the quasistatic model, which assumes that the motor occupancy at the MT-end is instantaneously determined by the solution to the steady-state Eq. 18. This solution is valid if the motor occupancy at the end changes quickly compared to other timescales in the problem. The results are shown in Fig. 9. We note that the quasistatic approximation gives results similar to the full mean-field model except at the lowest motor off-rates. This is intuitively reasonable, since slower motor off-rate at the MT-end increases the timescale for motor dynamics at the MT-end, decreasing the validity of the quasistatic approximation.
Figure 9.
Length of crossover to length-dependent depolymerization, as a function of the bulk motor concentration and the motor off-rate at the MT-end. The horizontal dashed line is the motor off-rate at the MT-end estimated from the experiments of Varga et al. (A) Mean-field model. (B) Quasistatic approximation, where the motor occupancy at the MT-end is assumed to change quickly compared to other dynamics in the problem.
Length-dependent depolymerization controlled by initial conditions
The experiments of Varga et al. do not begin with very long MTs such as those discussed in the previous section. As a result, we expect the dynamics to show a lag relative to the steady depolymerization observed when starting with long MTs (see Fig. 7). To address conditions relevant to experiments, in this section we characterize the effects observed in this transient regime.
For the mean-field calculations presented here, we numerically integrated Eq. 8 using a time-dependent motor density away from the end:
| (21) |
| (22) |
The initial conditions are L(t = 0) = L0 and ρe(t = 0) = 0. The time dependence of the density away from the end, ρ(L, t) is described by
| (23) |
with τ = 1/(koff + konc) and λ = vτ (as discussed above; see Eqs. 3 and 4, and Fig. 4). This form of the density is an approximation that assumes the density approaches its steady-state distribution with dynamics controlled by the slowest timescale in Eq. 2. Note that we assume that at time t = 0 motors are introduced to the system, as in the experiments of Varga et al.
In Fig. 10, we illustrate the solutions to these equations for an assumed bulk motor concentration of 5 nM. The dynamics vary with the initial length of the MT assumed; the maximum depolymerization rate varies by almost a factor of 10 with a comparable change in L0.
Figure 10.
Dynamics under conditions of transient shortening depend strongly on the initial MT length. (Black solid lines) Simulations (average of 500 runs). (Blue dashed lines) Mean-field model. At t = 0, motors are introduced to the system. The bulk motor concentration was 5 nM. (A) MT length as a function of time. (B) Depolymerization rate as a function of MT length.
We compared these results to the experimental data of Varga et al. by considering varying initial MT lengths and bulk motor concentrations. For each curve, we determined the maximum depolymerization rate (the peak of the curve in Fig. 10 B). The results are shown in Fig. 11, where we show how the maximum depolymerization rate varies with L0 and bulk motor concentration. The slope of depolymerization rate versus initial MT length is shown as well, with the results of Varga et al. shown for comparison. The results are reasonably similar—the model predictions are within a factor of 2 of the experimental results.
The model predictions show a linear dependence of the slope of depolymerization rate on initial MT length, while the data of Varga et al. suggest a nonlinear dependence of the slope on bulk motor concentration (Fig. 11). This nonlinearity could result from motor cooperativity, which would lead to a nonlinear dependence of the depolymerization rate on the motor density at the MT-end. This would be an interesting direction for future experiments to explore.
Conclusion
We have developed a theory of MT depolymerization by kinesin 8 and demonstrated agreement between our theory and currently available experiments. The model incorporates biased motor motion toward MT plus-ends, motor-catalyzed depolymerization of plus-ends, motor binding and unbinding, and motor crowding effects. Our theory quantitatively reproduces the experiments of Varga et al. using purified Kip3p, the budding yeast kinesin 8.
In developing a theory of kinesin-8 motors, we addressed a limit that has not been considered in previous theoretical work (18–20,22). Experiments have revealed that clumps of kinesin 8 form on the MT plus-end and change significantly during MT depolymerization (12,15). This observation suggests that MT shortening and motor density changes occur on similar timescales. Therefore, a steady-state mathematical analysis is likely to be a poor approximation to experiments. We have therefore developed and analyzed a time-dependent equation for the MT-end that couples MT depolymerization, motor arrival and dissociation, and motor crowding effects. The results of the equation for MT-end dynamics agree well with full Monte Carlo simulations of the model.
Despite the good agreement between our theoretical results and experiments, there are several uncertainties in our model. We have estimated the motor binding rate constant, which has not been precisely quantified in experiments. The most significant effect of this uncertainty is that it leads to uncertainty in the depolymerization processivity, as illustrated in Fig. 3. In addition, changing the on-rate constant would alter the dependence of the crossover length d on motor concentration, changing the predictions of Fig. 9. We also assumed that when a motor catalyzes dimer removal, it falls off the MT if another motor is bound directly behind it. This assumption is supported by in vivo experiments with fluorescently-labeled Kip3p, which show that a clump of motors accumulates at the MT plus-end when the MT is growing, but the clump shrinks during MT shortening (12,15). Finally, we did not consider possible effects of motor cooperativity in depolymerization; cooperativity is a possible explanation for the apparent nonlinearity of the experimental data shown in Fig. 11. Our best-fit parameters did lead to quantitative agreement between the theory and the experiments of Varga et al. Errors in our determination of the parameters would lead to changes in the quantitative predictions of the theory, but we verified that the qualitative predictions are insensitive to the exact parameter values chosen.
We observed length-dependent depolymerization of MTs in the model, as seen experimentally by Varga et al. (15) and theoretically by Govindan et al. (18). However, this phenomenon occurs only below a crossover length d; MTs much longer than d will depolymerize at a constant rate. The crossover length is controlled by key parameters of the model, particularly the bulk motor concentration, the motor translocation processivity, and the depolymerization processivity. In particular, using the best-fit experimental parameters we predict that the crossover length will decrease from 16 μm to 4 μm if the bulk motor concentration is increased from 5 to 50 nM. This strong concentration dependence may explain the observation of length-dependent depolymerization in vitro by Varga et al. (15) and not by Gupta et al. (12). (Note that the experiments differed in other ways, such as the observed motor velocity.)
Length-dependent depolymerization is not specific to motors with biased motility (18). For example, length-dependent depolymerization could occur for the kinesin-13 MCAK, which diffuses on MTs. The crossover to length-dependent depolymerization is sensitive to motor processivity. As a result, we expect length-dependent depolymerization will be much more important in the kinesin-8 family of proteins because they have a much higher processivity than do kinesin 13s (∼12 μm for Kip3p versus ∼1 μm for MCAK) (12).
The fact that the crossover length is so parameter-dependent highlights the need for care in interpreting experimental results. In cells, the bulk motor concentration and other parameters may be different from the in vitro values. If the key features of our model do apply in the more complicated cellular environment, we can make some speculative predictions. In particular, an overexpression experiment, which increases motor concentration, would lead to both shorter MTs and to a decrease in the crossover length d, and therefore a decrease in the range of lengths over which there is length-dependent depolymerization.
Our results are most consistent with processive depolymerization by kinesin-8 motors, suggesting that multiple tubulin dimers can be removed by a single motor. In particular, the experimental data can be fit to a nonprocessive model only if 1), the motor on-rate is a factor-of-20 higher than the one estimated from experiments; and 2), GMPCPP MTs are intrinsically unstable, so removal of one dimer from one row of tubulin subunits leads to the removal of all 13 dimers around the MT. We note that processive depolymerization has been observed for the kinesin-13 motor MCAK (21), so kinesin 13s and 8s may share some features in their depolymerization activity.
We have shown that processive depolymerization tends to increase the fluctuations of MT length about its average (Fig. 3). Therefore, the roughness of the MT length versus time during depolymerization could be used to quantify the depolymerization processivity. While we emphasize that our theory may not be directly relevant in cells, our results on MT length fluctuations do have interesting implications for some recent experiments. Although kinesin 8s serve, on average, to decrease MT length, the large fluctuations that result from processive depolymerization would introduce a significant variance about this average behavior. In addition, higher protein concentrations should decrease these fluctuations (Fig. 8 C). If this were true in cells, it could explain two recent and puzzling observations on kinesin 8 in vivo. Stumpff et al. found that kinesin 8 overexpression decreased the amplitude of metaphase chromosome oscillations, while reduction in kinesin-8 concentration by RNAi increased it (13). Unsworth et al. found that deleting the kinesin-8 genes (completely eliminating the protein) from fission yeast decreased MT length fluctuations (14), as would be expected if physiological levels of kinesin 8 contribute significantly to length fluctuations. Although our simple mathematical model does not describe the full complexity of the mitotic spindle, it does highlight the potential role of motor-induced fluctuations in spindle behavior.
Acknowledgments
This work was supported in part by an National Institutes of Health Training grant (No. GM65103, to L.E.H.) and the Alfred P. Sloan Foundation (to M.D.B.).
Footnotes
L. E. Hough and Anne Schwabe contributed equally to this article.
References
- 1.Caudron M., Bunt G., Bastiaens P., Karsenti E. Spatial coordination of spindle assembly by chromosome-mediated signaling gradients. Science. 2005;309:1373–1376. doi: 10.1126/science.1115964. [DOI] [PubMed] [Google Scholar]
- 2.Yeh E., Yang C., Chin E., Maddox P., Salmon E.D. Dynamic positioning of mitotic spindles in yeast: role of microtubule motors and cortical determinants. Mol. Biol. Cell. 2000;11:3949–3961. doi: 10.1091/mbc.11.11.3949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bieling P., Laan L., Schek H., Munteanu E.L., Sandblad L. Reconstitution of a microtubule plus-end tracking system in vitro. Nature. 2007;450:1100–1105. doi: 10.1038/nature06386. [DOI] [PubMed] [Google Scholar]
- 4.Howard J., Hyman A.A. Microtubule polymerases and depolymerases. Curr. Opin. Cell Biol. 2007;19:31–35. doi: 10.1016/j.ceb.2006.12.009. [DOI] [PubMed] [Google Scholar]
- 5.Goshima G., Wollman R., Stuurman N., Scholey J.M., Vale R.D. Length control of the metaphase spindle. Curr. Biol. 2005;15:1979–1988. doi: 10.1016/j.cub.2005.09.054. [DOI] [PubMed] [Google Scholar]
- 6.West R.R., Malmstrom T., Troxell C.L., McIntosh J.R. Two related kinesins, Klp5+ and Klp6+, foster microtubule disassembly and are required for meiosis in fission yeast. Mol. Biol. Cell. 2001;12:3919–3932. doi: 10.1091/mbc.12.12.3919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.West R.R., Malmstrom T., McIntosh J.R. Kinesins Klp5+ and Klp6+ are required for normal chromosome movement in mitosis. J. Cell Sci. 2002;115:931–940. doi: 10.1242/jcs.115.5.931. [DOI] [PubMed] [Google Scholar]
- 8.Mayr M.I., Hummer S., Bormann J., Gruner T., Adio S. The human kinesin Kif18A is a motile microtubule depolymerase essential for chromosome congression. Curr. Biol. 2007;17:488–498. doi: 10.1016/j.cub.2007.02.036. [DOI] [PubMed] [Google Scholar]
- 9.Garcia M.A., Koonrugsa N., Toda T. Two kinesin-like Kin I family proteins in fission yeast regulate of metaphase and the on the establishment set of anaphase A. Curr. Biol. 2002;12:610–621. doi: 10.1016/s0960-9822(02)00761-3. [DOI] [PubMed] [Google Scholar]
- 10.Garcia M.A., Koonrugsa N., Toda T. Spindle-kinetochore attachment requires the combined action of Kin I-like Klp5/6 and Alp14/Dis1-MAPs in fission yeast. EMBO J. 2002;21:6015–6024. doi: 10.1093/emboj/cdf611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Buster D.W., Zhang D., Sharp D.J. Poleward tubulin flux in spindles: regulation and function in mitotic cells. Mol. Biol. Cell. 2007;18:3094–3104. doi: 10.1091/mbc.E06-11-0994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gupta M.L., Carvalho P., Roof D.M., Pellman D. Plus end-specific depolymerase activity of Kip3, a kinesin-8 protein, explains its role in positioning the yeast mitotic spindle. Nat. Cell Biol. 2006;8:913–923. doi: 10.1038/ncb1457. [DOI] [PubMed] [Google Scholar]
- 13.Stumpff J., von Dassow G., Wagenbach M., Asbury C., Wordeman L. The kinesin-8 motor Kif18A suppresses kinetochore movements to control mitotic chromosome alignment. Dev. Cell. 2008;14:252–262. doi: 10.1016/j.devcel.2007.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Unsworth A., Masuda H., Dhut S., Toda T. Fission yeast kinesin-8 Klp5 and Klp6 are interdependent for mitotic nuclear retention and required for proper microtubule dynamics. Mol. Biol. Cell. 2008 doi: 10.1091/mbc.E08-02-0224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Varga V., Helenius J., Tanaka K., Hyman A.A., Tanaka T.U. Yeast kinesin-8 depolymerizes microtubules in a length-dependent manner. Nat. Cell Biol. 2006;8:957–962. doi: 10.1038/ncb1462. [DOI] [PubMed] [Google Scholar]
- 16.Mitchison T., Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312:237–242. doi: 10.1038/312237a0. [DOI] [PubMed] [Google Scholar]
- 17.Bicout D.J. Green's functions and first passage time distributions for dynamic instability of microtubules. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1997;56:6656–6667. [Google Scholar]
- 18.Govindan B.S., Gopalakrishnan M., Chowdhury D. Length control of microtubules by depolymerizing motor proteins. EPL. 2008;83:40006. [Google Scholar]
- 19.Parmeggiani A., Franosch T., Frey E. Totally asymmetric simple exclusion process with Langmuir kinetics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:046101. doi: 10.1103/PhysRevE.70.046101. [DOI] [PubMed] [Google Scholar]
- 20.Nowak S.A., Fok P.-W., Chou T. Dynamic boundaries in asymmetric exclusion processes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76 doi: 10.1103/PhysRevE.76.031135. 031135–11. [DOI] [PubMed] [Google Scholar]
- 21.Helenius J., Brouhard G., Kalaidzidis Y., Diez S., Howard J. The depolymerizing kinesin MCAK uses lattice diffusion to rapidly target microtubule ends. Nature. 2006;441:115–119. doi: 10.1038/nature04736. [DOI] [PubMed] [Google Scholar]
- 22.Klein G.A., Kruse K., Cuniberti G., Julicher F. Filament depolymerization by motor molecules. Phys. Rev. Lett. 2005;94:108102. doi: 10.1103/PhysRevLett.94.108102. [DOI] [PubMed] [Google Scholar]
- 23.Muller-Reichert T., Chretien D., Severin F., Hyman A.A. Structural changes at microtubule ends accompanying GTP hydrolysis: information from a slowly hydrolyzable analogue of GTP, guanylyl (α,β)methylenediphosphonate. Proc. Natl. Acad. Sci. USA. 1998;95:3661–3666. doi: 10.1073/pnas.95.7.3661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.VanBuren V., Odde D.J., Cassimeris L. Estimates of lateral and longitudinal bond energies within the microtubule lattice. Proc. Natl. Acad. Sci. USA. 2002;99:6035–6040. doi: 10.1073/pnas.092504999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.VanBuren V., Cassimeris L., Odde D.J. Mechanochemical model of microtubule structure and self-assembly kinetics. Biophys. J. 2005;89:2911–2926. doi: 10.1529/biophysj.105.060913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hyman A., Salser S., Drechsel D., Unwin N., Mitchison T. Role of GTP hydrolysis in microtubule dynamics: information from a slowly hydrolyzable analogue, GMPCPP. Mol. Biol. Cell. 1992;3:1155–1167. doi: 10.1091/mbc.3.10.1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shaevitz J.W., Block S.M., Schnitzer M.J. Statistical kinetics of macromolecular dynamics. Biophys. J. 2005;89:2277–2285. doi: 10.1529/biophysj.105.064295. [DOI] [PMC free article] [PubMed] [Google Scholar]