All-Atom Contact Model for Understanding Protein Dynamics from Crystallographic B-Factors

Abstract

An all-atom local contact model is described that can be used to predict protein motions underlying isotropic crystallographic B-factors. It uses a mean-field approximation to represent the motion of an atom in a harmonic potential generated by the surrounding atoms resting at their equilibrium positions. Based on a 400-ns molecular dynamics simulation of ubiquitin in explicit water, it is found that each surrounding atom stiffens the spring constant by a term that on average scales exponentially with the interatomic distance. This model combines features of the local density model by Halle and the local contact model by Zhang and Brüschweiler. When applied to a nonredundant set of 98 ultra-high resolution protein structures, an average correlation coefficient of 0.75 is obtained for all atoms. The systematic inclusion of crystal contact contributions and fraying effects is found to enhance the performance substantially. Because the computational cost of the local contact model scales linearly with the number of protein atoms, it is applicable to proteins of any size for the prediction of B-factors of both backbone and side-chain atoms. The model performs as well as or better than several other models tested, such as rigid-body motional models, the local density model, and various forms of the elastic network model. It is concluded that at the currently achievable level of accuracy, collective intramolecular motions are not essential for the interpretation of B-factors.

Introduction

Advances in x-ray crystallography and NMR spectroscopy have allowed the determination of a large number of protein structures, as is reflected in the rapid growth of the Protein Data Bank (PDB) (1). Although most proteins adopt a highly specific average three-dimensional structure, they also exhibit significant amounts of fluctuations that play an important role in protein function. For the protein backbone, for example, heteronuclear NMR relaxation spectroscopy yields time-resolved dynamic information about reorientational motions of bonds, such as the backbone amide N-H bonds (2,3). Amino acid side-chain dynamic information from NMR, on the other hand, is much more sparse, with the exception of methyl-bearing side chains (4).

X-ray crystallography provides information about protein mobility through Debye-Waller temperature factors, or B-factors, for both backbone and side-chain atoms (5). The B-factor is a measure of the uncertainty of the atomic position, which includes the effects of noise due to model errors and lattice defects, in addition to the positional variance of thermal protein motion. The amount of noise is generally lowest for the highest-resolution structures (<1 Å).

There is significant interest in reproducing experimental protein dynamics data by computational methods to assess the quality of the latter. Among computational methods, molecular dynamics (MD) computer simulations provide the most comprehensive view of protein motions (6). Experimental dynamics parameters serve as useful benchmarks for the assessment of molecular mechanics force fields, sampling of conformational space, and computational protocols (7). The sampling issue can be bypassed, at the cost of accuracy, by using normal-mode analysis where the force field in the vicinity of the native state is replaced by its multivariate quadratic expansion. This allows the compact representation of protein dynamics by the superposition of motional fluctuations along normal modes with individual amplitudes (8–13).

More recently, a new class of coarse-grained harmonic models known as elastic network models (ENM) (14) has been developed that includes Gaussian network models (GNM) (15), anisotropic network models (16–18), and a combination of the two (19). In these models, the interactions between amino acids that lie within a given cutoff distance, r_c, are modeled as Hookean springs. The resulting eigenmodes yield a description of the protein fluctuations in terms of collective motions. These models have been tested against experimental protein B-factors as benchmarks, typically yielding at least qualitative agreement with experiment. ENM also provides directional information about internal motions (20,21). An ENM-based model that achieves the best B-factor prediction so far is the chemical network model (CNM) (22), which employs the closest distance between two residues, rather than their C_α-C_α distance, as well as different spring constants between bonded and nonbonded residue pairs. For a set of 98 high-resolution protein structures, an average Pearson correlation coefficient between predicted and experimental B-factors of 0.75 was obtained. Reorientational generalizations of ENM, which are the reorientational contact-weighted ENM (23) and the network of coupled rotators (24), were successfully used for the reproduction of NMR spin-relaxation-derived N-H order parameters.

In all these models, calculation of motional amplitudes involves inversion of a Kirchhoff or Hessian matrix, which makes them computationally expensive when the number of residues is large. Due to their coarse-grained nature, the calculation of B-factors of atoms other than C_α atoms, including functionally important side-chain atoms, is not readily possible.

It has long been recognized that B-factors not only report on intramolecular motions but are also sensitive to the presence of rigid-body motions (25). A model termed translation, librations, and screw (TLS), proposed recently (26), uses 10 fitting parameters for each protein and produces a relatively high average correlation coefficient with respect to experimental B-factors (>0.8).

Halle (27) introduced a fundamentally different interpretation of crystallographic B-factors, the local density model (LDM), which relates the B-factors to local atom density. It assumes that each atom moves in a quadratic potential of mean force (PMF) generated by the neighboring atoms fixed at their equilibrium positions. All neighboring atoms that lie within a cutoff distance of ∼7.35 Å of a given atom contribute equally to the effective force constant of this atom. Thus, the atom with the largest neighbor-atom density will have the lowest B-factor.

NMR S² order parameters (28) describe the reorientational restrictions of bond vector fluctuations and thereby can be viewed as the reorientational counterpart to B-factors (29). It has been empirically demonstrated that backbone N-H 1-S² values are closely related to a contact sum that consists of terms with an exponential distance dependence between the surrounding atoms and the amide proton itself and carbonyl oxygen of the preceding amino acid (30). S² order parameters of side-chain methyl groups can be modeled similarly well by an extended local contact model (LCM) (23).

Here, we develop a model that combines features of the LDM and LCM for the prediction of B-factors for all atoms and analyzes a 400-ns MD trajectory of ubiquitin to test basic assumptions that go into this model. We then apply the model to a set of 98 crystal structures used previously (22) and compare the results with different models.

Theory and Methods

PDB set

All B-factor prediction calculations were applied to a set of 98 highest-resolution x-ray crystal structures previously used by Kondrashov et al. (22). This is a nonredundant set of protein structures that represents all major SCOP families. All of its members have at least 50 residues in a single chain with resolution ≤1 Å. For protein systems with more than one asymmetric unit, only the experimental B-factors from the first unit were used. For the back-calculation, the unit cell was surrounded by 26 nearest-neighbor cells to include crystal contact contributions between asymmetric units inside the unit cell and between different unit cells. The B-factors calculated in this way were then averaged over the asymmetric units for comparison with experiment. Only one side-chain conformation per amino acid was used. Local contacts between proteins and cofactors and ligands were included, whereas all contacts with water molecules were discarded.

MD trajectory

A 400-ns MD trajectory of ubiquitin in explicit SPC/E water at 300 K was performed using the AMBER9 package (31) with the AMBER99SB force field (32), as described previously (33). A total of 400,000 snapshots at a time increment of 1 ps are used to calculate a PMF(r_ij) between C_α atoms of amino acids 1 and 70 and all heavy atoms, where r_ij is the distance between the two atoms. An effective force constant between C_α atoms and all other heavy atoms was determined from the variance ${\sigma }_{ij}^2$ of r_ij, calculated over the trajectory according to

$$f_{ij}=k_{\text{B}}T/{\sigma }_{ij}^2,$$ (1)

where k_B is the Boltzmann constant.

Local contact model for crystallographic B-factor prediction

The PMF of atom i at equilibrium position r_i,0, defined with respect to the center of mass, is assumed to take the quadratic form

$$V_i\left({\mathbf{r}}_i\right)=\frac{1}{2}{f}_i{({\mathbf{r}}_i-{\mathbf{r}}_{i,0})}^2,$$ (2)

where r_i denotes the position of the atom i. The force constant, f_i, is determined from the interactions with all surrounding atoms j according to

$$f_i=\sum _{j\ne i}{f}_{ij},$$ (3)

where

$$f_{ij}=a\exp (-r_{ij}/r_0)+b\text{.}$$ (4)

The isotropic crystallographic B-factor of atom i is then determined by

$$B_i=\frac{8{\pi }^2}{3}({\sigma }_{i,x}^2+{\sigma }_{i,y}^2+{\sigma }_{i,z}^2)=8{\pi }^2{\sigma }_i^2=\frac{8{\pi }^2{k}_{\text{B}}T}{f_i},$$ (5)

where k_B is Boltzmann's constant and T is the absolute temperature. Hence, this model for the prediction of B-factors contains the three global parameters r₀, a, and b. As it turns out, b has only a modest effect on the results and can therefore be neglected, and a is an overall scaling factor, which does not affect the correlation coefficients between calculated and experimental B-factors. This leaves the interaction distance r₀ as the only essential parameter in this local contact model for the prediction of crystallographic B-factors (LCMB). It is sufficient to calculate the force constant between atom pairs within a certain cutoff. We use a cutoff of 15 Å in this work, as the effect of cutoff turns out to be negligible as long as it is >10 Å. To speed up the computation of the pairwise atomic distances, a classical cell subdivision algorithm (34) is employed, which renders the computational cost proportional to the number of protein atoms.

End effects

In proteins for which the N- and C-termini of proteins are not part of an α-helix or β-strand structure, the termini often exhibit fraying effects, manifested in an increase of their B-factors. This effect is included here by multiplying the calculated B-factors of the first and last residues by a factor of 1.5, the second and second-to-last by a factor of 1.4, and the third and third-to-last by a factor of 1.3, respectively. The LCMB with the termini treated in this way is termed the eLCMB.

GNM

The Gaussian network model was implemented in its standard form (15), where the variation Δr_ij of an atom pair distance r_ij = | r_j − r_i | is assumed to obey a Gaussian distribution

$$W(\Delta r_{ij})={(\gamma /\pi )}^{3/2}\exp (-\gamma \Delta r_{ij}^2)\text{.}$$ (6)

Here, γ is the force constant of the Hookean potential. In this model, the elements of the Kirchhoff matrix are given by

$${\Gamma }_{ij}=\left\{\begin{array}{c}\begin{array}{ll}-\gamma \hfill & i\ne j\text{and}{r}_{ij}\hfill \end{array}\le r_c\\ \begin{array}{cc}0& \text{i}\ne j\text{and}{r}_{ij}>r_c\end{array}\\ \begin{array}{cc}-\sum _{j\ne i}{\Gamma }_{ij}& i=j\end{array}\end{array}\right\},$$ (7)

where r_c is the cutoff distance that defines the interaction range. The mean-square fluctuations of the atoms are readily evaluated using

$$B_i=8{\pi }^2\frac{k_{\text{B}}T}{\gamma }{\left[\sum _{k=1}^{n-1}{\lambda }_k^{-1}{\mathbf{q}}_k{\mathbf{q}}_k^T\right]}_{ii}=8{\pi }^2\frac{k_{\text{B}}T}{\gamma }{\left[{\Gamma }^{-1}\right]}_{ii},$$ (8)

where λ_k is the eigenvalue of Γ to eigenmode q_k.

TLS model

The translation, libration, and screw (TLS) model was implemented as described recently (26). In this model, r_i is given by

$${\mathbf{r}}_i=\mathbf{c}+\omega \times ({\mathbf{r}}_{i,0}-{\mathbf{c}}_0)\text{.}$$ (9)

Here, c₀ is an arbitrarily chosen reference point, and c derives from c₀ by translational motion. It follows for the B-factor that

$$B_i=\frac{8{\pi }^2}{3}(\langle {\mathbf{r}}_i\cdot {\mathbf{r}}_i\rangle -{\mathbf{r}}_{i,0}\cdot {\mathbf{r}}_{i,0})\text{.}$$ (10)

The total number of fitting parameters is 10, which can be determined by singular value decomposition. For ∼10% of the proteins, this leads to unphysical fitting results (i.e., a rotation tensor that is not positive (26)), and hence these proteins were not included in subsequent statistical analyses.

A simplified version of the TLS model is obtained when translational and screw motions are removed and only isotropic rotation is allowed about the center of mass, which leads to the following distance dependence of the B-factors:

$$B_i=a{\left|{\mathbf{r}}_{i,0}\right|}^2\text{.}$$ (11)

Rotational amplitude, a, is the only fitting parameter of this rotation-only model (ROM).

Results

MD results

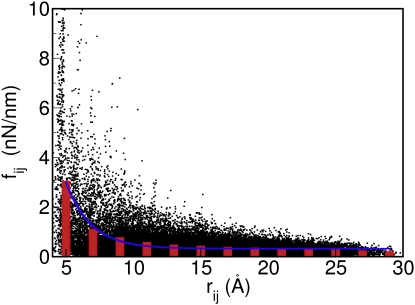
The 400-ns MD trajectory of ubiquitin was analyzed in terms of the fluctuation amplitudes (variances ${\sigma }_{ij}^2$) of interatomic distances between C_α atoms and all heavy atoms, which were converted into effective force constants f_ij according to Eq. 1. Fig. 1 shows f_ij as a function of the average distance r_ij. The vertical bars represent averages over 2-Å intervals starting at 4 Å, and the solid line is the fit to the vertical bars using the exponential function

$${\overline{f}}_{ij}\left(r_{ij}\right)=39.3\times \exp (-r_{ij}/1.9)+0.3$$ (12)

(in units of kg·s⁻² or nN/nm, with r_ij expressed in Å). Although individual force constants can considerably deviate from the average, especially for some of the smaller distances (<8 Å), the average force constants approximate very well the relationship of Eq. 4 (C_α-C_α pairs with a distance <4 Å have force constants that are ∼10 times larger than the average force constant found for the 4- to 6-Å interval and were not included in the fit).

Figure 1.

Force constants, f_ij, as a function of distance, r_ij, between all pairs of C_α atoms derived from a 400-ns MD trajectory of ubiquitin. The black dots are extracted directly from the MD simulation, whereas the vertical bars are averages over 2-Å distance intervals. The solid line is a least-squares fit given by the exponential function of Eq. 12.

To test the quality of this approximation, we calculated the C_α B-factors from the above model using the force constants extracted from the MD simulation (Fig. 1, dots), as well as the force constant derived from the best exponential fit (Eq. 12) and compared them with the B-factors directly calculated from MD simulations. The Pearson correlation coefficients, R, are 0.55 and 0.66, respectively, with the main discrepancies found for residue 8 and both termini. The corresponding Spearman correlation coefficients, which are more robust with respect to outliers, are 0.87 and 0.80, respectively. Hence, the MD simulation validates the basic assumptions underlying the LCMB (Eqs. 2–5). In the next section, the LCMB is tested against experimental B-factors.

eLCMB backbone C_α results

The eLCMB was next applied to the 98-protein set. When r₀ is set to 1.9 Å, the average Pearson correlation coefficient between predicted and experimental C_α B-factors is 0.72. The correlation can be further improved by optimizing r₀. For r₀ = 3 Å, an optimal average correlation coefficient of R = 0.74 ± 0.1 is found. When r₀ is optimized for each protein individually, its mean ± SD is r₀ = 3 ± 1.1 Å. Also, inclusion of the offset of 0.3 in Eq. 12 has a minimal effect and therefore will be neglected. The B-factor correction of the N- and C-terminal C_α triples has a more noticeable effect: without this correction, the correlation is 0.72 for r₀ = 3 Å.

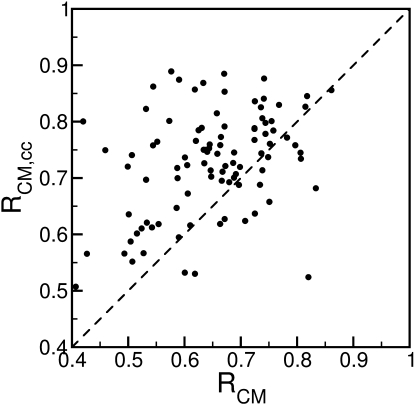
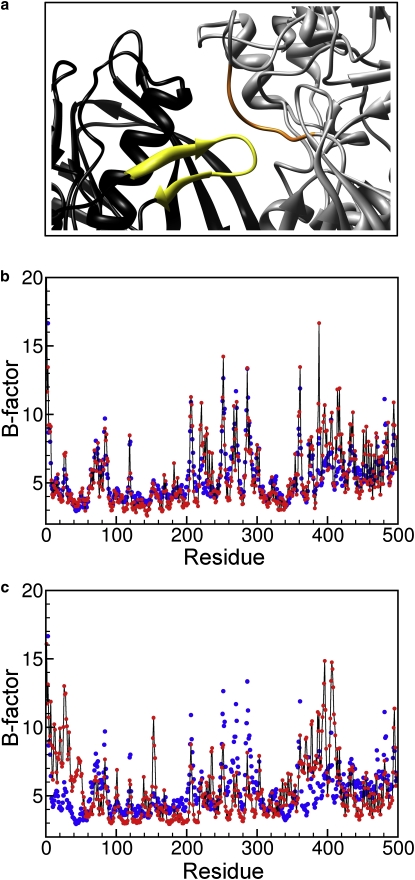
Crystal packing interactions make a significant contribution to the calculated B-factors (35). Without the inclusion of crystal packing effects, the average correlation coefficient is 0.64. A comparison of the performance of LCMB with and without crystal contact contributions for all 98 proteins is given in Fig. 2. It shows that for 81 of the 98 proteins, the prediction improves when crystal contacts are included. The kind of improvement of the B-factor prediction brought about by the inclusion of crystal contacts is exemplified for the 56-kDa cholesterol oxidase (PDB code 1N4W). Fig. 3, b and c, shows the predicted B-factors with and without crystal contacts, respectively, together with the experimental B-factors. The correlation coefficients are 0.84 (Fig. 3 b) and 0.72 (Fig. 3 c), respectively. The intermolecular interactions between two asymmetric units within the unit cell are displayed in Fig. 3 a. The protein fragment colored in yellow around residue 380 of the black unit makes extensive contacts with the orange part around residue 35 of the gray unit. These crystal contacts reduce the B-factors of the interacting regions, as indicated in Fig. 3, b and c. Other crystal contacts not shown in Fig. 3 a are presented in Fig. S1 in the Supporting Material.

Figure 2.

Effect of including crystal contacts on the LCMB model performance for a set of 98 ultra-high resolution protein structures. The Pearson correlation coefficients between predictions and experiment are plotted along the x and y axes for C_α B-factors without and with, respectively, the inclusion of crystal contacts.

Figure 3.

Illustration of the effect of crystal contacts on C_α crystallographic B-factors in the eLCMB for the 56-kDa protein cholesterol oxidase (1N4W). (a) Parts of two copies of the protein (black and gray) in the crystal, with the segments that make extensive crystal contacts colored in yellow (around amino acid 380) and orange (around amino acid 35), respectively. (b and c) Predicted (red dots) and experimental (blue dots) B-factors, with (b) and without (c) the inclusion of crystal contacts. The predicted values are uniformly scaled and shifted to optimally superimpose on the experimental values.

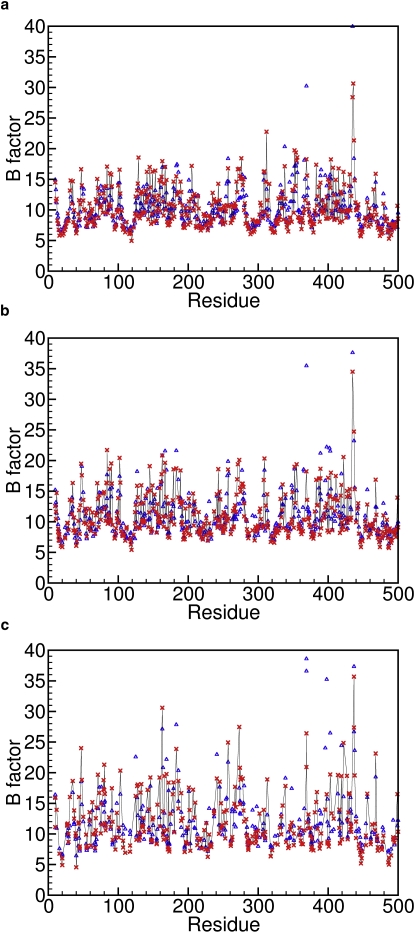
Due to its simplicity, the LCMB is applicable not only to C_α atoms, but also to any other atom in the protein. When the LCMB is applied to all main-chain and all side-chain atoms of the 98-protein set, an average correlation of 0.74 is obtained in the absence of B-factor correction of the N- and C-terminal residues for r₀ = 2 Å. After B-factor adjustment of the N- and C-terminal residues, R improves to 0.75. In Fig. 4, predicted and experimental B factors of Cβ, Cγ, and Cδ side-chain atoms are depicted, with correlation coefficients of 0.80, 0.75, and 0.77, respectively. The inclusion of crystal packing effects is critically important for all-atom B-factor predictions: when crystal packing effects are not taken into account, the average R drops to 0.65 for the protein set used here.

Figure 4.

Experimental (blue triangles) and predicted (red crosses) B-factors of the side-chain atoms of the 56-kDa protein cholesterol oxidase (1N4W) by eLCMB including the effects of crystal contacts for Cβ (a), Cγ (b), and Cδ (c) atoms, respectively.

A number of modifications of the eLCMB were made to test whether its performance can be further improved. In particular, contributions from atoms within the same amino acid were treated separately, as were contributions from atoms of residues that precede or succeed in sequence the residue that contains the atom of interest. None of these modifications yielded any further increase in the average correlation coefficient.

Discussion

Crystallographic B-factors of high-resolution crystal structures provide a wealth of experimental information at atomic resolution about the motional disorder of proteins. This explains why B-factors are frequently used to test motional models of proteins.

A key issue is the distinction between overall motion and intramolecular dynamics. The most general rigid-body motional model is the TLS model (25), which interprets the B-factors by combining overall anisotropic rotational, translational, and screw motions. It was recently combined with a random-walk model for the three N- and C-terminal residues, and an overall correlation was found that was notably high (26). For the protein set used in this work, the average correlation coefficient is 0.8. It must be kept in mind, however, that this model uses 10 fitting parameters compared to one actual fitting parameter (namely the overall scaling factor) for the LCMB. Although 10 is well below the number of C_α atoms of the proteins considered, residues with increased B-factors tend to cluster into groups of consecutive residues. These clusters are relatively localized in space, and they typically do not vastly outnumber the fitting parameters of the TLS model. To test the possibility of overfitting in the TLS model, a plane with random orientation was laid for each protein through the protein's center of mass, and the TLS model was fitted only to the atoms on one side of the plane. The fitting parameters were then used to predict the B-factors of the other protein half. The procedure was applied for 360 randomly chosen planes for each protein. An average correlation coefficient of 0.5 is obtained for the back-calculated B-factors. This strongly suggests that the TLS model is, to a significant degree, susceptible to overfitting.

A simplified version of the TLS model with a single fitting parameter is the rotation-only model (ROM) (Eq. 11), which allows isotropic rotation about the protein's center of mass only (i.e., no translational and screw motion). For the protein set used here, the ROM produces an average correlation coefficient of 0.56. In ROM, the predicted B-factors increase quadratically with the distance of the residue from the protein center (Eq. 11). ROM captures some of this trend, presumably because protein regions that exhibit increased experimental B-factors are often close to the protein surface. On the other hand, the TLS and ROM models explain neither the effect of local crystal packing on B-factors nor the sometimes sizeable differences between B-factors of atoms belonging to the same residue. This suggests that intramolecular disorder and dynamics are the dominant contributors to the B-factors for most systems. This conclusion is consistent with a MD study of staphylococcal nuclease in a crystalline environment, which found that ∼70% of the B-factor contributions are due to internal motion (36).

In the original LDM work (27), an improved agreement with experiment was found when crystal contacts were included. When applied to a set of 972 proteins, an average correlation coefficient of 0.51 was reported for the LDM, and this improves to 0.61 when 1/r-distance weighting is used (37). When the LDM is applied to the 98-protein set used in this work, the average correlation coefficient is 0.62 without and 0.68 with the inclusion of crystal contacts.

The LCMB introduced here combines features of LDM with the contact model (30). The latter was developed for the prediction of NMR order parameters and it also uses a contact sum with terms that follow the exponential-distance weighting of Eq. 4. The LDM and LCMB both represent mean-field approaches of protein dynamics, since they predict motions on a site-by-site basis with the other protein atoms fixed at their average positions. Therefore, these models neither invoke nor predict collective motions among protein atoms. The inclusion of fraying effects at the protein termini in the eLCMB model is an exception.

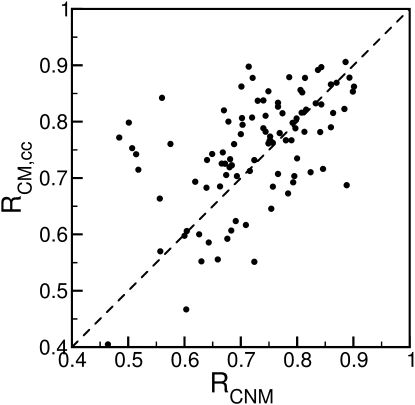
By contrast, elastic network models naturally provide a collective description of protein dynamics in terms of a superposition of motion along orthogonal normal modes. The B-factor prediction by the GNM produces, for the present protein set, a correlation of R = 0.59. The inclusion of crystal packing effects positively affects the GNM performance. For example, when crystal packing effects are combined with the chemical network model (22), R = 0.75 is obtained. Fig. 5 compares the CNM correlation coefficients (22) with the corresponding correlation coefficients of the eLCMB. The two models have virtually identical overall performance, although the performance can differ significantly for individual proteins.

Figure 5.

Comparison of correlation coefficients obtained from the CNM and eLCMB models for a 98-protein set. The two models have very similar overall performance, but distinct performance for individual proteins.

In the mean-field approximation underlying the LCMB, the distance dependence of the pairwise atomic interaction strength is derived from an all-atom MD simulation. We calculated the corresponding PMFs of the C_α atoms from the GNM model of ubiquitin with a 7.5-Å cutoff. For this purpose, we generated a canonical ensemble with 100,000 snapshots according to the quadratic energy function defined by the GNM model (Eq. 6) and calculated the pairwise distance-dependent force constant in analogy to the treatment of the MD trajectory (see Fig. S2), which yields a distance dependence for the force constants of

$${\overline{f}}_{ij}\left(r_{ij}\right)=7.3\times \exp (-r_{ij}/9.7)+2.1$$ (13)

(in units of kg·s⁻² or nN/nm, with r_ij expressed in Å). As is the case with the MD-derived relationship (Eq. 12), Eq. 13 shows an exponential distance dependence. It differs from the MD-derived relationship, however, in terms of both the size of the offset, which is quite large, and the decay constant in the exponent, which favors contributions from atoms that are farther away. It is important to note that the GNM underestimates the force constant between sequential C_α atoms by ∼10-fold. This explains the better performance of the CNM, which employs a 10-fold-increased force constant between neighboring residues and thereby substantially improves the correlation with experiment (22).

Besides the correlation coefficient, the variability of the overall scaling factors of the predicted versus experimental B-factors is another measure of the quality of the model. For a given protein, the overall scaling factor, s, is obtained by minimizing the mean-square difference ∑_i (s × B_pre,i − B_exp,i)², where the sum is over all C_α atoms. One might expect that for a given dynamics model the overall scaling factors, s, are similar for different proteins. To test this, we selected the proteins from the list whose x-ray diffraction data were collected at the same temperature, namely at 100 K. As shown in Fig. S3, for eLCMB, there is no clear correlation between the scaling factor, s, and protein size. The standard deviation of the scaling factors for the eLCMB is 30%, whereas it is 40% for the GNM. On the other hand, the overall scaling factor of the ROM shows a clear dependence on protein size, with smaller proteins having larger scaling factors, suggesting that in a crystalline environment, smaller proteins have larger rigid-body rotational amplitudes on average. Combining ROM with eLCMB by treating ROM (Eq. 11) as an additive term to Eq. 5 yields an optimized R value of 0.751, which slightly improves the correlation obtained by the eLCMB alone. When considering all atoms, on the other hand, the combination of ROM with eLCMB does not improve the correlation.

The eLCMB is computationally efficient. In its simplest implementation, its computational cost scales with O(N²), where N is the number of protein atoms. For larger proteins, the use of cell subdivision with appropriate cutoffs permits computational scaling by O(N). By contrast, the ENM models involve the inversion of a Kirchhoff or Hessian matrix of dimension M or 3M, which scales with O(M³), where M is the number of amino acids. For the 54-kDa protein cholesterol oxidase (1N4W), the eLCMB calculation with crystal contacts included takes on a 2.4 GHz opteron AMD processor <1 s.

A second advantage of the eLCMB is its applicability to all atoms of a protein, including all side-chain atoms. Protein side-chain atoms play a prominent role in protein function by their involvement in protein-protein and protein-ligand interactions. Therefore, rapid assessment of the atomic mobility of these entities and their changes upon complex formation is a useful complement to structural investigations.

This study demonstrates that, based on B-factors alone, it is difficult to judge whether ENM-type or LDM/LCMB-type models are physically more meaningful. The fact that a mean-field approximation, such as the local contact model, reproduces B-factors on a par with the CNM, which is now considered the most accurate ENM model, suggests that collective motions are not essential for the interpretation of B-factors at the level of accuracy achievable at the present time. Mean-field models represent an attractive alternative to collective motional models. This finding is consistent with recent results obtained with the reorientational contact-weighted ENM for the prediction of protein backbone order parameters (23). This model provides an improvement over the local contact model mainly for protein regions that undergo significant fraying effects. Similar to the modeling of the chain termini applied here, these can be treated without invoking a full ENM approach.

Conclusion

The extended local contact model is a mean-field approach to protein dynamics whose average pairwise atomic distance PMF is consistent with MD results. This model shows good agreement between predicted and experimental B-factors, comparable to that of a refined GNM model. The inclusion of crystal-contact effects is essential for obtaining accurate prediction in both types of models. This may have important implications also for the interpretation of dynamics data of protein crystals obtained by other methods, such as solid state NMR. Its computational efficiency makes the eLCMB model applicable to backbone and side-chain atoms of small and large proteins alike.

Supporting Material

Three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00473-1.