Inferring differentiation pathways from gene expression

Abstract

Motivation: The regulation of proliferation and differentiation of embryonic and adult stem cells into mature cells is central to developmental biology. Gene expression measured in distinguishable developmental stages helps to elucidate underlying molecular processes. In previous work we showed that functional gene modules, which act distinctly in the course of development, can be represented by a mixture of trees. In general, the similarities in the gene expression programs of cell populations reflect the similarities in the differentiation path.

Results: We propose a novel model for gene expression profiles and an unsupervised learning method to estimate developmental similarity and infer differentiation pathways. We assess the performance of our model on simulated data and compare it with favorable results to related methods. We also infer differentiation pathways and predict functional modules in gene expression data of lymphoid development.

Conclusions: We demonstrate for the first time how, in principal, the incorporation of structural knowledge about the dependence structure helps to reveal differentiation pathways and potentially relevant functional gene modules from microarray datasets. Our method applies in any area of developmental biology where it is possible to obtain cells of distinguishable differentiation stages.

Availability: The implementation of our method (GPL license), data and additional results are available at http://algorithmics.molgen.mpg.de/Supplements/InfDif/

Contact: filho@molgen.mpg.de, schliep@molgen.mpg.de

Supplementary information: Supplementary data is available at Bioinformatics online.

1 INTRODUCTION

Cell differentiation In all multicellular organisms somatic differentiated cells develop from embryonic stem cells in the formation phase and from adult tissue-specific stem cells in the adult phase. The study of triggers and molecular programs that drive cells through well-defined proliferation and differentiation stages is a central theme of developmental biology. In classical models of such processes external or internal factors initiate and drive differentiation steps in a non-reversible manner. They are conveniently depicted in diagrams that resemble genealogies of developmental stages, which we call developmental trees throughout this article. Recently, the gene expression programs of developmental trees have been studied extensively using microarrays, which helps to elucidate underlying molecular processes (Akashi et al., 2003; Anisimov et al., 2007; Ferrari et al., 2007; Hyatt et al., 2006; Tomancak et al., 2002).

Analysis Finding functional modules of co-regulated genes during the course of development with an unsupervised learning method is a crucial initial step in the large scale analysis of developmental processes. Ideally, the method of choice should exploit inherent dependencies arising from the data. It is, for example, well accepted that models taking temporal dependencies into account are superior for analyzing gene expression time-courses (Bar-Joseph, 2004).

In previous work we demonstrated how to exploit detailed knowledge about the differentiation pathways to infer gene modules with distinct developmental profiles from genome scale gene expression data (Costa et al., 2007b). There, we showed that the expression programs of developmental stages reflect the similarity of stages close by in the developmental tree. For exploring the dependencies arising from such similarities, we proposed the use of Dependence Trees (DTree) in which the known developmental tree imposed the dependence structure. We combined several of these DTrees in a mixture to model groups of co-regulated genes.

Novel contributions Here, we propose an extension of the above method for inferring developmental similarity and differentiation pathways as reflected in the dependence structure of modules of co-expressed genes, regardless of the underlying developmental tree. Our method estimates the structure of each component of a mixture of Dependence Trees (MixDTrees). Furthermore, we use maximum-a-posteriori (MAP) estimates for the parameters of the DTree, which makes the method robust to overfitting. We assess the performance of our model on simulated data and compare it with favorable results of other unsupervised methods.

We also infer differentiation pathways and predict functional modules in gene expression data of lymphoid development. Lymphoid development has been extensively studied, many developmental stages are known, and there is a large amount of available data on distinct stages of development and in several cell lineages (see Figure 3 (left)). We use biological annotation data from Gene Onotology (GO); (Ashburner, 2000) and Kyoto Encylcopedia of Gene and Genome (KEGG) (Kanehisa et al., 2006) to assist the interpretation of the inferred gene modules. The results show that the inference of DTree structures for modules of co-regulated genes helps to reveal differentiation pathways and functional relevant groups of genes. A comparison with other unsupervised methods commonly used for gene expression indicates the advantage of MixDTrees in terms of quality and interpretability.

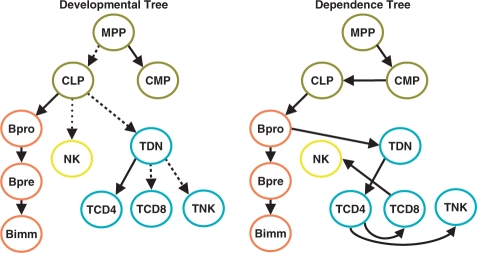
Fig. 3.

We depict the developmental tree with the stages contained in the Lymphoid dataset (left). Early hematopoietic cells are depicted in olive green, B-cells in orange, NK-cell in yellow and T-cells in blue. The dashed edges represent edges wrongly assigned in the DTree estimated from the Lymphoid data, which connect pairs of vertices with a path distant of one, while the dotted edge represents a edge with a path distance of three. We have in the right the DTree estimated from the Lymphoid data.

Related methods Mixtures of Dependence Trees are part of the graphical model (or Bayesian network) formalism (Friedman, 2004). They have been applied before, for example, in image recognition (Chow and Liu, 1968; Meila and Jordan, 2001) and detection of mutagenic trees (Beerenwinkel et al., 2004), but exclusively to data of discrete nature. Moreover, our method has some relations to bi-clustering (e.g. Brunet et al., 2004; Tanay et al., 2002), as it is able to find not only coexpressed genes but also developmental conditions with similar expression profiles. Nevertheless, bi-clustering methods make no implicit use of any dependencies (developmental or temporal) in these data sets. There is also a relation to the estimation of sparse covariance matrices, as Dependence Trees represent a subclass of them. Chaudhuri et al. (2007) apply an iterative conditional fitting method for computing sparse covariance matrices from arbitrary undirected graphs. This method, however, does not offer a solution for inferring the graph structure and has high computational cost. Schaefer and Strimmer (2005), who approach a similar problem in the context of gene association networks, use a shrinkage factor in a computationally efficient way for zeroing entries in the covariance matrix, while keeping it well conditioned. Both methods are not able to find association networks, which are specific for particular gene modules, as performed by MixDTrees.

2 METHODS

2.1 Dependence Trees (DTree)

Let X=(X₁,…,X_u,…,X_L) be a L-dimensional continuous random vector, where the variable X_u denotes the expression values of the developmental stage u and x=(x₁,…,x_L) denotes a realization of X representing gene expression values of a gene in the developmental stages 1,…,L. A DTree is defined as a probabilistic model representing dependencies between variables in X, which follow a tree structure.

Consider a directed graph (V,E) with |V|=L, where each vertex in V represents a variable in X, and a directed edge (v,u)∈E indicates that variable X_u is dependent on variable X_v. A directed graph is a directed tree, if the graph is connected, all vertices except the root have in-degree equal to 1, and there are no cycles in the graph. For simplicity, we represent a DTree structure by the parent map, pa:{1,…,L}↦{1,…,L}, where pa(u)=v means that (v,u)∈E. The root of the DTree structure, which has no incoming edges, is represented by pa(u)=u.

The probability density function (pdf) of a DTree is a second-order approximation of a joint pdf on a L-dimensional continuous random vector X (Chow and Liu, 1968),

(1)

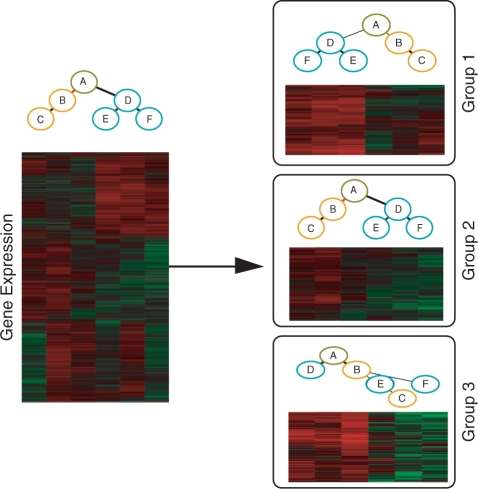
where we denote the model parameters by θ=(pa,τ₁,…,τ_u,…τ_L) and p_t is the pdf of a DTree. For example, for the DTree in Figure 1 left, we have p_t[x_A,x_B,x_C,x_D,x_E,x_F]=p[x_A]p[x_B|x_A]p[x_C|x_B] p[x_D|x_A] p[x_E|x_D]p[x_F|x_D].

Fig. 1.

Illustrative example of a developmental tree and its gene expression data (left). The developmental tree is constituted of a stem cell (stage A), an ‘orange’ lineage (Stages B and C) and a ‘blue’ lineage (Stages D, E and F). The red-green plot depicts the relative expression, where lines corresponds to gene profiles and columns to developmental stages ordered as in the above tree. In the right, we depict three groups of genes and their corresponding estimated tree structure as found by MixDTrees in the gene expression data in the left (see Section 2.3 for complete plot description).

We use conditional Gaussians (Lauritzen and Spiegelhalter, 1988) as probability densities, denoted as p[x_u|x_pa(u),τ_u] in Equation (1). Hence, for a given developmental profile x and a non-root developmental stage u with pa(u)=v, the pdf takes the form

(2)

where 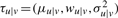are the parameters for one conditional density in the model. Intuitively, this conditional density models a linear fit of x_u on x_v, where w_u|v indicates the slope and μ_u|v the intercept. For the case of the root, pa(u)=u, we can simply set w_u|u=0 and Equation (2) will be equal to a univariate Gaussian (see Appendix A2 for parameter estimates).

2.2 Estimation of the Dependence Tree structure

For a given continuous random variable X the problem of estimating a DTree structure can be formulated as finding the p_t[x|Θ] that best approximates p[x]. We can measure the fit between p[x] and the approximation p_t[x] with the relative entropy (D) (Cover and Thomas, 1991), yielding the optimization problem

(3)

This is equivalent to finding a tree (Chow and Liu, 1968), here indicated by pa, which has maximal mutual information among tree edges, that is

(4)

where I denotes the mutual information (Cover and Thomas, 1991) (see Appendix A1 for derivations). This problem can be efficiently solved by calculating a maximum weight spanning tree from a fully connected indirected graph, where vertices are the developmental stages (1,…,L) and the weight of an edge (u,v) is equal to the mutual information between the corresponding variables (X_u,X_v) (Chow and Liu, 1968).

If p[x_u,x_v] follows a bivariate Gaussian pdf, the mutual information above can be computed (Cover and Thomas, 1991) by

(5)

Note that the mutual information is proportional to the correlation coefficient 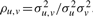. Hence, it measures the dependence between the two variables; I(X_u,X_v) = 0 if both variables are independent. Furthermore, as the mutual information is symmetric, I(X_u,X_v)=I(X_v,X_u), the estimation method does not determine direction of edges. Undirected and directed tree representations of DTree have equivalent pdfs (Meila and Jordan, 2001), directions of edges do not matter. For obtaining a directed tree, we select one particular node as root and direct all edges away from it.

2.3 Mixtures of Dependence Trees (MixDTrees)

We do not expect that all genes in a particular developmental process will share the same dependence structure, nor that the most likely DTree will exactly match the developmental tree per se. Indeed, we expect that some genes will be particularly correlated in particular developmental lineages, but not in others. For example, group 1 from Figure 1 has genes tightly overexpressed in the blue lineage ({X_D,X_E,X_F}), as does group 2 in the orange lineage ({X_B,X_C}). We also expect that some genes, which are important for earlier developmental stages, to be tightly coexpressed in stages near the root, but not in mature cell types (leaf vertices). See for example group 3 in Figure 1, which exhibits overexpression in all earlier stages ({X_A,X_B,X_D}). To infer these group-specific dependencies, we estimate a mixture of K DTrees, where each component can have a distinct tree structure.

We combine a set of K DTrees in a mixture model 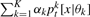, where θ_k=(pa_k,τ_1k,…,τ_Lk) denotes the parameters of the k-th DTree and α_k is proportional to the number of developmental profiles assigned to the k-th DTree; as usual α_k≥0 and 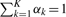. The mixture of Dependence Trees can be estimated with the Expectation–Maximization algorithm (Dempster et al., 1977). The estimation of the tree structures simply requires an additional computational procedure in the M-Step (Meila and Jordan, 2001).

Furthermore, we propose a MAP estimation to regularize the parameters w_u|v,k and 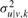of the pdfs from Equation (2) and prevent overfitting when there is little evidence for a given model (or for low α_k). We obtain the values of the hyper-parameters in an empirical Bayes fashion (Carlin and Louis, 2000), and use MAP point estimates at each M-Step of the Expectation–Maximization (EM) algorithm (see Appendix A2 for details on parameter estimates). The EM algorithm with MAP point estimates achieves results comparable to a more computationally expensive Markov Chain Monte Carlo method (Fraley and Raftery, 2007).

Note that in principle one could use a mixture of Gaussians (MoG) with full covariance matrix to model any arbitrary dependence in data with continuous variables. Due to the unbounded likelihood function, such method is prone to overfitting (McLachlan and Peel, 2000). To prevent this, several simplifications of the parameterization of the covariance matrix have been proposed (Banfield and Raftery, 1993; Celeux and Govaert, 1995), making distinct a priori assumptions of the variable dependencies. MixDTrees represents a new type of covariance matrix parameterization that is equivalent to inputing zeros on entries of the inverse of the covariance matrix on pairs of variables with no connecting edge (Lauritzen, 1996). Thus, the number of parameters required for representing a DTree is linear on the data dimensionality (3L−1), while it is quadratic for a multivariate Gaussian with full covariance matrix (L+L*(L−1)/2).

Visualization of gene groups To highlight the coexpression of developmental stages, as indicated by the estimated DTree, we perform the following. Gene groups are depicted as a heat-map with red values indicating overexpression and green values indicating underexpression (Eisen et al., 1998). There, the lines (gene profiles) are ordered as proposed in Bar-Joseph et al. (2001). This procedure orders genes with similar expression profiles to be close in the heat-map. Following this idea, for the columns (developmental stage profiles), we compute all possible columns orderings and select the one which has a minimal difference in the mutual information of adjacent columns. To further help the interpretation of individual groups, we compute strongly connected components (Cormen et al., 2001)—SCC for short—in the graph returned after thresholding the mutual information matrix. An optimal threshold parameter is obtained by evaluating the resulting SCC with the silhouette index (Kaufman and Rousseeuw, 1990). SCC is represented by dashed shapes around developmental stages and indicates, within a DTree, which developmental stages in a particular branch have similar expression profiles.

3 RESULTS AND DISCUSSIONS

3.1 Simulated data

To investigate general characteristics of MixDTrees and compare it with other methods, we use simulated data from mixture models with different degrees of variable dependence, and apply several unsupervised learning methods.

Data We generate data from mixtures with four types of variable dependence ranging from: Gaussians with diagonal covariance matrix (Σ^diag), DTree with low variate dependence (Σ^DTree−), DTree with high variate dependence (Σ^DTree+) and Gaussians with full covariance matrix (Σ^full). These choices range from the independent case (Σ^diag) to the complete dependent case (Σ^full). For each setting, we generate 10 such mixtures, and sample 500 development profiles from each. In all cases, we chose the μ from the range [−1.5,1.5], L=4, K=5 and mixture coefficients equal to α=(0.1,0.15,0.2,0.2,0.35). For Σ^diag , diagonal entries are sampled from [0.01,1.0], and non-diagonal entries are set to zero. For Σ^DTree, we randomly generate tree structures, one for each mixture component, and then choose 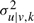from [0.01,1.0] and w_u|v,k from [0.0,0.5] for Σ^DTree− and w_u|v,k from [0.0,1.0] for Σ^DTree+. The generation of Σ^full is based on the eigenvalue decomposition of the covariance matrix (Σ=QΛQ^T) as in (Qiu and Joe, 2006), where Λ is drawn from [0.01,0.5]. The orthogonal matrix Q is obtained by sampling values from a lower triangular matrix M from the range [20,40], followed by the Gram–Schmidt orthogonalization procedure.

We apply MoG with full and diagonal covariance matrices and MixDTrees with MLE and MAP estimates to all datasets. The mixture estimation method is initialized with K=5 random DTrees (or multivariate Gaussians). Subsequently, we train the mixture model using the EM algorithm. To avoid the effect of the initialization, all estimations are repeated 15 times, and the one with highest likelihood is selected. We also performed clustering with k-means (McQueen, 1967), self-organizing maps (SOM) and spectral clustering (Ng et al., 2001). For all methods, the number of cluster was also set to five and for SOM, default parameters were used (Vesanto et al., 2000). We compare the class information from the data generation to compute the corrected Rand index (Hubbert and Arabie, 1985) and evaluate the clustering solutions.

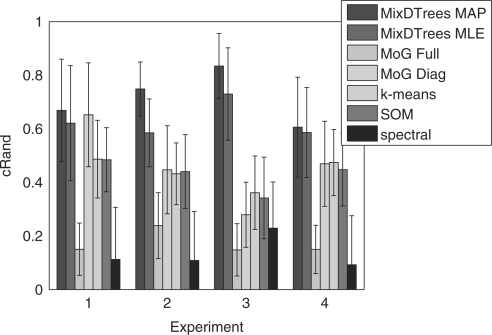
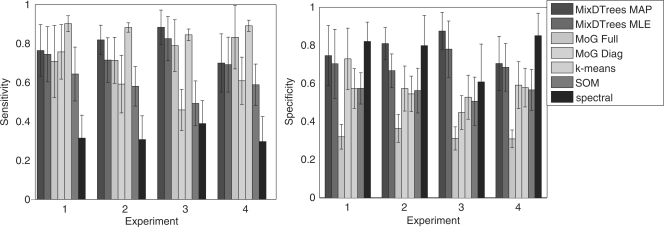
Results Every method performs well on the datasets generated with the corresponding model assumptions (Fig. 2). An exception is the MoG with full covariance matrices, which has low corrected Rand index for all datasets. An inspection on the specificity index (Fig. A1) indicates that the poor performance of MoG Full is caused by overfitting, since it tends to join real groups. Spectral clustering has a tendency to split real groups (see sensitivity plot in Fig. A1). In both datasets from Σ^DTree, MixDTrees MAP has higher mean values than MixDTrees MLE, which indicates a higher robustness of the MAP estimates (paired t-tests indicate superiority of MixDTrees MAP with P-values <0.05 in both Σ^DTree− and Σ^DTree+). Moreover, MixDTrees MAP achieves the highest values in all settings (paired t-tests indicate P-values <0.05), outperforming MoG Full, MoG Diagonal, k-means, SOM and spectral clustering, with the exception of MoG Diagonal in the Σ^diag data. These results show that MixDTrees MAP has a better performance on data coming from distinct dependence structures when compared to the other methods, and it is robust against overfitting.

Fig. 2.

We depict the mean corrected Rand index (Hubbert and Arabie, 1985) of true label recovery for distinct clustering methods (y-axis) against data generated with distinct model assumptions (x-axis) (1 for Σ^diag, 2 for Σ^DTree−, 3 for Σ^DTree+ and 4 for Σ^full). These choices range from the independent case Σ^diag to the complete dependent case Σ^full.

3.2 Lymphoid development

To evaluate the application of DTrees and MixDTrees to real biological data, we use gene expression data from lymphoid cell development. First, we compare the DTree structure inferred from the whole dataset with the lymphoid developmental tree. Then, we apply MixDTrees to find modules of co-regulated genes, and evaluate the results with GO and KEGG enrichment analysis. Finally, we compare our method with other unsupervised learning methods.

Data We produce an expression compendium of mouse lymphoid cell development by combining measurements of wild-type control cells from several studies (Akashi et al., 2003; Niederberger et al., 2005; Poirot et al., 2004; Tze et al., 2005; Yamagata et al., 2006) based on the Affymetrix U74 platform. In detail, our data contain four stages of early development hematopoietic cells (Akashi et al., 2003) [hematopoietic stem cell (HSC), multipotent progenitor (MPP), common lymphoid progenitor (CLP), common myeloid progenitor (CMP)]; three B-cell lineage stages (Tze et al., 2005) [pro-B cells (Bpro), pre-B cells (Bpre) and immature B-cells (Bimm)]; one natural killer (NK) stage (Poirot et al., 2004); and four T-cell lineage stages [double negative T-cells (TDN) (Niederberger et al., 2005), cd4 T cells (TCD4), cd8 T-cells (TCD8) and natural killer T-cells (TNK; Yamagata et al., 2006)]. The developmental tree describing the order of differentiation of the cells is depicted in Figure 3 left. We preprocess the data as follows: we apply variance stabilization (Huber et al., 2002) on all chips, take median values of stages with technical replicates, use HSC values as reference values and transform all expression profiles to log-ratios. We keep genes showing at least a 2-fold change in one developmental stage. The final data consists of 11 developmental stages and 3697 genes.

Inferring the DTree structure An initial question is how well we can recover the original developmental tree, as agreed upon by developmental biologists (Fig. 3 left), if we apply the structure estimation method described in Section 2.2 to the complete gene expression data (see Fig. 3 right for the estimated DTree). To quantify the difference between these trees, we compute the path distance between all pairs of vertices, and calculate the Euclidean distance between the resulting distance matrices (Steel and Penny, 1993), which indicates a distance of 15.74. To assess the statistical significance of this distance, we generate 1000 random trees with the same distribution of outgoing edges per vertex as the developmental tree. For each random tree, we compute the distance with the developmental tree. This test indicates a P-value of 0.002 of finding a distance as low as 15.74. Looking at these differences in detail, we can observe that 5 out of the 10 edges are correctly assigned, 4 edges connects vertices pairs with a path distance equal to 1 (i.e. MPP and CLP, CLP and TDN, TDN and TCD8 and TDN and TNK), and one edge connect vertices with a path distance of 3 (NK is connected to TCD8 instead the CLP). Furthermore, wrong edges have a tendency to be connected to vertices in the same level of the developmental tree (e.g. TCD8 and TNK both connected with the TCD4).

Another important question is how well does the DTree capture dependence in the data? One simple way to assess this is to measure the proportion of the mutual information represented in the tree edges, in comparison to the total mutual information on all pairs of variables. For a DTree structure pa, the treeness index can be defined as

(6)

For example, the score for the developmental tree (Fig. 3 left) is 0.22, whereas for the estimated DTree (Fig. 3 right), the ‘treeness’ index is 0.42. For measuring the statistical significance of this, we generate random data (1000 times) by shuffling values of gene expression profiles x_i, estimate a DTree from this random data, and measure its corresponding treeness index. This test indicates a P-value of 0.01 of finding a treeness index as high as 0.42.

Inferring Gene Modules with MixDTrees We estimate MixDTrees with MAP estimates from the Lymphoid data following the protocol in Section 3.1. The Bayesian information criterion (McLachlan and Peel, 2000) indicates 13 groups as optimal. We analyze the functional relevance of the groups of genes found by enrichment analysis (Beissbarth and Speed, 2004) with GO and pathway data from the KEGG (Kanehisa et al., 2006). For the GO (or KEGG) enrichment analysis, we use the statistic of the Fisher-exact test to obtain a list of GO terms (or KEGG pathways), whose annotated genes are overrepresented in a group. We correct for multiple testing following Benjamini and Yekutieli (2001). All results, group plots, list of genes per cluster, KEGG and GO enrichment analysis can be found at http://algorithmics.molgen.mpg.de/Supplements/InfDif/

First, we measure the average treeness of the MixDTrees (we calculate Equation (6) and take the sum weighted by α). For the MixDTrees MAP this value was 0.54, which indicates an increase of 28% over the treeness index for the single DTree. This reinforces our point that mixture of Dependence Trees with estimated structures is more successful in modeling dependencies in the data.

In relation to the groups of coexpressed genes found by MixDTrees, overall, stages from the same developmental lineage are at the same branches of the estimated DTree structure. Furthermore, groups present prototypical expression patterns such as overexpression in cells from a particular lineage, but not in other lineages (e.g. groups 2 and 5 for B-cells, groups 4 and 6 for T-cells and group 11 for NK-cells) or groups displaying under-expression in particular lineages (e.g. groups 7 and 12 for T-cells and groups 10 and 12 for B-cells).

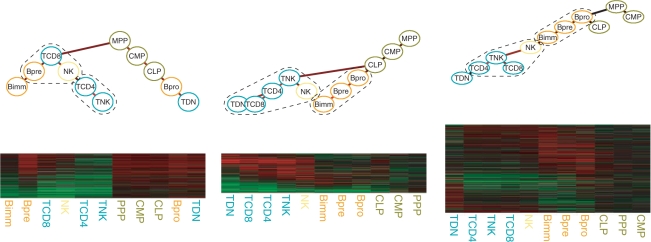
In Figure 4, we display some of these groups, which we discuss in more details. Group 1 is an interesting case, where the DTree structure differs drastically from the developmental tree. The right branch, which is formed by stages MPP, CLP, CMP, TDN and Bpro, has only early developmental stages, and all display high overexpression patterns. On the other hand, the majority of stages in the SCC of the left branch (Bimm, Bpre, TCD8, NK, TCD4, TNK) are immature developmental stages (leaves in Fig. 3 left). Enrichment analyses from GO and KEGG show that group 1 is overrepresented for cell cycle and DNA repair genes (P-values <0.001). This matches the biological knowledge that earlier differentiation stages of development are cycling cells, while immature cells are resting (Matthias and Rolink, 2005; Rothenberg and Taghon, 2005). Group 4 contains an SCC (left branch) with all T-cell stages plus the closely related NK-cell. At these stages, genes display an overexpression pattern. Enrichment analysis indicates overrepresentation for GO terms such as T-cell activation, differentiation and receptor signaling; and KEGG pathways such as T-cell signaling and NK-cell mediated cytotoxicity (P-values <0.001). Similarly, group 5 has a SCC with all B-cell stages. Furthermore, for B-cell stages, genes are preferentially overexpressed. GO analysis also indicates enrichment for terms such as B-cell activation (P-values <0.001), while KEGG analysis indicates enrichment in pathways such as Hematopoietic cell lineage and B-Cell receptor signaling (P-values <0.05). These results indicate how MixDTrees can be used in finding groups of biologically related genes, as well that the associated DTree structure adds relevant information regarding expression similarly of developmental stages.

Fig. 4.

We depict the DTree and expression profiles of groups 1, 4 and 5 from MixDTrees MAP. Dashed shapes around developmental stages represent the SCC. See Section 2.3 for complete description of plotting procedure.

Comparison with other methods For comparison purposes, we also perform clustering of the Lymphoid data with other methods: k-means, SOM, MoG with full covariance matrix, MoG with diagonal matrix and the bi-clustering methods Samba (Tanay et al., 2002) and non-negative matrix factorization (Brunet et al., 2004). Additionally, we evaluate distinct variations of the MixDTrees: MAP and MLE with DTree structure estimation and MAP estimates with the DTrees fixed to the structure from Figure 3 left, as in our previous approach (Costa et al., 2007b). For SOM and Samba, default parameters were used (Vesanto et al., 2000 , Tanay et al., 2002). For the mixtures, NMF, k-means and SOM, the number of clusters was set to 13. Samba, which detects the number of clusters automatically, determined 19 clusters.

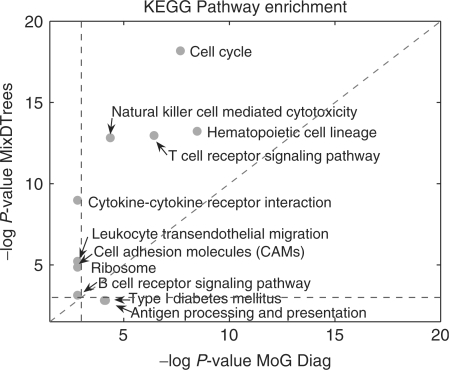
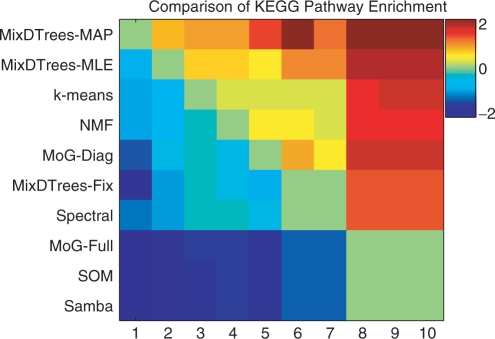
To evaluate the performance of the methods, we use a heuristic of comparing P-values of KEGG enrichment analysis in a similar way as Ernst et al. (2005). The results of the comparison of MixDTrees MAP and MoG Diag can be seen in Figure 5. In short, the best method should present a higher enrichment for a higher number of KEGG pathways, i.e. MixDTrees MAP was superior to MoG Diag in 9 out of 11 pathways. Furthermore, most of the 11 KEGG pathways enriched with a P-value <0.05 in one of the methods (points depicted in Fig. 5) are directly involved in immune system and developmental processes. We apply the same procedure for all pairs of methods and count the events {P-value m₁ <P-value m₂}, where m₁ and m₂ are the two methods in comparison. As can be seen in Figure 6, MixDTrees MAP outperforms all methods, while MixDTrees MLE and k-means also obtained higher enrichment than other methods. Overall, SOM, MoG Full and Samba obtain poor enrichment results, and were outperformed by other methods. We repeat the same analysis for GO enrichment (see Supplementary Material). The result are in agreement with the KEGG enrichment analysis, again MixDTrees MAP had higher enrichment than all other methods, while SOM and MoG Full obtain poor results.

Fig. A1.

We depict the sensitivity and specificity of label recovery for distinct clustering methods (y-axis) for distinct model assumptions (x-axis) (1 for Σ^diag, 2 for Σ^DTree−, 3 for Σ^DTree+ and 4 for Σ^full). A low sensitivity is a indicator of joining real clusters; while a low specificity indicates a tendency to split real clusters.

Fig. 5.

We depict the scatter plot comparing the KEGG pathway enrichment of MoG Diag (x-axis) and MixDTrees MAP (y-axis). We use −log(P)-values, where higher values indicate a higher enrichment. The blue lines corresponds to −log(P)-value cut-off used (P-value of 0.05). Only KEGG pathways with a −log(P)-value higher than (2.99) in one of the results are included. MixDTrees MAP had a higher enrichment for 9 out of the 11 KEGG pathways.

Fig. 6.

Heat-map plot displaying the comparison of KEGG enrichment for 10 distinct clustering methods. More precisely, entries in the plot correspond to log(#{P-value m_y <P-value m_x }/#{P-value m_y >P-value m_x }), where red (or blue) values indicate that the method on the y-axis (m_y) had a higher (or lower) count of enriched KEGG pathways than the method on the x-axis (m_x); numbers on the x-axis correspond to the methods on the y-axis.

4 CONCLUSIONS

Understanding the details of cell differentiation is a central question in developmental biology and also of high relevance for clinical applications, for example, when considering lymphoid development. The full spectrum of differentiation paths is still unknown, as recent studies suggest that there exist alternative paths in lymphoid development (Graf and Trumpp, 2007).

Here we present a novel statistical model called DTree for gene expression data measured for cells in distinct differentiation stages and an unsupervised learning method for finding functional modules and their specific differentiation pathways in the course of development. We show that the DTree inferred from the whole dataset approximates the dependencies intrinsic to Lymphoid development well. Furthermore, by combining several DTrees in a mixture, we find models specific to groups of co-regulated genes displaying distinct differentiation pathways reflected by the distinct dependence structures. These groups usually have a lineage specific expression pattern supported by term enrichment analysis of gene annotation from KEGG and GO, which indicates development-specific module function. Moreover, the DTree structure, which indicates the dependence between the stages, is valuable for the biological interpretation of these groups. On simulated data MixDTrees compares favorably to other methods routinely used for finding functional modules, even for data arising from variable dependence structures. In particular, our method is not susceptible to overfitting, which is otherwise a frequent problem in the estimation of mixture models from sparse data.

Alternative paths of differentiation can be investigated with the use of statistical models with higher order dependencies (Chaudhuri et al., 2007; Thiesson et al., 1998), which currently do not provide an efficient and exact method for the estimation of relevant dependencies. As our probabilistic method is based on a well-studied statistical framework (Friedman, 2004), we can easily benefit from extensions to mixtures proposed to integrate, or fuse, further biological information, such as sequence (Schönhuth et al., 2006) or in situ data (Costa et al., 2007a). Thus we will be able to explore developmental regulatory networks controlling module-specific differentiation from fused genomics and transcriptomics data.

APPENDIX

A1 DTREE Structure estimation

For a given L-dimensional continuous variable X, the problem of a DTree structure estimation can be defined as finding the pdf p_t[x] that best approximates p[x]. We summarize here the solution proposed in Chow and Liu (1968), which considered trees on discrete distributions, and we describe our extension to continuous variates. The solution is based on finding the DTree structure that minimizes the relative entropy between the p[x] and the approximation p_t[x], or

(A1)

The relative entropy between p[x] and p_t[x] is defined as (Cover and Thomas, 1991)

From Equation 1, we have

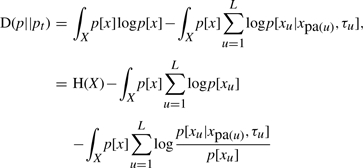By Bayes rule and the definition of entropy (H) and mutual information (I) (Cover and Thomas, 1991), this previous formula can be simplified to,

and hence,

(A2)

Since H(X) and H(X_u) are independent of p_t, Equation (A2) reduces to

(A3)

This problem can be efficiently solved by a maximum weight spanning tree algorithm on the fully connected undirected graph, in which vertices corresponds to the variables and edge weights to the mutual information between variables (Chow and Liu, 1968). This algorithm has a worst case complexity of O(L²logL).

We need to compute I(X_u,X_pa(u)) for a multivariate Gaussian. Given pa(u)=v, the mutual information is defined as,

(A4)

Expanding the terms

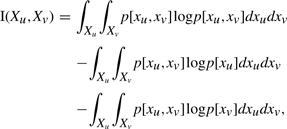and by definition of H, we have

(A5)

The entropy of a L-dimensional multivariate Gaussian pdf is defined (Cover and Thomas, 1991) as

(A6)

where Σ_X is the covariance matrix of X. By substituting Equation (A6) in Equation (A5), we obtain

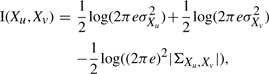given ,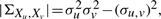

and hence,

(A7)

A2 MAP Parameters estimates

We use the Expectation Maximization algorithm with MAP point estimates for estimating the MixDTrees MAP. We describe here the derivations of the parameter estimates maximizing the MAP. This corresponds to the parameters used in the M-Step of the EM algorithm. All other parameters follow the basic EM framework, and we refer the reader to McLachlan and Peel (2000) for more details.

Let x_iu be the expression value of the gene i in development stage u, 1≤i≤N and 1≤u≤L. Then, x_i=(x_i1,…,x_iu,…,x_iL) is the developmental profile of gene i, and X corresponds to a data set with N observed genes.

In short, we want to find estimates maximizing

where y_i∈Y corresponds to the hidden variable indicating, which mixture component gene profile x_i belongs to. Since MixDTrees are based on first-order dependencies, it is sufficient to find the parameters in a simple bivariate scenario (X_u,X_pa(u)), where pa(u)=v. This simplifies the formula above to

(A8)

where

and thus

where 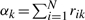and r_ik=p[y_i=k|x_i] is the posterior probability (or responsibility) (McLachlan and Peel, 2000) that gene i belongs to DTree k.

A2.1 Priors on parameters

We use the following conjugate priors to regularize the parameter w_u|v,k and 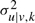and avoid overfitting when there is low evidence for a given model (or low α_k).

A2.1.1 Prior on deviation parameter

For simplicity of computation we work with a precision parameter . We define the prior of λ_u|v,k to be proportional to

where ν_u|v,k is the hyper-parameter.

A2.1.2 Prior on regression parameter

The prior of w_y|x,k is defined as

which is invariant to the scale of the variates X_u and X_v, and has β_u|v,k as a hyper-parameter.

A2.2 MAP estimates

The MAP estimates are obtained by taking the derivative of Equation (A8) in relation to each parameter, which leads to the estimates

(A9)

(A10)

When β_u|v,k→∞, the prior becomes non-informative; that is, the MAP and maximum likelihood (ML) estimates are equal.

(A11)

Again, when β_u|v,k→∞ and ν_u|v,k→∞, the prior becomes non-informative, and MAP and ML estimates are equal.

All the estimates make use of the following sufficient statistics

(A12)

(A13)

(A14)

A2.3 Hyper parameters estimates via empirical Bayes

In an empirical Bayes approach (Carlin and Louis, 2000), we can estimate the MAP value of β_u|v,k and ν_u|v,k from the data, by taking the derivative of Equation (A8) in relation to the hyper-parameters, that is

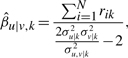(A15)

and

(A16)

Both empirical priors also penalize variables with large variances or with low evidence enforcing lower w_u|v,k and higher 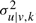, respectively.