Swelfe: a detector of internal repeats in sequences and structures

Abstract

Summary: Intragenic duplications of genetic material have important biological roles because of their protein sequence and structural consequences. We developed Swelfe to find internal repeats at three levels. Swelfe quickly identifies statistically significant internal repeats in DNA and amino acid sequences and in 3D structures using dynamic programming. The associated web server also shows the relationships between repeats at each level and facilitates visualization of the results.

Availability: http://bioserv.rpbs.jussieu.fr/swelfe

Contact: annela@abi.snv.jussieu.fr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Duplications play a major role in genome evolution by creating and modifying cellular functions (Marcotte et al., 1999). Duplications can be large, up to the entire genome, or small, down to small parts of genes. While genome and gene duplications have been extensively studied, few works have aimed at identifying and studying intragenic repeats. These arise in DNA but are selected for their functional and structural consequences. Therefore, the simultaneous study of repeats at DNA, protein sequence and protein structure levels is necessary to understand their biological role.

Currently, no tool allows for the integrated analysis of internal repeats at the three levels. Several programs efficiently detect large very similar DNA repeats [e.g. Reputer (Kurtz and Schleiermacher, 1999), Repseek (Achaz et al., 2007)], or tandem repeats [e.g. Tandem Repeat Finder (Benson, 1999)]. But there is a lack of methods to identify small, closely spaced and divergent repeats using appropriate substitution matrices and statistical procedures. Some programs detect structural similarities [Vast (Gibrat et al., 1996), CE (Shindyalov and Bourne, 1998), DALI (Holm and Sander, 1993)] but they are slow and not adapted to detect internal similarities. Our tool, Swelfe, uses conceptually the same algorithm to detect internal similarities at these three levels allowing to analyze the evolution of DNA repeats at the light of their effects on protein sequence and structure. This facilitates pinpointing sequence-structure associations and understanding the evolutionary forces acting upon the evolution of these elements.

2 ALGORITHM AND STATISTICS

Swelfe identifies repeats by alignment of DNA sequences, amino acids sequences and three dimensional (3D) structures. Preliminarily, 3D structures are encoded as linear sequences of α angles (α angle is the dihedral angle between four consecutive Cα) (Usha and Murthy, 1986) (supplementary Fig. 1). Strings of α angles have been shown to be very compact ways of representing protein backbones while conserving most of the structural features of the peptide skeleton (Carpentier et al., 2005). In Supplementary Materials we show comparisons with DALI showing that Swelfe is capable of finding very distant similarities even in the absence of classical secondary structural elements. Using this description we find repeats by dynamic programming with the Huang and Miller algorithm (Huang and Miller, 1991; Huang et al., 1990) on sequences and protein structures (Supplementary Fig. 2). The system of scores was adapted at each level (see Supplementary Table 1 for formulae and default parameters). In sequences, Swelfe uses any BLOSUM or PAM matrix for proteins while it generates a similarity matrix explicitly accounting for the frequencies of each nucleotide in DNA (Achaz et al., 2007). The structural score for two matching α angles increases when the circular difference between them decreases and also accounts for the relative frequencies of α-angles on the PDB (Supplementary Fig. 3). Thus very frequent angles, e.g. originating from α-helices or β-sheets, have a lower score.

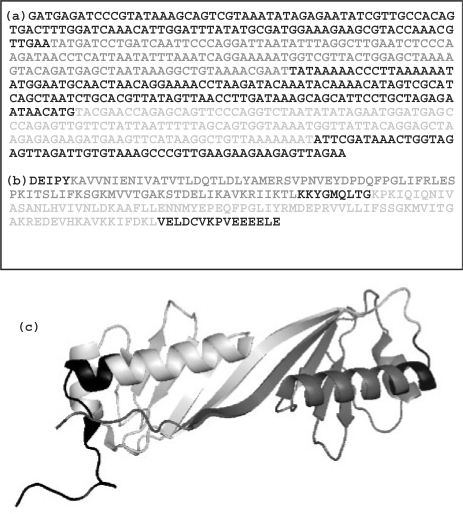
As post-processing steps we check that the sequence repeats are statistically significant (see below). Since a succession of non-perfectly matching α-angles could theoretically lead to poor overall superposition of repeats we check that the relative root mean square deviation (RRMSD) (Betancourt and Skolnick, 2001) between the two copies of the repeat is low. The default threshold (0.5) corresponds to a probability of 10⁻³ of finding such a low RRMSD in a 20 residues substructure. The vast majority of significant repeats we find in the PDB structures has much lower values of RRMSD (see histograms of RRMSD and RMSD distributions in Supplementary Material). Along with Swelfe we provide a python script that filters and simplifies the output of highly overlapping successive repeats (default: >50% overlap). Most parameters of Swelfe can be tuned as described in the manual. An example of protein exhibiting a repeat at the three levels is shown on Figure 1.

Fig. 1.

Example of repeat found at the three levels in the Tata-box Binding Protein (TBP) of Sulfolobus acidocaldarius (1MP9). (a) DNA (137 nt of repeat length), (b) amino acid sequence (82 aa), (c) 3D structure (83 aa). Repeats are shown in light gray and non-repeated regions are shown in black. Amino acid and 3D repeats are almost perfectly coincident, but the DNA repeat is smaller and within the region of the other repeats. Among homologous elements, similarity decreases with divergence time at different rates. It decreases quicker at the DNA and slower at the protein structural levels (Chothia and Lesk, 1986). This frequently results in smaller repeats in DNA than at the other levels. Edges of very degenerated repeats may also not precisely coincide at the different levels due to terminal mismatches at some but not at all levels. This is a typical feature of methods aiming at optimizing local alignments.

To assign a statistical significance for repeats in sequences we implemented the Waterman and Vingron method (Waterman and Vingron, 1994). The P-value is computed using the distribution of scores in a large number of random sequences computed by shuffling codons or amino acids of the original sequence. Full description can be found in Supplementary Material. We observed that drawing 100 random sequences is enough in most cases to obtain the most significant repeats (see Supplementary Fig. 4). The same authors also proposed a faster ‘declumping estimation’ method using fewer (e.g. 20) random sequences. We implemented it in Swelfe (see Supplementary Fig. 5). We find it to be 6 (DNA) to 10 (amino acids) times faster when calculating the same number of scores on random sequences, and we recommend it as a preliminary filter when scanning large databases.

On structural alignments there is no currently well-accepted method to assign statistical values to the alignment scores. We thus chose a conservative default score based on the analysis of the resulting structural alignments (250^○ followed by the RRMSD filter described earlier). This default value leads to finding approximately the same number of repeats at the level of amino acids and structures for the PDB proteins.

3 IMPLEMENTATION

Swelfe was written in C language and we offer a number of pre-compiled binaries (Linux and Mac OS X) and the source code. Swelfe is rather fast. Using a Xeon MacPro we analyzed the 9537 proteins from the subset ‘clusters50’ of PDB (i.e. structures having <50% sequence identity with each other) for which we found DNA and amino acid sequences. The program took less than a minute to find the 3D repeats or the amino acid repeats, 5 min for the DNA repeats. Statistical evaluation slows the program because it needs generating and analyzing the random DNA and protein sequences. Yet, when we made the same analysis including statistical evaluation for repeats using default parameters, the program took about 20 h for finding and classifying all DNA repeats and 30 min for the amino acid repeats. It uses ∼16 MB RAM for the DNA bank. The web server interface allows drawing relationships between the results at the three levels and visualization of the 3D structural results using Jmol (www.jmol.org). We also built a databank linking explicitly PDB structures with their genes and amino acid sequences through extensive similarity searches. This databank contains 85 845 entries, thus allowing extensive analyses at the three levels, and is available from the authors upon request.