Proliferating Cell Nuclear Antigen Uses Two Distinct Modes to Move along DNA

Abstract

Proliferating cell nuclear antigen (PCNA) plays an important role in eukaryotic genomic maintenance by topologically binding DNA and recruiting replication and repair proteins. The ring-shaped protein forms a closed circle around double-stranded DNA and is able to move along the DNA in a random walk. The molecular nature of this diffusion process is poorly understood. We use single-molecule imaging to visualize the movement of individual, fluorescently labeled PCNA molecules along stretched DNA. Measurements of diffusional properties as a function of viscosity and protein size suggest that PCNA moves along DNA using two different sliding modes. Most of the time, the clamp moves while rotationally tracking the helical pitch of the DNA duplex. In a less frequently used second mode of diffusion, the movement of the protein is uncoupled from the helical pitch, and the clamp diffuses at much higher rates.

Introduction

The proliferating cell nuclear antigen (PCNA)³ is a homotrimeric, ring-shaped protein that forms a closed circle around double-stranded DNA. The protein serves as a processivity factor for the eukaryotic replicative polymerases δ and ϵ by tethering them to the DNA (1). Additionally, PCNA interacts with a large number of replication, repair, and signaling factors to coordinate enzymatic processes at sites of replication and repair (2). This recruitment of nucleic-acid enzymes to a topological clamp around the DNA is a strategy employed in organisms ranging from bacteriophage to humans. The remarkable similarity of the ring-shaped structures of the Escherichia coli and bacteriophage T4 sliding clamps to PCNA underscores the evolutionary success of this molecular approach.

PCNA is a homotrimer consisting of 37-kDa subunits, each of which comprises two similar globular domains. The PCNA monomers are arrange in head-to-tail fashion, forming a ring with pseudo 6-fold symmetry. The central channel has a diameter of 34 Å, large enough to accommodate double-stranded DNA (3, 4). PCNA forms stable ring-shaped trimers in solution (5) that need to be opened to load onto DNA (6). The clamp loader, replication factor C (RFC), mediates the assembly of PCNA onto DNA at primer-template junctions (7) or at nicks in the DNA backbone (8) in a process that is dependent on ATP. The PCNA·DNA complex is very stable, exhibiting a half-life of tens of minutes (9, 10).

Although the interactions of various replication and repair proteins with PCNA are well studied (recently reviewed in Ref. 2), the interactions between PCNA and DNA are less well understood. Structural studies reveal that the central channel of the clamp is lined with highly conserved, positively charged residues (3, 4). Mutational analysis indicates that these residues may be more important for PCNA loading onto DNA than for sliding along DNA (11). Molecular dynamics simulations suggest that the positively charged residues interact with the phosphodiester backbone but that these interactions are highly dynamic and are frequently displaced by ions from solution (12).

The ring structure of PCNA and its relatively weak interaction with DNA allow it to move along the DNA in a diffusive fashion. Early work showed that PCNA can only be stably trapped on linear DNA when bound to polymerase δ on a primer-template (13). Further evidence for PCNA moving along DNA stems from a study, which measured UV cross-linking of PCNA to a chemically modified, double-stranded DNA template. On circular DNA, a high degree of cross-linking was observed, but linearization of the template dramatically reduced cross-linking, suggesting a rapid dissociation of PCNA from the DNA ends (14). In the absence of a more direct way to assess the motion of PCNA along DNA, it has been difficult to study the molecular nature of the PCNA·DNA interactions and to understand how translocation of the sliding clamp occurs.

In recent years, single-molecule techniques have been used to study diffusion of a variety of proteins along DNA. The earliest studies focused on the E. coli RNA polymerase, which is suggested to diffuse along DNA to find promoters (15–17). Other proteins studied include lac repressor (18) and p53 (19); the DNA damage surveillance and repair proteins oxoguanine DNA glycosylase 1 (hOgg1) (20), Rad51 (21), and Msh2-Msh6 (22); and the herpes simplex virus processivity factor UL42 (23). These studies allowed for a detailed biophysical characterization of diffusive protein motion along DNA and revealed a number of different mechanisms of translocation (24).

Here we use a single-molecule approach to show that PCNA diffuses along DNA using two distinct modes. In one diffusion mode, the clamp tracks the helical pitch of the DNA duplex, resulting in a rotational movement of the protein around the DNA. In the second mode, the protein undergoes a faster, predominantly translational motion. We speculate how these two diffusive mechanisms contribute to the activity of the different classes of proteins that are tethered to DNA by PCNA.

EXPERIMENTAL PROCEDURES

Protein Labeling and Characterization

Protein Expression and Labeling

The human PCNA open reading frame was amplified from Int pET19pps (kind gift from Dr. Tom Ellenberger) and was cloned into pET28b between the NdeI and BamHI restriction sites. The N-terminally hexahistidine-tagged protein was overexpressed in E. coli BL21(DE3) cells, purified over a nickel-nitrilotriacetic acid column (Qiagen), dialyzed into Storage Buffer (50 mm Tris, pH 8, 50 mm NaCl, 1 mm EDTA, 1 mm dithiothreitol, and 10% glycerol) and stored at −80 °C. Purified human RFC complex with an N-terminal RFC1 deletion, which increases PCNA loading efficiency, was a kind gift from Dr. Jerard Hurwitz (25, 26).

The purified PCNA was labeled by coupling AlexaFluor 555-maleimide (Invitrogen) to solvent-exposed cysteine groups on the protein. The human PCNA monomer contains six cysteine residues of which two are surface-exposed (PDB ID: 1AXC) (4), resulting in a total of six solvent-accessible cysteines per trimer. The labeling reaction was performed following the manufacturer's suggested protocol. Briefly, PCNA aliquots were thawed and dialyzed overnight at 4 degrees into labeling buffer (50 mm Hepes, pH 7.4, 50 mm NaCl). After reducing the protein with 10 mm Tris(2-carboxyethyl)phosphine, dye was added at a ratio of 10 dyes per PCNA trimer, and the reaction was allowed to proceed for 2 h at 22 °C. Finally, the reaction was quenched with 2 mm β-mercaptoethanol, and free dye was separated from labeled protein using a size exclusion column (PD10, Amersham Biosciences). Labeling stoichiometry was assessed using UV-visible spectrophotometry and determined to be 0.7 ± 0.3 AlexaFluor 555 per PCNA trimer. Fractions were aliquoted and stored at −80 °C.

Anti-X. laevis PCNA Antibody Production

Full-length Xenopus laevis PCNA (X. laevis PCNA) was cloned and expressed as described previously (27). The His₆-X. laevis PCNA was used to generate polyclonal antibodies in rabbits (Josman, LLC).

Primer Extension Assay

High speed supernatant (egg cytosolic) extract was prepared from X. laevis eggs as described previously (28). Endogenous PCNA was depleted to below 0.25% with a rabbit polyclonal anti-X. laevis PCNA antibody (characterized in supplemental Fig. S1A). The extent of depletion was determined by Western blotting with anti-PCNA mouse monoclonal antibody PC10 (Santa Cruz Biotechnology). Purified and labeled human PCNA was reintroduced to the depleted extract at a concentration of 1 μm monomers, and primer extension was measured. Extracts were supplemented with an ATP-regeneration system (2 mm ATP, 20 mm phosphocreatine, 5 μg/ml creatine kinase (all from Sigma)), 15 μg/ml nocodazole (Sigma), and [α-³²P]dATP (PerkinElmer Life Sciences). M13mp18 single-stranded DNA (New England Biolabs) was added at 15 ng/μl extract. Incorporation of radioactivity was measured after running the replication products on a 0.8% agarose-TBE gel.

Single-molecule Imaging

Buffers

Imaging buffers were based on the work of Ellison and Stillman (29). To obtain buffers with varying concentrations of potassium glutamate, stocks of Buffer A (50 mm Hepes, pH 7.5, 7 mm MgCl₂, 1 mm CHAPS, 1 mg/ml bovine serum albumin, 1 mm dithiothreitol, 0.001% Nonidet P-40) with 0 mm potassium glutamate and 500 mm potassium glutamate were prepared and mixed to achieve the desired salt concentration. The total ionic strength I of the buffers was calculated by using,

where c is the molar concentration of ion n, z is the charge number of that ion, and the sum is taken over all ions n. At pH 7.5, 47% of the 50 mm Hepes (free acid; pK_a = 7.55) in our solutions will be charged (z² = 1), resulting in an ionic strength of 12 mm. The sodium hydroxide used to achieve a pH of 7.5 contributes ∼13 mm to the ionic strength. Similarly, 7 mm MgCl₂ adds 21 mm ionic strength (for the divalent magnesium ions, z² = 4). In the absence of any potassium glutamate, these contributions add up to an ionic strength of 41 mm. Addition of potassium glutamate will change the ionic strength accordingly (z = 1). Viscous sliding buffers were based on Buffer B (50 mm Hepes, pH 7.5, 7 mm MgCl₂, 150 mm potassium glutamate) with glycerol, or PEG6000 added by weight to achieve the desired viscosity (5*η_water or 10*η_water) (47, 49).

Flow Cell, DNA, and Surface Tethering

Streptavidin-coated flow cells were constructed as reported before (20, 30, 31) with a flow-channel width of 1.5 mm and height of 0.12 mm. The inlet tubing had an inner diameter of 0.38 mm (PE20 from BD Biosciences) and 10-cm length to minimize the dead volume. Biotin-lambda-biotin DNA was prepared by ligating custom, 12-mer oligonucleotides with 3′Biotin modification (IDT) (BL1, 5′-AGGTCGCCGCCC-Biotin-3′; and BL2, 5′-GGGCGGCGACT-Biotin-3′) to their complementary, single-stranded ends of lambda DNA (PerkinElmer Life Sciences). To allow single-molecule observations of protein sliding along stretched DNA in the absence of hydrodynamic flow, we assembled stretched DNA onto the surface of the flow cell with both DNA ends coupled to the surface. To achieve this double tethering, 30 pm biotin-lambda-biotin DNA was flow stretched in Buffer A with 35 mm potassium glutamate. After the association of the first biotin with the streptavidin-coated surface, the DNA was stretched by the flow and the second biotin bound to the surface. By changing the flow rate that was applied when introducing the DNA into the flow cell, the length distribution of the DNA could be controlled (results not shown). To visualize DNA, we flow in a 100 nm solution of Sytox Orange (Invitrogen), a DNA intercalating dye, in Buffer A and image with 521 nm laser excitation at variable power. We only stain the DNA at the end of the experiment after PCNA sliding trajectories have been collected. The results described in the main text are obtained on DNA that was immobilized to the surface using a flow rate of 0.05 ml/min, resulting in a mean end-to-end distance of 11.5 ± 0.1 μm (corresponding to 70.3 ± 0.5% of the contour length of lambda-phage B-DNA) for DNA molecules upon which PCNA sliding was measured (see supplemental Fig. S4B). Typically, we observed 10–25 doubly tethered DNA molecules per 80 × 80 μm² field of view.

Loading Single PCNA Molecules

The typical single-molecule PCNA loading reaction contained 0.4 nm RFC (1/1000 dilution of stock immediately prior to use), 1 nm PCNA (1/2000 dilution immediately prior to use), and 1 mm ATP in 100 μl of Buffer A with 35 mm potassium glutamate. This reaction was drawn into the flow cell containing doubly tethered DNA molecules, was allowed to incubate for 20 min at room temperature, and then was flushed out with 40 flow-cell volumes of Buffer A with 500 mm potassium glutamate. Next, the buffer of interest was exchanged into the flow cell for 40 flow-cell volumes, flow was stopped, and event acquisition would begin. Typically, 0–3 PCNA molecules were observed per doubly tethered DNA molecule.

Quantum Dot Functionalization and Coupling to PCNA

QDots (605 nm) were functionalized with mouse monoclonal anti-histidine tag antibody (MCA1396 from AbD Serotec) using the Invitrogen QDot Antibody Conjugation Kit. For PCNA·QDot experiments, AlexaFluor 555- or mock-labeled PCNA was loaded as usual except that the initial wash included ∼1 nm anti-his QDots for 10 min. Next, the flow cell was washed with 40–100 flow cell volumes of Buffer A + 500 mm potassium glutamate to remove free QDots. Finally, the buffer of interest was exchanged into the flow cell for 40 flow-cell volumes, flow was stopped, and image acquisition was started.

Imaging Single PCNA Molecules

Fluorescence imaging of AlexaFluor 555-PCNA and PCNA·QDot complexes moving along DNA or QDot bound to DNA was performed as before (19). The AlexaFluor 555 dye and QDot (605 nm) emission were excited by the 521-nm line from an Ar/Kr laser (Coherent I-70 Spectrum), and fluorescence was collected by an EM-CCD (Andor iXon) after filtering scattered laser light (Chroma Technology). Typically, 2.5- to 5-fold less power was used for QDot imaging than for AlexaFluor 555 imaging. Typical frame rates were 19 Hz for AlexaFluor 555-PCNA and 4 Hz for PCNA·QDot. Data were analyzed by custom-written particle-tracking MATLAB® code (19).

Data Analysis

Particle Tracking

The positions of labeled particles were determined by fitting each single-molecule fluorescence image to a two-dimensional Gaussian distribution. This procedure allows the determination of a particle's position with a precision that can be better than the diffraction-limited optical resolution of the microscope used. The accuracy of position determination strongly depends on the signal strength corresponding to a single molecule and is given by,

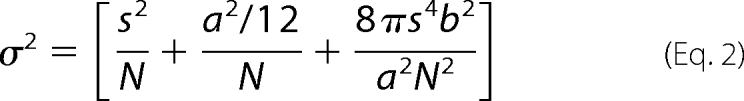where N is the number of photons collected (32). Typical signals from individual AlexaFluor 555 and QDot labels corresponded to 1000 ± 500 and 6000 ± 3000 photons per 50-ms integration. Using the standard deviation of the microscope point-spread function s (150 nm), the pixel size a (166 nm), and the background level b (13–19 photons for AlexaFluor 555 imaging and 4–12 photons for QDot imaging), we calculate the standard error of position determination to be σ = 12 nm for AlexaFluor 555-PCNA and σ = 2.2 nm for PCNA·QDot.

Determining Diffusion Coefficients

Using the experimentally obtained trajectories of individual sliding particles, we determined the diffusion coefficient D of each particle by plotting its mean square displacement (MSD) as a function of step interval m times the time interval, Δt,

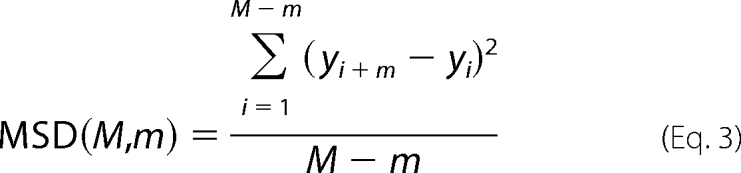Here, M represents the total number of steps in the trajectory, m ranges from 1 to M, and y_i is the displacement of the particle along the axis of the DNA in step i. Effectively, MSD(M,m) is the average of the squared displacements of the particle in the trajectory with length M, calculated from all pairs of positions that are m steps apart. According to the one-dimensional diffusion equation MSD(M,m) = 2DmΔt, we can obtain D by fitting the resulting data to a straight line using a weighted least-square fitting procedure. We measure the diffusion coefficient of the PCNA as half of the slope of the line fit to the MSD versus mΔt between steps m = 2 through m = 10. The lower end of this range was chosen, because many trajectories exhibit nonlinear behavior in the first step likely due to DNA fluctuations. The top of the range was limited by the shortest trajectories we accepted for fitting. Particles that were apparently immobile on the DNA or that showed bounded diffusion in the time window under consideration were excluded from analysis. Since bounded diffusion is apparent as a nonlinearity of the MSD versus mΔt, we report only particles for which the MSD(M,m) was correlated to mΔt with a Pearson correlation coefficient of 0.9 or higher.

Simulating Diffusion Trajectories of a Two-speed Stepper

Using MATLAB, we simulated a one-dimensional random walk of 100 steps, each consisting of the average of 100 sub-steps with normally distributed step sizes. Sub-steps were used to better approximate the averaging inherent to imaging a single molecule over a finite window of time (the exposure time Δt). Next, a single parameter was used to scale the step size distribution of the particles to a desired diffusion coefficient. As we did with our experimentally observed diffusion trajectories, we fit the mean-square displacement MSD versus time mΔt of these sample trajectories in the range of m = 2 through 10. Finally, we simulated one-dimensional diffusion trajectories of a stepper changing randomly between two different diffusion coefficients on timescales faster than Δt. We used two different step sizes as the only two parameters to scale the trajectories. The two step sizes were chosen such that their resultant diffusion coefficients matched the theoretical limits for helical and non-helical diffusion of PCNA along DNA. Subsequently, we used a probability f_hel for the stepper to use the step size associated with helical diffusion (and a probability (1 − f_hel) to use the step size corresponding to non-helical diffusion). f_hel was varied from 0 (100% maximal non-helical diffusion) to 1 (100% maximal helical diffusion). The mean diffusion coefficient from 100 of these 100-step trajectories was observed to vary linearly with f_hel.

RESULTS

Preparation of Active, Fluorescently Labeled PCNA

To visualize the movement of PCNA along DNA, a cysteine-reactive organic dye (AlexaFluor 555-maleimide) was used to fluorescently label His-tagged PCNA at one of its native cysteines. Human PCNA monomers have six cysteine residues of which only two, C27 and C62, are solvent exposed (PD BID: 1AXC) (4). Their positions are in loops distant from the DNA-interaction surface, making it unlikely that labeling would interfere with protein movement along DNA. Spectrophotometry performed after labeling revealed the presence of 0.7 ± 0.3 AlexaFluor 555 per PCNA trimer (see “Experimental Procedures”). To confirm that labeling did not inhibit PCNA function, we performed a primer extension assay using X. laevis egg extracts. A high speed supernatant of Xenopus egg cytoplasm supports PCNA-dependent replication of single-stranded DNA (33). Upon depletion of the endogenous X. laevis PCNA to <0.25% (supplemental Fig. S1A), primer extension on M13 single-stranded DNA was reduced ∼30-fold. Supplementing the depleted extracts with mock-labeled or AlexaFluor 555-labeled PCNA restored synthesis to 40% of the level seen in mock depleted extract (supplemental Fig. S1, B and C). This result shows that AlexaFluor 555-PCNA is able to support processive DNA synthesis just as actively as unmodified PCNA.

Loading and Visualizing Single PCNA Molecules

To track fluorescently labeled PCNA on DNA, we stretched and immobilized λ phage DNA on the glass surface of a microfluidic flow cell. To this end, we functionalized both ends of linearized λ DNA with biotin to allow binding to a streptavidin-coated surface. Introducing the biotinylated λ DNA into the flow cell at high flow rates caused the DNA to bind to the surface via streptavidin in a stretched state, with a length corresponding to ∼70% of its contour length. To minimize nonspecific interactions between the surface and protein or DNA, the glass was chemically functionalized with high molecular weight, biotinylated poly(ethylene glycol) (PEG) on top of which the streptavidin was deposited (30).

PCNA was loaded onto the stretched λ DNA in the flow cell. PCNA requires RFC and ATP for loading around DNA in the absence of DNA ends (6–8, 34). We reduced the concentrations of both RFC and PCNA in the loading reaction to limit the number of PCNA trimers loaded per λ DNA to less than one. After loading is complete, the RFC clamp loader releases from the DNA-bound clamp (35–37). However, to ensure that the molecules visualized were PCNA alone and not PCNA bound by the clamp loader, we washed the flow cell with 0.5 m potassium glutamate buffer to remove any residual RFC complexes or incompletely loaded PCNA (8). Furthermore, omission of ATP in the washing and imaging steps prevents residual RFC from binding to DNA or PCNA (36). Following these stringent washing steps, individual fluorescent complexes could be observed moving along the DNA for several hours. When ATP or RFC was omitted from the loading reaction, no sliding events were observed (data not shown). Taken together, these observations suggest successful loading and observation of individual fluorescently labeled PCNA complexes on DNA.

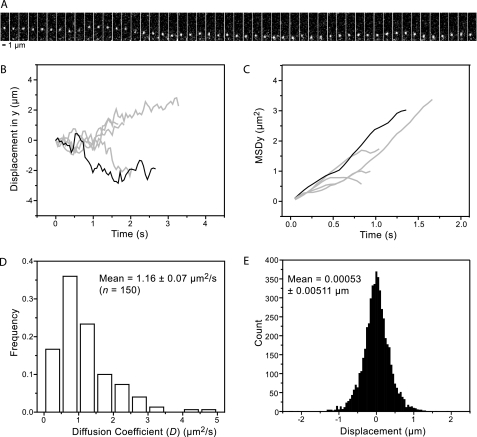
Once PCNA was loaded onto the stretched λ DNA, it was visualized using wide-field fluorescence microscopy. The fluorescence of individual, labeled PCNA molecules was imaged as a function of time with a charge-coupled device camera. Fig. 1A shows a representative time series of images of a single molecule of PCNA moving along λ DNA. The position of the clamp on the DNA through time was determined using particle-tracking algorithms (see “Experimental Procedures”). Fitting every diffraction-limited, fluorescence image with a two-dimensional Gaussian function determined the position of the protein. The precision of position determination is determined by the total amount of signal collected from a single molecule and can be much better than the resolution of the microscope (“Experimental Procedures”). This single-molecule analysis method was used previously to observe nanometer-scale motion of individual molecular motors (38). Fig. 1B shows the position of the molecule from Fig. 1A as a function of time, as determined from the fitting of the single-molecule images (black line). The gray lines depict the trajectories of additional single-molecule sliding events.

FIGURE 1.

Individual PCNA molecules diffusing on doubly tethered λ DNA. A, kymograph of a 50-step trajectory imaged at 19 Hz. B, relative protein position along the DNA axis (y) versus time. C, mean square protein displacement in y (MSDy) versus time. D, distribution of the diffusion coefficient observed from 150 trajectories of AlexaFluor 555-PCNA sliding along DNA in 150 mm potassium glutamate sliding buffer. The mean of this distribution is 1.16 ± 0.07 μm²/s (S.E.). E, distribution of displacements between subsequent frames (Δt = 52 ms) from trajectories of AlexaFluor 555-PCNA sliding in 150 mm potassium glutamate sliding buffer; n = 5037.

PCNA Moves along DNA in a Diffusive Fashion

Our single-molecule trajectories (Fig. 1, A and B) show that the PCNA moves in both directions along the DNA, suggesting a random walk along the duplex. For diffusive motion, the distance traveled is proportional to the square root of time (39). When describing the distance traveled as the MSD, a linear dependence on time t is obtained, with the diffusion coefficient D in the proportionality constant: MSD = 2Dt. The linear dependence of the MSD on time for the observed protein motion confirms its diffusive nature (Fig. 1C). The diffusion coefficient D can be obtained by fitting the slope of the MSD versus t curve (see “Experimental Procedures”). Fig. 1D shows the distribution of diffusion coefficients as obtained for 150 trajectories in the presence of 150 mm potassium glutamate.

This distribution has an arithmetic mean of 1.16 ± 0.07 μm²/s (all errors in diffusion coefficients are given as standard errors of the mean (S.E.)) and a standard deviation of 0.79 μm²/s. It is important to note that this large standard deviation does not reflect experimental errors, but describes the width of the measured distribution of diffusion coefficients. Similarly wide distributions in the diffusion coefficient have been observed in previous studies of protein sliding (17–23). The distribution of displacements between subsequent frames (Δt = 52 ms) is visualized in Fig. 1E. The mean of the distribution (0.53 ± 5 nm) is very close to zero, indicating the absence of a directional bias in the protein motion. Finally, given that our DNA is stretched an average to 70.3% of contour length, we can convert the mean diffusion coefficient into base pairs using the conversion factor (10.5 bp/(3.4 nm of B form DNA × 0.703 extension factor))² to obtain D = (2.24 ± 0.13) × 10⁷ bp²/s.

To exclude the possibility that the observed diffusion coefficients are overestimated by intrinsic motions of the DNA, we characterized the apparent diffusion of a fluorescent particle immobilized on the DNA. To this end, we used a doubly biotinylated λ-DNA construct bound with a QDot at roughly one-third of the DNA length from the terminus (site 33779 of GenBank^TM 9626243, supplemental Methods). The measured apparent diffusion coefficients of these DNA-coupled particles are below 0.015 μm²/s under the same conditions as those used for the PCNA imaging (supplemental Fig. S2), confirming that DNA motions do not significantly alter the measured diffusion coefficients of the PCNA.

To exclude the possibility that the observed diffusion coefficients are underestimated due to interactions of PCNA with the coverslip surface, we characterized diffusion on surface-to-bead tethered DNA. Here, one end of the DNA is raised 0.5 μm off of the coverslip surface. The measured diffusion coefficients from such sliding events are comparable to those obtained from DNA tethered on each end to the surface, confirming that the proximity to the surface does not significantly change the apparent diffusion coefficient (see supplemental text and supplemental Figs. S4 and S5).

PCNA Slides along the DNA while Maintaining Electrostatic Contact

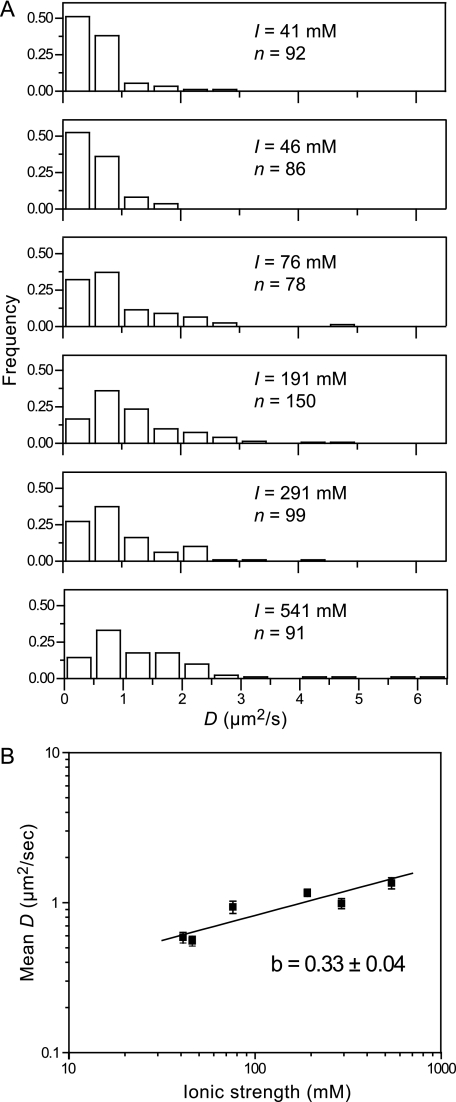
The diffusive motion of a protein along DNA can be explained by two different mechanisms: sliding or hopping (40). A sliding protein maintains continuous electrostatic contact with the DNA duplex as it diffuses, whereas a hopping protein translocates by transiently “hopping” off of the DNA, diffusing in solution, and then rebinding the DNA duplex. The closed topological shape of PCNA around DNA dictates that complete dissociations would have to be mediated by ring opening. Nevertheless, the difference between the inner diameter of the PCNA ring (3.4 nm), and the diameter of the duplex DNA (2.1 nm), suggests that the charges on both the protein and DNA surfaces could be screened by counter ions to allow effective disruption of electrostatic interactions, as envisioned in the hopping model. In the hopping model, a higher salt concentration will lower the binding affinity and will increase the fraction of the time the protein is not electrostatically interacting with DNA. As a result, the protein will be able to diffuse for longer times before rebinding, leading to an effective increase of the measured diffusion constant. In the sliding mode, however, electrostatic interactions are maintained, and the diffusion constant is independent of the ionic strength (Fig. 2B). This criterion has been used to distinguish between hopping and sliding mechanisms for a number of DNA-binding proteins (17, 19, 20, 22, 23). In particular, one protein shown to hop was the processivity factor UL42 from herpes simplex virus. UL42 is structurally homologous to PCNA but binds DNA as a monomer, facilitating transient dissociation from the DNA (41, 42). The diffusion coefficient of UL42 movement along DNA was shown to change by a factor of 4 upon increasing the ionic strength from 20 mm to 110 mm, underscoring the sensitivity of the diffusion kinetics of a hopping protein to ionic strength. We determined the diffusion coefficient of PCNA along DNA over a 13-fold change in ionic strength, from 41 mm to 541 mm (Fig. 2, A and B). We observe the diffusion coefficient to change only by 2.2-fold over a 13-fold change in ionic strength.

FIGURE 2.

Effect of ionic strength on the diffusion coefficient of PCNA. A, distributions of the observed diffusion coefficients for PCNA at ionic strengths of 41 mm (n = 92), 46 mm (n = 86), 76 mm (n = 78), 191 mm (n = 150), 291 mm (n = 99), and 541 mm (n = 91). B, the observed diffusion coefficients of PCNA along DNA versus ionic strength (mean ± S.E.) in log-log representation. The slope of the linear fit equals 0.33 ± 0.04 and represents the number of charge-charge interactions disrupted by increasing salt concentration.

A quantitative estimate of the number of electrostatic interactions that are disrupted by increasing salt concentration can be obtained by evaluating the relation between ionic strength and the microscopic equilibrium dissociation constant (40). Assuming that an increase in the time spent away from the DNA results in a proportionally higher diffusion coefficient, we used our experimentally obtained relation between ionic strength and diffusion coefficient to determine the number of screened charge-charge interactions. Analogous to the work of Berg (40), we recast our data as the logarithm of the diffusion coefficient versus the logarithm of the ionic strength (Fig. 2B). The slope of a line fit through these data provides an estimate of the number of screened charges. With a slope of 0.33 ± 0.04 our data suggest that only a fraction of a single charge-charge interaction is screened over this wide range of ionic strength. Our observation of only a very weak relation between ionic strength and diffusion coefficient suggests that PCNA maintains electrostatic contact with the DNA while moving.

Theoretical Estimates of Diffusion Coefficients

With evidence that PCNA slides along the DNA while maintaining electrostatic contact with the duplex, we set out to investigate the mechanistic details of this motion. Two scenarios can be envisioned that describe the sliding: 1) the protein tracks the helical pitch of the DNA, like a nut on a screw, resulting in a full rotation around the duplex every 10.5 bp, or 2) the protein moves along the DNA decoupled from the helical pitch, like a washer on a screw. For each of the scenarios, the maximum diffusion coefficient is described by the Einstein relation for Brownian motion D = k_BT/ξ, with ξ the frictional coefficient representing the frictional coupling between the protein and solution, k_B the Boltzmann constant, and T the absolute temperature (298 K in our experiments).

For purely translational, non-helical movement, the frictional coefficient ξ can be approximated (assuming the protein is a sphere) by 6πη_waterR, resulting in,

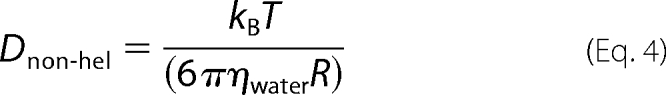with R representing the radius of PCNA (R = 4.0 nm (3)) and η_water is the viscosity of aqueous buffer (η_water = 10⁻³ Pa·s at room temperature). This description yields a maximum diffusion coefficient of 54 μm²/s, or 47-fold higher than our experimentally observed value.

However, if the protein rotationally tracks the helix while moving along the DNA, we must also consider the rotational drag. For a periodic pitch of one turn per 10.5 bp, Schurr (43) derived the rotational friction coefficient acting on the protein as follows.

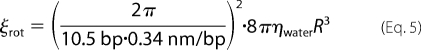Introducing both the translational and rotational frictional coefficients to the Einstein relation yields D_hel = k_BT/(ξ_trans + ξ_rot), resulting in a diffusion coefficient of 0.80 μm²/s as a theoretical upper limit for PCNA. This value is 68-fold slower than that of the protein diffusing along the DNA without tracking the helix, demonstrating that the diffusional properties of a protein tracking the DNA helix are almost entirely dominated by rotational drag. Note that a recent study of clamp sliding showed no significant difference between the diffusion coefficient as calculated using the spherical approximation for both the non-helical and helical diffusion coefficient and the diffusion coefficient calculated using the frictional drag term solved numerically for the molecular structure of the clamp (44). Our experimentally determined value for the diffusion coefficient, 1.16 ± 0.07 μm²/s (at 150 mm potassium glutamate) is very close to that predicted for a helical sliding model, suggesting that PCNA rotates around the DNA while moving.

PCNA Tracks the Helical Pitch When Sliding

To confirm that PCNA tracks the helix as it moves along DNA, we used low and high molecular weight viscogens (LMWV and HMWV, respectively) to differentially affect the rotational and translational components of diffusion. An LMWV, such as glycerol, slows both rotational and translational diffusion coefficients in a manner that is inversely proportional to the viscosity η. In contrast, HMWVs such as high molecular weight PEG, selectively affect translational diffusion (45, 46). In essence, the large size of the HMWV creates exclusion volumes that cause the viscosity for long range motion to be larger than for short range motion. Because rotational motion takes place on a shorter length scale than translational motion, rotation is less affected by the presence of the HMWV than translation. Thus, if a protein tracks the helix, with rotation being the dominant contributor to frictional drag, HMWV will change its diffusion coefficient by a factor less than η_HMWV/η_water. Conversely, if the protein does not track the helix and its motion is mainly determined by translational drag, the diffusion coefficient will decrease by η_HMWV/η_water-fold.

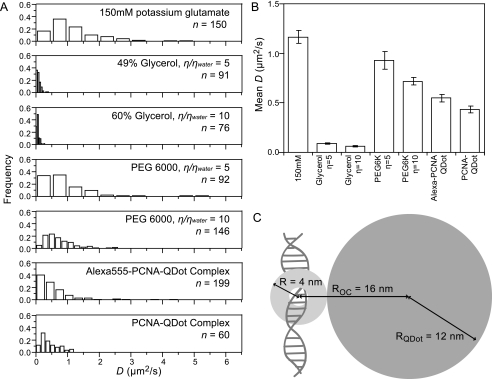
We showed that increasing the viscosity of the buffer solution by 5- and 10-fold with the LMWV glycerol significantly slowed down the diffusion coefficient of PCNA. We found that the apparent diffusion coefficient of PCNA decreased from 1.16 ± 0.07 μm²/s to 0.088 ± 0.08 μm²/s (13-fold decrease) for the 5*η_water buffer and 0.062 ± 0.005 μm²/s (19-fold decrease) for the 10*η_water, buffer (Fig. 3, A and B). Diffusion is slowed down more than expected, but the high concentration of glycerol required to achieve these viscosities, 49 and 60%, respectively (47), may affect the solvation of the DNA and/or PCNA. However, when we use the HMWV PEG6000 to change the viscosity by 5- or 10-fold, the diffusion coefficients remain almost constant. The mean diffusion coefficient decreases from 1.16 ± 0.07 μm²/s to 0.93 ± 0.09 μm²/s (1.2-fold decrease) in the 5*η_water PEG6000 solution and to 0.72 ± 0.04 μm²/s (1.6-fold decrease) in the 10*η_water PEG6000 solution (Fig. 3, A and B). The differential sensitivity of the diffusion coefficient to the molecular weight of the viscogens confirms the conclusion that PCNA tracks the helical pitch of DNA while moving.

FIGURE 3.

Effect of viscogens and geometry on the diffusion coefficient of PCNA. A, distributions of observed diffusion coefficients for conditions as noted. B, mean ± S.E. of diffusion coefficients for conditions as noted. C, scale drawing of the PCNA·QDot complex.

Increasing the Radius of PCNA Reveals Non-helical Movement

To further confirm the helical sliding of PCNA along DNA, we measured the diffusion coefficient of individual PCNA trimers carrying a large cargo. By attaching a large object to the PCNA, we increased its molecular radius and as a result, the frictional drag. Comparison of Equations 4 and 5 reveals that translational drag scales linearly with the radius of the moving object, whereas the rotational drag scales with the radius cubed. Consequently, a helically sliding protein should slow down more significantly upon increasing its radius than if it were diffusing in a non-helical fashion.

To increase the dimensions of PCNA, we functionalized 605 nm QDots with anti-histidine tag mouse monoclonal antibody and bound it to the histidine-tagged AlexaFluor 555-PCNA that had been preloaded onto DNA. Using the fluorescence of the QDot for imaging and tracking, we found that PCNA·QDot complexes had a mean diffusion coefficient of 0.55 ± 0.04 μm²/s (Fig. 3, A and B). We also bound the QDot to mock-labeled PCNA and observed a mean diffusion coefficient of 0.43 ± 0.04 μm²/s providing further confirmation that labeling with AlexaFluor 555-maleimide does not affect the mobility of the protein.

With an estimate of the hydrodynamic radius of the antibody-functionalized QDot (12 nm (22)), we can calculate the expected decrease in diffusion coefficient for the helically sliding PCNA bound to a QDot. Because the PCNA·QDot complex has a center of mass that is no longer positioned on the axis of the DNA (Fig. 3C), Equation 5 is no longer valid. For such a geometry, the rotational friction coefficient is derived, as in Ref. 48, as the sum of the rotational friction coefficients of the symmetric PCNA ring and the off-axis QDot,

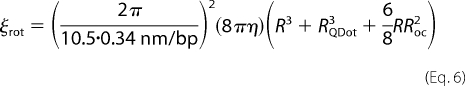R_QDot is the radius of the QDot, 12 nm, and R_OC is the distance from the center of mass of the QDot to the axis of the DNA, 16 nm. With these dimensions and the assumption that the translational friction is much smaller than the rotational one, we derive the expected diffusion coefficient for the helically tracking model to be 0.013 μm²/s, or 62 times slower than for PCNA alone. However, our experimentally measured values of 1.16 ± 0.07 μm²/s for PCNA alone and 0.55 ± 0.04 μm²/s for the PCNA·QDot complex show only a 2.1-fold reduction (Fig. 3, A and B).

The surprisingly small, 2.1-fold reduction in diffusion coefficient of PCNA upon binding of a large QDot is more consistent with a non-helical form of diffusion, where the diffusion coefficient is predominantly determined by the translational drag. To obtain an expression for the diffusion coefficient for a non-helically diffusing complex, one can simply add the radius of the QDot to the radius of the protein in the term describing the translational drag (Fig. 3B),

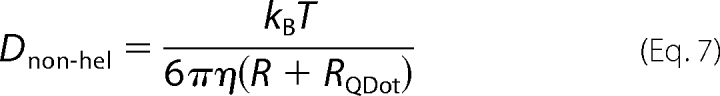Evaluating this expression, we find that D_non-hel = 13 μm²/s for a PCNA·QDot complex, a 4-fold decrease relative to the non-helical diffusion limit for PCNA alone (54 μm²/s). This 4-fold decrease is remarkably consistent with the experimentally observed reduction (from 1.16 ± 0.07 μm²/s to 0.55 ± 0.04 μm²/s (Fig. 3, A and B)). Thus, in apparent contradiction with our results described above, the observed dependence of the diffusion coefficients on size suggests that PCNA moves without tracking the helix.

Simulations of PCNA Alternating between Two Modes of Diffusion

Taken together, our HMWV experiments suggest a helical sliding mechanism for PCNA, whereas the coupling to a QDot seems to indicate a non-helical mode of diffusion. All our experimental observations can be explained by a model in which the protein uses both modes. If the clamp spends most of its time helically sliding, interrupted by short periods of the much faster non-helical, translational movement, we expect the diffusion coefficient to be largely insensitive to the presence of HMWV (which affects only the infrequently used non-helical motion). On the other hand, increasing the protein radius by coupling to a QDot will strongly slow down helical sliding. However, the ability of the protein to rapidly diffuse during its short excursions to the non-helical sliding state renders it only moderately sensitive to an increase in effective radius.

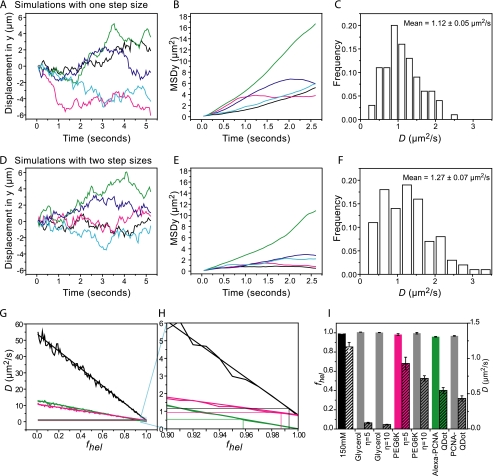
To quantitatively describe this scenario and rationalize our data, we simulated two types of random walks. First, we simulated a regular random walk of a particle along DNA by choosing step sizes out of a normal distribution centered around zero with a width normalized to result in a diffusion coefficient equal to the observed value in 150 mm potassium glutamate data (one-speed stepper). Examples of trajectories, their MSD versus t plots, and the distribution in diffusion coefficients from 100 such trajectories are shown in Fig. 4 (A–C). Next, we simulated the random walk of a protein that switches between two diffusional modes (two-speed stepper), corresponding to helical and non-helical diffusion. To do this, we chose steps from two different normal distributions, one scaled to match the theoretical limit for helical diffusion of PCNA along DNA and the second normalized to match non-helical diffusion. Furthermore, we assumed that the particle switches between these diffusion modes randomly and on time scales 100 times faster than the experimental imaging rate. We introduce this assumption to the simulations by averaging 100 simulated steps for a single step shown in the trajectory (see “Experimental Procedures” and supplemental Fig. S3). Finally, we used a probability f_hel for the stepper to use the step size associated with helical diffusion and the corresponding probability (1 − f_hel) to use the step size corresponding to non-helical diffusion. The value of f_hel was varied from 0 (100% non-helical diffusion) to 1 (100% helical diffusion). Sample trajectories of a two-speed stepper with f_hel = 0.99, their MSD versus t plots, and the distributions from 100 such trajectories are shown in Fig. 4 (D–F). As expected, we find that, upon varying the fraction of time that the molecule spends diffusing helically, f_hel, the simulated apparent diffusion coefficient D_app changes linearly (see Fig. 4G). We can summarize this linear relationship as follows,

and then solving for f_hel, we obtain Equation 9.

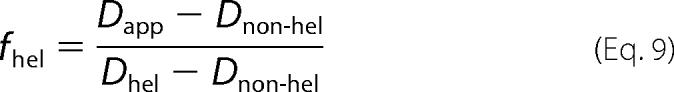FIGURE 4.

Simulating movement of PCNA along DNA with two different diffusion modes. A, sample 100-step trajectories of simulated random walks at 19 Hz with a single step size. Each step is the average of 100 substeps. Substeps normally distributed around zero are scaled to yield a mean diffusion coefficient matching the observed mean diffusion coefficient in 150 mm potassium glutamate buffer. B, MSDy versus time plots for trajectories in A. C, distribution of diffusion coefficients from 100 trajectories as in A. D, sample 100-step trajectories of simulated random walks at 19 Hz with two step sizes. Each step is the average of 100 substeps with f_hel = 99%. Substeps are scaled to match the calculated maximum diffusion coefficient for helical or non-helical models. E, MSDy versus time curves for trajectories in D. F, distribution of diffusion coefficients from 100 trajectories as in D. G, calculated (smooth line) and simulated mean (jagged line) diffusion coefficients for two step size model as f_hel (the fraction of time spent in the helical mode) is varied. Horizontal lines denote experimentally observed diffusion coefficients and vertical lines denote the f_hel value at which observed lines intersect the calculated lines. Black: step sizes scaled to D_non-hel and D_hel for diffusion of PCNA in buffer of viscosity η/η_water = 1 or experimentally observed diffusion coefficient of PCNA in 150 mm potassium buffer. Magenta: step sizes scaled to PCNA diffusion in buffer with HMW viscogen η/η_water = 5 or experimentally observed diffusion coefficient of PCNA in 150 mm potassium buffer with PEG 6000, η/η_water = 5. Green: step sizes scaled to diffusion of PCNA with QDot attached or experimentally observed diffusion coefficient of PCNA·QDot in 150 mm potassium buffer. H, 10-fold magnification of the selected region of the plot (shown in highlighted blue) in G. I, f_hel is calculated for conditions as noted in solid bars (left axis). Measured diffusion coefficients are indicated as dashed bars (right axis). Even though the different conditions give rise to very different values of mean diffusion coefficient, all the diffusion coefficients can be accurately described by values of f_hel that all fall in a very narrow range.

When we calculate f_hel using our experimentally observed diffusion coefficients and the theoretically calculated maxima for helical and non-helical diffusion mechanisms, we find that the fraction of time PCNA spends tracking the helix does not vary significantly between the different experimental conditions (Fig. 4, G–I). Comparing the experimental data with the theoretically expected values for helical and non-helical diffusion suggests that PCNA slides by tracking the helix 98 ± 1% of the time. During the rest of the time, it uses the much faster non-helical sliding mode. As described above, a scenario in which PCNA exclusively uses a helical or a non-helical mode of diffusion is inconsistent with our observations. Remarkably, our simple two-state model is consistent with all of our experimental conditions. A switching between the two modes with a value of 98 ± 1% for f_hel explains quantitatively why the diffusion coefficient changes only 1.2-fold in the presence of HMWV PEG6000, 5*η_water and why the diffusion coefficient only changes 2.1-fold when a QDot is bound to PCNA.

DISCUSSION

Using single-molecule techniques, we visualized the movement of human PCNA along double-stranded DNA. Analysis of the diffusive behavior of PCNA under various conditions allows us to describe the mechanisms of movement. We show that PCNA moves with a diffusion coefficient near or above the theoretical maximum for a helically tracking protein. In contrast, a recent fluorescence correlation spectroscopy study of the sliding behavior of the E. coli clamp β found that the diffusion coefficient is two orders of magnitude slower than predicted for the helically tracking model (44). Next, we demonstrated that the diffusion coefficient is only moderately dependent on the ionic strength, implying that PCNA maintains electrostatic contact with the DNA as it moves. Furthermore, we found that the diffusion coefficient does not change linearly with viscosity when a HMWV is used. This observation suggests that PCNA tracks the helical pitch of the DNA. Finally, we measured diffusion of a complex of PCNA with a QDot and found that the diffusion coefficient of this larger complex is much higher than expected for a helically tracking complex. To explain this inconsistency, we propose a model in which PCNA alternates between two modes of diffusion. One mode corresponds to helical sliding, in which PCNA undergoes a full rotation every 10.5 bp. In this mode, the viscous drag, and thus the diffusion coefficient of motion, is dominated by the rotational friction between protein and solvent. The second mode of diffusion corresponds to a state that allows for very fast non-helical tracking along the DNA, much faster than the rotational drag would allow.

Effect of Translocation Activation Barriers

A quantitative analysis of our data and comparison with simulations suggested that PCNA spends 97–99% of its time helically sliding along DNA and the remaining 1–3% in the non-helical translocation mode. It is important to realize that this partitioning ratio is based on the theoretical upper limits of the diffusion coefficient for each of the two translocation modes. These upper limits only take into account contributions from viscous hydrodynamic drag and assume that no other energy barriers exist to move from one position to another. In reality, the breaking and reforming of interactions between protein and DNA upon movement along the duplex will result in additional kinetic barriers and will lower the diffusion coefficient. The presence of an activation energy for movement and the resultant decrease of the diffusion coefficients for one or both modes of movement may change the partitioning between the helical and non-helical modes.

Previous single-molecule experiments have estimated values of the heights of these translocation barriers by comparing experimentally observed diffusion coefficients with those determined theoretically. Analysis of the diffusional movement of a transcription factor (19) and a DNA-repair protein (20) along the DNA resulted in an estimate of a 1–2 k_BT barrier for a single-base pair step. Assuming a mean activation free energy of 2 k_BT for each step, we can calculate the decrease of the theoretical diffusion coefficients and the resultant expected change in the partitioning between the two translocation modes. The Arrhenius relation (ΔG^‡/k_BT = ln(k_lim/k) can be used to relate the free energy of activation, ΔG^‡, with the ratio between the protein's random-walk stepping rate in the absence of kinetic barriers, k_lim, and presence thereof, k (20). Using ΔG^‡ = 2 k_BT results in a slowing down of the single-base pair stepping rate by a factor of e², or 7.39. The diffusion equation D = 〈x²〉/2t, with x the step size and t the time elapsed for every single step, shows that the diffusion coefficient D scales linearly with changes in the stepping rate. Taken together, introducing a translocation activation energy of 2 k_BT results in a decrease of the diffusion coefficient by a factor of 7.39. If the diffusion coefficients of both translocation modes are equally affected, the partitioning ratio between non-helical and helical sliding will remain unchanged.

A more likely scenario is one in which the activation barriers are not equal in both modes. For example, the helically tracking mode may require more DNA-protein contacts and thus have a 2-fold higher activation barrier of 4 k_BT while the non-tracking mode would have an activation barrier of 2 k_BT. In this particular example, the ratio would shift closer to 16%/84%. In summary, our results show a partitioning ratio between the two modes of diffusion of ∼2%/∼ 98%, in which the ∼2% of the time spent in the non-helical translocation mode is a lower limit based on the assumption that the diffusive process is entirely dominated by viscous drag.

Molecular Mechanisms of Translocation

Even though our experiments indicate the existence of helical and non-helical diffusion modes of PCNA along DNA, we can only speculate on the underlying molecular mechanisms. Previous molecular dynamics simulations of the interaction between PCNA and double-stranded DNA suggest an interpretation of our observations. The simulations revealed that the PCNA clamp encircles double-stranded DNA at a pronounced tilt of 20° with respect to the DNA axis (12). This tilt facilitates the formation of a large number of electrostatic interactions between the DNA phosphodiester backbone and the positively charged arginine and lysine residues lining the PCNA inner surface. The authors observed that contact breaking and formation along the inner surface of PCNA is very dynamic with competition between different protein residues for the same phosphodiester group.

Although the timescale of the molecular dynamics simulations was too short to directly observe translocation, the results suggest that the clamp is not stably associated with a single point on the DNA. Although tilted with respect to the DNA, the large number of protein-DNA interactions along the two strands of the minor groove suggests a picture in which the clamp follows the helical pitch of the DNA while moving. The dynamic nature of these interactions may allow a large enough number of these DNA-protein interactions to be broken transiently to support a state in which the PCNA clamp is more perpendicular to the DNA. During these brief moments, the PCNA·DNA interactions may not be extensive enough to force the clamp to track helically along the phosphodiester backbone, allowing it to move rapidly in a non-helical fashion.

The presence of two translocation modes may assist PCNA in carrying out its multitude of biological roles. The helical sliding mode could be used while PCNA is clamping a polymerase to the DNA-primer template. Because the polymerase needs to maintain a fixed position relative to the phosphodiester backbone near the 3′ terminus of the primer, a fixed orientation of the PCNA with respect to the helical pitch may improve the overall stability of the holoenzyme. The other, non-helical diffusion mode may be used intermittently to speed up diffusion to the next primer template. Moreover, the non-helical diffusion mode allows the clamp to change its position relative to the phosphodiester backbone charges. This rotational freedom may be necessary when the clamp binds an enzyme partner whose relative orientation with respect to the DNA needs to be optimal to commence enzymatic activity. For example, the activity of PCNA-bound Fen-1 or DNA ligase 1 at the junction between Okazaki fragments may only take place when the enzyme is properly juxtaposed with respect to the nick. Given the 3-fold rotational symmetry of PCNA and its sites of interaction with these protein partners, a mechanism must exist to allow the clamp to rotate freely around the DNA.