Analysis of the effects of ultrafine particulate matter while accounting for human exposure

Abstract

Particulate matter (PM) has been associated with mortality in several epidemiological studies. The US EPA currently regulates PM₁₀ and PM_2.5 (mass concentration of particles with diameter less than 10 µm and 2.5 µm, respectively), but it is not clear which size of particles are most responsible for adverse heath outcomes. A current hypothesis is that ultra-fine particles with diameter less than 0.1µm are particularly harmful because their small size allows them to deeply penetrate the lungs. This paper investigates the association between exposure to particles of varying diameter and daily mortality. We propose a new dynamic factor analysis model to relate the ambient concentrations of several sizes of particles with diameters ranging from 0.01 to 0.40 µm with mortality. We introduce a Bayesian model that converts ambient concentrations into simulated personal exposure using the EPA’s Stochastic Human Exposure and Dose Simulator, and relates simulated exposure with mortality. Using new data from Fresno, CA, we find that the four-day lag of particles with diameter between 0.02µm and 0.08µm is associated with mortality. This is consistent with the small particles hypothesis.

1 Introduction

Several epidemiological studies have shown an association between air pollution and adverse health outcomes (Dockerty et al., 1992; Schwartz, 1994; Pope et al., 1995; American Thoracic Society and Bascom 1996a, 1996b). Most of the recent work in this area has focused on PM₁₀ and PM_2.5, the mass concentrations of particles less than 10µm and 2.5µm, respectively. However, it is not clear which sizes of particles are most responsible for adverse heath outcomes. A current hypothesis is that ultrafine particles with diameter less than 0.1µm are particularly harmful because their small size allows them to deeply penetrate the lungs. The literature on ultrafine particles is relatively sparse compared to the literature on PM₂₅ and PM₁₀. Pekkanen et al. (2002) demonstrated an association between ultrafine particle levels and cardiovascular symptoms, while de Hartog et al. (2003) Timonen et al. (2004) failed to find a relationships between ultrafine concentration and cardiorespiratory symptoms. Wichmann et al. (2000) and Stölzel et al. (2006) showed that ambient ultrafine concentration levels were associated with daily mortality in Europe.

This paper uses a new data set to investigate the association between different sizes of particulate matter and mortality. Pollution data is measured at a single monitoring station in downtown Fresno, CA. The ambient concentrations of PM₁₀, PM_2.5, and several sizes of particles with diameters ranging from 0.01 to 0.40 µm are recorded hourly for 2001 and 2002. The health outcome is non-accidental mortality in elderly residents of Fresno, CA.

We develop a novel dynamic factor model to analyze the multivariate time series of particles with diameter less than 0.40 µm and to relate the various PM diameters with mortality. Bayesian latent factor models are common in health research (e.g., Wang and Wall, 2003; Biggeri et al., 2005; Lui et al., 2005) and in multivariate time series analysis (Aguilar et al., 1998; West and Harrison, 1997). The dynamic factor model reduces the dimension of the multivariate pollution time series to a small number of temporally-correlated latent time series factors. In our setting, the natural ordering of the diameters suggests an extension of the usual dynamic factor model that makes use of the similarity between adjacent diameters. This extension of the usual dynamic factor model borrows strength across diameters, thereby reducing variability in the latent factors. The latent factors are used as predictors of mortality. This results in a supervised factor analysis in that the factors are not only chosen to model PM data, but also to form predictive groups of diameters to be related with mortality.

A common limitation of observational studies of the effects of air pollution on human health is that ambient concentrations are used as surrogates for personal exposures, and a single value is used to represent the exposure of each individual in a geographic region. It is difficult to extrapolate a single ambient concentration to the entire population of interest because for a given ambient concentration level personal exposure can vary widely across individuals with different activity patterns. Assuming a common value of exposure holds for the entire population of individuals leads to the “ecological fallacy” (Selvin, 1958; Wakefield and Shaddick, 2005), and can result in bias.

We propose a new method for studying the association between PM and mortality while accounting for variability in personal exposure. Although direct measurements of personal exposures are not available, the population exposure distribution is estimated using the Stochastic Human Exposure and Dose Simulation model for particulate matter (SHEDS-PM), developed by Burke et al. (2001). This stochastic model uses information about human activity patterns, census data, and daily diurnal pollution cycles to estimate the daily population exposure distribution. Meshing the exposure simulator into our Bayesian framework allows us to investigate the association between personal exposure and mortality, and to compare these results to the association between mortality and ambient concentration.

Our approach extends the work of Holloman et al. (2004) who use a method similar to SHEDS-PM to compute the mean PM_2.5 exposure for a number of counties in North Carolina and relate the mean exposure to cardiovascular mortality. Our hierarchical model benefits from the full implementation of SHEDS-PM by using the actual output distributions produced by the model for daily exposure to the ambient PM level. By approximating the daily exposure distributions with normal distributions, we incorporate the SHEDS-PM exposure distributions (not just the mean value) in the model with mortality data to account for both the variability in exposures across the population each day and the uncertainty in the modeled exposures. Also, we applied the SHEDS-PM model for multiple PM diameters to investigate the joint effect of exposure to different particle sizes.

The paper proceeds as follows. Section 2 describes the Fresno data set. The dynamic latent factor model relating ambient concentrations with daily mortality is developed in Section 3. Details of SHEDS-PM are provided in Section 4, along with a model for relating SHEDS-PM output with mortality via the integrated population relative risk. Section 5 analyzes the effect of ambient concentrations on mortality and Section 6 demonstrates the effects of using simulated exposure, rather than ambient concentrations, as predictors of mortality. Section 7 concludes.

2 Description of the data

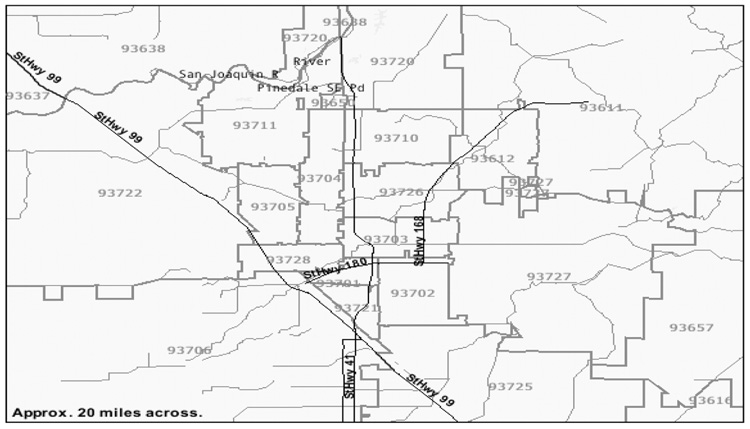
The city of Fresno is a located in central California. Its metropolitan area has approximately one million people. Particulate matter was monitored at a single monitoring station in downtown Fresno, located in zip code 93726 about 1km east of Highway 41 (Figure 1), a residential area in central Fresno. There are major highways to the east and west of the station and Fresno Yosemite International Airport is roughly two miles east of the station.

Figure 1.

Map of Fresno, CA. The monitoring station is located in zip code 93726 about 1km east of Highway 41.

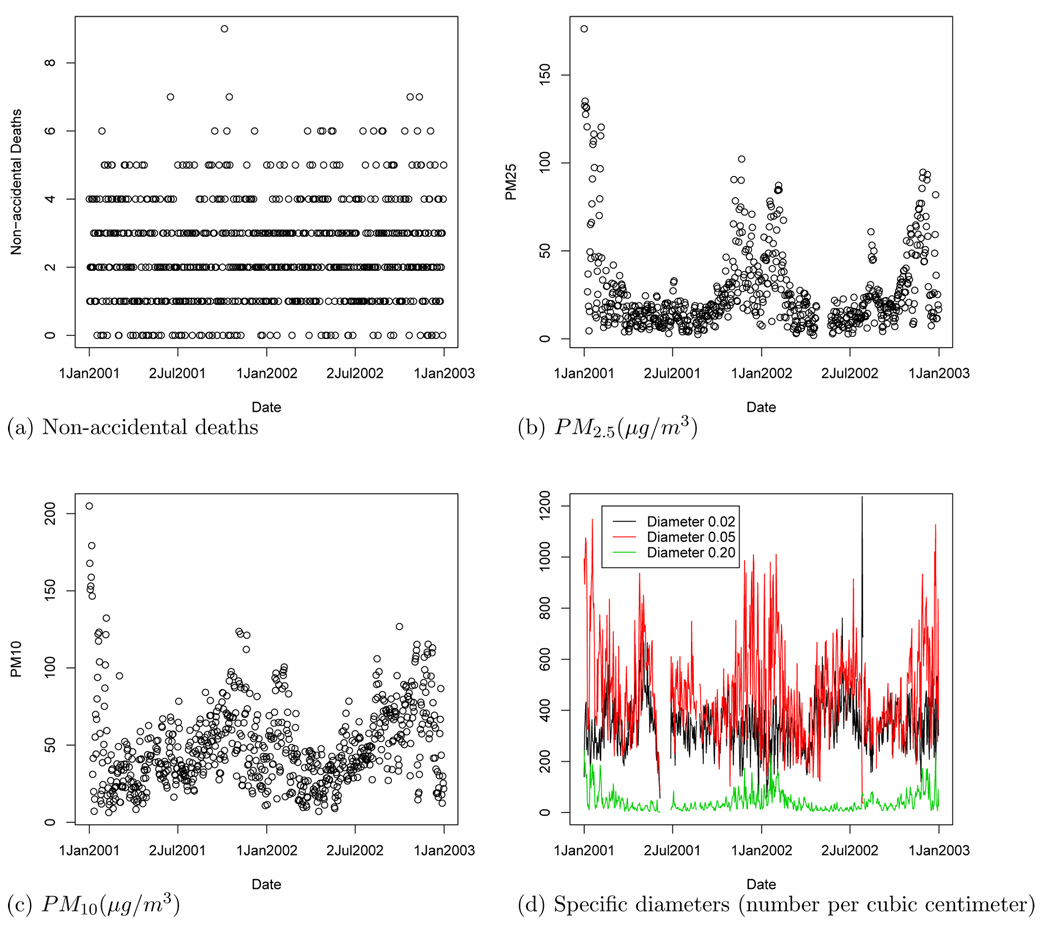
Daily non-accidental mortality counts (ICD 10^th Revision codes less than 291) for 18 zip codes in the Fresno metropolitan area (Figure 1) for 2001 and 2002 were obtained from the California Center for Health Statistics. We consider only the elderly (> 64 years old) population because the elderly are most susceptible to the effects of PM. According to the 2000 US census 9.3% of Fresno’s population is over 64 years old. Figure 2a plots the daily mortality counts (zeros indicate a day without deaths for this subpopulation).

Figure 2.

Time-series plots of the Fresno raw data.

Hourly pollution data for 2001 and 2002 were downloaded from the University of Maryland’s Supersites Integrated Relational Database System (http://supersitesdata.umn.edu). The sizes of PM we consider are PM₁₀, PM_2.5, and 17 ranges of fine PM with diameters ranging from 0.01 to 0.40 µm. For the diameters less than 0.40µm, the data are recorded as number concentration (number per cubic centimeter) rather than mass concentration. The daily average concentration for several pollutants are plotted in Figure 2. The concentrations of most PM diameters are highest in the winter, especially January, 2001. Daily carbon monoxide values were provided by the EPA. The weather covariates temperature and relative humidity are recorded hourly.

3 A model relating ambient PM with mortality

3.1 A latent factor model for ambient PM levels

In this section we propose a latent factor model for the ambient concentrations of particles with diameter less than 0.40µm. While PM_2.5, PM₁₀, and carbon monoxide are used as predictors of mortality, they are not included in the factor analysis because we would like to use the factor analysis to find combinations of diameters less than 0.40µm that are predictors of mortality after accounting for the effects of these copollutants.

Let y_dt be the observed average daily concentration for diameter d at day t, d = 1,…,D and t = 1,…,T. The vectors of observations for each diameter are standardized to have mean zero and unit variance. The dynamic Bayesian factor analysis model (Aguilar et al., 1998; West and Harrison, 1997) assumes the mean of y_dt is a linear combination of J ≤ D independent latent time series, i.e.,

$$y_{dt}={\theta }_{dt}+{ϵ}_{dt},$$ (1)

$${\theta }_{dt}={\mu }_d+{\displaystyle \sum _{j=1}^J{w}_{dj}{f}_{jt},}$$ (2)

where θ_dt is the true concentration for diameter d at time t, μ_d is the intercept for diameter d, w_dj is the loading of the j^th factor for diameter d, f_jt is the value of the j^th latent factor at time t, and ${ϵ}_{dt}~N(0,{\sigma }_d^2),$ independent across d and t.

We model the latent factors f_j = (f_j1, …, f_jT)′ as independent, stationary time series with mean zero and lag-h covariance functions ρ_j(h). In dynamic factor analysis, vague priors are typically selected for the loadings. However, in our setting the model can be improved by exploiting the natural ordering of the diameters. Let w_j = (w_1j,…,w_Dj), the vector of loadings for the j^th factor, have prior mean zero and cov(w_d1j, w_d2j) = γ_j (|d₁ − d₂|). This prior is used to borrow strength across adjacent diameters.

The induced prior covariance of two true concentrations θ_d1t and θ _d2t+h is

$$\text{Cov}({\theta }_{d_{1}t},{\theta }_{d_{2}t+h})={\displaystyle \sum _{j=1}^J{\gamma }_j(|d_1-d_2|){\rho }_j(h)}.$$ (3)

That is, the covariance between a pair of true concentrations is the sum of the products of the autocovariance functions for time and diameter of the J latent time series. At this level of generality, the factor analysis model results in a non-separable (between diameter and time) covariance function.

In the analysis of Section 5, the latent time series are taken to be independent AR(1) processes and loading vectors are taken to be independent intrinsic AR(1) processes. That is,

$$f_{jt}~N({\rho }_j{f}_{jt-1},{\tau }_j^2)\text{and}{w}_{dj}~N(w_{d-1j},{\delta }_j^2)$$ (4)

where ρ_j ∈ (−1, 1). The factors for the first time point f_j0 are given vague independent normal priors.

Restrictions are necessary to ensure that the model is well-identified. The variances ${\tau }_j^2\text{and}{\delta }_j^2$ appear in the covariance in (3) only through the product ${\tau }_j^2{\delta }_j^2$. Therefore to identify the scale we fix the conditional variances of the factors to be one, that is ${\tau }_j^2\equiv 1$ for all j. Following Aguilar and West (2000), for the first factor, we constrain the loading for the smallest diameter w₁₁ to be one. For the second factor, we set the loading for the smallest diameter w₂₁ to zero and, to make identification as strong as possible, restrict the loading for the largest diameter w_2D to be one. The third loading vector has w₃₁ = w_3D = 0 and w₃₂ = 1, and so on.

3.2 Relating the latent factors with mortality

Including all D = 17 diameters as predictors of mortality leads to substantial multicollinearity and misleading estimates. Clearly, some form of dimension reduction is needed. The factor analysis model of Section 3.1 represents the ambient concentrations as a linear combinations of the latent time series f₁, …, f_J. To circumvent multicollinearity, the latent factors are used as predictors of mortality. This results in supervised factor analysis, in that the loadings and latent factors are chosen not only to provide a reasonable fit to the observed ambient concentrations, but also to help explain the health outcome.

The number of deaths on day t, M_t, has a Poisson distribution with expected value

$${\eta }_t=\text{exp}\left({\mathbf{x}}_t\beta +{\displaystyle \sum C_j(t-l_j){\alpha }_j}\right),$$ (5)

where x_t is the vector of confounders, C_j(t−l_j) is the lag l_j ambient level of pollutant j, and β and α are the vectors of regression parameters. We include the pollutants PM_2.5, PM₁₀, carbon monoxide, and the latent factors f₁, …, f_J. Long-term trend, temperature, humidity, and an indicator of weekday are included as confounding variables in x_t. Following Dominici et al. (2002), we use a natural spline function of time to capture long-term trends in mortality. Temperature and humidity are also smoothed with natural spline functions. The effect of the number of degrees of freedom of the spline functions on the estimates of the effects of PM on mortality is investigated in Section 5.2.

In many studies of the health effects of particulate matter, the lags l_j are fixed at a particular value suggested by past experience or exploratory analysis. However, for these data several lags fit the data equally-well and the choice of lag qualitatively influences the results. To account for this uncertainty, we model the lags as random variables. Since the lags are typically chosen to be within a few days of the event (Stölzel et al., 2006; Holloman et al., 2004; Pekkanen et al., 2002; Dominici et al, 2002; Smith et al., 2000), the lag parameters l_j are given independent discrete uniform priors on the values {0,1, …, 7}.

To complete the Bayesian model, we specify priors for the hyperparameters. The variance parameters ${\sigma }_d^2\text{and}{\delta }_j^2$ are given independent InvGamma(0.01,0.01) priors (parameterized to have mean 1, variance 100) and the ρ_j are given Uniform(−1,1) priors. The intercepts μ_j and the regression parameters β and α have vague normal priors with mean zero and variance 100.

4 A model relating exposure with mortality

4.1 Simulating exposure using SHEDS-PM

A full description of the SHEDS-PM model can be found in Burke et al. (2001); a brief summary is given below. The SHEDS-PM model estimates the population distribution of exposures by simulating personal exposure for a set of I hypothetical individuals chosen to represent the study population in terms of age, gender, employment, housing type, and smoking status. Each day, the activities of the hypothetical individuals are generated by randomly selecting a diary from EPA’s Consolidated Human Activity Database (CHAD). CHAD contains personal diaries of over 22,000 individuals from exposure studies conducted around the US. The diaries describe the activity pattern of the individual throughout the day and are selected to match the hypothetical individual based on personal characteristics, housing type, season, day of the week, and average daily temperature.

SHEDS-PM considers nine microenvironments: outdoors, vehicles, residences, offices, schools, stores, restaurants, bars, and other indoor environments. The average exposure for individual i on day t, E_i(t), is the sum of the exposures accumulated in the nine microenvironments. Let C_mh(t) and T_imh(t) be the PM concentration and time spent, respectively, in microenvironment m for individual i during hour h. Then, the average daily exposure is

$$E_i(t)=\frac{1}{24}{\displaystyle \sum _{h=1}^{24}{\displaystyle \sum _{m=1}^9{E}_{imh}(t)}=}\frac{1}{24}{\displaystyle \sum _{h=1}^{24}{\displaystyle \sum _{m=1}^9{C}_{mh}(t)T_{imh}(t)}.}$$ (6)

The PM concentration for microenvironment m is assumed to be a linear function of the ambient concentration, i.e., C_mh(t) = a_m + b_mC_amb,h(t) where C_amb,h(t) is the known ambient PM level for hour h on day t. The coefficients for the residential microenvironment are modelled using a mass balance equation and have the form

$$a_{\mathit{\text{res}}}=\frac{E_{\mathit{\text{smk}}}{N}_{\mathit{\text{cig}}}+E_{\mathit{\text{cook}}}{t}_{\mathit{\text{cook}}}+E_{\mathit{\text{other}}}}{(\mathit{\text{ach}}+k)V}\text{and}{b}_{\mathit{\text{res}}}=\frac{P\times \mathit{\text{ach}}}{\mathit{\text{ach}}+k},$$ (7)

where P = penetration factor; k = deposition rate; ach = air exchange rate; E_smk = emission rate for smoking; N_cig = number cigarettes smoked; E_cook = emission rate for cooking; t_cook = time spent cooking; E_other = emission rate for other sources; and V = residential volume.

Exposure simulation via SHEDS-PM requires reliable prior information for the parameters in the mass balance equation for residential concentration and the linear equations for non-residential concentrations. The priors for several parameters for residential concentration are based on exposure studies conducted in California and are given in Table 1. The priors for the remaining parameters are taken from Burke et al. (2001). Since no data are available for non-ambient source exposure (e.g., smoking and cooking) for diameters other than PM₂₅, we only consider exposure from ambient sources.

Table 1.

Prior distributions for selected SHEDS-PM parameters. “Tri(a,b,c)” refers to the triangular density with minimum a, mode b, and maximum c.

Parameter	Category	Variability	Uncertainty dist. of μ	Uncertainty dist. of σ
Air exchange ratea	Winter	LogN(μ, σ2)	N(−0.68, 0.10)	Tri(0.55,0.65,0.75)
	Spring	LogN(μ, σ2)	N(−0.48, 0.10)	Tri(0.57,0.67,0.77)
	Summer	LogN(μ, σ2)	N(−0.05, 0.10)	Tri(0.81,0.91,1.01)
	Fall	LogN(μ, σ2)	N(−0.88, 0.10)	Tri(0.61,0.71,0.81)
Penetration	0.02µmb	N(μ, σ2))	N(0.70, 0.10)	N(0.08, 0.01)
	0.05µmb	N(μ, σ2)	N(0.65, 0.10)	N(0.08, 0.01)
	0.20µmb	N(μ, σ2)	N(0.65, 0.10)	N(0.08, 0.01)
	$P{M}_{2.5}^c$	N(μ, σ2)	N(1.00, 0.10)	N(0.08, 0.01)
Deposition	0.02µmb	N(μ, σ2)	N(2.50, 0.50)	N(0.50, 0.10)
	0.05µmb	N(μ, σ2)	N(0.80, 0.10)	N(0.20, 0.04)
	0.20µmb	N(μ, σ2)	N(0.50, 0.05)	N(0.20, 0.04)
	$P{M}_{2.5}^c$	N(μ, σ2)	N(0.27, 0.07)	N(0.10, 0.02)

The references are a=Murray and Burmaster (1995), b=Vette et al. (2001), and c=Özkaynak et al. (1996a,b).

The two-stage priors for the SHEDS-PM parameters (e.g., in Table 1) reflect both the inherent variability from person-to-person and day-to-day, and our uncertainty about the hyperparameters that control the variability distributions. To include both types of randomness in our simulation, each day we simulate the exposure of M independent populations of size I. The parameters for all individuals within the same simulated population have the same draw from the uncertainty distribution, but vary from person-to-person based on the variability distribution.

The model described above could theoretically be incorporated into a fully-Bayesian analysis. However, exploratory analysis suggests that the daily exposure distributions can be approximated by normal distributions; the level 0.05 Kolmogorov-Smirnov test of normality rejects the hypothesis that the exposure distribution follows a normal distribution for less than 1% of the simulated distributions for each of the PM diameter analyzed with SHEDS-PM in Section 6. Therefore, we assume the model

$$E_i(t)~\mathit{\text{Normal}}(m(t),v(t)),$$ (8)

Uncertainty in the exposure distribution on day t is captured by the priors for mean m(t) and variance v(t). Let {x̄₁(t),…,x̄_M(t)} and $\{s_1^2(t),\dots ,s_M^2(t)\}$ be the sample means and variances, respectively, of the M simulated exposure distributions for day t. Then m(t) is given a normal prior with mean and variance matching the sample mean and sample variance of {x̄₁(t),…,x̄_M(t)}, and v(t) is given a gamma prior with mean and variance matching the sample mean and sample variance of $\{s_1^2(t),\dots ,s_M^2(t)\}$. Combining the distributions of human activity, hourly PM levels, and priors for SHEDS-PM parameters into priors for m(t) and v(t) dramatically reduces the computational burden while still reflecting uncertainty in exposure distribution and allowing the exposure distribution to be updated by the mortality data.

4.2 Relating exposure to mortality

Each day, the exposure distribution is estimated using SHEDS-PM for PM_2.5 and several diameters of ultrafine particles suggested by the dynamic factor analysis. Let E_fi(t) be the exposure to pollutant f for individual i on day t. Since mortality is rare, the distribution of the event of individual i dying on day t can be approximated with Poisson distribution with expected value

$$\text{exp}\left(\mu +{\mathbf{x}}_t\beta +{\displaystyle \sum _{f=1}^F{E}_{fi}(t-l){\tilde{\alpha }}_f}\right),$$ (9)

where α̃₁, …, α̃_F are the regression parameters associated with the simulated exposures.

Following Richardson et al. (1987), the population average risk on day t is

$${\eta }_t=\text{exp}(\mu +{\mathbf{x}}_t\beta ){\displaystyle \prod _{f=1}^F{\displaystyle \int \text{exp}}}(E_f(t-l_f){\tilde{\alpha }}_f)p(E_f(t-l_f))d{E}_f(t-l_f),$$ (10)

where the exposure distribution on day t for pollutant f has density p(E_f(t)). Given η_t, M_t follows a Poisson(η_t) distribution, independent across t.

We assume that E_f (t) follows a normal distribution with mean m_f(t) and variance v_f(t), where

$$\begin{array}{c}{m}_t~N({\overline{m}}_f(t),{\tau }_f^2(t))\hfill \\ v_t~\mathit{\text{Gamma}}(a_f(t),b_f(t))\hfill \end{array}$$ (11)

Under the normal model for the population exposure distributions, the population average risk conditional on $({\mu }_f(t),{\tau }_f^2(t))$ can be written in closed form as

$${\eta }_t=\text{exp}\left(\mu +{\mathrm{x}}_t\beta +{\displaystyle \sum _{f=1}^F{m}_f(t-l_f){\tilde{\alpha }}_f+\frac{1}{2}{\displaystyle \sum _{f=1}^F{v}_f(t-l_f){\tilde{\alpha }}_f^2}}\right).$$ (12)

Comparing (12) with the expected number of deaths as a function of ambient pollution levels in (5) shows that the effect of ambient concentration equals the effect of personal exposure if each personal exposure equals the ambient concentration (m_f = C_f and v_f = 0) or if α̃_f = 0, i.e., the pollutant has no effect on mortality. Also, the effect of the population mean exposure m_f equals the effect of personal exposure if v_f = 0. Therefore, we expect the bias caused by using a single ambient concentration to represent the exposure of each individual in the population to be large if the variation in exposure within the population is large and the pollutant has a large effect on mortality.

When fitting these models to the Fresno data, we choose between models using the deviance information criterion (DIC) of Speigelhalter et al. (2002), defined as DIC = D̄ + P_D where D̄ is the posterior mean of the deviance, P_D = D̄ − D̂ is the effective number of parameters, and D̂ is the deviance evaluated at the the posterior mean of the parameters in the likelihood. The model’s fit is measured by D̄, while the model’s complexity is captured by P_D. Since modelling mortality is the primary focus, only the likelihood associated with mortality is used in computing DIC, and the likelihood associated with the ambient concentrations is ignored. Models with smaller DIC are preferred. All MCMC simulations are carried out in WinBUGS (http://www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml)

5 Analysis of the effect of ambient PM on mortality

This section analyzes the effect of ambient PM of various diameters on non-accidental mortality. We first use the Bayesian factor model of Section 3.1 to investigate the relationships between the fine PM diameters less than 0.4µm. In Section 5.2 we apply the full supervised factor model of Section 3 to study the effects of PM on all-non-accidental mortality and respiratory-related mortality.

5.1 Dynamic factor analysis of fine PM diameters

To understand the relationships between the fine PM diameters less than 0.4µm, we temporarily set aside the mortality data and fit the latent factor model of Section 3.1. A principal components analysis shows that the first three principal components explain 95% of the variance in the daily ambient concentrations, therefore we present results of the three- factor model.

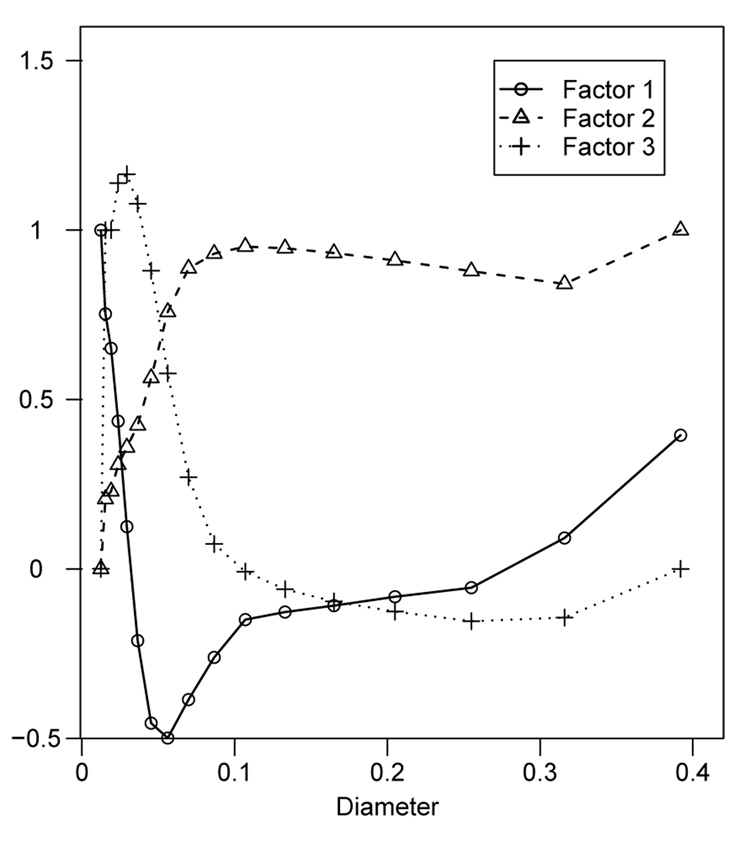
Figure 3 plots the posterior medians of the loadings. The loadings vary smoothly from one diameter to the next, in part due to the prior for the loadings which encourages borrowing strength across nearby diameters. DIC favors the model that smooths the loadings across diameter (DIC = −1030) over the model with vague independent normal priors for the loadings (DIC = −913).

Figure 3.

Posterior medians of the loadings of the dynamic factor model for the fine PM diameters.

The three factors roughly correspond to diameters less than 0.02µm (factor 1), diameters between 0.02 and 0.08µm (factor 3), and diameters greater than 0.08µm (factor 2). These results are similar to the principal components analysis, indicating the identifiability constraints described in Section 3.1 are not affecting the posteriors of the loadings.

5.2 Analysis of mortality

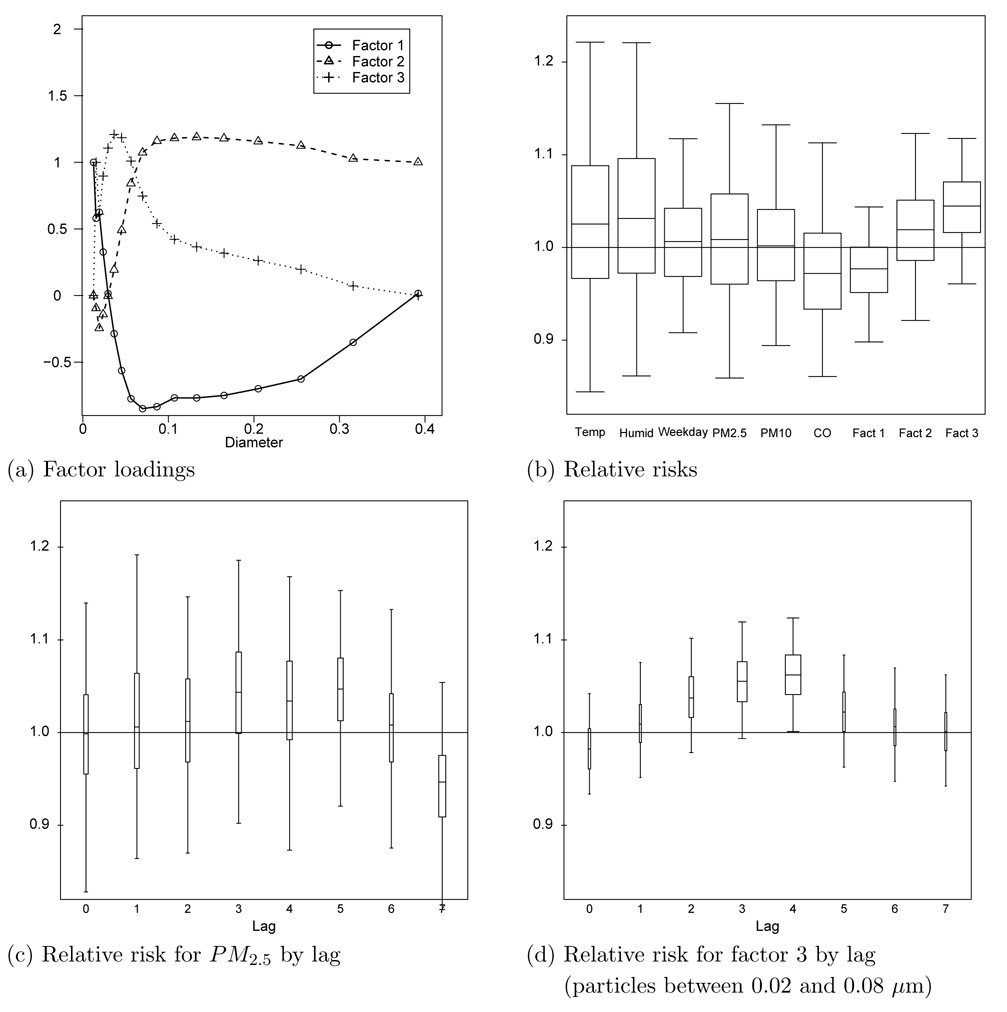
In this section, we present the results of the supervised factor analysis that makes use of both PM and mortality data. The medians of the factor loadings in Figure 4a are slightly different under this supervised factor analysis than under the PM-only analysis in Section 5.1 (Figure 3). For example, the loadings for diameters greater than 0.10µm for factor 1 are smaller than the PM-only analysis. However, generally speaking, the three factors divide the 17 diameters into the same three predictive groups as the PM-only analysis: diameters less than 0.02µm (factor 1), diameters between 0.02 and 0.08µm (factor 3), and diameters between 0.08 and 0.40µm (factor 2).

Figure 4.

Summary of the analysis of the effects of ambient pollution levels on non-accidental mortality. Panel (a) shows the posterior medians of the factor loadings. Panel (b) shows the posteriors of the relative risks of the predictors of mortality. The whiskers of the boxplots represent 95% intervals and the relative risks represent a one standard deviation increase. Panels (c) and (d) plot the relative risk associated with PM_2.5 and factor 3 for each lag. The width of the boxplots are proportional to the posterior probability of the lag.

The posteriors of the relative risks are plotted in Figure 4b. Each 95% interval covers one. However, the third factor (diameters between 0.02µm and 0.08µm) emerges as a signficant predictor of mortality in the plot of its relative risk by lag (Figure 4d). The width of the boxplots indicate that the four-day lag has the highest posterior probability. A four-day lag was also found by Stöolzel et al. (2006). Conditional on this lag, the 95% interval for the relative risk excludes one. For the remaining pollution-related predictors, the relative risk intervals cover one for all lags and the posteriors of the lag parameters are relatively flat (none of the possible lag values have posterior probability greater than 0.30 for any of these predictors).

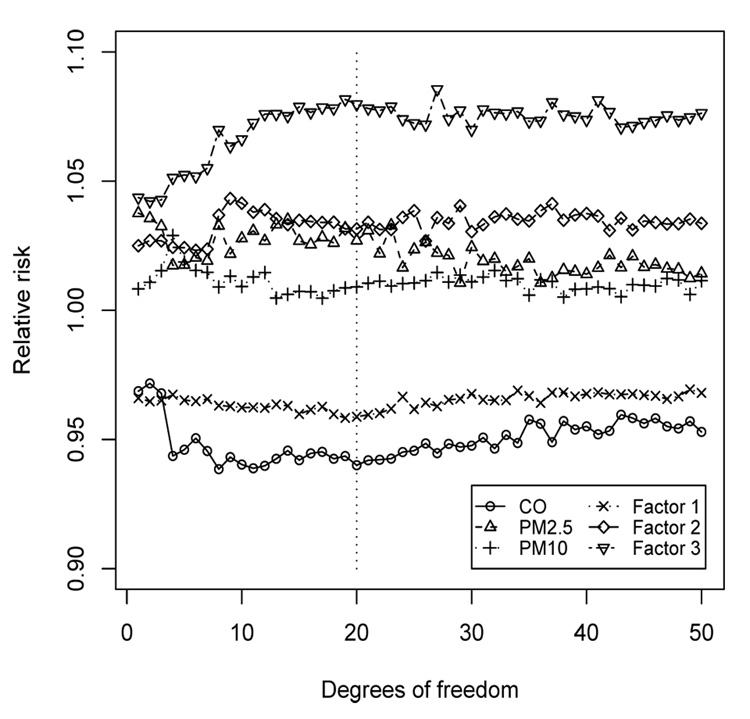
To investigate the influence of the smoothness of the long-term trend and weather co-variates, Figure 5 plots the relative risks for the pollution covariates for various of degrees of freedom for the spline smoothers. For each fit the factors are fixed at their posterior medians under the 20 degrees of freedom model and the posterior mode lag is used for each pollution covariate. The relative risks for all six pollutants remain fairly constant after 20 degrees of freedom. Therefore, our choice of degrees of freedom does not appear to be affecting our results. Also, we excluded the extremely large PM values in January 2001 (Figure 2) and the results were similar.

Figure 5.

Plots of the median relative risk for the pollutants against the degree of freedom in the spline smooth for the seasonality/weather covariates.

6 Analysis of the effect of exposure on mortality

As described in Section 1, using a single value of ambient PM levels to represent the entire population’s exposure as in Section 5’s analysis can lead to bias. In this section, we use SHEDS-PM to compare the effects of ambient pollution levels and the effects of simulated personal exposure. The population distribution of exposure is simulated for four PM diameters: 0.02, 0.05, 0.20 µm, and PM_2.5. To estimate the exposure distributions, for each day, we simulated the exposure for M = 20 populations of I = 100 elderly Caucasians in the census tract that includes the monitoring station. The demographics of elderly Caucasians is fairly constant throughout the Fresno area so these exposure distributions are representative of the exposure distributions in the entire Fresno area.

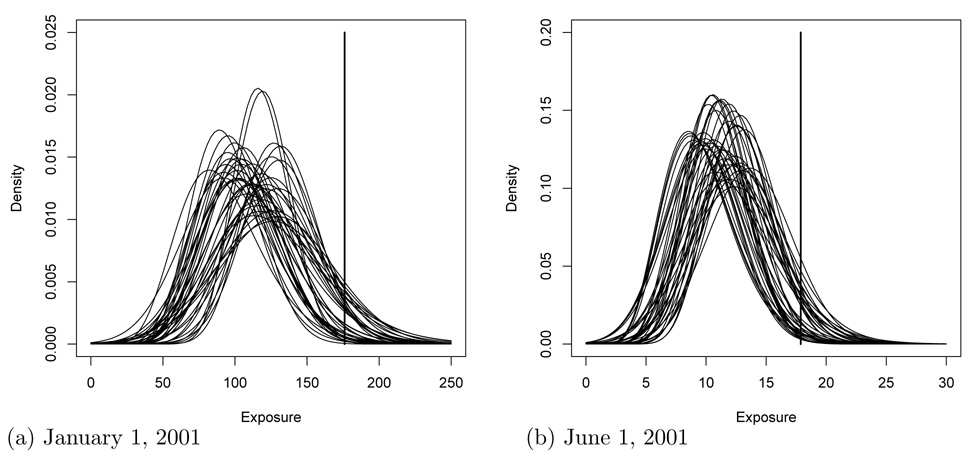
Figure 6 illustrates the variability and uncertainty in the exposure distribution for PM_2.5 on two days in 2001. For each simulated population, a normal density is fit by matching the first two moments of the sample distribution. For each of the 20 simulated populations, there is substantial variability in personal exposure within the population. For example, the average ambient PM_2.5 concentration on January 1, 2001 was 176 µg/m³, and PM_2.5 exposure ranges from 50 to 200 µg/m³. There is also considerable uncertainty about the true exposure distribution, as evident by the differences in the fitted densities. For the 20 populations on January 1, 2001 the mean exposure ranges from 91 to 132 µg/m³ and the standard deviation of exposure ranges from 20 to 41 µg/m³.

Figure 6.

Fitted density curves for 20 simulated PM_2.5 exposure distributions on (a) January 1, 2001 and (b) June 1, 2001. The vertical lines are the ambient concentrations.

The ratio the daily population mean exposure and the average daily ambient concentration varies considerably across diameter. Table 2 shows that the ratio of exposure to ambient concentration is smaller for ultrafine particles than for PM_2.5. This is due in large part to the small penetration factor and large deposition rate for ultrafine particles (Table 1). Table 2 also shows that the ratio of exposure to ambient concentration depends on the season and the day of the week. For each particle size, people are exposed to the largest proportion of the ambient concentration on summer weekends, times when people are generally more active and spend more time outdoors. The majority of the variability in the ratio the daily population mean exposure and the average daily ambient concentration is explained by season and day of the week, as the standard deviation within each season/weekday combination is small relative to the change across season/weekday combinations. However, there is also considerable variation within each season/weekday combination due to factors such as day-to-day variation in human activity and the diurnal cycle of pollution.

Table 2.

Mean (sd) of the daily ratios of the population mean exposure (averaged over all uncertainty runs) to daily average ambient concentration by season, weekday, and diameter.

Diameter	0.02µm	0.05µm	0.20µm	PM2:5
Winter, weekday	0.27 (0.026)	0.36 (0.078)	0.44 (0.140)	0.65 (0.004)
Winter, weekend	0.23 (0.029)	0.33 (0.024)	0.40 (0.021)	0.66 (0.006)
Spring, weekday	0.30 (0.047)	0.39 (0.032)	0.45 (0.018)	0.64 (0.003)
Spring, weekend	0.27 (0.039)	0.36 (0.022)	0.42 (0.017)	0.65 (0.006)
Summer, weekday	0.34 (0.034)	0.46 (0.020)	0.52 (0.015)	0.76 (0.002)
Summer, weekend	0.38 (0.068)	0.49 (0.042)	0.53 (0.027)	0.79 (0.008)
Fall, weekday	0.23 (0.023)	0.32 (0.016)	0.38 (0.017)	0.62 (0.002)
Fall, weekend	0.27 (0.036)	0.35 (0.024)	0.41 (0.026)	0.64 (0.013)

To determine the effect of incorporating the exposure simulator into our analysis, Table 3 compares the results using simulated exposure as opposed to ambient levels as predictors of mortality. Each model includes smooth functions for long-term trend, temperature, humidity, a weekday indicator, and ambient levels of PM₁₀ and carbon monoxide. The first model also includes the daily average ambient level of PM₂₅ and several fine diameters chosen to represent the latent factors of Section 5.2. The posterior mode lag is used for each pollution covariate. As in the supervised factor analysis of Section 5, PM with diameter 0.05µm (which represents Section 5’s factor 3) is the strongest predictor of mortality. However, perhaps due to the correlation between predictors, none of PM variables are significant predictors of mortality.

Table 3.

Median (95% interval) for the relative risks of non-accidental mortality for the pollution covariates for models using the ambient levels of PM₁₀ and carbon monoxide along with covariates for the fine PM diameters. The first model uses ambient concentration of the fine PM diameters, the second model uses the exposure distribution. The relative risks are the relative risk due to a one standard deviation increase in ambient concentration.

Diameter	Ambient Concentration	Exposure Distribution
DIC (pD)	2170.9 (10.0)	2172.2 (10.6)
0.02µm	1.008 (0.946, 1.073)	1.020 (0.796, 1.319)
0.05µm	1.038 (0.978, 1.115)	1.060 (0.948, 1.207)
0.20µm	0.945 (0.885, 1.003)	0.945 (0.882, 1.019)
PM2.5	0.975 (0.921, 1.032)	0.958 (0.875, 1.056)

The second model replaces the ambient concentrations of PM₂₅ and the three particles with diameter less than 0.40µm with their estimated exposure distributions as described in Section 4.2. The relative risks are similar for both models, so it does not appear that adding the exposure model has removed any systematic bias for these data. For example, the estimated relative risk for diameter 0.05µm increases from 1.038 using ambient concentrations to 1.060 using the exposure distribution. However, the 95% interval for this relative risk is more than 50% wider for the exposure model than for the ambient concentration model due to variability and uncertainty in the population exposure distribution. This illustrates the potential importance of accounting for variability and uncertainty in the population exposure distribution when making inferences about the relationship between PM and mortality.

7 Discussion

This paper presents a supervised dynamic factor model to relate a multivariate time series of pollutants with daily mortality. The model extends the usual dynamic factor model by borrowing strength across neighboring diameters, which leads to an improvement in DIC. Under this model, none of the latent factors for fine ambient PM levels are significantly associated with mortality while accounting for lag uncertainty. However, conditional on a four-day lag, ultrafine particles with diameter between 0.02µm and 0.08µm are shown to significantly predict mortality.

Our latent factor analysis used three factors because three factors seemed to be enough to capture the major trends in the multivariate time series of fine particles. We tried varying the number of factors to larger than three and in no case were any of the additional latent factors significant predictors of mortality. Of course, there are more sophisticated methods for choosing the number of factors. For example, the stochastic search variable selection procedure of George and McCulloch (1993) to determine the probability of each factor being included in the predictive model. Alternatively, Lopes and West (2004) assume the number of factors is unknown and use reversible jump MCMC. However, allowing the number of factors to be unknown in the SHEDS-PM model would be very difficult, so we elected to use a fixed number of factors throughout the analysis.

The dynamic factor model proposed in Section 3 could be adapted to model a single pollutant that is repeatedly measured at multiple locations. In this spatiotemporal setting, each site would be assigned a vector of loadings and the loadings for each latent factor would be smoothed with a spatial prior. This would result in a flexible spatiotemporal model that could be fit to non-stationary and non-separable data, as shown in (3).

We also analyze mortality using simulated exposure. The exposure distributions from SHEDS-PM model show that actual personal exposures differed for the various PM size fractions, which is important to account for when investigating the joint effects of multiple pollutants on daily mortality as in this study. For these data, the relative risk estimates were only slightly changed by adding the simulated exposure, but the 95% posterior intervals were widened by accounting for both the variability and uncertainty in the population exposure distributions.

Data from only a single monitoring location was available for this study; therefore, the daily exposure distributions were all estimated relative to a single ambient concentration, which may explain why the relative risk estimates did not change significantly when the exposure distributions were used. It is important to note that the SHEDS-PM model can be applied using data from multiple monitors to produce spatial fields of exposures. Exposure distributions that vary spatially may have a greater impact on relative risk estimates in models of spatial differences in health effects. To apply SHEDS-PM on a large spatial domain, the normal approximation for the exposure distribution and associated integrated relative risk presented here would be helpful in creating a computationally-feasible model.