Structural and Electrostatic Characterization of Pariacoto Virus: Implications for Viral Asembly

Abstract

We present the first all-atom model for the structure of a T=3 virus, pariacoto virus (PaV), which is a non-enveloped, icosahedral RNA virus and a member of the Nodaviridae family. The model is an extension of the crystal structure, which reveals about 88% of the protein structure but only about 35% of the RNA structure. Evaluation of alternative models confirms our earlier observation that the polycationic protein tails must penetrate deeply into the core of the virus, where they stabilize the structure by neutralizing a substantial fraction of the RNA charge. This leads us to propose a model for the assembly of small icosahedral RNA viruses: nonspecific binding of the protein tails to the RNA leads to a collapse of the complex, in a fashion reminiscent of DNA condensation. The globular protein domains are excluded from the condensed phase but are tethered to it, so they accumulate in a shell around the condensed phase, where their concentration is high enough to trigger oligomerization and formation of the mature virus.

Pariacoto virus (PaV), a T=3, non-enveloped, icosahedral virus, is a member of the Nodaviridae family. It was originally isolated in Peru from the Southern Armyworm, Spodoptera eridania (1). Its genome consists of two positive-sense ssRNAs (2). RNA1 (3011 nucleotides) codes for protein A, the catalytic subunit for the host RNA replicase, which enables the RNA-dependent RNA replicase to start replicating the viral RNA. RNA2 (1311 nucleotides) codes for capsid precursor protein α. 180 of these α proteins and the genome assemble together to make up the virus. Ever since it was isolated, PaV has been extensively studied using various techniques (3–6). The relatively small size (20nm diameter) and the ease with which it can be produced in various cell lines (7) make PaV and other members of the Nodaviridae family easy to characterize at the molecular level (8–10).

Structural studies of viruses are very important to understand protein-protein and protein-RNA interactions as well as to understand assembly pathways in RNA viruses (11–14). In the last few years, many studies have been done on RNA viruses using molecular modeling as supplementary method when other methods such as x-ray crystallography and cryo-electron microscopy (cryo-EM) do not give sufficient structural information. An all-atom model was derived for Satellite Tobacco Mosaic Virus (STMV), a T=1 virus, using molecular modeling (15). Those authors also carried out molecular dynamics simulations on the model to study the stability of the protein capsid and the RNA genome (15). Electrostatic interactions between RNA and the protein capsid were studied in Cowpea Chlorotic Mottle Virus (CCMV) by modeling the virus using coarse-grained modeling and representing RNA nucleotides by unconnected spheres that were distributed using the Monte Carlo method (16). In that study, no attempt was made to model the RNA structure. Other electrostatic studies of RNA viruses have also been aimed at understanding the molecular interactions and their effects on virus structure (17, 18).

The 3.0Å x-ray crystal structure of PaV reveals an asymmetric unit with three quasi-equivalent protein subunits (A, B and C) and one strand of a 25 base pair RNA duplex (6). Sixty of these units combine to form the icosahedral capsid, with 30 RNA duplexes lying along subunit contacts across the icosahedral 2-fold axes, forming a dodecahedral cage inside the capsid. The A, B, and C subunits (residues 83–321) are folded into an eight-stranded antiparallel β-sandwich, similar to proteins in other nodaviruses. Complementing the x-ray studies, cryo-electron microscopy showed the overall structure of PaV at 23Å resolution, which matched well with a low resolution model derived from the atomic coordinates (6). Cryo-EM also confirmed that the part of the RNA genome that was resolved in the x-ray structure forms the edges of the dodecahedral cage inside the protein capsid.

Although x-ray crystallography and cryo-EM have provided a lot of information regarding the structure of PaV (6), the complete atomic structure has not been determined. RNA at the dodecahedral edges accounts for only 35% of the total genome. The remaining 65% of the RNA lies inside the dodecahedral cage and is not resolved in the crystal structure because it lacks icosahedral symmetry. In addition, the 20 vertices at which the RNA duplexes are connected could not be resolved, presumably because different vertices have different structures. Similarly, protein subunit A is missing 6 residues at the N terminal end and 15 at the C-terminal in the crystal structure, while the B and C subunits are missing about 50 residues at the N-terminus and 19 residues at the C-terminus in the crystal structure (6).

In this paper, we report a model for the complete virus and examine the interactions of the basic N-terminal tails with the RNA genome, and their role in the stability of the mature virus. We built a model of the missing 65% of the genome and the unresolved protein residues. We built our models using coarsegrained modeling, representing unresolved nucleotides and amino acids by pseudoatoms and interpolating the pseudoatomic models to all-atom using special algorithms. We generated two all-atom models for the virus that differed in the conformations of the N-terminal protein tails and the extent to which they penetrate into the RNA genome. We tested these against the experimental radial density distributions from cryo-EM, and we evaluated the relative stabilities of the two models by comparing their energies. The result is the first all-atom model for a complete T=3 virus. Further, this effort has led to a new model for the assembly of small, non-enveloped icosahedral RNA viruses.

Methods

RNA modeling

The modeling of the Pariacoto virus genome posed several challenges because of the limited amount of available structural data. To begin with, the secondary structure for the PaV genome is not known. We used a hypothetical secondary structure mapped onto the dodecahedral cage (Figure 1). This is the same secondary structure that we proposed earlier (19). Those parts of the RNA genome that do not form the edges of the dodecahedral cage come inwards towards the center of the capsid as “stalactites”. The exact number of these connections is not known, but we used a combination of 3-way junctions and 4-way junctions as structural motifs connecting the RNA on the dodecahedral cage with the RNA in the interior (Fig 3). Nothing at all is known about the RNA structure in the interior, so we have to postulate a collection of plausible structures for the stalactites. We used twelve copies of a structure derived from domain IV (residues 1764–1988) of the E. coli 23S RNA to represent these. Although the twelve stalactites all have the same initial conformation, these become quite varied during the refinement of the model (Supplementary Fig. 1).

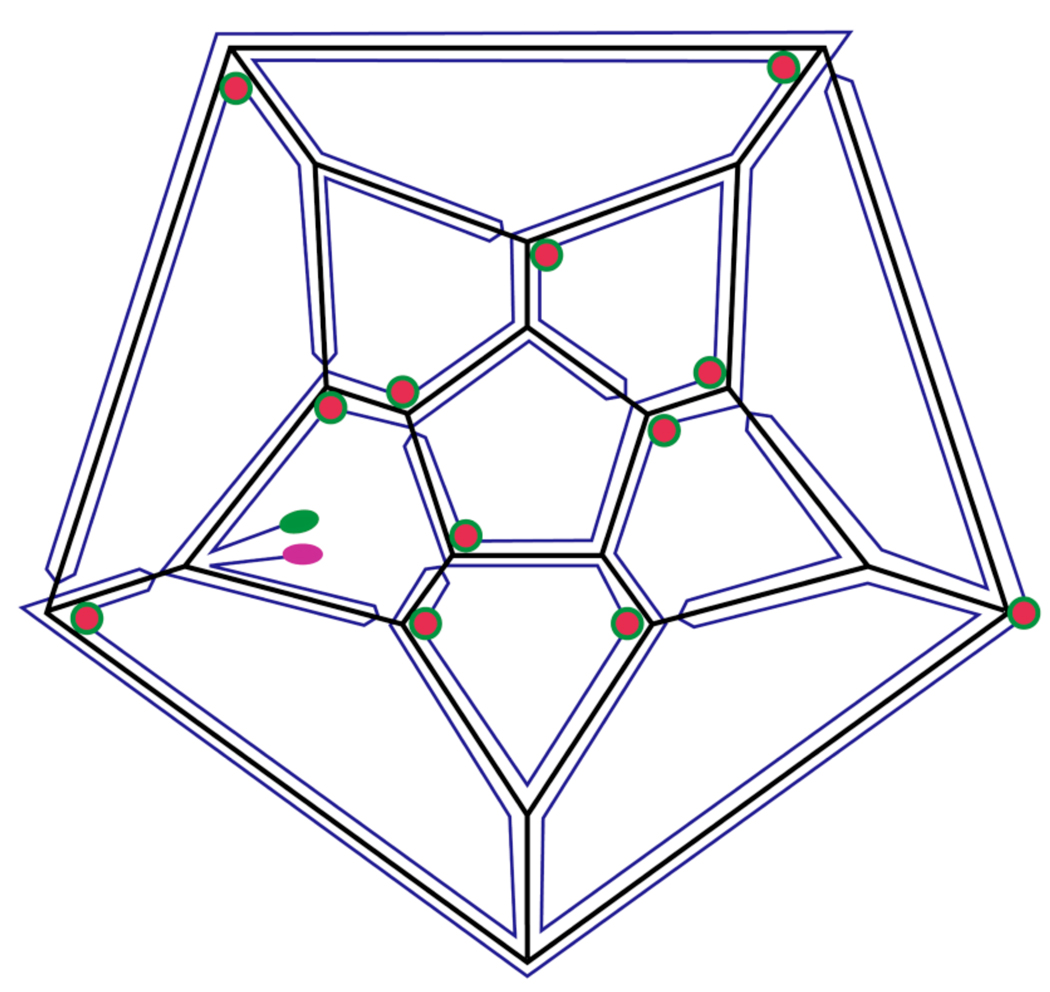
Figure 1.

Secondary structure map for the Pariacoto virus genome, adapted from our earlier model (19). The PaV RNA secondary structure is not known, nor is it known whether all base pairing in RNA1 and RNA2 is intramolecular, or whether there are base pairs between RNA1 and RNA2. In the absence of such information, we have represented the bipartite genome as one single strand. Each edge of the dodecahedral cage contains an antiparallel RNA double-helix. The 5’ and 3’ ends are highlighted in pink and green, respectively. Red circles indicate those vertices where RNA “stalactites” drop down into the interior of the virus to connect with that part of the RNA not on the dodecahedral cage.

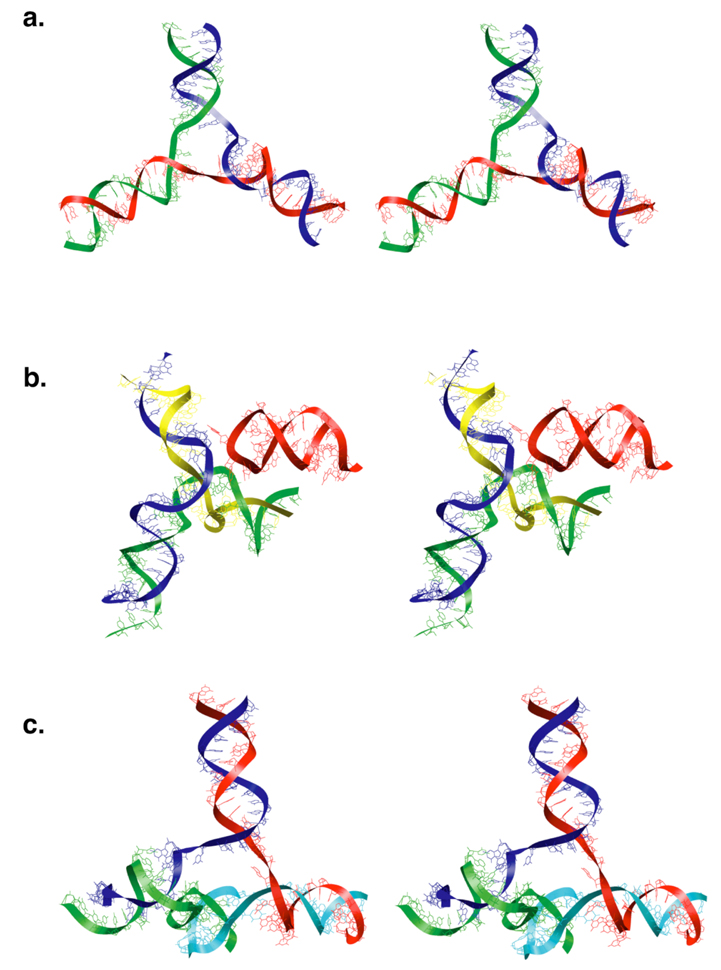
Figure 3.

Stereo images of model RNA junctions at the vertices. a. Three-way junction at a vertex with no stalactite. The three RNA duplexes lie on three edges of the dodecahedral cage. b. Three-way junction with two duplexes on edges of the dodecahedral cage and the third duplex (green and yellow) forming a stalactite that drops into the interior of the virus. The third edge of the dodecahedral cage is occuplied by a stem-loop (red) that comes from a neighboring vertex. c. Four-way junction connecting three RNA duplexes on the edges of the dodecahedral cage and a stalactite (cyan and green).

General approach

The volume inside the dodecahedral cage is too small to attach stalactites coming inwards from each of the twelve vertices without interpenetration. To solve this problem, we expanded the diameter of the dodecahedral cage by a factor of two, which increased the overall volume of the dodecahedral cage eight–fold. This allowed us to add the stalactites from the vertices without interpenetration. The expanded model was then contracted to the actual size in twelve scaling steps, with extensive energy minimization at each step (Figure 2).

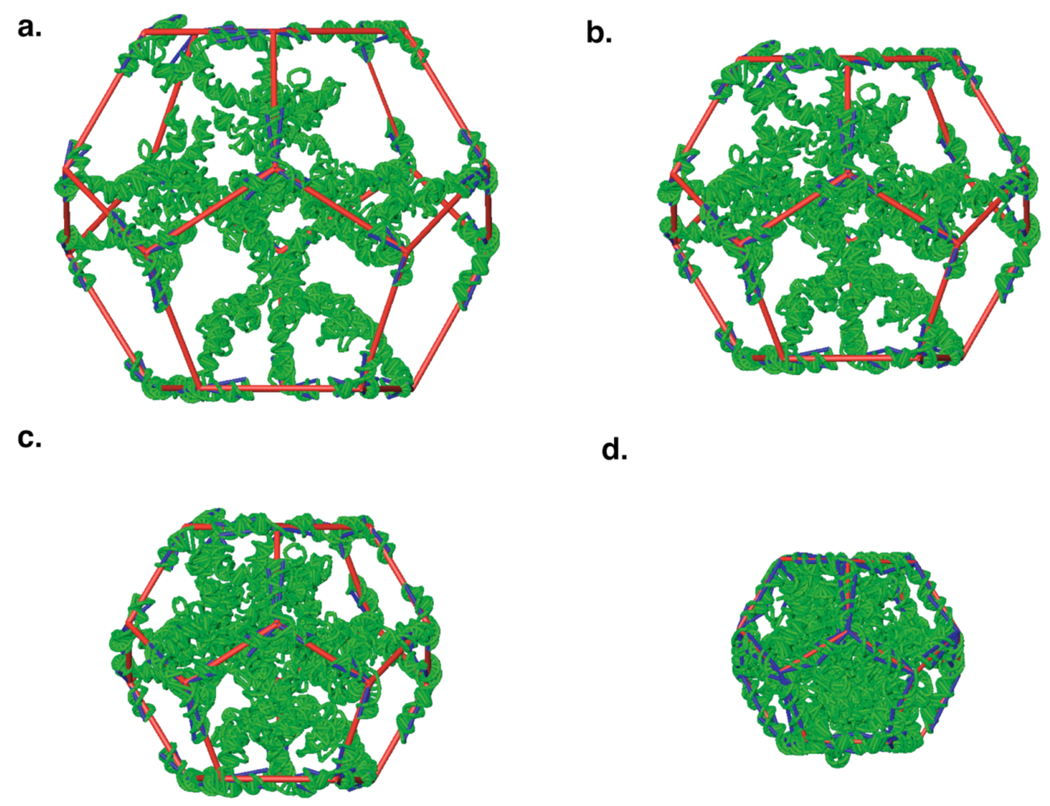
Figure 2.

Building and optimization protocol for the RNA genome (green). a. Initial model, showing dodecahedral framework (red) with diameter doubled from that of the final structure, so the volume is eight times the final volume. The RNA duplex along each edge of the framework is cut in the middle, and each half is rigidly attached to the corresponding edge and vertex. Pseudobonds from each vertex to the ends of each duplex are shown in blue; they restrain the RNA duplexes to their crystallographic conformations during minimization. Stalactites drop down from twelve of the vertices. b. After four rounds of scaling and minimization, the volume is about six times the final volume. c. After eight rounds of scaling and minimization, the volume is about three times the final volume. d. The final model, after twelve rounds of scaling and minimization.

Initial RNA genome model

The crystal structure of PaV (1F8V.pdb) is available from the RCSB Protein Data Bank (20). The dodecahedral RNA cage was generated by applying the BIOMT TRANSFORMATION matrix given in the file, using the oligomer generator tool in the VIPER database (21). The vertex structures were defined by the secondary structure (Figure 1). Each vertex had either three or four extensions of RNA coming out of it (Figure 3). Short stems were added at twelve vertices, as stubs to which the stalactites were subsequently added. Twenty pseudoatoms were also added at the vertices of the dodecahedral cage, to form a framework that could be easily expanded and contracted; we call these “vertex pseudoatoms”.

The size of the framework was increased by doubling the values of the x, y and z coordinates of each vertex pseudoatom. We cut the RNA duplex on each edge in half, moving each half to the appropriate vertex of the expanded framework, along with the connecting RNA vertex structures and the associated stubs. Stalactites were then attached to each of the twelve stubs. The initial model was generated on a Silicon Graphics workstation using the Builder module of INSIGHT II graphics software. This initial model (Figure 2a) contained all 4322 RNA residues.

Coarse-grained modeling and minimization

The initial model is quite large and the experimental data available for modeling are quite limited, so coarse-grained modeling is appropriate for refining the model. We converted the all-atom initial model to coarse-grain representation, with each nucleotide represented by a single pseudoatom at the phosphate position. A more complete description of this “all-P” representation is available elsewhere (22), along with a full description of the corresponding force field.

The edges of the dodecahedral cage were decreased to the original length in multiple steps, decreasing the ideal bond length (b₀) of the framework by 5Å in each step and minimizing until convergence (Figure 3). The minimization was done using our in-house molecular mechanics tool, YAMMP (22). The harmonic energy terms used in the minimization are given in Table 1. Since all the terms used in the potential energy function of all-P models are harmonic, minimization of the model should lead to zero energy, if all restraints can be satisfied.

Table 1.

Energy terms used in RNA modeling

Energy Ter	Equation	Atom Type	Force constant
Bond	Eb = kb (b b0)2 where b0 is the distance in the initial model, derived from crystal structure.	Crystallographic	kb = 20kcal/(mol•Å2)
		Stalactites	kb = 2 kcal/(mol•Å2)
Angle	Eθ = kθ (θ – θ0)2 where θ0 is the angle in the initial model, derived from crystal structure.	Crystallographic	kθ = 20kcal/mol
		Stalactites	kθ = 2kcal/mol
Improper torsion	Ei = ki (i – i0)2 where i0 is the improper torsion between four atoms in the initial model, derived from crystal structure.	Crystallographic	ki = 20 kcal/mol
		Stalactites	ki = 2kcal/mol
Non-bond exclusion	Enbn = kij (dij d0)2 if d < d0, d0 = 10Å		kij = 2kcal/(mol•Å2)
Radial restraint	$E_{noe}=\{\begin{array}{cc}{k}_{hi}{(r-r_{hi})}^2,\hfill & ifr>r_{hi}\hfill \\ 0,\hfill & ifr\le r_{hi}\hfill \end{array}$ where r is the distance from the center of the virus to atom i. rhi was changed at each scaling step.		khi = 2kcal/(mol•Å2)
Stud	Est = kst[(x–x0)2 + (y– y0)2 + (z–z0)2] where (x,y,z) is the current position of atom i and (x0,y0,z0) is the desired position.		kst = 40kcal/(mol•Å2)

During minimization, the stalactites RNA were relatively free to move and adjust their conformations, to avoid steric overlap. This was achieved by giving the intra-stalactite energy terms softer force constants than those for the RNA duplexes on the dodecahedral cage (Table 1). The latter were restrained by using strong force constants in the energy terms, and by the addition of pseudobonds connecting each vertex pseudoatom to the ends of the RNA duplexes at each edge (Figure 2). The duplexes on the dodecahedral cage did not deviate significantly from the crystal structure during the contraction/minimization cycles.

Conversion of refined coarse-grained model to all-atom model

Generating an all-atom model from phosphate positions is a challenging problem. The bond and angle restraints in the all-P models are based on observed distributions of P–P distances and P-P-P angles in the Nucleic Acid Database (22). With only these restraints, groups of four or more successive P atoms in any all-P model may have conformations that differ somewhat from those in real RNA structures. As a consequence, all-atom models can be generated fairly easily in double-helical regions, but all-atom models for other regions (loops, bulges, single-strands) are necessarily more speculative. This is not inappropriate, considering the modesty of our overall goal: generate a plausible RNA model, in terms of connectability along the backbone and the absence of serious steric problems. Here we discuss how plausible all-atom models can be built for all regions of the all-P model.

Briefly, the procedure used here builds all-atom models using a database of nucleotide conformations derived from all RNA-containing structures in the PDB as of April, 2006. In base-paired regions, four phosphate positions (0 and +1 on each strand) serve as anchor points, and a pair of nucleotides from the database must be fit to the structure, one on each strand. In non-base-paired regions, the four anchor phosphates are those −1, 0, +1 and +2 relative to the nucleotide being placed. The compatibility of all examples in the database with a particular position is assessed by requiring that the base be identical to the one being modeled, and that the root mean square deviations of the four phosphate positions in the example be within 1.5Å of the anchor phosphates in the all-P model. Only examples that pass this compatibility test are kept within the search space of each nucleotide.

The modeling problem then becomes one of exploring the search space of the whole molecule to determine which combination of examples gives the most plausible structure, where plausibility is defined as the lowest energy (van der Waals plus electrostatics, using the AMBER 8 force field). This optimizes base pairing and stacking, while minimizing steric clashes. Searching is done in a piecewise fashion, focusing on individual regions, to optimize performance. The most plausible structure is then refined by optimization of the ribose conformations, followed by energy minimization and a short annealing of the entire model, using molecular dynamics.

Protein modeling

For modeling the missing protein residues, we followed a similar methodology as in the case of RNA modeling, expanding the capsid, adding missing amino acids, and then shrinking the capsid back to its original size in multiple steps, with minimization at each step. Coarse-grained modeling was the initial step in modeling the missing residues of the capsid proteins. After refinement of the coarse-grained model, it was converted to an all-atom model, followed by final refinement.

Coarse-grained protein modeling

First, the capsid was expanded three times in length by simply multiplying the coordinates for the capsid proteins by 3. The crystallographic residues facing towards the RNA were converted into a model where two consecutive residues were represented by a single pseudoatom (2C–model). The rest of the crystallographically-resolved protein domains were represented by twelve pseudoatoms each, defining the face, edge and vertices of the equilateral triangle of each asymmetric unit. The missing N-terminal residues were generated in extended linear form pointing towards the RNA genome at the center. C-terminal residues were generated as a random coil. Residues for both the N- and C-terminal tails were represented by one pseudoatom per residue (Figure S2). The starting capsid model was scaled back down to the original size in a series of steps, testing different scaling ratios and van der Waals (vdw) diameters for the pseudoatoms of the protein tails. We examined scaling ratios between 0.95 and 0.99, finding that different scaling ratios did not significantly affect the configurations of the protein tails (data not shown). However, changing the vdw diameters from 8 to 12 Å significantly affected the penetration of the protein tails into the RNA genome [Figure 5b]. The resulting structures, designated model_8 and model_12, have dramatically different conformations for the protein tails. In model_8, the tails penetrate deeply into the RNA core, while they lie mostly on the outside of the RNA core in model_12

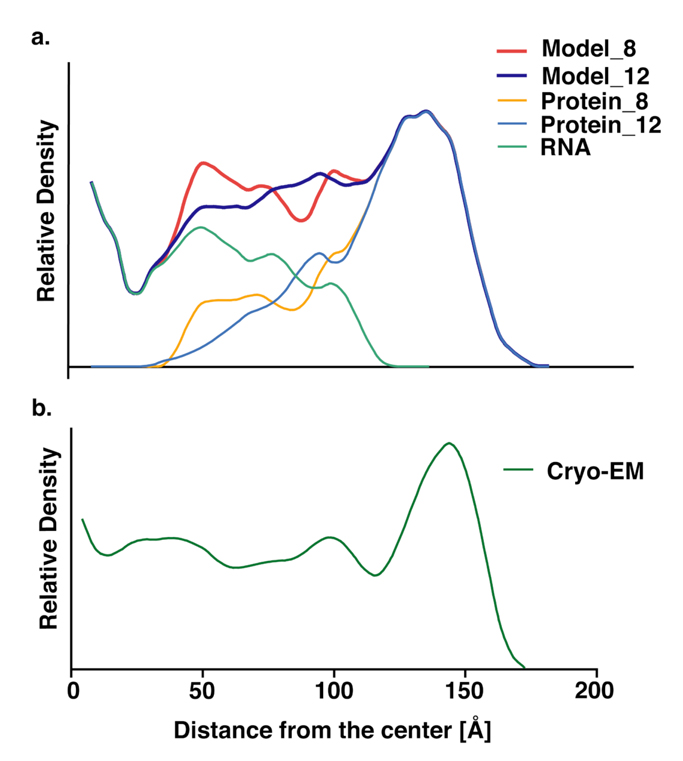
Figure 5.

Comparison of radial density distributions for model_8 and model_12 (a) with the experimental density distribution (b). The protein tails in model_8 reach more deeply into the interior (orange) than do those for model_12 (light blue). As a consequence, the total density for model_8 (red) matches the experimental density better than does that for model_12 (dark blue). Note that the density at radii less than about 30Å would be very sensitive to small changes in the model, because the volume of each shell is proportional to r² , so the density is proportional to r⁻².

All-atom protein modeling

Model_8 and model_12 were converted into all-atom representation using PULCHRA (22). PULCHRA converts Cα models to all-atom models using a rotamer library prepared from the statistics of Cα distances in the Protein Data Bank. The complete all-atom models, including all residues of the RNA genome and the capsid proteins, were energy minimized with NAMD, using the CHARMM force field.

Electrostatic calculations

Calculations of the electrostatic potential were performed using the Adaptive Poisson-Boltzmann Solver (APBS) (23). CHARMM27 forcefield radii and charges were assigned to the minimized all-atom structures of Model_8 and Model_12 using the PDB2PQR routine (24), yielding a charge of +46e for each of the 60 capsomers and −4320e for the RNA genome, where e is the charge on the proton. This resulted in a net charge of −1560e for the complete virus. The nonlinear version of the Poisson-Boltzmann equation was solved numerically on the 225×225×225 grid with an initial grid spacing of 2.0 Å, followed by focusing with the grid spacing reduced to 1.5 Å. The dielectric constants of the interior and exterior of the macromolecules were set to 10 and 78.5, respectively. The ionic strength was set to 100 mM, using only monovalent ions. The resulting potentials were visualized using Chimera (25) by mapping them onto the solvent-accessible surface of the models generated at the coarse-grained level.

Model Evaluation

The coarse-grained pseudoatomic model of the genome was checked for the presence of possible knots using the “knot” program (26). Our RNA model does not contain any knots. The all-atom genome model reconstructed from the pseudoatomic model was checked for interpenetration of rings and correct stereochemistry using PROCHECK, provided in the RCSB PDB website (http://www.pdb.org). There are no ring penetrations or other stereochemical problems. The RNA and protein distributions inside the complete all-atom models of the virus were compared with the native virus by generating density maps and corresponding radial density distribution functions (Figure 5) from the final all-atom models using SPIDER (27).

Results and Discussion

The 65% of the genome that was not resolved in the crystal structure was generated and packaged within the dodecahedral cage. Even though all twelve stalactites had the same starting structure, they have significantly different conformations in the final model (Supplementary Figure 1). The protein tails missing in the crystal structure were also generated, and their final conformations also vary significantly in the final model.

Generation of models for PaV with two different conformations of the N-terminal protein tails offers an opportunity to study their role in stabilizing the virus. The different positions of the tails in the two models are reflected in different density distributions (Figure 5). In model_12 most of the tails are packed in a shell about 100Å from the center, which is between the genome and the capsid. For model_8, many protein tails were able to penetrate inside the genome, and they contribute significantly to the density peak at a radius of about 50Å (Figure 5a). Peaks around this radius have been found in PaV (Figure 5b) and in other nodaviruses (19). Thus, model_8 is structurally more consistent with native viruses than is model_12. This is also consistent with density maps in Flock House virus (FHV), which is closely related to PaV. The radial density distribution for wild-type FHV has a peak at R∼32Å, but that peak is missing in mutant FHV in which 30 amino acids have been deleted from the amino terminus (19).

Single point energy calculations on the two models show that model_8 is also energetically more favorable than model_12. The electrostatic interaction energy between the RNA and the PaV capsid is much lower for model_8 (-3910 kcal/mol) than for model_12 (-523 kcal/mol). This is easily explained by the structural data (Figure 5): protein tails that penetrate deep into the core of the virus stabilize PaV by neutralizing a large fraction of the charge of RNA genome.

Figure 6 depicts the electrostatic potential mapped onto the solvent-accessible surface area of PaV. The external surface of PaV is almost neutral (Figure 6a), whereas the interior of the virus bears both positive charges (the protein tails) and negative charges (RNA). The lower panels of Figure 6 show the potential calculated for the virus without (Figure 6c) and with (Figure 6d) RNA, mapped onto the surface of the empty capsid. The positively charged tails (blue in Figure 6c) are fully neutralized and even reveal some negative potential on their surface due to the close proximity of RNA (figure 6d). This is probably because the total charge of RNA is almost a factor of two greater than that of the capsid.

Figure 6.

Electrostatic potential mapped onto the solvent-accessible surface of PaV. Total potential is mapped onto the surface of the RNA and one hemisphere of the capsid shell in a side view (a) and a perspective view (b). c. Potential of the empty capsid, mapped onto the surface of one hemisphere of the empty capsid. d. Potential of the entire virus, mapped onto the surface of one hemisphere of the empty capsid. Colors vary from red at a potential of -5kT/e to blue at a potential of +5kT/e, where k is Boltzmann’s constant, T is temperature (300K), and e is the charge on the proton.

Conclusions

There are three pieces of evidence that the polycationic protein tails penetrate deeply into the interior of nodavirus genomes. First, mutant FHV that lack 30 N-terminal amino acids are missing the 32Å peak seen in the cryo-EM radial density distribution for wild-type FHV (19). Second, our model_8 reproduces the experimental radial density distribution much better than model_12, and tails in the former penetrate much deeper into the genome than those in the latter model. Finally, electrostatic calculations show that deep penetration of the tails has a stabilizing effect, because of greater neutralization of the RNA charge.

This observation has important implications for viral assembly.

The assembly of small icosahedral RNA viruses like PaV and FHV is quite different from bacteriophage assembly. Interactions between phage capsid proteins are strong enough that capsids assemble spontaneously. The DNA genome is then forced into the pre-formed capsid by an ATP-dependent motor; there is little or noattraction between the DNA and the capsid proteins, in order to promote ejection of the genome upon infection of the host bacterium. In contrast, protein-protein interactions are weak in nodaviruses, and RNA-protein interactions are strongly attractive. As a consequence, capsids are only formed when the proteins and RNA are both present, and empty capsids do not exist.

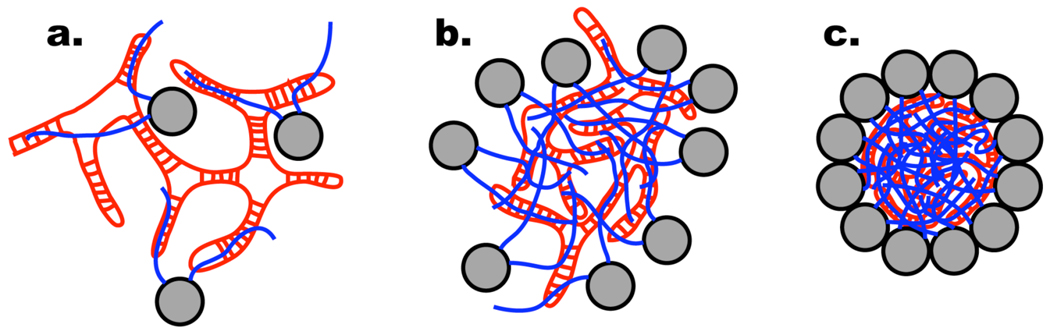
We propose a simple mechanism for the assembly of nodaviruses. Positively charged protein tails bind to the RNA (Figure 7a), with RNA replication, protein synthesis and RNA-protein binding occurring very closely in time and space (28, 29). When a sufficient quantity of the RNA charge is neutralized, the resulting complex collapses in a process reminiscent of DNA condensation (Figure 7b). We believe that most of these interactions are nonspecific, although in the mature virus there is evidence of a specific interaction between RNA2 and the N-terminal tail (30). In addition, the crystal structure (6) shows ordered interactions between the RNA and 36 N-terminal residues of subunit A, and between the RNA and eight residues of the C-terminus of subunit A, although the RNA sequence involved in these interactions cannot be determined. We hypothesize that the globular domains of the capsid proteins are squeezed to the outside of the collapsed state, as shown in Figure 7b. This provides a sufficiently high local concentration that the relatively weak protein-protein affinity is overcome, leading to oligomerization and the formation of the mature capsid (Figure 7c).

Figure 7.

Hypothesized mechanism for the assembly of small, non-enveloped, icosahedral RNA viruses. a. Positively charged amino- and carboxy-terminal protein tails (blue) bind to RNA (red). b. When a sufficient fraction of the RNA charge is neutralized, the complex of RNA and protein tails collapses, in a fashion resembling DNA condensation by polyvalent cations. This squeezes the globular domains of the capsid proteins (grey) into a shell surrounding the collapsed structure, where their concentration becomes sufficiently high to promote the specific protein-protein associations needed for capsid formation, leading to the formation of the mature virus (c).

One remarkable observation suggests that this mechanism might apply to many single-stranded viruses. Belyi and Muthukumar examined 16 wild-type and three mutant viruses (both DNA and RNA viruses) with genomes ranging from about 1 kb to 12 kb (31). They found that the ratio of the genome size to the net charge on the terminal protein tails is 1.61±0.03, an unexpectedly uniform ratio. Such a narrow range might be explained by our model, because the initial collapse would require sufficient charge neutralization to overcome RNA-RNA repulsions, but not so much as to lock the condensed state into a rigid, fixed configuration that might inhibit assembly of the mature capsid structure around the condensed mass.

This model provides a simple mechanistic basis for explaining how the relatively weakly associating proteins can force RNA into a small compact volume: the very strong electrostatic interactions between the polyanionic RNA and the polycationic protein tails provide a sufficiently favorable change in enthalpy to overcome the unfavorable entropic penalty associated with the dramatic reduction in RNA conformational space.

In summary, we present the first all-atom model of a complete T=3 virus. Although there are insufficient experimental data to allow the development of a completely rigorous three-dimensional model, our model is consistent with all the available data, and it is sterically plausible. Most important, it leads to a simple mechanistic hypothesis for the assembly mechanism of small non-enveloped RNA viruses. It will be exciting to test this model both experimentally and computationally.

Figure 4.

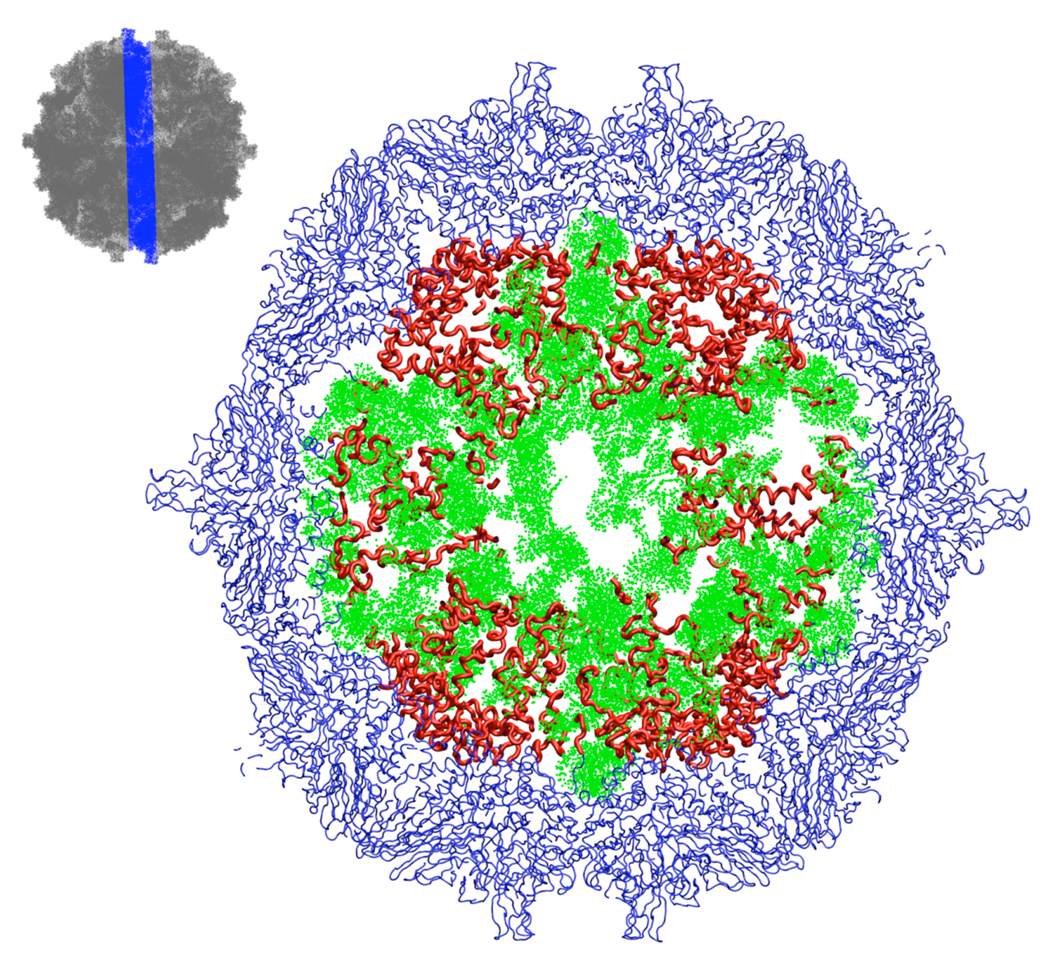
A 20Å section through the center of the final model (model_8). The thumbnail sketch at upper left shows the location and thickness of the slice by omitting the capsid proteins (dark grey) in the slice. In the main figure, those parts of the capsid proteins whose structures were restrained to the crystallographic conformation are shown in blue; they have icosahedral symmetry. Our model for those parts of the protein tails whose structures were not resolvable in the crystal structure are shown in red; these do not have icosahedral symmetry. RNA is shown in green.