Abstract
In the process of cell division, chromosomes are segregated by mitotic spindles—bipolar microtubule arrays that have a characteristic fusiform shape. Mitotic spindle function is based on motor-generated forces of hundreds of piconewtons. These forces have to deform the spindle, yet the role of microtubule elastic deformations in the spindle remains unclear. Here we solve equations of elasticity theory for spindle microtubules, compare the solutions with shapes of early Drosophila embryo spindles and discuss the biophysical and cell biological implications of this analysis. The model suggests that microtubule bundles in the spindle behave like effective compressed springs with stiffness of the order of tens of piconewtons per micron, that microtubule elasticity limits the motors’ power, and that clamping and cross-linking of microtubules are needed to transduce the motors’ forces in the spindle. Some data are hard to reconcile with the model predictions, suggesting that cytoskeletal structures laterally reinforce the spindle and/or that rapid microtubule turnover relieves the elastic stresses.
1. Introduction
Mitosis, the process by which the chromosomes are segregated in the dividing cell, is driven by a complex macromolecular machine—the mitotic spindle [1–4]. The characteristic fusiform (spindle-like) shape of this machine, wide in the middle and tapered at both ends (figure 1), is determined by microtubules (MTs)—polar dynamic filaments—the minus ends of which are anchored at or near the centrosomes (spindle poles), while the plus ends reach the spindle ‘equator’. The spindle dynamics are regulated by a host of molecular motors in addition to MTs (figure 1(C)) [5].
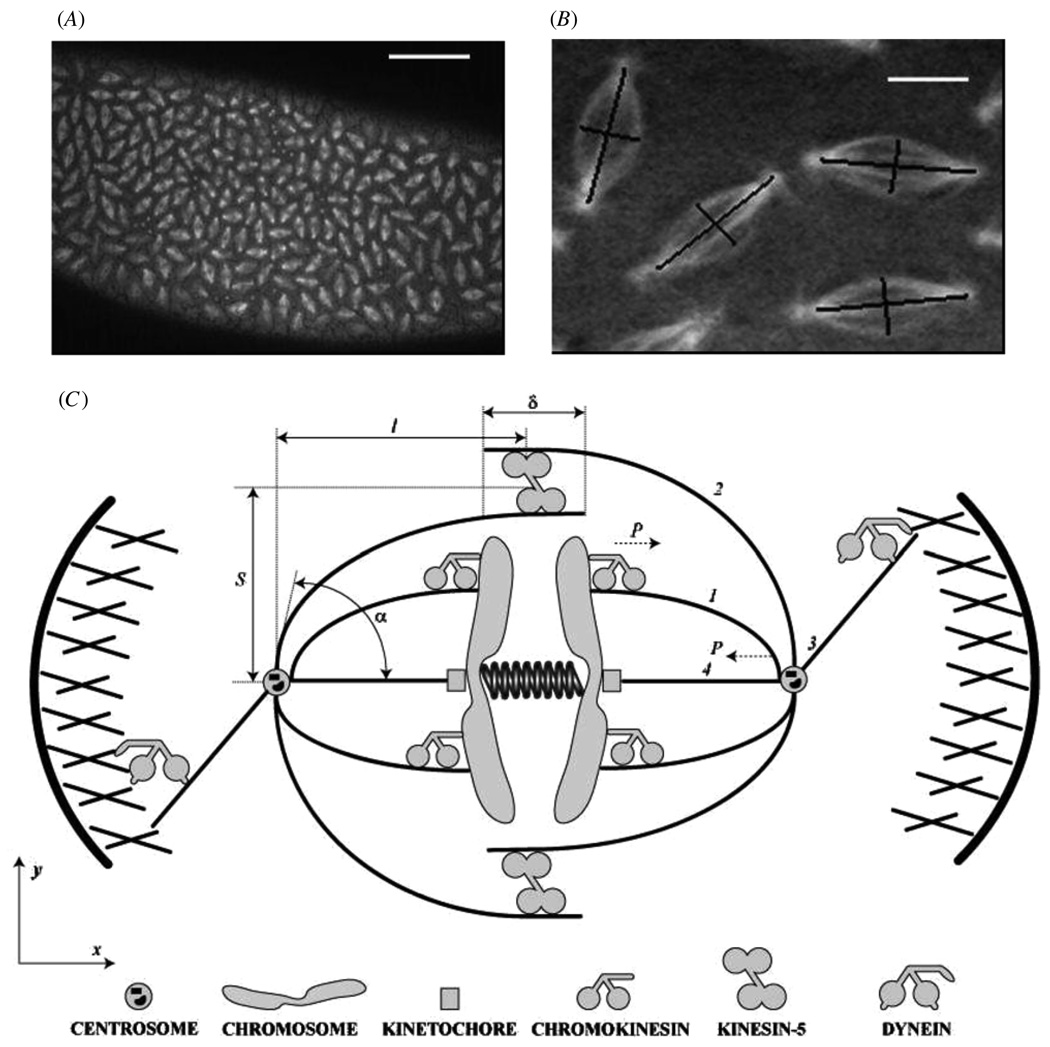
Figure 1.
(A) Confocal micrograph from a living Drosophila melanogaster syncytial embryo injected with fluorescent tubulin shows images of hundreds of synchronously dividing spindles. (Data obtained by Sharp et al as described in [8]; bar, 50 µm.) (B) Enlarged image of four spindles from A; the aspect ratio of the spindles is estimated as the ratio of the spindle length (segment connecting the spindle poles) to its width (segment at the spindle equator normal to the pole–pole axis). Bar 5 µm. (C) Schematic depiction of the spindle. Only a small fraction of mitotic motors is shown. Four functionally distinct MTs are shown: chromosomal MT (1), interpolar MT (2), astral MT (3) and kinetochore MT (4).
The dynamic spindle evolves through a number of stages [3]. After the centrosomes (two anchoring organelles focusing MT asters that constitute the spindle) are separated around the nucleus in prophase, the nuclear envelope breaks down, and in prometaphase the spindle self-assembles by establishing connections between the centrosomes and kinetochores—specialized organelles on the chromosomes. The chromosomes align at the spindle equator in metaphase, after which cohesion between the sister chromatids is dissolved, and the chromatids are segregated to the opposite pole in anaphase A, while the poles themselves separate in anaphase B [1–3]. This complex sequence of events is mediated by (i) astral MTs reaching from the poles to the cell cortex, (ii) kinetochore MTs connecting the centrosomes and kinetochores, (iii) chromosome arm MTs (chrMTs) reaching from the poles to the chromosome arms and (iv) interpolar MTs (ipMTs) overlapping at the spindle equator (figure 1(C)) [6].
What orchestrates the spindle assembly is not completely clear (and depends on the organism). Several distinct molecular processes, such as force balancing, limiting concentrations of spindle components, morphogen gradients and others acting in various combinations are the candidates for this role [7]. There is strong evidence that the motor-generated force balance is the principal mechanism in a number of organisms [3, 6, 8]. Even when different mechanisms govern the spindle dynamics in other systems [9], the spindle often functions as a mechanical machine [7], and the forces’ effects have to be considered. We emphasize though that there may be stages in the spindle development in some systems, or even its whole duration, when the chromosomal MT arrays are being emitted from the spindle equator and focused at the pole in an almost forceless fashion [4]. Our analysis does not apply to this pathway of the spindle assembly.
Here, we will focus on only a couple of outward forces that contribute to stabilizing and/or segregating the spindle poles in prometaphase, metaphase and anaphase. Both of these forces are developed by plus-end-directed molecular motors. One of the forces is generated by the sliding action of kinesin-5 motors that are able to cross-link and slide apart the anti-parallel overlapping ipMTs at the spindle equator [5, 8, 10, 11] (figure 1(C)). Another is exerted by chromokinesins on the chromosome arms that push the chrMTs away [12, 13] (figure 1(C)). Alternatively, MT polymerization itself can push on the chromosome arms [14]. Complemented by the outward force of dynein motors at the cell cortex as they pull on the astral MTs reaching the cortex and by the internal tension created by a host of other molecular motors in the kinetochore MTs, this antagonistic outward/inward force balance underlies the spindle structure and function (figure 1(C)) [6].
The motor-generated forces are applied to deformable spindle components, elasticity of some of which (centromeres [15] and chromosomes [16]) was investigated. MT elasticity in a number of cell biological systems was recently studied in a number of elegant papers [17–22], but the relevance of the internal MT elastic forces and for the spindle shape was not examined in quantitative detail. (An insightful qualitative discussion of this issue in [23] was an inspiration for our study.) In the following section, we describe the model of the elastic MTs in the spindle bent by the motor forces. Then, we analyze the scales of forces and deformations and solve (in order of mathematical complexity) the elasticity theory equations for chrMTs, for ipMTs with small overlap at the spindle equator, and finally for ipMTs with significant overlap between the anti-parallel ipMTs. We then compare these solutions with shapes of early Drosophila embryo spindles and discuss implications of the model for other spindles.
One of the results of this study is that cross-linking of MTs into bundles of ~10 filaments and clamping them at the spindle pole is essential for the force transduction of the motor forces across the spindle. We estimate effective stiffness of such bundles in the spindle as ~30 pN µm−1 and conclude that this stiffness limits the maximal motor sliding force at the spindle equator. We also discuss discrepancies between the model predictions and some published data, and speculate that either additional lateral stabilizing structures or rapid MT turnover in the spindle, or both, are important for its proper function.
2. Elastic bending of chromosomal MT bundles
2.1. Mathematical model for chrMT bundles
Mechanically, MT polymers are stiff rods with an elastic modulus comparable to that of plexiglass [24]. In vivo, MT-associated proteins and mechanical stresses in the cell can affect the MT mechanics [25, 26]. In particular, MTs are often bundled by various cross-linking proteins [27], which presumably increases the effective MT stiffness further [28]. Each MT is a thin elastic rod characterized by its flexural rigidity YI, where Y ~ 109 pN µm−2 is the MT Young’s modulus, and I ~ 10−8 µm4 is the second moment of inertia of the MT cross section [24]. We assume that the bundle consists of N elastic MTs; if the MTs are tightly cross-linked, the bundle’s flexural rigidity scales as ~N2, while if the cross-linking is flexible, the scaling is ~N [28]. Therefore, the order of magnitude of the MT bundle’s flexural rigidity can vary from B ~ YIN to B ~ YIN2. In the calculations described below we used the value N = 10 and assumed tight cross-linking, B = 100YI; we will discuss the consequences of varying these assumptions below. The bundle’s rigidity, in principle, can vary along the length due to many factors including spatial variance of the number of MTs, density of the cross-linking, and local mechanochemistry of the cell. Here we assume that the flexural rigidity is constant.
Let us consider a chrMT bundle of length L, with minus ends anchored at the spindle pole located at a distance l < L from the spindle equator (figure 1(C)). Mathematically, the shape of the bundle can be described with the arc length parametrization: the x- and y-coordinates of the material points of the bundle are {x(s), y(s)}, where 0 ≤ s ≤ L is the arc length. We assume that the plus end of the bundle is clamped at the chromosome arm in the horizontal (along the pole–pole axis) direction, and the chromokinesin motors and/or MT polymerization push the bundle’s plus end outward with force P. We also assume that the bundle’s plus end may slide freely in the vertical direction. Thus, mathematically, the force P = {−P, 0} is applied to the bundle’s plus end. We consider two possible types of anchoring of the minus end of the MT to the pole—clamped and hinged.
Let us introduce the unit vector tangential to the bundle t(s) = {x′(s), y′(s)} (here and below ′ denotes the derivative with respect to the arc length). In the appendix, we derive the equation for the bundle shape:
| (1) |
where θ(s) is the variable angle between the tangent to the bundle and the vertical direction. We use the bundle length L ~ 10 µm as the characteristic length scale, and its flexural rigidity divided by the bundle length squared, B/L2 ~ 10 pN, as the characteristic force scale in the system. Using these scales to non-dimensionalize the variables and parameters (we will keep the same notations for the non-dimensional variables), s → sL, P → PB/L2, we derive (see the appendix) the non-dimensional equation for the bundle shape:
| (2) |
The boundary conditions are determined by the assumption that the plus end is clamped in the horizontal direction (θ(s = 1) = π/2) and that the minus end at the spindle pole is either clamped at the prescribed angle (θ(s = 0) = π/2 − α) or hinged (θ′(s = 0) = 0). Thus
| (3) |
| (4) |
2.2. Model predictions for the shape of the chromosomal MT bundles
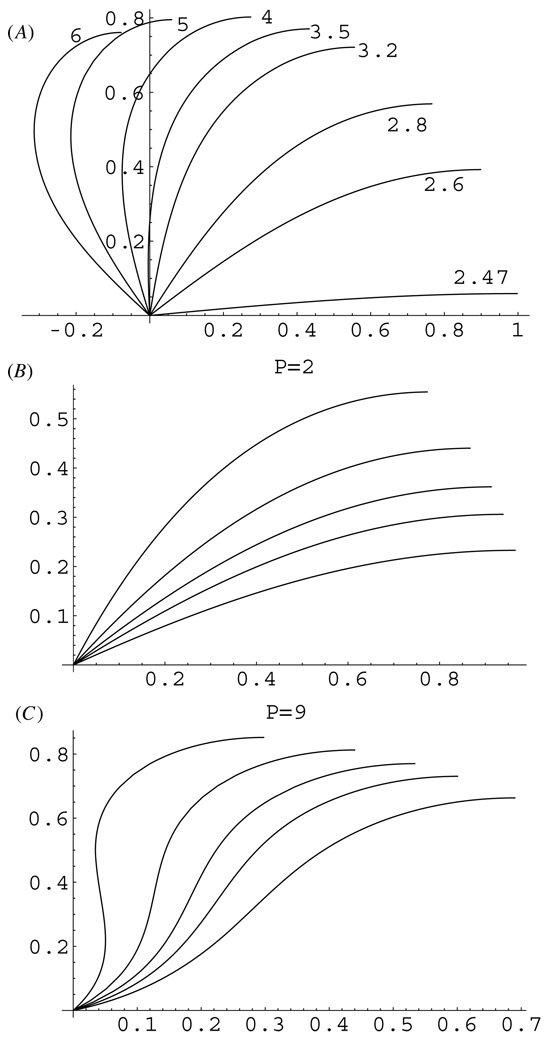
Model parameters and predicted observables are listed in table 1. In the appendix, we found analytical solutions of equations (2)–(4) in the form of elliptic functions [29] and plotted these solutions in figure 2. (As a control, we also solved these equations numerically using the shooting method; numerical solutions are in agreement with the analytical solutions.) Figure 2(A) illustrates the predicted shapes of chrMT bundles when there is a flexible hinge connection at the spindle pole. When the pushing force P at the chromosome arm is less than the critical force of ~25 pN, the bundle is stiff enough not to be deformed by such force and remains straight. At greater forces, the bundle buckles, and as the pushing force increases to ~30 pN, the bundle bends significantly into the shape that resembles the characteristic fusiform shape of MT bundles in the spindle (figure 1(B)). However, as the chromokinesin or polymerization pushing force increases beyond ~30 pN, the bundle deforms to an extent not observed in the spindles. These calculations suggest that the hinge connection at the centrosome would not support the spindle architecture robust to fluctuations of the motor forces: only a very narrow region of 25–30 pN per bundle gives realistic shapes, while the data and modeling indicate that the spindle has to be a robust structure as force changes within an order of magnitude.
Table 1.
Model parameters and predicted observables.
| Model parameters | ||
|---|---|---|
| Notation | Meaning | Value |
| P | Outward pushing or sliding force | ~0 − 100 pN (N/d: 0–10) |
| L | MT bundle length | ~10 µm (N/d: 1) |
| N | Number of cross-linked MT in the bundle | ~10 |
| B = N2YI | MT bundle flexural rigidity | ~103 pN µm2 |
| α | Clamping angle at the pole | π/8 to π/3 |
| γ | Sliding force at the ipMT overlap | ~0–200 pN µm−1 |
| Observables predicted by the model | ||
| l | Spindle half-length | 0 − L (N/d: 0–1) |
| S | Spindle half-width | 0 − L (N/d: 0–1) |
| l/S | Spindle aspect ratio | 0.2–5 |
| K | Effective spring constant of the MT bundle | ~1–30 pN µm−1 |
Figure 2.
(A) Predicted shapes of the chrMT bundles for the hinge connection at the centrosome as functions of the force in the range of 25–60 pN per bundle. (B), (C) Predicted shapes of the chrMT bundles clamped at the centrosome at angles α = π/8, π/6, π/5, π/4, π/3 at forces 20 (B) and 90 (C) pN per bundle. Distances are shown in units of 10 µm; forces are in units of 10 pN.
Figures 2(B), (C) show the predicted shapes of chrMT bundles when the MTs are clamped at various angles at the spindle pole. We found that for smaller pushing forces of a few tens of piconewtons, the bundles are bent into the characteristic spindle-like shapes (figure 2(B)). However, when the pushing force exceeds a characteristic critical force, which is clamp-angle dependent and varies from ~50 pN for α ~ π/3 to ~70 pN for α ~ π/6, the bundles bend so much that an inflection point emerges in the middle of them (figure 2(C)). At such super-critical force, the bundle shape near the centrosome becomes convex up, which is not observed in the spindles (figure 1(B)). Thus, the clamped connection at the spindle pole is more robust than the hinged one: the bundles are bent into the realistic shapes by the pushing forces ranging from zero to ~50 pN per bundle for realistic clamp angles.
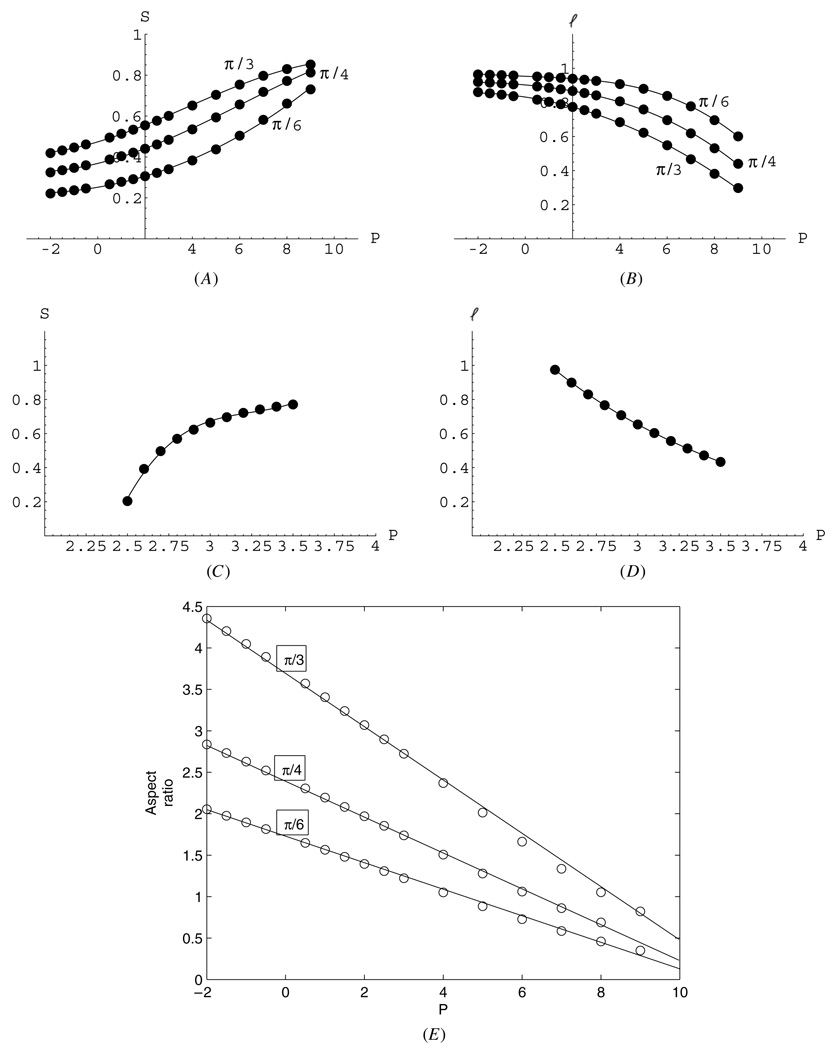
To compare the mathematical results with the observations and better understand the mechanical properties of the spindle, we plotted the spindle half-length (pole-to-equator distance), half-width (see figure 1(B)), and aspect ratio (length over width) (figure 3). Figures 3(B), (D) illustrates that the bending MT bundles effectively act as springs: greater force P compressing the spindle causes shorter spindle length. Figures 3(B), (D) allow us to evaluate the effective spring constant, K, of the MT bundle by estimating the inverse slope in the length–force relation: the effective spring constant can be defined as K = ΔP/Δl. The spring is nonlinear, so the spring constant depends on the range of the applied forces. For the hinge connection (figure 3(D)), the chrMT bundle behaves as a very weak spring characterized by K ~ 1 pN µm−1. On the other hand, the clamped bundle behaves as a relatively stiff spring characterized by K ~ 30 pN µm−1 for forces up to 50 pN per bundle. At greater forces, the bundles buckle, exhibiting the inflection in bent shapes, and the effective spring weakens to K ~ 10 pN µm−1.
Figure 3.
Predicted half-width (A), (C) and half-length (B), (D) of the spindle for hinge (A), (B) and clamp (C), (D) connections at the centrosome as functions of the force per bundle. (E) Predicted aspect ratios (l/S) for the spindles with the clamped connection at the centrosome as functions of the force per bundle. Circles represent the computed values, curves—quadratic (linear for (E)) polynomial approximations. Distances are shown in units of 10 µm, forces—in units of 10 pN. It is not clear if negative (pulling) forces at the chrMT bundle tips are biologically realistic, but mathematically they lead to realistic shapes for the clamped connection.
To change the spindle width significantly, forces have to change by ~10 pN per bundle for the hinged connection and by ~100 pN for the clamped connection (figures 3(A), (C)). The model predicts that the (clamped) spindle aspect ratio linearly decreases with force per bundle (figure 3(E)), changing from ~4 to 2 for greater clamp angles and from ~2 to 1 for smaller clamp angles as the force increases to ~50 pN per bundle.
3. Interpolar MT bundles bent by great sliding forces
Let us consider the ipMTs overlapping at the spindle equator in an anti-parallel fashion (figure 1(C), figure 4(A)). At the overlap, bi-polar kinesin-5 motors (sometimes resisted by other proteins) attempt to reach the plus ends of the overlapping MTs, and as a result generate the forces sliding the anti-parallel bundles apart in a fashion opposite to the well-known actin–myosin contraction in muscles. We characterize this sliding motor action by the parameter γ (table 1)—the force exerted per unit length of the overlap—equal to the force per motor multiplied by the average number of the motors per unit length.
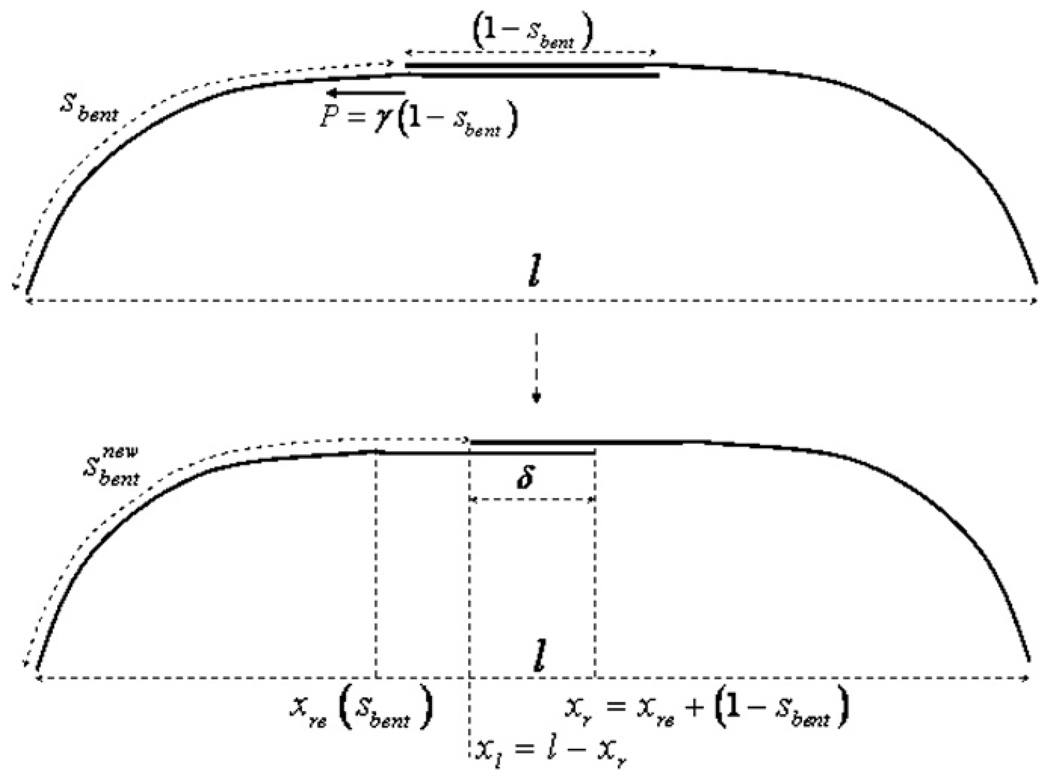
Figure 4.
Iteration procedure for computing the ipMT bundle shape for great sliding forces; see the appendix for the details.
Here we investigate the simple limiting case when the sliding force γ is great, of the order or greater than ~100 pN µm−1, while the spindle length is kept constant by the inward forces generated by the tension of the kinetochore MTs. If this is the case, then the length of the ipMT overlap at the equator, δ (figure 4), is small compared to the whole bundle length and spindle length. Indeed, if the overlap length is equal to a few microns, then with γ equal to 100 or more pN µm−1, the total sliding force amounts to hundreds of piconewtons, which would bend each of the ipMT bundles drastically away from the spindle equator (as is clear from the previous section), so the overlap would decrease to a sub-micron range. But then, the overlap length is an order of magnitude smaller than the lengths of the whole bundle and spindle, and the curvature of the overlap region can be neglected. Effectively, the overlap region can be represented by a short straight segment at the spindle equator, parallel to the spindle axis (figure 4).
Mathematically, the following iteration procedure can be used to find the ipMT bundle shape in this case (figure 4). First, we start with an arbitrary length of the bent part of the bundle, sbent, find the length of the overlap, (1 − sbent) and the resulting sliding force P = γ(1 − sbent). Then, without changing the spindle length, we use the analytical formulae in the appendix to find the shape of the curved part of the bundle. This gives us the new, updated shape of the ipMT bundle, from which we obtain the updated value of the overlap length, and therefore the updated values of the sliding force and arc length of the bent part of the bundle (see the detailed description in the appendix). We checked numerically that this iteration process converges; the resulting stable ipMT shape can be found analytically (see the appendix).
The result of these calculations is very simple and intuitive: for γ equal to 100 or more pN µm−1, the ipMT overlap at the equator is so small that it can be mathematically considered point-like, and so the shape of the bundle is well approximated by the results of the previous section for chrMTs. In particular, the hinged connection at the pole is not robust; for the clamped connection, the ipMTs are bent into realistic shapes by forces on the poles not exceeding ~50 pN per bundle, and the bundle behaves effectively as a spring with a spring constant ~30 pN µm−1. Note also that the case of possible ipMT bundles cross-linked at the spindle equator, rather than being pushed by active molecular motors, is also mathematically equivalent to this case.
4. Interpolar MT bundles bent by small sliding forces
4.1. Mathematical model for chrMT bundles
The case of smaller sliding forces, when γ is of the order of 10 pN µm−1, is mathematically the most difficult, because the overlapping region between anti-parallel MTs is not small compared to the spindle length, and curvature of the overlap region cannot be neglected. In this case, a direct solution of the elasticity theory equations for the bent rods becomes prohibitive, because the bending forces and moments exerted by motors and MAPs cross-linking the MT rods depend on the rod shape, which in turn depends on these forces and moments. This interdependence of the forces and shapes makes the problem too difficult for even a numerical analysis of the differential equations [30]. (A numerical investigation treating the MTs as short segments connected by angular springs and motors as linear springs [22] could be feasible in the future.)
Here we overcome this difficulty by modeling the kinesin-5 motors and other possible proteins at the middle part of the bundle of length δ as sliding cross-links keeping the MTs tightly bundled at the overlap, but sliding freely relative to each other. This allows us to approximate the whole overlapping ipMT array that spans the space from one pole to another as a single elastic rod. For simplicity, we do not consider possible heterogeneity of its effective stiffness. The simplest case is when the kinesin-5 motors do not generate sliding forces, but are just freely sliding cross-links.
Then, the ipMT bundle shape can be found as follows: we consider the bundle’s ends clamped at an angle α at the spindle poles at the fixed distance 2l from each other. The total ipMT bundle length is (2L − δ), where δ is fixed, but unknown, overlap length. An unknown force P, physically generated by the astral and kinetochore MTs, restrains the bundle at the poles. We analytically solve the elasticity theory equation for the bundle’s shape:
| (5) |
(see the appendix, where the non-dimensional version of the equations is solved). We find the solutions for any value of the parameter δ, so that the value of force P is determined by this parameter, and other parameters and boundary conditions, P = P(δ, α, L, l). Then, we compute numerically the elastic free energy [31] of the ipMT bundle, which is given by the integral
| (6) |
The energy is parametrized by the unknown value of the overlap: ϒ = ϒ(δ). Numerically minimizing the elastic free energy, we obtain the value of δ, force P and the shape of the bundle for given values of L, l and α.
This model can be generalized to the case when kinesin-5, possibly with other motors, applies tangential sliding forces γ per unit length of the overlapping ipMTs. We assume that these forces are independent of the bending elastic forces, and that the motor forces are additive. Note that we do not explicitly solve the elasticity theory equations for the rods bent by these forces for the reasons discussed above. Indeed, these forces are applied to the individual MTs within the bundle, but are canceled when integrated over the bundle’s cross section, because the forces on the antiparallel MTs are opposite to each other. However, clearly, these forces slide the anti-parallel MTs apart, increasing the bundle length and decreasing δ. This effect can be accounted for by adding the potential energy of the sliding motors to the elastic energy. The former can be estimated by integrating the force γs, sliding apart the anti-parallel sub-bundles overlapping over the distance s, with respect to s from 0 to δ. The resulting work (motor potential energy) is γδ2/2. Thus, the total energy in the active motor case is
| (7) |
In the appendix, we compute this energy, minimize it, and thus numerically obtain the value of δ, force P and the shape of the bundle for given values of L, l, γ and α.
4.2. Model predictions for the shape of the interpolar MT bundles at small sliding forces
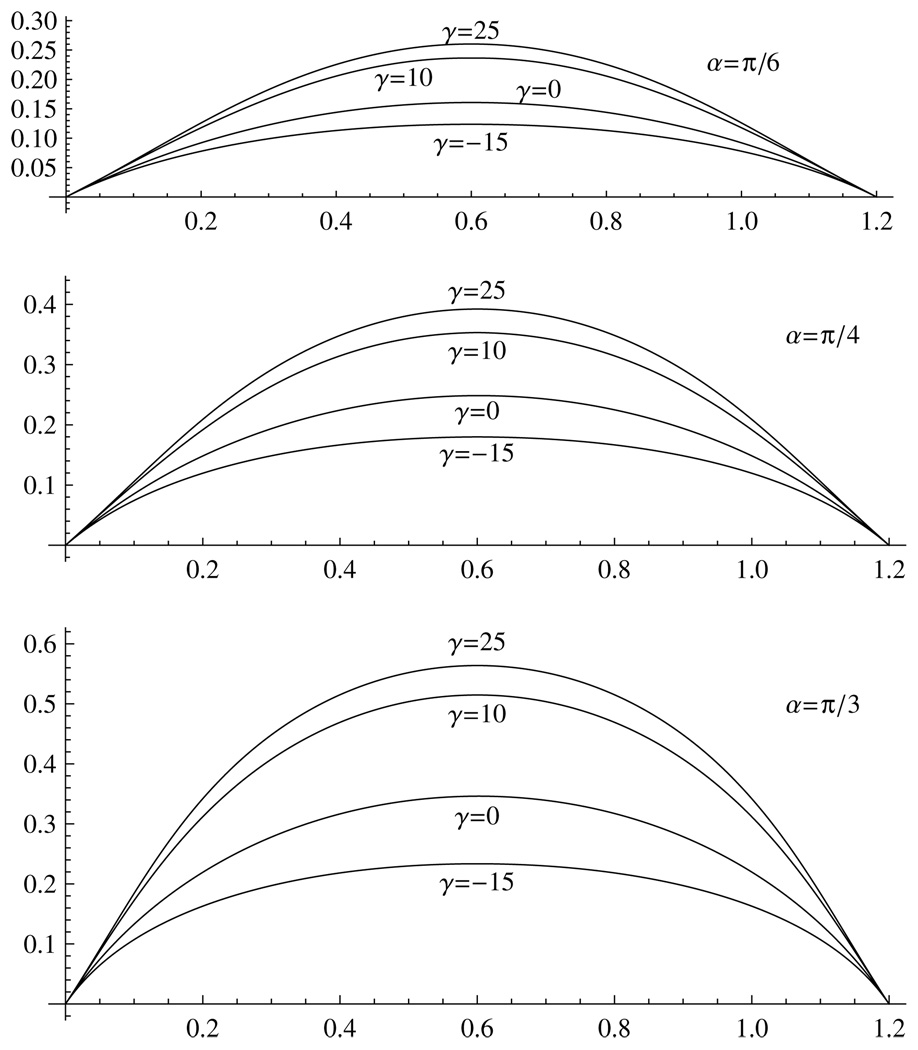
The resulting ipMT bundle shapes are shown in figure 5 for various clamping angles and motor forces. (For the hinged connection, the results are not shown because of the non-robustness of the shape in response to small force changes.) When the motors are passive, γ = 0, the ipMT bundle’s shape is an almost perfect circular arc (see the appendix), and no force is needed to restrain the poles. The spindle’s aspect ratio is between 2 (at α = π/3) and 4 (at α = π/6). When the motors exert sliding forces (γ = 10–25 pN µm−1), the MTs are bent outward, and the aspect ratio decreases, changing from 1.2 (at α = π/3) to 2.5 (at α = π/6).
Figure 5.
Predicted shapes of the ipMT bundles clamped at the centrosome at angles α = π/6, π/4, π/3 at weak outward (γ = 10, 25) and inward (γ = −15) sliding forces. Distances are shown in units of 10 µm; parameter γ – in units of 1 pN µm−1.
Note that the parameter γ has the same dimension, pN µm−1, as the effective elastic spring constant K, and in fact the overlapping ipMT region works as a spring: when the spindle length decreases, the ipMT overlap increases, and the outward sliding force grows with the overlap length. However, there is no simple linear relation between the force P applied to the poles and the overlap: P ≠ γδ. One reason is that the sliding force is not applied exactly in the pole–pole direction, plus, the force-dependent elastic bending mediates the resulting force at the poles. By varying the pole–pole distance 2l and computing the resulting force P, we estimated the effective spring constant of the combined effective motor/elastic spring. Its value, K ~ 10 pN µm−1, is insensitive to the value of γ. Thus, at significant, a few microns long, overlap between the ipMTs, the force of tens of piconewtons per ipMT bundle has to be generated by the kinetochore MTs to stabilize the spindle in metaphase.
The model also shows, in agreement with intuitive expectations, that if there is a net outward force from a collective action of astral and kinetochore MTs trying to segregate the poles, and if the ipMTs are pulled inward (i.e., by kinesin-14; γ is negative), then the aspect ratio of the spindle increases (figure 5). The computed shapes can also be representative of the shapes of the kinetochore MTs under tension, if they are cantilevered at the poles.
5. Discussion
5.1. Biophysical implications
Our analysis suggests that a flexible, hinge-like connection between the MT bundles and the centrosome (spindle pole) is not robust and is an ineffective way of transducing the motors’ forces in the spindle: in this case, the tightly cross-linked bundle of 10 MTs is equivalent to a weak spring characterized by K ~ 1 pN µm−1, so just one additional molecular motor would be able to significantly deform the spindle. Also, the change of forces in the narrow range of 25–35 pN per bundle would drastically deform the spindle aspect ratio from 10 to 1, which was never observed.
If the MTs are clamped at the spindle poles, the mechanical properties of the spindle become more robust: each MT bundle would be able to withstand up to 50 pN of pushing or sliding force before buckling. In this regime, the MT bundles behave as effective compressed springs. Respective stiffness of these ‘elastic springs’ is of the order of K ~ 30 pN µm−1, so only tens of motors would deform the spindle noticeably. When a bundle buckles at forces exceeding ~50 pN, the model predicts a characteristic inflection point (figure 2(C)) in the middle of the bundle.
In summary, our model suggests that the MT bundles in the spindle can be considered as a series of springs compressed by the molecular motors. The chrMT bundle is an elastic spring with effective stiffness K ~ 30 pN µm−1, while the ipMT bundle is an elastic spring with similar stiffness K ~ 10 pN µm−1. Note that all of these springs are under compression, assuming that both kinesin-5 and chromokinesin motors exert the outward forces on the spindle pole (not canceled completely by other motors, i.e. kinesin-14). The spindle poles in this situation are kept in equilibrium by inward forces, most notably by forces generated on kinetochore MTs that keep those MTs under tension [32]. Note also that the chrMT bundle spans half-spindle, while the ipMT bundle connects the poles; effective stiffness of the pair of the chrMT bundles in series is ~15 pN µm−1, so the stiffness of the whole spindle composed of a few tens of bundles would be in the range of hundreds of piconewtons per micron.
For chrMT bundles, it is natural to assume that the pushing force is generated by one motor per MT plus end. The respective force, either of kinesin or of MT polymerization is in the range of a few piconewtons [33], so N ~ 10 MTs, if they are tightly bundled and clamped at the spindle pole, would not be able to buckle and transduce the motor force effectively within the spindle. The pushing force scales as N, while the stiffness of the bundle scales as N2 at tight cross-linking, so either decreasing the number of bundled MTs or making the cross-linking loose would destabilize the spindle. Increasing the number of bundled MTs would make the bundle more robust, but the spindle clearly has to have many bundles for structural stability, so it is tempting to speculate that N ~ 10 MTs is the minimal required number per bundle, and that the cell regulates the bundle thickness to allow both mechanical stability and maximizing the number of the bundles.
For ipMT bundles, the parameter γ is probably scaling as N, and it is likely that ~10 motors per micron of the overlap between a MT pair are engaged [23]. This would put the value of γ in the range of hundreds of piconewtons per micron for N ~ 10 MTs per bundle, and thus into the regime in which the value of γ does not affect the spindle’s overall elastic properties. In this regime, the spindle geometry and effective stiffness would be sensitive to the forces generated by astral and kinetochore MTs and respective motors. This argument also holds when either N or cross-linking decreases. The important conclusion is that too many outward pushing molecular motors would simply waste their power by bending the spindle MTs out of shape and not transducing their force to the spindle poles. Even in the limit of the low motor density or force, we demonstrated that the force at the spindle poles is not very sensitive to the total sliding motor force, so the assumptions of the previous one-dimensional force balance models [6] that the whole motor force is transduced to the spindle poles have to be re-examined.
Finally, the possible dispersal of the MT bundle length is an interesting issue. The bundle’s stiffness is inversely proportional to the square of its length, so MT bundles much longer than the half-length of the spindle would not contribute much to the spindle mechanics, and moreover would be buckled drastically, which has never been observed, to the best of our knowledge. This makes it likely that the effective length regulation of the MTs in the spindle [34–36] has an important mechanical function.
5.2. Comparison with mitotic spindles in the early Drosophila embryo
Electron microscopy of the mitotic spindle in the early Drosophila embryo shows the average length of the ipMT overlap of the order of 1 µm [23] in metaphase. It also shows that tens of bundles consisting of 2–4 MTs overlap at the spindle equator [23]. In anaphase, the number of the ipMT bundles is likely to decrease to ~10 [37], and probably the MT number per bundle increases. These data are consistent with the regime in which the elastic bending of the ipMTs would have to be significant and sensitive to the characteristic forces. The latter are in the range of hundreds of piconewtons in prometaphase and metaphase and close to 100 pN in early anaphase [6]. Divided by the number of ipMT bundles, this suggests that ~10 pN is applied per bundle of ~3 MTs in prometaphase and metaphase, and ~10 pN is applied per bundle of ~10 MTs in anaphase. Our physical estimates suggest that in anaphase the clamped ipMT bundles can easily sustain such forces, while in prometaphase and metaphase the characteristic forces would have to buckle the ipMT bundles, unless the bundles are additionally reinforced (see below).
We measured the average aspect ratio of tens of the Drosophila spindles in metaphase and anaphase (figure 1(B)) and observed that the spindle’s average aspect ratio increases 1.5 times from 1.8 ± 0.2 in metaphase to 2.7 ± 0.3 in anaphase. From the micrographs, we estimate the clamping angle α ≃ π/6 − π/4. In principle, both values of the aspect ratios are in agreement with the characteristic aspect ratios predicted by our theory (figure 3(E), figure 5), as is the increase of the aspect ratios in anaphase, when the force decreases and the bundles stiffen.
However, some data are harder to explain by the model. First, buckling MTs in metaphase are not observed. Second, we measured the aspect ratio of the spindles when some motors were inhibited (kinesin-14, effectively diminishing the sliding force of kinesin-5), and did not observe any significant changes in the aspect ratios of the perturbed spindles. In principle, these observations can be reconciled with the theory if the total motor force is smaller than suggested by recent models and inferred from crude measurements. Below, we discuss other plausible reasons for these inconsistencies.
5.3. Budding yeast spindle
In the future, it would be interesting to examine the MT elasticity in the budding yeast spindle, which is a prime candidate for modeling because of its relative simplicity compared to other eukaryotes [38, 39]. The low number of MTs (about 20) in each half-spindle will make it possible to consider each individual MT, especially because the MTs do not seem to be bundled. The yeast spindle appears to be barrel shaped; there are few interpolar MTs and they are straight [40]. It is highly likely that sliding by forces of the order of 100 pN [38] underlies spindle elongation [41] in this system.
The budding yeast spindle is short compared to other eukaryotes, thus MT bundling may not be necessary; however, it was suggested that some cross-linking takes place and keeps MTs from buckling [39]. It is interesting to note that occasionally some spindle MTs appear bowed [38], as if they are buckled by compression forces. Our theory predicts for short unbundled ipMTs in the yeast spindle that they should remain straight both if the overlap is very small and if it is great. Buckling, however, is possible in longer spindles with moderate overlaps between the MTs. One additional aspect to consider is the fact that in yeast, ipMTs are surrounded by cohesin and kinetochore MTs [38], which is curiously the optimal mechanical design reinforcing the ipMTs laterally.
5.4. Model limitations and biological implications
How are some other spindles built? In generic animal cells, electron microscopy [42] suggests that ipMTs in metaphase and anaphase are not heavily bundled, while bundling increases in anaphase. The length of the equatorial overlap is in the micron range, and forces of hundreds of piconewtons [43] are operating in the spindles. This suggests that mechanically these spindles are similar to the Drosophila spindles considered above, so it is likely that some additional strengthening of the spindle is necessary in early stages of mitosis. In our opinion, the prime candidates for this are numerous MTs that orient laterally [44, 45], rather than along the spindle axis, and so, if cross-linked with the ipMTs can serve as trusses and struts stiffening the spindle. Additional or alternative strengthening can be provided by embedding the spindle in an actin meshwork [46], a lipid membrane envelope [47], other cytoskeletal elements [19], i.e. MAPs, or ‘spindle matrix’ networks [48].
Additional arguments for the spindle’s mechanical reinforcement is the observation that when a cricket or grasshopper spermatocyte spindle is cut by a micro-needle half-way between one of the poles and the equator, or across the equator diagonally, the shapes of the two resulting parts do not change drastically compared to how they appear in the intact spindles [49]. (One would expect the MTs to spring loose and straighten without lateral restrictions.) Similarly, halves of the spindles in fertilized eggs and blastomeres of the sand dollar, derived from breaking the spindles by stretching, kept their fusiform shapes [50]. However, after the cuts and breaks, the spindles look a little ‘frayed’, as if some MTs are splayed. Spindle’s stretching in these organisms indicates too high mechanical strength of the spindles [50]: a stretching force of up to 104 pN does not change the spindle length and shape in metaphase, while our theory predicts that a force in the range of a few hundreds of piconewtons would deform the chrMT and ipMT bundles noticeably. However, kinetochore MT fibers connecting the poles and chromosomes in metaphase are already stretched, and further stretching of these fibers are not likely to be broken or deformed by relatively great forces. These fibers are in parallel with chrMTs and ipMTs, which can explain the results of the stretching experiment. Our theory predicts that if instead the spindle is compressed, it has to appear much weaker mechanically than if stretched.
Besides strengthening of the ipMT and chrMT bundles laterally with cytoskeletal elements, other factors that could significantly change the process of mechanical stabilization of the spindle are very high dynamicity of the MTs in the spindle [34], regulation of MT properties by non-motor proteins [51] and length and width regulation of the MT fibers [52]. The former could ensure that elastic deformations and stresses do not have time to develop before individual MTs disassemble, and the latter could be the reason that very long buckled MTs are absent. We would like to stress again that our analysis does not apply to the systems where the spindle dynamics is dominated by the almost forceless (Listeria-actin-tail-like [4]) emission of the chromosomal MTs, focusing them at the poles or other potential shape-forming mechanisms [9, 53].
Another issue important for the spindle mechanics that we did not consider in detail is that chromosomes, in addition to MTs, are also elastic deformable elements. The following argument suggests that chromosomal deformations are moderate and do not change drastically the spindle shape. The polymerizing MTs, and/or chromokinesin pushing forces applied to the chromosome arms are in the tens of piconewtons range (a few piconewtons per MT times ~10 MTs per chromosome). These forces are applied to the chromosome arm over an area of ~1 µm2, resulting in the pressure of tens of pN µm−2. The effective stiffness of the chromosome arm is ~100 pN µm−2 [16], so the chromosomes are deformed only moderately. (Pressure divided by stiffness, ~0.1–0.5, gives the effective elastic strain.) The fact that chromosomal deformations are not huge is due to the spindle geometry: the MT lattice is much stiffer than the chromosome arms, but MTs are long and thin, while chromosomes are short and thick, plus the forces applied to the MTs are focused near their ends, while those applied to the chromosome arms are spread over their area. Nevertheless, the chromosomes’ role in the spindle mechanics will have to be more thoroughly examined in the future: at significant deformations, chromosomes could become crowded, start behaving like a ‘visco-elastic’ aggregate and dominate the spindle behavior.
Finally, our prediction that the MTs have to be clamped at the spindle poles raises questions about the molecular nature of the connections between the MT minus ends and the centrosomes (similarly, molecular details of the chrMT plus end interactions with the chromosome arms have to be investigated). Indeed, the moment of the bending forces of the order of hundred pN µm is applied to the MT bundle’s minus ends. If the MTs are cantilevered in the centrosomes, the size of which is but about 1 µm (and so the effective lever arm is about 1 µm), then such moment means that force of the order of 100 pN per bundle would be deforming the centrosome. Such forces would probably break the centrosome, so it is likely that larger relatively rigid structures surround the centrosomes serve as a ‘block of cement’ in which the MTs can be clamped. One candidate for such a structure is the NuMA protein network [54]. It would be informative to see what are the consequences for the spindle shape from perturbations of the mechanical strength of such a network.
6. Conclusion and outlook
We examined the role of elastic forces bending MTs in shaping the mitotic spindle. Our theory predicts that a flexible, hinge-like connection between the MTs and the spindle poles would make the spindle mechanically unstable. On the other hand, if the MTs are clamped at the spindle poles, the mechanical properties of the spindle become more robust. Based on the theory, about ten tightly cross-linked MTs are the minimal required number per bundle keeping the spindle stable. The model suggests that each chromosomal and interpolar MT bundle in the spindle can be considered as a spring, with a stiffness of the order of ~20–30 pN µm−1. The model also hints that the cell has to limit the power of the outward-pushing molecular motors: too many of them would simply waste their power by bending the spindle MTs out of shape and not transducing their force to the spindle poles.
A mathematical ‘proof’ that certain mechanism works in the cell is rarely convincing, because models are based on simplifying assumptions and because of complexity and redundancy of the cell phenomena. The value of mathematical models is in their ability to either demonstrate that a hypothesis, though qualitatively plausible, does not conform with physical laws and quantitative constraints imposed by available data, or to make clear predictions about which data are or are not consistent with the theory, thereby suggesting further experiments and modeling refinements. Our model is able to explain the fusiform shape of the mitotic spindles in metaphase and anaphase in the early Drosophila embryo. However, some data, such as insensitivity of the spindle shape to motor inhibitions, to cutting the spindle, and very high rigidity of the spindle, indicate that the MT elasticity may not be the whole story. It is possible that after the spindle is assembled in prometaphase and shaped by the elastic forces, some additional reinforcement is put in place in metaphase. Candidates for such reinforcement are (not mutually exclusive) additional short MTs or MAPs that can serve as trusses and struts, actin, ‘spindle matrix’ and lipid membrane networks enveloping the spindle. Another possibility is that the MT length is regulated in the spindle by motor-induced forces.
In order to quantitatively understand the spindle mechanics, besides detailed microscopy of the spindle, accurate mechanical measurements of the forces and rheologies of the spindle elements have to be made. Indeed, at the present the motor-generated forces are either inferred or crudely estimated; rapid MT turnover can make the spindle more ‘fluid’, than solid like. To test some of the model predictions, it could be useful to look for long MTs with characteristic buckled shapes in the spindles, to measure spindle deformations by stresses of various frequency and localization, and to strengthen or weaken the protein networks near the spindle poles and to observe consequent shape changes. Perhaps the main message of this study is that the mitotic spindle shape can reveal important information about the molecular mechanisms of the mitotic machinery, and that elastic forces of the bending MTs have to be taken into account to understand the spindle dynamics quantitatively.
Acknowledgments
This work was supported by the National Institutes of Health grant GM068952 to AM. We thank R Wollman, J Scholey, K Bloom and T Mitchison for useful discussions and D Sharp and J Scholey for sharing the data.
Glossary
List of abbreviations
- MTs
microtubules
- chrMTs
chromosome arm MTs
- ipMTs
interpolar MTs
Glossary
- Mitotic spindle
Fusiform-shaped bi-polar array of overlapping dynamic microtubules that segregate chromosomes with the help of multiple molecular motors.
- Microtubules
Linear dynamic polymers with static minus end and dynamic plus end. In the spindle, the minus end is focused at or near the spindle poles. The plus ends of the astral microtubules reach the cell boundaries; the plus ends of the interpolar microtubules reach the spindle mid zone; and the plus ends of the kinetochore and chromosomal microtubules reach the chromosomes.
- Molecular motors
Proteins able to use the chemical energy of ATP hydrolysis to generate mechanical force and movement. Specifically, mitotic motors of Dynein and Kinesin families exert sliding, pushing and pulling forces on microtubules and chromosomes in the spindle.
- Clamp
A rigid structure holding an elastic rod (microtubule) in a fixed position and orientation.
- Hinge
A type of bearing that connects an elastic rod (microtubule) with the spindle pole, allowing an angle of rotation between them.
- Spring constant, or stiffness
Measure of the ‘strength’ of a spring (has units of force per unit length): the proportionality coefficient between force and extension in the Hooke’s law.
Appendix A. Derivation of the equation for the shape
Introducing the moment of the internal stresses on the cross section of the MT bundle M(s) and the resulting internal stress on the cross section F(s), we can determine the equilibrium shape of the bundle from the linear elasticity theory [31]:
| (A.1) |
At the plus end, F = P = {−P, 0}, and since F′ = 0, then at all points along the bundle we have F = P, and
| (A.2) |
Using the non-dimensionalization F → FB/L2, M → MB/L, and introducing the angle θ(s) according to t = {sin θ, cos θ}, we obtain from the first of equation (A.2) the only nonzero component of the moment Mz = −θ′. Substitution of this expression into the second of equation (A.2) leads to
Appendix B. Analytical solutions of the shape equation
The solution of equations (2)–(4) can be found analytically in the form of the elliptic functions [29]:
| (B.1) |
where m is an integration constant, and am(u|m) denotes the inverse of the elliptic integral of the first kind:
Using the properties of the elliptic functions, it can be shown that the solution of equation (B.1) and its derivative at s = 0 have the form
| (B.2) |
where . Substituting the above expressions into the corresponding boundary conditions at the left end we obtain the equations for the integration constants:
| (B.3) |
where cn = cos(ϕ). After constants m1,2 are found, the shape of the bundle is obtained by integration:
| (B.4) |
Let us denote
so that θ(s) = π/2 − 2ψ(s).
Consider the indefinite integral equation (B.4) which can be rewritten as
| (B.5) |
Recall the formula for integration of cn(u|m) = cos(am(u|m)):
where is the elliptic integral of the second kind, and sgn(x) = x/|x|. Equation (B.5) becomes
| (B.6) |
The indefinite version of equation (B.4) is given by
| (B.7) |
We have ψ(1) = u(1) = 0, ψ(0) = ψ0 = am(u0|m), u(0) = u0.
Finally, the shape of the bundle is determined parametrically as follows:
| (B.8) |
| (B.9) |
Noting that am(0|m) = sn(0|m) = E(0|m) = 0, cn(0|m) = dn(0|m) = 1, we find from equation (B.9) that y(1) = (2/mu0)[1 − dn(u0|m)]. The general formulae (B.8), (B.9) can be simplified for two types of the boundary conditions discussed above.
Hinge at the pole
In this case, we have m = m2, dn(u0|m2) = 0, and dn(u|m2) ≥ 0, so the bundle shape is given by the formulae
| (B.10) |
| (B.11) |
It should be noted that there exists a critical value of the force Pcr = π2/4, such that for P < Pcr equation (B.3) admits no solution with positive y2. This critical force corresponds to the first eigenvalue of the buckling problem.
Clamp at the pole
In this case, we have ψ0 = α/2, and , where the plus sign is chosen for P < Pcr, and for P > Pcr the sign depends on the value of s. Here Pcr is a critical force which depends on the clamping angle α. For P ≥ Pcr the shape of the MT bundle has an inflection point (see below).
Consider these two cases separately, starting from P < Pcr. Since u′(s) = −u0 < 0, the function dn(u(s)|m1) is increasing, so that function dn(u(s)|m1) does not change its sign. This leads to the following expressions for the bundle shape:
| (B.12) |
| (B.13) |
As the elliptic integral of the second kind E(ϕ|m) has a positive derivative, the derivative of the horizontal coordinate x′(s) is also positive. The same statement is valid for the derivative of the vertical coordinate y′(s), so that the bundle has no inflection points for P < Pcr.
The case P > Pcr is more complicated, since the function dn(u(s)|m1) at some value s = s* changes its sign. This value s* is found from the relation . The smallest positive zero of the periodic function cn(u|m) is given by u* = K(m), where K(m) = F(π/2, m). Using this result, we find . The corresponding angle , thus we find .
The change of dn(u(s)|m1) at s = s* from a negative to a positive value means that the function f0(s, m1) = E(am(u|m1)|m1) sgn(dn(u|m1)) increases its value by 2E*. As we want to have a continuous and smooth solution with respect to s, we compensate for this change in sign by introducing a smooth function f(s, m1) in place of the discontinuous function f0(s, m1):
which can also be written in the form f(s, m1) = E(ψ(s)|m1) sgn(dn(u|m1)) − E*[1 + sgn(dn(u|m1))]. Thus, we finally have the bundle shape in the case P > Pcr:
| (B.14) |
| (B.15) |
The bundle shape defined parametrically by equations (B.14), (B.15) has the inflection point at s = s*.
B.1. Analytical solutions for ipMT bundles with great sliding force
The numerical solution is obtained by iterations over the value sbent. The iteration step consists of the following stages:
Having the current values of sbent, the length of the parallel overlap is (1 − sbent), find the force P = γ(1 − sbent).
Use the formulae in the previous subsection to find the shape of the curved part of the bundle. This gives the abscissa of the right end of this part, xre = x(sbent).
Compute the abscissa of the right end of the bundle as xr = xre + (1 − sbent).
Find the updated value of abscissa of the left end of the cross-linked overlap of the anti-parallel bundles xl = l − xr. Thus, we obtain the updated value of the overlap length δ = xr − xl = 2(xre + (1 − sbent)) − l.
Find the updated arc length of the bent part of the left bundle .
If the iteration process converges, we arrive at the equilibrium shape of the bundles which depends on the pole–pole distance 2l. The convergence point of the iteration process satisfies the condition 1 − sbent = 2(x(sbent) + (1 − sbent)) − l, where x(sbent) also depends on P = γ(1 − sbent). Thus, we can write this condition as
| (B.16) |
This equation gives a way to an analytic solution of the problem.
Hinge at the pole
There is a lower bound of γ at which the nontrivial solution exists given by the condition P > Pcr which takes the form .
The function s2(1 − s) has a maximum equal to 4/27 reached at s = 2/3. This gives the lower bound γl = 27π2/16 ≈ 16.66. The pole–pole distance 2l imposes an additional restriction on the value of γ. In order to have the nontrivial solution, the unperturbed structure with both horizontal bundles should be unstable: the condition P > Pcr should be valid for sbent = l − 1. This gives the additional condition γ > π2/(4(l − 1)2l), which means that when the pole–pole distance is small, close to the MT bundle length, the values of γ ~ 100 are required to buckle the ipMT bundle.
From (B.10) we have
We determine the modulus of the elliptic functions m2 from the condition . Using the smallest positive zero u* = K(m) of the periodic function cn(u|m), we obtain m2 as an implicit function of γ and . The amplitude ψ0 satisfies the condition 1 − m2 sin2 ψ0 = 0, from which we find , and finally
| (B.17) |
Clamp at the pole
In the case , equation (B.12) gives
| (B.18) |
where m1 is found as a function of γ and α from the equation: . When P > Pcr, we have
| (B.19) |
B.2. Unstressed interpolar bundle is shaped as a circular arc
Consider an elastic rod of a length (2 − δ) clamped at both ends at an angle α. The positions of the left and right ends are at the origin and at (2l, 0), respectively. In the case when there is no force applied to the rod at the poles, the force balance equation reads
| (B.20) |
Due to the mirror symmetry about the midpoint of the rod, the equivalent problem is
| (B.21) |
The rod shape {x(s), y(s)} is determined by a set of equations:
| (B.22) |
The solution of this simple problem is θ(s) = As + α, A = −α/(1 − δ/2). Integrating equation (B.22), we have
| (B.23) |
Using the condition x(1 − δ/2) = l, we have x(1 − δ/2) = −A−1 sin α = l, and obtain the value of δ = 2(1 − (αl)/(sin α)) and of A = −sin α/l. Excluding s from equation (B.23), we find the rod shape (x − l)2 + (y + l cot α)2 = (L/sin α)2, as a circular arc of the radius l/sin α. The elastic energy of the half rod is
B.3. Semi-analytical solutions for the shape of the interpolar bundle
We extend the treatment of the previous subsection to consider the general case when the nonzero force P, the value of which is unknown and has to be found, is applied to the interpolar bundle at the spindle poles. As above, the ends are clamped at a distance 2l(1/2 < l < 1). Due to the problem’s symmetry, we consider only the left half of the system: the left end is clamped at the origin at an angle α; the right end has coordinates {l, yr} (yr is unknown), and the tangent at that point is parallel to the horizontal axis. The arc length position of the right end point is sm = 1 − δ/2 < 1. The solution for P = 0 found above corresponds to .
The force balance equation in this case is
| (B.24) |
and the rod shape is determined by the set of equations x′(s) = sin θ, y′(s) = cos θ. The solution of equation (B.24), similarly to equation (B.1), has the form
| (B.25) |
where m is an integration constant, and am(u|m) is the inverse of the elliptic integral of the first kind (see section 6.2). The solution of equation (B.25) at s = 0 has the form . Substituting the above expression into the corresponding boundary conditions at the left end, we obtain the equations for the integration constant m:
| (B.26) |
After the constant m is found, the shape and elastic energy of the rod are obtained by integration:
| (B.27) |
We can substitute u(θ) = θ′(s) into equation (B.24) to re-write it in the form uu′ = P cos θ, and after integration, we find
| (B.28) |
Let us denote
so that θ(s) = π/2 − 2ψ(s). To compute the constant C, we differentiate equation (B.25) to have u = 2u0 dn(u|m) and . On the other hand, sin θ = cos 2ψ = 2 cos2 ψ − 1 = 2 cn2(u|m) − 1. Using these relations in equation (B.28), we have (4P/m) dn2(u|m) = 2P(C + 2 cn2(u|m) − 1), and recalling the relation for the elliptic functions dn2(u|m) = 1 − m + m cn2(u|m), we arrive at 2/m(1 − m + m cn2(u|m)) = 2 cn2(u|m) − 1 + C and obtain C = (2 − m)/m. Thus, we have
| (B.29) |
It is easy to see that in the case of zero force, P = 0, we have from equation (B.26) m = 0. Comparing equation (B.29) with the results of the previous subsection, we find in the limit P, m → 0: A2 = sin2 α/l2 = 4P/m. Substituting equation (B.28) into equation (B.27), we have
which gives the final expression for the elastic energy:
| (B.30) |
We established earlier that for P < Pcr = (π/2sm)2,
The horizontal position of the right end at s = sm is l, and we have u(sm) = 0, so
| (B.31) |
As the value of the parameter m depends on sm as defined in equation (B.26), the relations (B.26), (B.31) determine the values of sm and m for given value of P. Substituting equation (B.31) into equation (B.30), we arrive at , where both P and m depend on sm.
Using the definition of F(u|m) and equation (B.26), we obtain
| (B.32) |
so that
| (B.33) |
Substituting equation (B.32) into equation (B.31), we have
| (B.34) |
Expressions (B.25), (B.33), (B.34) implicitly solve the problem of the interpolar bundle shape: equation (B.34) determines the parameter m for given l, α and sm; substituting the result into equation (B.33) and minimizing the elastic energy, we can find the value of sm corresponding to the minimal energy. Equation (B.26) gives the value of the force P. Finally, the shape is given by equation (B.25).
Specifically, expressing sm from equation (B.34) and substituting it into equation (B.33), we find
| (B.35) |
In the limiting case when m = 0, the expression in the square brackets becomes equal to sin α/(mα), so that at m = 0 we find , and equation (B.35) gives ϒ(0) = α sin α/2l = ϒ0, so the case m = 0 corresponds to the unstressed circular-arc-shaped bundle.
The minimal value of the elastic energy can be found by differentiating equation (B.35) with respect to the parameter m, ∂ϒ/∂m = 0. For an arbitrary value of α, the minimum corresponds to the value m = 2. (In addition, there is a minimum at m = 0 at a special angle α = α*, where α* satisfies the equation (α*/sin α*)2 + (α*/sin α*) cos α* = 1. However, as the left-hand side of this equation increases for positive values of α*, one finds only the trivial solution α* = 0.) Thus, the minimum of the elastic energy
is reached at m = 2.
The corresponding values of sm and P are computed as
| (B.36) |
We used equation (B.36) to compute the bundle length and force needed to stabilize it corresponding to the minimal elastic energy at a given clamping angle and pole–pole distance. Then we computed and plotted the bundle’s shape using the formula
| (B.37) |
In fact, this shape is very close to the circular arc, and corresponding force P is very small.
Equation (B.37) gives the bundle’s shape when the motors at the microtubules’ overlap at the spindle equator only cross-link, but do not push the microtubules apart. In order to compute the shape in the presence of the active pushing motors, we used the Taylor expansion for the elastic energy as a function of sm in the vicinity of s̃m:
| (B.38) |
where the coefficients ak(l, α) can be found as follows. Expanding the expression for sm into the Taylor series around m = 2, we have sm = s̃m + lG(α)(m − 2) + O(m − 2), so that m − 2 = (sm − s̃m)/lG(α). Expanding also equation (B.35), we obtain
Here G(α) and Fk(α) denote very cumbersome expressions containing the elliptic integrals that we computed, but do not show here. Comparing the last relation with equation (B.38), we find an explicit expression for the coefficients ak(l, α) = 2Fk(α)/(Lk+1Gk(α)).
The molecular motors distributed over the overlapping part of the bundle increase the system energy by adding γδ2/2 to the elastic energy 2ϒ in equation (B.38). The total energy ϒ̅ then reads
(We kept only first four terms in the Taylor series, which gives a very accurate approximation.) The minimum of total energy corresponds to ∂ϒ̅/∂δ = 0, i.e.,
| (B.39) |
We solved equation (B.39) numerically to find δ, and then obtained the corresponding value of sm = 1−δ/2. Substituting this value into equation (B.34), we numerically find the parameter m. Then, using equation (B.26), we numerically find the value of P, and finally calculate and plot the shape from equation (B.25).
References
- 1.Bray D. Cell Movements. New York: Garland; 2002. [Google Scholar]
- 2.Karsenti E, Vernos I. The mitotic spindle: a self-made machine. Science. 2001;294:543–547. doi: 10.1126/science.1063488. [DOI] [PubMed] [Google Scholar]
- 3.Scholey JM, Brust-Mascher I, Mogilner A. Cell division. Nature. 2003;422:746–752. doi: 10.1038/nature01599. [DOI] [PubMed] [Google Scholar]
- 4.Karsenti E, Nedelec F. The mitotic spindle and actin tails. Biol. Cell. 2004;96:237–240. doi: 10.1016/j.biolcel.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 5.McIntosh JR, Grishchuk EL, West RR. Chromosome–microtubule interactions during mitosis. Annu. Rev. Cell Dev. Biol. 2002;18:193–219. doi: 10.1146/annurev.cellbio.18.032002.132412. [DOI] [PubMed] [Google Scholar]
- 6.Wollman R, Civelekoglu-Scholey G, Scholey JM, Mogilner A. Reverse engineering of force integration during mitosis in the Drosophila embryo. Mol. Syst. Biol. 2008;4:195. doi: 10.1038/msb.2008.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mitchison TJ, Maddox P, Gaetz J, Groen A, Shirasu M, Desai A, Salmon ED, Kapoor TM. Roles of polymerization dynamics, opposed motors, and a tensile element in governing the length of Xenopus extract meiotic spindles. Mol. Biol. Cell. 2005;16:3064–3076. doi: 10.1091/mbc.E05-02-0174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sharp DJ, Brown HM, Kwon M, Rogers GC, Holland G, Scholey JM. Functional coordination of three mitotic motors in Drosophila embryos. Mol. Biol. Cell. 2000;11:241–253. doi: 10.1091/mbc.11.1.241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Burbank KS, Mitchison TJ, Fisher DS. Slide-and-cluster models for spindle assembly. Curr. Biol. 2007;17:1373–1383. doi: 10.1016/j.cub.2007.07.058. [DOI] [PubMed] [Google Scholar]
- 10.Hoyt MA, Geiser JR. Genetic analysis of the mitotic spindle. Annu. Rev. Genet. 1996;30:7–33. doi: 10.1146/annurev.genet.30.1.7. [DOI] [PubMed] [Google Scholar]
- 11.Kapitein LC, Peterman EJ, Kwok BH, Kim JH, Kapoor TM, Schmidt CF. The bipolar mitotic kinesin Eg5 moves on both microtubules that it crosslinks. Nature. 2005;435:114–118. doi: 10.1038/nature03503. [DOI] [PubMed] [Google Scholar]
- 12.Tokai-Nishizumi N, Ohsugi M, Suzuki E, Yamamoto T. The chromokinesin kid is required for maintenance of proper metaphase spindle size. Mol. Biol. Cell. 2005;16:5455–5463. doi: 10.1091/mbc.E05-03-0244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mazumdar M, Misteli T. Chromokinesins: multitalented players in mitosis. Trends Cell Biol. 2005;15:349–355. doi: 10.1016/j.tcb.2005.05.006. [DOI] [PubMed] [Google Scholar]
- 14.Laan L, Husson J, Munteanu EL, Kerssemakers JW, Dogterom M. Force-generation and dynamic instability of microtubule bundles. Proc. Natl. Acad. Sci. USA. 2008;105:8920–8925. doi: 10.1073/pnas.0710311105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bouck DC, Bloom K. Pericentric chromatin is an elastic component of the mitotic spindle. Curr. Biol. 2007;17:741–748. doi: 10.1016/j.cub.2007.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marshall WF, Marko JF, Agard DA, Sedat JW. Chromosome elasticity and mitotic polar ejection force measured in living Drosophila embryos by four-dimensional microscopy-based motion analysis. Curr. Biol. 2001;11:569–578. doi: 10.1016/s0960-9822(01)00180-4. [DOI] [PubMed] [Google Scholar]
- 17.Howard J. Elastic and damping forces generated by confined arrays of dynamic microtubules. Phys. Biol. 2006;3:54–66. doi: 10.1088/1478-3975/3/1/006. [DOI] [PubMed] [Google Scholar]
- 18.Cosentino Lagomarsino M, Tanase C, Vos JW, Emons AM, Mulder BM, Dogterom M. Microtubule organization in three-dimensional confined geometries: evaluating the role of elasticity through a combined in vitro and modeling approach. Biophys. J. 2007;92:1046–1057. doi: 10.1529/biophysj.105.076893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Brangwynne CP, MacKintosh FC, Kumar S, Geisse NA, Talbot J, Mahadevan L, Parker KK, Ingber DE, Weitz DA. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell Biol. 2006;173:733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wiggins CH, Riveline D, Ott A, Goldstein RE. Trapping and wiggling: elastohydrodynamics of driven microfilaments. Biophys. J. 1998;74:1043–1060. doi: 10.1016/S0006-3495(98)74029-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kozlowskiz C, Srayko M, Nedelec F. Cortical microtubule contacts position the spindle in C elegans embryos. Cell. 2007;129:499–510. doi: 10.1016/j.cell.2007.03.027. [DOI] [PubMed] [Google Scholar]
- 22.Nedelec F. Computer simulations reveal motor properties generating stable antiparallel microtubule interactions. J. Cell Biol. 2002;158:1005–1015. doi: 10.1083/jcb.200202051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sharp DJ, McDonald KL, Brown HM, Matthies HJ, Walczak C, Vale RD, Mitchison TJ, Scholey JM. The bipolar kinesin, KLP61F, cross-links microtubules within interpolar microtubule bundles of Drosophila embryonic mitotic spindles. J. Cell Biol. 1999;144:125–138. doi: 10.1083/jcb.144.1.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sunderland, MA: Sinauer; 2001. [Google Scholar]
- 25.Mickey B, Howard J. Rigidity of microtubules is increased by stabilizing agents. J. Cell Biol. 1995;130:909–917. doi: 10.1083/jcb.130.4.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Odde DJ, Ma L, Briggs AH, DeMarco A, Kirschner MW. Microtubule bending and breaking in living fibroblast cells. J. Cell Sci. 1999;112:3283–3288. doi: 10.1242/jcs.112.19.3283. [DOI] [PubMed] [Google Scholar]
- 27.Rieder CL. Formation of the astral mitotic spindle: ultrastructural basis for the centrosome-kinetochore interaction. Electron Microsc. Rev. 1990;3:269–300. doi: 10.1016/0892-0354(90)90005-d. [DOI] [PubMed] [Google Scholar]
- 28.Claessens MM, Bathe M, Frey E, Bausch AR. Actin-binding proteins sensitively mediate F-actin bundle stiffness. Nat. Mater. 2006;5:748–753. doi: 10.1038/nmat1718. [DOI] [PubMed] [Google Scholar]
- 29.Abramowitz M, Stegun IA. Handbook of Mathematical Functions. New York: Dover; 1964. [Google Scholar]
- 30.Popov EP. Theory and Calculation of Flexible Elastic Rods. Moscow: Nauka; 1986. [Google Scholar]
- 31.Landau LD, Lifshitz EM. Theory of Elasticity. New York: Reed; 1986. [Google Scholar]
- 32.Maddox P, Straight A, Coughlin P, Mitchison TJ, Salmon ED. Direct observation of microtubule dynamics at kinetochores in Xenopus extract spindles: implications for spindle mechanics. J. Cell Biol. 2003;162:377–382. doi: 10.1083/jcb.200301088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schliwa M, editor. Molecular Motors. New York: Wiley-VCH; 2002. [Google Scholar]
- 34.Cheerambathur DK, Civelekoglu-Scholey G, Brust-Mascher I, Sommi P, Mogilner A, Scholey JM. Quantitative analysis of an anaphase B switch: predicted role for a microtubule catastrophe gradient. J. Cell Biol. 2007;177:995–1004. doi: 10.1083/jcb.200611113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gardner MK, Pearson CG, Sprague BL, Zarzar TR, Bloom K, Salmon ED, Odde DJ. Tension-dependent regulation of microtubule dynamics at kinetochores can explain metaphase congression in yeast. Mol. Biol. Cell. 2005;16:3764–3775. doi: 10.1091/mbc.E05-04-0275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Varga V, Helenius J, Tanaka K, Hyman AA, Tanaka TU, Howard J. Yeast kinesin-8 depolymerizes microtubules in a length-dependent manner. Nat. Cell. Biol. 2006;8:957–962. doi: 10.1038/ncb1462. [DOI] [PubMed] [Google Scholar]
- 37.Brust-Mascher I, Civelekoglu-Scholey G, Kwon M, Mogilner A, Scholey JM. Model for anaphase B: role of three mitotic motors in a switch from poleward flux to spindle elongation. Proc. Natl. Acad. Sci. USA. 2004;101:15938–15943. doi: 10.1073/pnas.0407044101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bouck DC, Joglekar AP, Bloom KS. Design features of a mitotic spindle: balancing tension and compression at a single microtubule kinetochore interface in budding yeast. Annu. Rev. Genet. 2008;42:335–359. doi: 10.1146/annurev.genet.42.110807.091620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gardner MK, et al. The microtubule-based motor Kar3 and plus end-binding protein Bim1 provide structural support for the anaphase spindle. J. Cell Biol. 2008;180:91–100. doi: 10.1083/jcb.200710164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Winey M, Mamay CL, O’Toole ET, Mastronarde DN, Giddings TH, McDonald KL, McIntosh JR. Three-dimensional ultrastructural analysis of the Saccharomyces cerevisiae mitotic spindle. J. Cell Biol. 1995;129:1601–1615. doi: 10.1083/jcb.129.6.1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hagan IM, Hyams JS. Forces acting on the fission yeast anaphase spindle. Cell Motil Cytoskeleton. 1996;34:69–75. doi: 10.1002/(SICI)1097-0169(1996)34:1<69::AID-CM7>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 42.Mastronarde DN, McDonald KL, Ding R, McIntosh JR. Interpolar spindle microtubules in PTK cells. J. Cell Biol. 1993;123:1475–1489. doi: 10.1083/jcb.123.6.1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nicklas RB. Measurements of the force produced by the mitotic spindle in anaphase. J. Cell Biol. 1983;97:542–548. doi: 10.1083/jcb.97.2.542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.McDonald KL, O’Toole ET, Mastronarde DN, McIntosh JR. Kinetochore microtubules in PTK cells. J. Cell Biol. 1992;118:369–383. doi: 10.1083/jcb.118.2.369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nicklas RB, Kubai DF, Hays TS. Spindle microtubules and their mechanical associations after micromanipulation in anaphase. J. Cell Biol. 1982;95:91–104. doi: 10.1083/jcb.95.1.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Silverman-Gavrila RV, Forer A. Evidence that actin and myosin are involved in the poleward flux of tubulin in metaphase kinetochore microtubules of crane-fly spermatocytes. J. Cell Sci. 2000;113:597–609. doi: 10.1242/jcs.113.4.597. [DOI] [PubMed] [Google Scholar]
- 47.Bobinnec Y, Marcaillou C, Morin X, Debec A. Dynamics of the endoplasmic reticulum during early development of Drosophila melanogaster. Cell Motil Cytoskeleton. 2003;54:217–225. doi: 10.1002/cm.10094. [DOI] [PubMed] [Google Scholar]
- 48.Johansen KM, Johansen J. Cell and molecular biology of the spindle matrix. Int. Rev. Cytol. 2007;263:155–206. doi: 10.1016/S0074-7696(07)63004-6. [DOI] [PubMed] [Google Scholar]
- 49.Nicklas RB, Lee GM, Rieder CL, Rupp G. Mechanically cut mitotic spindles: clean cuts and stable microtubules. J. Cell Sci. 1989;94:415–423. doi: 10.1242/jcs.94.3.415. [DOI] [PubMed] [Google Scholar]
- 50.Hiramoto Y, Nakano Y. Micromanipulation studies of the mitotic apparatus in sand dollar eggs. Cell Motil Cytoskeleton. 1988;10:172–184. doi: 10.1002/cm.970100122. [DOI] [PubMed] [Google Scholar]
- 51.Manning AL, Compton DA. Abstract structural and regulatory roles of nonmotor spindle proteins. Curr. Opin Cell Biol. 2008;20:101–106. doi: 10.1016/j.ceb.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Maiato H, Khodjakov A, Rieder CL. Drosophila CLASP is required for the incorporation of microtubule subunits into fluxing kinetochore fibres. Nat. Cell Biol. 2005;7:42–47. doi: 10.1038/ncb1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gaetz J, Gueroui Z, Libchaber A, Kapoor TM. Examining how the spatial organization of chromatin signals influences metaphase spindle assembly. Nat. Cell Biol. 2006;8:924–932. doi: 10.1038/ncb1455. [DOI] [PubMed] [Google Scholar]
- 54.Chakravarty A, Howard L, Compton DA. A mechanistic model for the organization of microtubule asters by motor and non-motor proteins in a mammalian mitotic extract. Mol. Biol. Cell. 2004;15:2116–2132. doi: 10.1091/mbc.E03-08-0579. [DOI] [PMC free article] [PubMed] [Google Scholar]