Functional Grading of Mineral and Collagen in the Attachment of Tendon to Bone

Abstract

Attachment of dissimilar materials is a major challenge because high levels of localized stress may develop at their interfaces. An effective biologic solution to this problem exists at one of nature's most extreme interfaces: the attachment of tendon (a compliant, structural “soft tissue”) to bone (a stiff, structural “hard tissue”). The goal of our study was to develop biomechanical models to describe how the tendon-to-bone insertion derives its mechanical properties. We examined the tendon-to-bone insertion and found two factors that give the tendon-to-bone transition a unique grading in mechanical properties: 1), a gradation in mineral concentration, measured by Raman spectroscopy; and 2), a gradation in collagen fiber orientation, measured by polarized light microscopy. Our measurements motivate a new physiological picture of the tissue that achieves this transition, the tendon-to-bone insertion, as a continuous, functionally graded material. Our biomechanical model suggests that the experimentally observed increase in mineral accumulation within collagen fibers can provide significant stiffening of the partially mineralized fibers, but only for concentrations of mineral above a “percolation threshold” corresponding to formation of a mechanically continuous mineral network within each collagen fiber (e.g., the case of mineral connectivity extending from one end of the fiber to the other). Increasing dispersion in the orientation distribution of collagen fibers from tendon to bone is a second major determinant of tissue stiffness. The combination of these two factors may explain the nonmonotonic variation of stiffness over the length of the tendon-to-bone insertion reported previously. Our models explain how tendon-to-bone attachment is achieved through a functionally graded material composition, and provide targets for tissue engineered surgical interventions and biomimetic material interfaces.

Introduction

The tendon-to-bone insertion connects two vastly different, highly ordered hierarchical tissues across a millimeter-wide region (Fig. 1) (1,2). Tensile modulus of tendon is ∼0.4 GPa in the direction of muscle force during physiologic loading conditions (3), and ∼20 GPa for bone (1). Structural interfaces with such severe material mismatches are prone to stress concentrations and failure (4). Tendon-to-bone insertion physiology is believed to result in a tougher interface through adaptations at the macroscopic level (e.g., the outward splay of the tissue) and the microscopic level (e.g., tissue composition and structure) (5,6). Our long-term goal is to develop a biomimetic strategy for attaching dissimilar materials using the tendon-to-bone insertion as a model biological system. This study contributes what we believe are new biomechanical models of how the tendon-to-bone insertion derives its mechanical properties.

Figure 1.

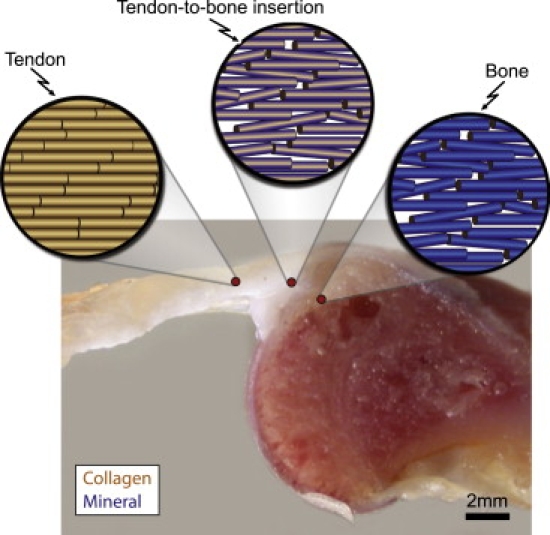
Tendon-to-bone insertion connects two very different, hierarchical tissues. A schematic of the collagen fibers is shown above a cross-sectional view of the tendon-to-bone insertion. Collagen fiber dispersion increases from tendon to bone. Blue shading in the schematic views indicates the concentration of mineral within each fiber. The schematic is representative of the diffuse model shown in Fig. 2b.

The traditional understanding of the tendon-to-bone insertion involves four discrete zones (5). Zone one, tendon, contains 90% by volume of well-aligned collagen fibers, predominantly type I, with small amounts of the proteoglycan decorin and the remaining volume primarily water (2,7). Tendon structure is hierarchical from the molecular- to the tissue-level. Triple-helix collagen molecules (tertiary structure, 1.5 nm diameter) aggregate in groups of five in a quarter-stagger array to form microfibrils (quaternary structure, 4 nm diameter) (8,9). Microfibrils aggregate in an approximately triclinic lattice to form fibrils (up to 0.5 μm in diameter) (10); fibrils aggregate to form fibers (3–7 μm in diameter); fibers aggregate to form fascicles (150–300 μm in diameter); fascicles combine to form tendon (millimeters in diameter). Zone two, fibrocartilage, contains collagen types II and III, with small amounts of types I, IX, and X and of the proteoglycans aggrecan and decorin (6,7,11,12). Zone three, mineralized fibrocartilage, is demarcated by the “tidemark,” interpreted by others as a mineralization front and a boundary between soft and hard tissue (5). Mineralized fibrocartilage contains type II collagen, with significant amounts of type X collagen and aggrecan (6,7,11,12). Zone four, bone, contains ∼40% by volume type I collagen following the hierarchical structure of tendon and contains ∼50% by volume of a stiff, carbonated apatite mineral (apatite). Apatite is situated predominantly within fibrils in ∼1–4 nm thick crystalline mineral platelets in gaps at the ends of collagen molecules; debate exists about the existence of mineralization outside of these gaps (13,14). Mechanically, zones two and three are approximately half as stiff as tendon (zone one); bone (zone 4) is nearly two orders of magnitude stiffer than tendon (6,15,16). The structural features responsible for this experimentally observed region between tendon and bone that is more compliant than either tendon or bone are unknown.

Traditionally, the attachment of tendon to bone has been described as occurring across distinct zones. This design (i.e., a four zone attachment) is fundamentally different from engineering design strategies for attachment of two dissimilar engineering materials. An abrupt transition between tendon and bone, as implied by the four-zone description, would lead to stress concentrations between zones and increased risk of failure at the interfaces. This challenge has led to the concept of “functional grading” (i.e., the gradual variation in composition and structure over a volume resulting in changes in the mechanical properties of the material) to alleviate stress concentrations (17). Whereas functional grading can occur at any length scale, it is typically incorporated into materials at the microscale. Based on this concept we hypothesized that, at the tissue hierarchical level, the tendon-to-bone insertion is a continuous, functionally graded material with respect to its mineral concentration, collagen fiber orientation distribution, and biomechanical properties. Our goal in this study is to define composition-structure-function relationships at the tendon-to-bone insertion. Specifically, we determined the spatial variations in mineral concentration and collagen fiber orientation in tendon-to-bone tissue samples. We then combined these experimental observations with observations reported elsewhere (6) to generate new tissue-level biomechanical models of the tendon-to-bone insertion.

Materials and methods

Study design

We used Raman spectroscopy to measure mineral content and polarized light microscopy to measure collagen fiber orientations along the tendon-to-bone insertion. These fiber-level (microscale) data supported a new model of the tendon-to-bone insertion that replaces the picture of four discrete zones with one of continuous functional grading, prompting us to characterize the structure-function relationships predicted by our data. As our Raman spectroscopy data indicated a spatial variation in the degree of mineralization, and as the degree of mineralization is known to affect cross-species variations in bone biomechanics (18,19), we quantified the ramifications of observed gradations in mineral volume fraction on tendon-to-bone insertion biomechanics. We then used our polarized light microscopy data and data from the literature to develop a mathematical model of structure-function relationships in the tendon-to-bone insertion by linking the fiber hierarchical level to the tissue hierarchical level.

Mathematical models

Relationship between mineral volume fraction and fiber mechanics

The first step in the modeling effort was characterizing the effect of observed gradations in mineral volume fraction on the effective stiffness tensor, C^(f)(ϕ), of a representative volume (“unit cell”) containing one partially mineralized fiber (Fig. 2 a). Mineral concentration was represented by the normalized mineral volume fraction, ϕ(x), defined as the ratio of the mineral volume fraction f_mineral(x) at a normalized position x to the volume fraction of mineral in the typical bone, $f_{\text{mineral}}^{\text{bone}}$ = 0.49 (14): ϕ(x) = f_mineral(x)/$f_{\text{mineral}}^{\text{bone}}$. The normalized position, x, along the centerline of the tendon-to-bone insertion, was defined with x = 0 at the end of the tendon (ϕ = 0) and x = 1 at the start of the bone (ϕ = 1).

Figure 2.

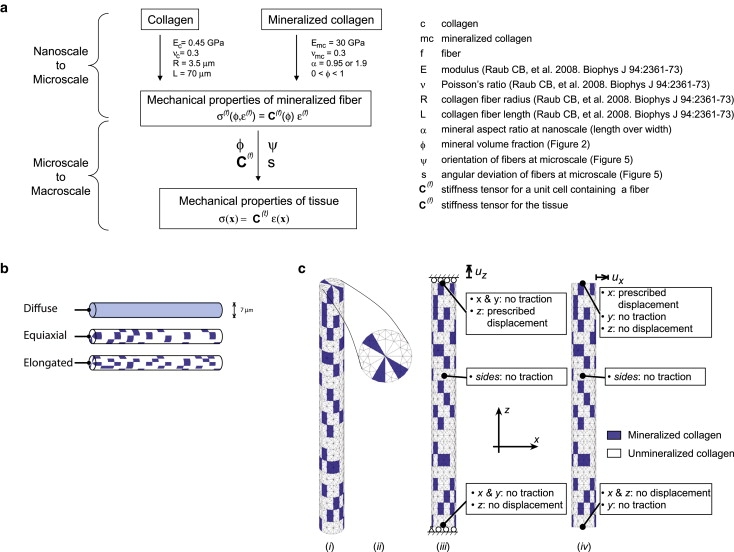
(a) Properties of mineralized and nonmineralized collagen at the nanoscale were incorporated with experimental measures of mineral content and collagen orientation to model the tendon-to-bone insertion at the microscale. (b) Three fiber-level models of mineral accumulation were studied. (c) Details for finite element model (i and ii) for Monte Carlo simulations to estimate the stiffness of partially mineralized fibers, and boundary conditions applied in extension (iii) and shear (iv).

Because our experimental measures were on the micrometer scale and because the details of the spatial accommodation between collagen and mineral at smaller length scales are still under investigation (14,20), we relied on bounds and plausible estimates within these bounds at this stage in the modeling. Specifically, we used the Hashin-Shtrikman homogenization bounds (21,22) to estimate limits on the stiffening effect of mineralization (Supporting Material, Section A), and we used three models to estimate the stiffening effects of the following submicrometer physiological features: the presence of preferential mineral nucleation sites in pockets of fibrils, the size and shape of the resulting enhanced mineralization regions, and the interconnectedness of such regions. Although these physiological details are unknown for partially mineralized fibers, stochastic variations in the spatial distributions of proteins that enhance apatite crystal nucleation should lead to pockets of stiffer (more mineralized) fibrils within partially mineralized fibers (23,24). Such heterogeneity in mineral distribution would be on the tens to thousands of nanometer scale, mostly below the resolution of the Raman microprobe. The three model mineral distributions described in the following paragraphs represent plausible, limiting cases (Fig. 2, b and c).

The first was a “diffuse” model, the Hashin-Shtrikman lower bound representing the extreme in which mineral accumulates uniformly at the micrometer length scale of interest (25); for example, according to this model, all fibers at a point in the tendon-to-bone insertion where ϕ = 0.5 contained half of the mineral of fibers in bone. The Hashin-Shtrikman lower bound corresponds to the case in which mineral accumulates in randomly sized, noncontacting spheres that are infinitesimally small compared to the radius and length of the fiber (26).

The second (“equiaxial”) model incorporated effects of nonuniform mineral accumulation. Fibers (radius R = 3.5 μm, length L = 70 μm; e.g., Raub et al. (27)) passing through the midpoint of the tendon-to-bone insertion contained an average of exactly half the mineral that would appear in an identical fiber in bone, but this mineral was distributed unevenly along fibers. All material within fibers was modeled as linearly elastic and isotropic; justification of this approximation is presented in the Supporting Material (Section B). Mineralized portions were prescribed mechanical properties representative of mineralized collagen fibers (isotropic, Young's modulus E_mc = 30 GPa, Poisson's ratio ν_mc = 0.3, where mc = mineralized collagen; see Discussion for justification of these values). The remaining, unmineralized regions were prescribed mechanical properties representative of unmineralized collagen (Young's modulus E_c = 0.45 GPa, Poisson's ratio ν_c = 0.3, where c = collagen; see Discussion for justification of these values). Randomly distributed, wedge-shaped clusters of mineralized collagen were distributed among pure (unmineralized) collagen. Clusters were assigned dimensions such that the exposure on the outer fiber surface was 3.5 μm × 3.67 μm (Fig. 2 b). The enhanced light-scattering caused by the fine-scale multiple interfaces of the tissue degraded the spatial resolution of the Raman microprobe sufficiently that we could not distinguish between the diffuse and the equiaxial models of mineral distribution. Clusters were permitted to adhere to neighboring clusters but not to overlap.

The third model (“elongated”) was identical to the second model except that regions of enhanced mineralization were elongated along the fiber axis (3.5 μm × 1.83 μm on the outer edge of the fiber, Fig. 2 b).

The effective stiffness tensors, C^(f), of fibers containing the equiaxed or elongated regions of enhanced mineralization were estimated as a function of ϕ through Monte Carlo simulations. Repeated finite element simulations assessed how nonuniform distribution of mineral affects the axial modulus, E_a, and the axial-transverse shear modulus, G_at, of partially mineralized fibers. The remaining three constants required to assemble an effective stiffness tensor were estimated by assuming: i), unit cells containing fibers were isotropic in their transverse planes (28); ii), the modulus for stretching in the plane of transverse isotropy was E_t = 0.175 E_a; iii), the Poisson's ratio for lateral contraction within the plane of transverse isotropy resulting from uniaxial loading in this plane was ν_tt = 0.3; iv), the Poisson's ratio for lateral contraction resulting from uniaxial loading along a fiber axis was ν_at = 0.3; and v), the stiffness tensor for a unit cell containing a single fiber was proportional to the stiffness of a fiber, with the constant of proportionality being the combined volume fraction of mineral and collagen, f_total, at each point; for example, the shear modulus of such a unit cell was f_totalG_at. Standard definitions were then applied to calculate the transversely isotropic stiffness tensor C^(f) from these engineering constants (26). Our assumptions were deemed reasonable because, when combined with the methods of the next section, they yielded estimates of tissue-level moduli that are consistent with data from the literature (29,30).

Boundary conditions for the repeated finite element simulations approximated extension and shear of fibers. In extension, the lower fiber surface was restrained from displacement in the axial (z) direction, whereas points on the upper surface were displaced a prescribed distance u_z in the z direction and allowed to move freely in the transverse plane (Fig. 2, c, iii). The remaining surfaces and directions were free of mechanical loads (traction-free boundary conditions). In shear, the lower surface was additionally restrained from displacement in the x direction, and the upper surface was displaced a prescribed distance u_x in the x direction, constrained from displacement in the z direction, and left free to displace in the y direction (Fig. 2 c, iv).

Equations were solved using commercial finite element software (Comsol, Newton, MA). Fibers were discretized into a minimum of 20,000 3D, quadratic-interpolation, tetrahedral elements (Fig. 2 c), and h-type convergence studies were carried out (4). Over 250 simulations with random mineral volume fractions were analyzed for each of the two clustering schemes (elongated and equiaxial) to estimate axial and shear moduli of a unit cell enclosing a partially mineralized fiber. The axial modulus, E_a, was calculated from the force F needed to displace the upper surface of the fiber by u_z: E_a = (FL)/(πR²u_z); the shear modulus, G_at, was calculated from the force F needed to displace the upper surface of the fiber by u_x: G_at = (FL)/(πR²u_x).

The solutions to the first (diffuse) model actually coincide with the Hashin-Shtrikman (31) lower bound (equations listed in the Supporting Material, Section A), which provided an estimate for the degree to which mineralization increased E_a. The shear modulus G_at was estimated from E_a through the linear elasticity solution for a laterally displaced beam (4): G_at = 3βE_a (R/L)², where (R/L) = 1:20 was the aspect ratio for fibers in the simulations, and β is a function of Poisson's ratios (β = 1.07 for an isotropic material with ν = 0.3). The remainder of the stiffness tensor was calculated as above. This procedure was also followed for the Hashin-Shtrikman upper bound.

Linking fiber mechanics to tissue mechanics through the volume fraction and fiber orientation distribution

Mechanical properties of individual mineralized collagen fibers were related to tissue mechanics by averaging over the measured fiber orientation at each point in the insertion (Fig. 2 a). C^(f)(ϕ) varied as a function of normalized mineral volume fraction, ϕ(x), so that the relationship between the strain ɛ^(f) and stress σ^(f)(ϕ,ɛ^(f)) in a unit cell containing each fiber was:

$${\mathbf{\sigma }}^{\left(\text{f}\right)}(\varphi ,{\mathbf{\varepsilon }}^{\left(\text{f}\right)})={\mathbf{C}}^{\left(\text{f}\right)}\left(\varphi \right){\mathbf{\varepsilon }}^{\left(\text{f}\right)}\text{.}$$ (1)

The total stress σ at a normalized position x in the tendon-to-bone insertion is the sum of the stresses in all fibers crossing that point, calculated by averaging over the fiber orientation distribution and weighting by the combined volume fraction f_total of collagen and mineral. Averaging over the unit sphere, Ω:

$$\begin{array}{l}\mathbf{\sigma }\left(x\right)={\int }_{\Omega }{f}_{\text{total}}\left(x\right){\left(\mathbf{R}\left(\mathit{n}\right)\right)}^{\text{T}}\left({\mathbf{\sigma }}^{\left(\text{f}\right)}(\varphi \left(x\right),{\mathbf{\varepsilon }}^{\left(\text{f}\right)}\left(\mathit{n}\right))\right)\mathbf{R}\left(\mathit{n}\right)p(\mathit{n},s\left(x\right))d\Omega \left(\mathit{n}\right)\\ =f_{\text{total}}\left(x\right){{\int }_{\Omega }\left(\mathbf{R}\left(\mathit{n}\right)\right)}^{\text{T}}\left({\mathbf{C}}^{\left(\text{f}\right)}\left(\varphi \left(x\right)\right){\mathbf{\varepsilon }}^{\left(\text{f}\right)}\left(\mathit{n}\right))\right)\mathbf{R}\left(\mathit{n}\right)p(\mathit{n},s\left(x\right))d\Omega \left(\mathit{n}\right),\end{array}$$ (2)

where p(n) is the probability density for finding a fiber whose axis is parallel to the unit vector n, ɛ^(f)(n) is the matrix of components of the strain tensor resolved with the n direction along the axis of material symmetry in such a fiber, R transforms a vector from this coordinate system to the global coordinate system, and n includes all directions over the unit sphere Ω (e.g., Marquez et al. (32)). The distribution p(n,s(x)) was axisymmetric and spherical, fit to the measured angular deviation of the fiber distribution, s (radians). If ψ is an angle relative to the mean fiber direction at a point, and −π/2 ≤ ψ ≤ π/2 (28),

$$p(\psi ,s)=\frac{{\text{exp}}^{-{\psi }^2/2{\text{s}}^2}}{\sqrt{2\pi }s{\text{exp}}^{-{\text{s}}^2/2}}\text{.}$$ (3)

Applying the assumption of affine deformation, the local strain field ɛ^(f) in each fiber equals the macroscopic tissue strain ɛ(x), and Eq. 2 can be rewritten:

$$\mathbf{\sigma }\left(x\right)=\left(f_{\text{total}}\left(x\right){\int }_{\Omega }{\left(\mathbf{R}\left(\mathit{n}\right)\right)}^{\text{T}}{\mathbf{C}}^{\left(\text{f}\right)}\left(\varphi \left(x\right)\right)\mathbf{R}\left(\mathit{n}\right)p(\mathit{n},s\left(x\right))d\Omega \left(\mathit{n}\right)\right){\mathbf{\varepsilon }}^{\left(\text{f}\right)}\left(x\right)\equiv {\mathbf{C}}^{\text{tissue}}\left(x\right){\mathbf{\varepsilon }}^{\left(\text{f}\right)}\left(x\right),$$ (4)

where C^(tissue)(x) is the effective stiffness tensor of the tissue at position x.

Moduli of collagen within tendon fibers and of mineralized collagen within bone fibers were estimated by backing out E_a using Eqs. 3 and 4 and data from the literature. For a tendon with angular deviation s = 2°, E_max = 0.4 GPa, E_min= 0.15 E_max, and f = 0.9 (29,30), this procedure predicts an effective modulus of collagen within collagen fibers of E_c = 450 MPa. For bone (s = 7.1°, E = 20 GPa, f = 0.87), this yields an isotropic modulus of mineralized collagen of E_mc = 30 GPa. The estimated Poisson's ratio mismatch between collagen and mineralized collagen was small and therefore neglected, with both materials assigned a Poisson's ratio of 0.3.

Experimental characterizations

Mineral concentration across the tendon-to-bone insertion site

We examined apatite mineral content using confocal Raman microprobe spectroscopy (RMS) as described previously (33). For sample preparation, the supraspinatus tendon-to-bone insertion sites of normal Fisher rat shoulders (N = 7) were dissected and sliced into 1–2 mm sections in the coronal plane using an Isomet low speed saw at 130 rpm. We used the rat supraspinatus tendon due to its relevance to the human shoulder (34). This tendon is a part of the rotator cuff, a structure that has significant clinical relevance due to its high incidence of injury and limited ability to heal (35). All animal procedures were in compliance with the Animal Studies Committee regulations at Washington University School of Medicine.

Individual RMS analyses (beam diameter, 1–2 μm) were made across the insertion site on the unfixed samples on glass slides within 48 h of thawing (rats were fresh frozen immediately after sacrifice). Linear distances between scan points were recorded via photo documentation. Samples were moistened only with phosphate buffered saline. Analysis was carried out with a fiber-optically coupled Raman microprobe based on an axial spectrograph with volume holographic transmission gratings (HoloLab Series 5000 Raman Microscope, Kaiser Optical Systems, Ann Arbor, MI). The 532-nm excitation was delivered by a frequency-doubled diode-pumped solid-state Nd-YAG laser (Coherent, Santa Clara, CA) that was coupled to a Leica microscope (Wetzlar, Germany) via an 8-μm, single-mode, optical fiber. An 80× ultra-long-working-distance objective (Olympus, Tokyo, Japan) with a numerical aperture of 0.75 and a working distance of 8 mm was used to focus the light onto the sample with a lateral resolution of ∼1 μm and a power of ∼5 mW at the sample surface.

An individual Raman spectrum was collected for each data point in a traverse orthogonal to the bone surface across the insertion site; each data point consisted of the averaged sum of 32 acquisitions at 4 s. GRAMS 32 commercial software (Galactic Industries, Salem, NH) was used to deconvolve complex spectral peaks and compare spectra from different points on a sample or among different samples. The output of the GRAMS 32 deconvolution program is a list of bands with their associated positions, widths, and areas. The ratios of the band areas within a given spectrum are a measure of the relative concentrations of those components; specifically, the ratio of the area of the symmetric P-O stretching band of apatite at 960 Δcm⁻¹ to the area of the C-H stretching bands at 2940 Δcm⁻¹ (one of the many bands for the organic component collagen) indicates the relative concentration of mineral. Changes in the ratio of apatite to collagen monitored and calculated for individual micrometer-sized spots across several tendon-to-bone insertion sites.

Angular orientation distribution of collagen fibers

Supraspinatus tendon-to-bone insertions from Fisher rats (N = 5) were processed for standard histology (paraffin embedded), sectioned in the transverse plane, and stained with a 0.1% Picrosirius Red. Collagen fiber orientation distributions were measured at the bone end of the tendon-to-bone insertion, within the “Level 4” patterning of fibers, just below the organizational level of osteons (36). A polarized light method for quantitative collagen orientation analysis was used to quantify collagen fiber orientation (6). Tissue sections were analyzed using a polarized light microscope (Olympus BX51P) and a digital microscope camera (Olympus DP70). The specimen was viewed with light filtered through a polarizer (East–West position) and analyzer (North-South position). Images were captured at section orientations from 0° to 180° in 5° increments. A compensator (λ/4 wave plate) was then engaged in a diagonal position (NW–SE) and additional images were recorded at section orientations from 0° to 180° in 5° increments. Software designed with MATLAB (The MathWorks, Natick, MA) was used to determine the angle of extinction, θ, by locating the angle associated with the minimum light intensity at grid points on each image. To determine whether the collagen orientation was at θ or θ ± 90° (i.e., aligned with the analyzer or the polarizer), the color hue was examined at θ ± 45° using images taken with the compensator in place. The angular deviation of the collagen orientations for all grid points was then calculated to describe the orientation distribution of the collagen fibers (37).

Results

The tendon-to-bone insertion is a continuous tissue

Our data show a continuous, approximately linear (R² = 0.8) increase in the integrated intensity of the 960 Δcm⁻¹ band (characteristic of the phosphate in the apatite mineral) relative to that of the 2940 Δ cm⁻¹ band (characteristic of the C-H stretch from the collagen and other organic components) (Fig. 3). No abrupt change in mineralization was observed at the approximate location of the tidemark. These observations reveal a new functional definition and model of the tendon-to-bone insertion as the region of tissue in which mineral accumulates in fibers, extending between bone ($\varphi =f_{\text{mineral}}/f_{\text{mineral}}^{\text{bone}}=1.0$) and tendon $\varphi =f_{\text{mineral}}/f_{\text{mineral}}^{\text{bone}}=0$). Our data suggest an approximately linear increase in mineral volume fraction between tendon (x = 0) and bone (x = 1):

$$\varphi \left(x\right)\approx x\text{.}$$ (5)

Figure 3.

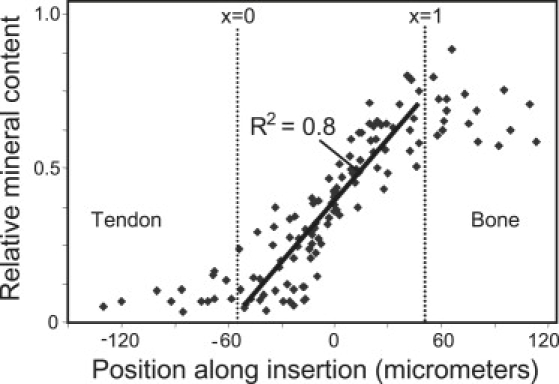
Relative concentration of mineral (i.e., apatite) estimated from RMS measurements, displayed as the ratio of the areas of the 960 Δcm⁻¹ PO₄ peak to the 2940 Δcm⁻¹ collagen peak, across the tendon-to-bone insertion. Approximate regions of tendon and bone are indicated.

Mineral content contributes strongly to collagen fiber stiffness above a critical volume fraction

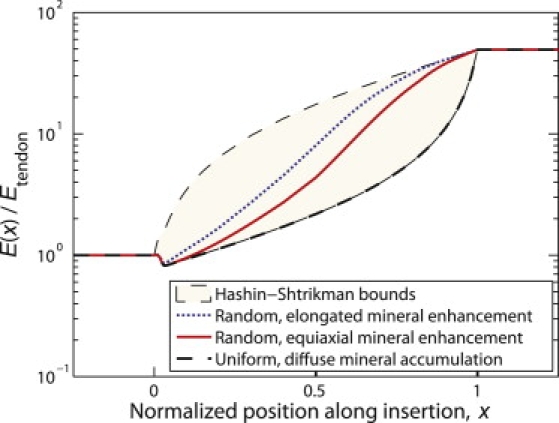
The diffuse model, approximated the Hashin-Shtrikman lower bound representing the extreme in which mineral accumulates with strict spatial uniformity (25). Because, in this model, a lack of connectivity exists until very high degrees of mineralization, this model predicted that 90% of the stiffening due to mineralization occurred over the final 10–20% of the tendon-to-bone insertion (Fig. 4). The second, equiaxial model, incorporated effects of nonuniform mineral accumulation. As with many other composite systems (21), including biological systems (32), the stiffening effect of mineral increased dramatically at the percolation threshold, where the concentration of mineral became sufficiently high that a mechanically continuous network of mineralized collagen forms (ϕ ≈ 0.5, Fig. 4, blue (right) arrow). The third, elongated model was identical to the second except that regions of enhanced mineralization were elongated along the fiber axis. The degree of mineralization corresponding to the percolation threshold was lower for elongated regions of enhanced mineralization than for equiaxed regions (Fig. 4, red (left) versus blue (right) arrow).

Figure 4.

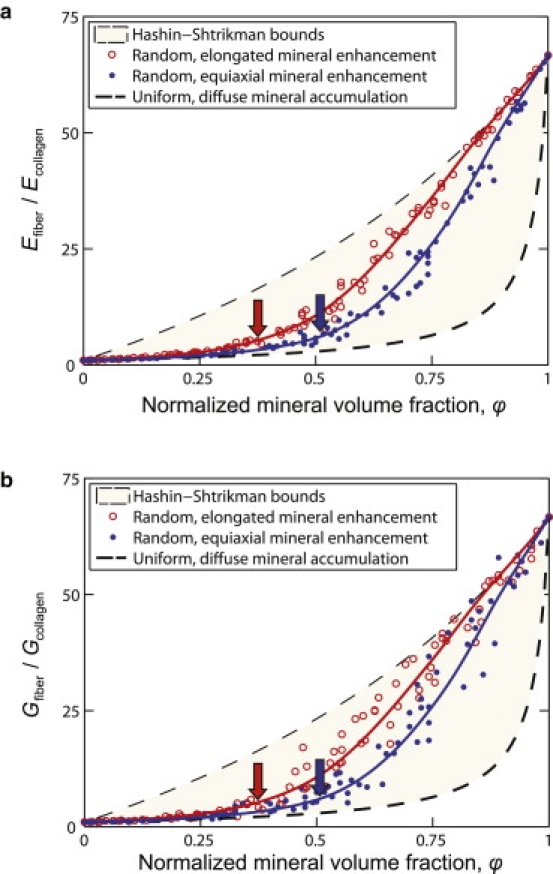
Bounds and estimates for the axial elastic modulus (E) and axial-transverse shear modulus (G) of a partially mineralized fiber. Mineral stiffens fibers dramatically at volume fraction above the percolation threshold (ϕ ≈ 0.5), indicated by the arrows. Percolation occurs at lower volume fraction for regions of enhanced mineralization elongated parallel to the fiber axis.

Angular dispersion of collagen fibers occurs across the tendon-to-bone insertion

If mineral stiffens the collagen fibers monotonically along the tendon-to-bone insertion site, why is fibrocartilage less stiff than tendon? The answer lies partly in the distribution of fiber orientations. We presented microscopic data previously showing that angular deviation, s, increases from tendon to bone (6,28). We now add observations of the angular deviation of the orientation distribution in bone at the single osteon level, relevant to the level of collagen fibers. Although compact bone exhibits on average a nearly isotropic orientation distribution of collagen fibers at the macro- (millimeter-) scale, our new observations show that, at the relevant micrometer-scale, local bundles of collagen fibers exhibit a degree of alignment; this is the Level 4 patterning of fibers, just below the organizational level of osteons (36). We reported that angular deviation values for the rotator cuff tendon-to-bone insertion site in rats reached a peak (i.e., fibers were least aligned) just before the tidemark (28), and we now observe that the fiber orientation distribution changes little beyond this point (Fig. 5 a). Collagen fibers in both bone and the tendon-to-bone insertion are far less aligned than those in tendon.

Figure 5.

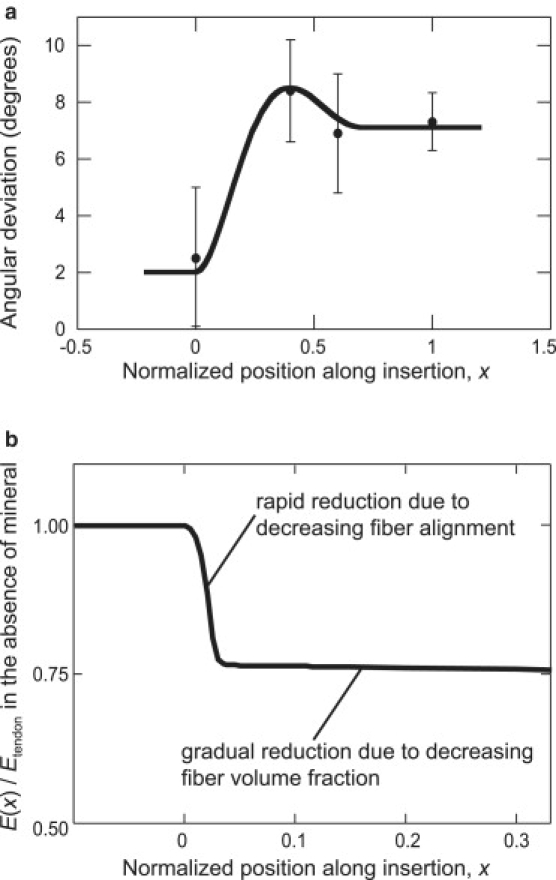
(a) Alignment of collagen fibers is greatest (angular deviation is lowest) in tendon, and angular deviation is highest in the tendon-to-bone insertion. (b) The spatially varying elastic modulus of a hypothetical tendon-to-bone insertion containing no mineral. The decreasing fiber alignment leads to a rapid drop in tissue stiffness in the first few percent of the tendon-to-bone insertion.

Reduced fiber alignment along the tendon-to-bone insertion reduces tissue stiffness

We assessed how the experimentally measured collagen fiber orientation distribution (Fig. 5 a) affects tissue mechanics by considering spatial variations in the elastic modulus of a hypothetical unmineralized tendon-to-bone insertion. This hypothetical tendon-to-bone insertion contained a uniform volume fraction of collagen fibers with a spherical orientation distribution (Eq. 3) of measured angular deviation, s, but with no mineral. The elastic modulus of this hypothetical unmineralized tendon-to-bone insertion dropped precipitously a few percent of the way along the insertion (s ≈ 2.5°), as the angular deviation, and hence the fraction of rope-like fibers that deflect predominantly in bending rather than in stretching, increased (Fig. 5 b; a quantitative model of this is included in the Supporting Material, Section C).

The combination of reduced fiber alignment and increasing mineral content explains the nonmonotonic variation in tissue stiffness observed along the insertion

Thomopoulos et al. (6) observed that the tangent modulus of some tissue in the supraspinatus tendon-to-bone insertion is more compliant than that of either tendon or bone. Similar results have been reported for patellar-tendon-to-bone and meniscus-to-bone insertions (15,16). The two experimentally measured components (collagen fiber orientation and mineral concentration) were combined by integrating a 3D generalization of the fiber's mechanical properties, adjusted to incorporate the linear spatial variation in mineral accumulation, over the measured spherical orientation distribution. The combination of these two factors led to values concordant with experimentally reported decrease and then increase in stiffness of tissue along the tendon-to-bone insertion (Fig. 6). Nonuniformity in the accumulation of mineral reduced the region over which tissue modulus dropped below that of the tendon, and elongation of mineralized regions along fiber axes enhanced this effect.

Figure 6.

Combination of decreasing collagen organization and increasing mineral content leads to a decrease in modulus followed by an increase in modulus.

Discussion

Effective attachment of tendon to bone is a remarkable engineering achievement. The tendon-to-bone insertion transfers mechanical loads across an interface with a nearly two order of magnitude stiffness mismatch and with a large difference in material organization. Analysis and modeling using our experimental data motivate what we believe is a new tissue-level understanding of the tendon-to-bone insertion and of the organizational and material strategies that endow the tissue with its specific mechanical properties. These structure-function relationships serve as a target for our current efforts to develop strategies for improved surgical repair of the tendon-to-bone insertions, and for our efforts to apply biomimetic design principles to synthetic material interfaces.

Our experimental and modeling results support our hypothesis that the tendon-to-bone insertion is a continuous, functionally graded material with respect to its mineral concentration, collagen fiber alignment, and biomechanical properties, but do not support the traditional understanding of four discrete zones (5). The tidemark between the unmineralized (zone 2) and mineralized fibrocartilage (zone 3) was traditionally thought to represent a boundary between soft and hard tissue (5), but our Raman analyses show that the tidemark does not represent a discontinuity in the tissue's mineral content. Rather, mineral content increases linearly over the tendon-to-bone insertion, consistent with analogous changes in the organic components (6). The tidemark may simply represent a threshold of mineral at which the tissue picks up stain. However, it remains unclear what its physical meaning is.

The gradation likely serves to improve stress transfer. In several engineering applications, the absence of functional grading of material properties reduces toughness of interfaces (38). Absence of functional grading after natural healing and surgical repair may similarly account for the subsequent susceptibility to re-injury. After tendon-to-bone healing, the transitional tissue is absent (39), and the resulting stress concentrations may contribute to subsequent re-injury susceptibility, chronic pain, and disability (28). Surgical reattachment of tendon to bone is challenging clinically, with mixed outcomes. Rotator cuff tears, repaired by suturing tendon to bone (40), present recurrent tears in up to 94% of cases (35,40,41). Tendon-to-bone repairs to avulsions of the hand's flexor tendons have poor clinical outcomes (42). Although success rates are higher in anterior cruciate ligament reconstruction involving tendon grafts through bone tunnels, grafts loosen frequently due to poor tendon-to-bone healing (43). This interpretation motivates our ongoing efforts to develop surgical intervention strategies that recreate the natural functional grading of the tendon-to-bone insertion.

Our modeling results indicate that collagen-mineral interactions and collagen fiber architecture at the micro scale are dominant factors in determining the macroscale tensile mechanical behavior of the tendon-to-bone insertion. Increasing mineral content across the tendon-to-bone insertion causes a stiffening of collagen fibers that becomes significant for mineralization at volume fractions beyond the morphology-dependent percolation threshold (Fig. 4). Before reaching this threshold, the mechanical behavior of the fiber is dominated by the compliance of the collagen. When connectivity of mineral exists from one end of the fiber to the other, force transferred through this mineral becomes significant relative to that transferred through the collagen, and so the modulus of the fiber increases overall. Polarized light microscopy showed that collagen fiber alignment decreases across the tendon-to-bone insertion, reducing tissue stiffness precipitously when the angular deviation exceeds s ≈ 2.5° (Fig. 5). Mechanically, the fiber orientation distribution is the dominant factor determining the stiffness of the tendon-most extremity of the tendon-to-bone insertion. Thus, despite the presence of mineral, there exists a region of transitional tissue that is more compliant than either tendon or bone. However, beyond the position at which the percolation threshold of mineralization is reached, the tissue stiffness rises dramatically to approach that of bone (Fig. 6).

The homogenization bounds investigated lend support to the above results, despite uncertainty in the physiological distribution of mineral along the tendon-to-bone insertion. The dimensions chosen for regions of enhanced mineralization in the simulations are the largest that could exist in fibers within the tendon-to-bone insertion without being spatially resolved by our Raman microprobe analyses in this optically complex tissue. The models therefore provide a reasonable bound on the greatest degree to which nonuniform mineralization might affect mechanics of the tendon-to-bone insertion. The numerical estimates followed the Hashin-Shtrikman lower bound at low mineral concentration (Fig. 4), as has been observed experimentally for many particulate-strengthened materials (25). Thus, the Hashin-Shtrikman lower bound provides a good estimate in this range not only for the diffuse, uniform mineralization hypothesized for bone development (14), but also for the minimum modulus values for any reasonable spatial nonuniformity in mineralization. Simulations followed the Hashin-Shtrikman upper bound at high mineral concentration (Fig. 4). Note that because the Hashin-Shtrikman bounds apply only to a perfectly uniform distribution of mineral apatite, stiffnesses outside of these bounds were possible, especially at the lowest and highest mineral concentrations considered. Nevertheless, a model tendon-to-bone insertion following even this extreme lower bound at low mineral concentrations, when combined with fiber orientation and mineral distribution data, predicts spatial stiffness variations like those reported (6,15,16).

Although the degree to which mineral stiffens collagen fibers is uncertain, the elastic modulus of 30 GPa adopted for the collagen/apatite composite in mineralized fibers was consistent with reported measurements. Nano-indentation studies of bone suggest elastic moduli values of at least E_mc = 30 GPa for mineralized collagen fibers (44), below the apatite elastic modulus of E_a ∼ 110 GPa (13), but orders of magnitude stiffer than collagen. Almer and Stock (45) suggest slightly lower moduli, with E_mc ∼ 18–25 GPa, and E_a ≈ 40 GPa. Yoon and Cowin (46) find elastic moduli on the order of 20 GPa for single osteons, suggesting still higher stiffness values for mineralized collagen fibers. Recent evidence suggests that when mineralized collagen fibers from bone are loaded, the mineral particles stretch marginally less than the collagen, as expected for a system with a concentration of stiff mineral close to the percolation threshold (47).

Although collagen in fibers is certainly not linear in its stress-strain behavior, a linear material model was used. The justification is that mineral, nominally linear in its response, is dominant in determining the stiffness of mineralized fibers; the effect of nonlinearity of response in collagen material is relatively small at the low and high mineral concentrations of importance to the conclusions in this article (Supporting Material, Section B). Including nonlinearity in the simulations would shift the percolation threshold to a marginally lower value of mineral content, as strain becomes localized in isolated pockets of unmineralized collagen, thereby stiffening this collagen. However, we defer determining the precise, small degree to which collagen nonlinearity affects percolation until accurate data on the nonlinear mechanical response of individual collagen fibers become available.

Our model explains how mineralization and collagen fiber distribution define stiffness across a continuous tendon-to-bone insertion. Understanding why this gradation exists will require a characterization of the effect of structural variations on the strength and toughness of tissue within the insertion. Defining the failure criteria for partially mineralized tissues along the insertion will require additional experimental data, as will developing an understanding of how toughness variations combine with the macroscopic structure of the tendon-to-bone insertion to achieve effective load transfer. We hypothesize that toughness will be greatest at points where stiffness is lowest, meaning that the compliant region within the tendon-to-bone insertion may serve as an energy absorbing band.

Our model has a number of limitations. First, our model does not account for varying collagen types or the presence of proteoglycans across the interface. Whereas the collagen in tendon and bone is largely type I, the collagen at the interface is a mix of type I and type II. There have been no reports, however, indicating that there are differences in the mechanical properties of these two collagen types. Therefore, the effect of collagen type was not incorporated into our model. It is possible that proteoglycan content at the insertion contributes to the observed changes in tensile stiffness across the insertion. These macromolecules play an important role in providing articular cartilage with a high compressive stiffness (48). Although their mechanical role at the tendon-to-bone insertion is unknown, the contribution of proteoglycans to tensile behavior is likely to be small compared to their role in compressive behavior (48). Second, our model accounts for mineralization by assuming that regions of collagen fibers are mineralized rather than modeling dispersed collagen fibers within a ground substance with varying mineral content. This approach was necessary due to the uncertainty of fiber-fiber and mineral-fiber interactions. Finally, there may be differences between the rat and the human with respect to insertion site structure and function. Our study first models individual fibers and then combines multiple fibers to model the insertion at the tissue level. We do not expect that any cross-species differences exist at the fiber level. At the tissue level, the human insertion is larger in volume that the rat insertion. However, we expect that the stiffness will scale linearly with the number of fibers in the cross-section of the tendon-to-bone insertion difference in volume, so that conclusions in our study are relevant to human tissue.

Conclusions

The body forms a functionally graded interface between tendon and bone. The model for the tendon-to-bone insertion that emerges from this work is one of a gradual and continuous change in: 1), the orientation distribution of collagen fibers; and 2), the relative concentration of the organic and inorganic tissue constituents. Mineral volume fraction varies approximately linearly across the tendon-to-bone insertion, with no abrupt mineralization front apparent at the tidemark.

Comparison of our modeling results with literature-based measurements of mechanical properties of mineralized tissue indicates that features at the micrometer scale are important factors explaining variations in the axial and shear moduli of tissue within the tendon-to-bone insertion. This is the scale of a number of microscope-based analytical techniques. Models of randomly but inhomogeneously distributed mineralization account for gradational, but nonlinear changes in mechanical properties across the tendon-to-bone insertion. Although addition of mineral to collagen increases the stiffness of the latter, the greatest stiffening response does not occur until the degree of mineralization has reached a value that is recognized as the percolation threshold. At this level of mineralization, the tissue acts as if the mineral were part of an interconnected network.

The stiffness of tissue in the tendon-to-bone insertion is likely controlled on the tendon end by collagen fiber alignment; reduction in fiber alignment here causes a reduction in tissue stiffness. Farther along the insertion, beyond where the mineral concentration reaches the percolation threshold, mineralization likely dominates tissue stiffness.

These data are important for developing improved surgical interventions that recreate the mechanics of the tendon-to-bone insertion in healing. The remaining questions of why the body forms this particular functional grading and whether this grading is truly optimal remains open. The answer to this question will undoubtedly be of value in designing biomimetic bimaterial interfaces.

Supporting Material

Additional text, equations, and figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01050-9.