Abstract
Cytochrome c oxidase is a transmembrane proton pump that builds an electrochemical gradient using chemical energy from the reduction of O2. Ionization states of all residues were calculated with Multi-Conformation Continuum Electrostatics (MCCE) in seven anaerobic oxidase redox states ranging from fully oxidized to fully reduced. One long-standing problem is how proton uptake is coupled to the reduction of the active site binuclear center (BNC). The BNC has two cofactors: heme a3 and CuB If the protein needs to maintain electroneutrality, then 2 protons will be bound when the BNC is reduced by 2 electrons in the reductive half of the reaction cycle. The effective pKas of ionizable residues around the BNC are evaluated in Rhodobacter sphaeroides cytochrome c oxidase. At pH 7, only a hydroxide coordinated to CuB shifts its pKa from below 7 to above 7 and so picks up a proton when heme a3 and CuB are reduced. Glu I-286, Tyr I-288, His I-334, and a second hydroxide on heme a3 all have pKas above 7 in all redox states, although they have only 1.6–3.5 ΔpK units energy cost for deprotonation. Thus, at equilibrium, they are protonated and cannot serve as proton acceptors. The propionic acids near the BNC are deprotonated with pKas well below 7. They are well stabilized in their anionic state and do not bind a proton upon BNC reduction. This suggests that electroneutrality in the BNC is not maintained during the anaerobic reduction. Proton uptake on reduction of CuA, heme a, heme a3, and CuB shows ≈2.5 protons bound per 4 electrons, in agreement with prior experiments. One proton is bound by a hydroxyl group in the BNC and the rest to groups far from the BNC. The electrochemical midpoint potential (Em) of heme a is calculated in the fully oxidized protein and with 1 or 2 electrons in the BNC. The Em of heme a shifts down when the BNC is reduced, which agrees with prior experiments. If the BNC reduction is electroneutral, then the heme a Em is independent of the BNC redox state.
Heme–copper oxidases are the terminal electron acceptors in anaerobic organisms. These transmembrane proteins reduce dioxygen and convert the released chemical energy into an electrochemical gradient, across the eukaryotic mitochondrial membrane or the bacterial cell membrane (1–4). Cytochrome c oxidases are the most prevalent heme–copper oxidases. In this protein 4 electrons, provided by 4 cytochromes c, are used to reduce dioxygen to water. The 4 protons needed to make water are taken from the negative cytoplasmic side of the membrane, adding to the electrochemical gradient. Four additional protons are pumped across the membrane (5). Thus, each dioxygen molecule reduced by cytochrome c oxidase is coupled to the transfer of 8 charges across the membrane.
The first step of electron transfer is from cytochrome c to CuA, a dicopper center in subunit II which extends beyond the membrane on the proton release side of the protein (Figure 1). After receiving the electron, CuA reduces the 6-coordinate, low-spin, bis-His–heme a, which is in the center of the membrane-embedded subunit I. Heme a then sequentially passes 2 electrons into the binuclear center (BNC),1 formed by a heme with a single His ligand (heme a3) and a Cu with three His ligands (CuB). The BNC and heme a are deeply buried in the protein, approximately 20 Å from the proton input side and 15 Å from the proton release side of the membrane.
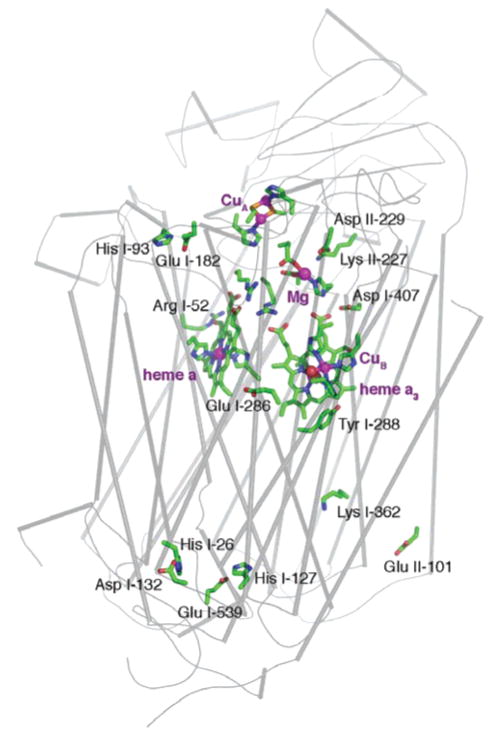
Figure 1. Rb. sphaeroides.
cytochrome c oxidase (PDB code 1M56). Backbone trace of subunits I and II. Subunits III and IV used in the calculations are not shown. Ionizable residues contributing to proton uptake or those on the proton transfer pathway are shown. Bound ions are shown as spheres. Cofactor metals are in purple and water bound to CuB is in red. Heme a3 and CuB make up the binuclear center (BNC).
Two channels, D and K, have been identified for protons to travel from the input side of the protein into the BNC. The D channel begins with Asp I-132 near the protein surface and ends with Glu I-286 near the BNC (6–8). The K channel begins with Glu II-101(9, 10), passes Lys I-362 (11), and ends with Tyr I-288. Both channels are more than 20 Å long and are assumed to be filled with water (12–14). It has been suggested that the single electron reduction of the fully oxidized oxidase is coupled to proton uptake via the K channel (7, 15–17) and that the second reduction is coupled to proton uptake via either the D (7) or K channel (18).
Electron transfer through oxidase changes the charge state of the redox cofactors. The favorable charge–dipole interaction of a charge with water, referred to as the solvation (reaction field or Born) energy, strongly stabilizes ionized states in water (19–22). If the charge is buried in the protein, then this favorable interaction is reduced. Consequently, the loss of solvation energy always shifts reaction equilibria in a protein, favoring states with the smaller net charge. The reduced CuA, heme a, and heme a3 have a charge of 0, and there is a +1 on the reduced CuB. Cofactor oxidation in the protein, which increases the positive charge, is destabilized relative to the same redox reaction in aqueous solution by the solvation energy loss. Removal from water also shifts the pKas of the surrounding acids and bases to favor their neutral forms. However, pairwise interactions with nearby charged groups or dipoles can stabilize buried charged residues and cofactors, compensating for the loss of solvation energy (23). The final in situ cofactor Ems and residue pKas reflect the relative contribution of these different terms. Significant perturbations, either stabilizing or destabilizing the charged forms, are well-known within proteins. For example, bis-His–hemes have Ems ranging from −410 to +360 mV, exhibiting the ability of the protein to modify the chemical properties of buried groups. The Em shifts for hemes with the same ligand have been shown to be caused by differences in the heme electrostatic environment within the protein (24–28).
It has been proposed that in the anoxygenic reductive half of the reaction cycle, when 2 electrons are transferred to the fully oxidized enzyme reducing heme a3 and CuB, 2 protons are bound near the BNC (29–31). This requires two groups with in situ pKas below the ambient pH in the oxidized enzyme, allowing them to be potential proton acceptors. Then when the cofactors are reduced, their pKas would need to shift to be higher than the solution pH so each can bind a proton. If there is tight coupling between proton and electron transfers, the reaction would be electroneutral, ensuring that the oxidized and reduced BNC complexes have the same net charge. There have been several proposed proton acceptors including a hydroxide bound to CuB (29, 32, 33) or heme a3 (34), the heme a3 propionic acids (12, 29, 35–37), or one of the His ligands of CuB (38–40).
Various computational techniques have been used to study cytochrome c oxidase. Continuum electrostatics calculations carried out on the Paracoccus denitrificans (33) and bovine oxidase (39, 41, 42) showed ionization changes and long-range coupling between the BNC and the distant residues (33). Density functional theory (DFT) calculations have analyzed the energetics of the oxygen bond splitting reaction (43, 44) and proton and electron affinities of the BNC cofactors and nearby residues (45). Molecular dynamics (MD) simulations have studied the behavior of water and polar residues in both the proton uptake channels and the cavities near heme a and the BNC (13, 14, 46). Computations have also suggested that the movements of Glu I-286 (47), water (12, 48) near the BNC, and Thr 359 (49) play a role in proton pumping. The electrostatics and DFT calculations have suggested that a hydroxyl group in the BNC (33), the heme propionic acids (45), and/or a His ligand to CuB (39, 40) contribute to the proton uptake.
MCCE (Multi-Conformation Continuum Electrostatics) calculates the shift in Em and pKa induced by the protein (27, 50–52). Given measured aqueous pKas and Ems (pKa,sol and Em,sol) for acidic and basic groups and redox cofactors, MCCE provides these values in the protein. The program is able to calculate pKas for amino acids (51), heme propionates (27), hydroxides ligated to hemes (53), and Ems for hemes in a variety of cytochromes (25, 27) through benchmark calculations on simpler proteins. Prior studies on photosynthetic reaction centers (52, 54, 55), bacteriorhodopsin (56), and quinol:fumarate reductase (57) show that MCCE provides a good match to experimental values for cofactor Ems and both cofactor and amino acid pKas in large transmembrane proteins.
In the work presented here, MCCE was used to calculate proton uptake during the individual stages of anaerobic reduction of Rhodobacter sphaeroides cytochrome c oxidase. The in situ pKas and proton uptake were determined for all residues. The stoichiometry of proton uptake for anaerobic reduction of the protein (18, 58, 59) and the Em of heme a with the BNC cofactors in different ionization states (31, 60–62) were computed by MCCE and compared to published experiments. There have been a variety of attempts to measure the proton uptake occurring at specific steps of the reaction cycle (18, 58, 59). There is disagreement among the reported estimates for the stoichiometry for the first two reductive steps (18, 31, 58, 59, 63, 64). The main focus of the work reported here is to determine, given the structure of the Rb. sphaeroides oxidase, the residues near the BNC whose equilibrium ionization states allow them to couple proton uptake to cofactor reduction and to determine if there are two proton acceptors to keep BNC reduction electroneutral.
METHODS
Subunits I–IV of the first model of the Rb. sphaeroides cytochrome c oxidase structure in the PDB file 1M56 (65) are analyzed with MCCE. Water molecules are removed and the internal cavities treated as a high dielectric space in the electrostatics calculation. A 32 Å slab of neutral atoms is added to provide a low dielectric membrane, with the slab position optimized to bury the fewest surface ionizable residues using the program IPECE (56). Buried lipids are removed.
Residue ionization is calculated with Multi-Conformation Continuum Electrostatics (MCCE2.0) (50, 51). The standard MCCE subroutine is used for all amino acids and the heme propionic acids (manuscript in preparation, www.sci.ccny.cuny.edu/~mcce). Additional side chain rotamers are generated in 120°increments around each rotatable bond. This generates a relatively modest number of conformers. These are then pruned, removing rotamers with Lennard-Jones clashes of >10 kcal/mol with the backbone or with itself. The remaining rotamers are chosen by a randomized packing routine, where each residue finds a conformer that does not clash with the rest of the protein. The protein is packed 5000 times, and rotamers that are occupied in >5% of the packed structures are kept (manuscript in preparation). Rotamer making and pruning are carried out without protons. After pruning, protons are placed on each rotamer, and ionization and hydroxyl conformations are created for all polar and ionizable residues. In the final model there are 5062 conformers for the 1134 residues. On average, each of the 122 ionizable residues have 20 conformers and polar residues have 5–10 conformers, while nonpolar residues have 1–4 conformers.
Look-up tables are calculated for both electrostatic and nonelelctrostatic self-energies and conformer–conformer pairwise interactions (50). The electrostatic pairwise interactions and reaction field (solvation) energies are calculated with a finite-difference technique to solve the Poisson–Boltzmann equation, using the program DelPhi (66–68). Amino acids are given PARSE charges and radii (69). Four focusing runs (70), each with 1003 grids, give a final resolution of 2.0 grids/Å. The protein and a 32 Å membrane slab are given a dielectric constant (ε) of 4, while the surrounding water has ε= 80 with a salt concentration of 150 mM. The Lennard-Jones interactions are calculated with AMBER parameters (71) with the energies divided by 4 (50). This rescaling is needed because the Lennard-Jones parameters are optimized with electrostatic interactions calculated with ε= 1, while in MCCE ε= 4 is used. A smaller Lennard-Jones repulsion is needed with ε= 4 to ensure that hydrogen bonds have the correct distance dependence.
Possible microstates of the system are subjected to Monte Carlo sampling. A microstate is made up of one conformer for each residue, cofactor, and water. The energy of microstate n (ΔGn) is the sum of the electrostatic and nonelectrostatic energies (27) defined by
| (1) |
where the summation is over the total M conformers of all residues in the protein; for each conformer i, δI= 1 if it is present in the current microstate n and 0 if it is not. Each residue has one conformer with δi = 1 and the rest δi = 0. In the double summation δi and δj are both 1 only when conformers i and j are from two different residues. kbT is 0.59 kcal/mol (25.8 meV); mi is 1 for bases, −1 for acids, and 0 for polar groups and waters. ni is the number of electrons gained or lost compared to the ground state conformer. For example, if an oxidized conformer is defined as the ground state, it has ni = 0 and the reduced conformer has ni = 1; F is the Faraday constant. pKsol,i is the pKa and Em,sol,i the midpoint potential of the ith cofactor in solution. ΔΔGrxn,i is the difference between the conformer reaction field energy in solution and in the protein (desolvation energy). ΔGpol,i is the pairwise electrostatic and nonelectrostatic interaction of the conformer with the backbone and with side chains that have no conformational degrees of freedom. The torsion energy for each conformer is added to ΔGpol,i. ΔGij is the electrostatic and Lennard-Jones pairwise interaction between each pair of conformers in the microstate. The limits on the summation of the interconformer terms ensure that each interaction is counted once. Monte Carlo sampling establishes the Boltzmann distribution of the different conformers of each residue at 25°C. Residue pKas and Ems are determined from the fraction group ionization in a series of Monte Carlo simulations at different pHs or Ehs (eq 1). Multiflip (72) between closely coupled residues is implemented (56). The SOFT function is not used (51). Four hundred million steps of Monte Carlo sampling are carried out. Each reported calculation represents the average of five Monte Carlo runs. The Monte Carlo uncertainty of the conformer occupancy is ±0.01. The uncertainty of calculated Ems is ±4 mV and ±0.07 for pKas.
MCCE calculates the shift in Em or pKa when a group is transferred from solution into the protein (27, 52). Thus
| (2) |
| (3) |
where m is −1 for an acid and +1 for a base. Preferably, Em,sol and pKa,sol are obtained from measurements in aqueous solution. pKa,sol for amino acids are taken from studies of peptides (73, 74). Systematic shifts are applied to the reference reaction field energies (ΔΔGRXN,sol) of the ionized form of ionizable residues on the basis of the pKa benchmark studies (51; manuscript in preparation). The shift is 0.76 ΔpK unit to Asp, 0.36 ΔpK unit to Glu, 1.75 ΔpK units to Arg, 0.10 ΔpK unit to Lys, 0.67 ΔpK unit to His, 0.59 ΔpK unit to Tyr, 1.32 ΔpK units to the C-terminus, and 0.41 ΔpK unit to the N-terminus. On the basis of the pKa and Em studies of aquo–heme proteins (53), −0.74 ΔpK unit is added to ferric hydroxyl–heme and 0.5 ΔpK unit to ferrous water–heme. The heme propionic acids are treated as previously described with a pKa,sol of 4.9 (27). Tyr I-288 is cross-linked to His I-284. The heavy atom rotamer conformation of Tyr 288 is fixed in the position found in the crystal structure. The cross-link shifts the Tyr pKa,sol to 8.9 (75), lower than the standard Tyr pKa,sol of 10.2. As the Tyr–His bonded interaction is included in pKa,sol, no additional nonbonded, pairwise interactions between these two groups are included in the calculations. The non-redox-active ions, Ca2+ and Mg2+, are each given a charge of +2. The residues that serve as ligands to these ions are fixed in their crystal structure positions and given PARSE charges (69). Acidic ligands are constrained to remain ionized.
Parameters for Em and pKa Calculations of the Cofactors
CuA is a dicopper complex with eight side chain and backbone groups serving as ligands. The copper atoms and ligands are treated as a complex, and the charge distribution is obtained with Gaussian 98 (76). The B3LYP method (77) with the LANL2DZ basis set (78) was used, and the CHELPG (79) algorithm was used to fit atomic charges. This charge set is able to recover measured Ems of the designed di-Cu–azurin and of the oxidase soluble domain from different species (manuscript in preparation).
Both heme a3 and CuB have one open coordinate position to bind water or hydroxyl. Conformers are built for water–heme a3, hydroxyl–heme a3, water–CuB, and hydroxyl–CuB. On heme a3, the Fe–O bond is oriented perpendicular to the porphyrin plane, and the bond length is 1.95 Å with square bipyramidal geometry (53). The oxygen position for CuB is determined by DFT optimization calculations using the B3LYP method (77) and LANL2DZ basis set (78) for an isolated cupric hydroxyl–3His–Cu complex. The CR and Cβ atoms of all His ligands and the Cu are fixed in their crystal positions during optimization. This yields a distorted tetrahedral Cu geometry. The resultant O–Cu–Nε(His I-333) bond angle is 136° and the Cu–O bond length is 1.9 Å. Hydrogens are located with tetrahedral oxygen geometry and bond lengths of 0.96 Å. On each cofactor, conformers of water and of hydroxyl are created by rotating the protons by 30° around the Fe–O or Cu–O bond, yielding 12 water and 12 hydroxyl positions on each cofactor. Thus, there are 48 different conformers for heme a3 and for CuB given their two ionization states each with 24 possible water or hydroxyl positions. CuB has an additional set of conformers described below, which include the possible ionization change of a His ligand.
The approach used here to calculate the Ems of cofactors and pKas of the water ligands treats the metal and their ligands as a complex. The assigned Em,sol and pKa,sol are taken from the measurements of a model system for the complex in solution. The reaction field energy is also calculated, treating the whole complex. Any nonbonded pairwise interactions among the metal and its ligands are ignored since these interactions are included in the Em,sol and pKa,sol. Treating cofactors and ligands as a complex thus avoids the errors inherent in using classical electrostatics to calculate the bonding energies joining them together. However, this approach requires prior knowledge of Em,sol and pKa,sol for the desired complex.
In this study, an Em,sol of −120 mV is assigned to the a-type bis-His heme found in the heme a site (28). An a-type heme has an extra electron-withdrawing formyl group that favors reduction (28). With the same ligands, the Em of heme a is 100 (28) to 160 (80, 81) mV more positive than that of c-type bis-His heme microperoxidase 8 (MP8) (82, 83). For calculating the pKa of water ligands, a pKa,sol of 9.6 is assigned to the oxidized ferric His–aquo–heme and 10.9 for the reduced ferrous His–aquo–heme, as measured with a c-type MP8 heme (86, 87). It is assumed that water pKas are the same in c-type and a-type hemes because the water to be protonated is not in the porphyrin plane and so should not be influenced by the formyl group on the porphyrin edge. There are fewer measurements that can be used to model the water pKa in the CuB complex. A pKa,sol of 9.4 is used for aquo–CuB(II). This is taken from measurements of a tripodal ligand tris[2-(methylamino)ethyl]amine complex (88, 89), which is similar to the CuB complex. A measured pKa,sol of aquo–CuB(I) has not been found in the literature. It is likely to be higher than that of CuB(II) due to the smaller positive charge on the metal. A conservative pKa,sol of 9.4 will be assigned to aquo–CuB(I) and the effects of this choice discussed below.
A metal-centered charge set is used for heme a, heme a3, and CuB. Hemes a and a3 have a +2 or +3 charge placed on Fe and −0.5 on each N atom of the porphyrin. CuB has a +1 or +2 charge on Cu. PARSE charges are used for the neutral His ligands. TIP3 charges are used for water ligands. CHELPG charges for the hydroxide and a His− are calculated in isolation with the B3LYP method using the 6–31G* basis set. The metal-centered charge distribution differs from that determined by DFT calculations for the complex where some of the metal positive charge is shifted to the ligands. A +0.3 charge is placed on the formyl group C and −0.3 on the electron-withdrawing formyl group of the a-type hemes. This simple metal-centered charge set has been used successfully in heme benchmark calculations for bis-His and His–aquo hemes (25, 27, 53).
It has been proposed that His I-334, a ligand to CuB, forms an anionic imidazolate during the reaction cycle (39, 40). To calculate the pKa of this His ligand, two approaches are used. The first is the same as used for the pKa calculations of the BNC water ligands. CuB and all of its His and aquo ligands are treated as one complex. There is no experimental pKa,sol available for such a complex with a deprotonated imidazolate. However, a pKa,sol of 9.0 has been calculated with DFT for a isolated CuB complex with water and 3 His ligands (40). A conformer with ionization state H2O–His−–CuB(II) is added to compete with H2O–His0–CuB(II) and OH−–His0–CuB(II) ionization states to determine the in situ His I-334 pKa. DFT calculations were not reported with both His− and OH− bound on CuB(II) or any pKas with a reduced CuB so these states cannot be addressed by treating CuB as a complex with its ligands. An alternative approach allows estimation of the His pKa in the presence of OH−, the OH− in the presence of His−, and the pKas with reduced CuB. Here His is treated as an isolated group separate from CuB with its bound water and the two other His ligands. The pKa,sol of the free imidazolate of 14.4 is used. The reaction field energy of the His and the smaller CuB complex are each calculated. Explicit nonbonded electrostatic interactions between His or His− and the different redox and protonation states of the smaller CuB complex are included. This approach has been shown to work for some heme ligands (25), but with a metal-centered charge, continuum electrostatics often overestimates the favorable interactions between a metal and an anionic ligand.
On the basis of a study of aquo–heme pKas and Ems in various proteins (53), the Poisson–Boltzmann continuum electrostatics calculations are found to overestimate the interactions of ferric heme a3 with CuB. That study compared the energies of a positive charge near a ferric aquo–heme in a vacuum calculated with DFT and with Coulomb’s law. For the neutral, ferric His–hydroxyl–heme, Coulomb’s law reproduces the favorable change in the heme energy found in the DFT calculations within 10%. The correlation between the Coulomb interaction and the DFT energies has a slope of 1 and is independent of the position of the external charge. Thus, the DelPhi continuum electrostatics calculations in MCCE should provide the correct interaction energies. However, there are position-dependent systematic errors in the large, unfavorable interactions with the cationic, His–water–heme complex. While interactions with negative charges, with charges in the heme plane, such as the propionic acids, and with distant charges, such as heme a, are well represented by Coulomb’s law, when a charge is near the face of the heme, the interactions are overestimated. Interactions with groups close to the heme also need correction in the benchmark calculations of the aquo–heme pKas in sperm whale and Aplysia myoglobin, hemoglobin I, heme oxygenase 1, and horseradish peroxidase (53).
The interaction between heme a3 and CuB is investigated with DFT calculations (see Supporting Information). Different heme a3 and CuB redox states, ligand protonation states, and hydrogen positions created in MCCE are tested. The correlation between DFT and Coulomb’s law interactions cannot be described by a simple scaling factor. But, these results showed that the ranking of the energies between different states of the BNC agrees in the two calculations. Thus, MCCE calculations are first carried out using uncorrected Poisson–Boltzmann (PB) interactions to find the equilibrium hydrogen positions in each BNC redox and protonation state. The DFT and Coulomb’s law interactions are then calculated with the equilibrium conformations. The scaling factor required to bring the Coulomb’s law interactions into agreement with the DFT calculations in a vacuum is applied to the PB interactions, and the scaled values are used in the pKa calculations. Conformers that are not occupied in the calculations with uncorrected PB interactions are omitted in the pKa calculations. DFT, Coulomb’s law, uncorrected DelPhi PB, and interactions between heme a3 and CuB used in the pKa calculations can be found in Supportinng Information (Table S1).
Analysis of the MCCE pKas and Ems
In the continuum electrostatics-derived MCCE analysis, the Em or pKa shifts found on moving a group from solution to its position in the protein (ΔΔGprotein) can be broken down as (27, 52)
| (4) |
All terms describe how the difference in free energy of reactant and product redox or protonation state changes when the group is moved from water to protein. The differences in solvation energy (ΔΔGrxn) and electrostatic and nonelec- trostatic interactions with the backbone (ΔGpol) are independent of the distribution of other conformers and so are independent of pH and Eh. Interactions of the group of interest with residues having conformational flexibility (ΔGres) are obtained from ΔΔGprotein, given the Em and pKa calculated by Monte Carlo sampling (eqs 2 and 3). ΔGres includes the energy of rearranging the conformers, as well as the interaction of the conformers with a site of interest (27, 52).
The pKas derived from the Monte Carlo sampling as function of pH to determine the pH where 50% of the group of interest is ionized are the appropriate value to compare to experimental pKas (51). However, changes in net protein charge with pH alter the electrostatic potential at each site of interest. This yields in situ pKas that are pH dependent; consequently, the free energy of ionization does not change with pH simply by pKa–pH, as it would in solution. The free energy of ionization at a given pH (ΔGpH) can be estimated from
| (5) |
where is the mean field interaction of the Boltzmann-weighted distribution of conformers of the residue of interest with the Boltzmann-weighted occupancy of all other conformers in the protein at this pH (27, 52). It therefore misses the energy needed if other residues change ionization or conformation state when the site of interest changes protonation state. Thus, ΔGpH, the vertical energy for changing the protonation state of a residue at pH 7, is
| (6) |
where
| (7) |
Given the protein equilibrated at pH 7, pK′7 describes the pH where the protonation free energy would be zero (when pH = pKa). ΔG7 is the best measure of the stability of a given ionization state at pH 7 when the pKa is far from 7. Thus, for residues with very high or low pKas equilibrium ionization changes are calculated at a high or low pH where the ionization states of the rest of the protein are different than they are in the physiological pH range.
RESULTS
Ionization states of all residues in the three-subunit Rb. sphaeroides cytochrome c oxidase were calculated with Multi-Conformation Continuum Electrostatics (MCCE) in seven different anoxygenic redox states (1): fully oxidized (OOOO, O state), singly reduced states with CuA reduced (ROOO), heme a reduced (OROO), or CuB reduced (OOOR, E state), mixed valence states with heme a and CuB (OROR) or both heme a3 and CuB (OORR, R state) reduced, and the fully reduced state (RRRR). Sites where proton uptake or internal transfer is coupled to electron transfer are identified by the calculated differences in residue protonation in different redox states (Table 1). In addition, pK′7 (eq 7) was calculated for key residues, which provides the energy required to move away from the equilibrium protonation state at pH 7 (Table 2).
Table 1.
Ionization States of Key Residuesa
| A. Net charge | OOOO | ROOO | OROO | OOOR | OROR | OORR | RRRR |
|---|---|---|---|---|---|---|---|
| Release side Cluster | |||||||
| His 1-93 | 0.05 | 0.17 | 0.12 | 0.08 | 0.12 | 0.08 | 0.22 |
| Glu 1-182 | −0.69 | −0.37 | −0.49 | −0.56 | −0.47 | −0.54 | −0.27 |
| Total | −0.64 | −0.20 | −0.37 | −0.48 | −0.35 | −0.46 | −0.05 |
| PropA (Heme a) | −1.00 | −1.00 | −1.00 | −1.00 | −1.00 | −1.00 | −0.79 |
| BNC Cluster | |||||||
| aquo-Heme a3 | 0.00 | 0.00 | 0.00 | −0.87 | −0.09 | 0.00 | 0.00 |
| aquo-CuB | −1.00 | −1.00 | −1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Glu 1-286 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Tyr 1-288 | −0.06 | −0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Total | −1.06 | −1.04 | −1.00 | −0.87 | −0.09 | 0.00 | 0.00 |
| Uptake side Cluste | |||||||
| His 1-127 | 0.31 | 0.29 | 0.48 | 0.37 | 0.44 | 0.44 | 0.50 |
| Glu 1-539 | −0.62 | −0.62 | −0.67 | −0.59 | −0.64 | −0.66 | −0.66 |
| Total | −0.31 | −0.33 | −0.19 | −0.22 | −0.20 | −0.22 | −0.16 |
| Whole protein | −4.30 | −4.70 | −4.80 | −4.90 | −4.80 | −4.90 | −5.80 |
|
| |||||||
| B. Proton uptake relative to OOOO state | ROOO | OROO | OOOR | OROR | OORR | RRRR | |
| Release side Cluster | - | 0.44 | 0.27 | 0.16 | 0.29 | 0.18 | 0.59 |
| BNC Cluster | - | 0.02 | 0.06 | 0.19 | 0.97 | 1.06 | 1.06 |
| Uptake side Cluster | - | −0.02 | 0.12 | 0.09 | 0.11 | 0.09 | 0.15 |
| Whole Protein | - | 0.60 | 0.50 | 0.40 | 1.50 | 1.40 | 2.50 |
| OOOO | ROOO | OROO | OOOR | OROR | OORR | ||
| C. Step-wise proton uptake | → | → | → | → | → | → | |
| ROOO | OROO | OOOR | OROR | OORR | RRRR | ||
|
| |||||||
| Release side Cluster | - | 0.44 | −0.17 | −0.11 | 0.13 | −0.11 | 0.41 |
| BNC Cluster | - | 0.02 | 0.04 | 0.13 | 0.78 | 0.09 | 0.00 |
| Uptake side Cluster | - | −0.02 | 0.14 | −0.03 | 0.02 | −0.02 | 0.06 |
| Whole Protein | - | 0.60 | −0.10 | −0.10 | 1.10 | −0.10 | 1.10 |
MCCE calculated ionization of key residues of Rb. sphaeroides cytochrome c oxidasein selected redox states. Charges on the aquo ligands of heme a3 and CuB are shown, while the charges on the metal center and the His ligands are not included in the number. The whole protein ionization includes charges on groups not explicitly noted here. Redox states of the four cofactors are represented by the four-letter key ordered CuA, heme a, heme a3, and CuB (O, oxidized; R, reduced). The A and D propionic acids are identified by their connection to the A and D rings in the PDB file.
Table 2.
pK′7 of Residues Implicated in Oxidase Activitya
| OOOO | ROOO | OROO | OOOR | OROR | OORR | RRRR | |
|---|---|---|---|---|---|---|---|
| BNC cluster | |||||||
| aquo–heme a3 | 10.7 | 11.1 | 12.4 | 5.9 | 8.4 | 21.5 | 22.6 |
| aquo–CuB | −9.4 | −9.1 | −7.8 | 26.2 | 16.8 | 18.8 | 20.7 |
| Glu I-286 | 9.7 | 9.5 | 11.3 | 11.2 | 10.6 | 10.9 | 12.8 |
| Tyr I-288 | 8.6 | 8.8 | 9.8 | 15.7 | 11.3 | 15.6 | 16.9 |
| His I-334 (a)b | 10.3 | 10.9 | 12.0 | NA | NA | NA | NA |
| His I-334 (b)b | 15.8 | 16.4 | 17.5 | 22.9 | 31.8 | 25.5 | 27.7 |
| PropA heme a | −1.7 | 0.0 | 2.1 | −0.1 | 3.5 | 0.4 | 6.1 |
| PropD heme a | −9.3 | −7.7 | −6.4 | −7.5 | −4.8 | −7.3 | −3.7 |
| PropA heme a3 | −8.0 | −7.2 | −6.1 | −4.5 | −2.3 | −3.9 | −1.6 |
| PropD heme a3 | −7.5 | −6.6 | −5.4 | −3.8 | −1.6 | −3.6 | −0.8 |
| release side cluster | |||||||
| His I-93 | 6.5 | 7.6 | 7.2 | 6.9 | 7.6 | 6.9 | 8.5 |
| Glu I-182 | 6.3 | 7.3 | 6.9 | 6.7 | 7.3 | 6.7 | 8.1 |
| uptake side cluster | |||||||
| His I-127 | 7.8 | 7.7 | 8.0 | 8.0 | 8.3 | 8.0 | 8.4 |
| Glu I-539 | 6.9 | 7.0 | 7.1 | 7.0 | 7.2 | 7.1 | 7.2 |
| D and K channel residues | |||||||
| Asp I-132 | 0.5 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 |
| Lys I-362 | −2.7 | −2.7 | −2.9 | −2.1 | −2.8 | −2.0 | −1.2 |
| Glu II-101 | 2.1 | 2.1 | 2.2 | 2.3 | 2.4 | 2.4 | 2.4 |
pK′′7 gives the effective pKa calculated with the protein ionization and conformation states fixed at pH 7 providing the free energy of a site changing ionization at pH 7 (eqs 5 and 6). pK′7 depends on the ionization states of other residues. is calculated with the key residue ionization states given in Table 1.
pK′7 for deprotonation of His I-334 to form the anion is calculated in two ways, as described in Methods. (a) The His has a pKa,sol of 9.0 in the oxidized water–CuB complex (40); pK′7 is calculated with a hydroxyl on heme a3 and water on CuB in OOOO, ROOO, and OROO states. This value is used for the OOOO state in Table 4 and Figure 6. (b, in italics) The His pKa is calculated, starting with a pKa,sol of 14.4 and explicit, nonbonded pairwise interactions with CuB and its ligands. The equilibrium state here has a hydroxyl on CuB in the OOOO state. This value is used for the OORR state in Figure 6.
Residues responding to the redox state changes can be assigned to three clusters. The BNC cluster contains the hydroxyl groups coordinated to heme a3 and/or CuB (32–34). In addition, the heme a and a3 propionic acids (45), Glu I-286 (6–8), Tyr I-288, Lys I-362, and His I-334 (38, 39) are essential ionizable residues in the vicinity of the BNC, which are in a position to couple proton uptake to cofactor reduction (Figure 2). On the proton release side of the protein, His I-93 and Glu I-182 form a cluster which changes ionization as the oxidase cofactors change charge (Figure 3A). The third cluster which includes His I-127 and Glu I-539 is found on the proton entry side near the D channel Asp I-132 (Figure 3B).
Figure 2.
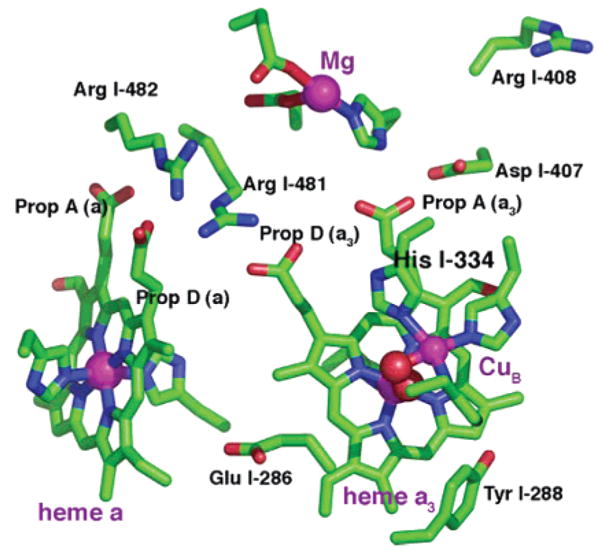
Hemes a and a3, CuB, the Mg cluster, and nearby ionizable residues. Mg and cofactor metal atoms are shown as purple spheres. The oxygens of the BNC water ligands are in red. The heme a3 water oxygen is behind that of CuB. The only labeled cofactor or ion ligand is His I-334, a CuB ligand whose pKa is studied here.
Figure 3.
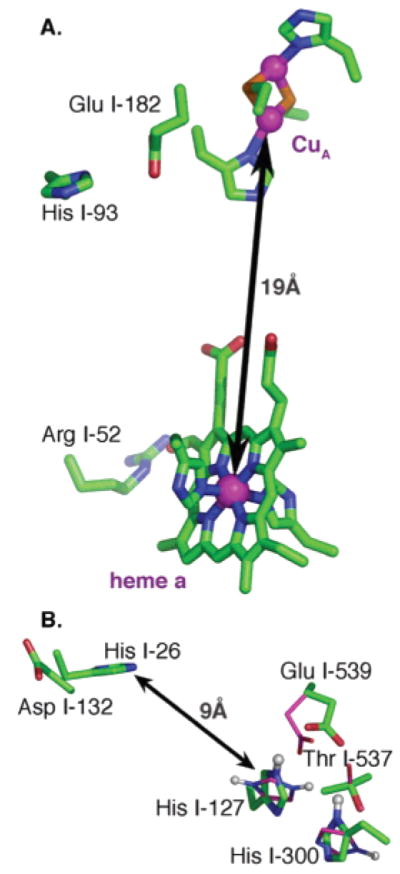
(A) CuA and heme a with their ligands, Arg 52, and the proton release side cluster, His I-93 and Glu I-182. (B) Asp I-132 and His I-26 at the D channel entrance and the proton entry side cluster, His I-127 and Glu I-539, together with His I-300 and Thr I-537. Conformational changes in the cluster when I-127 is protonated are shown with thinner purple sticks. Protons bonded to nitrogens of His I-127 and His I-300 are shown as spheres. Glu I-539 and Asp I-132 are ≈30 Å from CuB.
BNC Hydroxyl pKas
In the absence of oxygen, CuB and heme a3 each bind one water or hydroxide as their fourth and sixth ligand, respectively. To couple proton uptake to BNC reduction, the hydroxyl pKa must be lower than the solution pH in the fully oxidized state and higher following reduction. The pKa,sol for deprotonation of an oxidized His–aquo–heme has been measured to be 9.6 (86), while that of an oxidized Cu(II) with 3 His ligands is estimated to be 9.4 (88, 89). In the fully oxidized protein, MCCE Monte Carlo sampling places a hydroxyl on CuB down to a pH below 4 and a water on heme a3 beyond pH 11. Using the Boltzmann-sampled ionization states of all other residues at pH 7 (Table 1), the pK′7 of −9.4 for aquo–CuB indicates that 16.4 ΔpK units (22.3 kcal/mol) are needed to protonate the hydroxyl at pH 7 (eq 6, Table 2). The heme a3 pK′7 is 10.7, indicating that the cost of removing a proton from this water is 3.7 ΔpK units (5.0 kcal/mol).
The factors that determine pK′7 can be analyzed using eq 4 (Table 3). The oxidized hydroxyl–CuB has a net charge of +1. When a water is bound, its charge is +2. The oxidized hydroxyl–heme a3 has a net charge 0, and it is +1 when a water is bound. The larger charge means that the water complexes lose more solvation energy (ΔΔGrxn) than the hydroxyl complexes when they are moved into the protein. The difference stabilizes the hydroxyl form, lowering the in situ aquo–cofactor pK′7. The ΔΔGrxn lowers the heme a3 pK′7 by only 3.9 pH units, while it destabilizes the water–CuB by 14.7 ΔpK units (Table 3). The favorable interaction of each hydroxyl with the positive charge on the other BNC metal center lowers the pK′7 by >10 ΔpK units. The interaction of either hydroxyl with the rest of the protein (ΔGpol and ) raises its pK′7 by ≈6 ΔpK units (Table Gres,73). The pK′7 of aquo–CuB is −9.4 when a water is bound to heme a3 (Table 2), while the aquo–heme a3 pK′7 is −5.0 with water on CuB. As a result, at least one hydroxyl is very stable in the oxidized BNC. However, the repulsion between the two hydroxyls destabilizes the ionization of both by 15.7 ΔpK units. This is consistent with earlier MCCE1.0 calculations on P. denitrificans, which also found one hydroxyl group in the BNC in the fully oxidized enzyme (33). CuB with the lower pK′7 binds the hydroxyl, while a water is bound to heme a3. This is in agreement with the optical absorbance measurements, which have shown a high-spin heme a3 in oxidized cytochrome c oxidase (90). Hydroxyl–hemes are expected to be in a low-spin state (34, 91), while water–hemes are generally in a high-spin state (34). EXAFS and ENDOR experiments support the presence of a hydroxyl–CuB in the oxidized enzyme (32).
Table 3.
Energy Terms Used To Calculate pK′7a
|
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| net charge |
OOOO |
OORR |
RRRR |
|||||||||
| reactant | product | pKa,sol | ΔΔGrxn | ΔΔGpol | BNC | RES | BNC | RES | BNC | RES | ||
| ferric aquo–heme a3 | 0 | +1 | 9.6 | 3.9 | 0.4 | 0.2 | −5.7 | |||||
| ferrous aquo–heme a3 | −1 | 0 | 10.9 | −10.4 | 0.4 | 4.0 | −4.6 | 4.0 | −5.7 | |||
| cupric aquo–CuB | +1 | +2 | 9.4 | 14.7 | 0.4 | 10.0 | −6.3 | |||||
| cuprous aquo–CuB | 0 | +1 | 9.4 | −4.7 | 0.4 | 1.1 | −6.2 | 1.1 | −8.1 | |||
| Glu I-286 | 0 | −1 | 4.8 | 6.8 | 0.8 | −4.3 | 1.6 | −2.7 | 1.2 | −2.7 | 3.1 | |
| Tyr I-288 | 0 | −1 | 8.9 | 10.4 | 0.3 | −12.4 | 1.3 | −4.8 | 0.7 | −4.8 | 2.1 | |
| His I-334b | +2 | +1 | 9.0 | −8.5 | −2.1 | 2.2 | 9.7 | NA | NA | NA | NA | |
| 0 | −1 | 14.4 | 14.0 | −2.1 | −20.0 | 9.7 | −9.0 | 8.6 | −9.0 | 10.4 | ||
| PropA heme a | 0 | −1 | 4.9 | 10.4 | −5.5 | −3.8 | −7.7 | −1.8 | −7.5 | −1.8 | −1.8 | |
| PropD heme a | 0 | −1 | 4.9 | 9.8 | −7.3 | −4.3 | −12.3 | −2.1 | −12.5 | −2.2 | −8.8 | |
| PropA heme a3 | 0 | −1 | 4.9 | 7.1 | −1.3 | −10.4 | −8.3 | −5.1 | −9.6 | −5.1 | −7.3 | |
| PropD heme a3 | 0 | −1 | 4.9 | 6.5 | −3.2 | −9.9 | −5.8 | −5.2 | −6.7 | −5.2 | −3.8 | |
| His I-93 | 0 | +1 | 6.5 | 2.9 | −0.7 | 0.7 | −2.9 | 0.4 | −2.9 | 0.4 | −4.5 | |
| Glu I-182 | 0 | −1 | 4.8 | 4.8 | −2.7 | −0.7 | 0.2 | −0.4 | 0.2 | −0.4 | 1.6 | |
| His I-127 | 0 | +1 | 6.5 | 4.8 | 4.4 | 0.7 | −11.3 | 0.3 | −11.1 | 0.3 | −11.5 | |
| Glu I-539 | 0 | −1 | 4.8 | 6.7 | −4.1 | −0.5 | 0.0 | −0.2 | −0.1 | −0.2 | 0.1 | |
| Asp I-132 | 0 | +1 | 4.8 | 3.3 | −2.9 | −0.3 | −4.3 | −0.2 | −4.4 | −0.2 | −4.4 | |
| Lys I-362 | 0 | +1 | 10.8 | 10.9 | −0.7 | 2.6 | 1.2 | 1.6 | 1.0 | 1.7 | 0.2 | |
| Glu II-101 | 0 | −1 | 4.8 | 2.7 | −1.2 | −0.6 | −3.5 | −0.3 | −3.6 | −0.3 | −3.5 | |
The net charge of the reactant and product states is given. The reference reactant state is neutral for Prop, Glu, Lys, and His and has a neutral His I-334 and a hydroxyl on heme a3 and CuB. pKa,sol: pKa of isolated group in aqueous solution. ΔΔGrxn: double difference of desolvation (reaction field) energy [product −reactant]in protein − [product − reactant]in water. This is generally a positive, unfavorable term when the product charge is larger than that of the reactant. ΔGpol and : differences in electrostatic and nonelectrostatic interactions of product and reactant states with the backbone (ΔGpol), with the binuclear center cofactors and their water or hydroxyl ligands (BNC ), and with the protein side chains and other cofactors (RES ). uses a mean field energy interaction with the ionization states found by MCCE sampling at pH7 (see Table 1 for key residues). Thus, in the OOOO state there is a water on heme a3 and a hydroxyl on CuB. The hydroxyl moves to heme a3 in the OOOR state. There are no hydroxyls in the BNC in any other redox states. For example, the BNC term for ferric aquo–heme a3 in the OOOO state is the (ferric water–heme a3)–(ferric hydroxyl–heme a3) interaction with the cupric hydroxyl–CuB, the MCCE calculated equilibrium state for CuB. The interaction of the ferric water–heme and each of the CuB states is reduced as shown in Supporting Information (see Methods and ref 53).
pK′7 of His I-334 deprotonation is calculated in two ways, as described in Methods. The top entry uses a Cu(II)–water–His complex. This does not allow calculations with a hydroxyl on Cu(II) or any Cu(I) states. The BNC interactions are with hydroxyl–heme a3 and its ligands only. In the bottom entry, the BNC term includes the nonbonded interactions of the Cu, the other two CuB His, and its aquo ligands, as well as heme a3 with His I-334.
When CuB is reduced forming the OOOR state, a single hydroxide is calculated to remain in the BNC. A pKa,sol for an aquo–Cu(I) CuB analogue is not found in the literature. The reduced CuB, with its smaller charge, should have a higher aquo–heme pKa than the Cu(II) complex. The calculation shows that, even leaving the pKa,sol for the reduced hydroxyl–CuB at 9.4, the hydroxyl in the BNC shifts to the oxidized heme a3. The desolvation penalty, which strongly destabilizes the water–CuB(II), now favors water–CuB(I) (Table 3). Although the reduced water–CuB(I) complex has the larger net charge, the hydroxyl complex has a large dipole moment and more reaction field energy in water. The pK′7 of hydroxyl–CuB is 12.5 with water on the oxidized heme a3, while the aquo–heme a3 pK′7 is 5.9 with water on the reduced CuB (Table 2). As in the fully oxidized protein, the mutual repulsion of the two hydroxyls means that only one will be found. Thus, there is little proton uptake into the BNC on the reduction of CuB, but the hydroxide migrates from CuB to heme a3.
In the OROR state, the aquo–heme a3 pK′7 shifts up to 8.4 (Table 2). Hence, a proton will be taken into the BNC at pH 7 coupled to the reduction of heme a if CuB is already reduced. The change in pK′7 from the OOOR to OROR state is due to the aquo–eme a3 interaction with the neutral, reduced heme a being 2.5 ΔpK units smaller than it is with the cationic, oxidized heme. After 2 electrons enter the BNC to form the R (OORR) intermediate, the aquo–ofactor’s pKas are greater than 7 so both remain protonated as calculated previously (33). This result agrees with experiments that show little proton release at pH 7 when CO is photolyzed off the mixed valence complex, initiating back-electron transfer moving from the OORR to OROR state (34). The pKa obtained from the fractional site ionization in Monte Carlo sampling as a function of pH for aquo–eme a3 is 8.6, in good agreement with the measured pKa of 9 for proton release.
The pKas of the BNC aquo– cofactors have been calculated by Siegbahn and colleagues using the hybrid density functional method (44). Since no other residues are allowed to change ionization, their pKas are equivalent to pK′7 In the DFT study, the pK′7 is < − 10 for the first deprotonation with 2 waters in the site and 8 when forming two hydroxides in the OOOO state. In the MCCE calculations, the pKas are −9.4 and 10.7. Thus, both studies agree that there will be at least one hydroxyl in the BNC. But, the stability of the system with two hydroxides differs by 3 ΔpK units. In the DFT calculations, 10% of the oxidized BNCs would have two hydroxyls, while MCCE predicts none will.
The protein is treated differently in the two simulations. MCCE includes the whole protein in the model, while the DFT calculations include only the cofactors, their ligands, the propionates, and Tyr 288. The DFT simulation region is well chosen to make the net interaction of the BNC with other parts of the protein small. The missing interactions from the rest of the protein favor the hydroxyl groups by only ≈1 ΔpK unit. A more significant difference is that the DFT calculation assumes that the BNC is in a uniform medium with ε =4, while MCCE puts ε =80 into protein cavities. The high dielectric cavity stabilizes the more highly charged water–cofactor species, shifting the aquo–heme a3’s pK′7 up by ≈1 pH unit and the hydroxyl–CuB by ≈5 pH units. This term destabilizes the second hydroxide in the MCCE calculations. MCCE calculations were made, eliminating the continuum water in the cavities and the interactions with parts of the protein outside of the DFT simulation region. Here the pK′7s are −15.1 for aquo–CuB as it loses the first proton and 8.3 for aquo–heme a3 forming the second hydroxyl in the BNC, significantly closer to the DFT values. In the OOOR state there is only one stable hydroxyl in either calculation. It has a pKa of 7.6 in the DFT calculations and 5.9 in the standard MCCE calculations. In the MCCE calculations using DFT assumptions, the extra solvation energy drops the aquo–heme a3 pK′7 to 5.2.
Ionization of Tyr I-288
Tyr I-288 is at the end of the K channel, hydrogen-bonded to the water on heme a3 (Figure 2). Oxygen reduction chemistry is likely to involve a coupled electron (92–94) and proton (75, 95, 96) transfer from this Tyr to O2. The Tyr could also serve as a proton acceptor when the BNC is reduced, if it is deprotonated in the fully oxidized state. The MCCE calculated pKa is 8.7 (pK′7 8.6), so it is 6% deprotonated at pH 7. The relatively high pKa,sol and large desolvation energy destabilize its ionization, while the BNC positive charge favors ionization (Table 3). The pK′7 is lowered by the pKa,sol, being 8.9, 1.3 pH units lower than a standard Tyr, because of its attachment to His I-284 (75). Thus, this Tyr is neutral even in the oxidized protein, but there is only a 2.2 kcal/mol penalty for forming the anion at pH 7 in the equilibrated protein with a hydroxyl on CuB.
Ionization of Glu I-286
Glu I-286 is an essential residue which been proposed to shuttle chemical protons from the D channel to the BNC and pumped protons to the outside at the appropriate steps in the reaction cycle (6–8). In the fully oxidized protein, Glu I-286 is calculated to be fully protonated with a pKa of >10 (pK′7 9.9). Despite the low pKa,sol of 4.8, the loss of reaction field energy destabilizes the ionized form, keeping the Glu neutral (Table 3). Nearby cavities leading to the D channel (46, 47), and to heme a3 (12), solvate the Glu to lower pK′7. Interactions with the protein, mostly contributed by the oxidized BNC, further stabilize Glu−. The balance of favorable interaction with the protein and the large desolvation energy tunes the pK′7 so that it takes only 4 kcal/mol to deprotonate the Glu at pH 7. This puts the ionized state low enough in energy that it can serve as an intermediate in proton transfer.
Glu I-286 has been measured to have a pKa of 9.4 in the F state (97). The F state with a water–CuB(II) and a ferryl heme a3 [Fe(IV)=O2−] has the same net charge as the water–CuB(II) and ferric hydroxyl–heme a3. In the latter state, the Glu I-286 pK′7 would be 8.9 while it is 10 for Tyr I-288. Here Glu I-286 is 3% ionized at pH 7 and becomes 50% ionized at 10.9, titrating with a shallow pH dependence in reasonable agreement with the experimental value. The calculated Tyr pKa is much higher than its pK′7 which is obtained at pH 7 where Glu I-286 is neutral. Unfavorable interactions with the Glu which is ionized first with increasing pH make it harder to deprotonate the Tyr. Thus, the ionization states of the Glu and Tyr are tightly coupled with an interaction energy of 2.6 ΔpK units. Once one of them is ionized, the pKa of the other moves well above 10. The charge distribution in the BNC determines which amino acid is ionized first. In an OOOO state with a hydroxyl–heme a3 (similar to the F state charge distribution), the pKa for the Glu is lower than that of the Tyr. But in the lower energy OOOO state with hydroxyl–CuB, the Tyr has the lower pKa.
Ionization of the Heme Propionic Acids
All of the heme propionic acids are calculated to be deprotonated in the fully oxidized state (Table 1). The propionates on the A- and D-rings (nomenclature as in the PDB file) of heme a3, and on the D-ring of heme a, are close to the BNC and have been suggested to lie on the proton pumping pathway (12, 35–37). All of the propionic acids are stabilized by the presence of Arg I-481 and I-482. Each D-ring propionate is within hydrogen-bonding distance of an Arg. The heme a3 A-ring propionate is further stabilized by the Mg2+ and its ligands: His I-411, Asp I-412, and Glu II-254. Even though the net charge of the Mg cluster is 0, the propionate is closer to the Mg2+ than to its anionic ligands (Figure 3). A hydrogen bond from the neutral His I-411 further stabilizes the charged state. The heme a A-ring propionic acid is stabilized by Arg 52. The heme a3 propionate pK′7s remain below 0 in all of the oxidation states, despite their increasing 2–5 pH units when the BNC is reduced (Table 2). Any changes in protonation of the propionic acids would need to be coupled to movement of the adjacent Arg, as well as to reduction of the BNC (98). There is little difference in the propionic acid pK′7s for OOOR and OORR states, because the second reduction of the BNC is coupled to the protonation of the hydroxide; therefore, it is electroneutral with little long-range electrostatic impact (Table 2).
The heme a A-ring propionic acid has a pK′7 near physiological pH (Table 2). It remains fully ionized when the BNC is reduced (OORR). But, when the BNC and CuA and heme a are reduced (RRRR), its pK′7 is 6.1, so it is partially protonated at pH 7 (Table 1). However, this proton binding in the fully reduced protein is to the propionate furthest from the BNC, and it is coupled to the reduction of CuA and heme a, not the BNC cofactors.
The heme a3 A-ring propionic acid pK′7 has also been estimated by Siegbahn and colleagues using DFT calculations (44). They found that in the fully oxidized protein it is 5.2, while MCCE finds it to be −8.0. This large difference is a result of the DFT calculations being centered at the BNC cofactors, locating the propionic acids at the edge of the simulation region about 8 Å from the heme iron. Arg I-481, I-482, and the Mg2+ complex are not included in the calculation. These groups together stabilize the acid ionization by over 13 ΔpK units. MCCE calculations with only the groups used in the DFT calculations give a pK′7 of 6.6, in reasonable agreement with the DFT analysis. In the OOOR state, DFT calculates the propionate pK′7 to be 11.5, while it is −4.5 in MCCE considering the whole protein and 11.4 calculated by MCCE considering only the residues included in the DFT simulations. In the OORR state, the pK′7 is calculated to be 11.5 with DFT calculations, −3.9 with MCCE considering the whole protein, and 12.0 with MCCE considering the same residues as in the DFT calculation. Hence, the classical electrostatics calculations can reproduce the DFT pK′7s when the same region of the protein is considered. The simple classical calculation has the advantage of being able to routinely include the whole protein.
Ionization of His I-334
His I-334, a CuB ligand, has also been proposed to act as a residue whose protonation state is coupled to the BNC redox state. Earlier work by Wikström suggested that this His might break its bond to CuB and be doubly protonated in a His shuttle (38). More recently, Stuchebrukhov proposed that the His becomes a fully deprotonated imidazolate, coexisting with a hydroxyl group on CuB in the fully oxidized state (39). This His− could then serve as a second proton acceptor, keeping the BNC reduction electroneutral (39, 41). A pKa,sol for deprotonation of a His ligand on an oxidized water–CuB of 9.0 was calculated with DFT (40). Because the His− reduces the water–CuB charge, the His–water–CuB(II) pKa is lowered by ≈14 ΔpK units when it is moved to a uniform medium with ε =4 in the MCCE calculations and by 12.3 in the DFT self-consistent reaction field calculations (40). This difference is likely to be due to differences in the charge distribution in the two calculations. Within the protein, cavities and the large unfavorable interactions with the heme a3 propionates destabilize His− (Table 3). The resultant pK′7 of 10.3 with a hydroxyl–heme a3 indicates that the His will remain neutral in the fully oxidized state. Earlier calculations by Stuchebrukhov using a similar model for the His–CuB interaction and a continuum electrostatic-based methodology similar to that found in MCCE (99–103) reported a His− pKa of ≈6 in the oxidized protein with a hydroxyl on CuB (39). That calculation used a pKa,sol for the deprotonation of the water–CuB–His complex of 7. With this change in pKa,sol the pK′7 for His I-334 reported here would move down to 8.3. More recent calculations from the Stuchebrukhov group used a DFT-derived pKa,sol of 9 in aqueous calculations with (104) or without (41) a ferryl–heme a3 included. The pKa of His I-334 is 2.1 (41) or 5.4 (104) in the OORO state. The latter calculation includes the ferryl–heme a3 in the reference state. In the Stuchebrukhov nomenclature R indicates any electronic state of heme a3 with a net charge of 0 (i.e., ferrous–water, ferric–hydroxyl, or ferryl) while the O designation for CuB indicates that it is oxidized with a water ligand. The His I-334 pK′7 for this state calculated by MCCE is 10.3. MCCE reports different values for both solvation energy and pairwise interactions with the other groups in the protein, contributing to the disagreement with the earlier studies (41, 104).
Although the first approach is more accurate using the pKa,sol of the complex, the pK′7 cannot be estimated for His deprotonation with a hydroxyl on CuB, because the needed pKa,sol is not available. To estimate this pK′7, a second approach is used (see Methods). Here pK′7 is estimated by starting with an isolated imidazolate pKa,sol of 14.4 and then including explicit nonbonded pairwise interactions between the His and CuB. Despite the fact that this model is likely to overstabilize the anionic ligand due to the strong interaction between the metal center and the ligand, the His pK′7 is 15.8 (Table 3).
Protonation Changes on Residues outside the Active Site
At equilibrium, after reducing both cofactors in an initially oxidized protein, one hydroxide on a BNC cofactor has picked up a proton. In addition, other more distant residues change ionization state, contributing to the net proton uptake. The protonation of distant sites can be perturbed either by changes in the long-range electrostatic potential when the BNC is reduced or by changes in local environment if conformational rearrangements are triggered by reduction of the BNC cofactors. Electroneutral reduction of the BNC cannot yield long-range electrostatic changes. In the analysis presented here, where no backbone motions are allowed, there must be a change in the net BNC charge for proton uptake to distant residues to be coupled to electron transfer. The residues that are sensitive to small shifts in the long-range electrostatic potential are partially protonated with pKas near 7. Two clusters, one on the proton input and one on the release side, make the largest contributions to the total proton uptake. On cofactor reduction, there are shifts in charge distribution within these clusters as well as changes in net cluster ionization.
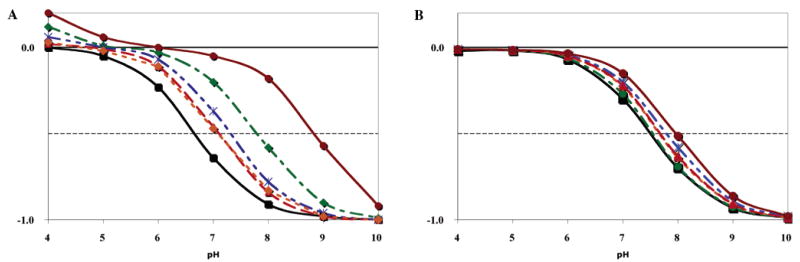
The ionization states of His I-93 and Glu I-182, 5 Å apart on the proton output side of the protein, are coupled together (Figure 3A). At low pH (<5) 1 proton is bound with 13% HisH+Glu− 87% His0GluH0. Both microstates have a net charge of 0 and similar energies, so both are occupied. The doubly ionized state is destabilized by the desolvation penalty for the two ionized groups but stabilized by the favorable interaction between them (105). The cluster titrates with a pKa of 6.7 in the OOOO state, producing a net charge of −0.64 at pH 7 (Figure 4A, Table 2). An electron on CuA shifts the pKa up to 7.7, while the pKa is 7.2 when heme a is reduced. The pKa shifts of 1.0 and 0.5 lead to average protonation changes of 0.44 or 0.27 going from OOOO to ROOO or OROO states (Table 1). The pKa shifts down to 6.9 with the first reduction of the BNC. The cluster pKa is the same in the OOOR and OORR states, since the second reduction is coupled to the protonation of the BNC hydroxyl group and so is electroneutral. When the BNC is doubly reduced, this cluster has 0.09 more protons bound than in the fully oxidized protein. Upon the anaerobic 4-electron reduction, the cluster binds 0.59 proton. Earlier calculations on P. denitrificans showed Lys II-191 (229 here) changing protonation rather than the residues shown here (33). This Lys was also suggested to be involved in proton release in the bovine oxidase calculations (42).
Figure 4.
pH and redox state dependence of the net charge on clusters in cytochrome c oxidase. (A) Proton release cluster: His I-127 and Glu I-539. (B) Proton entry cluster: His I-93 and Glu I-182. States: (black) OOOO (6.5, 7.4), (green) ROOO (7.6, 7.4), (blue) OROO (7.2, 7.6), (orange) OOOR (6.9, 7.5), (red) OORR (6.9, 7.6), and (brown) RRRR (8.6, 8.0). The pKa for the cluster 0 to −1 transition for the (release, entry) cluster is given in parentheses. The pKa for the OROR state is (7.6, 7.9) (not shown).
His I-127 and Glu I-539 form a cluster on the proton uptake side of the protein, close to Asp I-132 at the D channel entry (Figure 3B). These are far from any cofactor and more weakly coupled to cofactor redox changes than the output-side cluster. In the OOOO state, the cluster has a pKa of 7.4, which shifts to 8.0 in the RRRR state, leading to the uptake of 0.15 proton for 4-electron reduction at pH 7.0 (Figure 4B). Conformational changes of Glu- I-539, His I-300, and Thr I-537 are calculated to be coupled to the cluster ionization changes. This reorganization of the hydrogen-bonding network could slow the cluster ionization changes, modifying the proton transfer to this cluster, which is ≈9 Å from the D channel entry.
Asp I-132 is at the D channel entrance (106). It is always ionized with a pK′7 <1 in all oxidase redox states (Table 2). Since Asp I-132 is not deeply buried, it has a small desolvation penalty (Table 3). In addition, nearby backbone dipoles and an ionized His 26 stabilize the ionized Asp. Glu II-101 is at the K channel entrance (9, 10, 33). It is also kept ionized by a small desolvation penalty and favorable interactions with the backbone and other nearby residues including His II-96, which is ≈30% ionized at pH 7. This residue is equivalent to Glu II-78 in P. denitrificans, a residue that was previously calculated to become more protonated as the BNC is reduced (33). Lys I-362 is an essential conserved residue on the K channel (11). Although there are some suggestions that it is ionized (107), MCCE calculates it to be fully neutral with a pK′7 <0 in all redox states. It is deeply buried and has few favorable interactions with neighboring residues or backbone dipoles that would stabilize the charged state. It is far enough from the BNC that its ionization is only moderately destabilized by the cofactor positive charges.
Net Proton Uptake on Reduction of Cytochrome c Oxidase
MCCE calculates that the reduction of CuA in the fully oxidized enzyme is coupled to the uptake of 0.6 proton to the proton exit cluster and a few nearby groups (Table 1). When the electron is transferred from CuA to heme a, the release side cluster loses 0.17 proton back to solution, while the uptake side cluster picks up 0.14 proton. All together, 0.5 proton is bound on reduction of heme a relative to the fully oxidized state. The calculations show negligible additional proton uptake as the electron is transferred from heme a to CuB.
There is a wide range of reported experimental values for the stoichiometry of proton uptake coupled to CuA and heme a reduction. Oxidation of the fully reduced oxidase with a CO ligand to heme a3 (RRRR to OORR states) shows release of 0.3 (63), 0.4 (58), 0.6 (59), and 0.8 (64) protons in bovine and 0.8 proton in P. denitrificans (18) oxidase. However, the Ems of CuA and heme a (31, 64) vary by no more than 20 mV per pH unit. This is in better agreement with the smaller estimates of proton uptake. The proton uptake coupled to CuA and heme a reduction in a protein, with the BNC reduced, is calculated to lead to the binding of 0.9 H+/2e−. Almost all of the change is in the exit cluster, with a small amount in the proton input cluster. There are no changes in the BNC-associated residues moving from OORR to RRRR states. The MCCE value of 0.5 H+/e− CuA and heme a would each have Ems with a pH dependence of at least 30 mV per pH unit. The overestimation here is most probably due to the sensitivity of the His I-93 and Glu I-182 cluster to the electrostatic potential of CuA. This cluster binds 0.44 proton on the oxidation of CuA and releases 0.28 proton as the electron is transferred to the BNC.
The second reduction, forming either the OROR or OORR mixed valence states at pH 7, leads to the binding of 1 proton to the hydroxyl–heme a3. The pKa of the aquo–heme a3 is 8.3 in the OROR state; so it is ≈90% protonated. Thus, with CuB reduced, the reduction of heme a, not heme a3, is calculated to be coupled to the proton binding into the BNC (Table 1). When the second electron is transferred from heme a into the BNC, there are only small changes in total protonation, in agreement with the experiments photolyzing the CO–heme a3 bond in the mixed valence OORR state (34). Reduction of all four cofactors moving from the OOOO to RRRR state is coupled to the uptake of 2.5 protons (Table 1). Most of this is accounted for by the hydroxide in the BNC, proton uptake and release side clusters, and the heme a A-ring propionate, together with small changes on a few other distant groups. This is in agreement with the total proton uptake of 2.4 upon full reduction, which was measured in bovine oxidase (58, 59). Yet, it is smaller than a recent measurement of 3.3 H+/4 electrons in P. dinitrificans (18).
The Em of Heme a
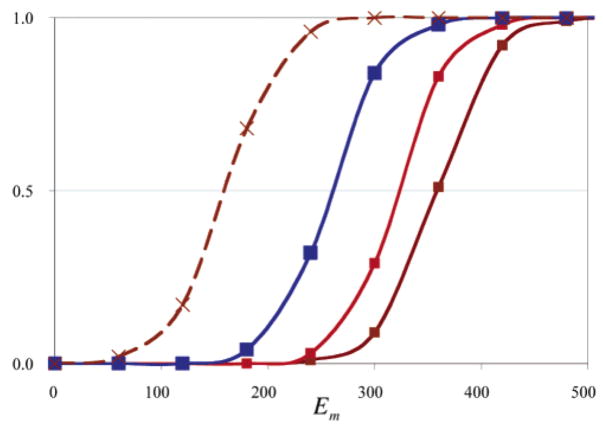
MCCE has been used successfully to calculate the heme Ems in different bis-His cytochromes (27). This allows the heme a Em to be calculated with no free parameters. The calculated Em of 360 mV, when the other cofactors are oxidized, is in agreement with the experimental values of 340 mV (31) to 430 mV (60). The Em is shifted 480 mV from the Em,sol of −120 mV mostly by the desolvation penalty and the positive potential from the backbone amide dipoles. Although the BNC and groups such as the heme propionates, Arg I-481 and I-482, individually have a large effect on the heme Em, these roughly cancel. Therefore, all residues lower the Em by only 70 mV. This match between experimental and calculated Em is obtained with all of the heme propionates ionized; despite earlier suggestions by DFT calculations that the Em would be too low (−150 mV) without protonation of one of the heme a propionates (45). Essentially one of the propionic acid charges was removed from the DFT calculations to compensate for not including the nearby Arg in the simulation region.
The heme a Em has been found to depend on the BNC redox state. It is lowered by 80–135 mV when both CuB and heme a3 are reduced (31, 61, 62, 108). In the OORR state, the Em is calculated to be 260 mV, 100 mV lower than in the oxidized enzyme, in good agreement with experiment. Simply adding 2 electrons to the cofactors and 1 proton to the BNC hydroxide lowers the Em by 150 mV. Proton uptake to other distant residues diminishes the Em shift. If the BNC reduction were electroneutral with 2H+/2e−, the heme Em would be independent of the BNC redox state. If there are two hydroxyls in the oxidized BNC, the heme a Em is 260 mV, the same as calculated in the fully reduced BNC, which is significantly lower than measured in the oxidized protein.
The heme a Em was also calculated with Arg 52 mutated to Met. This has been observed to lower the heme a Em by about 260 mV in P. denitrificans oxidase (108). In MCCE with the Rb. sphaeroides structure, removal of the Arg charge causes the protein to bind ≈0.5 proton. About half of this is to the heme a A-ring propionate. The resultant heme a Em with the other cofactors oxidized is calculated to be lowered by 200 mV, in reasonable agreement with experiment.
DISCUSSION
The number of protons bound at each stage of the electron transfer cycle in cytochrome c oxidase has been the subject of intensive study (1–4). The desolvation penalty for reducing the deeply buried BNC has been suggested to be the primary source of the tight coupling between electron and proton transfers needed for pumping in oxidase (29, 58, 109). Transferring an electron to a cofactor deep in the protein introduces a large desolvation penalty, which can be diminished by burying another charge with an opposite sign, such as a proton, nearby. Anions in the surroundings stabilize oxidation of the deeply buried cofactors, and cofactor reduction increases their pKas to favor proton binding (Table 2). However, the large desolvation penalty can also be compensated by pairwise interactions with nearby charged groups or dipoles (23). Here in the equilibrium calculations on the Rb. sphaeroides oxidase, only one group, the hydroxyl on CuB, shifts its pKa from below 7 to above 7 to pick up a proton when 2 electrons are transferred into the BNC. Similar conclusions were found in the MCCE analysis of the P. denitrificans structure, where only 1 proton is also taken up on formation of the R (OORR) state (33). Only 1 proton is needed for the O–O bond splitting chemistry of bound O2 in the A to PR transition (29, 110, 111). This proton and an electron are proposed to be donated by Tyr I-288, forming a hydroxyl on CuB and unprotonated heme a3 ferryl species (Fe4+=O2−) (75, 92–96).
At some point in the reaction cycle following O2 bondsplitting, heme a3 and CuB each will have a hydroxyl ligand with a bound chemical proton (29). This work has shown that the stable BNC has one hydroxide and one water in the fully oxidized state, which marks the end of the oxidative phase and the beginning of the reductive phase. Thus three chemical protons would need to be bound before reaching the stabilized fully oxidized state. However, in the O state, a deprotonated Tyr I-288, a hydroxyl on heme a3, or an anionic His- I-334 is only 1.6–3.5 ΔpK units higher than the equilibrated state. Thus, states with a second anion in the BNC may be accessible in the oxidative phase. This raises the possibility that the equilibrated O state observed in MCCE calculations is that of the stabilized “resting” (110, 112) enzyme, while a fully oxidized protein with two deprotonated groups in the BNC is a higher energy, metastable state which occurs during the reaction cycle.
Relative Energy of Different BNC Ionization States
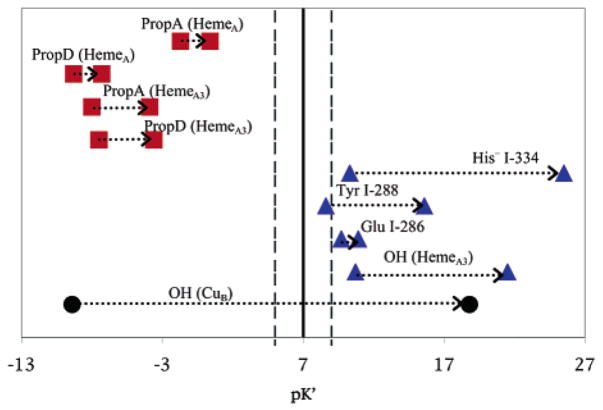
In order for a group to be a proton acceptor when the BNC is reduced, it must have a pKa below 7 in the oxidized protein and above 7 when the cofactors are reduced. Only the hydroxyl–CuB satisfies the criteria for a group whose protonation state is tightly coupled to the BNC reduction (Figure 6). All propionic acid pK′7s remain below 7 in OOOO and OORR states. The pK′7s of His I-334, aquo–heme a3, Glu I-286, and Tyr I-288 remain above 8. These ionization patterns are in agreement with previous calculations on P. denitrificans (33) and bovine (39) oxidase. Tyr I-288, with a pKa of 8.7 (pK′7 8.6) in the fully oxidized state, has a pKa in the different redox states closest to what would be needed for it to be involved in proton-coupled electron transfer. The Tyr is calculated to be ≈5% deprotonated in the OOOO state; so it contributes a small amount to the proton uptake coupled to the first BNC reduction. Proton uptake via the K channel, as would likely be used to deliver protons to the Tyr, has been found experimentally on the first reduction of the BNC (15, 16). The relatively low Tyr pKa relies on its pKa,sol being lowered 1.3 pH units by its covalent linkage to His I-284 (75). With a standard pKa,sol of 10.2, the cost of deprotonating the Tyr would be 2.9 ΔpK units and the Tyr pK′7 would be 9.9.
Figure 6.
pK′7 of the residues near the BNC in OOOO and OORR states. In all cases, pK′7 moves to higher values in the more reduced protein. pK′7 fixes all other residues in their lowest energy ionization state in MCCE calculations at pH 7 (Table 1). Thus, there is a hydroxyl on CuB in the OOOO state and no hydroxyls in the BNC in the OORR state. The four propionic acids are found to be ionized, and Tyr I-288, Glu I-286, and His I-334 are neutral in both states.
The energy of the different ionization states of the possible proton acceptors, including the hydroxyls on heme a3 and CuB, Tyr I-288, and His I-334, can be compared in the fully oxidized Rb. sphaeroides cytochrome c oxidase (Table 4). The highest energy state is where none of these groups are ionized, and the lowest has the hydroxyl–CuB as the sole anion. The hydroxyl–heme a3, water–CuB state is 4.4 ΔpK units higher. States with a single anion on the Tyr, or His, are at still higher energy. Thus, the lowest energy state has only one group that can serve as a proton acceptor when the BNC is reduced. The dianion hydroxyl–CuB, ionized Tyr state is only 1.6 ΔpK units (2.2 kcal/mol) higher, so this is the most accessible state with 2 proton acceptors. All other dianion states are at higher energy, even in the fully oxidized protein. However, the calculations do show that the single state and several dianionic states are close in energy. Additional simulations using improving methodology and comparing results from different oxidase structures and from different species will show how robust these conclusions are.
Table 4.
Relative Energy of Different Protonation States of BNC Cluster Residues in the Fully Oxidized BNCa
| state energy, pH 7 (ΔpK units) | OH− heme a3 | OH− CuB | His I-334b | Tyr I-288 | site pK′7c |
|---|---|---|---|---|---|
| neutral state | |||||
| 16.4 | 0 | 0 | 0 | 0 | |
| single anion | |||||
| 0 | 0 | −1 | 0 | 0 | −9.4 |
| 4.4 | −1 | 0 | 0 | 0 | −5.0 |
| 10.7 | 0 | 0 | 0 | −1 | 1.3 |
| 11.7 | 0 | 0 | −1 | 0 | 2.3 |
| dianionic states | |||||
| 1.6 | 0 | −1 | 0 | −1 | |
| 3.3 | −1 | 0 | −1 | 0 | |
| 3.7 | −1 | −1 | 0 | 0 | |
| 10.1 | 0 | 0 | −1 | −1 | |
Proton binding on each reduction of the BNC has been studied experimentally. There is evidence that the stoichiometry should be 2H+/2e− upon reduction during the O to R transition, rather than 1.4, with only 1 proton bound into the BNC, as found here (Table 1). Using photoexcited ruthium bispyridyl to deliver single electrons to the P. denitrificans oxidase BNC, electrometric measurements of wild type and Lys I-362 to Met mutants showed that one electrometric phase is inhibited in the mutants, suggesting that the first reduction is coupled to the proton uptake via the K channel (15, 16). Multiple excitation accumulates the doubly reduced enzyme, which is associated with a slower electrometric phase, attributed to a second proton uptake (16). Proton uptake during anaerobic reduction of the fully oxidized, CO-bound oxidase also supports a model where there are 2 protons bound on the 2-electron reduction of the BNC (58).
In contrast, the good match between the calculated and measured shift in the heme a Em when the BNC is reduced provides evidence that there is only 1H+/2e− (31, 61, 62, 108). If the BNC reduction is electroneutral, there is insufficient change in the long-range electrostatic potential to shift the Em of a residue 13 Å away. In addition, the lack of proton release at pH 7 moving from the OORR to OROR states, following flash photolysis of a bound CO (34), is in good agreement with the protonation of the BNC being coupled to heme a reduction in the OOOR state, as found here.
Assumptions and Uncertainties in the Analysis
The conclusion reported here, that there is one anionic group in the fully oxidized BNC that is strongly coupled to reduction, relies on a number of assumptions. The repulsion between the cationic oxidized water–heme a3 and the hydroxyl–CuB-(II) in the fully oxidized (OOOO) and mixed valence (OROR) states has been shown, by comparison between Gaussian 98 and Coulomb’s law, to be overestimated in a continuum electrostatics treatment (53). Using the uncorrected interactions, the pKa of the aquo–heme a3 is low enough that both of the BNC cofactors bind hydroxyl in the fully oxidized protein. The same correction for interactions between nearby charges is needed to obtain benchmark pKas, in agreement with experiment for aquo–hemes in two other proteins (53). In addition, measurements in a model system with a CuB analogue inserted into myoglobin also show a surprisingly small change in the water–heme Em when a Cu or a Zn is added, indicating a small interaction between the heme and the nearby metal (113).
A very simple metal-centered charge distribution is used for the cofactors in the BNC. The long-range interactions are only affected by the net charge, but local interactions are sensitive to the partial charges on individual atoms. Using Gaussian 98 charges for the hydroxyl–3His–CuB complex moves some of the positive charge from the copper to the His ligands, further from the hydroxyl on heme a3. This shifts the aquo–heme a3 pKa up by ≈2 pH units, indicating that both of the hydroxyls are even less likely to coexist in the oxidized BNC with a more distributed charge model.
Protein cavities are filled with high dielectric continuum water, instead of explicit water in the calculations. Buried waters have been suggested to be important for oxidase activity (12–14, 46, 48, 114). Earlier studies of bacteriorhodopsin have shown that the calculated pKas are similar with either continuum or explicit water, even for active site residues (56). In addition, if explicit waters are not placed carefully, necessary hydrogen bonds cannot be formed to compensate for the desolvation penalty incurred by filling in the cavities with explicit waters, introducing additional errors.
Kinetic vs Thermodynamic Control of Ionization States
This analysis provides a view of the equilibrium protonation states throughout the protein in the Rb. sphaeroides oxidase crystal structure. The MCCE calculated pK′7 provides the free energy needed to change the ionization of a residue, providing clues to which higher energy ionization states can be kinetically accessible. Glu I-286 and Tyr I-288 are both near the BNC at the end of the proton uptake channels. They have pK′7s between 9 and 10 in the fully oxidized state, as well as in the PR and F states in the oxidative phase. Hence, they are protonated at equilibrium, but they need only 2.5–4 kcal/mol for them to give up their proton. In contrast, the heme propionates on the output side of the protein have pK′7s below 0, making it very difficult for them to be protonated without changes in the protein structure. These calculations may overestimate the cost of deprotonating the propionates since Arg motion could diminish the cost of acid protonation, raising the pKa.
Calculations on the bacteriorhodopsin proton pump show that small changes in the structure can lead to directional protonation shifts between residues, while each residue remains in equilibrium in the given structure. These calculations were carried out with high-resolution structures trapped in different states of the bacteriorhodopsin reaction cycle. MCCE (56) and MEAD (115) calculations with structures differing by <1 Å RMSD show changes in the active site ionization, as predicted by experiment (116). The agreement between the kinetic measurements and equilibrium calculations shows that the protonation states remain in equilibrium with the structure, at least for processes occurring on the slow microsecond time scale. The challenge for studies of cytochrome c oxidase is to find the appropriate conformational changes required to stabilize the proton transfer intermediates. Glu I-286 has been found changing conformation during an MD simulation (117). If this Glu can move toward the positively charged BNC, the ionized form would be stabilized, lowering the pKa. The propionic acids are hydrogen-bonded to a pair of Arg’s. If propionic acids and the Arg move apart to break the ion pair, one of the propionic acids could be protonated (98). His I-334 is hydrogen-bonded to two propionic acids. If the propionic acids move away from the His, the unfavorable interaction between negative imidazolate and the propionic acids would be reduced, perhaps allowing His I-334 deprotonation. Analyses of protonation states of residues equilibrated around these modified positions are ongoing.
Supplementary Material
Figure 5.
Redox titration of heme a with (brown) the BNC fully oxidized (Em =359 mV), (red) heme a3 oxidized and CuB reduced (Em =322 mV), (blue) the BNC doubly reduced (Em =258 mV), and (brown dashed) the BNC fully oxidized with neutral Arg 52, as in the Arg to Met mutation (Em =161 mV).
Acknowledgments
We gratefully acknowledge Junjun Mao for developing and continually improving the MCCE code and Martin Wikström and Alexei Stuchebrukhov for a careful reading of the manuscript.
Footnotes
This work is supported by NIH Grant RO1-GM64540.
Abbreviations: BNC, binuclear center containing heme a3 and CuB and their axial ligands; pK′7, in situ pKa of a site calculated with a mean field approximation (all other protein residue and cofactor ionization and conformation states fixed in their Boltzmann distribution at pH 7); ΔG7, free energy of ionization of a group at pH 7 obtained from pK′7; pKa,sol, pKa of base or acidic group in aqueous solution; Em,sol, electrochemical midpoint potential (Em) of a model for the redox cofactor in aqueous solution; MCCE, Multi-Conformation Continuum Electrostatics. Key for oxidase redox states (cofactors listed in the order CuA, heme a, heme a3, and CuB): O, oxidized; R, reduced; O state (OOOO), all oxidized; E state (OOOR), CuB reduced; R state (OORR), heme a3 and CuB reduced. Aerobic states: A state, OORR state with oxygen bound; PR state, after oxygen is reduced [heme a3(IV)=O2−, CuB(II)–OH−, and deprotonated neutral Tyr I-288 radical state]; F state [heme a3(IV)=O2−, CuB(II)–OH−, and protonated neutral Tyr I-288]. The propionic acids are designated A and D as found in the PDB structure file. The IUPAC nomenclature calls them respectively propionate D and C.
SUPPORTING INFORMATION AVAILABLE
A table of interactions between heme a3 and CuB in different aquo protonation and cofactor redox states, values being calculated in a vacuum by Coulomb’s law, by DFT using Gaussian 98, by solving the Poisson–Boltzmann equation using DelPhi in the protein, and by (ΔGPBΔGDFT/ΔGCoulomb) to be used in MCCE pKa and Em calculations. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Brzezinski P. Redox-driven membrane-bound proton pumps. Trends Biochem Sci. 2004;29:380–387. doi: 10.1016/j.tibs.2004.05.008. [DOI] [PubMed] [Google Scholar]
- 2.Gennis RB. Some recent contributions of FTIR difference spectroscopy to the study of cytochrome oxidas. FEBS Lett. 2003;555:2–7. doi: 10.1016/s0014-5793(03)01150-5. [DOI] [PubMed] [Google Scholar]
- 3.Ferguson-Miller S, Babcock GT. Heme/copper terminal oxidases. Chem Rev. 1996;96:2889–2907. doi: 10.1021/cr950051s. [DOI] [PubMed] [Google Scholar]
- 4.Wikström M. Cytochrome c oxidase: 25 years of the elusive proton pump. Biochim Biophys Acta. 2004;1655:241–247. doi: 10.1016/j.bbabio.2003.07.013. [DOI] [PubMed] [Google Scholar]
- 5.Babcock GT, Wikström M. Oxygen activation and the conservation of energy in cell respirations. Nature. 1992;356:301–308. doi: 10.1038/356301a0. [DOI] [PubMed] [Google Scholar]
- 6.Junemann S, Meunier B, Fisher N, Rich PR. Effects of mutation of the conserved glutamic acid-286 in subunit I of cytochrome c oxidase from Rhodobacter sphaeroides. Biochemistry. 1999;38:5248–5255. doi: 10.1021/bi9830112. [DOI] [PubMed] [Google Scholar]
- 7.Wikström M, Jasaitis A, Backgren C, Puustinen A, Verkhovsky MI. The role of the D- and K-pathways of proton transfer in the function of the haem-copper oxidases. Biochim Biophys Acta. 2000;1459:514–520. doi: 10.1016/s0005-2728(00)00191-2. [DOI] [PubMed] [Google Scholar]
- 8.Ådelroth P, Karpeforsa M, Gildersona G, Tomsonc FL, Gennis RB, Brzezinski P. Proton transfer from glutamate 286 determines the transition rates between oxygen intermediates in cytochrome c oxidase. Biochim Biophys Acta. 2000;1459:533–539. doi: 10.1016/s0005-2728(00)00194-8. [DOI] [PubMed] [Google Scholar]
- 9.Branden M, Tomson F, Gennis RB, Brzezinski P. The entry point of the K-proton-transfer pathway in cytochrome c oxidase. Biochemistry. 2002;41:10794–10798. doi: 10.1021/bi026093+. [DOI] [PubMed] [Google Scholar]
- 10.Tomson FL, Morgan JE, Gu G, Barquera B, Vygodina TV, Gennis RB. Substitutions for glutamate 101 in subunit II of cytochrome c oxidase from Rhodobacter sphaeroides result in blocking the proton-conducting K-channel. Biochemistry. 2003;42:1711–1717. doi: 10.1021/bi026750y. [DOI] [PubMed] [Google Scholar]
- 11.Junemann S, Meunier B, Gennis RB, Rich PR. Effects of mutation of the conserved lysine-362 in cytochrome c oxidase from Rhodobacter sphaeroides. Biochemistry. 1997;36:14456–14464. doi: 10.1021/bi971458p. [DOI] [PubMed] [Google Scholar]
- 12.Wikström M, Verkhovsky MI, Hummer G. Water-gated mechanism of proton translocation by cytochrome c oxidase. Biochim Biophys Acta. 2003;1604:61–65. doi: 10.1016/s0005-2728(03)00041-0. [DOI] [PubMed] [Google Scholar]
- 13.Zheng X, Medvedev DM, Swanson J, Stuchebrukhov AA. Computer simulation of water in cytochrome c oxidase. Biochim Biophys Acta. 2003;1557:99–107. doi: 10.1016/s0005-2728(03)00002-1. [DOI] [PubMed] [Google Scholar]
- 14.Olkhova E, Hutter MC, Lill MA, Helms V, Michel H. Dynamic water networks in cytochrome c oxidase from Paracoccus denitrificans investigated by molecular dynamics simulations. Biophys J. 2004;86:1873–1889. doi: 10.1016/S0006-3495(04)74254-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ruitenberg M, Kannt A, Bamberg E, Ludwig B, Michel H, Fendler K. Single electron reducton of the oxidized state is coupled to proton uptake via the K pathway in Paracoccus denitrificans cytochrome c oxidase. Proc Natl Acad Sci USA. 2000;97:4632–4636. doi: 10.1073/pnas.080079097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Verkhovsky MI, Tuukkanen A, Backgren C, Puustinen A, Wikström M. Charge translocation coupled to electron injection into oxidized cytochrome c oxidase from Paracoccus denitrificans. Biochemistry. 2001;40:7077–7083. doi: 10.1021/bi010030u. [DOI] [PubMed] [Google Scholar]
- 17.Giuffre A, Barone MC, Brunori M, D’Itri E, Ludwig B, Malatesta F, Muller HW, Sarti P. Nitric oxide reacts with the single-electron reduced active site of cytochrome c oxidase. J Biol Chem. 2002;277:22402–22406. doi: 10.1074/jbc.M201514200. [DOI] [PubMed] [Google Scholar]
- 18.Forte E, Scandurra FM, Richter OMH, D’Itri E, Sarti P, Brunori M, Ludwig B, Giuffre A. Proton uptake upon anaerobic reduction of the Paracoccus denitrificans cytochrome c oxidase: A kinetic investigation of the K354M and D124N mutants. Biochemistry. 2004;43:2957–2963. doi: 10.1021/bi035863u. [DOI] [PubMed] [Google Scholar]
- 19.Bockris JOM, Reddy AKN. Modern Electrochemistry. Vol. 1. Plenum; New York: 1973. [Google Scholar]
- 20.Kassner RJ. A theoretical model for the effects of local nonpolar heme environments on the redox potentials in cytochromes. J Am Chem Soc. 1973;95:2674–2676. doi: 10.1021/ja00789a044. [DOI] [PubMed] [Google Scholar]
- 21.Warshel A, Russell ST. Calculations of electrostatic interactions in biological systems and in solutions. Q Rev Biophys. 1984;17:283–422. doi: 10.1017/s0033583500005333. [DOI] [PubMed] [Google Scholar]
- 22.Rashin AA, Honig B. Reevaluation of the Born model of ion hydration. J Phys Chem. 1985;89:5588–5593. [Google Scholar]
- 23.Kim J, Mao J, Gunner MR. Are acidic and basic groups in buried proteins predicted to be ionized? J Mol Biol. 2005;348:1283–1298. doi: 10.1016/j.jmb.2005.03.051. [DOI] [PubMed] [Google Scholar]
- 24.Churg AK, Warshel A. Control of the redox potential of cytochrome c and microscopic dielectric effects in proteins. Biochemistry. 1986;25:1675–1681. doi: 10.1021/bi00355a035. [DOI] [PubMed] [Google Scholar]
- 25.Gunner MR, Honig B. Electrostatic control of midpoint potentials in the cytochrome subunit of the Rhodopseudomonas viridis reaction center. Proc Natl Acad Sci USA. 1991;88:9151–9155. doi: 10.1073/pnas.88.20.9151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Voigt P, Knapp EW. Tuning heme redox potentials in the cytochrome c subunit of photosynthetic reaction centers. J Biol Chem. 2003;278:51993–52001. doi: 10.1074/jbc.M307560200. [DOI] [PubMed] [Google Scholar]
- 27.Mao J, Hauser K, Gunner MR. How cytochromes with different folds control heme redox potentials. Biochemistry. 2003;42:9829–9840. doi: 10.1021/bi027288k. [DOI] [PubMed] [Google Scholar]
- 28.Reedy CJ, Gibney BR. Heme protein assemblies. Chem Rev. 2004;104:617–649. doi: 10.1021/cr0206115. [DOI] [PubMed] [Google Scholar]
- 29.Michel H. The mechanism of proton pumping by cytochrome c oxidase. Proc Natl Acad Sci USA. 1998;95:12819–12824. doi: 10.1073/pnas.95.22.12819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Michel H. Cytochrome c oxidase: catalytic cycle and mechanisms of proton pumping—a discussion. Biochemistry. 1999;38:15129–15140. doi: 10.1021/bi9910934. [DOI] [PubMed] [Google Scholar]
- 31.Moody AJ, Rich PR. The effect of pH on redox titrations of heme a in cyanide liganded cytochrome c oxidase— Experimental and modeling studies. Biochim Biophys Acta. 1990;1015:205–215. doi: 10.1016/0005-2728(90)90022-v. [DOI] [PubMed] [Google Scholar]
- 32.Fann YC, Ahmed I, Blackburn NJ, Boswell JS, Verkhovskaya ML, Hoffman BM, Wikström M. Structure of CuB in the binuclear heme-copper center of the cytochrome aa3-type quinol oxidase from Bacillus subtilis: an ENDOR and EXAFS study. Biochemistry. 1995;34:10245–10255. doi: 10.1021/bi00032a019. [DOI] [PubMed] [Google Scholar]
- 33.Kannt A, Lancaster CRD, Michel H. The coupling of electron transfer and proton translocation: electrostatic calculations on Paracoccus denitrificans cytochrome c oxidase. Biophys J. 1998;74:708–721. doi: 10.1016/S0006-3495(98)73996-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Branden M, Namslauer A, Hansson O, Aasa R, Brzezinski P. Water-hydroxide exchange reactions at the catalytic site of heme-copper oxidases. Biochemistry. 2003;42:13178–13184. doi: 10.1021/bi0347407. [DOI] [PubMed] [Google Scholar]
- 35.Puustinen A, Wikström M. Proton exit from the heme-copper oxidase of Escherichia coli. Proc Natl Acad Sci USA. 1999;96:35–37. doi: 10.1073/pnas.96.1.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mills DA, Ferguson-Miller S. Influence of structure, pH and membrane potential on proton movement in cytochrome oxidase. Biochim Biophys Acta. 2002;1555:96–100. doi: 10.1016/s0005-2728(02)00261-x. [DOI] [PubMed] [Google Scholar]
- 37.Behr J, Michel H, Mantele W, Hellwig P. Functional properties of the heme propionates in cytochrome c oxidase from Paracoccus denitrificans. Evidence from FTIR difference spectroscopy and site directed mutagenesis. Biochemistry. 2000;39:1356–1363. doi: 10.1021/bi991504g. [DOI] [PubMed] [Google Scholar]
- 38.Wikström M, Bogachev A, Finel M, Morgan JE, Puustinen A, Raitio M, Verkhovskaya M, Verkhovsky MI. Mechanism of proton translocation by the respiratory oxidases. The histidine cycle. Biochim Biophys Acta. 1994;1187:106–111. doi: 10.1016/0005-2728(94)90093-0. [DOI] [PubMed] [Google Scholar]
- 39.Popovic DM, Stuchebrukhov AA. Electrostatic study of the proton pumping mechanism in bovine heart cytochrome c oxidase. J Am Chem Soc. 2004;126:1858–1871. doi: 10.1021/ja038267w. [DOI] [PubMed] [Google Scholar]
- 40.Quenneville J, Popovic DM, Stuchebrukhov AA. Redox-dependent pKa of CuB histidine ligand in cytochrome c oxidase. J Phys Chem B. 2004;108:18383–18389. [Google Scholar]
- 41.Popovic DM, Quenneville J, Stuchebrukhov AA. DFT/electrostatic calculations of pKa values in cytochrome c oxidase. J Phys Chem B. 2005;109:3616–3626. doi: 10.1021/jp046535m. [DOI] [PubMed] [Google Scholar]
- 42.Popovic DM, Stuchebrukhov AA. Proton exit channels in bovine cytochrome c oxidase. J Phys Chem B. 2005;109:1999–2006. doi: 10.1021/jp0464371. [DOI] [PubMed] [Google Scholar]
- 43.Blomberg M, Siegbahn PEM, Babcock G, Wikström M. O–O bond splitting mechanism in cytochrome oxidase. J Inorg Biochem. 2000;80:261–269. doi: 10.1016/s0162-0134(00)00080-5. [DOI] [PubMed] [Google Scholar]
- 44.Siegbahn PE. The catalytic cycle of tyrosinase: peroxide attack on the phenolate ring followed by O–O cleavage. J Biol Inorg Chem. 2003;8:567–576. doi: 10.1007/s00775-003-0449-4. [DOI] [PubMed] [Google Scholar]
- 45.Siegbahn PEM, Blomberg MRA, Blomberg ML. Theoretical study of the energetics of proton pumping and oxygen reduction in cytochrome oxidase. J Phys Chem B. 2003;107:10946–10955. [Google Scholar]
- 46.Xu J, Voth GA. Computer simulation of explicit proton translocation in cytochrome c oxidase: The D-pathway. Proc Natl Acad Sci USA. 2005;102:6795–6800. doi: 10.1073/pnas.0408117102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pomes R, Hummer G, Wikström M. Structure and dynamics of a proton shuttle in cytochrome c oxidase. Biochim Biophys Acta. 1999;1365:255–260. [Google Scholar]
- 48.Seibold SA, Mills DA, Ferguson-Miller S, Cukier RI. Water chain formation and possible proton pumping routes in Rhodobacter sphaeroides cytochrome c oxidase: A molecular dynamics comparison of the wild type and R481K mutant. Biochemistry. 2005;44:10475–10485. doi: 10.1021/bi0502902. [DOI] [PubMed] [Google Scholar]
- 49.Cukier RI. A molecular dynamics study of water chain formation in the proton-conducting K channel of cytochrome c oxidase. Biochim Biophys Acta. 2005;1706:134–146. doi: 10.1016/j.bbabio.2004.10.004. [DOI] [PubMed] [Google Scholar]
- 50.Alexov EG, Gunner MR. Incorporating protein conformational flexibility into the calculation of pH-dependent protein properties. Biophys J. 1997;72:2075–2093. doi: 10.1016/S0006-3495(97)78851-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Georgescu RE, Alexov EG, Gunner MR. Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins. Biophys J. 2002;83:1731–1748. doi: 10.1016/S0006-3495(02)73940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhu Z, Gunner MR. Energetics of quinone-dependent electron and proton transfers in Rhodobacter sphaeroides photosynthetic reaction centers. Biochemistry. 2005;44:82–96. doi: 10.1021/bi048348k. [DOI] [PubMed] [Google Scholar]
- 53.Song Y, Mao J, Gunner MR. Electrostatic environment of hemes in proteins: pKas of hydroxyl ligands. Biochemistry. 2006;45:7949–7958. doi: 10.1021/bi052182l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gunner MR, Nicholls A, Honig B. Electrostatic potentials in Rhodopseudomonas viridis reaction center: Implications for the driving force and directionality of electron transfer. J Phys Chem. 1996;100:4277–4291. [Google Scholar]
- 55.Alexov EG, Gunner MR. Calculated protein and proton motions coupled to electron transfer: electron transfer from QA− to QB in bacterial photosynthetic reaction centers. Biochemistry. 1999;38:8253–8270. doi: 10.1021/bi982700a. [DOI] [PubMed] [Google Scholar]
- 56.Song Y, Mao J, Gunner MR. Calculation of proton transfers in bacteriorhodopsin bR and M intermediates. Biochemistry. 2003;42:9875–9888. doi: 10.1021/bi034482d. [DOI] [PubMed] [Google Scholar]
- 57.Haas AH, Lancaster CR. Calculated coupling of transmembrane electron and proton transfer in dihemic quinol: fumarate reductase. Biophys J. 2004;87:4298–4315. doi: 10.1529/biophysj.104.042945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mitchell R, Rich PR. Proton uptake by cytochrome c oxidase on reduction and on ligand binding. Biochim Biophys Acta. 1994;1186:19–26. doi: 10.1016/0005-2728(94)90130-9. [DOI] [PubMed] [Google Scholar]
- 59.Forte E, Barone MC, Brunori M, Sarti P, Giuffre A. Redox-linked protonation of cytochrome c oxidase: the effect of chloride bound to CuB. Biochemistry. 2002;41:13046–13052. doi: 10.1021/bi025917k. [DOI] [PubMed] [Google Scholar]
- 60.Hellwig P, Grzybek S, Behr J, Ludwig B, Michel H, Mantele W. Electrochemical and ultraviolet/visible/infrared spectroscopic analysis of heme a and a3 redox reactions in the cytochrome c oxidase from Paracoccus denitrificans: separation of heme a and a3 contributions and assignment of vibrational modes. Biochemistry. 1999;38:1685–1694. doi: 10.1021/bi982282+. [DOI] [PubMed] [Google Scholar]
- 61.Babcock GT, Vickery LE, Palmer G. The electronic state of heme in cytochrome oxidase II. Oxidation-reduction potential interactions and heme iron spin state behavior observed in reductive titrations. J Biol Chem. 1978;253:2400–2411. [PubMed] [Google Scholar]
- 62.Carithers RP, Palmer G. Characterization of the potentiometric behavior of soluble cytochrome oxidase by magnetic circular dichroism. Evidence in support of heme-heme interaction. J Biol Chem. 1981;256:7967–7976. [PubMed] [Google Scholar]
- 63.Verkhovsky MI, Belevich N, Morgan JE, Wikström M. Proton linkage of cytochrome a oxidoreduction in carbon monoxide-treated cytochrome c oxidase. Biochim Biophys Acta. 1999;1412:184–189. doi: 10.1016/s0005-2728(99)00053-5. [DOI] [PubMed] [Google Scholar]
- 64.Capitanio N, Capitanio G, Minuto M, DeNitto E, Palese LL, Nicholls P, Papa S. Coupling of electron transfer with proton transfer at heme a and CuA redox Bohr effects in cytochrome c oxidase. Biochemistry. 2000;39:6373–6379. doi: 10.1021/bi0003137. [DOI] [PubMed] [Google Scholar]
- 65.Svensson-Ek M, Abramson J, Larsson G, Tornroth S, Brzezinski P, Iwata S. The X-ray crystal structures of wild-type and EQ(I-286) mutant cytochrome c oxidases from Rhodobacter sphaeroides. J Mol Biol. 2002;321:329–339. doi: 10.1016/s0022-2836(02)00619-8. [DOI] [PubMed] [Google Scholar]
- 66.Nicholls A, Honig B. A rapid finite difference algorithm utilizing successive over-relaxation to solve the Poisson–Boltzmann equation. J Comput Chem. 1991;12:435–445. [Google Scholar]
- 67.Bharadwaj R, Windemuth A, Sridharan S, Honig B, Nicholls A. The fast multipole boundary element method for molecular electrostatics: An optimal approach for large systems. J Comput Chem. 1995;16:898–913. [Google Scholar]
- 68.Rocchia W, Alexov E, Honig B. Extending the applicability of the nonlinear Poisson–Boltzmann equation: multiple dielectric constants and multivalent ions. J Phys Chem B. 2001;105:6507–6514. [Google Scholar]
- 69.Sitkoff D, Sharp KA, Honig B. Accurate calculation of hydration free energies using macroscopic solvent models. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 70.Gilson MK, Honig B. Calculation of the total electrostatic energy of a macromolecular system: solvation energies, binding energies, and conformational analysis. Proteins: Struct Funct, Genet. 1988;4:7–18. doi: 10.1002/prot.340040104. [DOI] [PubMed] [Google Scholar]
- 71.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 72.Beroza P, Fredkin DR, Okamura MY, Feher G. Protonation of interacting residues in a protein by a Monte Carlo method: application to lysozyme and the photosynthetic reaction center of Rhodobacter sphaeroides. Proc Natl Acad Sci USA. 1991;88:5804–5808. doi: 10.1073/pnas.88.13.5804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Richarz R, Wüthrich K. Carbon-13 NMR chemical shifts of the common amino acid residues measured in aqueous solutions of the linear tetrapeptides H-Gly-Gly-X-L-Ala-OH. Biopolymers. 1975;17:2133–2141. [Google Scholar]
- 74.Matthew JB, Gurd FRN, Garcia-Moreno B, Flanagan MA, March KL, Shire SJ. pH-dependent processes in proteins. CRC Crit Rev Biochem. 1985;18:91–197. doi: 10.3109/10409238509085133. [DOI] [PubMed] [Google Scholar]
- 75.McCauley KM, Vrtis JM, Dupont J, van der Donk WA. Insights into the functional role of the tyrosine-histidine linkage in cytochrome c oxidase. J Am Chem Soc. 2000;122:2403–2404. [Google Scholar]
- 76.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Zakrzewski VG, Montgomery J, Stratmann RE, Burant JC, Dapprich S, Millam JM, Daniels AD, Kudin KN, Strain MC, Farkas O, Tomasi J, Barone V, Cossi M, Cammi R, Mennucci B, Pomelli C, Adamo C, Clifford S, Ochterski J, Petersson GA, Ayala PY, Cui Q, Morokuma K, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Cioslowski J, Ortiz JV, Baboul AG, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Gomperts R, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Andres JL, Gonzalez C, Head-Gordon M, Replogle ES, Pople JA. Gaussian 98, Revision A. Gaussian, Inc.; Pittsburgh, PA: 1998. [Google Scholar]
- 77.Becke AD. Density-functional thermochemistry. 3 The role of exact exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 78.Hay PJ, Wadt WR. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J Chem Phys. 1985;82:270–283. [Google Scholar]
- 79.Breneman CM, Wiberg KB. Determining atom-centered monopoles from molecular electrostatic potentials–The need for high sampling density in formamide conformational-analysis. J Comput Chem. 1990;11:361–373. [Google Scholar]
- 80.Vanderkooi G, Stotz E. Reductive alteration of heme a hemochromes. J Biol Chem. 1965;240:3418–3424. [PubMed] [Google Scholar]
- 81.Vanderkooi G, Stotz E. Oxidation-reduction potentials of heme a hemochromes. J Biol Chem. 1966;241:3316–3323. [PubMed] [Google Scholar]
- 82.Battistuzzi G, Borsari M, Cowan JA, Ranieri A, Sola M. Control of cytochrome c redox potential: axial ligation and protein environment effects. J Am Chem Soc. 2002;124:5315–5324. doi: 10.1021/ja017479v. [DOI] [PubMed] [Google Scholar]
- 83.Wilson GS. Electrochemical studies of porphyrin redox reactions as cytochromes models. Bioelectrochem Bioenerg. 1974;1:172–179. [Google Scholar]
- 84.Marques HM, Cukrowski I, Vashi PR. Coordination of weak field ligands by N-acetylmicroperoxidase-8 (NAcMP8), a ferric haempeptide from cytochrome c, and the influence of the axial ligand on the reduction potential of complexes of NAcMP8. J Chem Soc. 2000;2000:1335–1342. [Google Scholar]
- 85.Santucci R, Reinhard H, Brunori M. Direct electrochemistry of the undacapeptide from cytochrome c (microperoxidase) at a glassy carbon electrode. J Am Chem Soc. 1988;110:8536–8357. [Google Scholar]
- 86.Munro OQ, Marques HM. Heme-peptide models for hemoproteins. 1 Solution chemistry of N-acetylmicroperoxidase-8. Inorg Chem. 1996;35:3752–3767. doi: 10.1021/ic9502842. [DOI] [PubMed] [Google Scholar]
- 87.Vashi PR, Marques HM. The coordination of imidazole and substituted pyridines by the hemeoctapeptide N-acetyl-ferromicroperoxidase-8 (FeIINAcMP8) J Inorg Biochem. 2004;98:1471–1482. doi: 10.1016/j.jinorgbio.2004.05.016. [DOI] [PubMed] [Google Scholar]
- 88.Anderegg G, Gramlich V. Metal complexes of bivalent cobalt, nickel, copper, zinc, and cadmium with the tripodal ligand tris[2-(dimethylamino)ethyl]amine: their stabilities and the X-ray crystal structure of its copper(T1) complex sulfate. Helv Chim Acta. 1994;77:685–690. [Google Scholar]
- 89.Thaler F, Hubbard CD, Heinemann FW, Eldik Rv, Schindler S, Fabian I, Dittler-Klingemann AM, Hahn FE, Orvig C. Structural, spectroscopic, thermodynamic and kinetic properties of copper(II) complexes with tripodal tetraamines. Inorg Chem. 1998;37:4022–4029. doi: 10.1021/ic971295t. [DOI] [PubMed] [Google Scholar]
- 90.Liao GL, Palmer G. The reduced minus oxidized difference spectra of cytochromes a and a3. Biochim Biophys Acta. 1996;1274:109–111. doi: 10.1016/0005-2728(96)00014-x. [DOI] [PubMed] [Google Scholar]
- 91.Sitter AJ, Shifflett JR, Terner J. Resonance Raman spectroscopic evidence for heme iron-hydroxide ligation in peroxidase alkaline forms. J Biol Chem. 1988;263:13032–13038. [PubMed] [Google Scholar]
- 92.Proshlyakov DA, Ogura T, Shinzawa-Itoh K, Yoshikawa S, Kitagawa T. Resonance Raman/absorption characterization of the oxo intermediates of cytochrome c oxidase generated in its reaction with hydrogen peroxide: pH and H2O2 concentration dependence. Biochemistry. 1996;35:8580–8586. doi: 10.1021/bi952096t. [DOI] [PubMed] [Google Scholar]
- 93.MacMillan F, Kannt A, Behr J, Prisner T, Michel H. Direct evidence for a tyrosine radical in the reaction of cytochrome c oxidase with hydrogen peroxide. Biochemistry. 1999;38:9179–9184. doi: 10.1021/bi9911987. [DOI] [PubMed] [Google Scholar]
- 94.Proshlyakov DA, Pressler MA, Demaso C, Leykam JF, Dewitt DL, Babcock GT. Oxygen activation and reduction in respiration involvement of redox-active tyrosine 244. Science. 2000;290:1588–1591. doi: 10.1126/science.290.5496.1588. [DOI] [PubMed] [Google Scholar]
- 95.Boulatov R, Collman JP, Shiryaeva IM, Sunderland CJ. Functional analogues of the dioxygen reduction site in cytochrome oxidase: mechanistic aspects and possible effects of CuB. J Am Chem Soc. 2002;124:11923–11935. doi: 10.1021/ja026179q. [DOI] [PubMed] [Google Scholar]
- 96.Cappuccio JA, Ayala I, Elliott GI, Szundi I, Lewis J, Konopelski JP, Barry BA, Einarsdottir O. Modeling the active site of cytochrome oxidase: synthesis and characterization of a cross-linked histidine-phenol. J Am Chem Soc. 2002;124:1750–1760. doi: 10.1021/ja011852h. [DOI] [PubMed] [Google Scholar]
- 97.Namslauer A, Aagaard A, Katsonouri A, Brzezinski P. Intramolecular proton-transfer reactions in a membrane-bound proton pump: the effect of pH on the peroxy to ferryl transition in cytochrome c oxidase. Biochemistry. 2003;42:1488–1498. doi: 10.1021/bi026524o. [DOI] [PubMed] [Google Scholar]
- 98.Wikström M, Ribacka C, Molin M, Laakkonen L, Verkhovsky M, Puustien A. Gating of proton and water transfer in the respiratory enzyme cytochrome c oxidase. Proc Natl Acad Sci USA. 2005;102:10478–10481. doi: 10.1073/pnas.0502873102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.You TJ, Bashford D. Conformation and hydrogen ion titration of proteins: a continuum electrostatic model with conformational flexibility. Biophys J. 1995;69:1721–1733. doi: 10.1016/S0006-3495(95)80042-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Bashford D, Gerwert K. Electrostatic calculations of the pKa values of ionizable groups in bacteriorhodopsin. J Mol Biol. 1992;224:473–486. doi: 10.1016/0022-2836(92)91009-e. [DOI] [PubMed] [Google Scholar]
- 101.Bashford D, Karplus M. Multiple-site titration curves of proteins: An analysis of exact and approximate methods for their calculation. J Phys Chem. 1991;95:9556–9561. [Google Scholar]
- 102.Antosiewicz J, McCammon JA, Gilson MK. Prediction of pH-dependent properties of proteins. J Mol Biol. 1994;238:415–436. doi: 10.1006/jmbi.1994.1301. [DOI] [PubMed] [Google Scholar]
- 103.Antosiewicz J, McCammon JA, Gilson MK. The determinants of pKas in proteins. Biochemistry. 1996;35:7819–7833. doi: 10.1021/bi9601565. [DOI] [PubMed] [Google Scholar]
- 104.Quenneville J, Popovic DM, Stuchebrukhov AA. Combined DFT and electrostatics study of the proton pumping mechanism in cytochrome c oxidase. Biochim Biophys Acta. 2006 doi: 10.1016/j.bbabio.2005.12.003. (in press) [DOI] [PubMed] [Google Scholar]
- 105.Honig BH, Hubble WL. Stability of “salt bridges” in membrane proteins. Proc Natl Acad Sci USA. 1984;81:5412–5416. doi: 10.1073/pnas.81.17.5412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Mills DA, Florens L, Hiser C, Qian J, Ferguson-Miller S. Where is “outside” in cytochrome c oxidase and how and when do protons get there? Biochim Biophys Acta. 2000;1458:180–187. doi: 10.1016/s0005-2728(00)00067-0. [DOI] [PubMed] [Google Scholar]
- 107.Branden M, Sigurdson H, Namslauer A, Gennis RB, Adelroth P, Brzezinski P. On the role of the K-proton-transfer pathway in cytochrome c oxidase. Proc Natl Acad Sci USA. 2001;98:5013–5018. doi: 10.1073/pnas.081088398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Kannt A, Pfitzner U, Ruitenberg M, Hellwig P, Ludwig B, Mantele W, Fendler K, Michel H. Mutation of Arg-54 strongly influences heme composition and rate and directionality of electron transfer in Paracoccus dinitrificans cytochrome c oxidase. J Biol Chem. 1999;274:37974–37981. doi: 10.1074/jbc.274.53.37974. [DOI] [PubMed] [Google Scholar]
- 109.Mitchell R, Mitchell P, Rich PR. Protonation states of the catalytic intermediates of cytochrome c oxidase. Biochim Biophys Acta. 1992;1101:188–191. [PubMed] [Google Scholar]
- 110.Wikström M, Verkhovsky MI. Proton translocation by cytochrome c oxidase in different phases of the catalytic cycle. Biochim Biophys Acta. 2002;1555:128–132. doi: 10.1016/s0005-2728(02)00267-0. [DOI] [PubMed] [Google Scholar]
- 111.Brzezinski P, Larsson G. Redox-driven proton pumping by heme-copper oxidases. Biochim Biophys Acta. 2003;1605:1–13. doi: 10.1016/s0005-2728(03)00079-3. [DOI] [PubMed] [Google Scholar]
- 112.Bloch D, Belevich I, Jasaitis A, Ribacka C, Puustinen A, Verkhovsky MI, Wikström M. The catalytic cycle of cytochrome c oxidase is not the sum of its two halves. Proc Natl Acad Sci USA. 2004;101:529–533. doi: 10.1073/pnas.0306036101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Zhao X, Yeung N, Wang Z, Guo Z, Lu Y. Effects of metal ions in the CuB on the redox properties of heme in heme-copper oxidases: spectroelectrochemical studies of an engineered heme-copper center in myoglobin. Biochemistry. 2005;44:1210–1214. doi: 10.1021/bi0479151. [DOI] [PubMed] [Google Scholar]
- 114.Olsson MH, Sharma PK, Warshel A. Simulating redox coupled proton transfer in cytochrome c oxidase: looking for the proton bottleneck. FEBS Lett. 2005;579:2026–2034. doi: 10.1016/j.febslet.2005.02.051. [DOI] [PubMed] [Google Scholar]
- 115.Onufriev A, Smondyrev A, Bashford D. Proton affinity changes driving unidirectional proton transport in the bacteriorhodopsin photocycle. J Mol Biol. 2003;332:1183–1193. doi: 10.1016/s0022-2836(03)00903-3. [DOI] [PubMed] [Google Scholar]
- 116.Balashov SP. Protonation reactions and their coupling in bacteriorhodopsin. Biochim Biophys Acta. 2000;1460:75–94. doi: 10.1016/s0005-2728(00)00131-6. [DOI] [PubMed] [Google Scholar]
- 117.Hofacker I, Schulten K. Oxygen and proton pathways in cytochrome c oxidase. Proteins: Struct Funct, Genet. 1998;30:100–107. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.