Abstract
Patterns of population structure provide insights into evolutionary processes and help identify groups of individuals for genotype–phenotype association studies. With increasing availability of polymorphic molecular markers across genomes, the examination of population structure using large numbers of unlinked loci has become a common practice in evolutionary biology and human genetics. The two classes of molecular variation most widely used for this purpose, short tandem repeat polymorphisms (STRPs) and single-nucleotide polymorphisms (SNPs), differ in mutational properties expected to affect population structure. To measure the relative ability of these loci to describe population structure, we compared diversity at neighboring STRPs and SNPs from 720 genomic regions in the four populations that comprise the Human HapMap. Comparing loci from the same genomic regions allowed us to focus on the contribution of mutational differences (rather than variation in genealogical history) to disparities in population structure between STRPs and SNPs. Relative to average values for SNPs from the same regions, STRPs had lower Fst, but higher Gst′ and In values. STRP–SNP correlations in population structure across genomic regions were statistically significant but weak in magnitude. Separate analyses by repeat type showed that these correlations were driven primarily by tetranucleotide and trinucleotide STRPs; measures of population structure at dinucleotides and SNPs were not significantly correlated. Pairwise comparisons among populations revealed effects of divergence time on differences in population structure between STRPs and SNPs. Collectively, these results confirm that individual STRPs can provide more information about population structure than individual SNPs, but suggest that the difference in structure at STRPs and SNPs depends on local genealogical history. Our study motivates theoretical comparisons of population structure at loci with different mutational properties.
Keywords: SNP, microsatellite, recurrent mutation, population structure, marker informativeness, human genome
Introduction
Most species show evidence of genetic differentiation among populations. Measurement of this population structure leads to inferences about evolutionary processes, including the dynamics of migration and the timing of population divergence (Charlesworth et al. 2003; Hey and Machado 2003). Quantification of population structure is also required for the identification of randomly mating sets of individuals that can be used to find genetic variants that affect phenotypes in genomewide association studies (Hirschhorn and Daly 2005).
Surveying DNA polymorphism at multiple unlinked loci is a powerful approach to measuring population structure. Humans provide a useful case study because worldwide patterns of population structure have been intensively examined using large numbers of molecular markers throughout the genome. Although the number of genomic regions that have been fully resequenced in common panels of individuals is growing steadily (Livingston et al. 2004; Bustamante et al. 2005; Wall et al. 2008), most analyses of human population structure involving hundreds or more loci have focused on short tandem repeat polymorphisms (STRPs, or microsatellites; Rosenberg et al. 2002, 2005, 2006; Adeyemo et al. 2005; Manica et al. 2005; Wang et al. 2007, 2008; Friedlaender et al. 2008). Recent advances in genotyping technology and the increasing popularity of genomewide association studies have stimulated the measurement of population structure at very large numbers of single-nucleotide polymorphisms (SNPs) as well (International Human HapMap Consortium 2005, 2007; Conrad, Jakobsson, et al. 2006; Lao et al. 2006; Seldin et al. 2006; Steffens et al. 2006; Jakobsson et al. 2008; Kimura et al. 2008; Li et al. 2008; Olshen et al. 2008; Tian et al. 2008).
The availability of genomewide STRP and SNP data in large samples from human populations raises the question of how patterns of population structure at these two marker classes should compare. Two disparities in the mutational process can create differences between STRP and SNP population structure, even when genealogical histories are identical. First, STRPs typically mutate by addition or subtraction of repeats (via replication slippage; Levinson and Gutman 1987; Ellegren 2000), whereas SNPs usually mutate through changes in single base-pair identities. Second, new STRP alleles arise much faster (10−3–10−5 per locus; Weber and Wong 1993; Ellegren 2000) than new SNPs (10−8–10−9 per site; Nachman and Crowell 2000). By rapidly adding or subtracting repeats, the STRP mutation process can generate alleles that already exist in the population, resulting in chromosomes that are identical-by-state but not identical-by-descent. Such recurrent mutation, which occurs rarely at SNPs, can lead to underestimation of population structure. This effect is expected to be most severe when between-population coalescence times are long (relative to within-population times) or mutation rates are high (Rousset 1996; Hedrick 1999; Estoup et al. 2002). Nevertheless, the higher mutation rate of STRPs leads to more variation overall, so that individual STRPs can offer greater statistical power to detect population structure than SNPs under some circumstances (Rosenberg, Li, et al. 2003).
Rosenberg, Li, et al. (2003) discovered that STRPs (using data from the globally distributed human genome diversity panel) were more sensitive to population structure than SNPs (using data from African Americans, European Americans, and East Asians) when structure was quantified by an information-theoretic measure. Liu et al. (2005) also showed that (on average) STRPs were better able to discriminate between human populations than SNPs. Although these studies examined large numbers of loci in many individuals, further comparisons of STRPs and SNPs in the context of population structure are needed. Recent analyses of dense SNP genotypes from the human genome diversity panel (consisting of individuals who had already been surveyed at hundreds of STRPs) indicated that the fraction of diversity attributable to various hierarchical components of population structure (within populations, between populations within geographic regions, and between geographic regions) differs between STRPs and SNPs (Jakobsson et al. 2008; Li et al. 2008), motivating further comparisons on a locus-by-locus basis. Furthermore, direct comparisons between population structure at STRPs and SNPs from the same genomic regions have yet to be conducted on a genomewide scale, making it difficult to separate mutational and genealogical variation as causes of observed differences between marker classes. Here, we integrate STRP and SNP genotypes in the Human HapMap to examine the relationship between population structure at STRPs and nearby SNPs in a common set of individuals drawn from four populations. Our findings reveal effects of the mutational process on measures of human population structure and inform marker choice in genomic studies of evolutionary history.
Methods
Data
HapMap individuals were genotyped for STRPs from Marshfield 5 cM genomic linkage screening sets (http://research.marshfieldclinic.org/genetics/home/index.asp) by Dr. James Weber (Payseur et al. 2008). These STRPs were chosen to be uniformly spaced, highly informative, and easy to type accurately (Ghebranious et al. 2003). Genotyping was performed by the Mammalian Genotyping Service as previously described (Weber and Broman 2001).
We determined the genomic positions of 720 autosomal STRPs from the screening sets by comparing the consensus sequence to the human genome sequence using BLAT (hg17; Build 35) at the UCSC web site (www.genome.ucsc.edu). Of these 720 STRPs, 51 were dinucleotide repeats, 148 were trinucleotide repeats, 511 were tetranucleotide repeats, and 10 were pentanucleotide repeats. Genotypes for all SNPs found within 10 kb of each STRP were downloaded from the HapMap web site (public release 21). This window size was chosen based on patterns of SNP–SNP and STRP–SNP linkage disequilibrium in these samples (International Human HapMap Consortium 2005, 2007; Payseur et al. 2008).
Analyses
Analyses were restricted to unrelated individuals: 59 parents from CEU (individuals of northern and western European ancestry living in Utah from the Centre d'Etude du Polymorphisme Humain [CEPH] collection) trios, 60 parents from YRI (individuals from the Yoruba in Ibadan, Nigeria) trios, 45 CHB (Han Chinese individuals living in Beijing, China), and 45 JPT (Japanese individuals living in Tokyo, Japan). Only SNPs that were polymorphic in at least one population (CEU, YRI, CHB, or JPT) were analyzed.
To measure population structure, we calculated Fst (Wright 1951), Gst′ (Hedrick 2005), and In (Rosenberg, Li, et al. 2003) at each STRP and SNP, treating CEU, YRI, CHB, and JPT as four separate populations. Fst was calculated using the unbiased estimator of Weir and Cockerham (1984). Gst′ (Hedrick 2005) adjusts for the effect of levels of variation on population structure by comparing the observed Gst (a multi-allelic analogue of Fst; Nei 1973) to the maximum possible Gst, conditional on the observed within-population heterozygosity. Values of Gst′ should be more comparable than Fst values among STRPs and SNPs (Hedrick 2005). Possible values of Fst and Gst′ range from 0 to 1. We also calculated the informativeness for assignment (In) according to Rosenberg, Li, et al. (2003). In is an information-theoretic measure that estimates the amount of information that a marker provides about individual ancestry by gauging the potential for assignment of each allele to a particular population. In takes on values between 0 (when all alleles have equal frequencies in all populations) and the natural logarithm of the number of populations (when the number of alleles is equal to or greater than the number of populations and no allele is found in more than one population). This measure is especially useful for multi-allelic markers, including STRPs.
Population structure measures for SNPs within a window were summarized using the arithmetic average or the median. Statistical significance of population structure at each STRP was estimated by comparing the observed value to a distribution of 10,000 values obtained from randomizing the population membership of STRP alleles. In a separate set of analyses, we calculated the same population structure measures for each pair of populations. We compared STRP and SNP measures across windows using matched-pairs Wilcoxon signed-rank tests and Spearman's rank correlation tests.
Results
To compare population structure at STRPs and SNPs, we analyzed 720 autosomal STRPs in individuals from the four human HapMap populations, genotyped by Dr. James Weber (Payseur et al. 2008; genotypes available at http://payseur.genetics.wisc.edu/strpData). These populations were previously genotyped at more than 4 million SNPs (International Human HapMap Consortium 2005, 2007). Levels of population structure for each STRP were compared with arithmetic average values across all SNPs within 10 kb from the same region. The average number of SNPs in each 20 kb window (10 kb on either side of each STRP) was 26 (range: 2–86). There was strong statistical evidence for population differentiation at STRPs: 639, 635, and 680 (of 720) loci showed significant structure (at the P < 0.05 threshold) in permutation tests using Fst, Gst′, and In measures, respectively. Evidence for population structure at millions of SNPs in these samples has been described previously (Weir et al. 2005; Gao and Starmer 2007).
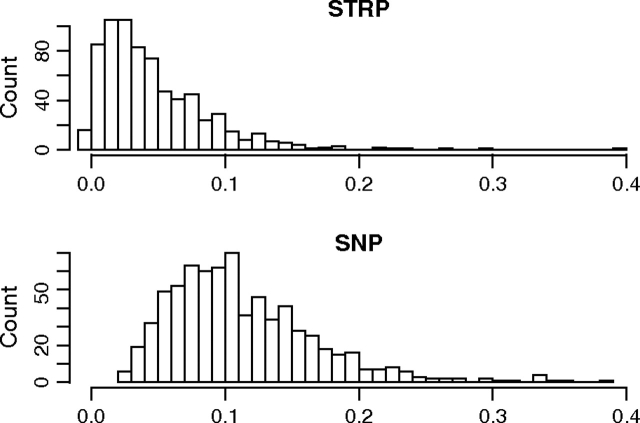
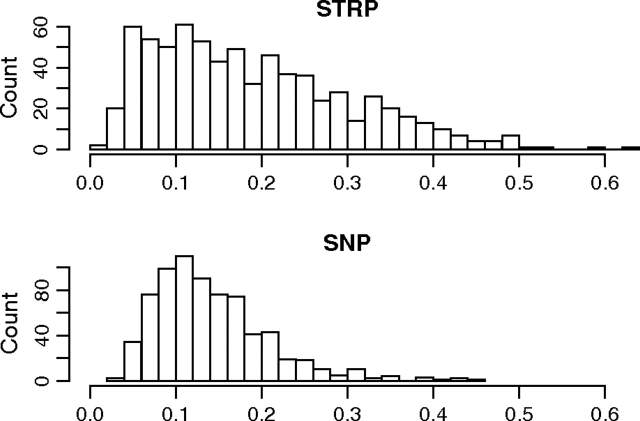
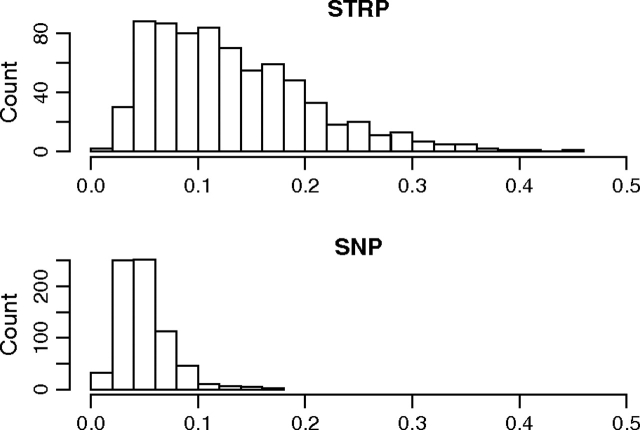
Summary statistics taken across the 720 regions are displayed in table 1. STRPs had lower Fst values than SNPs from the same genomic windows (P < 10−15; paired Wilcoxon signed-rank test; fig. 1). High within-population heterozygosity (such as that observed at STRPs) is expected to deflate Fst (Charlesworth 1998; Hedrick 1999). Consistent with this prediction, Fst was negatively correlated with the within-population component of heterozygosity among STRPs (Spearman's ρ = −0.24; P < 10−10). To address this issue, we also calculated Gst′ and In, which were both positively correlated with heterozygosity among STRPs (Gst′: ρ = 0.15; P < 10−4; In: ρ = 0.17; P < 10−5). Gst′ was higher at STRPs than at SNPs (P < 10−15; paired Wilcoxon signed-rank test; fig. 2). The disparity in evidence for population structure was further pronounced when In was used (P < 10−15; paired Wilcoxon signed-rank test; fig. 3), with STRPs showing higher values.
Table 1.
Population Structure at STRPs and SNPs in Four Populations
| STRP |
SNP |
|||||
| Mean | Median | SD* | Mean | Median | SD | |
| Fst | 0.05 | 0.04 | 0.04 | 0.11 | 0.10 | 0.06 |
| Gst′ | 0.19 | 0.17 | 0.11 | 0.14 | 0.13 | 0.07 |
| In | 0.13 | 0.12 | 0.07 | 0.05 | 0.04 | 0.02 |
Standard deviation (SD) across loci.
SNP values were calculated using the arithmetic mean across all SNPs in a window as individual data points.
FIG. 1.—
Histograms of Fst at STRPs and SNPs from the same genomic regions.
FIG. 2.—
Histograms of Gst′ at STRPs and SNPs from the same genomic regions.
FIG. 3.—
Histograms of In at STRPs and SNPs from the same genomic regions.
Because repeat type affects STRP mutation rate and polymorphism level (Chakraborty et al. 1997; Rosenberg, Li, et al. 2003; Zhivotovsky et al. 2003), repeat types can differ in patterns of population structure (Ruiz-Linares 1999; Rosenberg, Pritchard, et al. 2003). We compared the three repeat classes with large numbers of loci in our data: dinucleotides (n = 51), trinucleotides (n = 148), and tetranucleotides (n = 511). Consistent with previous results (Ruiz-Linares 1999; Rosenberg, Pritchard, et al. 2003), shorter repeat types showed stronger evidence for population structure (table 2).
Table 2.
Comparison of Population Structure among STRP Repeat Types in Four Populations
| Dinucleotide (n = 51) |
Trinucleotide (n = 148) |
Tetranucleotide (n = 511) |
|||||||
| Mean | SD | % Sig Loci* | Mean | SD | % Sig Loci | Mean | SD | % Sig Loci | |
| Fst | 0.07 | 0.04 | 100 | 0.07 | 0.05 | 99 | 0.04 | 0.04 | 85 |
| Gst′ | 0.30 | 0.09 | 100 | 0.25 | 0.11 | 99 | 0.16 | 0.10 | 84 |
| In | 0.23 | 0.07 | 100 | 0.17 | 0.07 | 100 | 0.11 | 0.06 | 92 |
Percentage of loci with P < 0.05 in permutation tests.
The correlation between levels of population structure at neighboring STRPs and SNPs is expected to exceed the correlation among loci from different parts of the genome because linked loci share genealogical histories. This prediction was supported by positive correlations between STRP and SNP population structure across genomic regions (table 3). Although these correlations were statistically significant, their magnitudes were weak (table 3; fig. 4). The strength of STRP–SNP correlations differed among repeat types, with trinucleotides showing the highest values, tetranucleotides showing the next highest values, and dinucleotides showing no significant correlations. To determine whether the relatively low correlations among dinucleotides were caused by the reduced number of surveyed markers in this repeat class, we calculated correlations on 1,000 randomly sampled sets of 51 loci (the number of dinucleotide loci) from each of the other repeat classes. Average correlations in these reduced data sets were very similar to the values observed in table 3 (and remained statistically significant), suggesting that differences among repeat types were not attributable to variation in the number of loci.
Table 3.
Spearman's Rank Correlations between-Population Structure at Neighboring STRPs and SNPs
| STRP Set | Measure | Correlation | P value |
| All | Fst | 0.18 | <10−6 |
| Gst′ | 0.19 | <10−6 | |
| In | 0.18 | <10−5 | |
| Dinucleotide (n = 51) | Fst | 0.24 | 0.09 |
| Gst′ | 0.10 | 0.49 | |
| In | −0.02 | 0.89 | |
| Trinucleotide (n = 148) | Fst | 0.40 | <10−6 |
| Gst′ | 0.39 | <10−5 | |
| In | 0.33 | <10−4 | |
| Tetranucleotide (n = 511) | Fst | 0.19 | <10−4 |
| Gst′ | 0.19 | <10−4 | |
| In | 0.20 | <10−5 |
FIG. 4.—
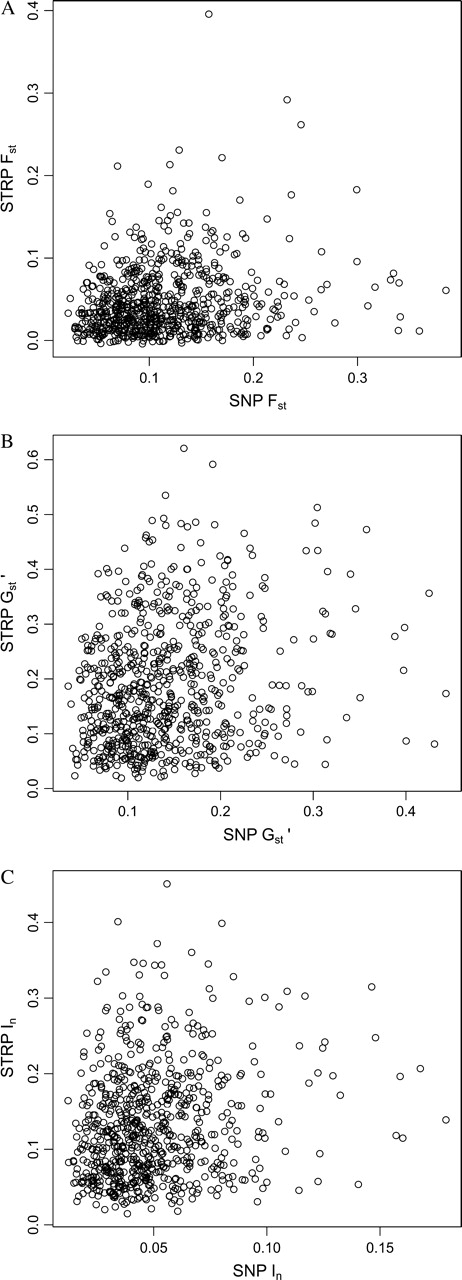
Scatterplots depicting relationships between STRP and SNP population structure. (A) Fst, (B) Gst′, and (C) In.
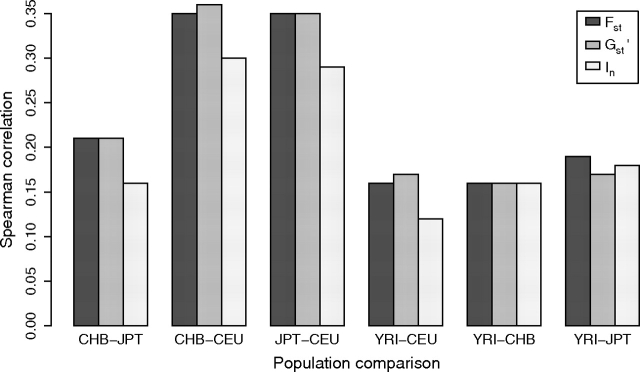
Collectively, the four HapMap populations represent a range of divergence times, providing an opportunity to examine the effects of timescale on relative levels of differentiation at STRPs and SNPs. We repeated the above analyses for all (six) pairs of populations. The magnitudes of genomic correlations between-population structure values at SNPs and STRPs in the pairwise comparisons were similar to those in the original, four-population analyses (fig. 5). The two population comparisons with intermediate levels of divergence (CEU–CHB and CEU–JPT) showed slightly higher correlations, raising three possible explanations. First, the CHB–JPT correlations might be reduced by statistical uncertainty in population structure estimates associated with small divergence between these populations (although analyzing only loci with nonzero values yielded similar correlations), thereby obscuring a decrease in the correlations with divergence time across the broader set of populations. Second, STRP and SNP variation might record genealogical history more similarly on intermediate timescales (divergence between Europe and Asia) than on older (divergence between Africa and non-Africa) and more recent (divergence between China and Japan) timescales. Finally, the genomic correlations between STRP and SNP population structure might be fairly insensitive to timescale. Distinguishing between these explanations will require comparisons among larger numbers of populations with variable divergence times.
FIG. 5.—
Spearman's rank correlations between STRP and SNP population structure measures across genomic regions for pairs of populations. Population pairs are ordered from most recent to most ancient divergence time.
Other results more clearly illustrated the differential effects of timescale on STRPs and SNPs. For example, we measured the STRP In/SNP In ratio in each genomic region and calculated the average of this ratio across regions for each pair of populations. The values were 10.6 (CHB–JPT), 4.3 (CHB–CEU), 4.4 (JPT–CEU), 3.0 (YRI–CEU), 3.0 (YRI–CHB), and 3.0 (YRI–JPT). Although several comparisons were not independent, these ratios suggest that the higher informativeness of STRPs compared with SNPs is most pronounced on recent timescales.
Discussion
The measurement of population structure using molecular markers has become a common practice in evolutionary biology and human genetics. Our genomic comparisons revealed substantial differences in levels of structure at linked STRPs and SNPs in human populations. By comparing loci from the same genomic regions, we could attribute these differences to variation in the mutational process rather than variation in local genealogical history.
Several mutational factors contribute to differences in population structure at the two marker classes. The stepwise mutation process thought to characterize STRPs produces alleles that are identical by state but not identical by descent. Fst and related estimators (including Gst′), which assume that each new mutation is unique, do not account for such recurrent mutation and are expected to be deflated by it. The underestimation of population structure will be most severe when mutation rates are high (indeed, high mutation rate affects homoplasy more strongly than does the stepwise mutation process; Rousset 1996). High levels of polymorphism suggest rapid mutation rates at the STRPs used in our study. In contrast, identical SNP alleles from different populations rarely result from multiple mutations, indicating that SNP Fst estimates should be closer to their parametric values. Our observation that STRP Fst is lower than SNP Fst supports this prediction. These results also agree with recent analyses of genomewide polymorphism in humans from 51 globally distributed populations (Jakobsson et al. 2008; Li et al. 2008). When these investigators used molecular analyses of variance to partition heterozygosity (in a manner analogous to Fst), the between-geographic-region component (the component most similar to the populations in our study) was higher for SNPs than for STRPs. Because of its emphasis on allele identity, Gst′ should also be differentially affected by recurrent mutation at STRPs.
A second reason to expect differences in Fst between STRPs and SNPs is the dependence of the multi-allele version of this statistic on within-population heterozygosity. When mutation rates are high, values of within-population and total heterozgyosity can approach one, constraining the maximum possible value of Fst to be small, even when populations share no alleles (Wright 1978; Charlesworth 1998; Hedrick 1999, 2005). The observations of lower Fst but higher Gst′ at STRPs (relative to SNPs) are consistent with this effect. Recent theoretical work has also shown that the effects of mutation on Fst can depend on the initial heterozygosity of the ancestral population (Ryman and Leimar 2008). Here, we focused on measures of population structure that could be calculated for both STRPs and SNPs, but additional metrics that are less dependent on the mutation rate or directly account for the stepwise mutation process might be better options for STRPs (Goldstein et al. 1995; Slatkin 1995; see Balloux and Lugon-Moulin 2002 for a discussion of this issue).
Regardless of these biases, the higher level of variation at STRPs relative to SNPs can provide increased power to detect population structure (Rosenberg, Li, et al. 2003). We observed much higher values of In at STRPs than at neighboring SNPs. Because In summarizes information more efficiently than Fst (Rosenberg, Li, et al. 2003), we conclude that STRPs are more sensitive indicators of population structure than SNPs in the HapMap populations. Nevertheless, our results highlight the challenges associated with comparing population structure at loci with disparate mutational properties and suggest that the measure of structure should be considered carefully.
Differences in population structure between STRPs and SNPs can also be affected by marker ascertainment biases. SNPs genotyped in the HapMap project were mostly discovered in small samples and are biased toward common variants as a result (International Human HapMap Consortium 2005; Clark et al. 2005). Although HapMap Phase 2 has added many rare SNPs (International Human HapMap Consortium 2007), the remaining bias toward common alleles could cause population structure to be underestimated because common alleles are more likely to be shared among populations (Clark et al. 2005). The STRPs in our study were originally selected based on their high heterozygosity (Ghebranious et al. 2003), a practice that could also affect population structure estimates (but see Romero et al. 2008). Future contrasts between SNPs and STRPs would benefit from population surveys of markers chosen to minimize these biases. It would also be useful to compare population structure at STRPs and SNPs in a wider range of populations (Romero et al. 2008) because the HapMap populations were intentionally chosen to maximize genetic differences.
In addition to providing direct comparisons among levels of population structure at STRPs and SNPs, our study is the first to quantify correlations in population structure among neighboring STRPs and SNPs on a genomewide scale. We detected significant correlations, indicating effects of shared genealogical history, but the magnitudes of the correlations were low. This finding has implications for genomewide studies of population structure. Although STRPs and SNPs show significant average differences across genomic regions, these marker classes appear to track population structure differentially across the genome. Two factors probably contribute to this pattern. First, jointly analyzing subsets of STRPs that show differing correlations with SNPs (e.g., dinucleotides and trinucleotides) could weaken overall correlations. These differences in correlation patterns could be caused by variation in mutation rate among repeat types. Disparities in mutation rate among STRPs with the same repeat type, which have been inferred from patterns of polymorphism (Xu et al. 2005), could also weaken genomewide correlations.
A second factor contributing to the low correlation in population structure is local genealogical history. Variation in the depth and shape of genealogies among genomic regions can affect the contrast between population structure measures at STRPs and SNPs. As a result, we should expect inferences about the dynamics of processes that affect population structure, such as population splitting times and migration rates, to differ among STRPs and SNPs. Because selective sweeps are detected through their distortion of local genealogies (which gives rise to patterns of variation that are unusual for the genome), our results also suggest contrasting properties for STRPs and SNPs in the context of genomewide scans for adaptive evolution that rely on patterns of population structure (Akey et al. 2002; Kayser et al. 2003; Storz et al. 2004; Beaumont 2005). The physical size of the genomic window we used (10 kb on either side of each STRP) might have grouped STRPs with some SNPs that have a different genealogical history, which could lead to the underestimation of correlations in population structure. The extent of this effect depends on the amount of recombination during the genealogical history of the HapMap individuals, which varies among genomic regions and populations (International Human HapMap Consortium 2005, 2007). The weakness of correlations between STRPs and SNPs seem to extend to within-population variation as well. The correlations in population structure documented here are analogous to patterns of within-population linkage disequilibrium in the same samples, where neighboring STRPs and SNPs show strong statistical evidence for associations but the magnitude of these associations is small (Payseur et al. 2008). Payseur and Cutter (2006) predicted low correlations between STRP and SNP diversities from coalescent simulations, and Väli et al. (2008) found no relationship between STRP and SNP heterozygosities (measured on the level of the individual) in populations of coyotes and wolves.
The relative ability of different classes of molecular markers to describe population structure depends on the timescale of the contributing evolutionary processes. The mutational stability of SNPs makes them well suited to detect population divergence or migration events that occurred long ago, whereas the rapid mutation rate of STRPs better reveals recent events (Mountain et al. 2002; Payseur and Cutter 2006). This difference is exemplified by the increase in relative informativeness of STRPs with decreasing population divergence time observed in our study. Because repeat types mutate at different rates (Weber and Wong 1993; Chakraborty et al. 1997), disparities in population structure between repeat types also suggest heterogeneity in the effects of timescale among groups of STRPs. In particular, the lack of significant correlation between dinucleotide and SNP population structures might be caused by especially large differences in mutation rate. The average variance in repeat number in our data was higher at dinucleotides (22.3) than at trinucleotides (8.8) and tetranucleotides (7.0). Because variance in repeat number increases linearly with mutation rate, this observation suggests that the dinucleotides surveyed here might mutate approximately three times as rapidly as the other STRPs.
Recent increases in SNP genotyping and resequencing capacity now allow high-density surveys of SNPs in large numbers of individuals. There are two reasons to expect these advances to shift genomewide examinations of population structure toward SNPs. First, although individual STRPs are more informative than individual SNPs about population structure, genomes contain many more SNPs than STRPs. Very large numbers of SNPs are likely to collectively identify population structure that would be missed by a smaller number of STRPs (Rosenberg, Li, et al. 2003; Liu et al. 2005). Second, when SNPs found near one another in the genome are analyzed, multi-SNP combinations can provide additional insight into population structure (Conrad, Jakobsson, et al. 2006; Jakobsson et al. 2008). Multi-SNP haplotypes share a desirable property with STRPs—higher information content—without suffering from the challenges of recurrent mutation. Interestingly, haplotype and STRP heterozygosities (averaged across the genome) are strongly correlated among human populations (Conrad, Jakobsson, et al. 2006), suggesting that the multi-allelic nature of these markers confers similar variation properties.
Nevertheless, STRPs continue to offer potential advantages over SNPs for the measurement of population structure. First, STRPs might be more powerful than SNPs in small or recently diverged populations. For example, closely related populations could harbor enough new variants at STRPs to detect structure, even if the number of new SNPs is too small (although very large numbers of SNPs seem able to detect fine-scale population structure; Novembre et al. 2008). Second, the effects of recombination rate can be safely ignored when using unlinked STRPs, whereas the inference of structure from multi-SNP haplotypes (whether phased or unphased) requires consideration of this additional, unknown variable. The ability of haplotypes to detect population structure depends on the relationship between the population mutation rate (θ; which determines the number of SNPs) and the population recombination rate (ρ; which determines how many SNPs have the same genealogical history and can be combined). In genomic regions that feature high θ/ρ, multi-SNP haplotypes are likely to outperform STRPs. Alternatively, STRPs could offer higher power to detect structure in genomic regions with low θ/ρ. Finally, the possibility of measuring population structure at large numbers of unlinked SNPs is still primarily limited to genetic model organisms (or their close relatives). The common practice of identifying a handful of highly variable STRPs and using these to describe population structure continues to be useful for nonmodel species.
Our investigation raises several questions that deserve theoretical attention. First, under which circumstances would the addition of STRPs to genomewide SNP surveys improve the characterization of population structure? Analytical approaches that combine linked variants at STRPs and SNPs have been shown to provide improved estimates of population divergence times (Ramakrishnan and Mountain 2004) and migration dynamics (Hey et al. 2004) relative to inferences based on either marker class in isolation. Similar investigations of the joint properties of unlinked STRPs and SNPs would be worthwhile. Second, what is the best way to compare patterns of population structure at loci with widely differing amounts of variation? Likelihood and Bayesian approaches that account for differences in variation and avoid the drastic data reduction inherent in popular summary statistics would be helpful. Finally, what are the mutational and demographic conditions that favor the use of one marker class over the other? Further investigations of the effects of departures from the stepwise mutation model on population structure at STRPs would be particularly useful (Estoup et al. 2002).
As the capacity to survey genomewide variation accelerates, opportunities to integrate different classes of variation to infer population history will increase. Genomic patterns of polymorphism at SNPs and STRPs can also be combined with variation at short indels (Weber et al. 2002) and large copy number variants (Conrad, Andrews, et al. 2006; Hinds et al. 2006; Locke et al. 2006) as information about the mutational properties of these loci becomes available. Harnessing the full power of molecular diversity for understanding population history will require consideration of the complete spectrum of genomic variation.
Supplementary Material
The STRP genotypes are available at http://payseur.genetics.wisc.edu/strpData.
Acknowledgments
We are very grateful to Jim Weber for collecting and sharing the STRP data. We thank Jim Weber, Phil Hedrick, Asher Cutter, Ryan Haasl, Beth Dumont, Sarah Tishkoff, and two anonymous reviewers for providing helpful comments on the manuscript. This research was supported by a Medical Education and Research Committee New Investigator Award (University of Wisconsin School of Medicine and Public Health) and an NHGRI grant (R01HG004498-01A1) to B.A.P., and by funding from the National Heart, Lung, and Blood Institute for the Mammalian Genotyping Service to Jim Weber.
References
- Adeyemo AA, Chen G, Chen Y, Rotimi C. Genetic structure in four West African population groups. BMC Genet. 2005;6:38. doi: 10.1186/1471-2156-6-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akey JM, Zhang G, Zhang K, Jin L, Shriver MD. Interrogating a high-density SNP map for signatures of natural selection. Genome Res. 2002;12:1805–1814. doi: 10.1101/gr.631202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balloux F, Lugon-Moulin N. The estimation of population differentiation with microsatellite markers. Mol Ecol. 2002;11:155–165. doi: 10.1046/j.0962-1083.2001.01436.x. [DOI] [PubMed] [Google Scholar]
- Beaumont MA. Adaptation and speciation: what can F(st) tell us? Trends Ecol Evol. 2005;20:435–440. doi: 10.1016/j.tree.2005.05.017. [DOI] [PubMed] [Google Scholar]
- Bustamante CD, Fledel-Alon A, Williamson S, et al. (13 co-authors) Natural selection on protein-coding genes in the human genome. Nature. 2005;437:1153–1157. doi: 10.1038/nature04240. [DOI] [PubMed] [Google Scholar]
- Chakraborty R, Kimmel M, Stivers DN, Davison LJ, Deka R. Relative mutation rates at di-, tri-, and tetranucleotide microsatellite loci. Proc Natl Acad Sci USA. 1997;94:1041–1046. doi: 10.1073/pnas.94.3.1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B. Measures of divergence between populations and the effect of forces that reduce variability. Mol Biol Evol. 1998;15:538–543. doi: 10.1093/oxfordjournals.molbev.a025953. [DOI] [PubMed] [Google Scholar]
- Charlesworth B, Charlesworth D, Barton NH. The effects of genetic and geographic structure on neutral variation. Ann Rev Ecol Evol Syst. 2003;34:99–125. [Google Scholar]
- Clark AG, Hubisz MJ, Bustamante CD, Williamson SH, Nielsen R. Ascertainment bias in studies of human genome-wide polymorphism. Genome Res. 2005;15:1496–1502. doi: 10.1101/gr.4107905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conrad DF, Andrews TD, Carter NP, Hurles ME, Pritchard JK. A high-resolution survey of deletion polymorphism in the human genome. Nat Genet. 2006;38:75–81. doi: 10.1038/ng1697. [DOI] [PubMed] [Google Scholar]
- Conrad DF, Jakobsson M, Coop G, Wen X, Wall JD, Rosenberg NA, Pritchard JK. A worldwide survey of haplotype variation and linkage disequilibrium in the human genome. Nat Genet. 2006;38:1251–1260. doi: 10.1038/ng1911. [DOI] [PubMed] [Google Scholar]
- Ellegren H. Heterogeneous mutation processes in human microsatellite DNA sequences. Nat Genet. 2000;24:400–402. doi: 10.1038/74249. [DOI] [PubMed] [Google Scholar]
- Estoup A, Jarne P, Cornuet JM. Homoplasy and mutation model at microsatellite loci and their consequences for population genetics analysis. Mol Ecol. 2002;11:1591–1604. doi: 10.1046/j.1365-294x.2002.01576.x. [DOI] [PubMed] [Google Scholar]
- Friedlaender JS, Friedlaender FR, Reed FA (11 co-authors) The genetic structure of Pacific Islanders. PLoS Genet. 2008;4:e19. doi: 10.1371/journal.pgen.0040019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao X, Starmer J, et al. Human population structure detection via multilocus genotype clustering. BMC Genet. 2007;8:34. doi: 10.1186/1471-2156-8-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghebranious N, Vaske D, Yu A, Zhao C, Marth G, Weber JL. STRP screening sets for the human genome at 5 cM density. BMC Genomics. 2003;4:6. doi: 10.1186/1471-2164-4-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein DB, Ruiz-Linares A, Cavalli-Sforza LL, Feldman MW. Genetic absolute dating based on microsatellites and the origin of modern humans. Proc Natl Acad Sci USA. 1995;92:6723–6727. doi: 10.1073/pnas.92.15.6723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick PW. Perspective: highly variable loci and their interpretation in evolution and conservation. Evolution. 1999;53:313–318. doi: 10.1111/j.1558-5646.1999.tb03767.x. [DOI] [PubMed] [Google Scholar]
- Hedrick PW. A standardized genetic differentiation measure. Evolution. 2005;59:1633–1638. [PubMed] [Google Scholar]
- Hey J, Machado CA. The study of structured populations–new hope for a difficult and divided science. Nat Rev Genet. 2003;4:535–543. doi: 10.1038/nrg1112. [DOI] [PubMed] [Google Scholar]
- Hey J, Won YJ, Sivasundar A, Nielsen R, Markert JA. Using nuclear haplotypes with microsatellites to study gene flow between recently separated Cichlid species. Mol Ecol. 2004;13:909–919. doi: 10.1046/j.1365-294x.2003.02031.x. [DOI] [PubMed] [Google Scholar]
- Hinds DA, Kloek AP, Jen M, Chen X, Frazer KA. Common deletions and SNPs are in linkage disequilibrium in the human genome. Nat Genet. 2006;38:82–85. doi: 10.1038/ng1695. [DOI] [PubMed] [Google Scholar]
- Hirschhorn JN, Daly MJ. Genome-wide association studies for common diseases and complex traits. Nat Rev Genet. 2005;6:95–108. doi: 10.1038/nrg1521. [DOI] [PubMed] [Google Scholar]
- International Human HapMap Consortium. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Human HapMap Consortium. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakobsson M, Scholz SW, Scheet P, et al. (23 co-authors) Genotype, haplotype and copy-number variation in worldwide human populations. Nature. 2008;451:998–1003. doi: 10.1038/nature06742. [DOI] [PubMed] [Google Scholar]
- Kayser M, Brauer S, Stoneking M. A genome scan to detect candidate regions influenced by local natural selection in human populations. Mol Biol Evol. 2003;20:893–900. doi: 10.1093/molbev/msg092. [DOI] [PubMed] [Google Scholar]
- Kimura R, Ohashi J, Matsumura Y, Nakazawa M, Inaoka T, Ohtsuka R, Osawa M, Tokunaga K. Gene flow and natural selection in oceanic human populations inferred from genome-wide SNP typing. Mol Biol Evol. 2008;25:1750–1761. doi: 10.1093/molbev/msn128. [DOI] [PubMed] [Google Scholar]
- Lao O, van Duijn K, Kersbergen P, de Knijff P, Kayser M. Proportioning whole-genome single-nucleotide-polymorphism diversity for the identification of geographic population structure and genetic ancestry. Am J Hum Genet. 2006;78:680–690. doi: 10.1086/501531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levinson G, Gutman GA. Slipped-strand mispairing: a major mechanism for DNA sequence evolution. Mol Biol Evol. 1987;4:203–221. doi: 10.1093/oxfordjournals.molbev.a040442. [DOI] [PubMed] [Google Scholar]
- Li JZ, Absher DM, Tang H, et al. (10 co-authors) Worldwide human relationships inferred from genome-wide patterns of variation. Science. 2008;319:1100–1104. doi: 10.1126/science.1153717. [DOI] [PubMed] [Google Scholar]
- Liu N, Chen L, Wang S, Oh C, Zhao H. Comparison of single-nucleotide polymorphisms and microsatellites in inference of population structure. BMC Genet. 2005;6(Suppl 1):S26. doi: 10.1186/1471-2156-6-S1-S26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingston RJ, von Niederhausern A, Jegga AG, Crawford DC, Carlson CS, Rieder MJ, Gowrisankar S, Aronow BJ, Weiss RB, Nickerson DA. Pattern of sequence variation across 213 environmental response genes. Genome Res. 2004;14:1821–1831. doi: 10.1101/gr.2730004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Locke DP, Sharp AJ, McCarroll SA, et al. (10 co-authors) Linkage disequilibrium and heritability of copy-number polymorphisms within duplicated regions of the human genome. Am J Hum Genet. 2006;79:275–290. doi: 10.1086/505653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manica A, Prugnolle F, Balloux F. Geography is a better determinant of human genetic differentiation than ethnicity. Hum Genet. 2005;118:366–371. doi: 10.1007/s00439-005-0039-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mountain JL, Knight A, Jobin M, Gignoux C, Miller A, Lin AA, Underhill PA. SNPSTRs: empirically derived, rapidly typed, autosomal haplotypes for inference of population history and mutational processes. Genome Res. 2002;12:1766–1772. doi: 10.1101/gr.238602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachman MW, Crowell SL. Estimate of the mutation rate per nucleotide in humans. Genetics. 2000;156:297–304. doi: 10.1093/genetics/156.1.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M. Analysis of gene diversity in subdivided populations. Proc Natl Acad Sci USA. 1973;70:3321–3323. doi: 10.1073/pnas.70.12.3321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novembre J, Johnson T, Bryc K, et al. (11 co-authors) Genes mirror geography within Europe. Nature. 2008;456:98–101. doi: 10.1038/nature07331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshen AB, Gold B, Lohmueller KE, et al. (18 co-authors) Analysis of genetic variation in Ashkenazi Jews by high density SNP genotyping. BMC Genet. 2008;9:14. doi: 10.1186/1471-2156-9-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payseur BA, Cutter AD. Integrating patterns of polymorphism at SNPs and STRs. Trends Genet. 2006;22:424–429. doi: 10.1016/j.tig.2006.06.009. [DOI] [PubMed] [Google Scholar]
- Payseur BA, Place M, Weber JL. Linkage disequilibrium between STRPs and SNPs across the human genome. Am J Hum Genet. 2008;82:1039–1050. doi: 10.1016/j.ajhg.2008.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramakrishnan U, Mountain JL. Precision and accuracy of divergence time estimates from STR and SNPSTR variation. Mol Biol Evol. 2004;21:1960–1971. doi: 10.1093/molbev/msh212. [DOI] [PubMed] [Google Scholar]
- Romero IG, Manica A, Goudet J, Handley LL, Balloux F. How accurate is the current picture of human genetic variation? Heredity. 2008;102:120–126. doi: 10.1038/hdy.2008.89. [DOI] [PubMed] [Google Scholar]
- Rosenberg NA, Li LM, Ward R, Pritchard JK. Informativeness of genetic markers for inference of ancestry. Am J Hum Genet. 2003;73:1402–1422. doi: 10.1086/380416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Mahajan S, Gonzalez-Quevedo C, et al. (12 co-authors) Low levels of genetic divergence across geographically and linguistically diverse populations from India. PLoS Genet. 2006;2:e215. doi: 10.1371/journal.pgen.0020215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Mahajan S, Ramachandran S, Zhao C, Pritchard JK, Feldman MW. Clines, clusters, and the effect of study design on the inference of human population structure. PLoS Genet. 2005;1:e70. doi: 10.1371/journal.pgen.0010070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, Zhivotovsky LA, Feldman MW. Genetic structure of human populations. Science. 2002;298:2381–2385. doi: 10.1126/science.1078311. [DOI] [PubMed] [Google Scholar]
- Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, Zhivotovsky LA, Feldman MW. Response to comment on “Genetic structure of human populations”. Science. 2003;298:2381–2385. doi: 10.1126/science.1078311. [DOI] [PubMed] [Google Scholar]
- Rousset F. Equilibrium values of measures of population subdivision for stepwise mutation processes. Genetics. 1996;142:1357–1362. doi: 10.1093/genetics/142.4.1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruiz-Linares A. Microsatellites and the reconstruction of the history of human populations. In: Goldstein DB, Schlotterer C, editors. Microsatellites: evolution and applications. Oxford: Oxford University Press; 1999. pp. 183–197. [Google Scholar]
- Ryman N, Leimar O. Effect of mutation on genetic differentiation among nonequilibrium populations. Evolution. 2008;62:2250–2259. doi: 10.1111/j.1558-5646.2008.00453.x. [DOI] [PubMed] [Google Scholar]
- Seldin MF, Shigeta R, Villoslada P, Selmi C, Tuomilehto J, Silva G, Belmont JW, Klareskog L, Gregersen PK. European population substructure: clustering of northern and southern populations. PLoS Genet. 2006;2:e143. doi: 10.1371/journal.pgen.0020143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M. A measure of population subdivision based on microsatellite allele frequencies. Genetics. 1995;139:457–462. doi: 10.1093/genetics/139.1.457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steffens M, Lamina C, Illig T, et al. (26 co-authors) SNP-based analysis of genetic substructure in the German population. Hum Hered. 2006;62:20–29. doi: 10.1159/000095850. [DOI] [PubMed] [Google Scholar]
- Storz JF, Payseur BA, Nachman MW. Genome scans of DNA variability in humans reveal evidence for selective sweeps outside of Africa. Mol Biol Evol. 2004;21:1800–1811. doi: 10.1093/molbev/msh192. [DOI] [PubMed] [Google Scholar]
- Tian C, Plenge RM, Ransom M, et al. (10 co-authors) Analysis and application of European genetic substructure using 300 K SNP information. PLoS Genet. 2008;4:e4. doi: 10.1371/journal.pgen.0040004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Väli Ü, Einarsson A, Waits L, Ellegren H. To what extent do microsatellite markers reflect genome-wide genetic diversity in natural populations? Mol Ecol. 2008;17:3808–3817. doi: 10.1111/j.1365-294X.2008.03876.x. [DOI] [PubMed] [Google Scholar]
- Wall JD, Cox MP, Mendez FL, Woerner A, Severson T, Hammer MF. A novel DNA sequence database for analyzing human demographic history. Genome Res. 2008;18:1354–1136. doi: 10.1101/gr.075630.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Lewis CM, Jakobsson M, et al. (26 co-authors) Genetic variation and population structure in native Americans. PLoS Genet. 2007;3:e185. doi: 10.1371/journal.pgen.0030185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Ray N, Rojas W, et al. (27 co-authors) Geographic patterns of genome admixture in Latin American Mestizos. PLoS Genet. 2008;4:e1000037. doi: 10.1371/journal.pgen.1000037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber JL, Broman KW. Genotyping for human whole-genome scans: past, present, and future. Adv Genet. 2001;42:77–96. doi: 10.1016/s0065-2660(01)42016-5. [DOI] [PubMed] [Google Scholar]
- Weber JL, David D, Heil J, Fan Y, Zhao C, Marth G. Human diallelic insertion/deletion polymorphisms. Am J Hum Genet. 2002;71:854–862. doi: 10.1086/342727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber JL, Wong C. Mutation of human short tandem repeats. Hum Mol Genet. 1993;2:1123–1128. doi: 10.1093/hmg/2.8.1123. [DOI] [PubMed] [Google Scholar]
- Weir BS, Cardon LR, Anderson AD, Nielsen DM, Hill WG. Measures of human population structure show heterogeneity among genomic regions. Genome Res. 2005;15:1468–1476. doi: 10.1101/gr.4398405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir BS, Cockerham CC. Estimating F-statistics for the analysis of population structure. Evolution. 1984;38:1358–1370. doi: 10.1111/j.1558-5646.1984.tb05657.x. [DOI] [PubMed] [Google Scholar]
- Wright S. The genetical structure of populations. Ann Eugen. 1951;15:323–354. doi: 10.1111/j.1469-1809.1949.tb02451.x. [DOI] [PubMed] [Google Scholar]
- Wright S. Evolution and the genetics of populations, variability within and among natural populations. Chicago: The University of Chicago Press; 1978. [Google Scholar]
- Xu H, Chakraborty R, Fu YX. Mutation rate variation at human dinucleotide microsatellites. Genetics. 2005;170:305–312. doi: 10.1534/genetics.104.036855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhivotovsky LA, Rosenberg NA, Feldman MW. Features of evolution and expansion of modern humans, inferred from genomewide microsatellite markers. Am J Hum Genet. 2003;72:1171–1186. doi: 10.1086/375120. [DOI] [PMC free article] [PubMed] [Google Scholar]