An Investigation of the Statistical Power of Neutrality Tests Based on Comparative and Population Genetic Data

Abstract

In this report, we investigate the statistical power of several tests of selective neutrality based on patterns of genetic diversity within and between species. The goal is to compare tests based solely on population genetic data with tests using comparative data or a combination of comparative and population genetic data. We show that in the presence of repeated selective sweeps on relatively neutral background, tests based on the d_N/d_S ratios in comparative data almost always have more power to detect selection than tests based on population genetic data, even if the overall level of divergence is low. Tests based solely on the distribution of allele frequencies or the site frequency spectrum, such as the Ewens–Watterson test or Tajima's D, have less power in detecting both positive and negative selection because of the transient nature of positive selection and the weak signal left by negative selection. The Hudson–Kreitman–Aguadé test is the most powerful test for detecting positive selection among the population genetic tests investigated, whereas McDonald–Kreitman test typically has more power to detect negative selection. We discuss our findings in the light of the discordant results obtained in several recently published genomic scans.

Introduction

Several recent papers have examined the abundance and distribution of Darwinian selection in the human genome (e.g., Akey et al. 2002; Clark et al. 2003; Bustamante et al. 2005; Carlson et al. 2005; Nielsen et al. 2005; Voight et al. 2006; Wang et al. 2006; Williamson et al. 2007). Although some of the results of these studies are concordant, others are not (e.g., Sabeti et al. 2006; Nielsen et al. 2007). One explanation for the lack of concordance is that different studies use different data and methods and may, therefore, capture different aspects of the evolutionary processes governing variation at the molecular level. In particular, some studies use comparative (between species) data, some studies use population genetic (within species) data, and some studies use a combination of both. Although much is known about the power of each type of method, there have been few efforts to establish the relationship between methods using intraspecific and interspecific data.

Neutrality tests using population genetic data have been based on allelic frequency configurations at individual loci (Ewens 1972; Karlin and McGregor 1972; Watterson 1978; Slatkin 1994, 1996), frequency distribution of segregation sites at multiple loci (e.g., Tajima 1989; Fu and Li 1993; Fay and Wu 2000), numbers of haplotypes (e.g., Fu 1996; Depaulis and Veuille 1998), haplotype diversity (Depaulis and Veuille 1998), haplotype partitions (Hudson et al. 1994; Innan et al. 2005), linkage disequilibrium and haplotype structure (e.g., Kelly 1997; Slatkin and Bertorelle 2001; Sabeti et al. 2002; Toomajian et al. 2003; Kim and Nielsen 2004), as well as differences in allelic frequencies between subpopulations (e.g., Lewontin and Krakauer 1973). Several thorough simulation studies comparing the statistical power of population genetic tests of neutrality have been carried out (e.g., Braverman et al. 1995; Simonsen et al. 1995; Fu 1997; Depaulis et al. 2003; Zeng et al. 2007).

The majority of methods for detecting selection based on comparative data rely on estimating ω = d_N/d_S, where d_N is the rate of replacement (nonsilent) substitutions and d_S is the rate of silent substitutions (e.g., Miyata and Yasunaga 1980; Goldman and Yang 1994; Muse and Gaut 1994; Nielsen and Yang 1998; Yang et al. 2000). The power and accuracy of these methods have been studied extensively (e.g., Yang and Bielawski 2000; Wong et al. 2004). The published simulation studies show that if the selective constraint at a single-codon position is fixed on all or part of an evolutionary tree, tests based on d_N/d_S ratios have considerable power. For example, in a data set of 30 species, the power to detect election at the 5% significance level is about 76% if 10% of sites evolve with ω = 1.5 and essentially 100% if 10% of the sites evolve with ω = 5 (Wong et al. 2004). However, for fewer species or if selective effects are not fixed among sites, the power can be much lower (e.g., Nielsen et al. 2005).

The third class of methods combines information from both comparative and population genetic data. The Hudson–Kreitman–Aguadé (HKA) test (Hudson et al. 1987) compares patterns of polymorphism and divergence at two or more loci. The HKA test is based on the premise that at neutral loci both variation within species and divergence between species depends only on the mutation rate. Significant deviations from a constant ratio of polymorphisms to divergence among loci may then indicate the presence of selection. The McDonald–Kreitman (MK) test (McDonald and Kreitman 1991) is similar to the HKA test but compares the ratio of nonsynonymous and synonymous mutations between and within species. The Poisson random field (PRF) model (Sawyer and Hartl 1992) gives a theoretical foundation for MK test. The statistical power and restrictions relating to the MK test and the PRF model have been studied by Akashi (1999) and Bustamante et al. (2001).

Previous studies have focused on comparing the statistical power among different population genetic tests or among different tests using only comparative data. The objective of this paper is instead to compare the statistical power of different classes of neutrality tests. One of the motivations for doing this is that several recent genomic scans for selection have provided quite different results when they have used different types of neutrality tests (recently reviewed in Nielsen et al. 2007; Sabeti et al. 2007). We focus on few of the most commonly used tests and we examine only the case of divergence between a pair of closely related species. The parameters are chosen to mimic human population genetic data and divergence times of magnitude around human–chimpanzee speciation split—the focus of many recent genomic scans. As we will show, much of the discrepancy between the results obtained from different genome scans can likely be explained by the differences in the statistical properties among different tests of neutrality.

Methods

Simulations

The methods used for simulating population genetic data are usually quite different from the methods used to simulate comparative data. In the absence of selection, population genetic data are usually simulated using coalescence methods (e.g., Hudson 2002), whereas forward simulations are used in the presence of selection (e.g., Williamson and Orive 2002). In contrast, comparative data are usually simulated by modeling the population fixation processes using Markov models that assume independence among nucleotide sites or codons (e.g., Yang 1997). Other aspects, such as mutational models, will often also differ between population genetic and comparative simulations. For example, population genetic simulations are typically based on the infinite alleles model or the infinite sites model (Kimura and Crow 1964; Kimura 1969), whereas simulations of comparative data usually use finite sites models which take multiple substitutions into account.

In this study, in order to examine the effects of recurrent mutation and selection within and between species, we use a forward simulation of a Wright–Fisher model similar to that used by Williamson and Orive (2002) but allow mutations to occur according to the Goldman and Yang (1994) codon-based model and allow two populations to evolve from a common ancestor existing T generations in the past. Every time a new mutation occurs, its position is chosen uniformly across the region. The type of the mutation (nonsynonymous or synonymous) is determined according to the number of nonsynonymous and synonymous sites in the specific codon where the mutation occurs. The fitness effect of the mutation depends on the selection model (see table 1). Mutation, selection, and recombination occur independently according to a standard Wright–Fisher model (Ewens 2004). Every time a mutation becomes fixed in the population, the codon underneath this mutation is updated according to Nielsen and Yang (1998) codon model conditioned on the type of the mutation. The initial population is simulated for 30 N generations at which time we assume stationary has been reached. Then, each of the two descendent populations, arbitrarily denoted by “right” and “left,” evolves for T generations. When the simulations are terminated, 1 haplotype sequence is sampled from the left lineage and 50 haplotypes are sampled from the right lineage for use in the population genetic tests. One haplotype is also sampled from the right lineage to construct d_N/d_S divergence comparisons.

Table 1.

Parameters Chosen in the Simulations

Schemes	Selection Models	Divergence (units of N)	Figure	θ	Fitness Schemes (S = 4Ns)
						Percent	Distribution
Random position	Recurrent positive selection on neutral background	15, 30	1	10, 30		Strong: 1%	Gamma (mean = 100, α = 1)
						Weak: 5%	Gamma (mean = 20, α = 1)
	Recurrent purifying selection on neutral background	15, 30	1	10, 30		Strong: 90%	Gamma (mean = 20, α = 1)
						Weak: 90%	Gamma (mean = 5, α = 1)
	Mosaic selection	30	3	30	Positive	Strong: 1%	Gamma (mean = 100, α = 1)
						Weak: 1%	Gamma (mean = 50, α = 1)
					Negative	Strong: [20%, 90%]	Gamma (mean = 20, α = 1)
						Weak: [20%, 90%]	Gamma (mean = 5, α = 1)
Divergence	Recurrent positive/negative selection under random position	[30, 100, 400]	4	30	Positive	Strong: 0.1%	Gamma (mean = 100, α = 1)
					Negative	Strong: 90%	Gamma (mean = 20, α = 1)
Sample size	Recurrent positive/negative selection under random position	30	4	30	Positive	Strong: 1%	Gamma (mean = 100, α = 1)
					Negative	Strong: 90%	Gamma (mean = 20, α = 1)
Fixed/random position	Mosaic selection (fixed)	30	4	30	Positive	[1–2.5%] codon positions	Gamma (mean = 50, α = 1)
					Negative	90% of the codon positions	Gamma (mean = 20, α = 1)
	Mosaic selection (random)	30	4	30	Positive	[1–2.5%]	Gamma (mean = 50, α = 1)
					Negative	90%	Gamma (mean = 20, α = 1)

Neutrality Tests

We implement three neutrality tests for comparative data: the HKA test (Hudson et al. 1987), the MK test (McDonald and Kreitman 1991), and the d_N/d_S likelihood ratio test (Nielsen and Yang 1998; Yang et al. 2000). We compare these tests with two tests based on population genetic data: 1) the Ewens–Watterson (EW) homozygosity test (Ewens 1972; Watterson 1978), which was found to be one of the most powerful tests of all population-based tests and to be robust against recombination (Zeng et al. 2007), and 2) Tajima's D test (Tajima 1989)—the most commonly used test based on the site frequency spectrum.

For the likelihood ratio test based on d_N/d_S ratios, we use a test based on models M7 and M8 from PAML package to detect positive selection (Yang et al. 2000). In the case of purifying selection, a likelihood ratio test is constructed by comparing likelihoods between strict neutrality (ω = 1.0 across all codons) and the M7 model (ω follows a beta distribution). The MK test is performed by applying a chi-square test to the contingency table. For the HKA test, a neutral locus of the same size as the selected locus is also simulated to construct the two-locus version of the HKA test. For both the Tajima's D test and the HKA test, neutral simulations are conducted to obtain empirical critical values. All tests are conducted at 5% significance level, and statistical power is evaluated based on 500 replicates.

Choice of Parameters

Exhaustively exploring the full range of all parameters is not computationally feasible. Instead, we choose parameter values compatible with observed levels of human polymorphism and “human–chimp divergence.” If we assume that a human population size is of N_e = 10,000, a human–chimp divergence time of 6 My, and an average generation time for both humans and chimps of 20 years, the divergence time is 6 × 10⁶/2 × 10⁴ × 20 = 15 measured in time units of 2N_e generations.

The size of the genomic regions is chosen to ensure sufficient levels of polymorphism to provide meaningful tests and to avoid computational and statistical issues arising from the analysis of data sets with very few polymorphic sites. Modeling human population genetic data, we assume that 1 kb in nucleotide sequences corresponds to θ = 4N_eμ = 1, where μ is the mutation rate per generation.

Directly simulating population sizes of 10,000 individuals is computationally challenging. Here, we present results based on haploid population of effective size of 500, but there is no reason to assume that our results do not generalize to larger populations. We also explore few other combinations of parameters. The frequencies of the 61 codons were assumed to be equal, and the ratio of transversion to transitions was set to 2.0.

Selection and Fitness Effects

In this study, we explore three selective scenarios: recurrent selective sweeps, recurrent purifying selection, and a mixture of the two. In each of the cases, we use two different assumptions: 1) “random positions,” where new selected mutations are equally likely to occur in any position in the genome independent of their fitness effects, and 2) “fixed positions,” where the selection coefficient acting on a new mutation depends on the site at which mutation occurs with a fixed selection coefficients for a particular site. The second model is comparable to models typically used for phylogenetic simulations (e.g., Wong et al. 2004).

In all cases, we restrict ourselves to multiplicative genic fitnesses, meaning that selection is acting at the haplotype level and the fitness of a specific haplotype is the product of fitness effects of individual mutations.

Following previous studies, we assume a gamma distribution to model the fitness effects of mutations (Williamson and Orive 2002). The gamma distribution depends on two parameters: the shape (α) and the scale parameter (β). The shape parameter controls the general shape of the distribution and allows variation from L-shaped similar to an exponential distribution to a symmetric distribution with a single mode similar to a normal distribution. The different parameter settings explored are summarized in table 1.

Results

Recurrent Positive Selection with Random Positions

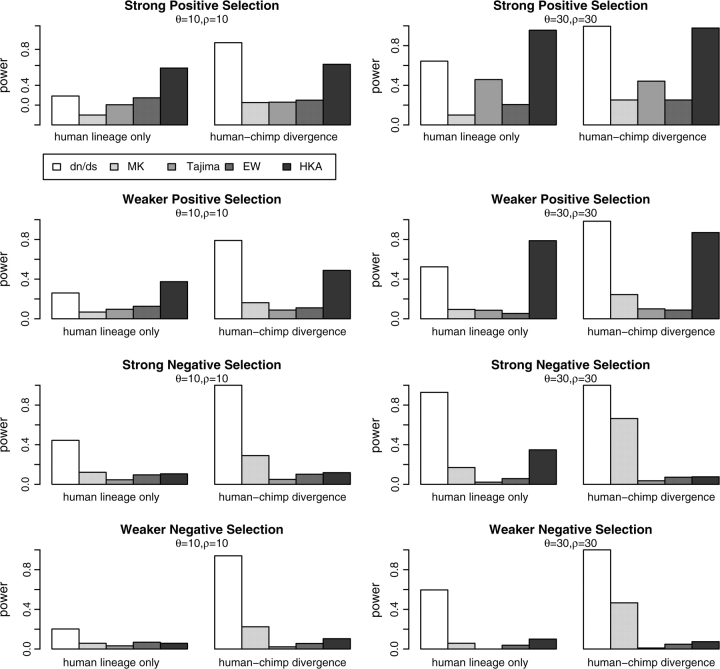
We first simulated two scenarios with random positions of the selected mutations. In the first scenario, 1% of nonsynonymous mutations have scaled selection coefficients S (=4Ns) sampled from a gamma distribution with parameters α = 1 and β = 100. This corresponds to relatively strong recurrent positive selection. In the other scenario, 5% of the nonsynonymous mutations have S sampled from a gamma distribution with parameters α = 1 and β = 20. In the second case, more of the mutations are experiencing positive selection, but the intensity of selection is weaker.

In addition to varying the intensity of selection, we also changed the proportion of time that selection acted on the population. We simulated cases where only the right lineage (corresponding to the human lineage) is under selection and cases where both lineages are under selection with different values of θ and ρ (fig. 1, top panels). As we can see from figure 1, the HKA and d_N/d_S test show reasonable statistical power, but the other tests, the MK test in particular, show little power. It may be surprising that the MK test has so little power in this scenario. The homogeneity of d_N/d_S ratios within and between species apparently captures little of the signal of positive selection at these levels of divergence because much of the variation in d_N/d_S ratios is among codon positions. When information from all sites is collected into a single table, some information is lost. However, the power of all the tests that use comparative data, including the MK test, increases as the divergence level increases.

FIG. 1.—

Statistical power of five neutrality tests assuming a random position model. Parameters are chosen as described in table 1 and discussed in the text. Two different values of θ and recombination rate (ρ = 4Nr) are simulated. “Human lineage only” corresponds to the cases where only the right lineage is under selection, whereas human–chimp divergence refers to the case where both lineages are under selection.

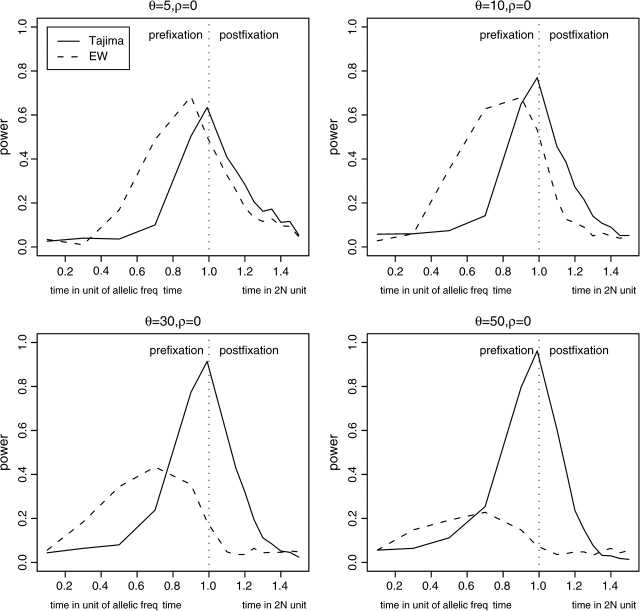
The tests based only on polymorphism have only little statistical power (fig. 1), which can be understood by noting that they have power to detect selection only while an advantageous allele is segregating in the population or shortly thereafter. A previous study found that the EW homozygosity test had very high power in detecting an ongoing selective sweep (Zeng et al. 2007). The fact that we find it to have very little power indicates that this test detects selection only in a narrow window around the time when a selected mutation reaches fixation. We confirmed this intuition by simulating a hitchhiking event on a nonrecombining segment of various sizes using SelSim (Spencer and Coop 2004). The advantageous allele with scaled selection coefficient S = 100 arises in the middle of the genomic region. A sample of 50 sequences is collected at several time points. As we can see from figure 2, the power of the EW test decreases quickly after the fixation of the advantageous allele. This effect is especially apparent when the segment is long. A similar effect is observed for Tajima's D, which does not gain power until very late in the selective sweep. However, the power of Tajima's D to detect this type of selection lasts for slightly longer than it does for the EW test. Tajima's D appears to have more power at the time of fixation when the mutant frequency is high and recombination is relatively weak (fig. 2).

FIG. 2.—

Statistical power of Tajima's D test and EW test on a single hitchhiking event with nonrecombining segments. The time to the left of the fixation event is measured in the frequency of the advantageous allele. The time to the right is measured in 2N generations. The selection coefficient (S = 2Ns) is set to be 100.

Recurrent Purifying Selection with Random Positions

We simulated two cases of purifying selection, one with 90% of all nonsynonymous mutations having scaled selection coefficient −S, where S is drawn from a gamma distribution with α = 1 and β = 5 in one case and α = 1 and β = 20 in the other.

In the lower panel of figure 1, we can see that population-based tests again have low power in detecting recurrent purifying selection. Previous studies have suggested that the effect of purifying selection on the shape of the gene genealogy is quite weak (e.g., Golding 1997; Krone and Neuhauser 1997; Neuhauser and Krone 1997; Przeworski et al. 1999; Slade 2000; Williamson and Orive 2002). Although selection tends to increase variance of the distribution of the number of mutations above that of a Poisson, the increase is small, thus accounting for the low power of many neutrality tests (e.g., Williamson and Orive 2002).

For the HKA test, the levels of polymorphism and divergence are both reduced, causing a decrease in statistical power. On the other hand, the d_N/d_S likelihood ratio test gains power because it detects multiple codon positions experiencing purifying selection. In contrast to the case of positive selection, the MK test now shows more power than any of the other tests except the d_N/d_S likelihood ratio test. The reduction in the rate on nonsynonymous mutation also increases the power of the MK test.

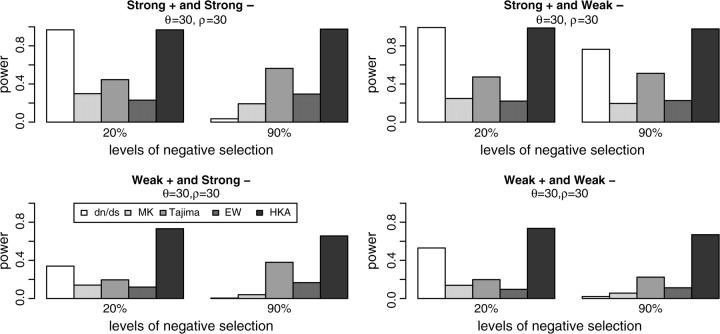
Mosaic Selection with Random Positions

We simulated four cases in which both purifying and positive selection are acting. In the case of strong positive selection, 1% of the nonsynonymous mutations have S following a gamma distribution with α = 1 and β = 100. For weaker positive selection, α = 1 and β = 50. Strong purifying selection has 20% or 90% of nonsynonymous changes with −S following gamma distribution (α = 1 and β = 20), whereas weaker purifying selection assumes a gamma distribution with α = 1 and β = 5. In all situations, we varied the levels of background purifying selection by allowing different proportions of nonsynonymous mutations to be negatively selected. In this setting, we evaluate the d_N/d_S test in terms of its power to detect positive selection. The results of the simulations are shown in figure 3.

FIG. 3.—

Statistical power of five neutrality tests under mosaic selection. Selection parameters are listed in table 1 and are also discussed in the text. Two different assumptions regarding the proportion of negatively selected mutations (20% or 90%) are used.

Because the same set of sites are experiencing both positive and negative selection in the model with random positions, the statistical power of d_N/d_S test depends on the relative magnitudes of positive and negative selection. Only with strong positive selection and relatively weak purifying selective does the d_N/d_S test show appreciable power to detect positive selection. Otherwise, the signal of negative selection will overwhelm the signal of positive selection.

The other four tests show patterns of statistical power somewhere between the two extreme cases in figure 1. It is interesting to note that test such as the Tajima's D test actually has increased power in the presence of background selection. There might be two reasons for this. First, both negative selection and recent selective sweeps will result in negative Tajima's D values. Therefore, selective sweeps and negative selection may work together to increase the power of this test. Second, the recovery phase after a selective sweep might be longer, because in our model, the effective rate of neutral mutation is reduced in the presence of negative selection. These two effects will tend to be counterbalanced by interference/Hill–Robertson effects (Hill and Robertson 1966).

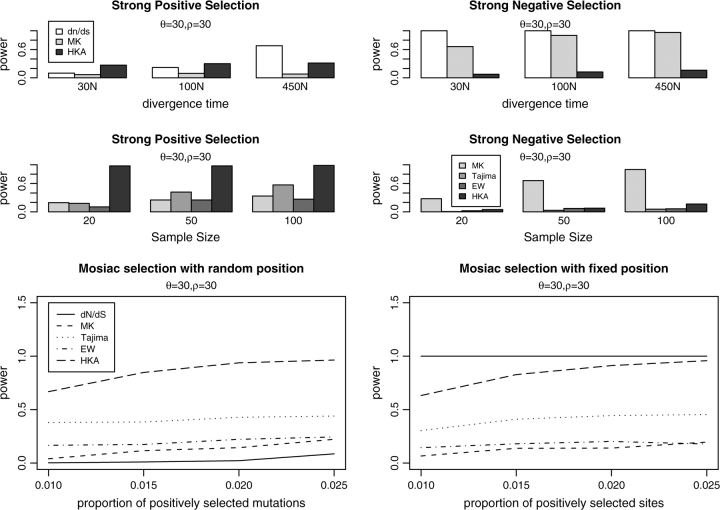
Factors Contributing to the Statistical Power

We investigate other factors that could influence the statistical power of the neutrality tests. We first examine the effect of changing the divergence time on the three tests using comparative data by simulating three levels of divergence: 30N, 100N, and 400N. Under the assumption of a molecular clock, these three divergence times correspond roughly to human–chimp (∼6 My), human–macaque (∼20 My), and human–mouse (∼80 My) divergence (e.g., Foote et al. 1999).

As we can see from figure 4 (top panel), the divergence time only weakly affects the power of the HKA test. The reason is apparently that most of the power of the HKA test comes from the transient reduction in variability occurring during a selective sweep. Increasing divergence levels has, therefore, only a small effect on this test. Similar patterns were found for the MK test. On the other hand, the d_N/d_S test is directly affected by the increased number of fixations observed with increased divergence times.

FIG. 4.—

Factors affecting the statistical power of several neutrality tests. In the top panel, we investigate the effect of divergence time on the statistical power of the d_N/d_S, MK, and HKA test. In the middle panel, we look at the relationship between sample size and statistical power for MK, Tajima's D, EW, and HKA test. In the bottom panel, difference between random position and fixed position are plotted. The parameters used in the simulations are listed in table 1 and are also discussed in the text.

In the presence of recurrent negative selection, both the d_N/d_S and the MK tests achieve increased power with increased divergence times. The HKA test, on the other hand, is less sensitive to changes in divergence times.

In addition to changing divergence time, we also examined the effect of sample size on the power of all the neutrality tests except d_N/d_S (fig. 4, middle panel). As expected, the power increases of all the tests with increased sample size for both recurrent positive and negative selection, in accordance with previous results (e.g., Braverman et al. 1995; Simonsen et al. 1995; Fu 1997; Depaulis et al. 2003; Zeng et al. 2007).

Fixed Positions of Selective Effects

So far we assumed that positively and negatively selected mutations are equally likely to occur in all sites. This assumption is probably not very realistic as different amino acid positions in a protein will typically experience different selective pressure. Often, only certain areas of a protein will be targeted by positive selection (e.g., the antigen-binding cleft of the major histocompatibility complex molecule or the antigenic sites of the HIV env protein; Hughes and Nei 1988; Nielsen and Yang 1998). We therefore carried out additional simulations in which the selection coefficients of new mutations are specific to the sites at which the mutations occur. In general, we find that the statistical power of the different tests using population genetic data is similar when this assumption is used instead of the previous one. However, the d_N/d_S ratio test has dramatically increased power to detect selection in the fixed-position model (an example is shown in fig. 4, bottom panel). When the distribution of selection coefficients differs among sites, the d_N/d_S ratio test may have considerable power to detect selection even in the presence of the type of mosaic selection under which it previously had reduced power (fig. 4, bottom panel).

Discussion

In this study, we investigate the statistical power of several tests of neutrality based on comparative and/or population genetic data, using traditional population genetic forward simulations. We have chosen to simulate data under a process where advantageous or deleterious mutations occur randomly and at a constant rate through time. Our conclusions are in some cases different from those of previous population genetic simulation studies which focused on the power of the tests at a specific time before or after fixation (e.g., Braverman et al. 1995; Simonsen et al. 1995; Fu 1997; Depaulis et al. 2003; Zeng et al. 2007). However, for the purpose of evaluating the relevance of the tests for genomic scans aimed at detecting selection, it seems more appropriate to find the power of the tests when averaged over a range of ages of selective sweeps, rather than focusing on a specific time after a beneficial mutation has arisen. To restrict the range of our analysis, we did not investigate other types of selection, such as balancing selection. We emphasize that the conclusions in this study may not necessarily generalize to balancing selection. Likewise, we have not investigated models of temporally changing selection coefficients, which would allow selection to act on standing variation (e.g., Teshima et al. 2006). Again, there is no guarantee that our conclusions generalize to the case where selection is acting on standing variation.

The evaluation of the d_N/d_S ratio test differs from previous studies in using an explicit population genetic model instead of using simulations based on superimposing a simple Markov chain of molecular evolution along the lineages of a phylogenetic tree (e.g., Wong et al. 2004). However, the results we find are largely concordant with previous results, presumably because there are only a limited number of selected mutations segregating simultaneously in our simulations aimed at mimicking human data. When that is true, interference among mutations is relatively weak or absent (Birky and Walsh 1988), and the divergence among species could potentially be modeled well by a simple Markov chain that assumes independence among mutations.

The power of the d_N/d_S ratio test depends strongly on assumptions regarding fixed or random positions of selected mutations. In the random position models with mosaic selection, that is, a mixture of positively and negatively selected mutations, the power of the d_N/d_S ratio test may be low. If mutations are distributed randomly along the sequence, and all sites are equally likely to experience positive and negative selection, the d_N/d_S ratio test will have power to detect selection only in extreme cases where the average level of positive selection is so large that the average d_N/d_S ratio exceeds one. Arguably, the assumption that the distribution of fitness effect is the same for all sites in a protein is unrealistic, and almost all empirical studies have reported strong variation in the d_N/d_S ratio among sites (e.g., reviewed in Yang and Bielawski 2000). In fact, most studies in which positive selection is detected using d_N/d_S ratio tests report estimates of the proportion of sites experiencing positive selection <5% (Yang and Bielawski 2000). However, it is not clear if this is because the dN/dS ratio test has power to detect positive selection only if it repeatedly affects the same set of sites or if it is because positive selection on most genes in fact tends to repeatedly happen in the same set of sites. Nonetheless, it is clear that under the assumption of a fixed-position model, the d_N/d_S ratio has more power to detect recurrent positive selection than any of the tests which use population genetic data. This conclusion is true even for the short divergence times mimicking human–chimp divergence. Arguably, the case of two closely related species investigated here is the scenario least favorable for d_N/d_S ratio tests. If more species were included and/or if the divergence time was longer, the power of d_N/d_S ratio tests would increase drastically (fig. 4; supplementary fig. 1, Supplementary Material online). The relationship between sample size, divergence time, and power has been evaluated in previous papers (Wong et al. 2004) and we will refer to these papers for further discussion.

It may be surprising that the d_N/d_S test has so much more power to detect recurrent positive selection than the population genetic tests do. The main reason is that the population genetic tests rely on capturing a selective sweep in action. If selective sweeps are common, the dN/dS ratio will be very large, providing even more power to the d_N/d_S ratio tests than to the population genetic tests. However, if selective sweeps are rare, the population genetic tests have very little power because they are unlikely to capture an ongoing selective sweep. Nonetheless, the tests using only population genetic data provide information regarding recent or ongoing selection. In this sense, even though these tests may typically have little power compared with the d_N/d_S ratio tests, they do provide additional valuable information regarding ongoing selection.

Among the tests using population genetic data, the HKA test appeared to have the most power to detect recurrent positive selection. In practice, the use of HKA tests has been quite limited mostly because of the lack of putatively neutral loci. Future studies might focus on evaluating the properties, power, and interpretation of the HKA test when different loci are targeted by varying degrees of positive and negative selection.

A bit surprisingly, the MK test was found to have only little power to detect positive selection but substantial power to detect purifying selection. The most important role of the MK test in population genetics might, perhaps, now appropriately be to test for negative selection, whereas other tests should be used to detect positive selection.

A previous study found that the EW homozygosity test is one of the most powerful tests of neutrality based on within-species variation and it is robust to deviations from assumptions regarding recombination (Zeng et al. 2007). However, from figure 2 of this paper, it is clear that the relatively high power of the EW homozygosity test is only maintained for a relatively narrow interval of time, mostly before the beneficial mutation reaches fixation. Similarly to what has been observed for Fay and Wu's H test (Fay and Wu 2000) and several other statistical test, the statistical power of the EW test decreases rapidly after the fixation event (e.g., fig. 3 in this report; Zeng et al. 2006). The time to fixation for a strong positively selected allele is quite short (Ewens 2004), and thus, the window for observing significant results is rather narrow.

There are a number of different tests we have not evaluated in this report, such as the long-range haplotype (LRH) test (Sabeti et al. 2002). Zeng et al. (2007) found that the power of this test depends on whether the selected site is correctly nominated as the core single-nucleotide polymorphism (SNP) in the LRH test. Only when the selected site is picked as the core SNP, will the LRH have high power (Zeng et al. 2007). However, even so, the LRH test only has power to detect selection in a very narrow window of time as well (Zeng et al. 2006). As the advantageous allele sweeps to fixation, the frequency of background haplotypes is being reduced. As a result, the LRH test loses power quickly as the selected allele approaches fixation (Sabeti et al. 2007). If we rank neutrality tests based on their cumulative power defined as sum of power over time, tests such as the Tajima's D test could be more powerful because they maintain power both before and after the fixation event (Simonsen et al. 1995; Fu 1997; Depaulis et al. 2003; Zeng et al. 2006).

Results from genomic scans for selection have shown very different results, often with very little overlap between the conclusions from different studies (Sabeti et al. 2006; Nielsen et al. 2007). The lack of concordance among studies may not be so surprising as the studies using only population genetic data will tend to detect very recent selection, whereas studies using comparative data will detect loci affected by repeated selective sweeps. The overall power of tests based only on population genetic data is low and relies in several cases on catching a rare event, a strong selective sweep, during a narrow window of time. There may possibly only be few loci in the human genome that are currently undergoing selective sweeps so strong that population genetic tests would detect them. This is an important point to keep in mind when interpreting the results of genome-wide scans based on detecting incomplete selective sweeps.

Comparative studies, in contrast, detect loci that repeatedly have been targeted by selection. These may not be the same loci as currently are undergoing selection. For example, a selective sweep currently affecting human populations in the lactase (LCT) locus (e.g., Bersaglieri et al. 2004; Burger et al. 2007; Tishkoff et al. 2007) is not detectable using comparative methods. There is no reason to assume that the lactase locus has been subject to repeated selective sweeps more than any other loci as the selection currently affecting this locus is caused by the unique event of human domestication of cattle. Additionally, the signal of positive selection in comparative data may in some loci be suppressed by the effect of negative selection, especially, when selection has not targeted the same sites repeatedly (e.g., fig. 3).

There are other reasons why results may differ between studies. For example, the data may differ between studies, some studies include only coding regions and others include both coding and noncoding regions, etc. In the light of this, we may turn the question around and, instead, ask why there, after all, are so many examples of concordance, such as in olfactory receptor–related genes and genes related to immunity and defense, where both methods aimed at detecting selective sweeps and comparative methods detect a signal. The explanation must be the existence of loci targeted by selective sweeps so frequently that the chance of catching an ongoing selective sweep in a population genetic study is high.

A major conclusion of this study is that, under suitable assumptions, comparative data provide much more power to detect genes that have been affected by positive selection than methods based solely on population genetic data. As population genetic tests, in addition, are struggling with issues relating to robustness to assumptions regarding demographic parameters and the pattern of recombination, while comparative methods do not rely on assumptions regarding recombination or demography, comparative methods are a much more natural choice of methodology if the objective is to identify genes, and categories of genes, that tend to be targeted by positive selection in general. However, it is important to emphasize that population-based tests have a number of advantages over tests based solely on comparative data. Most importantly, they can detect ongoing selection acting on both negative and positively selected segregating variants. Additionally, although comparative methods for detecting selection have been applied to noncoding regions (e.g., Andolfatto 2005; Pollard et al. 2006), there are no available methods quite similar to the d_N/d_S ratio as putatively neutral and selected sites are not easily identifiable and interspersed among each other in noncoding data. Most population genetic methods are more easily applicable to noncoding regions. Although comparative methods may be most suitable to identify categories of genes generally affected by selection, and to quantify the amount of selection in the genome, some of the most interesting and important questions regarding selection in recent human history can only be addressed using population genetic data.

In this paper, we have not discussed issues regarding robustness of the tests. It is well known that tests based on the distribution of allele frequencies or the site frequency spectrum are highly sensitive to assumptions regarding demography (e.g., Nielsen 2005). Haplotype-based tests have not been evaluated systematically in this regard but are thought to be more robust (Frazer et al. 2007; Sabeti et al. 2007). Additionally, all the population genetic tests may show some degree of sensitivity to assumptions regarding recombination, and some of them may also not be entirely robust to assumptions regarding mutation rates and the mutational process more generally (e.g., Andolfatto 2001; Wall et al. 2002; reviewed in Nielsen 2005). When choosing methods for analyzing hypotheses regarding selection, it will be of importance both to consider issues relating to power, the topic of this study, and the robustness of the statistical tests.

Supplementary Material

Supplementary figure 1 is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).