Robust microcircuit synchronization by inhibitory connections

SUMMARY

Microcircuits in different brain areas share similar architectural and biophysical properties with compact motor network known as central pattern generators (CPGs). Consequently, CPGs have been suggested as valuable biological models for the understanding of microcircuit dynamics and particularly, their synchronization. In the present paper we use a well known compact motor network, the lobster pyloric CPG to study principles of intercircuit synchronization. We couple separate pyloric circuits obtained from two animals via artificial synapses and observe how their synchronization depends on the topology and kinetic parameters of the computer-generated synapses. Stable in-phase synchronization appears when electrically coupling the pacemaker groups of the two networks, but reciprocal inhibitory connections produce more robust and regular cooperative activity. Contralateral inhibitory connections offer effective synchronization and flexible setting of the burst phases of the interacting networks. We also show that a conductance-based mathematical model of the coupled circuits correctly reproduces the observed dynamics illustrating the generality of the phenomena.

INTRODUCTION

Grouping neurons into functional ensembles called microcircuits has been proposed as a way of understanding the complexity of the brain (Grillner and Graybiel, 2006). Of the many types of microcircuits that have been studied, those that generate oscillatory dynamics and regulate rhythmic behavior such as swimming or breathing, so called central pattern generators (CPGs), have been particularly important. These circuits display a remarkable capacity for producing a wide variety of temporally coordinated patterns of neural output in response to behavioral needs or changes in the environment. More recently, the idea of considering CPG microcircuits as a conceptual framework for understanding cortical microcircuits has been suggested because of the similarities they share both in their morphological and dynamical properties (Yuste et al., 2005). These, in particular, include the general features of oscillatory behavior which underlie many forms of cortical activity (Buzsáki, 2006).

A fundamental requirement for the concept of microcircuits to be practical is that they can be coordinated with one another. Such coordination or synchrony may be transient or permanent but there must be reliable connections for producing coherent activity among various microcircuits. Each microcircuit found in the cortex, brainstem or spinal cord, is composed of hundreds to thousands of individual neurons. The precise cell to cell connectivity of these circuits can at present only be approximated and the synaptic linkage between them is generally represented by enclosing each microcircuit in a box and connecting the boxes with coordinating axons. It remains extremely difficult to reveal the dynamical mechanisms of intercircuit coordination by direct experimentation in vivo or in vitro. What kind of synaptic topology provides the most reliable but still flexible coordination of the units? Are excitatory or inhibitory connections preferable when synchronization over a wide dynamical range is desired?

Motivated by these challenges we developed a novel experimental approach to study mechanisms of microcircuit synchronization. We performed dynamic clamp experiments on the lobster pyloric central pattern generator (CPG), which has been a prime experimental model of oscillatory neuronal networks (Marder and Bucher, 2007). We took two separate pyloric CPGs from two different animals and connected them via computer controlled artificial synapses. We explored the specific synaptic connections necessary for the coordination of the two networks. The basic network architecture of the pyloric CPG is similar to those in microcircuits of more complex nervous systems, too. Particularly, a pacemaker group, functioning as an excitatory core, is embedded in a pool of inhibitory neurons sharing many reciprocal synaptic connections. Because the detailed circuitry of the pyloric CPG is well understood, we could examine precisely what types of synaptic configurations are the most effective in synchronizing the two separate circuits. Our experiments allowed us to actively probe intercircuit synchronization in the most direct way, eliminating the possibility of interactions via unknown synaptic pathways. The identical architecture of the coupled pyloric networks allowed us to suggest general rules that may be important for predicting the cooperative dynamics present in other microcircuits. In addition to our biological experiments, we used computer modeling to analyze the synchronization of pyloric circuits. The computer simulations reproduced our experimental results remarkably well and suggested that the mechanisms of intercircuit coordination we observed are applicable to other systems.

RESULTS

The lobster pyloric network produces a characteristic three-phase motor pattern. The circuit consists of well-identified neurons displaying cell-type specific voltage waveforms (Fig. 1B). The functional core of the pyloric circuit is the pacemaker group, a cluster of three electrically coupled neurons. These are the single anterior burster (AB) and two identical pyloric dilator (PD) neurons (Fig. 1A). Burst oscillations generated by the pacemaker group impose an entraining effect on the rest of the pyloric neurons, which also possess intrinsic bursting properties but are less regular oscillators than the AB and the PDs (Abarbanel et al., 1996). Consequently, natural or experimentally induced changes in the cycle period of the pacemaker neurons strongly affect the activity of the whole pyloric circuit (Hooper, 1997). The PD neuron, being less fragile than the small AB neuron, is a more preferable subject for dynamic clamp experiments.

Figure 1.

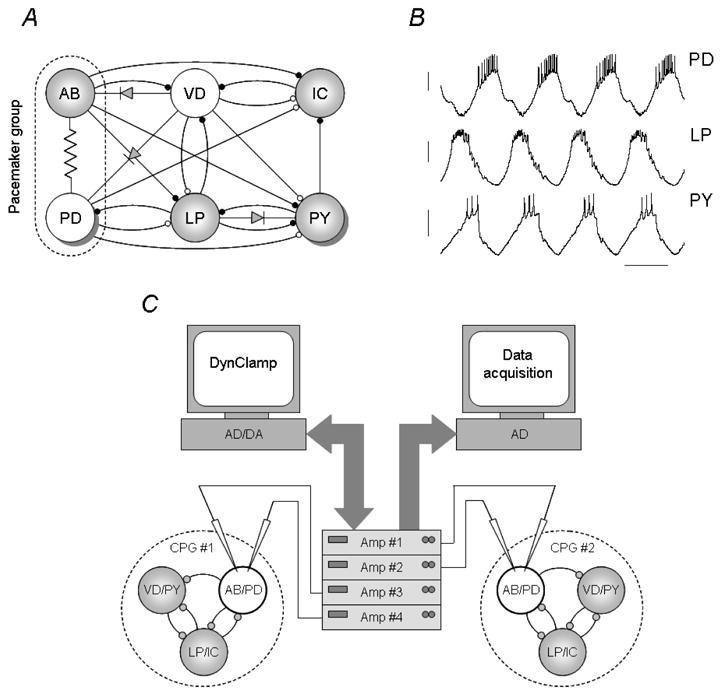
Connectivity of the lobster pyloric network and the experimental configuration used to couple two such circuits. The pyloric network consists of 14 identified neurons grouped in 6 groups (the PD and the PY neurons appear in 2 and 8 copies, respectively) (A). Cholinergic (white) and glutamatergic (gray) neurons are all inhibitory. Membrane voltage waveforms of the PD, LP and PY neurons (B). In a dynamic clamp experiment separate electrodes are used to measure the voltage output of the neurons and to inject the synaptic current (C). Here, PD neurons in both preparations are impaled with electrodes and a total of 4 intracellular amplifiers are connected to the computer running the dynamic clamp. A separate computer is used for acquiring the voltage output of the neurons.

When neuromodulatory inputs to the stomatogastric ganglion (STG) are kept intact, the pyloric oscillation appears as remarkably even. Yet, there are small variations in the long-term output of the network and they reflect synaptic interactions between the pyloric CPG and other circuits of the stomatogastric nervous system (e.g. the gastric modulation and cardiac sac episodes) (Ayali and Harris-Warrick, 1998; Bucher et al., 2006). In normal physiological saline and at 18 °C temperature the pyloric neurons produce nearly 2 bursts per second and this activity can be recorded for hours. In our experiments the observed mean burst cycle period was 0.517±0.013 s [mean ± S.E.M., n=29]. The degree of fluctuations caused by the gastric modulation (expressed as coefficient of variations of the mean values) was relatively small in our datasets: 3.6 ± 0.2 % for the burst cycle period [n=29]. Accordingly, separate pyloric networks from different animals would produce similar motor patterns although at slightly different frequencies.

Synchronization by electrical coupling of the pacemaker groups

Electrical coupling is an effective way of synchronizing the activity of neuron populations and has been observed in a wide range of neural systems (Connors and Long, 2004; Malyshev and Norekian, 2002; Perez Velazquez and Carlen, 2000; Tresch and Kiehn, 2000). In the STG, the 3 pacemaker neurons of the pyloric network are also electrically coupled and the neurons produce visually similar and tightly locked voltage waveforms.

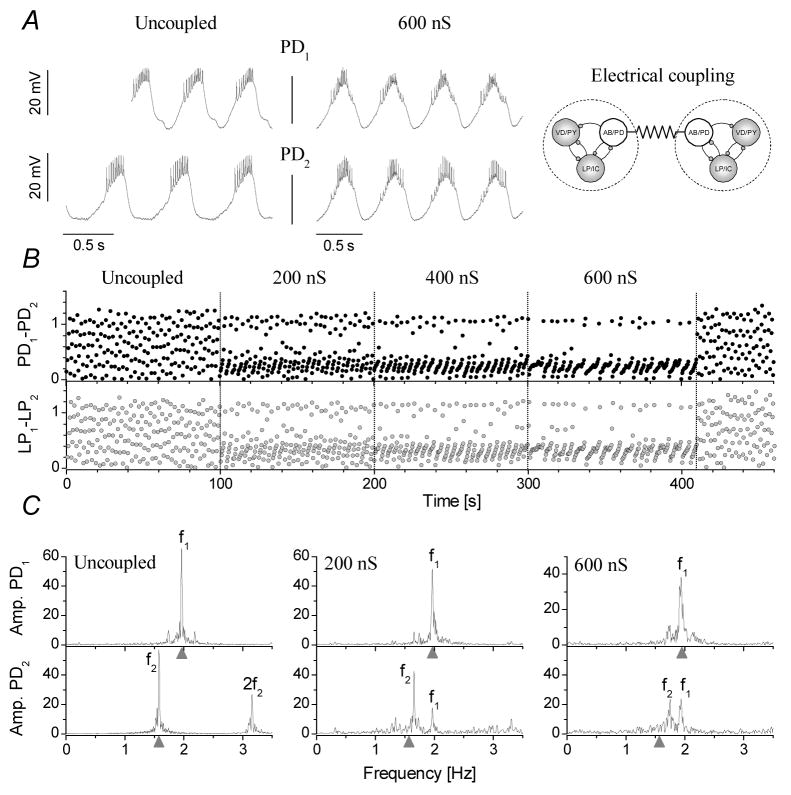
It is therefore intuitive to initially test the ability of electrical coupling of the pacemaker groups in synchronizing two pyloric CPGs. If synchronization of the pacemaker neurons occurs, would the other neurons of the two CPGs participate in an overall joint rhythm? To answer these questions, we first established electrical connections between the PD neurons of the two pyloric preparations. We varied the coupling strength by setting various levels of electrical conductance (100–600 nS) and analyzed the resulting burst patterns. Such epochs of electrical coupling lasted for 75–100 s. We used n_p=12 pairs of STGs in these experiments and coupled the circuits in n_e=80 separate epochs.

Depending on the relative difference between the intrinsic (free-running) frequencies of the preparations and the conductance of the electrical coupling, we observed either 1:1 phase-locked synchronization of the two pyloric circuits (n_s=30 epochs from a total of n_e=80) or asynchronized bursting with drifting phases between the PD neurons. There was a clear tendency toward tighter synchronization with stronger connections and with less difference between the intrinsic burst frequencies of the free-running CPGs. Fig. 2 shows an example of such experiments. In control conditions when the PD neurons are uncoupled, the preparations run at different burst frequencies (f₁ and f₂, Fig. 2C). Correspondingly, the relative burst phases of the PD neurons are drifting in an uncorrelated manner (Fig. 2B, Uncoupled). Connecting the PDs and increasing the coupling strength decreases the dispersion of phases (Fig. 2B). Fourier-amplitude spectra calculated from the two PD neurons’ spike density functions contain marked peaks at the intrinsic burst frequencies before coupling (Fig. 2C, left). When electrical connection between the PDs is established the spectra contain peaks at the burst frequencies of both preparations (Fig. 2C, middle, right). As the coupling strength is gradually increased, the peaks of the intrinsic burst frequencies f₁ and f₂ move closer and they merge when 1:1 phase-locking is achieved. When the synchronization occurs, the two pacemaker groups produce tightly locked bursts and they become a functionally uniform neural oscillator. The follower neurons of the two preparations such as the LP and PY neurons synchronize with their own pacemaker groups and maintain their original phase-relationships. At the same time, LP neurons in the two preparations, although not directly coupled, become synchronized, too (Fig. 2B).

Figure 2.

Synchronization of two pyloric CPGs through electrical coupling of their pacemaker groups requires a strong connection. The burst waveforms of the two PD neurons are shown in A in control (Uncoupled) and when they are coupled with 600 nS electrical connection. B shows the relative burst phases between the PD and LP neurons from the two networks as a function of the elapsed time. The strength of the connection was increased in discrete steps from 0 nS to 600 nS. The phases show clustering with stronger connections, however, clear 1:1 synchronization is not achieved in this example. The panels in C are Fourier amplitude spectra calculated from the PD neurons’ spike density time series. f₁ and f₂ are the burst frequencies of the first and second preparations, respectively. Even at 600 nS the frequencies of the preparations are slightly different. Gray triangles mark the intrinsic (uncoupled) burst frequencies for PD₁ and PD₂.

Synchronization by mutual inhibition between the PD neurons

Pyloric neurons, all of which have conditional bursting properties, are commonly arranged in a mutually inhibiting configuration. In these neural circuits regular rhythmic activity is produced by bursting neurons forming reciprocal inhibitory synaptic loops (Marder and Calabrese, 1996) and the interacting neurons are often referred to as half-center oscillators. Reciprocal inhibition is also common in vertebrate motor systems such as the respiratory (Smith et al., 2007) or locomotory (Mentel et al., 2008) CPGs and appears as a basic architectural feature for oscillatory neural circuits.

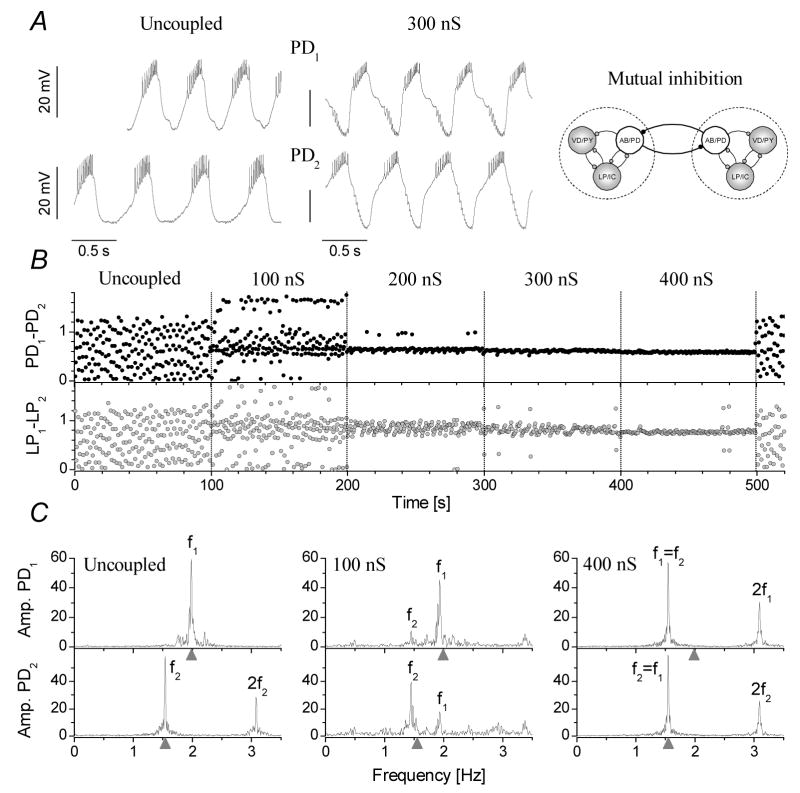
In the following set of experiments we established mutual inhibitory connections between the pacemaker groups of the two pyloric CPGs (n_p=17, n_e=163). The artificial synaptic connection was set in a way to obtain both spike mediated and graded inhibition in the postsynaptic cell. Fig. 3 demonstrates the synchronization of two pyloric CPGs in one of these experiments. As a general rule, reciprocal inhibition turned out to be more effective in synchronizing the pyloric circuits than the electrical coupling (n_s=82). The interconnected PD neurons together with their electrically coupled AB/PD neurons formed a complex half-center oscillator containing a total of 6 cells. The coupled PD neurons were bursting regularly in a phase close to 0.5 (180°). 1:1 anti-phase oscillations started at maximal conductances from 50–200 nS and maintained at stronger connections (Fig. 3B). The frequency of the joint oscillation f_joint (i.e. when f₁=f₂) depended both on the intrinsic frequencies and the strength of the connections. Commonly, the burst frequency of the joint network was close to that of the intrinsically slower preparation and our model simulations predicted the same behavior for this configuration (described later). Systematic, independent variation of the two maximal conductances (PD₁-PD₂ and PD₂-PD₁) showed that the phase-relationships of the two pacemaker groups had only a weak dependence on the strength of these connections, the relative phases always being close to 0.5. At the same time, the intrinsically slower PD neuron tended to start its burst later that the opposite PD neuron. Consequently, when the intrinsically faster PD neuron was used as reference, the relative burst phase was higher than 0.5 in the synchronized circuits (Fig. 3B). The Fourier-analysis revealed that mutual inhibitory connections not only resulted in stable anti-phase synchronization of the pyloric circuits, but their oscillations became more regular, too (Fig. 3C).

Figure 3.

Mutual inhibitory coupling of the pacemaker neurons effectively synchronizes the pyloric CPGs. A: membrane potential waveforms of the two PD neurons in the free-running preparations and when synchronized through 300 nS inhibitory coupling. B shows the relative phases between the PD and LP neurons against the time of experiment. The strength of the connection was increased in discrete steps from 0 nS to 400 nS. The panels of C show the Fourier amplitude spectra calculated from the PD neurons’ spike density data. f₁ and f₂ are the burst frequencies of the first and second preparations, respectively. Stable 1:1 phase-locked synchronization appears at 300 nS and above. Skipping behavior is occasionally observed at 200 and 300 nS.

Contralateral inhibition from the LP neurons to the pacemakers

A third possible route to synchronization was to connect the circuits via non pacemaker cells. One of those, the lateral pyloric (LP) neuron is an important component of the pyloric network, because it provides the only phasic input to the pacemaker group. The LP delivers potent glutamatergic IPSPs to the PD and this inhibition acts to stabilize the burst cycle period of the pacemaker (Mamiya and Nadim, 2004). The time course of the rebound depolarization in the PD neuron depends on the degree and duration of the LP-inhibition. Hence, the LP neuron plays an important regulating role in the operation of the pacemaker group and therefore affects the entire pyloric motor output.

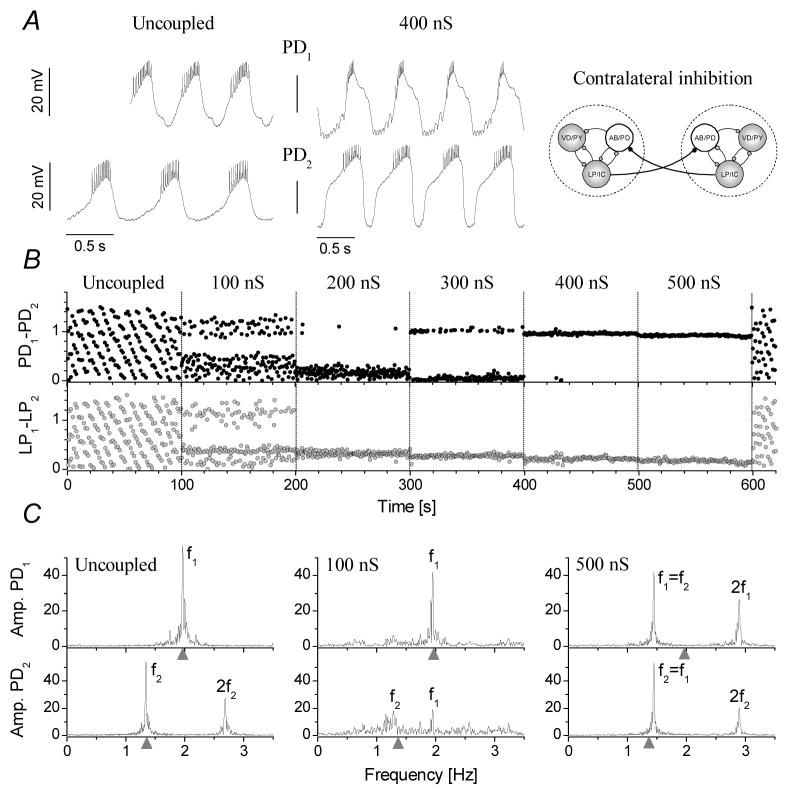
In the following experiments we used the LP neurons of both CPGs to mediate contralateral inhibition to the pacemaker groups in both preparations (n_p=11, n_e=90). Consequently, this experimental configuration doubled the number of PD neurons postsynaptic to each of the LP neurons. Hence, a burst in any one of the two LP neurons would simultaneously inhibit the PD neurons in both preparations. Would this concurrent inhibition of the pacemaker groups synchronize the activity of the two CPGs? Indeed, this is what we observed in the experiments. Fig. 4 demonstrates the burst patterns and relative phases of the two PD neurons under the action of inhibitory inputs from the LP neurons in the opposite circuit. Synchronization of the two CPGs was observed at conductances as low as 200 nS with a gradual increase in the phase-stability with stronger connections (n_s=48). Similarly to the mutual inhibition of the PD neurons, the joint oscillations were regular and periodic with sharp peaks in the Fourier-spectra. The frequency of the joint oscillations in the synchronized regime was closer to that of the intrinsically slower preparation. Nevertheless, f_joint depended on the intrinsic burst frequencies and the strength of the simulated LP-PD connections in a non-trivial manner. Changing the maximal conductances of the simulated LP-PD synapses caused apparent jumps in the phases of the two PD neurons. Independent variation of the two conductances also revealed a wide range of PD₁–PD₂ phases in the resulting joint rhythms. In this respect, the contralateral feedback inhibition of the PD neurons by the LP neurons not only effectively synchronized the two circuits, but it was also more flexible in setting the phases of the CPGs. We note that the simulated LP-PD connections are unidirectional; hence, there is no direct feedback from the PD neuron to the LP neuron in the opposite CPG. In this respect, it might be surprising that this synaptic configuration still proves to be successful in synchronizing the two circuits. Yet, there is a polysynaptic feedback pathway in the joint circuit, which transmits information from the PD neuron to the LP neuron in the opposite CPG. In both CPGs the PD neuron delivers (natural) cholinergic inhibition to its own LP neuron. This LP inhibits the alternate PD neuron via the dynamic clamp connection. In turn, the PD neuron receiving this inhibition will inhibit its own LP neuron. Hence, this complex feedback loop incorporates 4 neurons with 4 inhibitory synaptic connections and it works in both directions.

Figure 4.

Contralateral inhibition of the PD neurons effectively synchronizes the pyloric CPGs. A: burst oscillations of the two PD neurons in the free-running preparations and when receiving inhibition from the opposite preparations LP neuron through 400 nS inhibitory coupling. B: The phases of the PD and LP neurons display gradual shifts with increasing coupling strengths. Fourier amplitude spectra of the two PD neurons are shown in C in control and when receiving inhibition from the alternate LP neuron with different strengths (100 and 500 nS).

Joint burst frequency, phase entropy and zones of synchronization

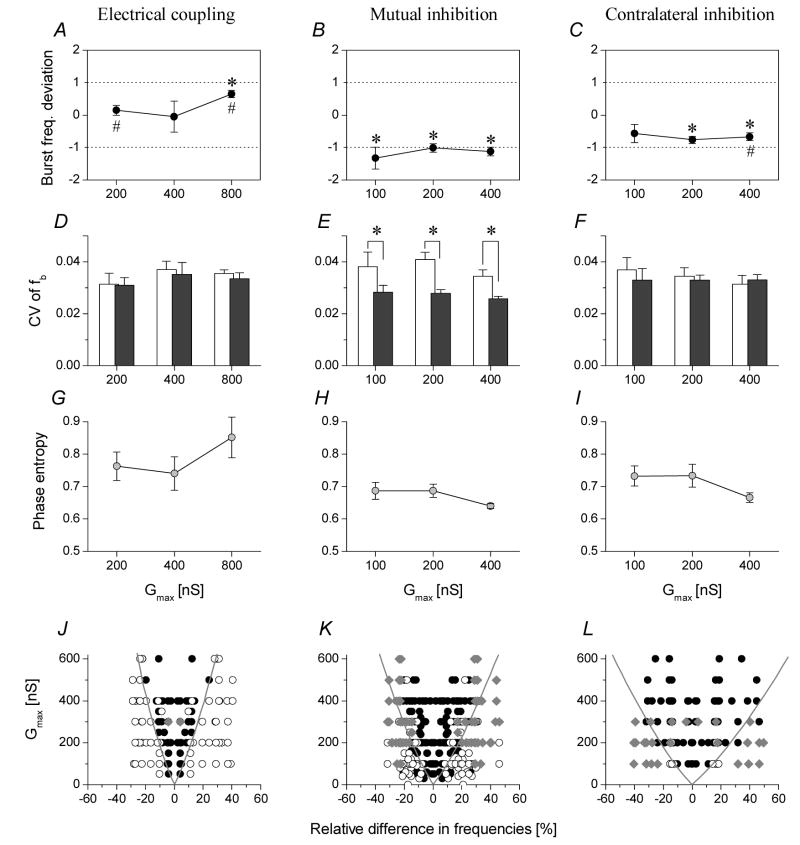
In motor systems the frequency and phasing of the interconnected CPGs are functionally critical parameters. Hence, it is also important to analyze the frequency, regularity and relative phasing of the motor patterns of coupled oscillators and the dependence of such parameters on the type of synaptic interconnections. As noted earlier, the difference between the intrinsic burst frequencies of the two preparations strongly affects whether the networks can synchronize and at what conductances. Apparently, pyloric circuits with widely different burst frequencies require stronger connections for synchronization. In the uncoupled preparations we observed relative differences between the f₁ and f₂ frequencies over a ±50 % range. To quantify the dependence of f_joint on the intrinsic burst frequencies and the type of synaptic interconnections, we introduced a parameter called the burst frequency deviation (BFD). This parameter indicates how f_joint differs from the arithmetic mean of the two intrinsic burst frequencies (f₁+f₂)/2. We compared this parameter for the three different types of coupling, different strength of connections and across preparations. As expected from our earlier observations, the BFD was close to zero for the electrotonic coupling indicating that f_joint was close to the mean of the two intrinsic frequencies (Fig. 5A). Here, the two pyloric CPGs change the frequency of their burst oscillations in the same degree but in opposite directions. When using strong electrical coupling (800 nS), we found that the BFD was significantly higher than zero (n_p=4, n_e=4) suggesting that the joint burst frequency got closer to that of the intrinsically faster preparation. As for the mutual inhibitory configuration, the BFD values were consistently negative. This observation shows that the burst frequency of the joint circuit is mainly determined by the inherently slower pacemaker and this is also verified by our model simulations. Here, the BFD values are found to be significantly different from zero but not different from −1 at p<0.05 level (one-sample t-test, n_p=6, n_e=9), corresponding to the burst frequency of the slower PD (Fig. 5B). Regarding the LP-PD contralateral connections, the BFD values are also negative, but slightly less than those for the PD-PD connections (BFD<0 for G_max=200 and 400 nS, p<0.05, n_p=5, n_e=9).

Figure 5.

Comparison of the three synaptic configurations’ performance in synchronizing the pyloric CPGs. All burst parameters were calculated from the time series of PD neurons. The panels in the top row show the burst frequency deviation parameter (mean ± S.E.M.) for increasing strengths of coupling (A–C). #: mean<>-1; *: mean<>0, p<0.05, one-sample t-test. Middle row: coefficient of variations of burst frequencies for the free-running preparations (white coumns) and for the synchronized joint circuits (gray columns, mean ± S.E.M.) (D–F). Significant regularization of burst frequency is observed for the PD-PD inhibitory configuration (*: p<0.05, paired t-test) (E). Bottom row: phase entropy values of the synchronized burst patterns (G–I). The electrotonic coupling (G) yields higher entropies than the inhibitory configurations (H and I). Zones of synchronization for the three synaptic configurations are shown in J–L. Different symbols indicate different regimes of cooperative dynamics. Black circles: phase-locked synchronization; Empty circles: drifting burst phases; Gray diamonds: irregular dynamics with frequent phase-resetting. Boundaries of the approximate regions of the 1:1 phase-locked modes (black circles) appear as cones. The zone of synchronization is the widest for the LP-PD contralateral inhibition.

As shown earlier, successive burst cycle periods, or, analogously, instantaneous burst frequencies (f_b) display some level of fluctuation in normal conditions and also when the CPGs are connected. The coefficient of variations (CV) is a convenient parameter to quantify the regularity of bursting and the accuracy of frequency-synchronization. While electrical coupling of the pacemakers and the LP-PD contralateral configuration did not change the regularity of bursting (Fig. 5D, F), a significant drop of CV values was seen with the PD-PD reciprocal configuration (Fig. 5E). This clearly shows that the reciprocal inhibitory connection between the pacemakers of the pyloric networks effectively dampens the intrinsic fluctuations in burst frequencies of the component networks and the joint system will be more periodic than the uncoupled CPGs. Regarding the accuracy of phase-synchronization we find that stronger coupling of the pyloric circuits leads to smaller dispersion of relative burst phases (e.g. Fig. 3B). The degree of regularity is well characterized by the phase entropy parameter. This parameter also quantifies the peakedness of the frequency distribution of relative phases. Precise synchronization would yield low entropy while a uniform distribution of relative burst phases (i.e. uncorrelated bursting) would result in the maximal entropy: equal to 1, due to normalization. The phase entropy is the lowest for the PD-PD inhibitory configuration. Increasing the strength of connections decreases the phase entropy in the PD-PD and LP-PD inhibitory configurations, but does not when using the electrical coupling (Fig. 5G).

As the final step of our analysis we created a series of diagrams by scatter-plotting the maximal conductance of the synaptic connection (as set by the experimenter) against the normalized difference between the intrinsic burst frequencies of the preparations. This latter parameter takes two values for each pair of frequencies and is calculated as

$$\frac{f_2-f_1}{f_1},\text{or}\frac{f_1-f_2}{f_2}.$$

This type of scatter plot contains as many as two times the number of experimental trials (with fixed maximal conductances within trials). Data point symbols are set according to the observed dynamics of the coupled system. Points with 1:1 phase-locked synchronization are black circles. The efficiency of the various artificial synaptic connections in coordinating the two pyloric CPGs is clearly shown by the extent of the zone of synchronization, i.e. the area occupied by the black points. Fig. 5J–L show the data for the three synaptic configurations described above. The LP-PD inhibitory configuration exceeds the electrical coupling and the mutual inhibition between the PDs. Interestingly, the V-shaped areas appearing in these diagrams are similar to Arnold’ tongues describing the dynamics of nonlinear oscillators under the action of periodic forcing (Szücs et al., 2001). Comparing the regions outside of the zone of synchronization we find that weak (sub-synchronization) electrotonic coupling typically gives rise to drifting behavior (quasiperiodicity) while more complex dynamics is observed with weak PD-PD inhibitory or LP-PD connections.

Synaptic configurations unable to synchronize the networks

Our experiments showed that contralateral feedback connections to the two pacemaker groups perform well in synchronizing the pyloric CPGs. Recognizing the ability of the LP neurons in coordinating the two pyloric CPGs we decided to test two additional synaptic configurations involving the LPs. We examined the possibility whether coupling the LP neurons via dynamic clamp without directly stimulating the PD neurons could synchronize the two circuits. We have already shown that sufficiently strong electrical connections between the PD neurons can phase-lock their activity and eventually synchronize the two CPGs. We would expect that connecting the LP neurons in a similar manner would then synchronize them as well. To test this idea we established an artificial electrical connection between the two LPs with conductances ranging from 100 to 600 nS (n_p=5, n_e=85). As expected, the electrical connection resulted in gradually more similar voltage waveforms in the two LP neurons with increased coupling strength. In this respect, the two LPs started behaving as a joint neural oscillator. Nonetheless, this configuration failed to synchronize the pacemaker groups and the two CPGs (n_s=0). Instead, the PD neurons kept their intrinsic burst frequencies and remained bursting as independent oscillators. It is therefore not sufficient to synchronize only the two LP neurons in order to phase-lock the two pacemaker groups and both CPGs. Due to the mismatch in the burst frequencies of the individual pacemaker groups and their synaptic effects on their own LP neurons, the voltage waveforms of the coupled LP neurons became irregular. The reason of such irregularity is that the LP neuron in preparation #1 receives natural inhibition from the PD neuron at frequency f₁ as well as an electrical input from the LP neuron in the pyloric circuit #2 at the frequency f₂ (not matching f₁).

In the next set of experiments we tested reciprocal inhibitory connections between the LP neurons established in a way similar to the PD-PD inhibition (n_p=4, n_e=43). Our anticipation was that the two LP neurons could form a half-center oscillator and initiate a regular anti-phase bursting effectively leading to anti-phase synchronization of their PD neurons, too. In fact, this configuration also failed in synchronizing the two pyloric networks (n_s=0). The two LP neurons displayed competing rather than cooperative behavior resulting in irregular, subthreshold oscillations and occasionally sharp rebounds in their activity under dynamic clamp. Not surprisingly, this behavior also prompted characteristic disruptions in the PD neurons’ rhythmic activity and synchronization was never achieved.

Like the LP, the ventricular dilator (VD) neuron strongly influences the activity of the pacemaker cells and the other postsynaptic pyloric neurons in the normal bursting preparation. There is a strong cholinergic inhibitory connection from the VD to the LP neuron (Fig. 1A). Besides, the VD neuron is weakly connected to the PD and AB neurons via electrical coupling. In the following experiment we tested the possibility that connecting the VD neurons from two separate pyloric circuits could lead to their synchronization. This experiment essentially showed the same kind of behavior as seen with the LP-LP coupling. Synchronization of the separate pacemaker groups was never achieved and there was only a weak correlation between the VD activity and the rest of the neurons (n_p=1, n_e=8, n_s=0).

Modeling the coupled pyloric circuits

We observed various modes of synchronization of two pyloric circuits under the action of specific inter-network connections, but whether these results can be generalized to other microcircuits remains to be tested. Also, it would be important to know how the biophysical properties of the neurons or their intra-network connections determine the observed modes of synchronization. To address this problem first we built a computational model of the pyloric circuit. We then coupled two such model circuits through synaptic connections as we did in our experiments. The computational model allowed us to adjust the intra- and inter-network parameters over a wide range and with much finer resolution than that was possible in the biological experiments. The model not only correctly reproduced the observed modes of synchronization but also showed that they were robust against manipulation of the intrinsic cellular properties and the strength of intra-network connections. Our reduced mathematical model of the CPG consisted of 3 ‘lumped’ neurons representing the 3 main phases of the motor pattern. Here, the PD, LP and PY neurons were connected via chemical inhibitory connections in a way that was topologically equivalent to that in the biological system. The model pyloric network reproduced several features of the voltage output of the real system including the overall shape and phasing of the bursts of the component neurons (Fig. 6A).

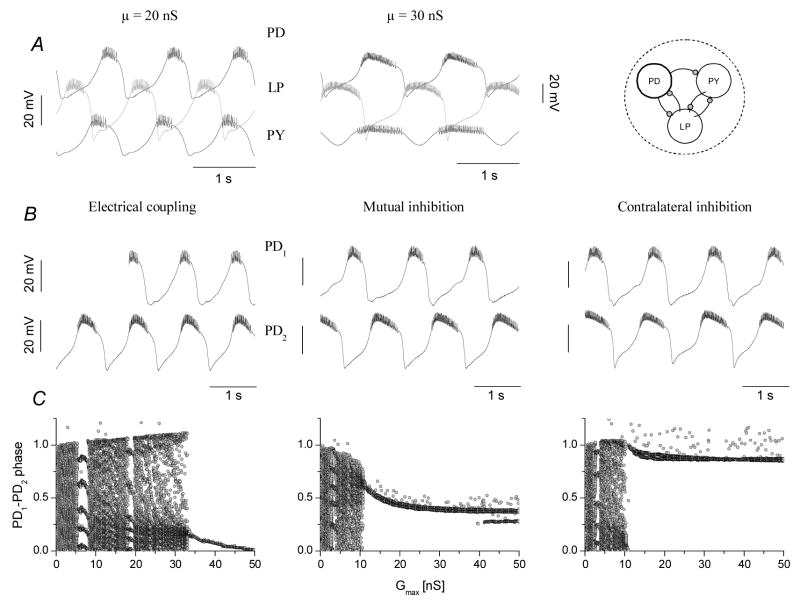
Figure 6.

The model pyloric circuit reproduces the modes of synchronization observed in the experiments. Depending on the strength of intra-network connection (μ) the circuit can operate in a faster three-phasic pattern or in a slower, two-phasic mode (A). Voltage traces of the coupled PD₁ and PD₂ neurons are shown in B (50 nS for the electrical and 40 nS for the two inibitory configurations). Electrical coupling of the circuits (left) brings the PDs into in-phase oscillations, similarly to the LP-to-PD contralateral inhibition (rightmost). Mutual inhibition (middle) results in anti-phase burst patterns. Panels of C show the relative burst phases as a function of the coupling strength. Synchronization occurs when the scattered point clouds collapse into narrow populations (bifurcation). Chaotic or quasiperiodic dynamics is observed before reaching the bifurcation point. Synchronization of the electrically coupled circuits arrives at stronger connections than that in the other two configurations. In-phase synchronization yields relative burst phases close to 0 (electrical) or 1 (contralateral), depending on which PD neuron is the leading one. Anti-phase bursting yields a burst phase close to 0.5 (mutual inhibition).

The burst frequency of the circuit was adjusted through the μ parameter, i.e. setting the strength of intra-circuit connections globally. Stronger intra-network connections resulted in a slower motor rhythm, but also induced phase shifts in the voltage output of the neurons. Consequently, low and high μ values produced either normal, pyloric-like 3-phasic oscillations or a two-phasic output (Fig. 6A). Coupling two model circuits was done by simulating internetwork connections of the kind used in our biological experiments. In the example of Fig. 6 we set μ=20 nS for CPG₁ and μ=30 nS for CPG₂. Therefore, CPG₁ displayed faster oscillations than CPG₂ prior to coupling. Electrical, mutual inhibitory and contralateral inhibitory configurations resulted in periodic and synchronized burst oscillations in the joint networks. Electrical coupling and contralateral inhibitory configurations facilitated in-phase synchronization while mutual inhibition of the PD neurons led to anti-phase synchronization (Fig. 6B). The model simulations nicely reproduced the qualitative patterns we observed with the biological system. Additionally, the strength dependence of inter-network burst phasing was also similar to that we observed in the real CPGs. Fig. 6C demonstrates how relative burst phases of the PD₁ and PD₂ neurons depend on the coupling strength for the 3 configurations. Here, the maximal conductance of the inter-circuit connections was gradually increased from 0 to 50 nS. The three scatter plots all display clear bifurcations when the two interconnected circuits begin synchronizing. Remarkably, electrical coupling requires higher strength than the two chemical inhibitory configurations to synchronize the CPGs – again, in agreement with the biological experiments.

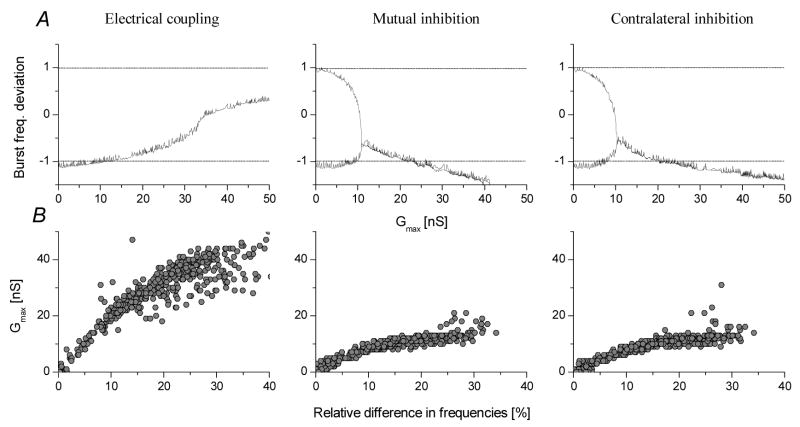
Regarding the burst frequencies of the joint circuits, we found that the mathematical model showed essentially the same behavior as we observed in the experiments. Fig. 7A displays the burst frequency deviation parameter as a function of the coupling strength for the three simulated configurations. Here, we used one pair of CPGs and increased the coupling strength of their connections in small steps. With no coupling, the inherently slower preparation corresponds to the −1 value, the faster one comes to +1. The burst frequencies of the two circuits are initially different but move closer together and eventually merge at the bifurcation point, i.e. when the coupling gets strong enough for synchronization. Increasing the coupling strength above the bifurcation moves the BFD curve into different directions depending on the type of the synaptic configurations. In the first case (electrical coupling), the BFD parameter slightly increases and remains above zero indicating that the inherently faster preparation has a stronger effect on the opposite one than vice versa. The mutual inhibitory configuration behaves differently, because the deviation parameter has a negative slope and moves below −1. Here, the intrinsically slower preparation determines f_joint. A similar effect is seen with the LP-PD contralateral configuration, however, the curve is less steep than for the mutual inhibition. Hence, the model correctly reproduces the burst frequency dependence of the coupled biological circuits (see Fig 5A for comparison).

Figure 7.

Bifurcation diagrams for the burst frequency reveal a cooperative dynamics similar to that observed in the biological circuits. In A, the burst frequency deviation parameter is plotted against the maximal conductance of the inter-network connection. Synchronization occurs when the slower and faster circuits equalize their burst frequencies and the curves merge in the bifurcation point. In electrical coupling configuration the joint burst frequency exceeds the arithmetic mean of the intrinsic f_Bs and gradually increases with G_max. The two inhibitory configurations display negative slope curves after the bifurcation points. Here, f_joint is set by the intrinsically slower circuit (the deviation parameter being close to −1 or below). Panels of B show the threshold conductances corresponding to the locations of the bifurcation points in 436 pairs of circuits each having different intrinsic burst frequencies. These graphs are analogous to the zone separating lines in Fig. 6 but are shown only for positive relative differences.

As the bifurcation diagrams of the relative burst phase and the BFD parameter show, the chemical inhibitory configurations are more effective in synchronizing the circuits than the electrical coupling. Is this valid also when the intrinsic burst frequencies of the model circuits vary in a wide range? By adjusting the global strength parameter μ of the intra-network connections, we were able to simulate many pyloric circuits running at different frequencies. A total of 436 pairs of them were coupled and their bifurcation diagrams were calculated. Fig. 7B shows the conductance threshold of synchronization (location of the bifurcation) as a function of the relative difference between the intrinsic burst frequencies. Hence, any conductance value above the critical values would result in synchronization of the two circuits. These diagrams show a similar behavior as seen on Fig. 5: electrical coupling requires stronger connections for synchronization than the two inhibitory configurations. Hence, the zone of synchronization (i.e. the area above the scattered points) is much wider for the inhibitory connections than for the electrical coupling. Our extensive datasets from the simulations also show that the dynamics and bifurcation properties of the joint circuits remain consistent when different μ parameters are used to set the intrinsic burst frequencies of the two networks.

DISCUSSION

Recent progress in systems neuroscience has shown that complex microcircuits of the brain and spinal cord have architectural and biophysical properties similar to those in compact motor networks (Grillner and Graybiel, 2006). Furthermore, synchronization of neural networks appears to be a widespread dynamical phenomenon linking separate groups of neurons into larger functional assemblies (Engel et al., 2001; Varela et al., 2001). In this respect, our experiments and model simulations with coupled pyloric networks might predict principles of intercircuit synchronization applicable to larger neural populations. Our results suggest that target-specificity of the intercircuit connections is one of the most important factors determining the robustness of synchronization (Table 1). Furthermore, inhibitory topologies provide more flexible and reliable synchronization of oscillatory networks than electrotonic coupling of the rhythm generating neurons.

Table 1.

A summary of the various synaptic connections and their performance in synchronizing the pyloric circuits. Tested configurations are shown in the leftmost column. Description of the other columns is as follows: Synch: qualitative efficiency of the configuration in synchronizing the circuits (checkmarks or crosses: promoting or not respectively); Regular: regularity of the burst oscillations in the coupled circuits (checkmarks: improving, crosses: worsening); Mode: in-phase or anti-phase synchronization (up-up or up-down arrows respectively); Dev. f_b: average deviation of burst frequency across three connection strengths; ΔCV: relative change of the coefficient of variation of burst frequency expressed as a percentage; Remark: a general description of the observed dynamics.

Config	Synch	Regular	Mode	Dev. fb	ΔCV	Remark
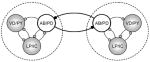
	✓	✓		+0.25	− 4%	Mutual ‘periodic forcing’ of the pacemaker groups
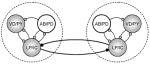
	✓	✓✓		− 1.15	− 28%	Regular rhythm but inflexible phasing of the coupled circuits
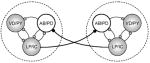
	✓✓	✓		− 0.66	− 3%	Robust and flexible synchronization depending on synaptic strenght
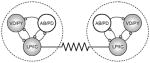
	✘	-	-	-	-	Pacemaker groups partially decouple from the LPs
	✘	✘	-	-	-	Competition between the LPs, ‘escape’ behavior, phase resetting
	✘	-	-	-	-	Very weak effect on the pacemakers

Using artificial synapses to study CPG network dynamics

The dynamic clamp technique has become a valuable experimental tool to manipulate synaptic and intrinsic biophysical properties of biological neural systems as well as to create hybrid circuits of living and artificial neurons (Le Masson et al., 2002; Oprisan et al., 2004; Prinz et al., 2004). Using this technique to study intercircuit coordination of neural oscillations, while a novel approach, offers several advantages over more traditional methods. Fully controllable artificial synaptic connections can be inserted into selected neurons in a network without disrupting the function of the existing biological connections. When connecting neural networks from two animals, the dynamic clamp establishes the only channel of communication between the two biological systems.

The artificial synaptic connections we established between the two CPGs resembled in many aspects to those existing within the pyloric network and already known to be crucial in regulating the frequency and phasing of the neuronal oscillations. However, a specific synaptic topology known to be effective in synchronizing neurons within one pyloric network might not be necessarily effective in coordinating two such networks. Consequently, coupling similar CPGs via artificial synaptic connections can reveal novel principles of network coordination. Our experiments have shown that even a small number of synaptic connections between CPGs can synchronize their activity when appropriate parameters are used. Electrical coupling of the pacemaker groups acted as mutual periodic forcing of neural oscillators with slightly different intrinsic frequencies (Szücs et al., 2001). While in-phase synchronization did occur with strong electrical coupling between the PD neurons, this configuration appeared sensitive to perturbations from extrinsic synaptic sources (such as CS episodes) and the joint oscillation was less regular than that observed with the inhibitory chemical connections. Despite the obvious simplicity of using electrotonic connections to synchronize two separate networks, the fact that the CPGs may be separated anatomically would make electronic connections impractical. In principle, chemical excitatory synapses could also be used to synchronize two motor circuits. Such excitatory synaptic connections have been already demonstrated in locomotor networks (Cangiano and Grillner, 2003). Weak unilateral excitation might force the follower circuit to become entrained to the driver circuit. Reciprocal excitation, especially when synaptic strength is large, however, can cause instabilities due to positive feedback. Indeed, the few times we attempted excitatory connections they produced unstable synchronization and ‘runaway’ burst oscillations. The failure of mutual excitation in synchronizing the pyloric CPGs is mainly due to the strong intrinsic bursting properties of the pacemaker neurons. Hyperpolarizing, voltage-dependent membrane conductances in reciprocal configuration are easily overtaken by the potent excitatory input from the opposite network leading to unstable behavior.

Inhibitory interconnections offer the best way for synchronization

A synaptic topology with reciprocally inhibiting PD neurons produces regular anti-phase burst oscillations in the connected networks and the joint oscillation is usually more regular than those observed in the separate networks. This finding highlights the importance of inhibitory synapses in intercircuit coordination and nicely ties in with earlier data on rhythm generation in compact neural circuits (Szücs et al., 2000). Hence, reciprocal inhibition appears not only as a fundamental building block for CPG networks (Friesen, 1994), but also as a neural mechanism effectively synchronizing larger populations of neurons (Wang, 2002). While stable synchronization is readily obtained in such configurations, the phases of the interacting PD neurons bursts weakly depend on the strength of the connections. In this respect, reciprocal inhibition of the pacemaker groups does not appear as an optimal topology when the phasing of the component neurons is expected to be set over a wide range. As our experiments with the LP-PD contralateral inhibition have shown, an indirect connection between the pacemaker groups performs better in that respect. Here, the synaptic feedback loop between the two CPGs involves more steps than in the direct configurations (PD-PD). As a result, the phasing of the two PD neurons and the follower neurons is determined by a number of synaptic as well as cellular parameters.

The failure of the LP-LP connections in synchronizing the pyloric circuits was somewhat unexpected. As demonstrated earlier, the natural input from the LP neuron to the PD neuron greatly affects the phasing and frequency of its burst (Mamiya and Nadim, 2004). However, it is well known that the pacemaker group can generate a stable rhythmic burst pattern even in the absence of the LP input. The burst frequency of the PD neuron appears slightly higher when the natural LP-input is absent (Bal et al., 1988; Mamiya and Nadim, 2005). When coupling two preparations, the burst frequency of the LP neurons will be initially determined by their own pacemaker neurons. Here, one of the LP neurons will burst intrinsically faster than the PD neuron in the opposite preparation. When the two LPs are coupled via electrical connection, they synchronize their voltage output, but become irregular, too. In such conditions the LP-PD synapses will likely show different amount of frequency-dependent depression in the opposite networks (Manor et al., 1997). As a result, the postsynaptic effects of the LP neurons on their PD neurons become weaker preventing the synchronization of the two networks.

Comparison with other motor systems

Coordinating unit CPGs bilaterally and intersegmentally are often accomplished by coordinating interneurons that in some cases are considered part of the rhythm generating mechanism (Buchanan, 1999; Cangiano and Grillner, 2005; Grillner, 2003). A good example of intersegmental coordination, the leech heart network contains rhythm generating interneurons in adjacent segments, which are coupled via coordinating fibers descending from an anterior ganglion (Peterson, 1983). While the leech heart segmental oscillators are not directly connected, their bursting is synchronized because they receive concurrent inhibition from the coordinating fibers (Masino and Calabrese, 2002). The LP-PD contralateral inhibitory configuration as tested in our experiments shows some resemblance to this circuitry. Indeed, both in the coupled pyloric networks and in the leech heart network the rhythm generating neurons produce nearly in-phase oscillations. At the same time, the joint burst frequency in our LP-PD and PD-PD configurations tended toward the one of the inherently slower oscillator unlike that in the leech circuitry where the inherently faster oscillator dominated the joint rhythm. Depending on the relative phase of the inhibitory input to the PD neuron its subsequent burst can be phase delayed or phase advanced. The phase response curve of the PD neuron as measured in dynamic clamp experiments shows that an inhibitory input arriving in a late phase of the burst cycle delays the next burst (Prinz et al., 2003). Consequently, the intrinsically slower PD (or LP) neuron delivers late-phase inhibition to the PD neuron in the opposite circuit and effectively decreases its burst frequency. Hence, the shape of the phase response curve and the duty cycle of the interconnected neurons largely determine the joint burst frequency of the coupled system. Regarding the biophysical mechanisms promoting such synchronization and the phase maintenance of the oscillations it is likely that the transient K-current I_A plays an important role (Greenberg and Manor, 2005). The PD neuron reportedly displays strong I_A (Tierney and Harris-Warrick, 1992), which current gets de-inactivated under the action of potent pre-burst inhibitory input, such as the one arriving from the opposite pyloric circuit in the PD-PD and LP-PD configurations. The voltage dependent activation of the A-current, in turn, delays the onset of the subsequent PD burst effectively decreasing the burst frequency. Model simulations of the inter-network synchronization such as those we performed can help better understanding these biophysical mechanisms. We have already performed a few preliminary studies in this direction. In this respect it is notable that removal of the A-current from the neurons of the interconnected model pyloric circuits does not destroy the synchronization but it requires stronger connection for the PD-PD inhibitory configuration. Additionally, the joint burst frequency of the coupled circuit will be higher in I_A-free circuits than in normal conditions.

Coordinating fibers have been shown to be responsible for maintaining proper phase relationships between different body segments or appendages on those segments. Crayfish legs and swimmerets for example produce a metachronal wave that has to be coordinated from segment to segment (Jamon and Clarac, 1995; Mulloney et al., 1998). The underlying cellular connectivity has been approached both experimentally and theoretically using modeling techniques (Jones et al., 2003). Here, coupled oscillator theory has been used to show how specific coordinating neurons in the crayfish swimmeret system could be used to provide phase synchronization between separate networks. Stable 90° phase relationships between adjacent CPG networks were effectively produced by two ascending and one descending fibers with specific connections to the interneuron pool. The fact that only specific synaptic connections were effective is quite similar to our results.

One of the best known vertebrate motor systems is the lamprey locomotory CPG. Here, bursting activity is generated in glutamatergic excitatory neurons in each hemisegments (Cangiano and Grillner, 2005; Grillner, 2003) and left-right coordination is mediated by glyciniergic interneurons. The out-of-phase operation of the circuit therefore relies on bilateral (reciprocal) inhibition, similarly to that in compact invertebrate CPGs and also as in our artificially coupled pyloric networks. Inhibition of the excitatory core neurons by the contralateral glycinergic cells has been also proposed in model studies and demonstrated experimentally in lesion studies (Cangiano and Grillner, 2005). This topology shows similarities to our LP-PD contralateral configuration and it might serve as a general mechanism for coordinating segmental oscillators. Lesion experiments in the lamprey also showed that contralateral inhibition reduces the burst frequency of the hemisegmental oscillators, i.e. their intrinsic frequencies are higher than in the coupled system (Cangiano and Grillner, 2003). This effect is similar to that we observe in the coupled pyloric circuits under reciprocal inhibition suggesting similar biophysical mechanisms.

Implications for synchronization in complex microcircuits

Although the concept of central pattern generator has been mainly used to uncover the bottom-up organization of motor systems, recent progress in the spatial and temporal resolution of brain mapping/recording techniques have revealed that self-contained and functional groups of neurons, similar to CPGs, can be identified in all levels of the nervous system (Grillner and Graybiel, 2006; Markram et al., 2004). These are commonly referred to as microcircuits. Also, CPGs have been proposed as a way of getting to the basic principles underlying cortical dynamics (Yuste et al., 2005). Specifically, microcircuits in various brain areas appear to function as sophisticated CPGs displaying a high degree of plasticity and capable of generating oscillations at multiple time scales. Indeed, CPGs and brain microcircuits share many similar topological and dynamical properties. A pacemaker group or excitatory core of neurons is commonly found in both types of networks (Grillner et al., 2005). Additionally, the excitatory core is embedded in a pool of inhibitory neurons which are typically reciprocally interconnected. As in CPGs, oscillations and synchronization are common in cortical microcircuits and increasing evidence suggests that these phenomena are causally responsible for eliciting specific brain functions (Buzsáki, 2006; Singer and Gray, 1995). Importantly, cortical microcircuits also demonstrate rich spontaneous dynamics in the absence of external input and are able to generate rhythmic spatiotemporal patterns (Silberberg et al., 2005; Yuste et al., 2005) - a hallmark of CPG dynamics. Synchronization of brain microcircuits is, however, often transient and episodic and associated with dynamical integration and reconfiguration of neuronal assemblies. These episodes of synchronization temporally link distributed brain areas in spite of their complex intrinsic structure and individual dynamics (Engel et al., 2001; Varela et al., 2001).

Our experiments showed that inhibitory connections provide robust but still flexible synchronization of oscillatory neuronal circuits. Considering the abundance of oscillations on multiple spatial and temporal levels of the brain, the ample variety of GABAergic interneurons in cortical microcircuits (Markram et al., 2004) and their wide-range projection patterns (Buzsáki et al., 2004), it seems more likely that inhibitory neurons play a central role in coordinating distinct neuronal groups into functional assemblies (Yuste et al., 2005). In this respect it is noteworthy that both spike responses (Bacci and Huguenard, 2006; Harsch and Robinson, 2000) and burst oscillations (Szücs et al., 2003) become more reproducible and regular under the action of inhibitory inputs. Clearly, inhibition acts to reset the postsynaptic membrane potential and de-inactivates populations of low-threshold voltage-gated channels, which, in turn, promote oscillatory dynamics. Nonetheless, tackling biophysical and dynamical mechanisms of intercircuit coordination in large population of neurons remains a challenging program. Our in vitro experimental model, with completely controllable artificial synaptic connections between the units, might provide a new opportunity to move forward in this direction.

EXPERIMENTAL PROCEDURES

Preparation and Electrophysiology

Adult spiny lobsters (58 animals, 28 paired preparations) were obtained from Don Tomlinson Commercial Fishing (San Diego, CA). The animals were kept in aerated and circulated seawater at 15–16 °C. Prior to dissection the animals were anesthetized by keeping them in ice for 40 min. For each experimental session we used two lobsters and began their dissection at the same time. The stomatogastric nervous system containing the stomatogastric ganglion (STG) and the anterior commissural and esophageal ganglia was separated from the stomach (Mulloney and Selverston, 1974) and pinned down in a silicone elastomer-lined Petri dish. Nerves interconnecting the anterior ganglia as well as the output motor nerves of the STG were left intact. The STG was enclosed in a small well made of petroleum jelly that served as a separate perfusion chamber of ~2 ml volume. The preparations were bathed in the standard Panulirus physiological saline composed of (in mM) 483 NaCl, 12.7 KCl, 13.7 CaCl₂, 10 MgSO₄, 4 NaSO₄, 5 HEPES, and 5 TES; pH was set to 7.40. The two STG preparations were moved into the experimental rigs each equipped with 4 manipulators, and 4 intracellular amplifiers (Neuroprobe 1600, A-M Systems Inc., Carlsborg, WA; and Axoclamp-2B) each operated in bridge mode. Microelectrodes were filled with 3 M K-acetate plus 0.1 M KCl solution with a resistance of 12–15 MΩ. Neurons used as postsynaptic cells in the dynamic clamp experiments were impaled with double electrodes. One electrode was dedicated for measuring the membrane potential while the other was used for current injection (separate amplifiers). In addition to the neurons coupled through artificial synapses one or two non-stimulated neurons were recorded from each STG.

Dynamic clamp and Data acquisition

To connect neurons from two distinct STGs we used a Windows-based dynamic clamp software (DynClamp4) earlier developed in our lab (Pinto et al., 2001). This program allowed the simulation of electrical and chemical synaptic connections at an update rate of 10 kHz. Inhibitory chemical connections were set up in a way to generate both spike-mediated and graded inhibition in the postsynaptic neurons. The reversal potential of the synaptic current was −100 mV, a value 30 mV more hyperpolarized relative to the trough of the PD membrane potential waveform and close to the value of the natural LP-PD synapse observed in our experiments. The threshold of transmitter release parameter V_th was chosen from −56 to −48 mV depending on the shape and amplitude of the presynaptic neurons burst waveform. Separate computers were used to run the dynamic clamp and to acquire the voltage waveforms of the neurons. The data acquisition computer was equipped with a PCI-MIO-16E-4 board (National Instruments, Austin, TX) and running the DasyLab 6.0 program (Datalog GmbH, Germany). Voltage data were sampled at 20 kHz on each channel. Action potential (spike) emissions were detected in real-time by calculating the first time-derivative of the intracellular membrane potential and observing the local maxima of the derivative time series. The arrival times of spikes of each recorded neuron were saved sequentially into separate ASCII files for later analysis.

Data analysis

Burst parameters were calculated from the spike arrival time series {t_i^k}={t₁^k, t₂^k, t₃^k,… t_N^k}, available for each recorded neuron k. Timing of the spikes relative to the preceding one was characterized by the interspike interval (ISI): ISI_i=t_i+1−t_i. Bursts were identified by analyzing the variations of successive ISI durations, i.e. by detecting short (intraburst) ISIs preceded by a long (interburst) ISI duration. Such an event indicated the onset of a burst in the recorded neuron. Successive burst arrival times {t_b,j^k}={t_b,1^k, t_b,2^k,…,t_b,M^k} were used to construct time series of burst cycle period data: BCP_j=t_b,j+1−t_b,j. The burst frequency was defined as the inverse of the burst cycle period. Phase relationship between two neurons was determined by pairing burst arrival times in the ‘follower’ neuron and the ‘reference’ neuron. The time interval between the burst onset of the reference cell and that of the nearest next burst onset in the follower cell was calculated and then divided by the burst cycle period of the reference cell. This parameter was called the relative burst phase of the two neurons. Phase entropy was calculated from probability distributions of relative burst phase data according to the formula

$$H=-\frac{{\displaystyle \sum _i^n}{p}_i{log}_2(p_i)}{{log}_2(n)}.$$

Here, values of burst phase distribution histograms were normalized to the total count and probabilities p_i were obtained. The denominator of the expression is the logarithm of the total number of values used in the density distribution (n bins). H is normalized into a unitless measure and it is scaled between 0 and 1. The firing activity of the neurons was characterized by the spike density function (SDF) obtained by convolving the spike arrival time series (discrete event times) with a Gaussian filter (Szücs, 1998). Fourier-amplitude spectra were calculated from selected stationary sections (50–100 s) of the SDF time series using 2 mHz resolution.

COMPUTATIONAL PROCEDURES

Individual model neuron

The neuron model is based on our earlier work (Huerta et al., 2000) and it consists of two compartments, one for the axon (fast generator) and another for the neuropil and soma (slow generator). The axon compartment produces the spikes and contains the sodium current I_Na, a delayed rectifier potassium current I_Kd, and a leakage current that is represented by I_L. The fast dynamics is described by C_AV̇_f = −I_Na − I_kd − I_L + I_vf,Vs where C_A=0.33 nF, V_F is the membrane potential in the axon while V_S is the membrane potential of the neuropil and soma. The slow dynamics is provided by C_sV̇_s = − I_Ca − I_K(Ca) − I_h − I_L − I_vf,Vs − I_syn + I_dc, where C_S=0.5 nF, I_Ca is the calcium current, I_L is the leakage current, I_h is a low threshold, hyperpolarization activated current, I_K(Ca) is the calcium dependent potassium current, I_A is the transient potassium current, I_dc is the external current, I_Vf,Vs = g_fs (V_s−V_f) is the current coupling the two compartments, and I_syn is the synaptic current that is modeled as in the dynamic clamp. The intracellular calcium dynamics is modeled by a simple first order kinetic equation: [Cȧ] = −αI_Ca − β [Ca] + γ, with α = 6.6×10⁻⁵μM/nAms, β = 1.21×10⁻³ms⁻¹, γ = 4.84×10⁻⁵μM/ms. The transient potassium current I_A is not incorporated in our earlier model. This current has the following form I_A = g_A n³h (V_s + 80 mV), where g_A can take values in the range g_A∈ [0,20] μS without markedly changing the dynamics of the coupled CPGs. The main action of the I_A current is that it delays the onset of the burst and reduces intraburst spiking rate. Furthermore, it induces variability across the neurons of both CPGs. Equations for the IA current are the same as in (Nowotny et al., 2008).

The CPG model

The model pyloric circuit is made of three neurons: a PD, an LP, and a PY. Each of the neurons is modeled by a two compartment conductance based model based on (Huerta et al., 2000). The network is formed by inhibitory connections as follows: $I_{\mathit{syn}}^j={\displaystyle \sum _{i=1}^3}{g}_{ji}{r}_i(t)(V_{\mathit{rev}}-V_j)$, where j=1, 2, 3 for the PD, LP and PY neuron, respectively. V_rev is the inhibitory reversal potential (set to −60 mV). The neurotransmitter release is governed by ${\beta }_r{\stackrel{.}{r}}_i=\frac{s_{\infty }(V_i)-r_i}{1-s_{\infty }(V_i)}$ where $s_{\infty }(V_i)=\frac{1}{2}(tanh((V_i-V_{th})/{\sigma }_{th})+1)$ with V_th=10 mV and σ_th=10 mV. The connectivity matrix is $\mathbf{g}=\mu \left(\begin{array}{ccc}0& 2& 0\\ 1& 0& 1\\ 1& 1& 0\end{array}\right)$ where the intrinsic parameter of the CPG μ is used as the global conductance to regulate the frequency of the oscillation of the circuit. A higher value for μ results in slower burst oscillations in the circuit.

Two connected CPGs

Synchronization of two model circuits is achieved by coupling them via synapses analogously to those in the biological experiments. Each CPG has slightly different parameters and the global conductance parameter μ is set independently for the CPGs. We explore three types of configurations, namely the PD-PD electrical coupling, the PD-PD mutual inhibitory connection, and the LP-PD contralateral inhibitory connections. The electrical connections yield Ohms law: $I_{\mathit{syn}}^{PD(\mathit{CPG}1)}=\lambda (V_{PD(\mathit{CPG}1)}-V_{PD(\mathit{CPG}2)}),I_{\mathit{syn}}^{PD(\mathit{CPG}2)}=\lambda (V_{PD(\mathit{CPG}2)}-V_{PD(\mathit{CPG}1)})$. Here, λ is the conductance of the electrical coupling. The PD-PD inhibitory connections are modeled as $I_{\mathit{syn}}^{PD(\mathit{CPG}1)}=\lambda r_{PD(\mathit{CPG}2)}(V_{\mathit{rev}}-V_{PD(\mathit{CPG}1)}),I_{\mathit{syn}}^{PD(\mathit{CPG}2)}=\lambda r_{PD(\mathit{CPG}1)}(V_{\mathit{rev}}-V_{PD(\mathit{CPG}2)}).$, where λ is the maximal conductance and the synaptic activation term r_PD(CPGx) follows a first order kinetics as in (Pinto et al., 2001). The LP-PD inhibition here is analogous to the previous ones.