Kinetic gating of the proton pump in cytochrome c oxidase

Abstract

Cytochrome c oxidase (CcO), the terminal enzyme of the respiratory chain, reduces oxygen to water and uses the released energy to pump protons across a membrane. Here, we use kinetic master equations to explore the energetic and kinetic control of proton pumping in CcO. We construct models consistent with thermodynamic principles, the structure of CcO, experimentally known proton affinities, and equilibrium constants of intermediate reactions. The resulting models are found to capture key properties of CcO, including the midpoint redox potentials of the metal centers and the electron transfer rates. We find that coarse-grained models with two proton sites and one electron site can pump one proton per electron against membrane potentials exceeding 100 mV. The high pumping efficiency of these models requires strong electrostatic couplings between the proton loading (pump) site and the electron site (heme a), and kinetic gating of the internal proton transfer. Gating is achieved by enhancing the rate of proton transfer from the conserved Glu-242 to the pump site on reduction of heme a, consistent with the predictions of the water-gated model of proton pumping. The model also accounts for the phenotype of D-channel mutations associated with loss of pumping but retained turnover. The fundamental mechanism identified here for the efficient conversion of chemical energy into an electrochemical potential should prove relevant also for other molecular machines and novel fuel-cell designs.

Cytochrome c oxidase (CcO) captures the energy from the reduction of oxygen to drive the translocation of protons across the inner mitochondrial (or bacterial) membrane (1–8). The resulting electrochemical gradient powers the production of ATP, the energy source of the cell. CcO takes up four electrons from the outside (P side) of the membrane and four protons from the inside (N side) for the reduction of one dioxygen molecule. Four additional protons are translocated across the membrane from the N side to the P side. Crystal structures of the enzyme from various organisms (3, 4, 9, 10) indicate the electron and proton pathways, formed by conserved residues and cofactors. Extensive experimental and theoretical studies have provided valuable information about these pathways, the reaction sequence, and energetic aspects of catalysis (5, 7, 9, 11–20). However, some key aspects of the fundamental mechanisms governing the coupling between the chemical reaction and vectorial proton translocation are still unclear.

Here, the objective is to explain how vectorial proton translocation is accomplished in CcO, with respect to both the driving forces (i.e., proton and electron affinities expressed as pK_a values and midpoint redox potentials, respectively, and Coulombic couplings) and the kinetic control (i.e., the “gating” effects that result from a dependence of kinetic barriers on the microscopic states). Specifically, we aim to construct a model of the proton pump that is consistent with the experimentally known thermodynamic and kinetic properties. All intermediate reactions are required to satisfy detailed balance, thus ensuring adherence to the second law of thermodynamics. The nonequilibrium pumping function is achieved by holding the concentrations of the reactants (oxygen, protons, and electrons) and the product (water) constant, thus establishing a steady state. Moreover, we require that the intermediate proton and electron transfer reactions are controlled by Coulombic interactions. With this model, we aim to elucidate the pumping function and to explain its high efficiency.

To gain insight into the mechanism of pumping while circumventing the complexities of a fully detailed model, we here use a reduced description. Only the key redox and proton sites are retained, with the effects of the other sites absorbed into effective free energies and rate coefficients in a master equation that governs the dynamics. Master equations provide a powerful framework in which to study nonequilibrium processes in enzymes and molecular motors (21–24), and have been used by us to show how redox-coupled proton pumping could be accomplished in principle (25). The model developed here is explicitly designed to reproduce known thermodynamic and kinetic properties of CcO. Optimization under the experimental constraints produces models that pump protons at ≈100% stoichiometric efficiency (i.e., two charges translocated across the membrane per electron consumed) at membrane potentials >100 mV. From the dependence of the kinetic barriers on the microscopic states, we identify the proton and electron transfer reactions that have to be gated. These gating effects are the key to the high efficiency of the pump and thus embody much of its mechanism.

Results and Discussion

Three-Site Kinetic Model of CcO.

In CcO, electrons are transferred from cytochrome c, bound at the P-side surface of the membrane, to the binuclear center (BNC) via two metal sites, Cu_A and heme a (see Fig. 1A). Protons for chemistry are transferred into the BNC via two distinct pathways, the so-called D and K channels (26–28). Pumped protons are delivered via the D pathway to a pump site located above the BNC toward the P side (Fig. 1A). It is generally believed that all four pumped protons and two of the chemical protons are transferred through the D pathway with Glu-242 at its end near the BNC (29). The remaining two chemical protons are transferred via the K pathway. A likely factor for this duality is the special role of Tyr-244 at the end of the K pathway, a residue implicated in the chemistry of dioxygen bond-breaking as a proton and electron donor (30, 31).

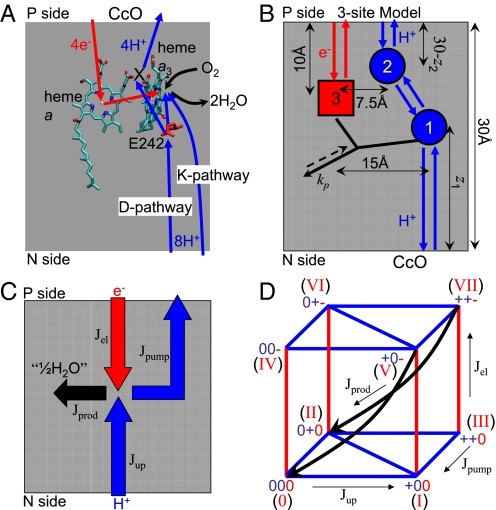
Fig. 1.

Schematic of CcO function and model. (A) Crystal structure (9) of two heme groups (a and a₃) and Glu-242 from bovine mitochondrial CcO. Electron transfer from P side (cytochrome c) via heme a to the BNC (heme a₃ and Cu_B) is indicated in red. Blue arrows indicate proton translocation, including uptake of both chemical and pumped protons from the negatively charged N side via D and K pathways and release of pumped protons from the pump site (X) on the positively charged P side. Black arrows indicate uptake of dioxygen and release of water. (B) Kinetic scheme of the three-site model for CcO. The circles and square show proton and electron sites, Glu-242, the pump site, and heme a, respectively. Arrows indicate proton (blue) and electron (red) transfer reactions. The black arrow denotes product formation, which can occur only if sites 1 and 3 are both occupied. The dashed reverse arrow indicates that here the detailed balance is broken. (C) Flux diagram of CcO proton pump. J_el is the electron flux, J_up is the proton uptake flux from the N side, J_pump is the net proton pumping flux to the P side, and J_prod is the product flux. Flux conservation requires that J_prod = J_el = J_up−J_pump. (D) Reaction diagram of the three-site kinetic model with a total of eight states labeled in roman numerals. Blue and red lines indicate proton and electron transfer, respectively, and black arrows represent the product formation reaction.

In our reduced model of CcO (Fig. 1B), heme a is the only electron site explicitly included along the electron-uptake pathway, with the Cu_A site absorbed into an effective rate coefficient for electron delivery into heme a. Similarly, for proton uptake into the BNC, we explicitly consider only Glu-242 at the end of the D pathway, thus ignoring the K pathway. In addition, we include a pump site that is protonically connected to both Glu-242 and the P side of the membrane. This model with 2³ = 8 states and 21 free parameters retains sufficient detail to recover the key thermodynamic properties of the CcO redox and protonation equilibria, and is simple enough to reveal the basic principles of redox-coupled proton pumping.

The dynamics of the model is described by a kinetic master equation. The resulting kinetic scheme is presented in Fig. 1D (with states labeled in roman numerals according to the binary code of their site occupancies). States are connected kinetically if they can interconvert by a single transfer or uptake/release of a proton or electron, or by product formation. All microscopic rate coefficients, except for product formation, satisfy the detailed balance condition consistent with the second law of thermodynamics (see Methods). To achieve steady-state turnover, we introduce a driving force of 500 meV (equal to the redox energy released per electron) to the forward product formation rate (see Fig. 1B and Methods). In this reaction step, the electron is irreversibly transferred to the BNC and used for the reduction of oxygen to water. For every electron consumed, half an equivalent of water is formed (“1/2 H₂O”; see Fig. 1C).

The relative locations of the redox and proton sites determine their Coulombic couplings. We fix the heme a site at 1/3 of the membrane width from the P side (Fig. 1B). During the model optimizations, the proton sites are free to move perpendicular to the membrane surface, thus changing the electrostatic couplings, with the restrictions that sites 1 (Glu-242) and 2 (pump site) are located below and above site 3 (heme a), respectively (see Fig. 1B and Methods). Their coordinates horizontal to the membrane surface are fixed (see Fig. 1B and Fig. S1).

Experimental Constraints on Thermodynamics.

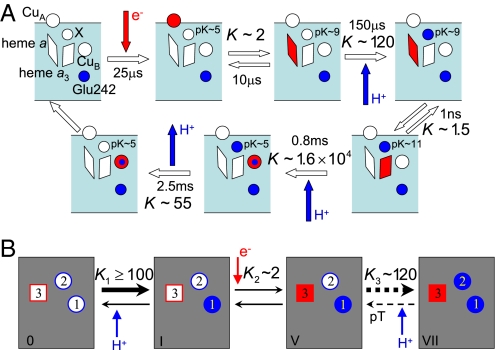
In the parametrization, we impose experimentally observed apparent pK_a values of the proton sites, and equilibrium constants for key reaction steps (20). Fig. 2A shows the measured equilibrium constants K (clockwise) along a schematic reaction cycle, and Fig. 2B illustrates how these values were imposed on the reaction steps in our model. In contrast, we do not enforce the midpoint potential of the redox site. Instead, we use its value, obtained by optimizing the pump, to validate the model by comparing against experiment.

Fig. 2.

CcO reaction cycle. (A) Measured equilibrium constants and rates along a proposed reaction sequence in the absence of membrane potential (red, electrons; blue, protons; X, pump site) (20). (B) Experimental equilibrium constants in terms of the states of the three-site model. The dashed arrows in the last reaction (V-VII) indicate that the reaction is a two-step process consisting of the pT followed by the uptake of a proton from the N side.

The apparent pK_a of site 1 (Glu-242) was deduced to be ≈9.4 from kinetic measurements (6), and >10 from thermodynamic measurements by using Fourier transform infrared spectroscopy (32). Such high pK_a values are consistent with the pK_a estimate (>11) of Asp-96 in bacteriorhodopsin (33), which serves a similar function as Glu-242. In our model, we restrict the pK_a of site 1 (Glu-242) in the oxidized state to vary between 9 and 12, such that its intrinsic free energy is bounded by −2.8 < G₁⁰ < −6.9 kcal/mol. The apparent pK_a of the pump site in the oxidized enzyme has been estimated to be 5.3 (8). Here, we limit the intrinsic free energy of site 2 to 1.4 < G₂⁰ < 4.1 kcal/mol, corresponding to pK_a values of the pump site between 4 and 6 in the oxidized state.

Proton Pumping Efficiency Against Membrane Potentials.

Even with five experimental restraints on pK_a's and reaction equilibria imposed, the 21 parameters of the model are not all determined. The reduced space of parameters is explored by Monte Carlo (MC) searching, with the goal of finding parameter combinations that lead to efficient proton pumping. Starting from a broad range of initial conditions, the system parameters are randomly varied to optimize the pumping efficiency η (defined as the number of protons pumped per electron consumed; see Eq. 4 and Methods), while maintaining the experimental restraints described above (see Methods).

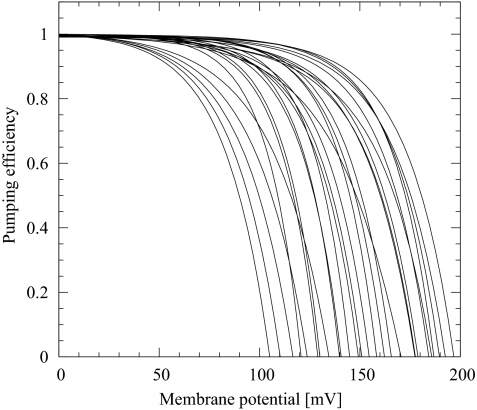
We find that even in the presence of the experimental thermodynamic constraints, it is relatively easy to obtain pumping solutions. The physical characteristics of the pumping solutions are remarkably diverse. Fig. 3 presents the pumping efficiency as a function of the opposing membrane potential for some of the solutions found by MC optimization. Note that we have assumed a pH of 7 at both sides of the membrane (for pumping against a pH gradient, see SI Text and Fig. S2). Importantly, in many models the efficiency remains at nearly 100% at voltages of >100 mV. Furthermore, protons are pumped against membrane potentials of ≈200 mV, close to the membrane potentials in mitochondria.

Fig. 3.

Pumping efficiency as a function of the opposing membrane potential for proton-pumping solutions of the three-site kinetic model found via MC optimization. These solutions satisfy the thermodynamic equilibrium constants shown in Fig. 2 at zero membrane potential.

Thermodynamics and Energetics of Proton Pumping.

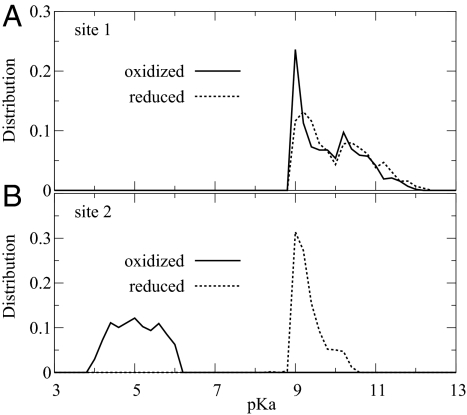
We find that in the steady state, site 1 (Glu-242) is protonated >99% of the time, consistent with measurements of pH effects on the kinetics (6). The pK_a values for the proton sites in the oxidized state are also consistent with the thermodynamic constraints (pK_a of site 1 between 9 and 12, and pK_a of site 2 between 4 and 6), as shown in Fig. 4. It is interesting that in the different optimized models, the pK_a of site 1 in the oxidized state is consistently near 9, which is at the lower end of the allowed range (Fig. 4A); in contrast, the pK_a of the pump site (or site 2) is almost uniformly distributed within the allowed range of 4 to 6 (Fig. 4B).

Fig. 4.

Protonation equilibria. Distributions of pK_a's for site 1 (A) and site 2 (B) when site 3 is oxidized (solid lines) and reduced (dashed lines), respectively.

The couplings between the proton and electron sites are essential for proton pumping. For the three-site model, the pK_a's of proton sites i = 1 and 2, with site 3 reduced (r) or oxidized (o), are related by pK_a^r = pK_a^o − ε_i3 / (1.4 kcal/mol), where ε_i3 is the electrostatic coupling between the proton and electron site. The geometric constraints on the sites (Fig. 1B) impose a limit on the coupling between site 1 and 3 as ε₁₃ ≥ −1.1 kcal/mol, suggesting that the pK_a change is bounded by ΔpK_a = pK_a^r − pK_a^o ≤ 0.8. This bound is confirmed in Fig. 4A, which shows little change in the pK_a of site 1 between the reduced and oxidized state. In contrast, the proximity of site 2 to site 3 leads to ε₂₃ ≥ −18.5 kcal/mol (see Methods). This bound implies that the pK_a change of site 2 (or pump site) has to be <13. However, despite this large allowed range, in nearly all optimized models ΔpK_a ≈4 for the pump site. Accordingly, the pK_a of site 2 in the reduced state is concentrated around 9 (Fig. 4B). This pK_a value is remarkably consistent with the experimental pK_a of the pump site when heme a is reduced (see Fig. 2A and ref. 8). Moreover, the relatively weak coupling between sites 1 and 2 and the strong coupling between sites 2 and 3 are consistent with the continuum electrostatics calculations of Kannt et al. (34), which gave pK_a shifts of ≈2 and 5 for Glu and the heme propionates, respectively, one of the latter being a likely pump site (8, 35).

In our model, the relative midpoint redox potential of site 3 was not restricted. We find that most of the pumping solutions have midpoint redox potentials between 15 mV and 30 mV relative to cytochrome c (or Cu_A), with a few models going as high as 240 mV (SI Text and Fig. S3). Without having imposed a constraint, the majority of the models thus produce midpoint potentials consistent with the measured differences between the potentials of heme a (270 mV) and either cytochrome c (270 mV) or Cu_A (250 mV) (8).

Proton-Pumping Mechanism and Gating.

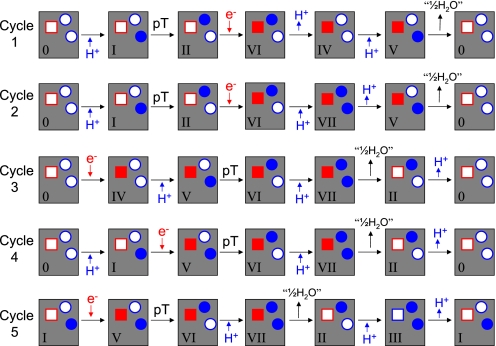
To explore the mechanism of proton pumping, we group the pumping solutions with midpoint potentials of site 3 <30 mV (relative to cytochrome c) based on their dominant pump cycles. For each model, fluxes are calculated along all possible pump cycles (21). The cycle that yields the maximum flux is designated as a dominant pump cycle. We find that of seven possible pump cycles, only five are dominant in at least one model, as illustrated in Fig. 5. The first two cycles show that the uptake of an electron from the P side (II → VI) is preceded by the internal proton transfer (pT) to the pump site (I → II), followed by the pumping of the proton to the P side (VI → IV, VII → V). The product formation (V → 0) then follows. In contrast, the last three cycles follow a different mechanism: The uptake of an electron (0 → IV, I → V) is followed by pT (V → VI), product formation (VII → II), and then proton pumping (II → 0, III → I).

Fig. 5.

Five pump cycles used in three-site kinetic models with midpoint potential of site 3 <30 mV relative to cytochrome c.

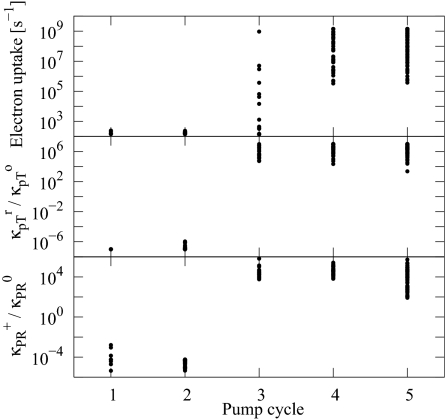
Which one of the five different pump cycles in Fig. 5 is most consistent with our experiment? To answer this question, we compare the measured kinetics of electron uptake to that predicted for the different models. The measured rate of electron uptake from Cu_A to heme a is in the microsecond range (Fig. 2A) (20, 36, 37). The rate coefficient for the reaction I → V should thus be of similar order. Fig. 6 shows the rates of electron uptake (I → V) for the different models separated according to their dominant pump cycle. We find that electron uptake is slow for all models dominated by the first two cycles, and most models dominated by cycle 3, with time constants of 1–10 ms. In contrast, electron uptake is fast in models dominated by cycles 4 and 5 (with rates exceeding 1/μs in almost all models). We conclude from this result that models dominated by cycles 4 and 5 are most likely to capture the mechanism of CcO, which differ only by the sequence of reprotonation of site 1 and the release of the pumped proton. In fact, a recently proposed model (8, 20) closely resembles the mechanism of cycle 5.

Fig. 6.

Gating mechanisms. (Top) Rate of electron uptake (transition I → V) for the different models as a function of their dominant pump cycle. (Middle) Ratio of the intrinsic internal pT rate (between Glu-242 and the pump site) with heme a reduced and oxidized. (Bottom) Ratio of the intrinsic product formation rates in the presence (κ_PR⁺) and absence (κ_PR⁰) of a proton in the pump site.

Which factors determine the dominant pump mechanism of a particular model? One key factor is the ratio of the intrinsic rates of pT between sites 1 (Glu-242) and 2 (pump site) in the reduced state (site 3 occupied) and oxidized state (site 3 empty). Fig. 6 shows the ratio of rate coefficients for transitions I → II and V → VI for the different models as a function of the pump cycle that dominates them. For models that pump protons by using cycles 1 or 2, the intrinsic internal pT rate in the oxidized state, κ_pT^o, is ∼10⁶ times larger than in the reduced state, κ_pT^r. In contrast, for models dominated by cycles 3 to 5, κ_pT^r is ∼10⁶ times larger than κ_pT^o. As a consequence, the pump site receives its proton from Glu-242 before heme a is reduced in cycles 1 and 2, and after reduction in cycles 3–5 (Fig. 5). Consistent with the early and late arrival of the proton in the pump site, in cycles 1 and 2 the pumped proton is released before the product is formed, whereas in cycles 3–5 the product is formed before the pumped proton is released (when “starting” the cycle with reduction of heme a) (see Fig. 5).

In the context of our model, a reaction step is gated if the associated barrier strongly depends on the state of the proton or electron site(s) not directly involved in the reaction. In Fig. 6, we find that in all models the internal proton transfer is strongly gated, depending on the reduction of heme a. Remarkably, proton pumping can be achieved both by a sharp enhancement of the internal proton transfer rate in the reduced state (cycles 3–5), and by a sharp reduction (cycles 1 and 2). Interestingly, in both cases the rates change by a factor of ∼10⁶, which amounts to a change in the free-energy barrier of the pT reaction of k_BTln10⁶ = 8.3 kcal/mol.

Based on the preceding arguments regarding the rate of electron uptake, we believe that models dominated by cycles 4 and 5 should best capture CcO function. In these models, reduction of heme a greatly enhances the rate of pT from Glu-242 to the pump site. This behavior matches the predictions of the water-gated model of proton pumping by CcO (16), and more recent analyses of the pump mechanism (8, 35). As shown in the bottom frame of Fig. 6, a second prediction of the water-gated model is also matched: The rate of product formation is greatly enhanced after a proton has been delivered to the pump site. In the water-gated model, these rate enhancements are achieved by a branched chain of water molecules inside a hydrophobic cavity next to the BNC (15, 38, 39). This chain serves as an efficient proton conducting wire (40) from Glu-242 to the pump site with heme a reduced, and to the BNC with the BNC reduced (16). Even though our analysis of master-equation models does not address the microscopic origin of the gating, it provides fully independent evidence that, based on kinetic requirements, the internal proton transfer rate has to be strongly gated. This gating is fully consistent with the water-gated model. Moreover, we can estimate the magnitude of the necessary gating effect as a rate enhancement by a factor of 10⁶, consistent with a drop in the barrier for pT by ≈8.3 kcal/mol, a value close to the 7.1 kcal/mol predicted by Siegbahn and Blomberg (35).

Effects of D Channel Mutations.

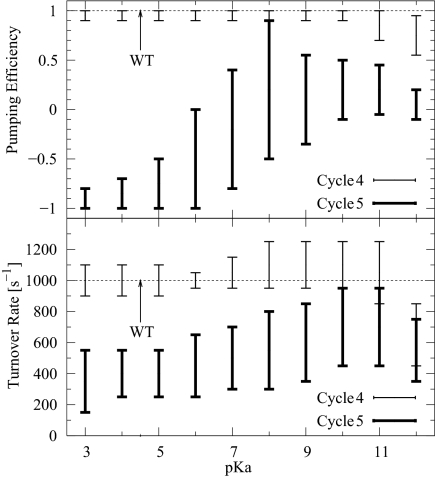
Relating the kinetic models to CcO mutation studies provides further insight into the pump mechanism. The N98D mutation introducing an aspartic acid into the D channel between Glu-242 and the N side of the membrane resulted in an interesting phenotype in which the enzymatic activity of the WT is retained but the proton-pumping ability is lost (41, 42). To explore this behavior within our kinetic scheme, we have added a proton site between the N side and site 1 (Glu-242) to already optimized three-site models (Fig. 3) and explored its effect on pumping and turnover over a broad pK_a range. This modification qualitatively mimics the introduction of the ionizable residue N98D on the D channel. We found that the majority of the models dominated by cycle 4 pump protons nearly as efficiently as the original three-site models (see Fig. 7). In contrast, nearly all models dominated by cycle 5 lose their pumping ability in a wide range of pK_a of the additional (N98D) proton site. At the same time, these models keep the enzymatic activity, although the turnover rate is slightly (by no more than a factor of two) diminished compared with the original ones. This behavior is qualitatively consistent with the experimental observations (41, 42). The detrimental effect of the N98D mutation stems from an effective shutdown of the internal proton transfer from site 1 (Glu-242) to site 2 (pump site). The kinetic model of the D-channel mutation suggests that cycle 5 is the most likely proton-pumping pathway and that the proton taken up from the N side repels the “pump proton” from site 2 to the P side, consistent with the reaction sequence deduced from experiment (20).

Fig. 7.

D-channel mutation. (Top) Range of pumping efficiency for the models of D-channel mutation as a function of the pK_a of the additional proton site (N98D). (Bottom) Rate of turnover vs. the pK_a of the N98D mutation. The horizontal line indicates the turnover rate of the original three-site models.

Concluding Remarks.

To explore the mechanism of proton pumping by CcO, and the role of gating, we have developed simple master-equation models of the proton and electron transfer reactions in CcO. The models rely on basic physical principles, and incorporate information about the structure of CcO and the energetics of the reaction steps. We find that a diverse group of very different models satisfies the experimental constraints on the structure, proton affinities, and equilibria of reaction steps, and is able to pump protons against membrane potentials of nearly 200 mV, and against pH gradients of ≈2. On the one hand, this diversity indicates that our coarse-graining procedure was successful in the sense that we did not eliminate any of the sites essential for pumping; on the other hand, it required us to use additional information to identify the models that best capture proton pumping in CcO.

We showed first that the majority of the models reproduced the experimental difference in midpoint potentials between cytochrome c and heme a, without having used this information as a constraint. In contrast, kinetic information for the rate of electron uptake allowed us to discriminate between the different models. In particular, we could show that models dominated by cycles 4 and 5 are most likely to reproduce CcO function. However, further study suggests that cycle 5 is the only pathway consistent with the experimentally observed D channel mutation. Under steady-state conditions, electron uptake is followed by the creation of a state with heme a reduced and both Glu-242 and the pump site protonated, after which the product is formed (i.e., the oxygen compound at the BNC is singly reduced and protonated), with the cycle completed by the release of the pumped proton.

The high pumping efficiency of these models (with nearly perfect stoichiometry of two charges translocated per electron consumed at 100 mV membrane potential) requires (i) strong electrostatic couplings between the pump site and the electron site (heme a), and (ii) a pronounced gating effect. Gating is achieved through a ∼10⁶-fold enhancement in the intrinsic rate of proton transfer from Glu-242 to the pump site when heme a is reduced. Remarkably, this gating mechanism is fully consistent with the predictions of the water-gated model of proton pumping (16), which was derived based on the atomistic dynamics of a short water chain connecting Glu-242, the BNC, and the D-propionate of heme a₃ leading into the presumed pump site. The motion of the Glu-242 side chain between a downward-facing position exposed to the D channel and an upward-facing position pointing toward the pump site (38, 39, 43, 44) provides an additional means of modulating the effective internal proton transfer rate. However, we want to stress that the models studied here do not rely on specific molecular mechanisms. Indeed, different oxidase families may use alternative mechanisms to gate the internal proton transfer [e.g., oxidases without Glu-242-equivalent residues (45)]. As more experimental information becomes available for different oxidases, kinetic models with greater complexity can be parametrized to provide further details of proton-pumping mechanisms.

It is interesting to compare and contrast the mechanism identified here for the pumping of protons by oxidase to that of other molecular machines. Transporters are membrane proteins that couple the translocation of a substrate molecule against a free-energy gradient to a second process that is “downhill” in free energy, such as the hydrolysis of ATP (46). Their mechanism appears to follow, roughly, that of a lock used to raise boats in a canal, with structural changes allowing access initially to the low (free)-energy side for substrate uptake and then to the high (free)-energy side for release. In oxidase, a “lock function” for the pumped proton is achieved by the arrival of an electron at site 3 that effectively closes the gate toward the N side. However, in contrast to transporters and canal locks, oxidase can couple the energetically “uphill” transport of the proton to the “downhill” chemistry of oxygen reduction without undergoing a large structural change. As a further complication, in oxidase the downhill process uses the same substrate (H⁺) and pathway. As our model shows, electrostatic effects combined with a modulation of the barriers for proton transfer are sufficient to achieve the gating required for highly efficient proton pumping. The mechanisms identified here for energy transduction by using redox chemistry may also be useful in studies of other molecular machines (24) and may aid in the design of novel bio-inspired fuel cells.

Methods

Master Equation.

The transition rate coefficients, k_ij, for the three-site model with a total of 2³ = 8 kinetic states (Fig. 1D), are constructed to satisfy detailed balance between forward and backward rates. Consider two states i and j that are connected by a single proton or electron uptake/release or transfer step between sites μ and ν (blue or red lines in Fig. 1D, respectively). The corresponding rate coefficient in the absence of a thermodynamic driving force, G_i = G_j, is defined as κ_ij, and is called the “intrinsic” rate coefficient between states i and j. The transition rate coefficient from i to j can then be written as

where κ_ij = κ_ji such that k_ji/k_ij = exp[−(G_j − G_i)/k_BT]. For simplicity, we here assume that the effects of a free-energy change are balanced between the forward and reverse reactions, corresponding to the factor 1/2 in the exponent in Eq. 2. Note that unlike the previous study (25), the intrinsic rate coefficients, κ_ij, now depend on the states i and j, thus creating more degrees of freedom and allowing us to explore the role of gating in the pump function.

Product formation is driven by a free energy gain of ΔG_p = 500 meV, corresponding to one quarter of the energy released from reducing the dioxygen molecule. Thus in addition to Eq. 2, the forward product-formation rates (black arrows in Fig. 1D) contain an extra factor equal to exp(−ΔG_p/k_BT). This factor breaks the detailed balance between the forward/reverse product-formation rates, and results in a nonzero steady-state flux.

The relative free energy G_i of state i is given by

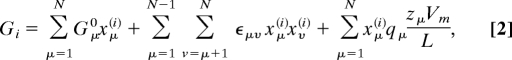where N = 3 is the number of sites, G_μ⁰ is the intrinsic relative free energy of site μ, and ε_μν is the electrostatic coupling between two sites μ and ν with the conducting boundary conditions at the membrane surfaces (47), and x_μ⁽ⁱ⁾ is zero when site μ is empty in state i, and one when it is occupied. Here V_m is the membrane potential, q_μ is the charge of the site μ, z_μ is the distance from the N side of the membrane to site μ, and L = 30 Å is the membrane width (Fig. 1B). Note, however, that care must be taken in specifying the voltage-dependent rate coefficients for proton or electron uptake, because of the broken symmetry of the two sides of the membrane.

The thermodynamic couplings, ε_μν, are restricted purely to electrostatics, i.e., ε_μν = q_μq_ν/Dr_μν where D is the dielectric constant and r_μν is the distance between two sites μ and ν determined from their corresponding Cartesian coordinates. To incorporate the thermodynamic data indicating strong coupling between heme a and the pump site (20, 48), we use D = 4 for ε₂₃ and D = 20 for the other couplings. With the geometric constraints for the three sites, i.e., 0 ≤ z₁ ≤ 20 Å and 20 Å ≤ z₂ ≤ 30 Å (see Fig. 1B), one obtains ε₁₂ ≤ 2.2 kcal/mol, ε₁₃ ≥ −1.1 kcal/mol, and ε₂₃ ≥ −18.5 kcal/mol.

Master Equation.

The probability of state i, P_i(t), satisfies the master equation

In the absence of the driving force (i.e., ΔG_p = 0), the probabilities would approach equilibrium without proton flux, P_i^eq/P_j^eq = exp[−(G_i − G_j)/k_BT]. For nonzero driving force, ΔG_p > 0, the system approaches a steady state (dP_i^ss/dt≡ 0) with nonzero fluxes, J_ij = k_ijP_j^ss − k_ji P_i^ss ≠ 0.

MC Optimization for Pumping Solutions.

Even though an explicit expression for the analytical steady-state solution exists, it is impractical to analyze the solution consistent with the thermodynamic constraints because of the large number of parameters. Thus, to find optimal pumping solutions that satisfy all of the thermodynamic constraints, we first numerically determine the steady-state solution of the rate equations for a given set of parameters. We define the pumping efficiency η as the number of protons pumped per electron consumed (Fig. 1C),

We note that because of flux conservation the net flux of protons released on the P side, J_pump, is equivalent to the net proton flux between sites 1 and 2.

To find optimal pumping solutions consistent with the thermodynamic constraints in the space of parameters, we define a target function, ψ, as

where K_i and K_i^obs are the calculated and observed equilibrium constants (Fig. 2) at zero membrane potential, and α₀ = 100, α₁ = 1, α₂ = 100, and α₃ = 10. The function ψ is then maximized by MC simulations in which the model parameters (intrinsic free energies, electrostatic couplings, and intrinsic rate coefficients) are randomly varied. In refining the model parameters, we put limits on the magnitude of the intrinsic free energy of the electron site, G₃⁰ (<12 kcal/mol), and rate coefficients (10² to 10⁹ s⁻¹) to keep them within certain physical ranges. Note that the intrinsic free energies of proton sites are limited to −2.8 < G₁⁰ < −6.9 kcal/mol and 1.4 < G₂⁰ < 4.1 kcal/mol in accordance with the apparent pK_a values measured experimentally. For each parameter set, the proton pumping efficiency η is calculated numerically at an initially low membrane potential, and the equilibrium constants K_i (i = 1,2,3) are computed at zero membrane potential. By performing simulated annealing in the multidimensional space of parameters and gradually increasing the membrane potential, we can locate optimal parameter combinations with maximal efficiency η, which, at the same time, yield the experimental equilibrium constants within a range ± 10%. The procedure is repeated from different starting points in parameter space to obtain a large number of possible parameter combinations.