Abstract
The mechanism of ligand binding coupled to conformational changes in macromolecules has recently attracted considerable interest. The 2 limiting cases are the “induced fit” mechanism (binding first) or “conformational selection” (conformational change first). Described here are the criteria by which the sequence of events can be determined quantitatively. The relative importance of the 2 pathways is determined not by comparing rate constants (a common misconception) but instead by comparing the flux through each pathway. The simple rules for calculating flux in multistep mechanisms are described and then applied to 2 examples from the literature, neither of which has previously been analyzed using the concept of flux. The first example is the mechanism of conformational change in the binding of NADPH to dihydrofolate reductase. The second example is the mechanism of flavodoxin folding coupled to binding of its cofactor, flavin mononucleotide. In both cases, the mechanism switches from being dominated by the conformational selection pathway at low ligand concentration to induced fit at high ligand concentration. Over a wide range of conditions, a significant fraction of the flux occurs through both pathways. Such a mixed mechanism likely will be discovered for many cases of coupled conformational change and ligand binding when kinetic data are analyzed by using a flux-based approach.
Keywords: kinetics, binding, folding, coupled equilibria, mechanism
The binding of ligands by macromolecules is crucial to a multitude of physiological processes. These include the cascade of reactions accompanying hormone binding to receptors (1, 2), enzyme reactions initiated by the binding of substrates to the enzyme (3, 4), gene regulation by the binding of molecules to DNA (5) and RNA (6), and the folding of unstructured proteins to produce biologically active molecules (7, 8). In virtually all cases, the binding of ligands and conformational changes go hand in hand. Consequently, considerable effort has been expended in assessing the detailed mechanism by which ligand binding and conformational changes are coupled (3, 4, 9). Two limiting mechanisms are generally considered: (i) “conformational selection,” whereby the ligand selectively binds to a form of the macromolecule that is present only in small amounts, eventually converting the macromolecule to the ligand-bound conformation; and (ii) “induced fit,” (9) whereby ligand binds to the predominant free conformation followed by a conformational change in the macromolecule to give the preferred ligand-bound conformation.
The 2 limiting mechanisms can be written as:
 |
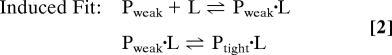 |
In these equations, Pweak and Ptight represent the tightly and weakly binding conformations of the protein (or other macromolecule), and L is the ligand. In point of fact, these 2 limiting mechanisms can be distinguished by kinetic measurements of the rate of the conformational change. In the simplest case, which often prevails, the ligand-binding step is assumed to be rapid relative to the conformational change, and the ligand concentration is much greater than the protein concentration. Under these conditions, the observed first-order rate constants for the 2 mechanisms are (4):
In these equations, kf and kr are the forward and reverse rate constants for the conformational change reaction as it is written, and Kd is the equilibrium dissociation constant for ligand binding. In the former case, the observed rate constant decreases as the ligand concentration increases, whereas in the latter case, the observed rate constant increases as the ligand concentration is raised. If the ligand and protein concentrations are comparable, kinetic experiments near equilibrium (relaxation kinetics) can be easily interpreted with simple analytical equations similar to the above (4). If the ligand-binding reaction and the conformational change reaction proceed at similar rates, the kinetic analysis becomes complex, although relaxation measurements can be analyzed without too much difficulty.
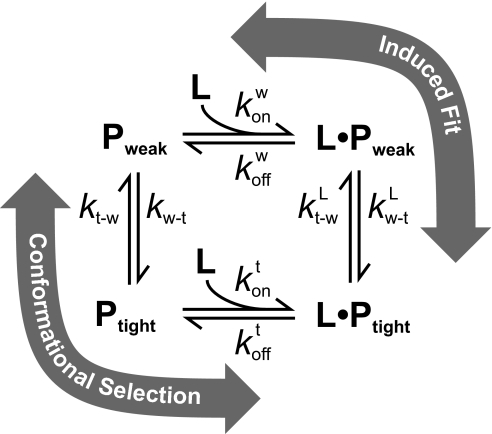
These 2 limiting cases are part of the general mechanism shown in Fig. 1. Here, we will show that in many cases both mechanisms may be occurring, and that the reaction path can be altered by changes in the ligand and protein concentrations. Determination of the reaction path followed requires knowledge of both the rate constants and the concentrations of all species. If these are known, the flux, F, through a given path can be readily calculated. The flux of a reaction is equivalent to the rate of change of the reactant concentrations with respect to time and is calculated by multiplying the reactant concentration(s) times the forward rate constant. The fractional flux through a given path is a precise measure of how much a reaction proceeds through that path. For complex mechanisms, the flux can be calculated following 2 simple rules:
where Fi is the flux of the ith reaction step. For a combination of serial and parallel paths, these 2 rules can be combined.
Fig. 1.
General mechanism for ligand binding coupled to conformational change. Pweak and Ptight represent macromolecule conformations with lower and higher affinity for the ligand, L.
The fluxes for forming Ptight·L from Pweak and L for the 2 pathways illustrated in Fig. 1 are as follows:
Conformational selection: Using F1 = kWT[Pweak] and F2 = konT[Ptight][L]f with Eq. 6:
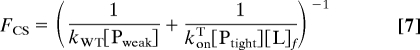 |
Induced fit: Using F1 = konW[Pweak][L]f and F2 = kWTL[Pweak·L] with Eq. 6:
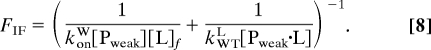 |
It is important to note that the ligand concentration ([L]f) in these equations refers to the free ligand concentration rather than the total concentration. Because total ligand concentration is usually the known quantity, one must derive the free concentration as described in Methods.
To illustrate the methodology of calculating fluxes, we consider 2 specific examples, the reaction of enzyme with a substrate and the coupling of protein folding with ligand binding.
Results
Enzyme Plus Substrate.
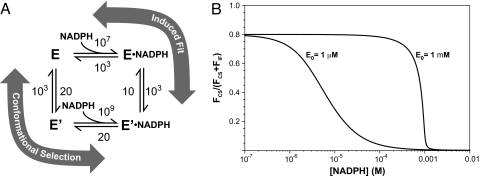
Dihydrofolate reductase (DHFR) is an enzyme that has been extensively studied with many different methods and in many different laboratories (10–25). It catalyzes the reduction of dihydrofolate by nicotinamide adenine dinucleotide phosphate (NADPH) to tetrahydrofolate and NADP+. A recent NMR study of DHFR demonstrates that an ensemble of enzyme conformations exists throughout the entire reaction and suggests that the reaction proceeds by a conformational selection mechanism (13). As a specific example, the binding of NADPH to the enzyme is considered. In terms of Fig. 1, Pweak and Ptight correspond to the E and E′ conformations of dihydrofolate reductase and the ligand is NADPH (see Fig. 2A.) The NMR study suggests that only ≈2% of the free enzyme exists in a conformation, E′, to which NADPH binds much more strongly than to the predominant conformation. The exchange rate constant observed is ≈1,000 s−1. This can be attributed to the sum of the rate constants for the interconversion of the 2 enzyme species. An alternative path for the formation of E′·NADPH is the binding of E and NADPH to form E·NADPH, which then forms E′·NADPH. The second order rate constant for the overall combination of enzyme and NADPH is ≈107 M−1·s−1 and the overall equilibrium dissociation constant is ≈1 μM (15, 25).
Fig. 2.
Mechanism of DHFR conformational change coupled to NADPH binding. (A) Mechanistic scheme for 2 alternative pathways where E and E′ represent the low and high affinity forms of DHFR, respectively. Labels on arrows represent first order rate constants (in s−1) except for the 2 ligand binding steps, which are second-order rate constants (in M−1·s−1.) Values given are based in part on estimates made by Boehr et al. (13) (see Enzyme Plus Substrate) (B) Fractional flux through the Conformational Selection path at 2 DHFR concentrations: 1 μM is near cellular concentrations and 1 mM is the concentration used for the NMR experiments. Fractional flux is plotted vs. total [NADPH].
Based on these results, reasonable rate constants have been assigned to the mechanism depicted in Fig. 2A. If NADPH is presumed to bind only to E, the corresponding second order rate constant would be approximately equal to the experimentally determined value, 107 M−1·s−1 (the estimate shown in Fig. 2). Whereas, if NADPH is presumed to bind only to E′, the approximate second order rate constant consistent with the experimental data is 109 M−1·s−1 (Fig. 2). Thus, the bimolecular rate constants are consistent with the experimental measurements of the overall rate constant for both the conformational selection and induced fit mechanisms. The sum of the rate constants for the interconversion of E and E′ is set equal to 1,000 s−1, with an equilibrium constant of 50 in favor of E, both from the results of NMR experiments. The sum of the rate constants for the interconversion of E·NADPH and E′·NADPH is also set equal to 1,000 s−1, with an equilibrium constant of 100 favoring E′·NADPH. This value of the equilibrium constant is somewhat arbitrary, but E′·NADPH is clearly the favored conformation. Note that with this equilibrium constant, the equilibrium dissociation constant for the binding of ligand to E is 5,000 times larger than that for binding to E′.
With the rate constants specified above, the fraction of the equilibrium flux proceeding through the conformational selection mechanism at various ligand concentrations is shown in Fig. 2B for 2 conditions, 1 mM total enzyme concentration as used in the NMR experiment and 1 μM total enzyme concentration, a condition closer to other types of experiments and the cell. The flux through each path is:
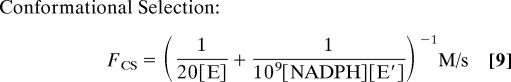 |
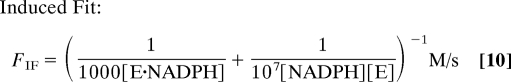 |
where [NADPH] corresponds to the free ligand concentration obtained from Eq. 11 in Methods. In both cases, the mechanistic path followed changes as the ligand concentration is varied. As is also readily apparent, the mechanistic path followed depends greatly on the enzyme concentration. Under the conditions used in the NMR experiments (1 mM enzyme, 10–50 mM NADPH), virtually none of the flux proceeds through the conformational selection mechanism. At very low ligand concentrations, ≈80% of the flux goes through the conformational selection mechanism, but this percentage drops off rapidly as the ligand concentration is increased. These calculations are illustrative only. In point of fact, insufficient information is available to determine which mechanism prevails. However, this example vividly illustrates that both mechanisms must be considered and that the pathway is not easily predicted, even if one of the conformations binds the ligand much more tightly. Furthermore, the mechanistic pathway depends very strongly on the ligand and enzyme concentrations. In order for a large fraction of the mechanism to proceed through the conformational selection mechanism at high ligand concentrations, the second order rate constant characterizing the binding of E and NADPH would have to be reduced several orders of magnitude. This is certainly possible, but seems unlikely.
Folding Plus Binding.
The marginal thermodynamic stability of many proteins under physiological conditions has increasingly been recognized in proteomes from a variety of organisms (26). The folding reaction of many proteins or individual domains is unfavorable in the absence of a binding partner (27). A large fraction of these so-called intrinsically disordered proteins fold only when bound to small ligands, nucleic acids or other proteins (8). Through thermodynamic linkage, the binding free energy of these complexes is used in part to promote folding of the intrinsically disordered protein (28). Even when a protein is stably folded in the absence of ligand, binding always enhances stability except in the unlikely event that the binding affinity of the unfolded protein is equal to or higher than that of the folded form. The mechanism by which these coupled folding and binding reactions take place has stimulated much recent interest (29–36).
Kinetically speaking, the key question is: which occurs first, folding or binding? Although claims of coincident or concurrent folding and binding have been made, this mechanism is extremely improbable because both folding and binding are relatively low frequency stochastic events, making their simultaneous occurrence an even lower frequency event (see refs. 37–39). A more appropriate interpretation of apparent coincident folding and binding is that one of the 2 reactions (probably binding) occurs with a rate constant higher than can be experimentally detected or the intermediate species is spectroscopically silent. Thus, folding and binding are almost certainly sequential steps and kinetic experiments must be carefully designed to determine their order.
Several recent studies have sought to determine the order of steps in sequential folding/binding reactions (8, 29, 32, 33, 36). The experiments require transient detection of the folding reaction in the presence of various concentrations of ligand (33). Alternatively, binding can be transiently detected under various conditions that produce various proportions of folded and unfolded protein. In either case, the folding/binding mechanism cannot be determined under a single set of conditions. Likewise, the relative free energies of the ground state species or their structures cannot be compared because these properties do not exclusively determine the relative flux. Only kinetic measurements under a variety of equilibrium conditions can quantitatively determine the relative importance of the binding-first and folding-first pathways.
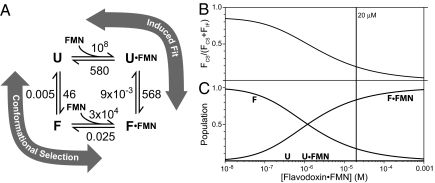
A recent example of a kinetic study of a coupled folding and binding system is the work of Wittung-Stafshede and coworkers on the folding of Desulfovibrio desulfuricans flavodoxin in the presence and absence of its cofactor, flavin mononucleotide (FMN) (30, 31). These workers measured the folding kinetics of apo- and holo-flavodoxin (31) and combined these results with their previous work on FMN binding kinetics in the same system (30) to estimate the rate constants for the mechanism depicted in Fig. 3A. The second-order rate constants for FMN association shown in Fig. 3A correspond to pseudofirst order rate constants for FMN binding of >1,000 s−1 for unfolded flavodoxin and ≈2 s−1 for folded flavodoxin at holo-protein concentrations of 20 μM. Likewise, the folding rate constants for apo- and holo-flavodoxin were estimated to be 46 s−1 and 570 s−1, respectively. Based on a comparison of these rate constants, the authors argued that the mechanism must occur exclusively via the binding-first (induced fit) pathway because the lowest rate constant step on this path (folding of holoflavodoxin) is hundreds of times faster than the lowest rate constant step (FMN binding by folded protein) on the alternative folding-first (conformational selection) path.
Fig. 3.
Mechanism of Desulfovibrio desulfuricans flavodoxin folding coupled to FMN binding. (A) Mechanistic scheme for 2 alternative paths where U and F represent the folded and unfolded forms of flavodoxin, respectively. Labels on arrows represent first order rate constants (in s−1) except for the 2 ligand binding steps, which are second order rate constants (in M−1·s−1.) Values given are based on estimates made by Muralidhara et al. (30, 31). (B) Fractional flux through the folding-first (Conformational Selection) pathway at various holoflavodoxin concentrations, calculated from the rate constants given in A. (C) Fractional population of each species shown in A. The vertical line at 20 μM indicates the holo-flavodoxin concentration used by Muralidhara et al. (31). Note that the populations of U and U·FMN are very small under all conditions and the mechanism is mixed over the concentration range shown.
This conclusion is incorrect under a wide range of conditions for the reasons outlined in the previous section. Using the authors' estimates for the rate and equilibrium constants, we have calculated the flux through each path as a function of holo-protein concentration. As depicted in Fig. 3B, the flux through the folding-first path represents 20% of the total flux at 20 μM holo-protein [the concentration used by Wittung-Stafshede and coworkers (30, 31)] and as much as 85% at lower concentrations. Thus, the mechanism is mixed over a very broad concentration range and inspection of rate constants alone does not allow the determination of mechanism.
The reason that the path with lower rate constants has significant flux can be understood by inspecting the fractional populations of the 4 forms of the protein in Fig. 3C. At all reasonable concentrations, the population of the folded unbound protein F vastly exceeds that of both unfolded forms. The relative contribution of the 2 steps in the folding-first pathway is strongly concentration dependent and at 20 μM holo-protein the folding step is flux-limiting (the true “rate-limiting” step) even though the rate constant for folding is 400 times higher than the pseudofirst order rate constant for binding to F (0.1 s−1). This is because [F] is 104 times greater than [U]. However, the relative contribution of the 2 steps in the binding-first pathway to the total flux through that path is concentration independent and under the conditions used by Muralidhara et al., both steps contribute equally, which means that the overall binding-first flux is half of the flux through each sequential step. Under these specific conditions, the relative importance of the folding-first pathway may be approximated by comparing the rate constant for folding of the unliganded unfolded flavodoxin (46 s−1) with the pseudofirst order rate constant of FMN binding to the same species divided by 2 (180 s−1). This calculation agrees with the estimate given above that 20% of the flux is through the folding-first path.
Discussion
These 2 examples of flux calculations indicate several important factors that should be considered in assessing the mechanism of processes that couple conformational changes to ligand binding. First, the mechanistic path followed depends on the protein and ligand concentrations. Second, the mechanism can only be assessed by considering all possible paths. Even when a given path may seem (with a strong emphasis on “seem”) thermodynamically unlikely, it can be a viable path because the path is determined by the flux, which is in turn determined by a product of concentrations and rate constants. This same caution applies when discussing “rate-determining steps:” the “rate-determining step” cannot be determined only by examining relative values of rate constants. The true rate-determining step in a sequential pathway is the step with the lowest flux because the reciprocal sum in Eq. 6 is dominated by the smallest Fi values. Thus, an alternative name for the “rate-determining” step is the “flux-determining step.”
An additional complication is that the mechanisms discussed thus far are simplifications of what actually occurs. Proteins exist in an ensemble of conformations (40, 41). For enzymatic reactions, an ensemble of conformations exists for each of the multiple intermediates that occur along the reaction pathway (12, 16, 42). Conformational ensembles are also important for protein folding. The calculation of fluxes for these more complicated situations is straightforward, but requires a detailed knowledge of the kinetics and thermodynamics of the reaction mechanism. When multiple conformations are involved, the distinction between conformational selection and induced fit mechanisms becomes blurred. For example, consider the case where the final conformation of the protein-ligand complex has a “lid” over the binding site (43). In this case, the assertion is usually made that an induced fit mechanism must occur. This is a statement about the kinetics of the ligand binding mechanism, namely the second-order rate constant for the combination of protein in the “lid-closed” conformation and ligand is very small. However, if an ensemble of conformations is present, the combination of protein and ligand may involve several ground state conformations that are significantly populated. The maltose binding protein is a good example of the situation. From crystallographic studies, the conformation of the protein without ligand is “open,” whereas the conformation with ligand bound that has a lid over the binding site is “closed.” Thus, the mechanism of ligand binding is cited as binding to the “open” state before a change in conformation to the “closed” state. However, recent NMR experiments have indicated that a significant fraction (≈5%) of the protein without ligand has a conformation in-between the “open” and “closed” states (44). If the binding of ligand involves this state mechanistically, then the mechanism could involve both conformational selection and induced fit mechanisms.
A flux-based approach to determine these mechanisms of conformational change coupled to binding has several conceptual and experimental advantages. Although rate constants are often estimated via equilibrium displacement time resolved experiments, this is not the only way to measure flux. Dynamic NMR experiments, including line shape analysis (45, 46) and relaxation dispersion experiments (47–50), detect equilibrium flux directly because no time dependent perturbation from equilibrium is necessary to observe the effect of chemical exchange between 2 or more magnetic environments. Because the data are not time-dependent, they can be analyzed without solving the differential equation(s) defined by the rate law. In some circumstances, for instance when the macromolecule concentration is much larger than the apparent Kd, this differential equation is second order and has no useful analytical solution. However, Eqs. 5 and 6 still apply under these conditions and can be used to model dynamic NMR data, allowing determination of kinetic parameters from estimates of flux. Thus, a flux-based analysis is ideally suited to dynamic NMR experiments.
In summary, we have shown that ligand-binding mechanisms involving multiple protein conformations can be complex. Moreover, the mechanism of ligand binding changes as the ligand and protein concentrations change. The mechanistic paths followed can be best assessed by using the concept of flux, but this requires a detailed knowledge of all of the rate constants and conformations involved. At the present time, the best way to determine this information appears to be from NMR, where both rates and populations can be determined, and from detailed kinetic studies.
Methods
All flux calculations were performed by using a Mathematica notebook, available for application to other systems from T.G.O. The key equations allow the calculation of free ligand and macromolecule concentrations from the known total concentrations and equilibrium constants:
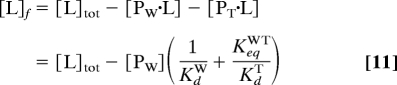 |
where [L]f and [L]tot are the free and total ligand concentrations; [PW·L] and [PT·L] are the concentrations of the ligand-bound forms of Pweak and Ptight; KdW and KdT are the dissociation constants of those species; KeqWT is the equilibrium constant for the Pweak ⇌ Ptight reaction in the absence of ligand; and [PW] is the concentration of Pweak given by:
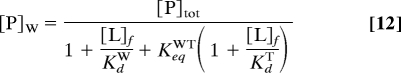 |
where [P]tot is the total macromolecule concentration. Substituting Eq. 12 into Eq. 11 yields a quadratic equation whose positive solution gives [L]f. The concentrations of the other species are:
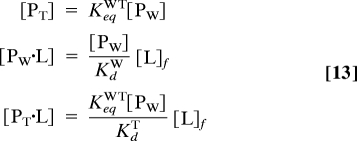 |
Acknowledgments.
This work was supported by National Institutes of Health Grants 5R01GM061367 and 5R01GM081666 (to T.G.O.).
Footnotes
The authors declare no conflict of interest.
References
- 1.Deupi X, Kobilka B. Activation of G protein-coupled receptors. Adv Protein Chem. 2007;74:137. doi: 10.1016/S0065-3233(07)74004-4. [DOI] [PubMed] [Google Scholar]
- 2.Weatherman RV, Fletterick RJ, Scanlan TS. Nuclear-receptor ligands and ligand-binding domains. Annu Rev Biochem. 1999;68:559–581. doi: 10.1146/annurev.biochem.68.1.559. [DOI] [PubMed] [Google Scholar]
- 3.Fersht A. Structure and Mechanism in Protein Sci: A Guide to Enzyme Catalysis and Protein Folding. New York: Freeman; 1999. [Google Scholar]
- 4.Hammes GG. Enzyme Catalysis and Regulation. New York: Academic; 1982. [Google Scholar]
- 5.von Hippel PH. From “simple” DNA-protein interactions to the macromolecular machines of gene expression. Annu Rev Biophys Biomol Struct. 2007;36:79–105. doi: 10.1146/annurev.biophys.34.040204.144521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Montange RK, Batey RT. Riboswitches: Emerging themes in RNA structure and function. Annu Rev Biophys. 2008;37:117–133. doi: 10.1146/annurev.biophys.37.032807.130000. [DOI] [PubMed] [Google Scholar]
- 7.Henkels CH, Kurz JC, Fierke CA, Oas TG. Linked folding and anion binding of the Bacillus subtilis ribonuclease P protein. Biochemistry. 2001;40:2777–2789. doi: 10.1021/bi002078y. [DOI] [PubMed] [Google Scholar]
- 8.Wright PE, Dyson HJ. Linking folding and binding. Curr Opin Struct Biol. 2009;19:31–38. doi: 10.1016/j.sbi.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Koshland D. The active site and enzyme action. Adv Enzymol Relat Subj Biochem. 1960;22:45–97. doi: 10.1002/9780470122679.ch2. [DOI] [PubMed] [Google Scholar]
- 10.Agarwal PK, et al. Network of coupled promoting motions in enzyme catalysis. Proc Natl Acad Sci USA. 2002;99:2794–2799. doi: 10.1073/pnas.052005999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Antikainen NM, Smiley RD, Benkovic SJ, Hammes G. Conformation coupled enzyme catalysis: Single-molecule and transient kinetics investigation of dihydrofolate reductase. Biochemistry. 2005;44:16835–16843. doi: 10.1021/bi051378i. [DOI] [PubMed] [Google Scholar]
- 12.Benkovic SJ, Hammes-Schiffer S. A perspective on enzyme catalysis. Science. 2003;301:1196–1202. doi: 10.1126/science.1085515. [DOI] [PubMed] [Google Scholar]
- 13.Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- 14.Cameron CE, Benkovic SJ. Evidence for a functional role of the dynamics of glycine-121 of Escherichia coli dihydrofolate reductase obtained from kinetic analysis of a site-directed mutant. Biochemistry. 1997;36:15792–15800. doi: 10.1021/bi9716231. [DOI] [PubMed] [Google Scholar]
- 15.Fierke CA, Johnson KA, Benkovic SJ. Construction and evaluation of the kinetic scheme associated with dihydrofolate reductase from Escherichia coli. Biochemistry. 1987;26:4085–4092. doi: 10.1021/bi00387a052. [DOI] [PubMed] [Google Scholar]
- 16.Hammes GG. Multiple conformational changes in enzyme catalysis. Biochemistry. 2002;41:8221–8228. doi: 10.1021/bi0260839. [DOI] [PubMed] [Google Scholar]
- 17.Liu H, Warshel A. The catalytic effect of dihydrofolate reductase and its mutants is determined by reorganization energies. Biochemistry. 2007;46:6011–6025. doi: 10.1021/bi700201w. [DOI] [PubMed] [Google Scholar]
- 18.Osborne MJ, Schnell J, Benkovic SJ, Dyson HJ, Wright PE. Backbone dynamics in dihydrofolate reductase complexes: Role of loop flexibility in the catalytic mechanism. Biochemistry. 2001;40:9846–9859. doi: 10.1021/bi010621k. [DOI] [PubMed] [Google Scholar]
- 19.Penner MH, Frieden C. Kinetic analysis of the mechanism of Escherichia coli dihydrofolate reductase. J Biol Chem. 1987;262:15908–15914. [PubMed] [Google Scholar]
- 20.Radkiewicz J, Brooks C. Protein dynamics in enzymatic catalysis: exploration of dihydrofolate reductase. J Am Chem Soc. 2000;122:225–231. [Google Scholar]
- 21.Sawaya MR, Kraut J. Loop and subdomain movements in the mechanism of Escherichia coli dihydrofolate reductase: Crystallographic evidence. Biochemistry. 1997;36:586–603. doi: 10.1021/bi962337c. [DOI] [PubMed] [Google Scholar]
- 22.Schnell JR, Dyson HJ, Wright PE. Structure, dynamics, and catalytic function of dihydrofolate reductase. Annu Rev Biophys Biomol Struct. 2004;33:119–140. doi: 10.1146/annurev.biophys.33.110502.133613. [DOI] [PubMed] [Google Scholar]
- 23.Wang L, Goodey NM, Benkovic SJ, Kohen A. Coordinated effects of distal mutations on environmentally coupled tunneling in dihydrofolate reductase. Proc Natl Acad Sci USA. 2006;103:15753–15758. doi: 10.1073/pnas.0606976103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wong KF, Selzer T, Benkovic SJ, Hammes-Schiffer S. Impact of distal mutations on the network of coupled motions correlated to hydride transfer in dihydrofolate reductase. Proc Natl Acad Sci USA. 2005;102:6807–6812. doi: 10.1073/pnas.0408343102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang Z, Rajagopalan PT, Selzer T, Benkovic SJ, Hammes G. Single-molecule and transient kinetics investigation of the interaction of dihydrofolate reductase with NADPH and dihydrofolate. Proc Natl Acad Sci USA. 2004;101:2764–2769. doi: 10.1073/pnas.0400091101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bloom JD, Labthavikul ST, Otey CR, Arnold FH. Protein stability promotes evolvability. Proc Natl Acad Sci USA. 2006;103:5869–5874. doi: 10.1073/pnas.0510098103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dyson HJ, Wright PE. Intrinsically unstructured proteins and their functions. Nat Rev Mol Cell Biol. 2005;6:197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
- 28.Wyman J. The binding potential, a neglected linkage concept. J Mol Biol. 1965;11:631–644. doi: 10.1016/s0022-2836(65)80017-1. [DOI] [PubMed] [Google Scholar]
- 29.Espinoza-Fonseca LM. Reconciling binding mechanisms of intrinsically disordered proteins. Biochem Biophys Res Commun. 2009;382:479–482. doi: 10.1016/j.bbrc.2009.02.151. [DOI] [PubMed] [Google Scholar]
- 30.Muralidhara BK, Wittung-Stafshede P. FMN binding and unfolding of Desulfovibrio desulfuricans flavodoxin: “Hidden” intermediates at low denaturant concentrations. Biochim Biophys Acta. 2005;1747:239–250. doi: 10.1016/j.bbapap.2004.11.012. [DOI] [PubMed] [Google Scholar]
- 31.Muralidhara BK, Rathinakumar R, Wittung-Stafshede P. Folding of Desulfovibrio desulfuricans flavodoxin is accelerated by cofactor fly-casting. Arch Biochem Biophys. 2006;451:51–58. doi: 10.1016/j.abb.2006.03.032. [DOI] [PubMed] [Google Scholar]
- 32.Narayanan R, Ganesh OK, Edison AS, Hagen SJ. Kinetics of folding and binding of an intrinsically disordered protein: The inhibitor of yeast aspartic proteinase YPrA. J Am Chem Soc. 2008;130:11477–11485. doi: 10.1021/ja803221c. [DOI] [PubMed] [Google Scholar]
- 33.Onitsuka M, Kamikubo H, Yamazaki Y, Kataoka M. Mechanism of induced folding: Both folding before binding and binding before folding can be realized in staphylococcal nuclease mutants. Proteins. 2008;72:837–847. doi: 10.1002/prot.21978. [DOI] [PubMed] [Google Scholar]
- 34.Shoemaker BA, Portman JJ, Wolynes PG. Speeding molecular recognition by using the folding funnel: The fly-casting mechanism. Proc Natl Acad Sci USA. 2000;97:8868–8873. doi: 10.1073/pnas.160259697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sugase K, Dyson HJ, Wright PE. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature. 2007;447:1021–1025. doi: 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
- 36.Turjanski AG, Gutkind JS, Best RB, Hummer G. Binding-induced folding of a natively unstructured transcription factor. Plos Comput Biol. 2008;4:e1000060. doi: 10.1371/journal.pcbi.1000060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Adilakshmi T, Bellur DL, Woodson SA. Concurrent nucleation of 16S folding and induced fit in 30S ribosome assembly. Nature. 2008;455:1268–1272. doi: 10.1038/nature07298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Milla ME, Brown BM, Waldburger CD, Sauer RT. P22 Arc repressor: Transition state properties inferred from mutational effects on the rates of protein unfolding and refolding. Biochemistry. 1995;34:13914–13919. doi: 10.1021/bi00042a024. [DOI] [PubMed] [Google Scholar]
- 39.Zeeb M, Lipps G, Lilie H, Balbach J. Folding and association of an extremely stable dimeric protein from Sulfolobus islandicus. J Mol Biol. 2004;336:227–240. doi: 10.1016/j.jmb.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 40.Dill KA, Chan HS. From Levinthal to pathways to funnels. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 41.Hilser VJ, García-Moreno E,B, Oas TG, Kapp G, Whitten ST. A statistical thermodynamic model of the protein ensemble. Chem Rev. 2006;106:1545–1558. doi: 10.1021/cr040423+. [DOI] [PubMed] [Google Scholar]
- 42.Benkovic SJ, Hammes G, Hammes-Schiffer S. Free-energy landscape of enzyme catalysis. Biochemistry. 2008;47:3317–3321. doi: 10.1021/bi800049z. [DOI] [PubMed] [Google Scholar]
- 43.Sullivan SM, Holyoak T. Enzymes with lid-gated active sites must operate by an induced fit mechanism instead of conformational selection. Proc Natl Acad Sci USA. 2008;105:13829. doi: 10.1073/pnas.0805364105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tang C, Schwieters CD, Clore GM. Open-to-closed transition in apo maltose-binding protein observed by paramagnetic NMR. Nature. 2007;449:1078–1082. doi: 10.1038/nature06232. [DOI] [PubMed] [Google Scholar]
- 45.Huang GS, Oas TG. Submillisecond folding of monomeric lambda repressor. Proc Natl Acad Sci USA. 1995;92:6878–6882. doi: 10.1073/pnas.92.15.6878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ropson IJ, Frieden C. Dynamic NMR spectral analysis and protein folding: Identification of a highly populated folding intermediate of rat intestinal fatty acid-binding protein by 19F NMR. Proc Natl Acad Sci USA. 1992;89:7222–7226. doi: 10.1073/pnas.89.15.7222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Burton RE, Huang GS, Daugherty MA, Fullbright PW, Oas TG. Microsecond protein folding through a compact transition state. J Mol Biol. 1996;263:311–322. doi: 10.1006/jmbi.1996.0577. [DOI] [PubMed] [Google Scholar]
- 48.Eisenmesser EZ, et al. Intrinsic dynamics of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 49.Igumenova TI, Brath U, Akke M, Palmer AG. Characterization of chemical exchange using residual dipolar coupling. J Am Chem Soc. 2007;129:13396. doi: 10.1021/ja0761636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mittermaier A, Kay LE. New tools provide new insights in NMR studies of protein dynamics. Science. 2006;312:224–228. doi: 10.1126/science.1124964. [DOI] [PubMed] [Google Scholar]