Abstract
DNA is a very important cell structural element, which determines the level of expression of genes by virtue of its interaction with regulatory proteins. We use electron (EM) and atomic force microscopy (AFM) to characterize the flexibility of double-stranded DNA (∼150–950 nm long) close to a charged surface. Automated procedures for the extraction of DNA contours (∼10–120 nm for EM data and ∼10–300 nm for AFM data) combined with new statistical chain descriptors indicate a uniquely two-dimensional equilibration of the molecules on the substrate surface regardless of the procedure of molecule mounting. However, in contrast to AFM, the EM mounting leads to a noticeable decrease in DNA persistence length together with decreased kurtosis. Analysis of local bending on short length scales (down to 6 nm in the EM study) shows that DNA flexibility behaves as predicted by the wormlike chain model. We therefore argue that adhesion of DNA to a charged surface may lead to additional static bending (kinking) of ∼5 degrees per dinucleotide step without impairing the dynamic behavior of the DNA backbone. Implications of this finding are discussed.
Introduction
DNA's charge properties and its high flexibility allow irreversible adhering of molecules onto a planar surface forming a two-dimensional object and thereby permitting visualization by means of electron microscopy (EM) and atomic force microscopy (AFM). In general, adhesion and immobilization are achieved by virtue of ionic interactions between DNA phosphates and surface charges. These processes lead to:
-
1.
A loss of one degree of freedom, thereby diminishing the number of possible DNA configurations.
-
2.
Potential distortions of the DNA double helix reflected in notable alterations in DNA conformation(s), which may lead to a change in the apparent persistence length.
A quantitative description of the apparent DNA conformation confined to a plane requires invoking the existing models for DNA conformation in solution (three-dimensional) and in plane as well. The wormlike chain (WLC) model treats DNA as a continuous, inextensible (elastic) rod and considers the deformations occurring at each infinitesimal point following Hooke's law (1,2). Another model is based on a discrete description of a DNA polymer chain attributing its conformational flexibility to the thermal fluctuations in the angles between adjacent basepairs (3). Similar to the WLC model, the discrete model describes DNA as a homopolymer. The main statistical quantities describing behavior of homopolymers by either model have similar analytical expressions, allowing the use of either description for the analysis purposes. Several extensions were made toward a more realistic model, such as the inclusion of static bends or kinks distributed randomly (in position and orientation) along the polymer chain (4–9).
Numerous examples demonstrate the power of EM and AFM in determination of DNA persistence length and the conformational state of DNA confined to an imaging plane (9–20). In many instances, the persistence length calculated close to 50 nm (10–14,16,21,22), a generally accepted value determined by other techniques exploiting mainly bulk measurements (15,17,18). However, smaller values (36 nm (23)) and larger values (∼80–140 nm (9,11,24,25)) were reported as well. In addition, there is disagreement about the state of the deposited molecules:
-
1.
Either molecules equilibrate on the imaging surface before their adhesion (called the two-dimensional state), or
-
2.
molecules are captured (i.e., trapped) by the imaging surface without their equilibration, leading to the conformation reflecting a projection of three-dimensional conformation in solution onto a two-dimensional plane (called the three-dimensional state).
A mixture of both two-dimensional and three-dimensional states can be present for each molecule or their ensemble, depending on the deposition procedure and DNA length. Both EM and AFM provide evidence(s) for a two-dimensional state (10,11,19) and a three-dimensional one (11,20,26). In this line, recent studies show that DNA flexibility may vary in a length-dependent manner, exhibiting an increased flexibility (via spontaneous large-angle bends) over distances <5 nm (16). Even the breakdown of the conventional elastic rod model is suggested for short DNA fragments (27).
In this article, we will argue that successful analysis of two-dimensional data sets requires both dedicated image processing and a model describing the statistical behavior of DNA molecules confined to a plane. We will show that DNA immobilized onto a surface can exhibit a notable variation in persistence length, yet showing its chain statistics as expected over long separation distances (in EM from 10 to 120 nm and in AFM from 10 to 300 nm) along the contour. By extending the number of statistical quantities, we prove a two-dimensional equilibrium state of immobilized molecules. A modification of the homopolymer WLC model was required to provide an adequate description of the DNA configuration in plane. To this end, we introduce local surface-induced static bends leading to an averaged heteropolymer WLC model (3–5,13). We also argue that modulations in apparent DNA persistence length due to interactions with the imaging surface are not a methodological artifact, but rather a general property of DNA that also manifests itself upon interaction with protein surfaces.
The developed software for the image and data analysis is provided as MATLAB (The MathWorks, Natick, MA) scripts, which can be freely downloaded from www.diplib.org/home22266. It provides the possibility to analyze images obtained from either EM or AFM imaging, given sufficient image quality, and provide DNA characterization as presented below. The software makes use of the MATLAB toolbox DIPimage (Technical University Delft, The Netherlands, www.diplib.org).
Materials and Methods
Sample preparation
Supercoiled pPGM1 plasmid DNA (2981 bp) was purified using Qiagen kits (Hilden, Germany) (28). Linear DNA fragments were obtained after digestion with either EcoRI (2981-bp fragment), EcoRI/ScaI (1444-bp and 1837-bp fragments), or PvuII (474-bp and 2507-bp fragments) and purified using gel filtration chromatography on a Superose 6 column (SMART system, Amersham Biosciences, Fairfield, CT). A 474-bp fragment was obtained by additional purification through an anion exchange Waters Gen-Pak FAX column (Milford, MA). All samples were stored in a buffer of 10 mM Tris-HCl, pH 7.5, 10 mM NaCl, and 0.1 mM Na3EDTA at a concentration of 200–400 μg/mL.
Electron and atomic force microscopy
Two different procedures were used for the deposition of DNA molecules for electron microscopy (28): adsorption to glow-discharged carbon film and to polylysine film. The samples were analyzed with a Philips CM12 electron microscope (Eindhoven, The Netherlands) in a dark-field mode at a magnification of 28,000–35,000. The sampling density of the digital images was 1.21 nm/pixel or 1.51 nm/px.
For AFM, DNA was deposited onto the surface of freshly cleaved mica (Muscovite, Plano, Germany). Samples were a drop of DNA solution (10 μL) at a concentration of 2 μg/mL from buffer (B) was placed onto the surface of freshly cleaved mica (Muscovite). Samples were scanned using a Digital Instruments MultiMode scanning probe microscope Nanoscope IIIa (Veeco, Plainview, NY) operating in Tapping mode. The sampling density of the digital images was 7.81 nm/pixel. For details, see the Supporting Material.
Image and data analysis
The image analysis software was custom-developed using the MATLAB toolbox DIPimage. The software is provided as MATLAB scripts (which can be freely downloaded from www.diplib.org/home22266). The algorithm uses an improved Fast Marching algorithm (29) shortly after identification of the relevant molecules to find the DNA centerline. The image analysis algorithm was extensively validated on images generated by Monte Carlo simulations. In the data analysis, extra precaution was taken in sampling the strands to avoid correlation. Reusing all data for computing the characteristic quantities for each length along the DNA yield highly correlated points. To avoid this, we divided each DNA strand into length segments randomly drawn from a predefined set of lengths such that no piece of strand is used twice. For details, see the Supporting Material.
Results
Image processing and analysis
Recently, we developed an automated procedure for finding a path through the centerline of stringlike structures, such as DNA, obtained, for instance, by high-resolution imaging techniques (29). Briefly, the method (see Materials and Methods) is based on a minimum-cost path algorithm and allows determination of a path whose distance to the true centerline is more than an order-of-magnitude smaller in areas of high curvature than traditional algorithms. The method has been successfully applied to several thousands of DNA molecules on high-resolution images obtained by EM and AFM. The paths extracted by this method stay in the middle of the DNA strand without cutting corners. As a consequence, the length measurement remains unbiased and the curvature is no longer underestimated. Fig. 1 shows a typical EM micrograph of 474-bp-long DNA fragment, an AFM image of a mixture of 474- and 2505-bp-long DNA fragments, and the convergence of the DNA centerline (from red via green to blue).
Figure 1.

(a) EM micrograph of 474-bp DNA fragment mounted onto polylysine film from 1 mM NaCl. (b and c) EM and AFM images of DNA digested with EcoRI and ScaI (1144-bp and 1837-bp fragments, respectively), and mounted from 5 mM HEPES, pH 7.5, 10 mM KCl, and 5 mM MgAc2; (d) cartoon showing convergence of automatic iterative image processing (from red via green to blue) as described in Materials and Methods to find the DNA backbone. Scale bars, 100 nm. Images a, b, and d are displayed using inverted grayscale.
The method was validated by Monte Carlo simulations of DNA molecules following WLC statistics in plane (see Materials and Methods). Validation of the method allowed us to analyze not only full-length DNA fragments, but also short segments after a magnification calibration. We found that isolated and non-self-intersecting strands behave identical to pieces of self-intersecting molecules, i.e., persistence lengths consistent within 1 nm (data not shown). This is very advantageous as longer molecules tend to intersect more and the chances of finding isolated molecules without self-intersection decreases.
Average statistical quantities were calculated as a function of length along the DNA based on all scored (without self-intersections) molecules as described in Materials and Methods after which we fitted the corresponding Eqs. 4–6 to the measured quantities. Special precautions were made to avoid intrinsic correlations between measured quantities for different distances along the molecule. Figs. 2 and 3, a–c, exemplify the results of estimations of persistence length calculated from average squared end-to-end distance (Eq. 4), average squared angular difference (Eq. 5), and average cosine of angular difference (Eq. 6), respectively. The data show very good agreement with theoretical expectations and remarkable consistency of persistence length calculated using different formulas. The uncertainty in determining the persistence length due to the fitting was in the range of 1–2 nm. We applied this procedure to the data drawn from various experiments and found very good consistency among the fit results obtained from the different formulas (see Table 1). Together with the Monte Carlo simulations, the results on the experimental data validate the procedure for image processing and data analysis.
Figure 2.
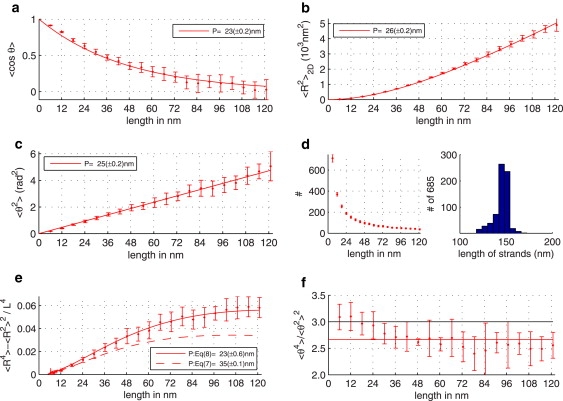
Example of the data analysis for the 474-bp DNA fragment mounted onto polylysine film from 1 mM NaCl and imaged by EM. Panels a–c show estimates of the persistence length based on 〈cosθ(L)〉 (Eq. 5), 〈R2(L)〉 (Eq. 4), and 〈θ2(L)〉 (Eq. 6), respectively. (d) Number of unique DNA strand elements used to compute the different descriptors per contour length L and the length distribution of the analyzed molecules. (e) Normalized difference (〈R2〉 − 〈R2〉2)/L4 (Eq. 9) with fits for the two-dimensional (Eq. 8) and three-dimensional (Eq. 7) case. (f) Kurtosis 〈θ4〉/〈θ2〉2 (which is equal to 3 for θ normally distributed around zero).
Figure 3.
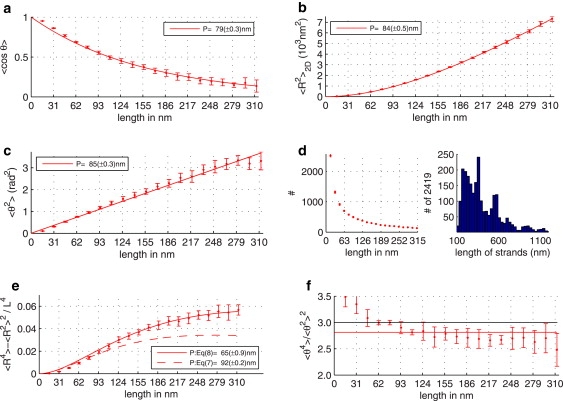
Example of the data analysis for 2981-bp DNA with 10 mM KCl, 5 mM MgAc2 mounted on mica and imaged with AFM; panels a–c show estimates of the persistence length based on 〈cosθ(L)〉 (Eq. 5), 〈R2(L)〉 (Eq. 4), and 〈θ2(L)〉 (Eq. 6), respectively. (d) Number of unique DNA strand elements used to compute the different descriptors per contour length L and the length distribution of the analyzed molecules. (e) Normalized difference (〈R4〉/〈R2〉2)/L4 (Eq. 9) with fits for the two-dimensional (Eq. 8) and three-dimensional (Eq. 7) case. (f) Kurtosis 〈θ4〉/〈θ2〉2 (which is equal to 3 for θ Gaussian distributed around zero).
Table 1.
Persistence length calculated using different statistical descriptors of the WLC model for various mounting and imaging conditions
| Mounting conditions | Scored length (nm) (No. molecules) | P〈R2〉 (nm) | P〈cos〉 (nm) | P〈θ2〉 (nm) | P〈D4〉 (nm) | Avg. (nm) |
|---|---|---|---|---|---|---|
| 2.5 mM NaCl∗ | ∼33,000 (210) | 30 | 29 | 29 | 29 | 29 |
| 10 mM NaCl∗ | ∼70,000 (451) | 31 | 31 | 33 | 34 | 32 |
| 50 mM NaCl∗ | ∼37,000 (235) | 35 | 31 | 32 | 30 | 32 |
| 100 mM NaCl∗ | ∼76,000 (490) | 25 | 25 | 26 | 25 | 25 |
| 1 mM NaCl, polylysine† | ∼107,000 (685) | 26 | 23 | 25 | 23 | 24 |
| 2.5 mM NaCl, polylysine† | ∼52,000 (332) | 28 | 26 | 27 | 23 | 26 |
| 10 mM KCl, 5 mM MgAc2†,‡ | ∼134,000 | 23 | 20 | 22 | 23 | 22 |
| 10 mM KCl, 5 mM MgAc2†,§ | ∼151,000 | 23 | 21 | 24 | 27 | 24 |
| 10 mM KCl, 5 mM MgAc2†,¶ | ∼112,000 | 21 | 19 | 22 | 26 | 22 |
| 10 mM KCl, 5 mM MgAc2†,‖ | ∼1,000,000 | 89 | 80 | 81 | 66 | 79 |
| 10 mM KCl, 5 mM MgAc2†,∗∗ | ∼563,000 | 101 | 91 | 91 | 76 | 90 |
474-bp DNA fragment, deposition onto glow-discharged carbon film, EM data.
474-bp fragment, deposition onto polylysine film, EM data.
Mixture of 1144-bp and 1837-bp fragments, deposition onto glow-discharged carbon film, EM data.
2981-bp fragment, deposition onto glow discharged carbon film, EM data.
Mixture of 474-bp and 2507-bp fragments, deposition onto glow-discharged carbon film, EM data.
2981-bp fragment, deposition onto mica, AFM data.
Mixture of 474-bp and 2507-bp fragments, deposition onto mica, AFM data.
Dimensionality of surface-immobilized DNA and its persistence length
The statistical quantities for the conformation description of homopolymers in a three-dimensional plane are
| (1) |
| (2) |
| (3) |
where L is the length along the DNA (or contour length) between two points on a polymer segment, P3D is the persistence length in three dimensions, and θ is the angle between two tangent vectors separated by a distance L along the DNA. Equations 1–3 used for the description of polymer chain statistics are similar for continuum (WLC) and discrete models (1–4) and do not account for self-avoiding behavior. For the two-dimensional case, the corresponding formulae are (10,11)
| (4) |
| (5) |
| (6) |
Note that Eqs. 4–6 and Eqs. 1–3 display identical mathematical structures. The only difference is a scaling of the persistence length between two and three dimensions, i.e., with the substitution 2P3D → P2D in Eqs. 1–3, the formulas are identical. In the remainder of this article, we will use P2D = 2P3D when explicitly referring to the two-dimensional model. In view of the above considerations, this implies that, in a strict sense, the persistence length can be determined with an uncertainty factor of two in absence of prior knowledge of the conformation dimensionality. To avoid this uncertainty, we computed the average fourth moment of the end-to-end distance for the molecules and compared the value with the model in two and three dimensions. For the WLC model, the expression has been derived in three dimensions (30):
| (7) |
For two dimensions, the expression is (see Eq. S12 (31) and Eq. C18)
| (8) |
Importantly, the formulae for 〈R4〉 do not scale from two to three dimensions. However, the difference vanishes for lengths exceeding ∼500 bp, after which . In contrast, the difference
| (9) |
does not vanish. Not even for a length up to 3000 bp and P3D ≈ 50 bp, after which (for P3D = 100 bp the difference can be detected up to ∼5000 bp). Therefore, the quantity 〈D4〉 provides reliable means for determining the dimensionality of the deposited molecules and hence the persistence length by selecting the correct model. Methodologically, it means that we fit two sets of Eqs. 1–3 and Eq. 7, respectively, to Eqs. 4–6 and Eq. 8, to the quantities measured from the experimental data. The test of Eq. 9 is used to make a proper choice for the dimensionality of the molecules and as a result determines the persistence length in three dimensions by selecting the corresponding set of formulae. The plots of 〈D4〉 for two- and three-dimensional cases are depicted in Fig. 2 e. It is clearly seen that
-
1.
the data can be described using the corresponding formula for two dimensions (Eq. 8); and
-
2.
the persistence length is very close to those calculated using Eqs. 4–6.
In contrast, using Eq. 7, we failed to fit the data for all distance separations up to 120 nm. The depicted curve is the closest approximation to the experimental data with P3D = 35 nm. The DNA molecules analyzed in Fig. 2 were 474-bp-long and imaged by EM. Convincingly, we found also for longer strands imaged by AFM in Fig. 3 e that 〈D4〉 best fits to the two-dimensional formulae, thereby supporting the conclusion that the DNA was imaged in a two-dimensional equilibrium state.
Having validated the image processing, data analysis, and the usage of the corresponding formulae (Eqs. 4–6 and Eq. 8), we calculated persistence lengths of DNA fragments ranging from 474 bp up to ∼3000 bp for different salt conditions (NaCl 0–100 mM, KCl, MgAc2), buffer composition (Tris, HEPES), and nature of the imaging surface (glow-discharged carbon film, polylysine film) by EM and AFM. The results show (compare Table 1) that all four quantities used for the persistence-length calculation give very similar results, supporting our approach even further. It implies that regardless of deposition and imaging conditions, DNA molecules behave as two-dimensional polymers for lengths in the range ∼10–120 nm (EM data) or ∼10–300 nm (AFM data). EM data show that the persistence length of the molecules deposited from 1 to 100 mM NaCl is in the range 25–32 nm, regardless of the nature of the deposition surface (glow-discharged carbon film or polylysine film). At zero NaCl concentration, we measured a smaller persistence length of 15–17 nm (not shown). Deposition from the 5 mM MgAc2 and 10 mM KCl solutions led to a small but detectable decrease in persistence length (22–24 nm). In contrast, using the latter conditions for the deposition on a mica surface (AFM data) leads to a dramatic increase of the persistence length to 80–90 nm as calculated by using either quantity (Table 1).
Kurtosis and static bending of DNA
The homopolymer model describes the DNA flexibility by assuming an harmonic potential in the bending angle θ. This model results in 〈θ〉 = 0. The kurtosis is defined as
| (10) |
and is always equal to 3, regardless of the dimensionality of the molecules in this model. We found that for AFM data the kurtosis is close to 3 for distances ∼50–80 nm along the DNA; for longer distances, it remains within the range 2.7–2.8 (see Fig. 3 f). However, for EM data the kurtosis was always below 3, showing a decrease to ∼2.5 for distances larger than 25 nm along the DNA (see Fig. 2 f). For a homopolymer model, a deviation of the kurtosis from the expected value may be indicative for either an inadequate procedure for image processing and/or analysis, or the presence of nonequilibrium processes during deposition. Another possibility implies that harmonic potential accounting for DNA bending is still quadratic but around a nonzero value (heteropolymer model). Having validated the image processing, the data analysis, and the applicability of the formulae used, we consider the last possibility. Therefore, we introduce a small, surface-induced static bending at each dinucleotide step. For the simple assumption that all static bends occur in plane with identical amplitude but random sign, we derived an expression for the kurtosis accounting for the average static bending angle and separation distance (see the Supporting Material). The kurtosis for the heteropolymer model,
| (11) |
shows that the kurtosis rapidly approaches 3 as the length along the DNA n increases. In this case, the sign of the static bends was chosen randomly with equal probabilities. To calculate the average amplitude of the static bends, we recall that , where and stand for the dynamic behavior of polymer chain and static bending, respectively (5,32). Using an identical procedure for DNA deposition as we used for EM analysis, Cognet et al. (13) found that for DNA molecules confined to a plane, /bp. Since we are looking for angle displacement in two dimensions, we have to use the corresponding value for the persistence length. Our EM measurements show that P3D is in the range of 15–32 nm (see Table 1), which corresponds to P2D ∼90–190 bp. It means that is in the range 3.7°–7.2°.
For an intermediate value of θstat = 5.3°, we performed Monte Carlo simulations of polymer chains and evaluated the expected kurtosis for different lengths along the DNA n and different probabilities p of positive and negative sign of θ0. Given the assumption of p = 0.5 and a large number of molecules (>104), the kurtosis is indeed exactly 3 for any n. If we decrease the number of molecules to similar numbers as encountered in the experiments (∼500), we find a decrease of the kurtosis with increasing n for any θstat ≠ 0 (see Fig. 4) for any value of p. Higher values of p yield smaller kurtosis for larger distances along the DNA similar to the experimental data, EM data in particular. Considering the fact that we only have a few hundred molecules, no conclusion can be drawn about the exact value of p. However, it must be in the range 0.5 ± 0.03, given the simulations. In control simulations with θstat = 0°, the kurtosis was always 3 for any number of molecules.
Figure 4.
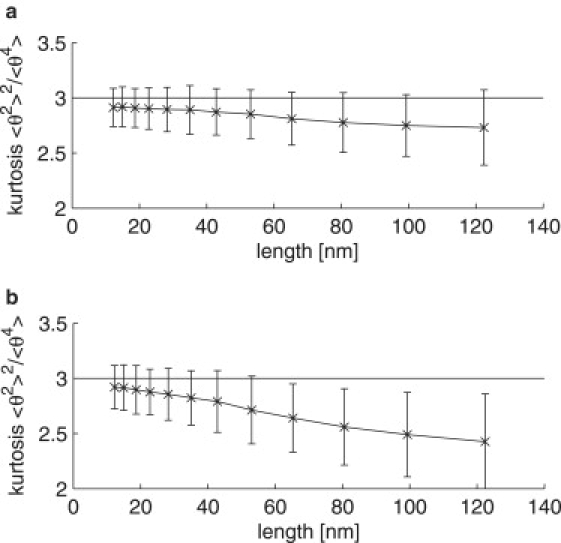
Simulated kurtosis for a nonzero static bending of θstat = 5.3° (a) probability p = 0.5 and (b) probability p = 0.53 of the sign. The simulation was performed on 500 molecules of 474-bp chain length (see Materials and Methods) and averaged over 500 independent realizations. The error bars indicate 1σ spread.
Therefore, it becomes evident that the experimental data can be explained by a modified homopolymer model accounting for static bending together with limited sampling. However, in contrast to AFM data, EM data require that static bending should be larger mostly due to surface-induced bending in addition to the intrinsic dynamic and static bendings.
DNA bending at short distances
We investigated flexibility or bending of DNA over very short distances as done by Wiggins et al. (16) in an AFM study. Their measurements imply that the elastic energy of highly bent DNA conformations is lower than predicted by the WLC model. That is, on short length scales, large angle bends occur more frequently than predicted by the WLC. In Fig. 5 c, we computed the negative logarithm of the observed bend-angle probability distribution function G(θ;L) for short distances L for the molecules investigated in Fig. 2. In Eq. 12, we have derived a formula (see the Supporting Material)
| (12) |
that takes binning effects in the probability density function of the bending angle θ into account. This enables exact fitting of the persistence length also from the histogram. The fitted persistence length is depicted in Fig. 5 b in blue. For three distances along the DNA L = 3.02, 4.54, and 6.05 nm, we found P ∼28 nm. We did not find any deviation from a Gaussian distribution of the bend angles over any distance, and in particular not over short distances (see Fig. 5 c). The data shown here are typical for all investigated supports and mounting conditions used for EM. For AFM data, we could not investigate the bending on such short length scales due to a lack of resolution.
Figure 5.
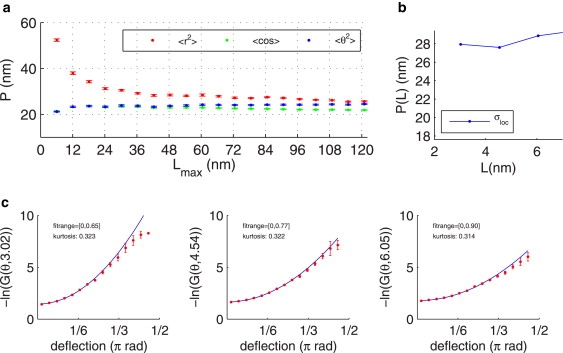
(a) Fitted persistence length based on 〈R2〉, 〈θ2〉, and 〈cosθ〉 as a function of the distance length L along the DNA for the same molecules as in Fig. 2. (b) Fitted persistence length (blue) for very short distances only based on the histograms shown in panel c. (c) Negative logarithm −ln G (Eq. 12) of occurrence of the deflection angle θ for very short segments (L = 3.02, 4.54, and 6.05 nm). The deflection angle histogram is computed from a few thousand bends.
Discussion
Microscopy techniques permit the analysis of conformations of long flexible polymer molecules, DNA in particular, in a dried state. The analysis requires that
-
1.
molecules irreversibly adhere to an imaging surface; and
-
2.
all segments along the length should be imaged in an identical manner, though possibly with some intensity modulations reflecting the processes of molecule deposition and/or detection.
However, these requirements do not ensure that the conformation of deposited molecules will be unique (two- or three-dimensional) and identical; moreover, molecules may be of mixed conformations. In addition, the apparent conformation of the molecules may depend on their length. The conformational state of deposited molecules is traditionally analyzed by fitting experimental datasets with the formulae accounting for statistical properties of equilibrated molecules either in two or three dimensions. Goodness of fit, the intrinsic conformity of the calculated values for the persistent length together with agreement with literature data, is often considered as a strong support for the techniques used for molecules deposition and image analysis. In contrast, inconsistency of the experimental data with theoretical expectations calculated using one of the descriptors, e.g., 〈R2〉, is often interpreted as a result of nonequilibrium processes before adhesion of the molecules, e.g., trapping of the molecules by the deposition surface (11). Goodness of fit, however, only shows the validity of the model used without guarantee that the persistence length will be close to ∼50 nm. Deviation of the measured persistence length (using, e.g., 〈R2〉 descriptor) from the expected value of ∼50 nm, in some instances, allowed authors to speculate about the projection of three-dimensional equilibrium DNA conformation onto a two-dimensional imaging plane (33).
Our data show that DNA molecules of ∼500–3000-bp-long deposited onto a solid support (either glow-discharged carbon film or polylysine film or mica) behave as an equilibrated two-dimensional polymer chain for distances along the DNA up to ∼120 nm (EM measurements, Fig. 2 e) or 300 nm (AFM measurements, Fig. 4 e), though of different persistence length. The overall procedure used for EM imaging (deposition onto glow-discharged carbon film together with uranyl staining) had been validated in a sense that it does not change DNA dynamic behavior, i.e., 〈〉 is close to 4.6° (13). However, it does modulate the apparent persistence length. We believe that these modulations of persistence length (decreasing) are mainly due to distortions of the DNA backbone. These distortions do not impair the harmonic potential of DNA flexibility at each dinucleotide step since the conformation of the molecules along long distances follow theoretical predictions with high accuracy. We rather believe that adhesion to a charged (imaging) surface induces an additional static bending. We note that intrinsic static bends, introduced to describe sequence-dependent DNA deformations, i.e., curvature (reviewed in (5)), can account for ∼3° (34) on average for the molecules confined to a plane. Our data show that the static bending should be in the range 3.7°–7.2° (in plane), most probably close to 5°, implying that deposition onto carbon film or polylysine film induces additional DNA bending (kinking). In this line, AFM data showing the kurtosis in the range 2.7–2.8 are in agreement with the heteropolymer model of DNA exhibiting intrinsic static bending that is supported by our Monte Carlo simulations (see Fig. 4).
In support of our conjecture of equilibrated two-dimensional polymers, we stress that conformity of DNA conformation to the theoretical expectations was found for distances along the DNA beyond 100–150 nm, a value after which a significant deviation of DNA conformation from the WLC model is usually found (9,20,26,35). This deviation is often interpreted as a three-dimensional state of imaged DNA due to surface trapping (9,20,26). Fig. 3 shows that under our deposition/preparation conditions, DNA conformation can be well fitted by any descriptor used here until separation distances ∼300 nm. Attempts to fit 〈R2〉 using scaling formulae for polymer wandering in two or three dimensions, as earlier suggested (20,26), did not produce any physically relevant result. Importantly, at all separation distances, DNA behaves in accordance with the WLC model for either combination of mounting/imaging conditions.
The whole analysis presented here is based on fitting the known homopolymer formulae (Eqs. 4–6 and 8) to the experimental data. However, as we argued in the case of EM mounting, an additional (induced) static bending is required; we have to justify usage of these formulae for heteropolymer molecules. Using Monte Carlo simulation, we generated a set of 474-bp-long molecules using the harmonic potential with different values of 〈θdyn〉 (corresponding to P3D ranging from ∼20 nm to ∼50 nm) and θstat = 5.3°, and thus, analyzed simulated molecules as described. The results (see Fig. S5) clearly show that
-
1.
fitting with Eqs. 4–6 and 8, give similar values for the apparent persistence using either descriptor; and
-
2.
thus calculated apparent persistence length is in a good agreement with the effective persistence length determined via Eq. S14 in the Supporting Material.
The kurtosis decreases from 3 to ∼2.5 as the length along the DNA increases up to ∼100 nm in agreement with EM data. Attempts to fit the data with Eq. 7, corresponding to the three-dimensional conformation of the molecules, failed for distances beyond 40 nm, implying their two-dimensional state. Importantly, fitting the model to short distances (4 nm and 6 nm) using Eq. 12, led to a persistence length similar to those calculated using Eqs. 4–6 and 8. Together, these results validate the usage of Eqs. 4–6 and 8, for the purpose of analysis of heteropolymer molecules.
It is known that, in general, the persistence length of DNA decreases as the concentration of monovalent cations increases in solution (15,17,18,36), reaching a value close to 50 nm. Similar behavior is observed for multivalent cations, though the limiting value for the persistence length may be somehow smaller (15,17,18,36). Deposition onto negatively charged surface, e.g., freshly cleaved mica, mediated by the divalent cations, e.g., Mg2+, may preserve persistence length close to 50 nm (11,35). In some instances, higher values (∼80–140 nm) were reported (9,11,24,25) using 〈R2〉 or 〈θ2〉 descriptors. In the latter case, a clear deviation from the expected strait line was found (11) for separations >100 nm, indicative for the contribution of excluded volume effects for molecules with contour lengths larger than 20 persistence lengths. In our case, AFM data show that either descriptor can be fit by the analytical formulas giving consisting values for the persistence length. Since the goodness of fit was high for DNA separations in the range ∼15–300 nm (see Fig. 3), we infer that apparent persistence length was similar regardless of separation along DNA, with the contour implying small contribution of excluded volume effect. Thus, our data are in accord with the results of Frontali and co-workers (10,19), showing absence of excluded volume effect for cytochrome c adsorbed DNA with contour lengths up to 30 persistence lengths.
Large values for the persistence length can be explained by modulation of preequilibrated DNA molecules close to the mica surface during rinsing step. Rinsing of the sample and its drying—steps that are required for the fixation of DNA onto surface and imaging in air—may lead to the modulation of apparent DNA conformation as described by Cherny and Jovin (28), in a way that depends on the forces occurring between preequilibrated molecules and mica surface. Since in many instances rinsing buffer is pure water, the Debye length increases, leading to an increase of persistence length (10,17,18,36). Deposition from low salt buffer onto positive charged surfaces may lead to a significant decreasing apparent persistence length from ∼40 nm to ∼11 nm, in a manner depending on surface charge density (35). The authors (35) proposed that surface charge density modulates a fractional neutralization of DNA phosphate groups, leading to a significant increase in DNA flexibility. We note that the glow-discharged carbon film and polylysine film used here are positive-charged surfaces. Therefore, we cannot rule out this mechanism accounting for the decreased persistence length of DNA molecules from EM experiments, although we believe that induced DNA static bending (kinking) is a more favorable one, in view of a notable modulation of the kurtosis.
Recent studies by Wiggins et al. (16) and Mathew-Fenn et al. (27) argued that the classical model of DNA duplex as an ideal elastic rod fails to describe either increased DNA flexibility (16) or end-to-end distance distribution (27) on short length-scales of 5–10 nm. For instance, Wiggins et al. (16) observed a non-Gaussian potential for the bend angle on these length scales. In our EM data, we had the resolution to test this finding. However, we do not see any deviation from a Gaussian distribution of the bend angle down to 3 nm, i.e., we do not find more high angles in the histograms of the negative logarithm –ln G(θ;L). Our estimation of the persistence length P as a function of distance L on experimental data is consistent from –ln G(θ;L) (Eq. 12) and P(L); compare Fig. 5 b. The fact that we do not observe an increased flexibility could be due to a lower persistence length of ∼20 nm in comparison to ∼50 nm in their study. A lower persistence length (higher flexibility) makes it less probable to observe deviations at the same separation distance as in Wiggins et al. (16). To observe angle fluctuation with the same probability, we would need to evaluate at the same P/L ratio, i.e., at separations L < 2 nm. This is beyond the imaging resolution and the subsequent image analysis. Note that our Monte Carlo simulations of the three short length-scales used show consistent estimation of P down to separations of L = 4 nm for similar noise levels as observed in the EM images (see Fig. S3 d). This rules out that the image-processing algorithm is too stiff to follow the DNA backbone exactly. We always find more of the higher angles than Gaussian distributions (see Fig. 5 c), but with so little occurrence that no significant conclusions can be drawn. Together, our findings neither confirm nor contradict these studies.
Lastly, we note that the analysis of specific DNA-protein complexes shows that in many circumstances the DNA backbone may be significantly distorted (relative to the solution structure), forming a bend or kink upon formation of specific DNA-protein complex (37). Recent data exploiting molecular dynamic simulations indicate that DNA flexibility and deformability (i.e., indirect readout) play a key role in discrimination-specific sequences and stabilization of the complex structure upon interaction with proteins (38,39). We therefore speculate that deformations of DNA backbone detected as induced bending/kinking upon its interaction with highly charged surface is in agreement with these data. Moreover, this behavior of DNA is an intrinsic property, the extent of which is possibly modulated by the strength of DNA-surface interactions.
Supporting Material
Methods, analysis, figures, equations, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01120-5.
Supporting Material
Acknowledgments
We thank G. Heim for help with the image acquisition and T. M. Jovin for discussion.
F.G.A.F. was partially supported by Rolling Grants program No. 94RG12 of the Netherlands Organization for Fundamental Research of Matter. D.I.C. was awarded by a Wellcome Trust VIP grant.
Footnotes
F. G. A. Faas and B. Rieger contributed equally to this work.
D. I. Cherny is on leave from the Institute of Molecular Genetics, Russian Academy of Sciences, Moscow, Russia.
Contributor Information
B. Rieger, Email: b.rieger@tudelft.nl.
D.I. Cherny, Email: dc114@le.ac.uk.
References
- 1.Kratky O., Porod G. Röntgenuntersuchungen gelöster Fadenmoleküle. Rec. Trav. Chim. Pays-Bas Belg. 1949;68:1106–1124. [Google Scholar]
- 2.Landau L., Lifshitz E. 2nd Ed. Part 1. Pergamon Press; Oxford, UK: 1969. Statistical Physics. [Google Scholar]
- 3.Schellman J. Flexibility of DNA. Biopolymers. 1974;13:217–226. doi: 10.1002/bip.1974.360130115. [DOI] [PubMed] [Google Scholar]
- 4.Schellman J. The flexibility of DNA: I. Thermal fluctuations. Biophys. Chem. 1980;11:321–328. doi: 10.1016/0301-4622(80)87004-9. [DOI] [PubMed] [Google Scholar]
- 5.Schellman J., Harvey S. Static contributions to the persistence length of DNA and dynamic contributions to DNA curvature. Biophys. Chem. 1995;55:95–114. doi: 10.1016/0301-4622(94)00144-9. [DOI] [PubMed] [Google Scholar]
- 6.Popov Y.O., Tkachenko A.V. Effects of kinks on DNA elasticity. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:051905. doi: 10.1103/PhysRevE.71.051905. [DOI] [PubMed] [Google Scholar]
- 7.Wiggins P.A., Phillips R., Nelson P.C. Exact theory of kinkable elastic polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:021909. doi: 10.1103/PhysRevE.71.021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wiggins P., Nelson P. Generalized theory of semiflexible polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:031906. doi: 10.1103/PhysRevE.73.031906. [DOI] [PubMed] [Google Scholar]
- 9.Moukhtar J., Fontaine E., Faivre-Moskalenko C., Arneodo A. Probing persistence in DNA curvature properties with atomic force microscopy. Phys. Rev. Lett. 2007;98:178101. doi: 10.1103/PhysRevLett.98.178101. [DOI] [PubMed] [Google Scholar]
- 10.Frontali C., Dore E., Ferrauto A., Gratton E., Bettini A. An absolute method for the determination of the persistence length of native DNA from electron micrographs. Biopolymers. 1979;18:1353–1373. doi: 10.1002/bip.1979.360180604. [DOI] [PubMed] [Google Scholar]
- 11.Rivetti C., Guthold M., Bustamante C. Scanning force microscopy of DNA deposited onto mica: equilibration versus kinetic trapping studied by statistical polymer chain analysis. J. Mol. Biol. 1996;264:919–932. doi: 10.1006/jmbi.1996.0687. [DOI] [PubMed] [Google Scholar]
- 12.Rivetti C., Walker C., Bustamante C. Polymer chain statistics and conformational analysis of DNA molecules with bends or sections of different flexibility. J. Mol. Biol. 1998;280:41–59. doi: 10.1006/jmbi.1998.1830. [DOI] [PubMed] [Google Scholar]
- 13.Cognet J., Pakleza C., Cherny D., Delain E., Cam E.L. Static curvature and flexibility measurements of DNA with microscopy. A simple renormalization method, its assessment by experiment and simulation. J. Mol. Biol. 1999;285:997–1009. doi: 10.1006/jmbi.1998.2322. [DOI] [PubMed] [Google Scholar]
- 14.Pastre D., Pietrement O., Fusil S., Landousy F., Jeusset J. Adsorption of DNA to mica mediated by divalent counterions: a theoretical and experimental study. Biophys. J. 2003;85:2507–2518. doi: 10.1016/s0006-3495(03)74673-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lu Y., Weers B., Stellwagen N. DNA persistence length revisited. Biopolymers. 2001;61:261–275. doi: 10.1002/bip.10151. [DOI] [PubMed] [Google Scholar]
- 16.Wiggins P., Heijden T.v.d., Moreno-Herrero F., Spakowitz A., Phillips R. High flexibility of DNA on short length scales probed by atomic force microscopy. Nature Nanotechnol. 2006;1:137–141. doi: 10.1038/nnano.2006.63. [DOI] [PubMed] [Google Scholar]
- 17.Hagerman P. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 18.Manning G.S. The persistence length of DNA is reached from the persistence length of its null isomer through an internal electrostatic stretching force. Biophys. J. 2006;91:3607–3616. doi: 10.1529/biophysj.106.089029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Frontali C. Excluded-volume effect on the bidimensional conformation of DNA molecules adsorbed to protein films. Biopolymers. 1988;27:1329–1331. doi: 10.1002/bip.360270811. [DOI] [PubMed] [Google Scholar]
- 20.Valle F., Favre M., del los Rios P., Rosa A., Dietler G. Scaling exponents and probability distributions of DNA end-to-end distance. Phys. Rev. Lett. 2005;95:158105. doi: 10.1103/PhysRevLett.95.158105. [DOI] [PubMed] [Google Scholar]
- 21.Abels J., Moreno-Herreo F., Heijden T.v.d., Dekker C., Dekker N. Single-molecule measurements of the persistence length of double-stranded RNA. Biophys. J. 2005;88:2737–2744. doi: 10.1529/biophysj.104.052811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.v Noort, Verbrugge J.S., Gossen N., Dekker C., Dame R. Dual architectural roles of HU: formation of flexible hinges and rigid filaments. Proc. Natl. Acad. Sci. USA. 2005;101:6969–6974. doi: 10.1073/pnas.0308230101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bussiek M., Mucke N., Langowski J. Polylysine-coated mica can be used to observe systematic changes in the supercoiled DNA conformation by scanning force microscopy in solution. Nucleic Acids Res. 2003;31:e137. doi: 10.1093/nar/gng137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fang Y., Spisz T., Hoh J. Ethanol-induced structural transitions of DNA on mica. Nucleic Acids Res. 1999;27:1943–1949. doi: 10.1093/nar/27.8.1943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zheng J., Li Z., Wu A., Zhou H. AFM studies of DNA structure on mica in the presence of alkaline earth metal ions. Biophys. Chem. 2003;104:37–43. doi: 10.1016/s0301-4622(02)00335-6. [DOI] [PubMed] [Google Scholar]
- 26.Joanicot M., Revet B. DNA conformational studies from electron microscopy. I. Excluded volume effect and structure dimensionality. Biopolymers. 1987;26:315–326. doi: 10.1002/bip.360260211. [DOI] [PubMed] [Google Scholar]
- 27.Mathew-Fenn R., Das R., Harbury P. Remeasuring the double helix. Science. 2008;322:446–449. doi: 10.1126/science.1158881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cherny D., Jovin T. Electron and scanning force microscopy studies of alterations in supercoiled DNA tertiary structure. J. Mol. Biol. 2001;313:295–307. doi: 10.1006/jmbi.2001.5031. [DOI] [PubMed] [Google Scholar]
- 29.Heekeren A.v., Faas F., Vliet L.v. Finding the minimum-cost path without cutting corners. In: Ersboll B.K., Perdersen K.S., editors. Lecture Notes on Computer Science. Vol. 4552. Springer Verlag; Berlin: 2007. pp. 263–272. [Google Scholar]
- 30.Porod G. X-ray and light scattering by chain molecules in solution. J. Polym. Sci. 1953;10:157–166. [Google Scholar]
- 31.Shi Y., He S., Hearst J. Statistical mechanics of the extensible and shearable elastic rod and of DNA. J. Chem. Phys. 1996;105:714–731. [Google Scholar]
- 32.Trifonov E., Tan R.-Z., Harvey S.C. Static persistence length of DNA. In: Olson W., editor. DNA Bending and Curvature, Structure and Expression. Vol. 3. Adenine Press; Schenectady, NY: 1988. pp. 243–253. [Google Scholar]
- 33.Kaji N., Ueda M., Baba Y. Direct measurement of conformational changes on DNA molecule intercalating with a fluorescence dye in an electrophoretic buffer solution by means of atomic force microscopy. Electrophoresis. 2001;22:3357–3364. doi: 10.1002/1522-2683(200109)22:16<3357::AID-ELPS3357>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 34.Goodsell D., Dickerson R. Bending and curvature calculations in B-DNA. Nucleic Acids Res. 1994;22:5497–5503. doi: 10.1093/nar/22.24.5497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Podesta A., Indrieri M., Brogioli D., Manning G., Malani P. Positively charged surfaces increase the flexibility of DNA. Biophys. J. 2005;89:2558–2563. doi: 10.1529/biophysj.105.064667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Baumann C., Smith S., Bloomfield V., Bustamante C. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. USA. 1997;94:6185–6190. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dickerson R.E., Chiu T.K. Helix bending as a factor in protein/DNA recognition. Biopolymers. 1997;44:361–403. doi: 10.1002/(SICI)1097-0282(1997)44:4<361::AID-BIP4>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 38.Perez A., Luque J., Orozco M. Dynamics of B-DNA on the microsecond time scale. J. Am. Chem. Soc. 2007;129:14739–14745. doi: 10.1021/ja0753546. [DOI] [PubMed] [Google Scholar]
- 39.Noy A., Luque J., Orozco M. Theoretical analysis of antisense duplexes: determinants of the RNase H susceptibility. J. Am. Chem. Soc. 2008;130:3486–3496. doi: 10.1021/ja076734u. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


