The surprisingly high human efficiency at learning to recognize faces

Abstract

We investigated the ability of humans to optimize face recognition performance through rapid learning of individual relevant features. We created artificial faces with discriminating visual information heavily concentrated in single features (nose, eyes, chin or mouth). In each of 2500 learning blocks a feature was randomly selected and retained over the course of four trials, during which observers identified randomly sampled, noisy face images. Observers learned the discriminating feature through indirect feedback, leading to large performance gains. Performance was compared to a learning Bayesian ideal observer, resulting in unexpectedly high learning compared to previous studies with simpler stimuli. We explore various explanations and conclude that the higher learning measured with faces cannot be driven by adaptive eye movement strategies but can be mostly accounted for by suboptimalities in human face discrimination when observers are uncertain about the discriminating feature. We show that an initial bias of humans to use specific features to perform the task even though they are informed that each of four features is equally likely to be the discriminatory feature would lead to seemingly supra-optimal learning. We also examine the possibility of inefficient human integration of visual information across the spatially distributed facial features. Together, the results suggest that humans can show large performance improvement effects in discriminating faces as they learn to identify the feature containing the discriminatory information.

Introduction

Perceptual learning, whereby humans are able to improve their performance for perceptual tasks via practice, is a well-documented phenomenon (Goldstone, 1998; Gilbert, Sigman & Crist, 2001; Fine & Jacobs, 2002). Most work has investigated this learning for low-level feature properties, such as orientation (Ahissar & Hochstein, 1997; Matthews, Liu, Geesaman & Qian, 1999), frequency (auditory, Hawkey, Amitay & Moore, 2004, and visual, Fiorentini & Berardi, 1980), textural segregation (Karni & Sagi, 1991; Karni & Sagi, 1993), and motion (Ball & Sekuler, 1982; Ball & Sekuler, 1987), to name a few. Studies suggest multiple possibilities for the genesis of this performance improvement, including tuning of basic sensory neurons early in the perceptual stream (a bottom-up effect; Saarinen & Levi, 1995; Li, Levi & Klein, 2004), increase in gain (i.e., stimulus enhancement; Dosher & Lu, 1999; Gold, Bennett & Sekuler, 1999), reduction of internal noise (Dosher & Lu, 1998; Lu & Dosher, 1998), re-weighting of visual channels (Dosher & Lu, 1998; Shimozaki, Eckstein & Abbey, 2003) to enhance task-relevant features and locations, and top-down attentional mechanisms (Ahissar & Hochstein, 1993; Ito, Westheimer & Gilbert, 1998; Gilbert et al., 2001), thus freeing computational constraints and reducing extraneous sources of noise.

Common to many of the sensory tuning and channel re-weighting mechanisms is the concept that the human perceptual system amplifies relevant information (the signal of interest) while suppressing irrelevant information (i.e., ambiguous data from irrelevant features).

Classic work by Eleanor Gibson has described how performance improvement in perceptual tasks is mediated by the observers’ ability to reduce the uncertainty about which features are relevant for the visual task (Gibson, 1963). Dosher and Lu present an account of this utilization improvement (1998). Their study demonstrates that a selective weighting of channels (e.g., enhancing or ignoring responses from neurons excited by specific, narrow frequency bands) can account for performance gains in a simple orientation discrimination task. This gain is attributed to a drop in additive internal noise through the reduction of contributing visual channels coupled with an enhancement, or narrowing, of a relevant perceptual filter or template.

In previous work we have pursued studying the process of feature re-weighting with computational approaches. In particular, we have developed a paradigm (Eckstein, Abbey, Pham & Shimozaki, 2004; Abbey et al., 2008) that allows us to systematically quantify how well human performance in a visual task improves relative to an ideal observer as humans discover which is the discriminating feature(s) from a set of many possible features (e.g., orientation, spatial frequency, contrast polarity, etc.).

Humans are also able to learn perceptual tasks involving more complex, higher-dimensional stimuli comprising an assortment of low-level features in a proficient manner. Anyone who has purchased a new set of luggage can attest to the difficulty of picking out their bags from the bedlam found at the airport baggage claim fracas. Initially, identifying our luggage might be quite difficult among the similar bags. Yet, after a modest amount of experience we may start to notice that our bag’s green handle and iridescent logo are somewhat rare among the otherwise nondescript (with regards to our selected visual features) brown lumps. As we develop more and more experience our ability to quickly and accurately spot our bag, with its distinguishing relevant feature, improves.

Here we investigated such a learning process with the ubiquitous yet complex set of stimuli comprising human faces. In order to measure these effects we implement the recently devised technique of the optimal perceptual learning (OPL) paradigm (Eckstein et al., 2004; Abbey, Pham, Shimozaki & Eckstein, 2007). Previous studies have shown humans are able to quickly learn to use task-relevant features to aide performance, with learning manifesting after a single trial. The essence of this paradigm is a task, such as localization of a bright bar, which can be performed more efficiently when a specific feature, such as the bar’s orientation, is attended to. Initially, the observer must complete the task without any prior knowledge as to the characteristics of a possibly useful feature. However, with feedback he or she can ascribe more “weight”, or a higher probability, to certain features of the visual scene. For instance, the observer can use location feedback to calculate the evidence for the target bar being of a certain orientation by comparing the data at the true location with bars of varying angles.

Unlike oriented Gaussian bars (Eckstein et al., 2004; Abbey et al., 2007) and letters (Eckstein et al., 2003), faces, like extreme versions of our orphaned luggage, are naturally intricate structures. Multiple complex features (e.g., eyes), themselves constructed from multiple lower-level features (e.g., contrast, frequency, orientation), are located and oriented according to a distinct configuration. Also, human faces are much more natural stimuli. Studying people’s learning and potential bias for identifying such objects may lead to different and interesting patterns of results compared to simpler, more artificial stimuli.

The theory and rationale of the ideal learner

A consistent increase in performance from trial to trial certainly implies a learning effect. However, it does not tell us how well, or efficiently, the observer has improved. The task’s stimuli may be inherently easier or more difficult to learn. Imagine a task where the observer is asked to locate a square among a large array of distracting pentagons. For each trial the color of the square remains constant while the pentagon colors are allowed to randomly vary (including the square’s assigned color). If the color is highly salient it is easy for an observer to inspect the location indicated by feedback and deduce the relevant color. A human would learn this task very well and very quickly. It is obvious, though, that this is an effect of the stimulus. We are really interested in the human’s perceptual and decision mechanisms and their efficiencies independent of task difficulty. Thus, we implement an ideal observer analysis (Burgess, Wagner, Jennings & Barlow, 1981; Liu, Knill & Kersten, 1995; Eckstein et al., 2004) to compare how well a human performs and learns a task against an absolute maximum, or standard. If a hypothetical task A is easy to learn, the ideal observer will quickly improve performance. A human must also increase performance quickly or lose ground to the ideal observer. In that case, the human has learned a lot, but not as much as he or she could have learned. On the other hand, there might be another task B in which human observers learn less than in task A but in which human learning is comparable to the ideal observer’s learning.

Thus, comparisons of human vs. ideal learning using efficiency measures can isolate human ability to learn from the inherent properties of the task.

In this paper we will explore if indeed humans can quickly learn to use discriminating features for a complex visual stimulus such as a face and compare the pattern of learning to that measured with simpler stimuli. Some researchers have termed humans “face experts” (Gauthier & Tarr, 1997; Kanwisher, 2000); here we see how efficient people actually are at using available evidence. With years of near-constant exposure to faces do humans develop specific learned strategies for face recognition? We will see if these strategies appear in the data, and, if so, can people efficiently learn to use an adaptive strategy given appropriate evidence.

Theory

Optimal perceptual learning paradigm (OPL)

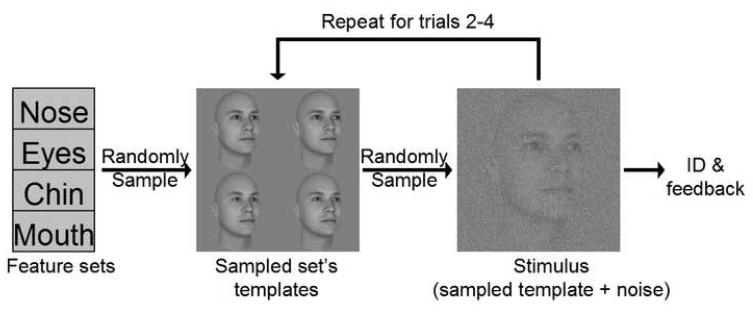
We conducted the study using an optimal perceptual learning (OPL) paradigm (Eckstein et al., 2004). For the purposes of this paper we shall define some terminology. A “feature set” is the collection of all exemplars (faces here) that are maximally discriminated by the same feature. For instance, all faces in the “nose set” contain the vast majority, though not all, of their identification evidence within a distinct nose region. A “learning block” is defined as a short set of consecutive trials, called learning trials, consisting of stimuli culled from a single feature set.

At the onset of each learning block a discriminating feature is randomly selected. Before each learning trial, one of four faces is randomly sampled from the chosen feature set. The face is embedded in white Gaussian noise and displayed to the observer. At the conclusion of a learning trial, the observer identifies which face he or she saw by selecting from the possibly presented faces (Figure 1). Performance is measured in terms of percent correct identification. While the observer selects both the identity and the feature, only the identity factors into performance.

FIGURE 1.

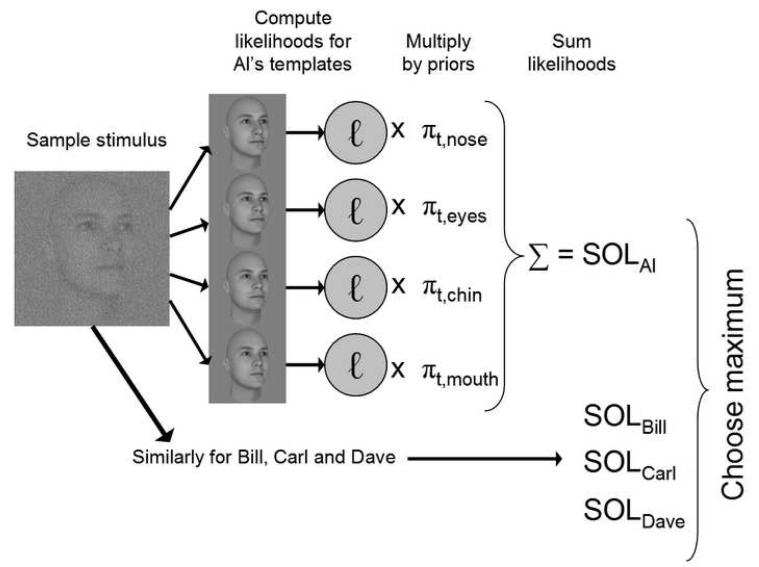
Ideal Observer for the OPL paradigm

The ideal observer computes the probability of a specific face (or target) being the one randomly selected for the trial given the observed (noisy) data. By comparing these probabilities and choosing the maximum the ideal observer is using a Bayesian decision rule to optimally identify the underlying identity.

Thus, on each trial the ideal observer computes the posterior probability of identity i being the displayed face given the observed image, g, denoted as P(i|g). We can compute this probability through Bayes’ rule (Peterson, Birdsall & Fox, 1954; Green & Swets, 1966), which states:

$$P(i\mid g)=P(i)P(g\mid i)∕P(g)$$ (1)

Here, P(g|i) is the probability of observing the data, g, given the underlying face presented corresponded to identity i. This is often called the likelihood, l. P(i) is the prior probability of the face with the i^th identity being present. Since the faces were randomly selected with equal probability, P(i) is constant across identities (P(i)=0.25). P(g) is the probability of observing the data, which does not change across possible identities and thus can also be taken as 1. The problem simplifies to computing the likelihoods for each identity given the observed data and choosing the maximum.

We are left with computing and comparing likelihoods for each of the I possible identities (I = 4 in the current study). Recall, though, that the face is a selection from a subset of all possible faces; namely, from one of the J possible feature sets (J = 4). Therefore, the ideal observer can preferentially weight the likelihoods from different feature sets based on past observations since it knows that a single feature set is used throughout a learning block. This leads to a weighted sum of likelihoods (SLR). The ideal observer computes individual likelihoods for each of the J templates associated with an identity. It then multiplies each likelihood by its corresponding prior probability, π_j, and sums across these weighted likelihoods, as illustrated by

$${\mathit{SLR}}_{i,t}=\sum _{j=1}^J{\pi }_{j,t}{\ell }_{i,t,j}$$ (2)

Here, ℓ_i,t,j is the likelihood of identity i on learning trial t for feature set j. π_j,t is the weight ascribed to feature set j for the t^th trial (the prior). On trial t the ideal observer selects the largest SLR_i,t as its best estimate for the displayed identity.

Recall each stimulus consists of an additive combination of a 256-level grayscale face and white Gaussian noise. In this case the likelihood for each template is (Peterson et al., 1954)

$${\ell }_{i,t,j}=\exp \left[\left({\mathbf{s}}_{i,j}^T{\mathbf{g}}_t-0.5E_{i,j}\right)∕{\sigma }^2\right]$$ (3)

with s_i,j representing a column vector which contains the template of the i^th identity in the j^th feature set (the two-dimensional picture is linearly re-indexed into a one-dimensional vector). Similarly, the column vector g_t represents the data (the observed stimulus) on trial t. E_i,j is the energy of the i^th identity in the j^th feature set (E_i,j=s_i,jTs_i,j; here, we equalized the energies across templates). Also, σ is the standard deviation of the noise (in levels of gray) at each pixel. Figure 2 shows a diagram of the ideal observer decision process.

FIGURE 2.

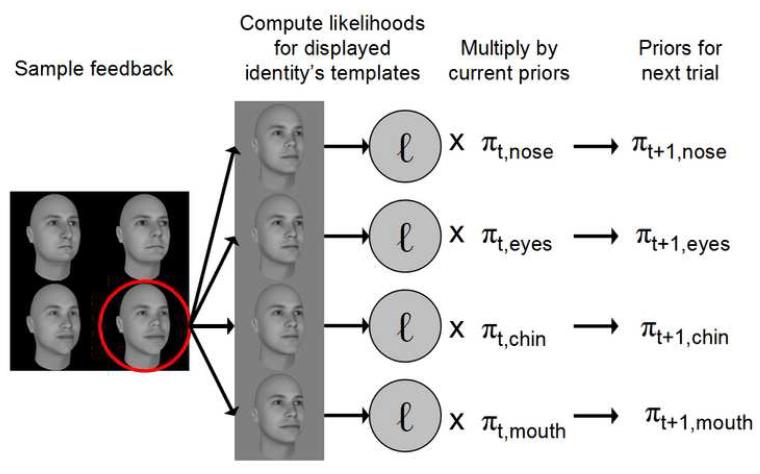
Now we need to compute the weights (or prior probabilities) for each trial for each feature set. The weights are identical on the first trial since the relevant feature set is chosen at random. At the conclusion of each trial the observer is given feedback as to the identity of the stimulus, which we will call ip for identity present. The ideal observer, utilizing its perfect memory, modifies these weights for the next trial, t+1, according to the likelihood (already computed above) of feature j being true given identity i was shown on trial t:

$${\pi }_{j,t+1}={\pi }_{j,t}{\ell }_{ip,t,j}={\pi }_{j,t}\exp \left[\left({\mathbf{s}}_{ip,j}^T{\mathbf{g}}_t-0.5E_{ip,j}\right)∕{\sigma }^2\right]$$ (4)

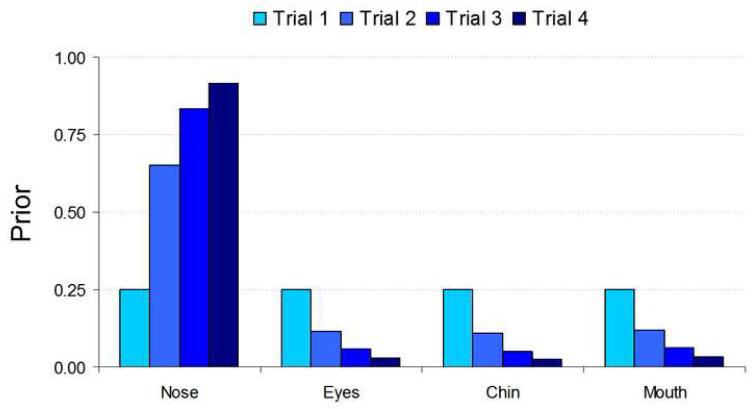
Figure 3 shows a diagram of the prior updating process. Across the four learning trials, on average, the ideal observer places more and more weight on the relevant feature. On average (across trials), the likelihood of the correct feature is greater than the likelihoods for the irrelevant features for the given identity. Figure 4 displays a progression of prior probabilities across learning trials for an example feature (the nose in this case) and averaged across many learning blocks.

FIGURE 3.

FIGURE 4.

Ideal observer analysis: Threshold energy and efficiency

We define the contrast energy of a signal as:

$$E=S{S}_{\mathit{ave}}{\mathit{ATC}}^2$$ (5)

where SS_ave is the sum of the squared average pixel values for all templates, A is the area of a pixel in degrees², T the stimulus’ display time in seconds and C the contrast of the image.

Following a classic definition of efficiency (Barlow, 1980; Abbey, Eckstein & Shimozaki, 2001), we define an observer’s efficiency for feature j on trial t as:

$${\eta }_{j,t}=\frac{E_{\mathit{IO}}\left({\mathit{PC}}_{j,t}\right)}{E_{\mathit{obs}}}\times 100\%$$ (6)

E_obs is the observer’s contrast energy (held constant through all trials) and E_IO(PC_j,t) is the contrast energy necessary to equate the ideal observer’s proportion correct to the observer’s for feature j on trial t. This is also called the threshold energy. The efficiency gives us a measure of how well the observer is utilizing the available discriminatory information.

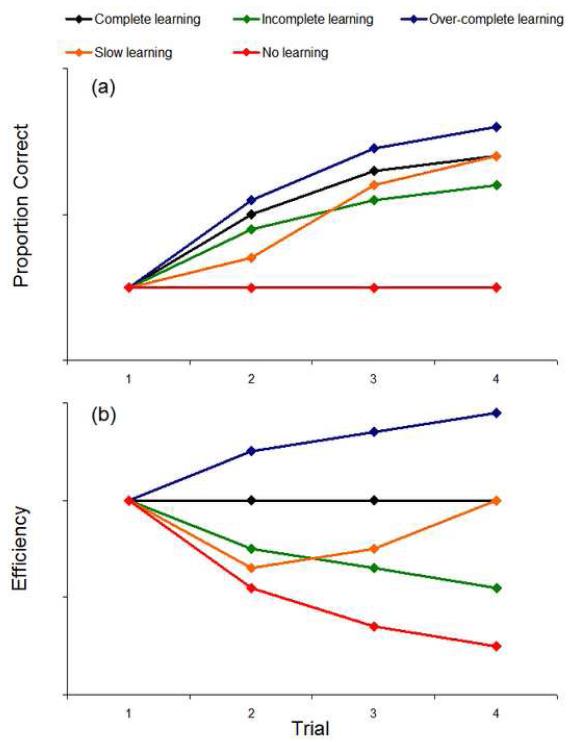
There are several ways in which a human observer’s efficiency relative to the ideal observer can change over the course of a learning block. Note, that we are interested in changes in efficiency across learning trials which is distinct from the initial level of absolute efficiency. A low initial task absolute human efficiency does not preclude a significant efficiency decrease. For example, if the human does not improve performance across a learning block and the ideal observer does, the human efficiency will decline across learning trials irrespective of the initial absolute efficiency. Figure 5 illustrates a few possible scenarios. The black line shows the ideal observer’s performance given the contrast level that leads to some (arbitrary) trial 1 proportion correct. This line also represents the performance of an observer who matches the ideal observer’s performance (with the lowered contrast) on each learning trial. By definition this observer’s efficiency stays constant. An observer who displays a learning signature like this is said to be a “complete learner”. On the opposite end of the spectrum is the red line. This “non-learner” shows flat performance across learning trials, leading to a precipitous efficiency loss when compared to the ideal observer’s Bayesian prior updating. The green line represents a “non-complete learner”, an observer whose performance increases but not as much as that of the ideal observer. In general, we would expect most learning signatures to share these major features of a non-complete learner’s learning profile. The orange line represents the case of an observer who learns as much as the ideal observer, but at a slower pace. Finally, we have the blue line, representing an “over-complete learner”. This is an observer who exceeds “ideal learning” by actually out-learning the ideal observer. A situation like this would require a careful investigation and explanation, as the observer is clearly doing something more than just prior updating.

FIGURE 5.

Methods

Stimuli

One of the major difficulties with face perception psychophysics is lack of control over the stimuli. This becomes especially problematic when we implement an ideal observer model which uses information at each pixel in an image perfectly. A small discrepancy (by human standards) between template and signal in a region with which we are not concerned can greatly affect the ideal observer’s identification performance. This can lead to mislocalization of diagnostic information.

We wanted to confine discriminating information to specific regions of the face; namely, the nose, eyes, mouth and chin. In order to control for the discriminating information across the features we opted to use the commercial software program FaceGen (Singular Inversions, Vancouver, British Columbia), which allowed us to change individual features on synthetic faces. Granted, the exact definitions and boundaries of these common features are somewhat arbitrary and ill-defined. In order to decrease ambiguity we selected and changed two distinct parameters for each feature (Eyes: size, distance between; Nose: bridge length, nostril tilt; Mouth: width, lip thickness; Chin: width, pointedness). The feature parameters were not completely independent, with some information “leaking” away from the region of interest. The dispersion was not egregious though, as we shall see shortly.

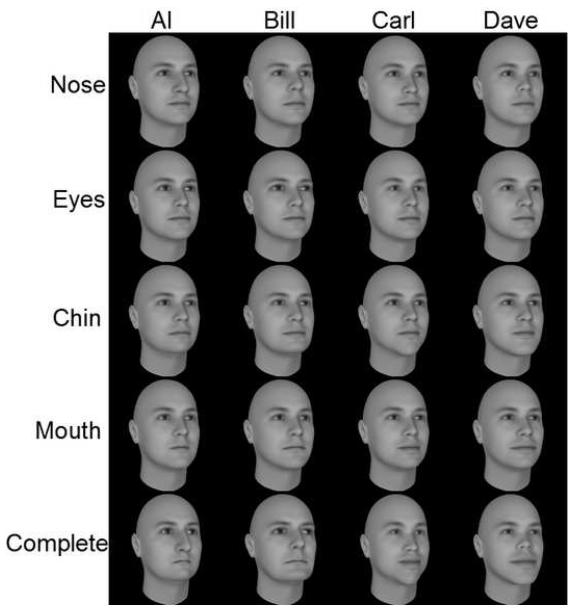
We started the stimulus-creation operation with a single “base face”. We then created 16 distinct stimuli arranged into four “feature sets” (nose, eyes, mouth and chin), each containing four distinct identities (Al, Bill, Carl and Dave; See Figure 6). For example, the nose set consisted of four faces which were identical except for the nose region. Each face was standardized for the same external size and shape. We lowered these faces’ contrast and embedded them in zero-mean, 20 gray-level (3.9 cd/m²) standard deviation white Gaussian noise for presentation. An identity was defined as a simple linear combination of the individual features (the base face with all four features changed).

FIGURE 6.

In order to measure the efficacy with which we confined the diagnostic discriminating information to specific spatial regions, we also created a separate set of “blocked” templates. We masked non-overlapping regions with black boxes, eliminating the visual information. Each of the original templates could have an associated eye, nose, mouth or chin mask (Figure 7).

FIGURE 7.

Experiment

Images were displayed on an Image Systems M17LMAX monochrome monitor (Image Systems, Minnetonka, MN) set at a resolution of 1024 by 768 pixels. A linear gamma function was used to map gray levels to luminance (256 levels of gray, 0-50 cd/m² luminance range). Images were 400 by 400 pixels with a mean luminance of 25 cd/m². Observers were kept 50 cm from the display, leading to each pixel and each image subtending 0.019 degrees and 7.68 degrees of visual angle, respectively. We ran the experimental program using MATLAB (The MathWorks, MA) and the PsychToolbox (Brainard, 1997).

Three human observers (MP, WS and RL; one female, aged 20-24 years with normal or corrected to normal visual acuity) participated in the study. Each participant completed an 800 trial training session followed by two distinct sections.

The first experiment focused on evaluating how well we were able to contain the diagnostic information to desired regions of the face. Observers participated in 32 sessions of 200 trials each, leading to a total of 6,400 trials (and, on average, 320 trials per data point). Each session sampled templates from a single feature set. Mask location was also randomly sampled (nose, eyes, chin, mouth or no mask). The observer started each trial by clicking a mouse button. An image (a combination of face, mask and noise) was displayed in the middle of the monitor for two seconds, after which he or she selected one of the four templates (displayed at the bottom of the screen, unlimited response time) comprising the current feature set. Feedback was then given regarding the true displayed template.

The second experiment utilized the aforementioned OPL paradigm. Observers participated in 50 sessions of 50 learning blocks each, which were further subdivided into four learning trials per block, leading to a total of 10,000 trials (and, on average, 625 trials per data point). Again, observers initiated each trial with a mouse click. A feature set was randomly sampled for each block, and an identity was randomly sampled from that feature set for each trial. An image (a combination of template and noise) was displayed in the middle of the monitor for two seconds, after which he or she selected one of the 16 templates (with unlimited response time). Feedback was given as to the identity.

Model simulations

Ideal observer analysis was run using MATLAB. We simulated 1,000,000 Monte Carlo trials per data point. The images were the same as in the human design except with varied contrast levels. Decision rules followed Equations 1 through 4.

Results

Blocked features

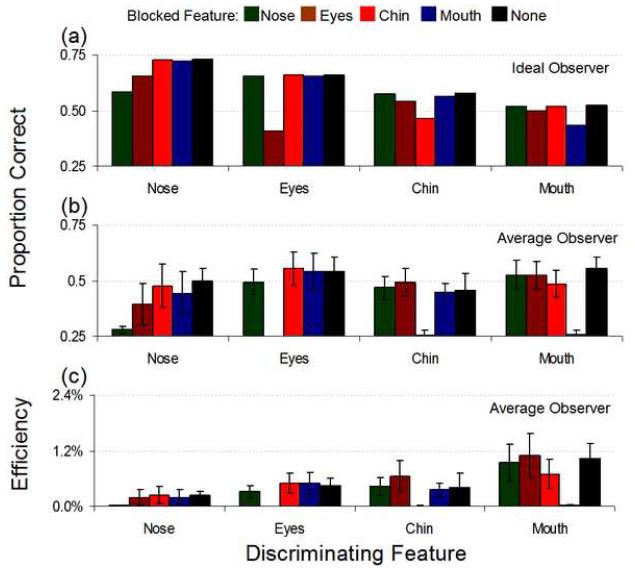
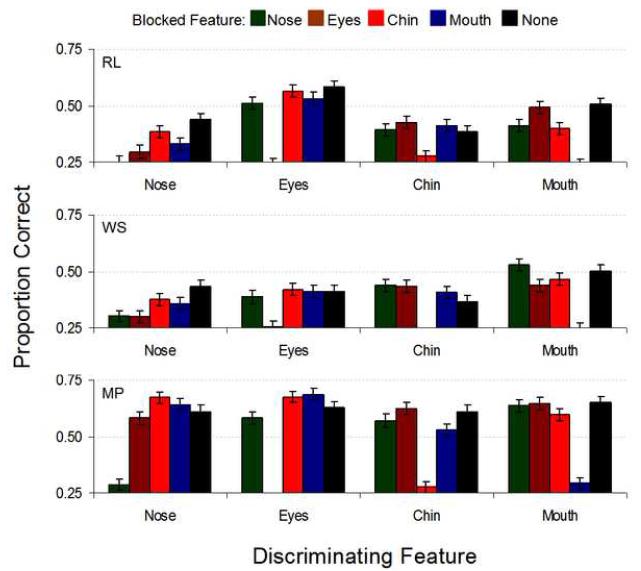
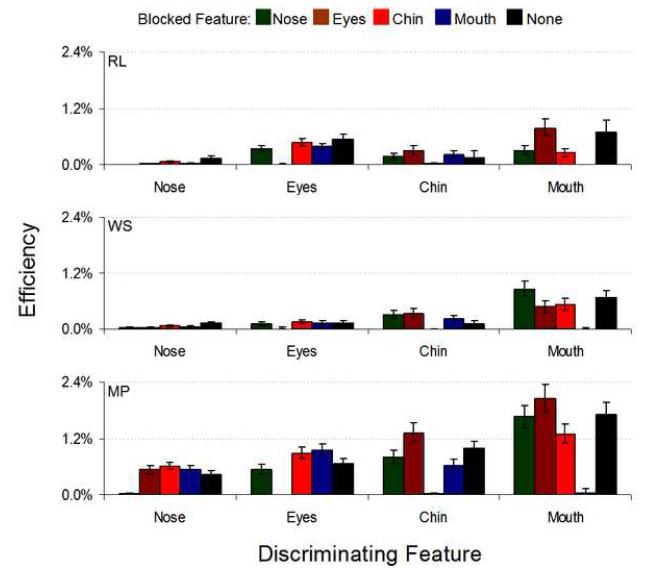
Mean identification performance across the three human observers as well as for the ideal observer (both measured in proportion correct) and the mean efficiency results for the masked-features experiment are shown in Figure 8. Within each feature set, human performance on trials where the relevant feature was blocked was significantly reduced from all other masking conditions. Figures 9 and 10 show individual subject data, displaying general consistency across observers. Again, when the relevant feature was blocked human performance was severely impaired (with the exceptions of WS, where blocking the eyes (p=.93), chin (p=.056) or the mouth (p=.12) in the nose set was not significantly different from blocking the nose, and RL, where blocking the eyes (p=.18) in the nose set produced similarly insignificant performance changes; otherwise, blocking the relevant feature decreased performance at p<.001; Figure 9 and Table 1 in the Supplementary Material). Indeed, performance on these conditions was not significantly different from chance (p>.1, again with WS causing an exception whereby we could marginally reject the null hypothesis of chance performance, p=.04, when the nose was blocked in the nose set; Table 1 in the Supplementary Material). While the ideal observer’s performance dropped significantly under these conditions compared to other masking locations, it did not fall to chance levels, leading to extremely low human efficiencies (Figure 10). However, the ideal observer did suffer the greatest performance drop when the relevant feature was blocked while falling only slightly in performance when an irrelevant feature was blocked. Thus, we were able to confine almost all of the discriminating information to the feature of interest (Figure 8a). Also, the nose set contained the most information according to the ideal observer, yet humans performed poorly in this condition. The mouth set, however, contained the least information yet led to consistently high human performance. These results show observers process information efficiently in the mouth region and inefficiently in the nose region.

FIGURE 8.

FIGURE 9.

FIGURE 10.

Learning

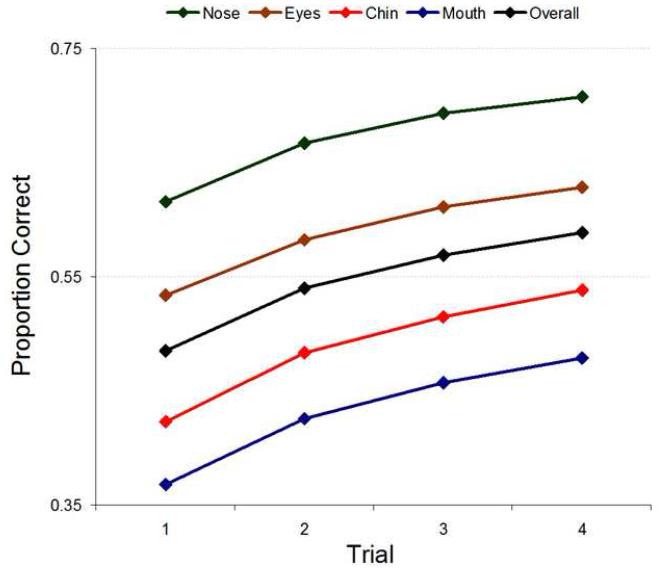
Figure 11 displays ideal observer performance at a set contrast level (lower than that used for the human trials in order to set performance at a commensurate level for display purposes) across learning trials. Feature-specific performances represent blocks where stimuli were drawn from the corresponding feature set. Overall performance is simply the average performance across all conditions for a given learning trial.

FIGURE 11.

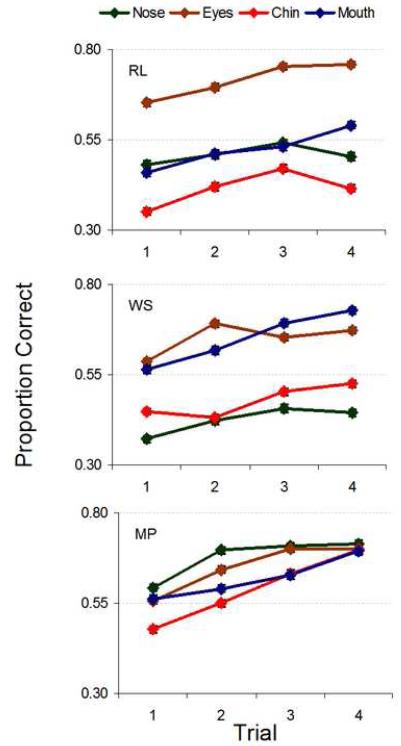
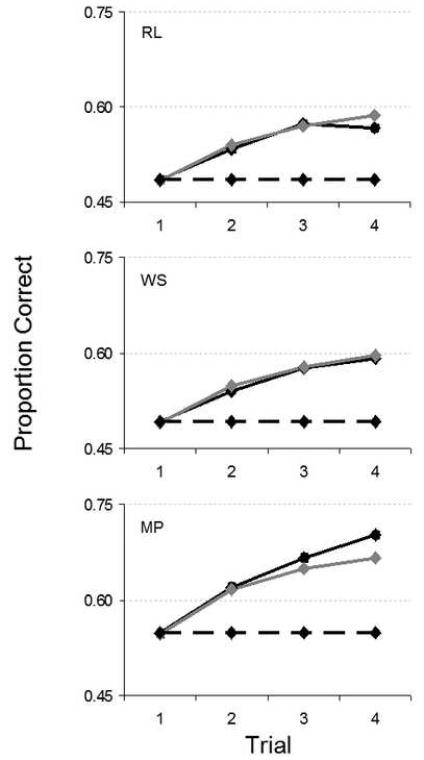
Figure 12 shows raw performance for each observer. Learning (measured as the difference in PC from first to fourth trial) was significant for all observers and all features (p<.001, with the exception of RL, who showed reduced yet still highly significant learning for the chin set (p=.02) but no significant learning for the nose set (p=.41); see Table 2 in the Supplementary Material).

FIGURE 12.

The ideal observer results show directly that the feature sets were not homogenous in their available information; indeed, faces in the nose set were the easiest to discriminate, followed by the eyes, chin, and mouth. However, this rank order did not hold for humans, implying non-ideal, non-uniform processing and/or identification strategies for different features. This can be quantified and clarified through the measure of efficiency.

Efficiency

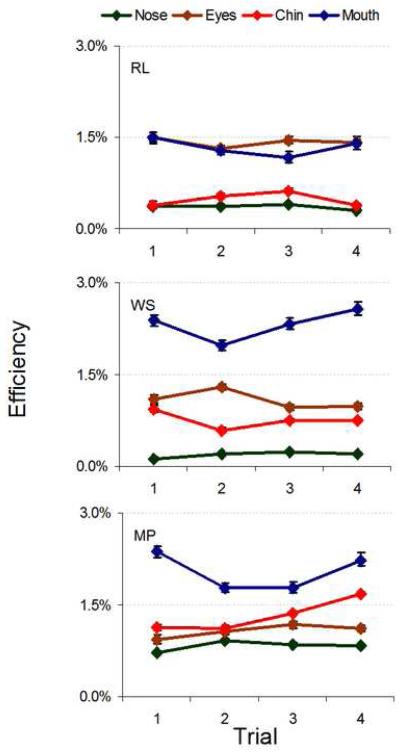
Efficiency across learning trials, shown in Figure 13, varied across features and observers. This follows directly from the varying performance levels exhibited in Figures 11 and 12. Changes in efficiency between the first and fourth learning trials, measured as the ratio between efficiency change and the efficiency on trial 1, ranged from losses of 19% to gains of 68% (see Table 3 in the Supplementary Material). These trends were highly idiosyncratic, with one observer displaying only gains, another only losses, and a third with both gains and losses. While the absolute changes in efficiency varied considerably, some clear trends emerged. In general, efficiency was highest when the mouth and eyes were relevant.

FIGURE 13.

Discussion

Efficiency of learning faces vs. simple stimuli

In previous OPL studies (Eckstein et al., 2004; Abbey et al., 2007) stimuli were small and simple, with exemplars differing along few dimensions (e.g. orientation, spatial frequency, contrast, etc). Although human performance improved across learning trials the efficiency dropped from trial 1 to trial 4. We define the overall change in efficiency from trial 1 to trial 4, Δη, and the normalized change in efficiency, Δη₀ as:

$$\Delta \eta ={\eta }_4-{\eta }_1$$ (7)

$$\Delta {\eta }_0=\frac{\Delta \eta }{{\eta }_1}$$ (8)

Eckstein et al. 2004 found an average Δη₀ across four learning trials for an oriented Gaussian bar localization of -23.3%, while Abbey et al., 2007 observed an average Δη₀ of -24.7% for a similar task

In the current study the stimuli were decidedly not simple. Each image contained four possible widely spatially distributed feature regions. Each feature in itself was visually large and complex. The gathering, processing and analyzing of the visual information offered by the faces requires a larger assortment of neural mechanisms than those needed for Gaussian blobs, Gabors and other comparable stimuli. Indeed, these simpler “objects” have correlates in the early stages of visual processing that can be approximated as linear detectors (Hubel & Wiesel, 1962, 1968), minimizing the need for computing sub-ideal, non-linear combinations of information from multiple independent detectors.

In order to see how well humans learned this task, overall, compared to an optimal learner we will first look at raw performance. Figure 14 shows learning signatures for each human observer collapsed across feature conditions. For comparison we have added the results from ideal observer simulations where the contrast has been set so as to match the human’s performance on trial 1. Surprisingly, individuals are able to match and even surpass the optimal learner’s improvement. This can also be seen as changes in efficiency in Figure 15.

FIGURE 14.

FIGURE 15.

Remarkably, efficiencies either dropped only slightly (RL; Δη=-0.08%; Δη₀=-0.17%; p=.018 one-tailed), remained essentially constant (WS; Δη= -0.03%; Δη⁰=-0.05%; p=.98 two-tailed), or actually improved (MP; Δη=+0.19%; Δη₀=+0.34%; p=.001 one-tailed) (see Table 3 in the Supplementary Material).

Why is this result surprising? It says that humans are able to match or surpass an ideal observer’s learning given their starting (trial 1) performance. This is in stark contrast to the aforementioned OPL studies with simple stimuli where efficiencies invariably dropped between each successive learning trial.

Indeed this is expected to be a hallmark of such a paradigm: the ideal observer learns ideally. The question that follows, then, is what is mediating the dichotomy in efficiency across simple and face stimuli?

A potential conclusion is that the relatively stable or increasing efficiency with faces vs. simpler Gaussian blobs or letters is related to specialized neural mechanisms in the human brain (e.g., the fusiform face area) dedicated to the evolutionary importance of face recognition. While possible, there are a number of alternative explanations related to visual processing that we consider:

1. Adaptive eye movement strategies

2. Differential feature-specific internal noise

3. Inappropriate bias in trial 1 to certain features

4. Inefficient integration of information across facial features in trial 1

The hypothesis related to eye movements is tested with a supplementary control study while the internal noise and inappropriate initial bias hypotheses are evaluated using computational modeling. Finally, the inefficient integration of information explanation is discussed in the context of previous results and a subset of our blocked facial features data.

Eye movements

Studies have shown normal human fixations concentrate on the eye and, to a lesser extent, the mouth regions during face recognition tasks (Dalton et al., 2005; Barton, Radcliffe, Cherkasova, Edelman & Intriligator, 2006). This strategy, applied to the foveated human visual system, may be a component of sampling inefficiency at the beginning of learning blocks. Recall, the ideal observer model does not have a fovea; rather, every pixel is sampled and processed equally regardless of spatial position. Conversely, humans must move their eyes about the stimulus to compensate for the lower information resolution in the periphery. If human fixations become more concentrated around the feature of interest across learning trials one would expect performance improvements related to the improved foveal sampling of the stimuli. Thus, the current ideal observer cannot capture improvements due to improved foveal sampling.

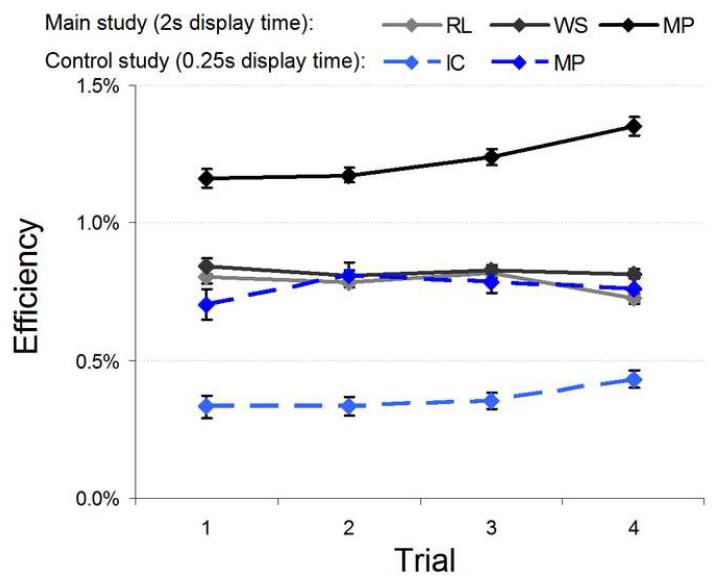
We tested this hypothesis with a control study using two observers (MP from the first study and a new, naïve observer, IC, a 22 year old male with normal acuity). The paradigm was the same as in the main learning study, but now the observers were forced to either fixate on the upper portion of the face (halfway between the eyes, midway down the bridge of the nose) or the lower portion (between the tip of the chin and the center of the mouth). One of these two fixations was randomly sampled before each learning block and kept through the four learning trials. The image was displayed for 250ms during which eye movements were prohibited (the image was the same as used in the main study except with a decreased noise amplitude, standard deviation of 15 gray levels or 2.93 cd/m², to compensate for the shorter viewing time).

The results from this study, summarized in Figure 16, show little support for the hypothesis that an improved fixation strategy can account for the pronounced human improvement. With the previous results from the main perceptual learning study shown as a reference we can see that even when eye movements are precluded human observers displayed a significant increase in efficiency across learning trials. Moreover, the main study incorporated a two second display time, allowing observers to foveally sample the entire face image (verified through self-reports). While the current results do not allow us to rule out the possibility that adapting eye movement strategies can be a source of enhanced human learning, we can safely say that eye movement strategies cannot fully account for the high learning of humans in this paradigm.

FIGURE 16.

Initial bias towards features

Aside from being more visually complex, faces are also more natural, familiar stimuli. More importantly, the face recognition task itself is performed many times a day effortlessly, rapidly, and reliably. It would not be unreasonable to expect this lifetime of experience to foster task-specific strategies; specifically, strategies honed through exposure to certain faces. This preexisting experience could lead to two possible confounding issues: a tendency to more heavily weight information from features which have been found to be reliable for face recognition in everyday life, and differential processing efficiency for different features due to disparities in amount of experience or inherent properties of the brain. Could either, or both, of these scenarios help explain the large measured human learning effects?

Recognizing bias

First we must ask if there is an indication of bias in the data. We define feature bias, FB, for feature j on trial t as:

$${\mathit{FB}}_{j,t}=\left(\frac{{\mathit{NR}}_{\mathit{obs},j,t}-N_{\mathit{obs},j,t}}{N_{\mathit{obs},j,t}}\right)-\left(\frac{{\mathit{NR}}_{\mathit{IO},j,t}-N_{\mathit{IO},j,t}}{N_{\mathit{IO},j,t}}\right)$$ (9)

Here, NR_obs,j,t is the number of times the human observer selected templates from feature set j on trial t, while N_obs,j,t represents the number of times the relevant feature was j on trial t. We apply the same calculation to the ideal observer. If an observer responds with a feature more often than that feature was actually presented, we may be tempted to call this a bias. However, we need to compare this to an ideal observer’s results since this over selection may be due to the stimuli (that is, if the signals from one feature set are inherently more discriminating, or contain more evidence, the ideal observer will tend to select templates from this set more often even for the equalized feature prior probabilities for trial 1).

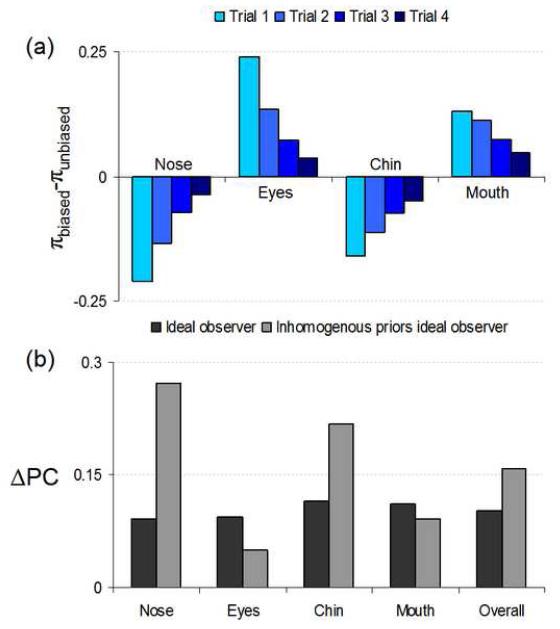
Figure 17a shows the ideal observer’s response frequency relative to the display frequency for trial 1. This “bias” is actually a product of the varying information in the stimuli as explained above and not the priors. This selection disparity is attenuated as the prior probabilities are updated across learning trials: the asymptotic drive toward complete certainty of the relevant feature dominates any one set’s preponderance of visual sensory evidence. The mistakes by the ideal observer become driven solely through uncertainty of the identity within the relevant set, and thus the most heavily contributing template to the final decision is increasingly likely to be a member of this group.

FIGURE 17.

Humans display a much different pattern (Figure 17b). Controlling for stimulus effects as per Equation 9 leads to human feature bias (trial 1 displayed in Figure 17c). The results are clear and strikingly consistent: humans are biased away from the nose, towards the eyes and mouth, and are essentially agnostic toward the chin. Next, we consider two ideal observer models with built-in human biases and the effects on learning. The human-biases in the ideal observer were simulated by using differential internal noise for each feature (Ahumada, 1987) and inhomogeneous initial priors across features.

Differential noise ideal observer

The first model we will consider is an ideal observer that encounters different levels of noise dependent on the relevant feature of the stimuli. In human terms, this corresponds to varying amounts of additive internal noise. Due to its additive nature we can supplant the ideal observer’s noise variance term for feature j, ${\sigma }_j^2$, as such:

$${\sigma }_j^2={\sigma }_{\text{external}}^2+{\sigma }_{\text{int ernal}\mid j}^2$$ (8)

The total noise level of a signal when feature j is relevant is a sum of the constant external noise level (standard deviation of 20 gray levels) and an internal noise level conditional on the feature of relevance. In order to set these internal noise levels we used a steepest descent optimization algorithm (Nocedal & Wright, 1999). We used four free parameters (σ_nose, σ_eyes, σ_chin, and σ_mouth) to minimize the difference between the ideal observer’s proportion correct on the first trial for each feature set and that of the human observers. We then allowed the ideal observer to perform the task as usual, updating prior probabilities in an ideal Bayesian manner, while keeping the differential noise levels constant throughout the learning blocks.

Looking at Figure 18 one result becomes immediately apparent: overall learning, defined here as the difference in performance between trials 1 and 4 collapsed across features, is, if anything, slightly decreased by differential noise. Learning with individual feature sets can change, but the increased learning of the lower noise conditions is more than offset by the decreased learning of the higher noise conditions. More learning is expected with lowered noise levels as stimulus evidence is stronger and thus the updating process is faster. It is also not surprising to find overall learning relatively unaffected: here, the non-ideality is the noise which remains unchanged across learning trials. Indeed, a more complicated model whereby the additive internal noise evolves across trials is quite possible but not explored here.

FIGURE 18.

Inhomogeneous priors ideal observer

It is possible that humans give different weights in the decision process to different feature sets. If, in the humans’ vast real-world experience, some features are generally more informative than others, it is entirely reasonable to expect a biased decision strategy which capitalizes on this property. Indeed, humans seem to preferentially use eye and mouth information (Schyns, Bonnar & Gosselin, 2002) and to predominantly fixate these features during face recognition (Dalton et al., 2005; Barton et al., 2006). In an ideal observer framework this would translate to non-uniform prior probabilities.

We attempted to model such an observer by matching feature-specific performance on trial 1 to human data through fixing of the initial prior probabilities. In this scheme we have four free parameters (three prior probabilities, the fourth being constrained because their sum must equal one, and signal contrast) and four values to fit (the PCs for each feature), leading to a unique solution. The fitted priors and their overall progression, relative to an unbiased ideal observer, are shown in Figure 19a. Essentially, the biased priors ideal observer “unbiases” itself through the prior updating process: evidence tempers bias.

FIGURE 19.

Does this unbiasing process affect learning? The results in Figures 19b and 19c confirm that indeed it does. Overall learning is increased relative to the ideal observer. An ideal update process pushes the non-ideal prior distribution toward ideal; this evidence-driven optimization leads the biased-priors ideal observer to an inherent increased learning. Broken down by feature (Figure 19c) we see this learning is driven by the most under-valued priors (usually the nose and chin). This is conceptually interesting: Human supra-learning could be at least partially explained by learning to weight, or not ignore, some features, an imperative when each feature is equally likely to be the singularly relevant one. If humans are simply ignoring or throwing out evidence due to misguided a priori weighting we would expect learning to be greatly facilitated through a trend toward a more egalitarian weighting distribution. Thus, our simulation results suggest that initial inhomogeneity of priors in humans might add to the inefficient spatial integration of features in explaining the dramatic human improvement in face discrimination performance.

Inefficient integration of information

On the first learning trial, observers (human and ideal alike) are unaware of the block-relevant feature and thus are required to integrate information across the different facial features. A possibility is that humans are inefficient at this integration process. By the fourth learning trial observers are well aware of the relevant feature. The growing dominance of the relevant feature’s information in the decision-making computations across learning trials minimizes the effects of human integration inefficiency.

Tasks using small, low-dimensional stimuli tend to produce quite high efficiencies. Examples include mirror symmetry detection of dot displays (25%; Barlow & Reeves, 1979), amplitude discrimination of sinusoids in noise (70-83%; Burgess et al., 1981), localization of oriented elongated Gaussians (15-27%; Eckstein et al., 2004) and detection (39-49%), contrast discrimination (24-27%) and identification (35-55%) of Gaussian and difference of Gaussians blobs (Abbey & Eckstein, 2006).

By comparison, tasks using complex stimuli comprised of multiple features and large spatial extent tend to produce much lower human efficiencies. Examples include general object recognition (3-8% efficiency; Tjan, Braje, Legge & Kersten, 1995), recognition of line drawings (0.1-3.75%) and silhouettes (0.08-3.23%; Braje, Tjan & Legge, 1995) and, most relevant to this study, human faces (around 0.4-2%, commensurate with our findings; Gold et al., 1999).

There are many potential reasons why human efficiencies are lower for larger stimuli composed of multiple feature dimensions. One of these is a human difficulty with binding information between spatial locations and features. Indeed, there is evidence that humans are inefficient at integrating spatially distributed information of complex stimuli. For instance, Pelli, Farell and Moore describe a word-length effect whereby the efficiency of recognizing common words in noise drops as the inverse of the number of letters (e.g., 4.8% efficiency recognizing a 3-letter word while the individual letters are recognized with 15% efficiency) (2003). This linear law suggests a failure of holistic processing, even for such commonly encountered stimuli as words.

This difficulty with efficient integration appears in studies of face perception as well. Using a range of Gaussian aperture sizes to selectively mask human face images, Tyler and Chen showed that near-threshold face detection improves with increasing size in a manner consistent with linear spatial summation up to an area roughly approximating the larger facial features. Performance continued to improve for larger apertures, but at a decreasing rate, until the entire central area of the face (constituting the eyes, nose and mouth) was visible, after which performance stabilized. While the task was face detection, not identification, the evidence points toward a deficiency in integration of visual information across larger facial features. If this were the case in the present study, greater than optimal learning could be a product of minimizing the effects of non-ideal integration as the human observer’s effective area of information summation shrinks from trial to trial.

Further evidence for human inefficiency at integrating spatial information for object recognition can be found in the blocked feature study we conducted. In the blocked sessions, the human observers knew explicitly the feature set being sampled. This led to high performance when the known relevant feature was visible. Essentially, the observers were cued on the task relevant feature and thus could weight and select information at the information-rich region. However, when the relevant feature was hidden, human performance plummeted to chance. The ideal observer, on the other hand, could still maintain relatively high performance, indicating that while the relevant feature possessed a high concentration of information, other areas contained useable (but more diffuse) information as well. These results attest to a crippling difficulty for humans relative to the ideal observer when faced with a need to integrate information across many features and large spatial regions. Tying back to the supra-optimal learning, as humans are able to ignore irrelevant features they perform the task by using the information at the relevant feature which can be processed in a much more efficient way. That is, humans reap large efficiency improvements when they do not need to integrate information across multiple features. However, there exists the possibility that human strategy was critically disrupted by the addition of the highly salient masks. Humans, knowing the relevant feature, may have simply given up when that feature was removed.

In the end, the data from this study cannot firmly state the contribution of integration inefficiencies toward the learning results. We believe further studies are needed to explore this possibility thoroughly and rigorously. However, the previous evidence and the blocked features study seem to hint at a human reliance on concentrated visual information and sparse feature-coding. Though speculative, it is possible that over learning trials the task evolves into one more easily accommodated by human visual processing strategy.

Implications for face recognition

The literature on object recognition and face recognition in particular is vast (Kanwisher, 2000; Haxby, Hoffman & Gobbini, 2000). Most studies have focused on the mechanisms humans may use for the task. Generally this has condensed down to three main possibilities: featural (Biederman, 1987; Carbon & Leder, 2005; Martelli, Majaj & Pelli, 2005), configural (Diamond & Carey, 1986; Maurer, Le Grand & Mondloch, 2002) and holistic, or template-based, processing (often mentioned in the same breath as configural; Tanaka & Farah, 1993; Farah, Tanaka & Drain, 1995; McKone, Martini & Nakayama, 2001; Michel, Rossion, Han, Chung & Caldara, 2006; for an overview and discussion on the definitions of these complex concepts, see Leder & Bruce, 2000). This study was concerned with the effects of manipulating individual features while leaving their relative configurations unchanged. We attempted to also eliminate holistic information by constraining the regions of discriminability (the fact that humans could not use the information separated and dispersed from the features, as shown in the blocked-features sessions, would actually tend to conflict with holistic theories, though the amount of information was very small and may not have aided humans even if the same amount of information had been completely restricted to the individual features). The consistently higher efficiencies seen with the eye and mouth sets implies either a more effective recognition strategy (i.e., directing more attentional weighting and gaze toward these regions), or some inherent or experience-driven advantage given to these features in the brain’s recognition system (such as increased gain or sharper tuning for specific features). In sum, humans can use individual features for recognition, provided they occur within the context of a human face. Features by themselves, divorced from this context, may lead to poor recognition performance even though the same amount of discriminating information is available. We are planning a study to test this possibility.

Conclusions

This study incorporated the natural, complex stimuli of human faces into a rapid perceptual learning paradigm (OPL). Similar to simpler stimuli, such as oriented bars, humans were able to learn which stimulus feature was relevant for identity recognition after a single trial, with performance increasing (at a declining rate) across four consecutive learning trials. Compared to an ideal observer, overall human efficiency was much lower than that observed in previous studies with less complex stimuli (though consistent with published object and face recognition efficiencies). However, across learning trials recognition efficiency did not consistently decrease as with previous simpler stimuli showing human learning that is comparable to that of an ideal learner. Modeling and a subsequent study controlling for eye movements suggest that the surprisingly high human efficiency at learning to recognize faces cannot be accounted for by eye movement strategies and might be a by-product of feature biases, as indicated by observers’ tendencies to select faces where the mouth and eyes were the relevant feature while avoiding the nose templates. This phenomenon might be related to observers’ experience with gazing at the eyes and mouth of real faces in social situations, or an experience-driven recognition strategy given the natural information distribution of real human faces. A dynamic eye movement strategy which allows the observer to foveate the feature relevant regions as the trials progress did not seem to be a significant source of increased efficiency. We also speculate based on previous studies and our blocked feature study that inefficient human integration of spatially distributed information in the initial learning trial could also be contributing to the larger performance gains across learning trials.