Quantitative Analysis of the Magnitude and Time Delay of Cyclic Variation of Myocardial Backscatter from Asymptomatic Type 2 Diabetes Mellitus Subjects

Abstract

Early detection of diabetic patients at high risk for developing diabetic cardiomyopathy may permit effective intervention. The goal of this work is to determine whether measurements of the magnitude and time delay of cyclic variation of myocardial backscatter, individually and in combination, can be used to discriminate between subgroups of individuals including normal controls and asymptomatic type 2 diabetes subjects. Two-dimensional parasternal long-axis echocardiographic images of 104 type 2 diabetic patients and 44 normal volunteers were acquired. Cyclic variation data were produced by measuring the mean myocardial backscatter level within a region-of-interest in the posterior wall, and characterized in terms of the magnitude and normalized time delay. The cyclic variation parameters were analyzed using Bayes classification and a nonparametric estimate of the area under the receiver operating characteristic (ROC) curve to illustrate the relative effectiveness of using one or two features to segregate subgroups of individuals. The subjects were grouped based on glycated hemoglobin (HbA1c), the homeostasis model assessment for insulin resistance (HOMA-IR), and the ratio of triglyceride to high-density lipoprotein cholesterol (TG/HDL-C). Analyses comparing the cyclic variation measurements of subjects in the highest and lowest quartiles of HbA1c, HOMA-IR, and TG/HDL-C showed substantial differences in the mean magnitude and normalized time delay of cyclic variation. Results show that analyses of the cyclic variation of backscatter in young asymptomatic type 2 diabetics may be an early indicator for the development of diabetic cardiomyopathy.

INTRODUCTION

Insulin resistance and type 2 diabetes are growing concerns in populations in which there is an increasing prevalence of obesity. Although diabetes is a well-known risk factor for coronary artery disease, and consequently, ischemia-related heart failure, there is increasing evidence that diabetes is also a risk factor for the development of heart failure apart from coronary disease, a so-called “diabetic cardiomyopathy” (Fang et al. 2004; Hamby et al. 1974; Kannel et al. 1974; Witteles and Fowler 2008).

The mechanisms for the development of diabetic cardiomyopathy are not completely known and likely involve multiple pathways including impaired renal function, sympathetic/parasympathetic imbalance, protein glycosylation, and upregulation of the renin-angiotensin-aldosterone system. Evidence is also emerging that hyperlipidemia plays a central role in the pathogenesis of heart failure in diabetic patients, independent of atherosclerosis. Type 2 diabetes is associated with elevated serum triglyceride and free fatty acid level (Barrett-Connor et al. 1982; Fraze et al. 1985; Hallgren et al. 1960). These elevated levels can increase the supply of fatty acid substrates to the heart, increase fatty acid utilization, and alter the lipid homeostasis of the tissue, particularly in the setting of insulin resistance (Augustus et al. 2003; Carley and Severson 2005; Peterson et al. 2004; Stremmel 1988). Several mouse models show that accumulation of lipids in non-adipose tissue such as the myocardium can lead to cell dysfunction and cell death, and ultimately result in cardiomyopathy, even in the absence of hyperglycemia (Borradaile and Schaffer 2005; Chiu et al. 2001; Chiu et al. 2005; Finck et al. 2003; Nielsen et al. 2002; Rijzewijk et al. 2008; Zhou et al. 2000). While the link between lipid metabolic abnormalities and cardiomyopathy in diabetic patients is less clear, evidence suggests that the myocardium of patients with type 2 diabetes is exposed to excessive free fatty acid and triglyceride delivery, which causes lipotoxicity and thereby contributes to the development of diabetic cardiomyopathy. This is supported by studies demonstrating increased myocardial triglycerides in hearts of diabetic patients at autopsy and in pathological examinations of failing hearts explanted from individuals with diabetes and cardiomyopathy who underwent orthotopic cardiac transplantation (Alavaikko et al. 1973; Sharma et al. 2004; Szczepaniak et al. 2003).

Cyclic variation of myocardial backscatter is a non-invasive approach for assessing myocardial structure and function. This form of tissue characterization analysis has been employed to characterize a number of cardiac pathologies including ischemia (Barzilai et al. 1984), myocardial infarction (Hancock et al. 2002; Iwakura et al. 2003; Ohara et al. 2005), cardiac hypertrophy (Losi et al. 2007; Masuyama et al. 1989), and changes in myocardial size, structure, and function (Di Bello et al. 1998; Giglio et al. 2003; Hu et al. 2003; Komuro et al. 2005; Madaras et al. 1983; Micari et al. 2006; Naito et al. 1996). One such study from our laboratory examined differences in magnitude and normalized time delay of cyclic variation of backscatter among type 1 diabetic patients with systemic complications and normal controls (Perez et al. 1992). In a follow up study, Wagner et al. extended this work by using Receiver Operating Characteristic (ROC) analysis to quantitatively assess the univariate and multivariate discriminating power of the cyclic variation parameters (1995). The results of that paper indicated that a combination of two or more cyclic variation parameters (magnitude of the septal wall, time delay of the septal wall, magnitude of the left ventricular free wall, and time delay of the left ventricular free well) yielded a larger area under the ROC curve than a single feature. Early detection of diabetic patients at high risk for developing diabetic cardiomyopathy might permit effective intervention. The long-term goal of this exploratory study is to determine whether myocardial tissue characterization based on measurements of the magnitude and time delay of cyclic variation of myocardial backscatter might be a useful non-invasive indicator of hearts at potentially higher risk for developing diabetic cardiomyopathy. Although a longitudinal study over many years would be required to determine the utility of this approach in modifying clinical outcomes, this preliminary study examines methodology that might be appropriate for such a longer-term investigation.

METHODS

Subjects Studied

A total of 148 subjects (44 normal controls and 104 asymptomatic type 2 diabetic patients) between the ages of 30 and 55 years old were recruited for the research study over a 3-year period. Subjects were enrolled in the study after signing informed consent forms approved by the Washington University Human Studies Committee. Subjects were excluded if they met the following criteria that are known to affect adversely heart function or metabolism independent of parameters being studied: participants who had greater than Stage 1 hypertension as defined by the seventh report of the Joint National Committee (Joint National Committee on the Prevention 2003); valvular disease including trace or mild valvular regurgitation; systolic dysfunction; ischemic heart disease as assessed by a screening stress echocardiography exam; or symptoms of heart failure. Subjects were also excluded if they were outside the age range of 30 to 55 years old, current smokers, postmenopausal, pregnant or lactating. Out of the 148 subjects enrolled, 7 subjects withdrew from the study, 4 subjects did not have all the plasma markers needed for analysis, and data from 12 subjects were not analyzed due to poor signal to noise ratios for the tissue characterization measurements. In the end, data from 125 subjects were collected and analyzed. These 125 subjects had an average age of 43 ± 7 years (mean ± standard deviation) and included 72 females and 53 males.

Laboratory Tests

Once a subject was enrolled in the study, laboratory tests were performed after an overnight fast. The tests included fasting glucose, glycated hemoglobin, lipid, and protein levels. The echocardiographic evaluation included standard measurements to assess cardiac function as well as study specific measurements such as tissue characterization.

Tissue Characterization Data Acquisition

A detailed description of the system calibration, backscatter data acquisition, and cyclic variation analysis can be found in Holland et al. (2006) and is summarized below. Subjects were imaged using a General Electric (GE) Vivid 7 clinical imaging system (General Electric Medical Systems, Waukesha, WI). Data was collected from the parasternal long-axis view in harmonic imaging mode with a transmit frequency of 1.7 MHz and a receive frequency of 3.4 MHz. The post-processing settings (compression, reject, dynamic range, data dependent processing (DDP)) of the imaging system were configured to optimize the dynamic range of images of the left ventricular free wall, and to provide a linear relationship between changes in the displayed grayscale value and changes in the level of ultrasonic backscatter expressed in decibels. This relationship was achieved by acquiring a succession of images of a tissue-mimicking phantom as the overall receiver gain was systematically changed in known decibel (dB) steps. The phantom images were analyzed offline using NIH ImageJ (National Institutes of Health, Bethesda, MD). In this approach, a region-of-interest was placed within each phantom image and the mean grayscale value was measured. Analysis of the measured mean grayscale level corresponding to each known gain setting was used to determine the relationship between changes in the displayed grayscale value and changes expressed in dB. Furthermore, this approach established the range where this relationship was linear. To obtain echocardiographic data from subjects, images from five consecutive heart cycles were digitally acquired with the overall gain of the imaging system configured to maximize the available dynamic range of backscattered signals. Subsequent analyses of the acquired image data were performed off-line using NIH ImageJ.

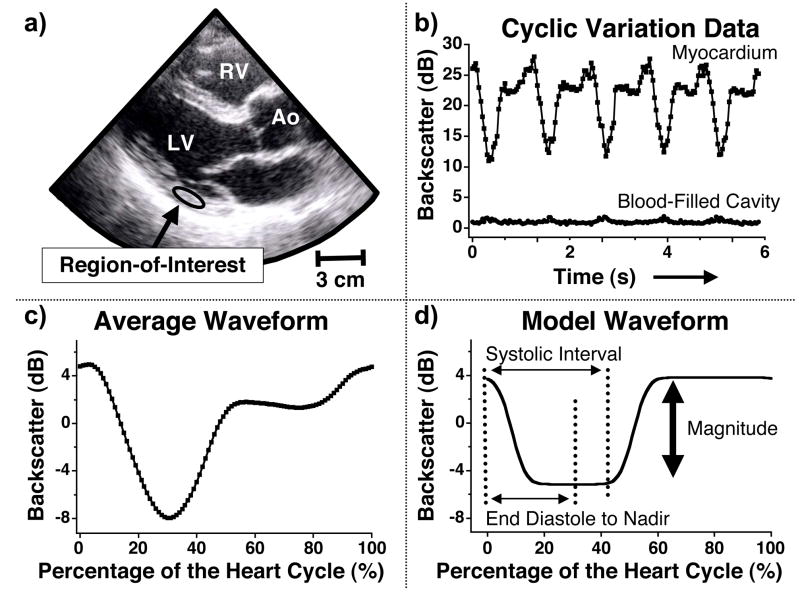
Backscatter data were generated from a region-of-interest that was manually tracked to stay within the mid-myocardium of the left ventricular free wall over the heart cycle. Figure 1a shows a representative echocardiographic image with a region-of-interest drawn in the posterior wall of the parasternal long-axis view. Previous studies have used this method of measuring backscatter data from a manually positioned region-of-interest and shown both intra- and inter-observer backscatter results are reproducible (Holland et al. 2009). For each image frame of the cineloop, the mean grayscale value of the region-of-interest was recorded and converted to backscattered energy expressed in decibels. The backscattered energy was plotted versus time (or frame number) to yield the systematic variation of backscatter from the heart. A similar procedure was performed for a region-of-interest placed in the blood-filled cavity of the left ventricle. This analysis was done to ensure clutter in the image did not strongly affect the measured backscatter energy from the myocardium and ultimately influence the cyclic variation results. Figure 1b shows the cyclic variation of myocardial backscatter over five heart cycles for the region-of-interest drawn in Figure 1a, and for a region-of-interest placed in the blood-filled cavity. The vertical scale in Figure 1b illustrates the relative difference between the measured backscatter energy in the myocardium and the blood-filled cavity, and does not represent the absolute level of backscatter. Figure 1c depicts the average cyclic variation waveform calculated by averaging the five separate heart cycles of myocardial backscatter in Figure 1b. The data are represented as a zero-mean curve and plotted as a percentage of the heart cycle. In this formalism, end-diastole is defined as the start (0%) and end (100%) of the heart cycle.

Figure 1.

a) Image showing a representative region-of-interest placed in the posterior wall of the parasternal long-axis view for one subject. RV = right ventricle LV = left ventricle Ao= aorta b) Cyclic variation of myocardial backscatter data from the region-of-interest shown in Figure 1a and backscatter data from the blood-filled cavity. The vertical scale illustrates the relative difference in backscatter results and does not represent an absolute measurement. c) Average waveform calculated from the five heart cycles illustrated in Figure 1b. The data are represented as a zero-mean curve and the heart cycle is defined as starting and ending with end diastole. d) A model waveform utilized in the automated analysis of cyclic variation data (Mohr et al. 1989) to calculate the magnitude and time delay of the cyclic variation of myocardial backscatter. The vertical arrow illustrates the magnitude of cyclic variation, and the normalized time delay is calculated as the time interval from end diastole to the center of the nadir divided by the systolic interval.

The systematic variation of the backscattered energy was quantified by analyzing the magnitude and normalized time delay of cyclic variation using an automated algorithm (Mobley et al. 1995; Mohr et al. 1989). The magnitude of cyclic variation was calculated as the difference between the average peak and average nadir values of the backscattered energy. The corresponding normalized time delay is expressed as a dimensionless ratio obtained by dividing the time interval from end-diastole to the nadir of the mean backscatter trace by the systolic interval. Mitral valve motion was used to identify the diastolic and systolic intervals. End diastole was defined as the frame just after the mitral valve closed and end systole corresponded to the frame before the mitral valve opened. The analysis of magnitude and normalized time delay of cyclic variation are illustrated in Figure 1d.

Data Analysis

For this preliminary study, analyses of the cyclic variation of myocardial backscatter were performed with subjects divided into quartiles based on each of three indices, glycated hemoglobin (HbA1c), the homeostasis model assessment of insulin resistance (HOMA-IR) as calculated by The Oxford Centre for Diabetes, Endocrinology, and Metabolism HOMA calculator (Wallace et al. 2004), and the ratio of triglyceride to high-density lipoprotein-cholesterol levels (TG/HDL-C). With regard to the choice of indices for these planned comparisons, HbA1c and HOMA-IR were selected for the data analyses because they represent useful indices for the monitoring of type 2 diabetic patients. The ratio of TG/HDL-C, which was previously employed as a predictor of insulin resistance and cardiometabolic risk in the Framingham offspring cohort (Kannel et al. 2008), illustrates a particular dislipidemia that could play a role in the pathogenesis of heart failure in diabetic patients. For each classification, cyclic variation measurements from subjects in the highest quartile (N=32) were compared with those in the lowest quartile (N=32). The quartiles were determined by rank ordering the subjects according to the index of interest, and grouping the 32 subjects with the largest rank as the highest quartile and the 32 subjects with the smallest rank in the lowest quartile. Our hypothesis was that subjects with a high percentage of HbA1c, large value for HOMA-IR, or large ratio of TG/HDL-C exhibited a less favorable profile than those subjects with lower values. In this sense, the lowest quartile might be considered to be the “healthier” of the two quartiles; however, the subjects in both groups have clinically normal hearts as assessed by a stress echocardiography exam. A subset of the laboratory results for these three subject groupings is presented in Table 1.

Table 1.

A summary of the laboratory results for the study population. The column headings represent how the subjects were divided for cyclic variation analysis and the rows represent a subset of the biological parameters reported. All values are expressed as a mean ± standard deviation. The p values were determined using a two-tailed unpaired student t-test. HOMA-IR = Homeostasis model assessment for insulin resistance, TG/HDL-C = Triglyceride to high density lipoprotein-cholesterol ratio, n.s. = not significant

	Hemoglobin A1c		HOMA-IR		Triglyceride to High-Density Lipoprotein Cholesterol ratio
	Lowest Quartile (N = 32)	Highest Quartile (N = 32)	Lowest Quartile (N = 32)	Highest Quartile (N = 32)	Lowest Quartile (N = 32)	Highest Quartile (N = 32)
Gender
M = male	M = 10	M = 15	M = 13	M = 14	M = 11	M = 16
F = female	F = 22	F = 17	F = 19	F = 18	F = 21	F = 16
Age (yrs)	39 ± 6	44 ± 6	41 ± 6	43 ± 7	41 ± 6	43 ± 8
	p < 0.05		p = n.s.		p = n.s.
Body Mass Index (kg/m2)	28 ± 7	36 ± 7	26 ± 5	38 ± 7	31 ± 8	34 ± 7
	p < 0.001		p < 0.001		p = n.s.
Hemoglobin A1c (%)	5.4 ± 0.2	9.1 ± 1.3	5.7 ± 0.7	7.4 ± 1.6	6.7 ± 1.6	7.5 ± 1.7
	p < 0.001		p < 0.001		p = n.s.
HOMA-IR	1.1 ± 0.7	2.8 ± 1.8	0.7 ± 0.2	4.7 ± 2.2	1.7 ± 1.9	3.1 ± 1.8
	p < 0.001		p < 0.001		p < 0.01
TG/HDL-C	3.0 ± 3.0	6.4 ± 8.0	2.7 ± 2.9	6.8 ± 7.7	1.2 ± 0.3	10.7±7.4
	p < 0.05		p < 0.01		p < 0.001

Cyclic variation data from the lowest and highest quartile-groups (small HbA1c, HOMA-IR, or ratio of TG/HDL-C and large HbA1c, HOMA-IR or ratio of TG/HDL-C respectively) served as the input data for Bayes classification. Bayes classification was employed to combine information from the magnitude and time delay of cyclic variation and assign a subject to the lowest or highest quartile. Once the result was calculated for each subject, Receiver Operating Characteristic (ROC) analysis was used to assess the performance of the Bayes classified data. A more detailed explanation of Bayes classification and ROC analysis is provided in the Appendix.

RESULTS

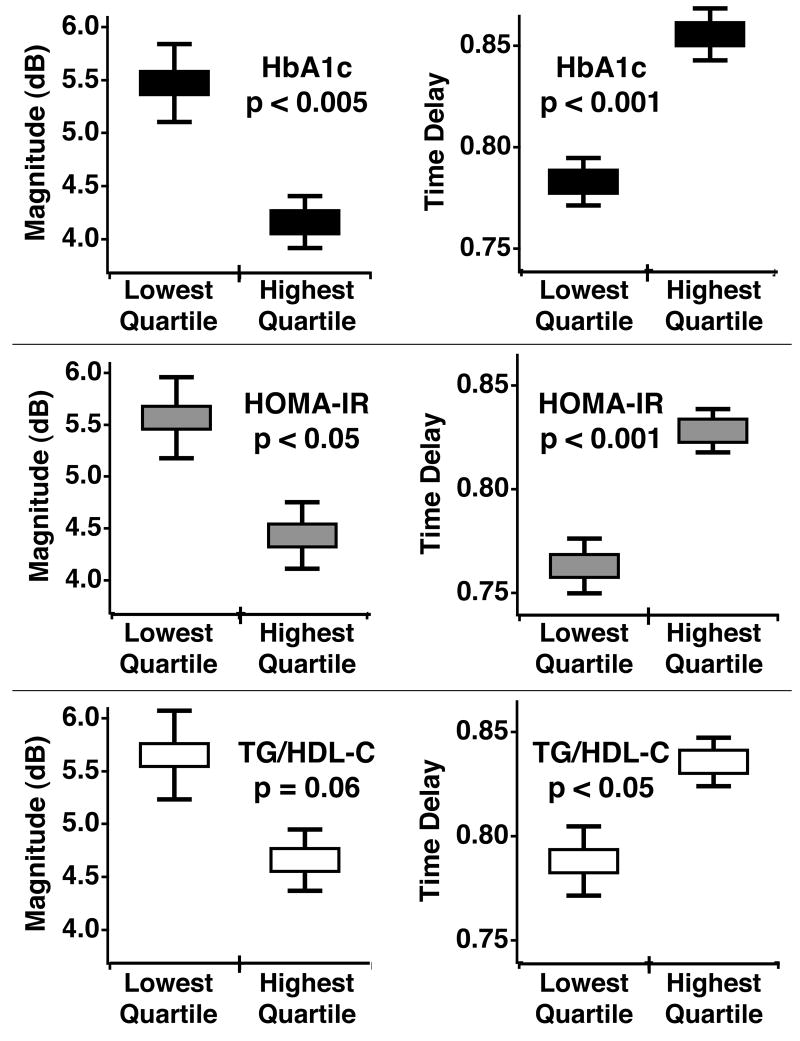
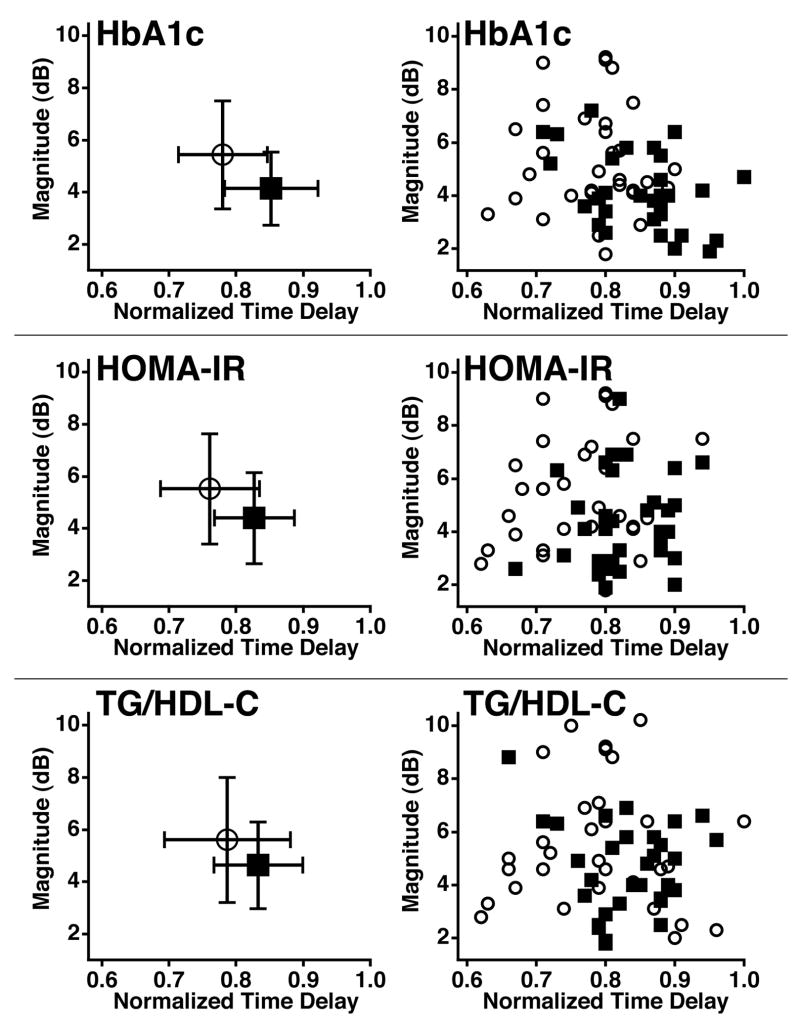
The mean and standard error for the magnitude and time delay of cyclic variation of myocardial backscatter were analyzed for the highest and lowest quartile groups of each metabolic parameter to quantify how the subjects separated on average. Figure 2 illustrates these results for three metabolic parameters, HbA1c, HOMA-IR, and TG/HDL-C. For each parameter, we observed a separation between the lowest and highest quartiles for the magnitude and the normalized time delay. In all but one case this separation between the results for the lowest and highest quartile was calculated to be statistically significant with a two-tailed, unpaired student t-test. Of the three metabolic parameters, HbA1c yielded the largest separation between the mean magnitude results, with the lowest quartile averaging 5.4 dB and the highest quartile averaging 4.1 dB. The average time delay measurements for this classification were 0.78 and 0.85 for the lowest and highest quartiles respectively. Dividing the subjects by HOMA-IR resulted in a similar separation of the average time delays as that seen in the HbA1c results. The results for subjects in the lowest and highest quartiles of HOMA-IR were mean time delays of 0.76 and 0.83, respectively, and mean magnitudes of 5.5 dB and 4.4 dB, respectively. TG/HDL-C yielded a less pronounced separation of the cyclic variation results than the other metabolic parameters. In this subject classification, the lowest quartile had an average magnitude of 5.6 dB and average time delay of 0.79 whereas the highest quartile had a mean value of 4.6 dB for the magnitude and 0.83 for the time delay. The magnitude and normalized time delay of cyclic variation are illustrated together in Figure 3. The left panels of Figure 3 show the means, and standard deviations for the magnitude and time delay of cyclic variation for the highest and lowest quartile groups of each metabolic parameter. The right panels display the individual data for the 64 subjects included in the HbA1c, HOMA-IR, and TG/HDL-C analysis. For the two cyclic variation parameters used in combination, the means suggest a modest separation of the data for all three subject classifications.

Figure 2.

The averages and standard errors of the magnitude (left panels) and normalized time delay (right panels) of cyclic variation for the lowest and highest quartiles in each subject division. The significance of each cyclic variation parameters was found using a two-tailed unpaired student t-test. HbA1c = Hemoglobin A1c, HOMA-IR = Homeostasis model assessment for insulin resistance, TG/HDL-C = Triglyceride to high density lipoprotein-cholesterol ratio

Figure 3.

The left panels are the mean, and standard deviations of the magnitude and normalized time delay of cyclic variation for the lowest and highest quartiles in each subject division. The right panels are individual subject results for the magnitude and normalized time delay of cyclic variation. In all the graphs, the open circles represent the 32 subjects in the lowest quartile of each subject division while the squares illustrate the results for the 32 subjects in the highest quartiles. HbA1c = Hemoglobin A1c, HOMA-IR = Homeostasis model assessment for insulin resistance, TG/HDL-C = Triglyceride to high density lipoprotein-cholesterol ratio

After the average cyclic variation results were obtained, ROC analysis was employed to quantify how magnitude and time delay could distinguish between populations, both individually and in combination. Table 2 summarizes the nonparametric estimate of the area under the curve and the associated standard error for the cyclic variation parameters analyzed individually as well as in combination. When the subjects are divided into quartiles of HbA1c, the magnitude of cyclic variation yielded an area and standard error of 0.69 ± 0.07. The normalized time delay, for these subjects, resulted in an area under the curve and standard error of 0.75 ± 0.06, and the combination of the magnitude and time delay of cyclic variation through Bayes classification gave an area and error of 0.78 ± 0.06. A similar trend is seen when the subjects are divided into quartiles of HOMA-IR. In this analysis the magnitude of cyclic variation resulted in an area and standard error of 0.63 ± 0.07, normalized time delay of cyclic variation yielded an area and error of 0.74 ± 0.06, and the combination of the two parameters gave an area and error of 0.76 ± 0.06. In the third measure, TG/HDL-C, the area under the curve and standard error for the magnitude of cyclic variation was 0.58 ± 0.07, and 0.64 ± 0.07 (area ± standard error) for the normalized time delay. The combination of magnitude and normalized time delay gave an area under the curve and standard error of 0.68 ± 0.07 for the TG/HDL-C grouping of subjects.

Table 2.

A summary of the nonparametric estimate of the area under the Receiver Operating Characteristic curve (AUC) and the associated standard errors (St.Err.). The first two rows represent the results when only magnitude or normalized time delay information is used. The third row reports the results when the magnitude and time delay results are combined through Bayes classification. HbA1c = Hemoglobin A1c, HOMA-IR = Homeostasis model assessment for insulin resistance, TG/HDL-C = Triglyceride to high density lipoprotein-cholesterol ratio

	HbA1c AUC ± St.Err.	HOMA-IR AUC ± St.Err.	TG/HDL-C AUC ± St.Err.
Magnitude	0.69 ± 0.07	0.63 ± 0.07	0.58 ± 0.07
Delay	0.75 ± 0.06	0.74 ± 0.06	0.64 ± 0.07
Combination	0.78 ± 0.06	0.76 ± 0.06	0.68 ± 0.07

DISCUSSION

Although the study subjects were considered to have clinically normal hearts as assessed by a stress echocardiography exam, and no greater than Stage 1 hypertension, differences in the magnitude and normalized time delay of cyclic variation were observed when the subjects were classified by hemoglobin A1c (HbA1c), homeostasis model assessment of insulin resistance (HOMA-IR), and the ratio of triglycerides to high-density lipoprotein cholesterol (TG/HDL-C). For each of these parameters, the cyclic variation of backscatter measurements behaved in a fashion similar to that observed in previous studies of subjects with type 1 and type 2 diabetes (Akdemir et al. 2001; Di Bello et al. 1995; Di Bello et al. 1996; Di Bello et al. 1998; Fang et al. 2003; Perez et al. 1992; Wagner et al. 1995). Those studies showed that the magnitude of cyclic variation is larger and the normalized time delay measurements are smaller in normal hearts than in diabetic hearts. Figures 2 and 3 demonstrate a similar trend in the current subject population. The subjects with more favorable profiles (low HbA1c, HOMA-IR, or TG/HDL-C) have a larger magnitude and smaller time delay of cyclic variation than the subjects in the highest quartiles of each classification. These differences in the cyclic variation parameters reach significance in all but one instance.

The cyclic variation results may suggest a trend toward a larger area under the ROC curve when information from magnitude and time delay of cyclic variation is combined using Bayes classification than when each feature is analyzed individually. However this observed improvement is relatively modest, suggesting the need for additional studies and the identification of additional features that may improve the approach used to characterize the cyclic variation waveform. Many laboratories only report the magnitude of cyclic variation, yet this study suggests an improved ability to distinguish between subject groups when both magnitude and time delay of cyclic variation are used together. This result is similar to that reported in the Wagner et al. study of type 1 diabetic patients with systemic complications versus normal controls (1995). Unlike the Wagner et al. study, the current study examined subjects who have clinically normal hearts and no systemic complications from diabetes. Yet in spite of this, the magnitude and time delay measurements show differences between the two groups. The 95% confidence intervals calculated in the current study are comparable to those reported in Figures 2, 3, and 4 of the Wagner et al. paper despite the different subject populations. In the current study, the difference between the area under the curve for the magnitude, time delay, and combination of cyclic variation parameters could increase if a quadratic classifier was used in the Bayes classification rather than the linear classifier used in this study (Fukunaga 1972; Wagner et al. 1995). Although the calculated values for area under the curve are quite modest, they are comparable to the areas obtained when the ratio of triglyceride to high-density lipoprotein cholesterol is used as a surrogate for insulin resistance (Kannel et al. 2008).

There are a number of limitations to the present study. First, because endomyocardial biopsy was not appropriate in these otherwise healthy subjects, we do not have direct evidence of myocardial abnormalities, either with regard to structure or metabolism. Second, the body mass index of subjects in the highest quartiles was substantially larger than that in the lowest quartiles for all three metabolic parameters. However, because obesity is a known risk factor for the development of type 2 diabetes, this finding is not unexpected. Studies suggest that there may be a link between obesity and the magnitude of cyclic variation of backscatter (Di Bello et al. 2006; Wong et al. 2004). This connection could be due to the influence of obesity on the load experienced by the myocardium. However, studies have shown that the magnitude of cyclic variation is relatively preload and afterload independent (Naito et al. 1996).

In summary, classifying subjects according to hemoglobin A1c, homeostasis model assessment of insulin resistance, and the ratio of triglycerides to high-density lipoprotein cholesterol resulted in differences in the magnitude and normalized time delay of cyclic variation between the lowest and highest quartile groups for each classification. In the long view, these results suggest that monitoring the hearts of patients with type 2 diabetes using the combination of magnitude and time delay of cyclic variation of backscatter might permit observation of changes associated with disease progression that may contribute to the development of diabetic cardiomyopathy.

APPENDIX

Bayes Classification

A detailed description of Bayes classification can be found in Introduction to Statistical Pattern Recognition by Fukunaga and is summarized below (1972). In this study Bayes classification analysis used cyclic variation results to calculate a decision rule that minimized the error of identifying a new subject with the wrong group. The Bayes decision rule incorporated both the magnitude and normalized time delay from the same subject and used information about the mean and covariance of the tests within both groups.

In general, when the two populations studied are normally distributed and their covariance matrices are equal, the Bayes decision rule simplifies to a linear classifier,

$$h(X)={(M_2-M_1)}^T{\mathrm{\sum }}^{-1}X+\frac{1}{2}(M_1^T{\mathrm{\sum }}^{-1}{M}_1-M_2^T{\mathrm{\sum }}^{-1}{M}_2)$$

where h(X) is the log likelihood ratio that the subject is in population 1 or 2, X is a vector of test results for one subject, M is a vector representing the means for each test, Σ is the covariance matrix, T the matrix transpose, and the subscripts 1 and 2 represent the two different populations (Fukunaga 1972). The elements of the covariance matrices were calculated using the formula

$${\sigma }_{mn}^2=\frac{1}{N-1}\sum _{k=1}^N(X_{mk}-{\mu }_m)(X_{nk}-{\mu }_n)$$

In the cyclic variation analysis, N is the number of subjects in the test population, x is the k^th subject’s test result for test m or n, and μ is the mean of test m or n, where m and n are indices corresponding to the diagnostic tests that are being compared. In this cyclic variation analysis, two tests (magnitude and time delay) were analyzed for each patient, so m and n both run from 1 to 2, and four covariance matrix elements are calculated. If the two populations studied (highest and lowest quartiles) do not have equal covariance matrices, the elements in the covariance matrix of population 1 can be averaged with the corresponding elements in the covariance matrix of population 2 to yield a common covariance matrix (Wagner et al. 1995). Alternatively a quadratic classifier can be calculated for the decision rule. In the present study, the covariance matrices for the two groups were averaged and a linear classifier was employed in order to make the results comparable to those presented in the Wagner et al. study of type 1 diabetic patients (1995). In the current study the h(X) values ranged from approximately -3 to 3 with negative h(X) values indicating a higher likelihood to be in population 1 and positive h(X) values signifying the subject is more likely to be in population 2.

The calculated linear classifier was estimated from a finite sample of subjects resulting in a decision rule that was derived from imperfect information. The performance of this classifier is expected to be inferior to a decision rule based on precise knowledge of the study population, but by using resampling techniques the effects of finite sample size can be reduced. The primary resample method was round-robin classification, also known as leave-one-out jackknife (Efron 1982; Wagner et al. 1995). In the round-robin resampling scheme, one of the samples was held out of the training set and the other samples were used to calculate or train the classifier. The left out sample was then classified using the trained decision rule and replaced into the original dataset. After replacement of the first left-out sample, a different sample was removed from the training dataset and the remaining samples were used to calculate the decision rule. The newly calculated decision rule was slightly different from the first rule because the training dataset included the previously left-out sample and did not include the latest sample that was removed. The removed sample was classified using the latest decision rule and then the sample was moved back into the original dataset. This process was repeated multiple times with different samples excluded from the training set until all the samples were classified and results could be used in ROC analysis.

Receiver Operating Characteristic (ROC) Analysis

A nonparametric estimate of the area under the ROC curve was used to assess the performance of the Bayes classified data by quantifying its ability to distinguish between the two populations. ROC analysis provides a description of the separability of two groups that is independent of a decision threshold, a test interpreter’s mindset, and prevalence of the disease. This method of analysis often relates the true positive fraction (the fraction of actually positive cases that are identified as positive by the test) to the false positive fraction (the fraction of actually negative cases that are called positive by the test) as a function of decision threshold. An ideal test with clear separation between test results of two groups would yield an area under the curve of 1.0. Conversely an area under the curve of 0.50 is representative of a random guess. In general an area under the curve between 0.50 and 0.70 indicates a poor test performance, an area between 0.70 and 0.80 is considered fair, 0.80 to 0.90 is good, and an area greater than 0.90 is considered excellent (Kannel et al. 2008).

The nonparametric estimate of area under the curve is also referred to as the Wilcoxon (Wilcoxon 1945) and the Mann-Whitney U-statistic (Mann and Whitney 1947). Several studies have shown that these unbiased estimators are analogous to that of the parametric area under the ROC curve (Bamber 1975; DeLong et al. 1988; Gallas 2006; Hanley and McNeil 1982). The Wilcoxon and Mann-Whitney U-statistic estimate the probability that a randomly selected result from one group will be greater than or equal to a randomly selected result from the other group. This statistic W is expressed as

$$W=\frac{1}{M·N}\sum _{j=1}^N\sum _{i=1}^M\mathrm{\Psi }\left(X_i,Y_j\right)\text{where}\mathrm{\Psi }(X,Y)=\{\begin{array}{ll}1\hfill & Y<X\hfill \\ \frac{1}{2}\hfill & Y=X\hfill \\ 0\hfill & Y>X\hfill \end{array}$$

In this formulation, the two subject groups are represented by X and Y, with subject populations M and N respectively. This figure of merit can be interpreted as the expected percent correct in a binary decision situation. As more test results are assigned to the correct population the statistic W gets closer to 1.0, in a fashion similar to that of the parametric area under the ROC curve. In this study all of the ROC results reported are from a nonparametric estimate of the area under the ROC curve.