Reduced amino acid alphabets exhibit an improved sensitivity and selectivity in fold assignment

Abstract

Motivation: Many proteins with vastly dissimilar sequences are found to share a common fold, as evidenced in the wealth of structures now available in the Protein Data Bank. One idea that has found success in various applications is the concept of a reduced amino acid alphabet, wherein similar amino acids are clustered together. Given the structural similarity exhibited by many apparently dissimilar sequences, we undertook this study looking for improvements in fold recognition by comparing protein sequences written in a reduced alphabet.

Results: We tested over 150 of the amino acid clustering schemes proposed in the literature with all-versus-all pairwise sequence alignments of sequences in the Distance mAtrix aLIgnment database. We combined several metrics from information retrieval popular in the literature: mean precision, area under the Receiver Operating Characteristic curve and recall at a fixed error rate and found that, in contrast to previous work, reduced alphabets in many cases outperform full alphabets. We find that reduced alphabets can perform at a level comparable to full alphabets in correct pairwise alignment of sequences and can show increased sensitivity to pairs of sequences with structural similarity but low-sequence identity. Based on these results, we hypothesize that reduced alphabets may also show performance gains with more sophisticated methods such as profile and pattern searches.

Availability: A table of results as well as the substitution matrices and residue groupings from this study can be downloaded from http://www.rpgroup.caltech.edu/publications/supplements/alphabets.

Contact: phillips@pboc.caltech.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Naturally occurring protein structures are observed to adopt ‘folds’, i.e. a common group of secondary structures with the same orientation and topology. Current estimates of the number of protein folds in nature is estimated to be between 1000 and 10 000 in total (Grant et al., 2004), an astonishingly low number compared with the huge space of possible amino acid sequences. From the wealth of structures and their associated sequences now available in the Protein Data Bank (PDB), it is clear that the same protein fold may be generated by different amino acid sequences; in effect, the structure of proteins is more conserved than their sequences (Chothia and Lesk, 1986). In some cases, the sequences underlying similar structures show almost zero sequence identity [see, e.g. Benson et al. (2004)]. This large degeneracy invites us to look for a coarse-grained sequence description that will reveal the underlying structural similarities between these apparently dissimilar sequences.

We take the inspiration for our coarse-grained, reduced alphabet study from the hydrophobic–polar (HP) model for protein folding, introduced by Dill (1985) to study the folding of globular proteins. This model derives from the observation that hydrophobicity will tend to dictate a minimum free energy protein conformation with hydrophobic residues buried in the interior and the hydrophilic residues exposed at the surface of a folded protein, suggesting that these gross features are dominant in dictating the fold. The HP model has been used fruitfully with lattice folding methods to generate structures with motifs analogous to those in natural proteins (Li et al., 1996) as well as to design de novo small globular proteins by patterning of polar and non-polar residues (Hecht et al., 2004).

Applying the idea of searching for classes of amino acids was applied with great success by Bork et al. (1992) to correctly predict in 1992 that MreB, FtsA and ParM would adopt the same ATPase fold as actin, nearly 10 years before any of those three proteins were crystallized. Bork et al. used a previously described ‘property pattern’ approach (Bork and Grunwald, 1990) to build up a profile of five motifs from actin, HSP70 and sugar kinase sequences and were then able to sensitively identify structural homologs by searching for matches against those conserved motifs.

Furthermore, previous experimental work with reduced amino acid alphabets in protein folding studies has shown that, in many cases, a reduced alphabet is sufficient to produce native-like proteins. The four-helix bundle protein Rop was studied by Munson et al. (1994) who showed that 32 amino acids in the hydrophobic core comprising eight different residues (ACEFILQT) could be replaced by patterning with just two amino acids (AL) to produce native-like proteins that showed activity in vitro, though only one mutant showed activity in vivo (Magliery and Regan, 2004). Schafmeister et al. (1997) designed de novo a 108-residue four-helix bundle with a seven-letter alphabet (AEGKLQS) and validated their results with a crystal structure. Riddle et al. (1997) were able to produce functional variants of the 57-residue Src SH3 β-sheet domain in which 38 of 40 targeted residues comprising 15 distinct amino acids were successfully mutated to a reduced alphabet of just five amino acids (AEGIK).

Given the success of the HP and other reduced alphabet models in reproducing important features of protein structure and folding together with the experimental success in designing native-like proteins from reduced alphabets, we surmize that these simple folding ideas might also be reflected in pairwise alignments of the sequences of structurally similar proteins. By properly grouping 20 naturally occurring amino acids into classes and thereby coarse-graining the scoring matrices, similarities in protein sequence that are not readily seen in the full 20-letter alphabet would be revealed. By all of the measures we used, reduced alphabets showed increased effectiveness at identifying structurally similar proteins as defined by the Distance mAtrix aLIgnment (DALI) database by a modest though statistically significant amount. Based on these gains in pairwise alignments and other past successes in the literature, we believe that the reduced alphabet approach applied to more sensitive methods, e.g. position-specific iterated basic local alignment search tool (PSI-BLAST) profile searches, holds promise for detecting structurally related proteins with weak sequence similarity.

The remainder of the article is organized as follows. In Section 2, we describe our procedure for coarse-graining substitution matrices, outline the reduced alphabet schemes tested and reference databases used in this study as well as describe the principal metrics for this work: area under the Receiver Operating Characteristic (ROC) curve (AUC), mean pooled precision and recall at 0.01 errors per query (EPQ). In Section 3, we present the results of all-versus-all sequence alignments using each of the reduced alphabets, showing the performance of reduced alphabets in comparison with various common full 20-letter substitution matrices. Finally, we compare the results of this study with other similar work and speculate on promising avenues for further development with the reduced alphabet concept.

2 METHODS

2.1 Substitution matrices

There are many amino acid substitution matrices that have been formulated for pairwise sequence database searches; one of the most commonly used matrices and the default choice for BLAST searches is BLOSUM62. The BLOSUM family of substitution matrices is based on a log-odds ratio of the observed and expected frequencies of amino acids in a reference set of alignments where a sequence identity cutoff has been applied (62% in the case of BLOSUM62). This method, originally proposed by Henikoff and Henikoff (1992), is described briefly here. Let us label the naturally occurring amino acids with indices 1–20; we may then derive a matrix c_ij with each entry of the matrix being the tally of the observed pairings of amino acid i with amino acid j in the reference alignments. Pairwise alignments do not distinguish between aligning e.g. AD and DA, so if the total count of ij and ji pairs is C (with i ≠ j) we assign c_ij=c_ji=C/2 to reflect this symmetry. The underlying reason for this symmetry is that we assume no a priori knowledge of the order in which the sequences arose; without such knowledge, the likelihood of a substitution from, e.g. A to G and G to A are equal. The observed probability matrix o_ij is the normalized c_ij matrix:

(1)

The frequencies of each of the amino acids p_i is now easily calculated from o_ij:

(2)

and the expected (random) probability of aligning amino acid i with j is:

(3)

The substitution matrix score m_ij is calculated from the observed and expected probabilities as a log-odds ratio:

(4)

where the base of the logarithm is usually chosen as b=2 so that m_ij has units of bits of information (though substitution matrix values are sometimes measured in half-bits or other fractional bit units). For convenience of notation, the BLOSUM series of matrices will be referred to hereafter as BL followed by the level of sequence identity used in building the matrix, e.g. BL62 for the BLOSUM matrix with 62% identity cutoff.

We follow this log-odds method in formulating matrices based on a reduced alphabet. Each reduced alphabet scheme clusters amino acids together into groups where all amino acids within a group are considered identical. Given N groups of amino acids defining a reduced alphabet, the new frequency of group I is calculated as:

(5)

where k runs over each amino acid in group I. The new expected and observed probabilities to align group I with group J are:

(6)

(7)

Finally, the new matrix entries in the reduced N × N matrix are:

(8)

(9)

This method differs from that used in some previous reduced alphabet studies (Li et al., 2003; Murphy et al., 2000), which used the arithmetic mean of the subsitution matrix entries; using the mean of the subsitution matrix scores is inconsistent with the log-odds probability scheme upon which the substitution matrices are based.

2.2 Reduced alphabet schemes

A reduced alphabet is any clustering of amino acids based on some measure of their relative similarity. Many such schemes have been proposed; the ones used in this study are briefly reviewed here together with the abbreviations used to refer to them. If a name for the scheme is given by the authors (e.g. SDM and DSSP) it has also been used here, otherwise abbreviations are formed by using the first letters of the names of the first and last authors. Thomas and Dill (1996) created a hierarchy of amino acid groupings based on intuitive physicochemical considerations (TD). Mirny and Shakhnovich (1999) (MS) constructed a six-letter alphabet based mostly upon intuition as well as a study of the effects of disulfide bonds on protein folding which suggested separating aliphatic hydrophobic and aromatic hydrophobic residues (Abkevich and Shakhnovich, 2000). Solis and Rackovsky (2000) posited clusters based on maximum preservation of structural information (DSSP and GBMR). Andersen and Brunak (2004) searched for clusters of amino acids based on the ability of standard methods to correctly predict secondary structure from the simplified sequences (AB). Cieplak et al. (2001) used the Miyazawa–Jernigan interaction matrix (Miyazawa and Jernigan, 1996) together with a distance-based clustering scheme to partition the naturally occurring amino acids into two- and five-letter groups (CB). Prlić et al. (2000) derived new substitution matrices based on structural alignments of proteins with low-sequence identity and then clustered the amino acids based on those matrices (SDM and HSDM). On the basis of a comparison of early substitution matrices, Landes and Risler (1994) proposed a 10-letter alphabet that showed promise for increasing the sensitivity of protein alignment searches (LR). Li et al. (2003) proposed grouping schemes based on preservation of information in global sequence alignments between a sequence and its reduced-alphabet version. They produced two groupings, one allowing amino acids to change their order or ‘interlace’ (LW-I) and one where they were not allowed to change order (LW-NI). The LW schemes were identical at the levels of 2, 3 and 15 through 19 letters. We also note that the CB and LW schemes were identical at the two-letter level. Melo and Marti-Renom (2006) created a five-letter clustering of amino acids based on the Johnson–Overington matrix (JO20) (Johnson and Overington, 1993), which they found performed well in aligning homologous sequences and fold assessment (MM). Murphy et al. (2000), inspired by experimental successes in designing proteins with reduced alphabets, proposed clusters of amino acids based on the BL50 substitution matrix (ML). Liu et al. (2002) studied the pair frequency counts in the Miyazawa–Jernigan and BL50 matrices to find deviations from a random background and based thereon proposed a clustering of amino acids (LZ-MJ and LZ-BL). Finally, Wang and Wang (1999) derived clusters from the Miyazawa–Jernigan matrix by preserving maximal similarity between a reduced-alphabet version of the matrix and the full 20 × 20 matrix (WW). They found a 5-letter alphabet (IKEAG) that matched with what Riddle et al. (1997) had found in their experimental study producing SH3 domains from reduced alphabets. Each of these schemes produced a hierarchy of amino acid classes. At each level in the hierarchy, the number of classes or ‘letters’ in the alphabet is increased. We tested each of the reduced alphabet schemes in the papers just cited; Table 1 shows the abbreviations for each scheme, the various levels of clusterings comprising the scheme and the frequency matrix and gap penalties used. In this work, reduced alphabet matrices will be referred to by the alphabet scheme (TD, SDM, HSDM, etc.) followed by the number of letters in the alphabet, e.g. HSDM17.

Table 1.

Reduced alphabet schemes investigated in this work

Scheme	Alphabet size(s)	Matrix	Gaps	Reference
AB*	2–19	BL62	11/1	Andersen and Brunak (2004)
CB*	2,5	BL62	11/1	Cieplak et al. (2001)
DSSP*	2–14	BL62	11/1	Solis and Rackovsky (2000)
GBMR*	2–14	BL62	11/1	Solis and Rackovsky (2000)
HSDM	2–10,12,14–17	HSDM	19/1	Prlić et al. (2000)
LR*	10	BL62	11/1	Landes and Risler (1994)
LW-I* / -NI*	2–19	BL62	11/1	Li et al. (2003)
LZ-MJ* / -BL	2–16	BL50	11/1	Liu et al. (2002)
ML	4,8,10,15	BL50	12/2	Murphy et al. (2000)
MM	5	JO20	140/0	Melo and Marti-Renom (2006)
MS	6	BL62	11/1	Mirny and Shakhnovich (1999)
SDM	2–4,6–8,10–14	SDM	7/1	Prlić et al. (2000)
TD*	2–10,14	BL62	11/1	Thomas and Dill (1996)
WW*	5	BL62	11/1	Wang and Wang (1999)

Abbreviations and references are listed in the first column; alphabet sizes, matrix used and gap penalties are also shown. Wherever possible, we used the matrices and gaps given in the original articles referenced, though we note that the starred schemes were proposed independently of any particular substitution matrix. In those cases, the BL62 frequency counts were used to derive the coarse-grained matrices with 11/1 gaps. In addition to the reduced alphabet schemes tested above, we also tested the following full 20 × 20 matrices: BL50 11/1, BL50 12/2, BL62 11/1, JO20 140/0, SDM 7/1 and HSDM 19/1. Data points at 20 letters for SDM or HSDM come from these last two matrices, respectively.

2.3 Pairwise sequence alignments

2.3.1 Protein database

We chose the DALI database (Holm and Sander, 1993), which uses fully automated methods to cluster protein domains based on their structural similarity as our ‘gold standard’ for determining the structural relatedness of proteins. DALI partitions each protein structure in the PDB into domains by maximizing criteria of compactness and recurrence of those domains (Holm and Sander, 1998). After determining the domains, all-versus-all structural alignments of the domains are executed and a Z-score estimated to indicate the statistical significance of those alignments (Holm and Sander, 1998). Finally, the domains are clustered into families based on Z-score cutoffs; a cutoff Z-score >2, indicating statistically significant structural similarity at the 2σ level, is used to define proteins with roughly the same ‘fold’ (Holm and Sander, 1998).

The sequence library for this study was drawn from the DALI pdb90 database using each of the representative sequences in the domain fold classes defined by the DALI Domain Dictionary (Dietmann et al., 2001; Holm and Sander, 1998), both available for download at the DALI website.¹ All pairs of sequences within the same domain fold class are considered to be structurally related ‘hits’ (true positives) in our database searches. In total, 13 351 sequences were drawn from the pdb90 database, representing 2780 fold classes. One domain fold class, number 1636, was not represented in the database because its representative sequence, 1mwxA_1, was not found in the latest version of pdb90 available for download. We also note that there were 1264 sequences which were singletons i.e. they were the only members of their DALI fold class; these sequences are in some sense undetectable since they have no true positive relationship to any other protein in the database. Nevertheless, to reflect the situation in actual practice where this information is not known a priori, the singletons were included in our analysis.

2.3.2 Alignment program

All-versus-all Smith–Waterman alignments were executed using SSEARCH version 3.4 from the FASTA sequence alignment suite (Pearson, 1991; Smith and Waterman, 1981); the alignments were ranked by E-value as calculated by the default SSEARCH statistics option (specified by the ‘-z 1’ command line option).

2.3.3 Generation of search results

We executed all-versus-all alignments, using each sequence in the DALI pdb90 database in turn as a query against the remaining sequences. The results of all these searches were then pooled into a single list of results ranked by the E-value assigned by SSEARCH; when true and false positives shared an E-value, the false positive alignments were ranked ahead of the true positives to obtain a conservative estimate of discriminating power.

2.3.4 Reference sequence alignments

Structural alignment of protein domains with the DALI method produces a reference list of structurally equivalent pairs of residues (Holm and Sander, 1993). We compared these structure-based alignments with the alignments produced by SSEARCH and tallied the fraction of structurally equivalent residues found by SSEARCH local alignments. The database of structurally equivalent residues, dali_fragments, was obtained from the DALI downloads web site (see footnote 1).

2.4 Metrics

A scoring matrix should ideally be able to both detect related pairs of proteins (true positives) and reject non-related pairs (false positives); these properties are termed sensitivity and selectivity, respectively, and in many instances they compete with one another in the sense that as a matrix is tuned to be more sensitive it often loses selectivity and vice versa. After pooling the results of querying the database with each sequence, we choose a particular E-value and consider all results at this E-value or lower to be ‘hits’. The recall, fall-out, precision and EPQ are calculated from the list of hits as follows:

(10)

(11)

(12)

(13)

where TP is the number of true positive hits, FP is the number of false positive hits and N_seq is the total number of sequences; P and N are the total number of positive and negative relationships in the database, respectively. Moving down the pooled list of search results, we generate successively larger groups of hits at increasing E-values with associated values for recall, fall-out, precision and EPQ. The three curves analyzed in this work are precision versus recall, recall versus fall-out (also called the ROC curve) and recall versus EPQ (also called the coverage versus EPQ plot), all parametrized by increasing E-value. We define the mean pooled precision to be the integral of the precision versus recall curve for the combined list of search results; this number gives the average precision achieved over the entire range of recall. The AUC measures the ability of a matrix to identify related pairs by assigning them lower E-values than pairs of proteins that are not related over the entire list of pooled results. Finally, the recall at 0.01 EPQ gives the number of true positives returned at a fixed, low error rate. Recall may be normalized in several ways, as defined by Green and Brenner (2002). Recall without normalization gives equal weight to each true positive relationship; quadratic normalization weights true positive hits so that each fold represented in the database has equal weight. Linear normalization is a compromise between these two, giving each sequence in the database equal weight and is meant to take into account the fact that folds are not equally represented in nature (Grant et al., 2004).

3 RESULTS

3.1 Mean pooled precision

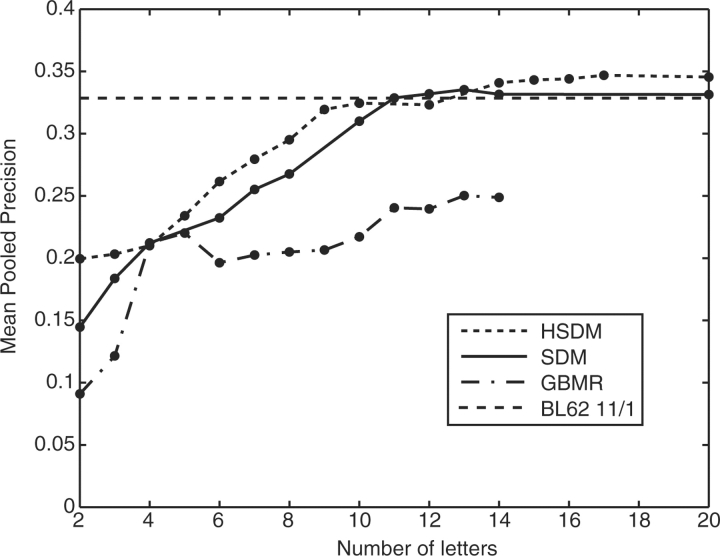
A perfect method would have a mean pooled precision value of unity, maintaining 100% precision until all true positives have been identified. The mean pooled precision for all of the HSDM, SDM and GBMR alphabets is plotted in Figure 1. Even the strongest performers in mean pooled precision cannot maintain a high level of precision beyond a recall value of about 0.4. This means that only ∼40% of the total number of true positives can be reliably identified before additional true positives in the list of hits become buried in a flood of false positives in a sort of ‘needle-in-a-haystack’ situation (see Supplementary Material for HSDM17, SDM12 and GBMR4 precision versus recall curves).

Fig. 1.

Reduced alphabet performance in mean pooled precision. Mean pooled precision indicates the average precision achieved by a matrix over the entire range of recall. Points indicate reduced alphabets that were tested; the connecting lines are a guide to the eye. A perfect method would achieve a mean pooled precision value of unity, with all true positives ranked ahead of false ones. The HSDM17 matrix is the top performer in this metric; the dashed black line shows the performance of BL62 11/1 for reference.

3.2 AUC

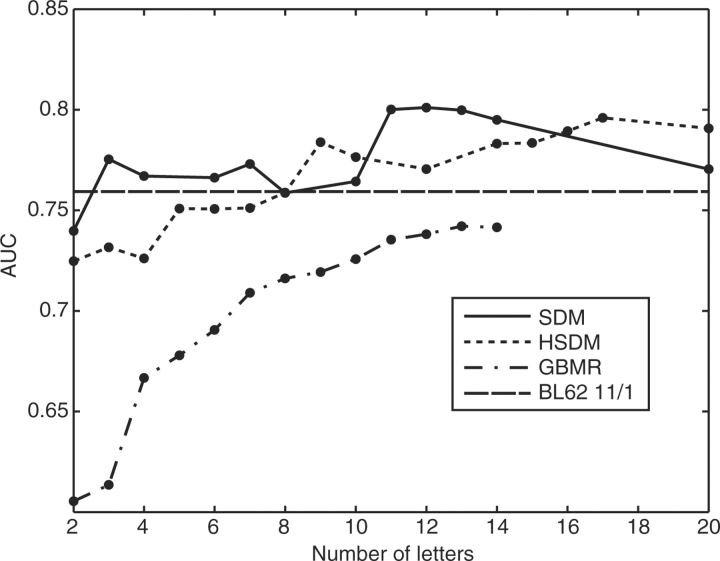
The AUC has a very specific interpretation: it is equal to the probability of assigning a lower E-value to a true positive than to a false positive (Hanley and McNeil, 1982). Therefore, it gives a measure of the sensitivity of a scoring matrix to related sequences over the entire pooled list of results. The top overall performer in detecting structurally related proteins by pairwise search is the SDM12 matrix; another notable high performer is LZ-MJ6 which finished in the top 10 with only six letters. The total AUC versus number of letters in these schemes is shown in Figure 2; note that the AUC does not necessarily increase monotonically with alphabet size.

Fig. 2.

Overall sensitivity of the HSDM, SDM and GBMR alphabets, as measured by the AUC. The integral of the ROC gives a measure of how well the entire pooled list of hits is sorted; a perfect method would have an ROC area of unity. The level of sensitivity of BL62 11/1 is shown with the black dashed line. Points indicate reduced alphabets that were tested; the connecting lines are a guide to the eye.

Although it is of interest that HSDM17 maintains the best selectivity as measured by mean pooled precision and SDM12 the best sensitivity as measured by the AUC, what is of most interest to a user of an alignment program with a query protein and a target database is to find a scoring matrix that will yield the most number of true positives at a fixed, low error rate. Operationally, a researcher will have an intuition for what E-values indicate hits that are likely to be significant and will ignore hits below that intuitive threshhold. In the DALI database, we used there are more than 150 times as many false positives as true positives, so that much of the advantage shown by HSDM17 and SDM12 is in a regime beyond what could be reasonably processed ‘by hand’. Therefore, we also examine the performance of reduced alphabets in recall of true relationships at an EPQ rate of 0.01.

3.3 Recall at 0.01 EPQ

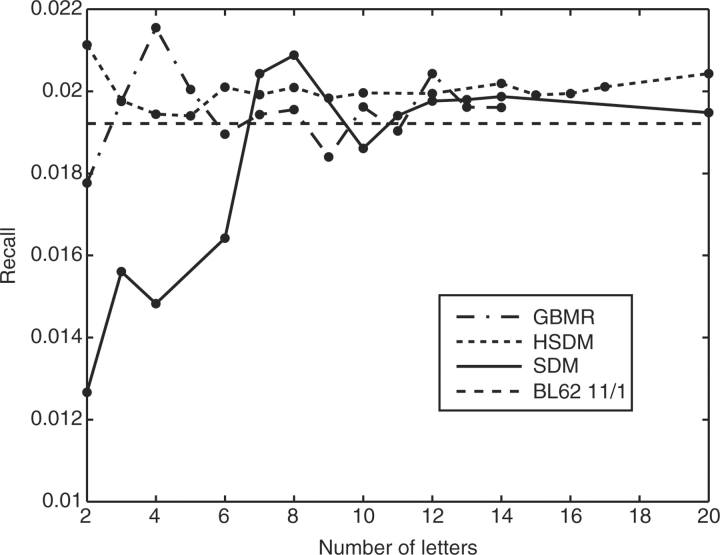
The second measure of the selectivity of each reduced alphabet scheme was calculated as the recall (also called coverage) at 0.01 EPQ; this is the metric of the most practical interest. Figure 3 shows the recall at 0.01 EPQ with linear normalization versus number of letters for the GBMR, SDM and HSDM alphabets.

Fig. 3.

Recall with linear normalization at 0.01 EPQ for various numbers of letters in the GBMR, HSDM and SDM reduced alphabet schemes. The level of performance of BL62 11/1 is shown with the black dashed line. Points indicate reduced alphabets that were tested; the connecting lines are a guide to the eye.

These results would seem to indicate that reduced alphabets offer an advantage of immediate practical value over currently used matrices based on the full alphabet. To further investigate this possibility we performed all versus all alignments with HSDM17, SDM12, GBMR4 and BL62 11/1 using proteins belonging to the same structural classification of proteins (SCOP) superfamily to define true positives. In the SCOP study, we found that BL62 11/1 outperformed GBMR4 in linearly normalized recall at 0.01 EPQ with both the scop40 and scop95 databases. However, the larger reduced alphabets maintained their advantage in selectivity and sensitivity: HSDM17 and SDM12 both achieved higher mean pooled precision, AUC and linear recall at 0.01 EPQ scores than BL62 11/1. (See the Supplementary Material for the full results.) This indicates that small reduced alphabets can show an increased sensitivity and selectivity for proteins that are structurally related, the only criteria used by DALI, but seem to lose selectivity when criteria such as function and evolution are taken into account, as is done with the human-curated SCOP superfamily classification (Murzin et al., 1995). To the extent that performance with the SCOP and DALI databases indicates real world performance, these results suggest that moderately reduced alphabets like SDM12 and HSDM17 offer increased sensitivity and selectivity over the standard BL62 11/1 matrix based on a full alphabet.

3.4 Statistical significance of results

The three top-performing alphabets (GBMR4, SDM12 and HSDM17) are shown in Table 2 together with the results of BL62 11/1 shown for reference. We used the Bayesian bootstrap method developed by Price et al. (2005) to evaluate the statistical significance of the successes of the reduced alphabets in comparison with the standard BL62 11/1 scoring matrix. First, the differences in performance are tabulated between each pair of bootstrap replicas, then a Z-statistic is calculated by dividing the mean of distribution of differences by its SD. This statistic, rather than the difference in mean performance, was found to be the most sensitive for evaluating the significance of differences in performance between two scoring matrices (Price et al., 2005). We find a strongly significant Z-score of 6.17 for the superior performance of SDM12 relative to BL62 11/1 in AUC, and marginally significant Z-scores of 1.33 for HSDM17 versus BL62 11/1 in mean pooled precision and 1.49 for GBMR4 versus BL62 11/1 in recall at 0.01 EPQ with linear normalization.

Table 2.

The top performing alphabets found in this study in linearly normalized recall at 0.01 EPQ (GBMR4), AUC (SDM12) and mean pooled precision (HSDM17) with the standard deviation of 1000 bootstrap replicas given in parentheses

Alphabet	Amino acid groups																				Recall	AUC	MPP
GBMR4	ADKERNTSQ									YFLIVMCWH									G	P	0.022 (0.001)	0.667 (0.004)	0.212 (0.006)
SDM12	A	D	KER			N	TSQ			YF		LIVM				C	W	H	G	P	0.020 (0.001)	0.801 (0.005)	0.332 (0.009)
HSDM17	A	D	KE		R	N	T	S	Q	Y	F	LIV			M	C	W	H	G	P	0.020 (0.001)	0.796 (0.004)	0.347 (0.008)
BL62 11/1	A	D	K	E	R	N	T	S	Q	Y	F	L	I	V	M	C	W	H	G	P	0.019 (0.001)	0.759 (0.005)	0.329 (0.009)

Results for BL62 11/1 are shown for comparison.

The bold values represent the best result in each column for Recall, AUC and MPP.

4 DISCUSSION

We wish also to note that many reduced alphabets beyond the three that we mentioned above outperform the BLAST default, BL62, with 11/1 gaps. Among the 151 scoring matrices tested in this work, BL62 ranked 38th overall in AUC, 18th in mean pooled precision, and 111th, 102nd and 104th in recall at 0.01 EPQ with no, linear and quadratic normalization, respectively. In the remaining plots, we will compare the top performers in mean pooled precision (HSDM17), AUC (SDM12) and recall at 0.01 EPQ (GBMR4) with one another, using BL62 11/1 as the baseline. Full results as well as the top 10 schemes in each category are presented in the Supplementary Material. The overall low performance of the reference matrix BL62 11/1 in mean pooled precision (∼0.03) and recall at 0.01 EPQ (∼0.02) indicate that those metrics represent a kind of ‘stress test’ for pairwise sequence alignment. This makes the task of sorting out the best performing matrices more obvious than if an easier test had been chosen where all matrices performed relatively well. In Section 5, we examine the statistical significance of our ranking of best matrices to determine whether the differences in performance are significant.

Some related previous work looked into the question of how many amino acid classes are necessary both for protein folding and for identification of related proteins. In their study of pairwise sequence alignment, Murphy et al. (2000) estimated that a minimum of 10–12 amino acid classes is necessary to design foldable sequences for most protein families. Fan and Wang (2003) found that the minimum alphabet size for protein folding requires ∼10 types of amino acids. In a recent study, Li and Wang (2007) observed optimal sequence alignment accuracy at an alphabet size of around 9 letters. We find a similar optimal size when maximizing the AUC (12 classes). The consensus from these diverse methods is that performance improvements can be made by properly grouping the amino acids into 9–12 clusters.

It is interesting that the top performing alphabets, shown in Table 2, are compatible with one another in the sense that SDM12 can be derived from GBMR4 and HSDM17 can be derived from SDM12 by simply breaking down larger clusters into smaller ones without needing to interchange the grouping of any of the amino acids. In the GBMR4, alphabet glycine and proline are singled out as being structurally dissimilar from the other amino acids; the remaining two groups reflect a hydrophobic (YFLIVMCWH) and polar (ADKERNTSQ) classification. In this sense, the GBMR4 alphabet is a modest refinement of the simple HP concept. The SDM12 alphabet maintains clusters for acidic/basic (KER), polar (TSQ), aromatic (YF) and mostly aliphatic (LIVM) groups. Two non-intuitive results in these groupings are the omission of aspartic acid from the acidic/basic KER cluster and the inclusion of methionine in the otherwise aliphatic LIVM cluster. In HSDM17, only the strongest associations among these are maintained: acidic/basic (KE) and aliphatic (LIV). By clustering together amino acids with similar properties in this way, we increase the signal to noise in our database searches and avoid over-assigning importance to differences among the naturally occurring amino acids.

We wish to note several promising avenues for further investigation which could not be pursued in this work for lack of time and computing resources. In theory, an optimum alphabet could be searched for at each alphabet size by, e.g. Monte Carlo search. Likewise, it would be ideal to optimize the gap penalties with respect to each reduced alphabet. Lack of sufficient computational resources made it impractical to carry out these optimizations. We chose to use the DALI database as our standard for determining structural relationships among proteins in the PDB over databases like SCOP (Murzin et al., 1995) because its determinations are informed only by structural similarity and require no human curation. Although we obtained some preliminary results with SCOP, it would be instructive to compare the results using the DALI database with what would be obtained by testing all the reduced alphabets in this work using SCOP superfamilies as the gold standard for structural relatedness. Given the encouraging results shown by SDM12 and HSDM17 with both SCOP and DALI, we believe that further investigation into the practical advantages of reduced alphabets for general use with pairwise alignment matrices merits additional exploration.

5 CONCLUSION

We find, perhaps counter to common intuition, that reduced alphabets increase the selectivity and sensitivity to pairs of proteins with structural similarity as measured by the mean pooled precision, AUC and recall at 0.01 EPQ (under all normalizations). In addition, we found that reduced alphabets can return more distantly related pairs of proteins. This is in contrast to some earlier studies (Li et al., 2003; Liu et al., 2002; Murphy et al., 2000) which found that reduced alphabets could only produce losses in performance relative to a full alphabet. Landes and Risler (1994) also observed improved sensitivity with reduced alphabets; in an early study with aminoacyl-tRNA synthetases, LR10 showed an increased ability to identify distant homologs over methods using the full alphabet. This work also adds to the encouraging results with reduced alphabets found by, e.g. Fan and Wang (2003), Melo and Marti-Renom (2006) and Li and Wang (2007). Melo and Marti-Renom tested the Johnson–Overington matrix against several small reduced alphabets: WW5, GBMR5, ML4, MM5 and 100 randomly reduced five-letter alphabets and used the resulting pairwise alignments as the initial seed for an optimal structural superposition. They found that the GBMR5 reduced alphabet produced performance gains over the full matrix in the final structural alignment, as measured by the root-mean-square deviation of Cα atoms.

A promising area for application of the results of this study is in the building of protein profiles or hidden Markov models. Such models are built up from a multiple alignment of many putatively homologous proteins. At each position in the alignment, a number can be assigned for the probability of observing a particular amino acid based on the sequences in the multiple alignment. The simplest type of protein profile is simply a consensus sequence of the most commonly occurring amino acid at each position. One current limitation of these methods is the limited sample of sequences with which to build up the multiple alignment; experimentally determined sequences account for only a fraction of the total sequence space available to a given protein fold. By thinking of a protein as being made up of amino acids drawn from classes with particular physical properties, we can leverage the physicochemical similarities of amino acids to help make up for this lack of statistics in our sampling of sequence space. This problem of undersampling was recognized by Sjölander et al. (1996) who developed a method of Dirichlet mixtures for use with multiple alignments to improve detection of remote homologs. The method of Dirichlet mixtures estimates the most likely expected distribution of amino acids at a given position in a multiple alignment and could be extended to estimate the most likely expected distribution of classes of amino acids, as studied here, instead of individual amino acids. A reduced alphabet approach to building up protein profiles may improve our ability to detect proteins with structural homology by leveraging our knowledge of the chemical properities of the amino acids in building up a physical picture of a fold.