Sequence physical properties encode the global organization of protein structure space

Abstract

It is demonstrated that, properly represented, the amino acid composition of protein sequences contains the information necessary to delineate the global properties of protein structure space. A numerical representation of amino acid sequence in terms of a set of property factors is used, and the values of those property factors are averaged over individual sequences and then over sets of sequences belonging to structurally defined groups. These sequence sets then can be viewed as points in a 10-dimensional space, and the organization of that space, determined only by sequence properties, is similar at both local and global scales to that of the space of protein structures determined previously.

Evaluating the degree of structural homology between protein sequences is a significant outstanding problem in biomedical research. That this problem remains open is apparent from the persistence of interest in the “remote homolog” problem—the observation that in any reasonably large group of sequences that fold to a specified, common architecture, there will be pairs of sequences that are not related by any currently known criterion.

Accurate methods for structural homology detection depend on an understanding of the sequence code underlying fold selection. There are intriguing hints that this code may be less complex than once thought. That the average amino acid compositions of proteins can give reasonably accurate classifications of structural class (1–3) and fold family (4–12) is well known. But a classification scheme gives no information about quantitative relationships between the classes under consideration, because it reflects only local details of the underlying space of protein structures. Quantitating those relationships requires a sequence-based metric function capable of objectively measuring the distance between 2 arbitrarily selected classes.

We have delineated the organization of structure space in previous work (13–15). Those results were obtained using only structural data, with no reference to sequence information. The picture that emerged, subseqently verified by Yee and Dill (16), is that of a structure gradient in which all-helical structures are concentrated at one extreme of the space and all-sheet/barrel structures are concentrated at the other extreme, with mixed alpha/beta structures in the intervening region.

In the present work we demonstrate that when protein sequences are represented appropriately, the average amino acid properties of those sequences encode a similar picture of the global organization of protein sequence space. We demonstrate the existence of a metric function, based entirely on sequence properties, that reproduces the known characteristics of structure space.

Sequence Model

Rigorous determination of the characteristics of protein sequences requires that they be analyzed numerically, using a representation that is both complete and nonredundant. Representations that rely on arbitrarily chosen sets of physical properties of the amino acids generally are both incomplete and correlated. This problem was addressed by Kidera and coworkers (17, 18), who performed a factor analysis on all available sets of physical properties of the 20 amino acids. They demonstrated that all of these data can be represented by a set of 10 property factors, which together carry 86% of the variance of the entire property database. Therefore, to a very good approximation, an amino acid X can be represented numerically as a 10-vector,

It follows that an N-residue sequence can be written as a set of 10 numerical strings of length N, each of which describes the variation of one of the property factors along the length of the protein. The property factors are linearly independent by construction, and therefore the 10 strings together give a complete, uncorrelated description of the physical properties of the sequence. The definitions of the property factors are given in supporting information (SI) Table S1.

Applying this representation requires a database of protein sequences. We have constructed a very large set of sequences taken from the CATH database (19, 20). The organization of CATH is ideal for this investigation, because domains are organized in a hierarchical fashion based (in order of increasing detail) on class, architecture, topology, and homology. In the present work, we wanted to use a comprehensive sequence/structure database that reflects the composition of the entire Protein Data Bank, rather than relying on selection criteria. A primary consideration in avoiding biased results is eliminating sequences with a high degree of similarity from the database. We therefore began with a subset of the entire CATH database, CathDomainSeqs.S35.ATOM.v3.1.020, which was selected by the CATH curators to be representative of the entire database while containing no pairs of sequences with sequence identity exceeding 35%. This value is generally considered to mark the lower limit of sequence relatedness, and thus our working database is composed entirely of sequence pairs that are in the “twilight zone.” It contains no pairs that can be considered homologs in the traditional sense.

We further adjusted the database by removing all sequences with missing residues and all sequences with fewer than 60 amino acids. We were left with a data set of 7,056 sequences known to be complete and unrelated by any standard criterion. The highest level of the CATH hierarchy consists of 4 classes. C = 1 contains all-helical structures, C = 2 contains sheet/barrel structures, and C = 3 contains mixed alpha/beta structures. The very small class C = 4 (73 sequences) contains proteins whose only common feature is a lack of regular structure, and is not considered in this work. Our final database contained 1,538 sequences with C = 1, 1,690 sequences with C = 2, and 3,755 sequences with C = 3. Sequences ranged in length from 60 to 1146 aa, and the total number of residues in the database was 1,114,667.

The sets of sequences in which we are interested here are those characterized by common values of the 3 identifiers C, A, and T. These are sequences known to fold to similar architectures but for which no specification of sequence homology is given. We restrict our attention to those CAT classes in the database that have at least 20 members. There are 59 such classes, constituting 6% of the 980 CAT classes in the database. These contain a total of 4,319 sequences—60% of the sequences in the database. The groups included in the present study are shown in Table S2. It should be noted that this database is significantly larger than the databases used in earlier work (13, 16).

For every sequence S in the database, we can define the sequence-averaged value of the mth property factor,

where N_S is the number of residues in the sequence. We can further average these quantities over the set of N_Q sequences that belong to some predefined set {Q},

The N_Q sequences in {Q} are then represented by the 10-vector of averaged property factors,

We refer to this as the averaged property factor (APF) representation of the sequence class Q. It should be noted that the sequence-averaged property factors in eq. (2) are the k = 0 Fourier transforms of the 10 numerical strings that together represent the sequence (21, 22). This observation provides a direction for further generalization of the results, through inclusion of higher Fourier components in the analysis of sequence space.

The 10-vectors Q_CAT for the 59 CAT classes can be thought of as the position vectors of these classes in 10-space. To understand the relationships between classes established by the Euclidean metric inherent in the APF representation, we need to visualize the distribution of the corresponding points. We therefore performed a principal components analysis (PCA) (23) of the 10-vectors.

Results

The PCA results are summarized in Table 1. The first 3 eigenvectors carry a total of 67.2% of the variance of the entire data set; therefore, a low-dimensional representation of the structure space is both feasible and meaningful. Each of the principal components includes contributions from all 10 property factors. The principal components are listed in Table 2.

Table 1.

Eigenvalues of the principal eigenvectors

Eigenvector	Eigenvalue	Variance proportion
e1	4.078	40.8
e2	1.426	14.3
e3	1.211	12.1
e4	0.949	9.5
e5	0.791	7.9
e6	0.541	5.4
e7	0.446	4.5
e8	0.272	2.7
e9	0.198	2.0
e10	0.088	0.9

Table 2.

The principal components

	〈f1〉	〈f2〉	〈f3〉	〈f4〉	〈f5〉	〈f6〉	〈f7〉	〈f8〉	〈f9〉	〈f10〉	C
U1	2.228	−2.388	2.584	−2.286	3.945	3.387	−4.775	3.279	−4.297	−1.229	1.426
U2	0.73	2.351	0.902	8.174	2.676	9.352	3.010	−2.851	−2.563	−17.233	3.218
U3	−2.391	−5.221	−3.168	3.897	−12.529	−5.277	−0.341	7.730	−7.368	−8.474	−5.181
U4	−1.203	−2.079	9.038	−0.529	−4.457	−9.396	−11.939	−10.586	3.692	−10.838	−3.366
U5	1.662	−2.123	−9.205	−10.71	−8.622	8.833	−3.014	−3.695	8.812	−14.255	3.23
U6	0.74	1.276	9.144	1.925	−25.742	15.313	6.211	−4.466	−5.774	13.654	2.01
U7	−1.126	−7.337	2.402	−8.596	9.415	−4.77	27.633	−10.987	−9.914	−6.868	−1.137
U8	−0.207	0.912	15.02	−4.479	−2.24	−1.763	17.849	22.849	23.702	−16.13	−0.544
U9	−11.163	−16.34	1.492	9.107	13.122	25.787	−5.281	−2.872	16.958	16.329	4.358
U10	23.277	−17.543	−4.64	26.19	−12.113	−14.568	14.858	−10.044	24.143	18.283	−9.952

The general form of the ith principal component is Ui = Σ_{n = 1}¹⁰ a_m〈fⁿ〉 where a_in is the (i,n)th element of the table and 〈fⁿ〉 is the average of the nth property factor.

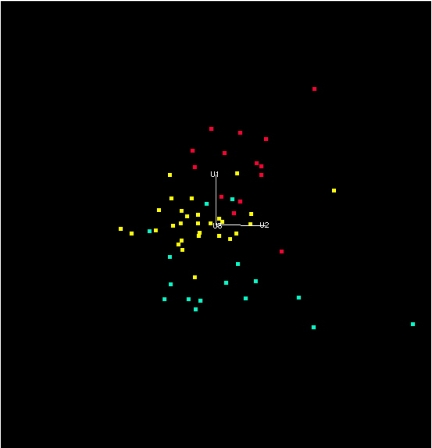
A projection of the APF space onto the first 3 eigenvectors of the PCA is shown in Fig. 1. It can be seen that the distribution of CAT groups, identified by structural class (i.e., by the value of the CATH classifier C), is isomorphic to that obtained from purely structural considerations, in that the all-helical and all-sheet/barrel groups occupy opposite extremes of the space, separated by alpha/beta structures. To make this observation quantitative, hyperplanes separating the regions corresponding to the 3 C classes were determined, using a minimum squared error (MSE) algorithm (23). The ability of these hyperplanes (which are defined in Table S3) to separate the classes is summarized in Table 3. It can be seen that the separation between classes, although not perfect, is very clean. The relatively few misclassfied groups arise from an inability of fairly simplistic, unoptimized hyperplane classifiers to completely separate the points in the 3 regions, and the misclassifications are entirely consistent with the large-scale structure of the space. P values were calculated for the observed distributions of groups with all 3 C values, and all satisfy P < .0001. Optimization of the hyperplanes, or use of a more flexible separation function, may produce a perfect classification of the 59 CAT groups.

Fig. 1.

Projection of the points representing the 59 CAT groups onto the first 3 principal components (see text). Groups for which C = 1 are coded green, those for which C = 2 are coded red, and those for which C = 3 are coded yellow.

Table 3.

Classification of the 59 CAT groups

	Number of CAT groups	CAT groups correctly classified	Number of proteins	Proteins correctly classified
C = 1	16	14 (88%)	762	703 (92%)
C = 2	14	13 (93%)	1,220	1,182 (97%)
C = 3	29	26 (90%)	2,337	2163 (93%)

A related question of potential interest is the predictive power of this approach. As a preliminary test, a test data set (Table S4) was constructed comprising 60 CAT groups from the original database that have between 10 and 19 members. By construction, the sequences in this data set have >35% pairwise sequence identity with each other and with the sequences in the 59-group development set. This data set is expected to be a challenging test of any classification procedure for two reasons: (i) The small size of the CAT groups makes the averages over sequence properties in eq. (3) less reliable, and (ii) the disjunction between CAT classes in the 2 data sets guarantees that the groups in the test database differ significantly from those in the development set.

Application of the MSE hyperplanes that classify the development set to the classification of the CAT groups in the test set gives an overall accuracy of 67.8% (Table 4). A more sophisticated classification was then carried out using a support vector machine (SVM), with an RBF (Gaussian) kernel, giving an overall accuracy of 81.7%. It is of interest to compare this result to other recent results on sequence classification. This comparison is complicated by 2 factors: (i) A wide spectrum of methods was used, some of which combine multiple classes of preoptimized descriptive properties whose statistical independence has not been investigated, and (ii) the training and testing sequence databases on which those studies are based differ widely in both size and difficulty.

Table 4.

Classification of the 60 CAT groups in the test set

	Number of CAT groups	CAT groups correctly classified	Number of proteins	Proteins correctly classified
C = 1	14	9 (64%)	195	129 (66%)
C = 2	11	6 (55%)	145	82 (56%)
C = 3	35	25 (71%)	481	352 (73%)

A recent study comparing results on class prediction using 16 different methods found accuracies between 77% and 99.5% (24). The data sets used in that study were those of Chou (25) and of Zhou (26), containing 204–498 sequences. The present work is based on a much larger data set, and, because it is directed toward delineating the global structure of sequence space, classifies CAT groups rather than individual sequences. More importantly, the sequence descriptors are not optimized for correspondence with a preexisting classification. Nevertheless, the SVM results are consonant with previous results.

Further confirmation of the power of the APF representation comes from a complete-linkage clustering of the 59 CAT groups. This gives a set of superclusters, the members of which are CAT groups, each containing at least 20 sequences. Cluster compositions at the 7-supercluster level are given in Table 5. Almost every cluster is dominated by one value of C, indicating that the APF parameters encode information capable of distinguishing the structure classes. At the same time, the clusters straddle the borders between classes in a manner consistent with the large-scale structure of sequence space, as revealed by the PCA and shown in Fig. 1.

Table 5.

Complete-linkage cluster composition

Cluster number	Fraction (C = 1)	Fraction (C = 2)	Fraction (C = 3)
1	0.0	0.9	0.1
2	1.0	0.0	0.0
3	0.5	0.0	0.5
4	0.83	0.08	0.08
5	0.0	0.67	0.33
6	0.07	0.0	0.93
7	0.09	0.0	0.91

Discussion

It should be emphasized that our results were obtained without using structural information, and that the chemical data used did not include the actual sequences of amino acids along the chain-only sequence- and group-averaged values of the amino acid property factors. Clearly, when amino acid physical properties are appropriately represented, their averages encode not only membership in fold families, but also the global organization of protein structure space.

We have demonstrated an unexpectedly simple connection between chemical constitution and structure in proteins. We have also shown that the principal components can be used as a metric function to quantitate the differences between groups. Further explorations of the implications of this metric are underway.