Bayesian hierarchically weighted finite mixture models for samples of distributions

Abstract

Finite mixtures of Gaussian distributions are known to provide an accurate approximation to any unknown density. Motivated by DNA repair studies in which data are collected for samples of cells from different individuals, we propose a class of hierarchically weighted finite mixture models. The modeling framework incorporates a collection of k Gaussian basis distributions, with the individual-specific response densities expressed as mixtures of these bases. To allow heterogeneity among individuals and predictor effects, we model the mixture weights, while treating the basis distributions as unknown but common to all distributions. This results in a flexible hierarchical model for samples of distributions. We consider analysis of variance–type structures and a parsimonious latent factor representation, which leads to simplified inferences on non-Gaussian covariance structures. Methods for posterior computation are developed, and the model is used to select genetic predictors of baseline DNA damage, susceptibility to induced damage, and rate of repair.

1. INTRODUCTION

Molecular epidemiology studies increasingly make use of samples of cells from immortalized cell lines corresponding to different individuals. Typically, the number of cells collected can be large even when the number of individuals (cell lines) is small to moderate. Although analysts often simplify the data by focusing on distributional summaries, the natural response for a study subject is a random distribution. The focus of inference is then on assessing how the random distribution changes across cell lines and with predictors. As in functional data analysis (Ramsay and Silverman, 1997), in which the response for an individual is a random function, it is appealing to limit parametric assumptions.

Our motivation is drawn from a study using single-cell electrophoresis (comet assay) to study genetic factors predictive of DNA damage and repair. The cell lines employed in this study come from the STET, a resequencing project including 90 unrelated male and female individuals from different ethnic backgrounds. For these individuals, unique combinations of single nucleotide polymorphisms (SNPs) were used to define haplotype categories for 20 candidate DNA repair genes. Single-cell electrophoresis, also known as comet assay (Östling and Johanson, 1984, Singh and others, 1988), was then used to measure the frequency of DNA strand breaks in cell lines for the 90 STET individuals. Replicate samples (100 cells) from each cell line were allocated to 1 of 3 groups: (1) analyzed without treatment, (2) analyzed immediately after exposure to a known genotoxic agent (hydrogen peroxide, H₂O₂), or (3) analyzed after allowing 10 min for DNA repair following exposure to H₂O₂.

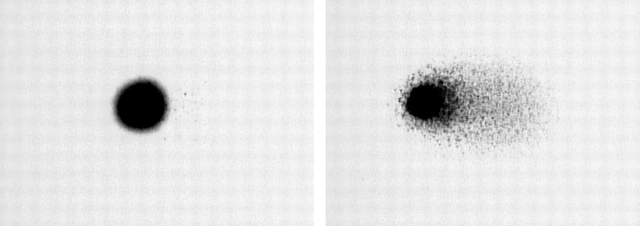
The comet assay is commonly used in genotoxicity experiments to quantify DNA damage arising from single-strand breaks and alkyl labile sites on the individual cell level. Figure 1 shows 2 cells analyzed with the comet assay. Cells with few strand breaks have a spherical shape, while those with a high frequency of strand breaks present a tail of DNA streaming out from the nucleoid, forming a comet-like appearance. Summary statistics of the amount of DNA in the tail are used as surrogates for the amount of damage. Motivated by the results of Dunson and others (2003), we focus in this article on one particular surrogate.

Fig. 1.

Comet images of typical lymphoblastoid cells following no treatment (left panel) or following treatment with 10 μM H₂O₂ for 20 min (right panel).

The Olive tail moment (Olive and others, 1990) is defined as the percentage of DNA in the tail of the comet multiplied by the length between the center of the comet's head and tail as is automatically calculated from the cell image by standard software like Komet™ or Vis Comet™.

To demonstrate the challenges involved in the analysis, we present in Figure 2 the distribution of the Olive tail moment for one of the cell lines in the sample at 3 time points of the Olive tail moment each based on 100 cells. Note that these distributions are non-Gaussian, violating the assumptions of typical analysis of variance (ANOVA) models, and that the shape of the distribution changes dramatically. Another issue is that our interest focuses not on estimating these distributions but in studying heterogeneity among individuals in susceptibility to damage and repair rates. Also, we do not expect samples at different times points to be uncorrelated. Indeed, cells from individuals with large initial damage might show increased susceptibility to damage, or individuals suffering a lot of damage might recover at a faster rate. Finally, we note that it is not possible to examine the same cells before and after damage because cells are destroyed in applying the comet assay. Therefore, longitudinal methods are not helpful in this setup. In summary, flexible models for random distributions are needed, which should allow for the inclusion of highly structured hierarchical models in order to account for the special characteristics of the data.

Fig. 2.

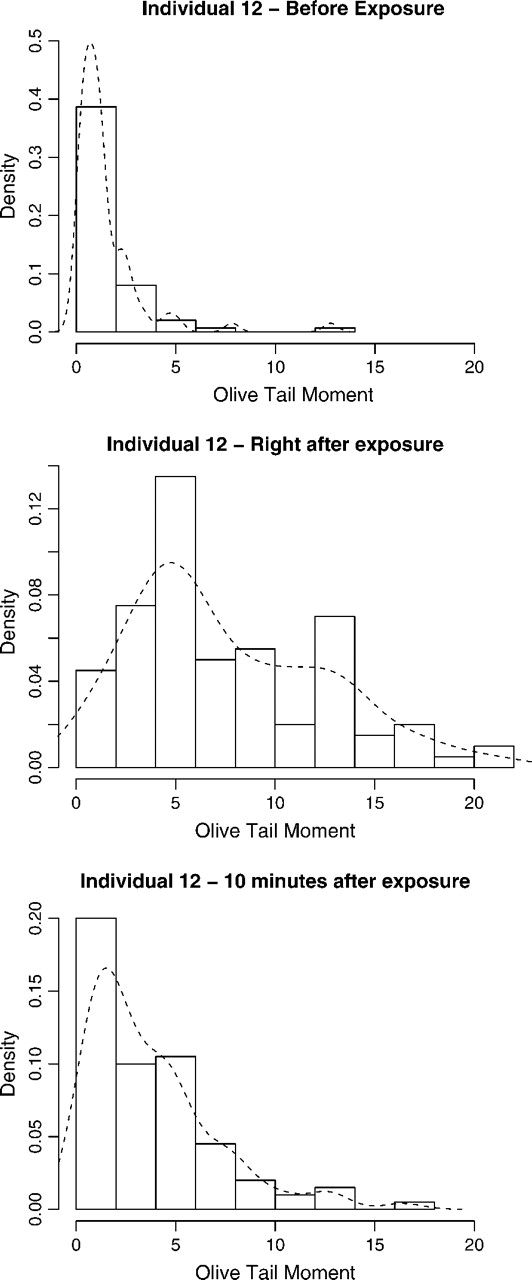
Histograms and smoothed kernel estimates for the distribution of the Olive tail moment for individual 12 based on 100 cells at each of the 3 observed time points.

In modeling hierarchical functional data, one can potentially allow heterogeneity among individuals in curve data by using a spline and/or wavelet model with individual-specific basis coefficients (Bigelow and Dunson, 2005), (Thompson and Rosen, 2008), (Morris and Carroll, 2006). When the data consist of random distributions instead of random curves, this approach can be modified by specifying the random distribution as a mixture of a finite number of basis distributions. In particular, mixtures of Gaussians provide an appealing choice; finite mixtures of a moderate number of Gaussians can produce an accurate approximation of any smooth density.

Our proposed approach is based on generalizing finite mixtures of Gaussians to place a hierarchical regression model on the mixture weights, while keeping the basis distributions constant across groups. A conceptually related approach for functional data analysis has recently been presented by Behseta and others (2005). In this paper, we focus on multilevel probit regression models, incorporating latent factors to allow flexible modeling of dependence. The idea of placing a regression model on the mixture probabilities is borrowed from the latent class modeling literature. Although latent class regression methods have previously been applied to functional data (Muthen and Shedden, 1999), to our knowledge such approaches have not been used to obtain flexible models of samples of distributions.

There is a growing Bayesian literature on models for dependent random distributions, most based on generalizations of the Dirichlet process (Ferguson, 1973, Ferguson, 1974, Sethuraman, 1994). Some relevant examples include the dependent Dirichlet process (MacEachern, 1999, MacEachern, 2000), which has spawned the works of DeIorio and others (2004) and Gelfand and others (2005), the order-dependent Dirichlet process (Griffin and Steel, 2006), the hierarchical Dirichlet process (Teh and others, 2006), and the linear combination of draws from independent Dirichlet processes (Müller and others, 2004, Dunson and others, 2007). However, although most of these methods are rather general in nature and provide full support on the space of absolutely continuous distributions, practical application and interpretation in large and complex hierarchical settings like the DNA repair study can be difficult. Indeed, these approaches do not allow for a hierarchical model specification like the one we describe in this paper.

As mentioned by several authors, including Mengersen and Robert (1996), Richardson and Green (1997), and Green and Richardson (2001), finite mixture models provide an accurate approximation to fully nonparametric Bayes approaches in many cases, with some distinct advantages. In developing our finite mixture model, we were motivated in particular by 2 issues: (1) interpretability and (2) ease of computation, given that the data in the National Institutes of Environmental Health Sciences (NIEHS) DNA repair study consist of information for over 20 000 cells. Fully nonparametric Bayes methods that allow the number of mixture components to be unknown tend to be both computationally intensive and subject to difficulties in interpreting latent class category-specific results, as the class definitions change across Monte Carlo Markov chain (MCMC) iterations.

The paper is organized as follows. Section 2 develops the general formulation of the hierarchically weighted finite mixture (HWFM) models and discusses prior elicitation, while Section 3 describes specific choices of the hierarchical structure in the context of the DNA repair study. Section 4 describes efficient computational implementations for this class of models. In Section 5, we apply the HWFM models to answer relevant questions on the DNA repair study. Finally, Section 6 contains a brief discussion on this class of models and the application at hand, as well as possible extensions.

2. HIERARCHICALLY WEIGHTED GAUSSIAN MIXTURES

2.1. Finite mixtures

Consider initially the case in which data consist of i.i.d. draws from a single unknown distribution, so that y_jf, for j = 1,…,m. For example, the data y = (y₁,…,y_m)′ may consist of measures of DNA damage for m untreated cells drawn from a single cell line. In this i.i.d. case, we focus on the following model:

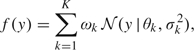(2.1)

where k ∈ {1,…,K} indexes the component number, ω_k is a probability weight on the kth component (0 < ω_k < 1, 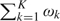=1), and {θ_k, σ_k²} are the normal mean and variance for the kth component density.

In order to generalize (2.1) to allow covariates and hierarchical dependency structures, one can potentially choose a hierarchical regression structure for the weights {ω_k} and/or the component-specific parameters {θ_k,σ_k}. However, by fixing the set of component-specific parameters, the components correspond to common, data-defined, latent classes that can be easily interpreted in the context of each specific application. For example, in exposing samples of cells to genotoxic agents, it is not possible to treat all cells with the same dose due to the inability to spread the compound equally over the entire cell culture tray, and a subset of cells may remain effectively untreated. Hence, at a given dose, the response distribution can be realistically modeled as a mixture of the distributions at lower doses and an innovation distribution. Similar behavior occurs as repair times vary, with cells that repair more rapidly mimicking cells that have suffered little damage but have slower rates of repair. In this setting, we find it appealing to visualize a set of (unknown but fixed) basis distributions, (·| θ_k, σ_k²), for k=1,…,K, representing different levels of cellular damage, with weights that vary depending on experimental conditions (before or after exposure, repair time) and measured/unmeasured genetic factors.

Prior to exposure to the genotoxic agent, the distribution of DNA damage among cells in the different cell lines could be characterized by assigning relatively high weight to component densities that allocate high probability to values close to 0. In contrast, after exposure, the weights on stochastically larger components would be expected to increase. Also, in characterizing the distributions of DNA damage following repair, the weights on stochastically larger basis densities may be relatively small for cell lines established for individuals having high rates of repair. Thus, by allowing the specific weights to vary across the different cell lines, heterogeneity can be accommodated.

2.2. Hierarchical structure

Consider now observations that are indexed by categorical variables, such as cell line (i=1,…,n) and treatment group (t=1,2,3). In order to allow the mixture weights to vary with treatment groups and (initially unmeasured) cell line–specific factors, one can define a model for the latent class indicator _itj ∈{1,…,K} for the jth cell in the tth treatment group for the ith cell line. Note that 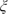_itj=k denotes that the cell belongs to the kth mixture component.

A computationally convenient and flexible structure is provided by the continuation ratio probit model:

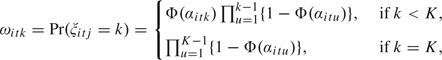where Φ(·) denotes the standard normal distribution function. Note that this model allows a different weight for each component in the mixture for every cell line × treatment group combination, effectively allowing the distribution of the cellular damage to change freely. The use of the probit transformation to define the weights allows us to restate the model using normally distributed latent variables (see Section 4), enabling us to incorporate most of the standard Bayesian machinery into the model for the distribution. Additionally, the probit transformation induces a natural scale in the transformed weights that simplifies prior elicitation, as discussed below. The use of a continuation ratio probit model is reminiscent of the stick-breaking construction for the weights of the Dirichlet process (Sethuraman, 1994). Indeed, if α_itu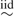N(α_itu|0,1), then Φ(α_itu)∼ Uni[0,1]= Be(1,1) and we recover a special case of the finite stick-breaking construction in Ishwaran and James (2001), creating independent priors for each cell line at each experimental condition. By allowing for different dependence across the αs, we allow the shape of the distributions to be dependent across individuals and experimental conditions while allowing for flexible and rich weight structures. Similar approaches, using a multinomial logit model, have been used in machine learning to construct spatially weighted mixtures for image segmentation (Figueiredo and others, 2007) and in latent class analysis (Muthen and Shedden, 1999).

For the parameters of the normal component, we propose standard, conditionally conjugate priors

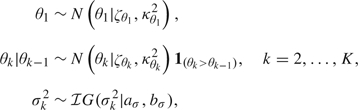where N(·|θ,σ²)1_A denotes the normal distribution with mean θ and variance σ² restricted to the set A. Order constraints on the parameters of the mixture components have been regularly used in the literature to ensure identifiability (see, e.g. Mengersen and Robert, 1996, and Richardson and Green, 1997) by attempting to prevent label switching due to the inherent symmetry of the parameter space in mixture model. However, label switching is not a concern for us since we are not interested in component-specific inference (Stephens, 2000). Instead, introducing an order constraint on the means allows us to interpret the components of the mixtures as corresponding to increasingly higher levels of cellular damage, as described above.

The specific form for the transformed weights α_itk has so far been left open, which endows the model with a great deal of flexibility and generality. In general, we assume that the vector of transformed weights α follows a parametric distribution, possibly dependent on a set of hyperparameters η, that is, α∼p(α|η). Choosing p to be a Gaussian distribution will typically yield conditionally conjugate distributions, simplifying computation through Gibbs sampling. In Section 3, we discuss 3 interesting choices for such models, in the context of the DNA repair studies.

2.3. Bayesian model selection and mixture priors

In this section, we present a brief review of Bayesian model selection; for a more detailed discussion see Kass and Raftery (1995). Given 2 models M₁:p(y|φ₁) and M₂:p(y|φ₁) with associated prior distributions p₁(φ₁) and p₂(φ₂), the Bayes factor of model 1 versus model 2 is defined as

Let π_i denote the prior probability of model i. Given prior odds for model 2 versus model 1, π₂/π₁, these can be updated using the Bayes factor to yield posterior odds, _O21=_B21π₂/π₁. The posterior odds measures the relative strength of the evidence in favor of each model provided by the data. Indeed, posterior odds can be transformed to posterior probabilities for each of the models by noting that Pr(M₁|y)=(1+_O21π₂/π₁)⁻¹. Posterior probabilities over 0.76 provide substantial evidence in favor of M₁, while probabilities over 0.99 provide decisive evidence (Jeffreys, 1961, Kass and Raftery, 1995).

Computation of Bayes factors can be a complex task, as they require the calculation of multidimensional integrals. Mixture priors (in contrast to the mixture likelihoods we discussed in Section 2.1) can be used to simplify this operation by transforming the model comparison problem into an inference problem. In the context of nested models, it is common to use zero-inflated priors

where p*(φ) is the prior for the parameter of interest under the alternative (more complex) model and 1_x(·) denotes the degenerate distribution with all its mass at x. The updated value π₂|y corresponds to the posterior probability of the null model (see George and McCulloch, 1997, and Clyde and George, 2004, for excellent reviews).

3. HIERARCHICAL MODELING IN DNA REPAIR STUDIES

3.1. Modeling and testing heterogeneity

Our first goal is to formally assess heterogeneity across individuals in the frequency of DNA strand breaks. Although exploratory analysis of the data reveals some important differences in the shape of the distributions across subjects, developing a formal test is a necessary preliminary step before building a more complicated model structure. Besides, the problem of identifying heterogeneity in populations of distributions is a complex problem that appears in many different applications.

Given this goal, an ANOVA-like structure for the transformed weights and suitable zero-inflated priors seem a natural choice. Therefore, we consider the model

(3.1)

where {γ_k} controls the baseline probability of latent class k, {δ_i} controls the baseline susceptibility of individual i, {β_t} controls the population-wide baseline damage at time t, and the remaining terms represent dependence of the weights on possible interactions. To ensure identifiability of the parameters, we let δ₁ = β₁ = (δβ)₁₁ = (δγ)₁₁ = (βγ)₁₁ = (δβγ)₁₁₁ = 0, so γ_u, u = 1,…,k, determines the probability of the kth component for the baseline damage in the first individual in the sample.

In this ANOVA-like structure, hypotheses related to differences between groups, cell line–specific effects, and interactions can be assessed by considering nested models, with appropriate terms in the linear predictor excluded. In particular, we are interested in testing differences attributable to cell line effects. We therefore write γ = (γ₁,…,γ_K)′ and let λ =(λ_(−r)′, λ_(r)′)′ denote the remaining parameters, with the subvector λ_(r)′ =(δ′,δβ′, δγ′, δβγ)′ denoting coefficients associated with cell line (individual)–specific effects and λ_(−r)′=(β′, βγ′) measuring differences attributable to repair time. Then, we let

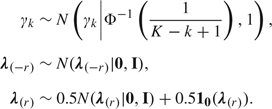This prior for γ and the identifiability constraints are intended to approximately enforce the same prior probability for each component. See Section 4.2 for details.

The prior on λ_(−r) has a ridge regression–type shrinkage structure intended to stabilize estimation, while the mixture prior for the cell line–specific coefficients λ_(r) allows us to assess evidence of heterogeneity among individuals. Zero values for these coefficients correspond to a null model with no heterogeneity. We choose a prior that assigns 0.5 probability to the model with no heterogeneity and choose independent standard normal priors for the coefficients included in the model. As we discussed in Section 2.3, related mixture priors have been widely used in model selection problems. Note that only 2 models are being considered in this particular setup, instead of all possible nested models. This greatly reduces computational burden and improves the mixing of our algorithm, without detracting from our goal. The unit prior variance was chosen to assign high probability to a range of plausible values for the regression coefficients included in the model, taking the probit scale into consideration.

3.2. Modeling heterogeneity in DNA repair

The main interest of the DNA repair study focuses on understanding heterogeneity in the rates of DNA repair, adjusting for baseline damage and susceptibility to induced damage. To address this goal, we need to place additional structure on the model: damage levels at different time points cannot be directly interpreted as the quantities of interest, as they might be correlated.

For this purpose, we replace the cell line–specific terms λ_(r) in the previous linear predictor in (3.1) by a factor analytic model containing cell line–specific latent traits

with {γ_k} intercepts as before, {β_t} group differences, {(βγ)_kt} interactions,

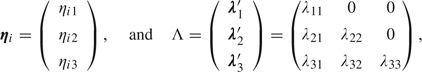where the upper diagonal terms of Λ have been set to 0 for identifiability. The factor analytic term, λ_t′ η_i, accounts for heterogeneity among the cell lines, with η_i1, η_i2, and η_i3 normal latent traits measuring the ith cell line's level of initial DNA damage, susceptibility to induced damage, and rate of repair relative to the other cell lines. Due to the conditional structure, η_i2 can be interpreted as a susceptibility adjusting for baseline damage, while η_i3 (measuring the change in the distribution along 10 min elapsed since the cells were damaged) can be interpreted as a repair rate adjusting for baseline and induced damage. Within-cell line correlation between groups is captured by the parameters λ₂₁, λ₃₁, and λ₃₂. To fix the scale of the latent traits for identifiability purposes, we let var(η_it)=1 for t = 1,2,3. In addition, we initially let E(η_it)=0 for t = 1,2,3, though we will later consider methods for incorporating diplotypes.

Under this structure, the level of heterogeneity among the cell lines is controlled by the magnitude of the factor loadings parameters λ_tt, t=1,2,3. The null hypothesis of homogeneity in baseline damage corresponds to λ₁₁ =0. The null hypothesis of homogeneity in susceptibility corresponds to λ₂₂ =0 and homogeneity in repair rates corresponds to λ₃₃ =0. Models excluding the main effects by letting λ_tt =0 should automatically exclude any correlation effects by also fixing λ_tt′ = 0, ∀ t′ < t, thereby reducing the number of models for the covariance structure to 30.

Again, by using mixture priors with point masses at 0 for the factor loadings, we can effectively move within this model space

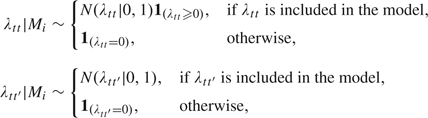in which the sign constraint on λ_tt is used to ensure identifiability. Because the total number of models involved is small and predictive densities can be calculated in closed form, we opt for sampling over the full model space instead of the one-component-at-a-time scheme typical of stochastic search variable selection (SSVS). This improves the efficiency of the Gibbs sampler, avoiding problems with slow mixing due to a tendency to remain in local regions of the model space for long intervals. The models are given equal probability a priori, Pr(M_i)=1/30 for all i.

3.3. Haplotype selection

The primary advantage of the model structure presented above is that it contains a single cell line-specific summary of DNA repair capability capturing the characteristics of the individual distributions. However, while differences in the repair rates are of interest, the main focus of the study is on relating those differences to genetic factors.

Suppose that G candidate genes have been preselected for study, with the gth gene having n_g variants in the population. Here, `variants’ refer to haplotypes, which are unique combinations of SNPs. An individual's diplotype for a specific gene is defined by the pair of haplotypes for that gene, one inherited from the mother and one from the father. For the 20 genes that were preselected in the NIEHS study, the number of diplotypes ranges from 3 to 24, with a total of 224. This results in a huge number of unique combinations of diplotypes for the 20 genes.

Given the small number of subjects and the large number of diplotypes involved in the analysis, we consider only additive effects of the genes on the latent factor, so that η_it=u_iμ_t, where u_i = (u_i1′,…,u_iG′)′ is a vector of indicators of the variant category for each of the G genes and μ_t is a vector of regression coefficients. Extensions to include interactions are straightforward but would not be useful in this specific example since the data on interactions are very sparse. Note that u_ig contains n_g−1 indicators when the gth gene has n_g haplotypes, and the intercept term is excluded for identifiability (for the same reason that E(η_it) was set to 0 previously).

Taking advantage of the normal linear regression structure of the models for each of the latent traits, we can apply Bayesian variable selection methods for subset selection in regression, using once again mixture priors with point mass at 0 for the regression coefficients. This structure can be formalized through prior distributions of the form

and a SSVS procedure can then be used to identify genes that can influence the repair capability. If a gene has no effect on the repair rate, the coefficients for each of the subcategories should be 0. The previous approach could be easily extended to identify genes associated with higher susceptibilities to damage in the individuals.

4. INFERENCE

4.1. Posterior computation

By augmenting the observed data with the latent class indicators, _itj}, and with latent normal random variables underlying each 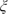_itj, we can obtain a simple Gibbs sampling algorithm for posterior computation. This algorithm relies on a strategy related to Albert and Chib (1993), but by using a continuation ratio probit instead of generalized probit structure, we avoid the problems in the updating of the threshold parameters mentioned in Johnson and Albert (1999). A related strategy was used by Dunson (2006) in multistate modeling of multiple event data.

Specifically, let z_itjk ∼N(α_itk,1) and define 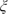_itj = k if z_itju < 0 for all u < k and z_itjk > 0, with 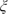_itj = K if z_itju < 0 for all u ≤_K−1. The joint posterior distribution of the parameters and latent variables is proportional to

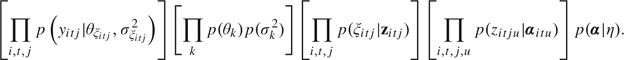Derivation of the full conditional posterior distributions for each of the unknowns in the model follows by standard algebra. After choosing initial values for the parameters, and given a specific form for p(α|η), the algorithm iterates through the following steps:

Step 1: The latent variables z_itjk and 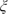_itj are updated in block by

1. Sampling 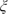_itj from a discrete distribution with probabilities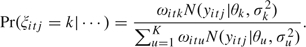

   
2. Generating z_itjk|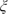_itj from

   

   with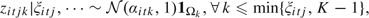

   

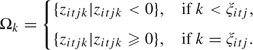
Step 2: The parameters for the normal components in the mixture can be generated from:

1. For the means, the first component is sampled from

   

   while for k = 2, …, K,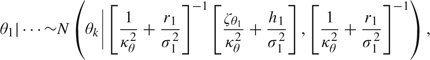

   

   where r_k =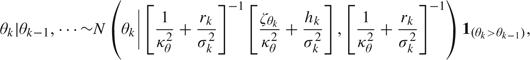 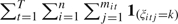and h_k = .
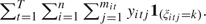2. The variances σ_k² are a posteriori conditionally independent, yielding

   

   where r_k = .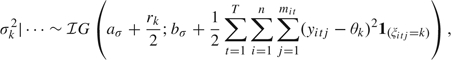

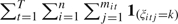Step 3: Sample α from

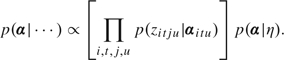Data augmentation strategies of this kind allow for implementations that rely only on Gibbs samplers, rather than on more general MCMC schemes requiring simultaneous proposals of large numbers of parameters or rejection samplers that could generate even worse mixing issues by forcing us to sample one parameter at a time.

4.2. Prior elicitation

Consider first eliciting hyperparameters {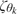}_k=1^K and {κ_θk²}_k=1^K corresponding to the location of the Gaussian components and a_σ and b_σ corresponding to their variances. These hyperparameters need to be chosen to ensure that the mixture spans the expected range of observed values with high probability. In practice, we have experimented with 2 types of choices, with essentially equivalent results: (1) Having all prior means {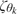}_k=1^K equal to the global mean (or global median) of all observations in the sample, and setting all κ_θk² equal to half the range of the observed data for all k (a rough estimate of dispersion), and (2) setting 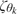equal to the k/(K+1) quantile of the sample, with κ_θk² equal to one-eighth of the range. Sensitivity was assessed by halving and doubling the values of κ_θk² under each of these 2 scenarios. Under a similar argument, a_σ and b_σ were chosen so that (σ_k²)=b_σ/(a_σ−1) is equal to half the range of the observations. Note that in every scenario we have employed proper priors to avoid identifiability issues with mixture models. See Mengersen and Robert (1996), Natarajan and McCulloch (1998), and references therein for a discussion of this point.

Next, we consider the prior structure on the weights ω_itk. As discussed above, the use of a continuation ratio probit model along with normal priors for the transformed weights is convenient, as it greatly simplifies implementation of the model. In particular, the transformed mixture weights {α_itk} can be sampled in step 3 above from conditionally normal distributions. Hyperparameter choice is also simplified. A common assumption in mixture models is that all components have the same probability a priori. In the current context, this can be approximately enforced by setting (α_jtk) = Φ⁻¹(1/(K−k+1)). Additionally, 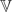(α_jtk)≈1 because we expect the continuation ratio Φ(α_jtk) to be between 0.002 and 0.998 with 0.99 probability. Smaller values for 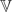(α_jtk) lead to strong restrictions on the set of weights, discouraging small ones (especially for the first few components in the mixture). On the other hand, larger variances do not impose restrictions on the set of weights but can adversely affect model selection.

We concentrate the rest of the discussion on the heterogeneity model described in Section 3.1, but similar arguments apply to the other models considered in the paper. It is well known that, unlike in estimation problems, the effect of the prior in model selection does not necessarily vanish as the sample size grows (Kass and Raftery, 1995). In particular, Bayes factors and posterior probabilities obtained using noninformative and flat priors tend to overly favor the null model even in large samples due to Lindley's paradox. In the heterogeneity model, this means that large variances for the normal component of p(λ_(r)) can seriously bias the results. Therefore, we avoid variances larger than 1 for these parameters. On the other hand, the parameters γ_k or λ_(−r) are common to both models under consideration, and improper or flat priors should produce reasonable results. Our sensitivity analysis confirms that model selection results are not dramatically affected by increasing their variances.

5. UNDERSTANDING HETEROGENEITY IN DNA REPAIR STUDIES

The data from the DNA repair study were analyzed using the models described in Section 3. Eight mixture components were judged sufficient to flexibly characterize changes in the density across cell lines and treatment groups, while limiting the risk of overfitting. Inferences were robust in our sensitivity analysis for K ranging between 8 and 15, but the quality of the fit, as assessed through the plots described in Section 5.5, was compromised for K < 8. We considered different options for the hyperparameters 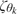, including 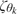= 8 for all k (about the empirical mean of the data) and fixing 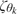to the k/(K+1)th quantile of the data, all leading to equivalent results. The prior variance was taken to be κ_θ² = 25, so as to cover the range of the data, while the hyperparameters for σ_k² were set to a_σ = 1.0, b_σ = 1/2, so that (σ_k²) = 2 a priori. Again, results were robust to reasonable changes in these parameters.

The Gibbs sampler was run for 60 000 iterations following a 10 000 iteration burn-in period. Code was implemented in FORTRAN, and the longest running time was around 26 h on a 2.80-GHz Intel Pentium 4 computer in the case of the haplotype selection model described in Section 3.3. Examination of diagnostic plots showed adequate mixing and no evidence of lack of convergence. In order to corroborate this observation, we used the Gelman–Rubin convergence test (Gelman and Rubin, 1992), which compares the variability within and between multiple runs of the sampler with overdispersed starting values; we monitored the mean, variance, and skewness of the fitted distributions as our parameters of interest. In every case, confidence intervals for the convergence statistic R contained the reference value 1, as expected for nondivergent chains. Agreement of fitted and empirical distributions, assessed through quantile–quantile plots (see Section 6.4), was adequate for most subjects and experimental conditions.

5.1. Simulation study

As a preliminary to the analysis of the DNA repair data set, a simulation study was run addressing some of the frequency properties of our density comparison approach. The study demonstrated that the models are indeed capable of detecting differences across populations as long a moderate number of components are incorporated in the mixture. This is true even for distribution that has similar mean and variances but differs in higher moments. Additional details can be found in Section 1 of the supplementary material, available at Biostatistics online (http://www.biostatistics.oxfordjournals.org).

5.2. Modeling and testing heterogeneity in Olive tail moment

The estimated posterior probability of the null hypotheses (homogeneity among the cell lines) was 0.0004, and the Bayes factor for the alternative hypothesis was ≈2500. Hence, there was clear evidence of heterogeneity among the cell lines, justifying a more detailed analysis of the data.

5.3. Modeling heterogeneity in DNA repair

The chain visited only 4 out of 30 models; since sampling was performed over the whole model space and not one variable at a time, we believe that lack of mixing is not an issue. The model with highest posterior probability (0.93) contains 4 factor loadings, corresponding to the main effects λ₁₁, λ₂₂, and λ₃₃, along with the correlation between susceptibility and repair rate λ₃₂. The other models include the same 4 variables plus λ₂₁, λ₃₁, or both, with respective posterior probabilities 0.03, 0.02, and 0.01. This reveals clear evidence of heterogeneity in the 3 latent traits, no evidence of dependence between initial damage and repair rate or susceptibility, and decisive evidence of a negative dependence between the repair rate and the susceptibility to damage (since Pr(λ₃₂≤0)≅1). This can be explained by the speed of the repair mechanisms for oxidative damage, with damage being actively repaired even as cells are being exposed.

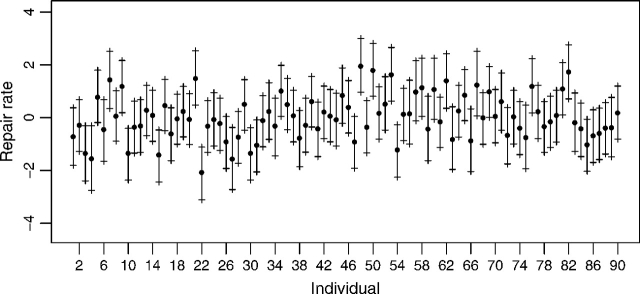
Figure 3 shows the estimated latent repair rates, η_i3, for each of the cell lines. It is important to emphasize that these values cannot be interpreted in absolute terms, but only relative to other members of the same population. For example, individuals 48, 50, 53, and 82 have the higher repair rates compared with other members of the population, while individuals 4, 15, 22, and 27 have a relatively very low repair rate. Therefore, only a careful choice of the study population, like in the STET project, allows generalizations to the general population.

Fig. 3.

Posterior median and 90% posterior credible intervals for the estimated latent repair rate (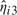) of the 90 cell lines in the population under study.

5.4. Haplotype selection

We focus on 20 candidate DNA repair genes for illustration, resulting in a total of 224 parameters characterizing differences among individuals in repair rates. The genes considered, along with their associated number of diplotypes and posterior probability of influence, are shown in Table 1.

Table 1.

List of 20 genes preselected to explain repair rates, with their number of diplotypes and posterior probability of influence

Gene	Number of diplotypes	Posterior probability
XRCC3	8	0.89
POLG	7	0.83
ADPRT	20	0.80
ERCC1	9	0.77
ERCC6	24	0.76
POLD1	15	0.75
XPA	20	0.66
POLI	11	0.64
ERCC5	14	0.63
XRCC2	10	0.54
ERCC3	10	0.50
FEN1	3	0.50
XRCC2	10	0.50
PCNA	9	0.49
OGG1	6	0.39
POLL	6	0.33
POLD2	10	0.30
LIG1	16	0.19
POLB	6	0.18
LIG3	10	0.15

Our prior probability on any gene being significant was set to π₀=0.5. Results for the factor loading are similar to those obtained in Section 5.3 and therefore not discussed again. Following convention, we consider genes with a posterior probability greater than 0.75 as potentially involved in the repair mechanisms of oxidative damage, yielding 6 candidates: XRCC3, POLG, ADPRT, ERCC6, POLD1, and ERCC1. At the other extreme, there were 3 genes that had less than 0.25 posterior probability, including LIG3, POLB, and LIG, which therefore do not seem to play a relevant role in this specific repair process.

Some additional information can be obtained by looking at the joint distribution of the diplotypes rather than at its marginal distribution. The 2 most visited models include XRCC2, XRCC3, POLD1, POLG, POLI, ERCC1, ERCC6, and PCNA with a posterior probability of 0.0015 (note that ADPRT is not in the list) and the second most visited model contains ADPRT, XPA, XRCC2, XRCC3, POLD1, POLD2, POLG, POLI, ERCC1, ERCC5, ERCC6, FEN1, and PCNA, with a posterior probability of 0.00145, showing that no combination of genes is clearly preferred to explain the variations across individuals. On the other hand, XRCC3, POLD1, POLG, and ERCC1 appear in all 15 most visited models, while ERCC6 and ADPRT are also often present among the most visited models (13 and 12 times, respectively), with no other gene present with similar regularity.

5.5. Assessing model fit

As a way to assess model fit, we computed quantile–quantile plots of the predictive distribution for each individual against its corresponding empirical distribution. As an illustration, we show in Figure 4 the resulting plots for one individual at each time point for the model in Section 5.4. Dotted lines correspond to a 95% probability interval for the quantile of the predictive distribution.

Fig. 4.

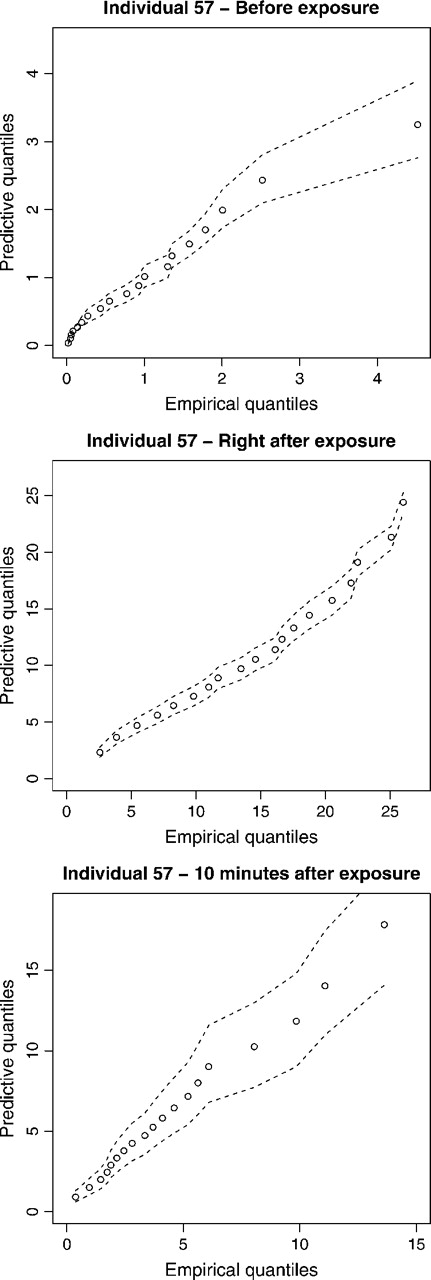
Quantile–quantile plot of the predictive distribution from our nonparametric model and their 90% credible interval versus the corresponding empirical distribution.

In general, these plots demonstrate a reasonable fit of the model to the data. However, a slight lack of fit can be observed for some individuals in the high quantiles of the distribution (typically, over 90%), where the predictive distribution would indicate slightly more extreme values than actually observed.

6. DISCUSSION

Motivated by data from comet assay studies of DNA damage and repair, this article has proposed an approach for Bayesian hierarchical density regression, allowing an outcome distribution to change flexibly with multiple predictors and across subjects. The basic idea underlying our method is to use a finite mixture model, with the probability weights following a hierarchical model. Efficient posterior computation is facilitated by using a continuation ratio probit structure with data augmentation. This scheme enables us to take advantage of the well-developed literature on Gaussian models and priors developed for variable selection in linear regression, even though the outcome distributions are clearly nonnormal. In this particular setting, the low dimensionality allows us to sample over the whole model space at once, ensuring good mixing and avoiding common pitfalls.

By incorporating latent factors measuring baseline damage, susceptibility, and rate of repair, we were able to perform inferences on the factors varying across cell lines in the STET database. The finding of clear evidence of heterogeneity in rate of repair raised our interest in identifying factors explaining the differences between individuals. Using candidate genes provided by the investigators, we ran a stochastic search variable selection procedure to identify genes that may be of interest for further study.

Some comments on our SSVS scheme are necessary. Note that our choice of π₀ = 0.5 implies that we expect, a priori, at least 6 genes to be significant with a probability 0.94, which is about the number of significant genes in our posterior analysis. This would seem to indicate that the relatively large posterior probabilities obtained might be driven in part by our prior selection. Therefore, our analysis at this stage is necessarily exploratory but allows us to provide some guidance as to where to focus future more detailed studies on repair mechanisms.

FUNDING

This research was partially supported by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences.