MCCE2: Improving Protein pK_a Calculations with Extensive Side Chain Rotamer Sampling

Abstract

Multiconformation continuum electrostatics (MCCE) explores different conformational degrees of freedom in Monte Carlo calculations of protein residue and ligand pK_as. Explicit changes in side chain conformations throughout a titration create a position dependent, heterogeneous dielectric response giving a more accurate picture of coupled ionization and position changes. The MCCE2 methods for choosing a group of input heavy atom and proton positions are described. The pK_as calculated with different isosteric conformers, heavy atom rotamers and proton positions, with different degrees of optimization are tested against a curated group of 305 experimental pK_as in 33 proteins. QUICK calculations, with rotation around Asn and Gln termini, sampling His tautomers and torsion minimum hydroxyls yield an RMSD of 1.34 with 84% of the errors being <1.5 pH units. FULL calculations adding heavy atom rotamers and side chain optimization yield an RMSD of 0.90 with 90% of the errors <1.5 pH unit. Good results are also found for pK_as in the membrane protein bacteriorhodopsin. The inclusion of extra side chain positions distorts the dielectric boundary and also biases the calculated pK_as by creating more neutral than ionized conformers. Methods for correcting these errors are introduced. Calculations are compared with multiple X-ray and NMR derived structures in 36 soluble proteins. Calculations with X-ray structures give significantly better pK_as. Results with the default protein dielectric constant of 4 are as good as those using a value of 8.

Introduction

The ionization state of protein side chains and ligands help control many important biological functions such as proton and electron transfer reactions, ion transport through channels, ligand binding, protein folding, and protein–protein association.^1–6 Asp, Glu, Lys, and Arg make up 25% of the residues in an average protein. The difference of their pK_as in solution and in situ provides insight into the local electrostatic environment of the protein.⁷ It is challenging to calculate these pK_as for a number of reasons. The short-range electrostatic interactions between charged sites are strong and very position dependent, whereas interactions between buried charges fall off slowly so that the ionization of sites are interdependent.^8–12 In addition, the protein response to changes in charge is heterogeneous, being dependent on the degree of charge burial as well as the local flexibility.^13–15 Successful calculations thus need to optimize the local structure, accounting for the structure changes when groups change ionization state, while considering the possibility of coupled ionization changes throughout the protein.

There has been significant progress in calculating pK_as and redox site electrochemical midpoints (E_ms) by various methods with significantly different levels of theory (see refs. ^4–6,14, and ^16–21 for reviews). Techniques using Monte Carlo sampling of ionization states with continuum electrostatics (CE) based energy functions provide a robust method for calculating pK_as, redox cofactor E_ms, and the coupling between them. The Poisson-Boltzmann (PB) equation of CE allows the electrostatic potential to be determined with a nonuniform distribution of dielectric material and solution ionic strength.^22–24 This represents a compact and efficient way to treat the large difference between the response of protein and the surrounding water to charge changes. Electrostatic energies can also be obtained by GB methods, which give CE energies via an analytical approximation.^25,26

In PB based approaches, the protein is defined as a region with a low dielectric constant embedded in a solvent with a high dielectric constant of 80. Moving an ionizable residue from water to the less polarizable protein diminishes the solvation energy always favoring the neutral form.^1,27–30 However, pairwise interactions with the surrounding protein charges and dipoles can replace the favorable interactions with water, stabilizing a buried ionized group.³¹ There is considerable uncertainty as to the best value for the dielectric constant of protein, with values as low as 4, especially inside of membrane proteins,^8,9,11,32,33 or 8³⁴ to 20 for smaller proteins,^35,36 to as high as 80³⁷ being used. The appropriate value depends both on the distribution of residues of differing polarity and on the local protein flexibility.^38,39 The uncertainty of ε_p has limited the usefulness and accuracy of the CE analysis. Several methods have begun to allow for coupling conformation and ionization moves in Monte Carlo sampling to introduce an explicit heterogeneous dielectric response. Adding side chain flexibility,^40–42 changes in hydrogen bond orientations.^43,44 and allowing heavy atom and hydroxyl rotamer searches as in multiconformation continuum electrostatics (MCCE)^34,45 have all been found to improve the accuracy of the calculations.

Other methods with quite different strengths and weaknesses are also being used to study ionization equilibria in proteins.^39,46–49 Empirical methods, which can provide good match between calculations and experiments for benchmark calculations, use knowledge-based parameters.^50–52 Equilibrium ionization states in proteins have also been well studied by the protein dipole Langevin dipole technique, which provides a semimicroscopic view of the protein and solvent response.^15,53–56 MD based analyses employ either constant-pH MD or free energy perturbation techniques.^47,57–63 QM and QM/MM methods also provide the means to calculate individual pK_as in the context of a protein.^64–69

MCCE is a technique that adds side chain and ligand conformational degrees of freedom to a CE analysis of pK_as and E_ms. Side chain conformation and ionization are sampled within the same Monte Carlo analysis. This lets the conformation remain in equilibrium with the changing charge throughout a titration. Previous versions of MCCE used a coarse rotamer library without extensive relaxation.⁴⁵ Even this limited conformer sampling improved the match between experiment and calculation for individual residues and diminished the dependence on the starting structure.³⁴ The work presented here adds more extensive rotamer sampling and relaxation, further improving the accuracy. Methods for choosing a subset of conformers to be subjected to accurate PB analysis are described. The additional rotamers are shown to produce some systematic errors. The added side chains increase the low dielectric region increasing pairwise interactions. In addition, rotamer making and clustering always produces more neutral than ionized conformers generating an entropy artifact that favors the neutral state. MCCE2 corrects these problems while allowing extensive, efficient side chain conformation sampling within pH titrations.

Methods

MCCE combines CE and molecular mechanics force fields to calculate the equilibrium distribution of ionization states and atomic positions.^34,45 The Boltzmann distribution of conformation and ionization states of protein side chains, buried waters, ions, and ligands is determined as a function of pH,¹¹ E_h^33,70,71 or in defined intermediates along a reaction coordinate.^72–76 The dielectric response of the system is composed of the implicit, continuum solvent with ε = 80, a low protein dielectric constant (ε_p) of 4 (default)^* and explicit side chain rearrangements. There are several significant improvements to the earlier program^34,45 including extensive multistep rotamer making, rotamer pairwise relaxation, rotamer pruning. Terms are added accounting for the van der Waals interactions with the implicit solvent⁷⁷ and correcting for entropy favoring ionization states for which there are more available conformers. A correction for errors in the dielectric boundary due to the presence of multiple conformations provides the most significant improvement in benchmark calculations.

MCCE2 is broken into four steps: (1) the Protein Databank file is checked and modified as needed; (2) a simplified energy function is used to select several thousand atomic positions for side chains and ligands from an initial group of tens of thousands of conformers. The final structure file is a protein model with multiple conformers representing all degrees of freedom in the calculation including appropriate acid/base or redox site ionization states, and side chain and ligand positions; (3) accurate energy look-up tables are calculated for the self-energy of each conformer and pairwise interactions between conformers. No higher order terms are considered; (4) the probability of finding each conformer for every residue or ligand in a Boltzmann distribution is determined by Monte Carlo sampling at defined solution conditions such as pH and E_h.

Step 1: Preparing the Protein

Residue topology files for each amino acid and ligand define the heavy atom bond connectivity, the number and position of hydrogens to be added to each atom, rotamer building rules, protonation and redox states to be considered, the atomic partial charges and conformer reaction field energy in solution for each ionization state, and the solution pK_a (pK_a,sol) and electrochemical midpoint potential (E_m,sol) for each residue. Each residue or ligand in the input protein structure file is compared with the appropriate parameter file. MCCE completes missing side chains as needed. Solvent exposed waters and ions with >5% solvent accessible area (default) are automatically removed. The subroutine IPECE¹¹ can add waters or ions into cavities and a low dielectric slab to simulate a membrane if desired. Residue or atom names are changed to match MCCE conventions. For example, by default chain termini have their names changed so they and their side chains can be titrated independently. Cys with terminal S atoms within 3.5 Å are identified as being in a disulfide bridge and are renamed and fixed in the neutral, unprotonated state in their initial positions. In addition, other groups such as propionic acids on hemes are renamed so that they can be ionized independently of the heme group,⁷⁰ or as in rhodopsins, the retinal and ligated lysine are renamed so the Schiff base is treated as one residue.¹¹ Bound small molecules such as waters, ions, or ligands have an additional, dummy conformer defined in the topology file.¹¹ This interacts only with the solvent, representing the group leaving the protein. Mutations can be made by deleting the original side chain and renaming the backbone atoms with the new residue name. Appropriate atoms will be added to build the desired side chain. If all side chains are removed the protein will be rebuilt and completely repacked without any bias from the original coordinates.

Step 2: Building the Multiconformer Model

The protein is divided into fixed backbone and flexible side chains. Standard side chain packing methods seek to find the minimum energy structure.^78–80 By contrast, MCCE needs to produce an ensemble of low energy side chain positions to allow the protein to remain in equilibrium with the different ionization states found for example in a pH titration. The process first selects heavy atoms rotamers, then adds and optimizes the proton positions, then prunes duplicate conformers (Supp. Info. Table S1). MCCE defines rotamers as side chains with different heavy atom positions, whereas conformers are the completed side chains with defined proton positions and ionization states.

Step 2a: Protein Side Chain Optimization and Relaxation

A set of ideal rotamers is created with ideal bond lengths, bond angles, and dihedral angles. The heavy atom rotamer closest to that found in the crystal structure is kept. Then all ideal rotamers for the protein are minimized using the steepest decent method^81,82 with Amber nonelectrostatic parameters, PARSE charges and a uniform dielectric constant of 6, assuming standard ionization states with His neutral. The protein is minimized five times, starting with the polar protons in randomly chosen torsion minima or tautomers. Resultant rotamers are compared. When no two atoms are >0.05 Å apart from the rotamers are considered duplicates and one is pruned. The starting, experimental conformer, the closest idealized rotamer and the remaining minimized, idealized side chain rotamers with the protons removed are added to the available positions for each residue. These rotamers are very close to the crystal structure, but are minimized in the force field used here. This creates a structure with on average 3–6 rotamers/residue.

Step 2b: Isosteric Rotamers

Isosteric rotamers are made by swapping OD1 with ND2 in Asn, OE1 with NE2 in Gln, CE1 with NE2, and ND1 and CE1 with CD2 and NE2 in His. These atoms of similar mass can rarely be unambiguously assigned in crystal structures. These extra rotamers will let the protein remake the hydrogen bond networks throughout a titration without significantly changing the protein shape or packing.⁴³

Step 2c: Heavy Atom Rotamer Generation and Pruning

Starting from the closest idealized rotamer, new rotamers are added at 60° intervals (default). Substrates bound in protein cavities can have additional translational and rotational degrees of freedom defined in the topology files. For residues with symmetric structures, conformers with identical structures but distinguishable atom names are built. For example, after three 60° steps Asp OD1 will overlap with the OD2 in the initial rotamer. Conformers where atoms of the same element type are within 0.001 Å of each other are considered duplicates and only one is kept. The default calculation starts with ≈250 rotamers/residue ranging from 1296 for LYS to 1 for Ala (Supp. Info. Table S1).

The AMBER⁸³ nonelectrostatic intrarotamer torsion and Lennard-Jones (LJ) interactions within a rotamer and with the backbone are calculated. In all LJ calculations, the 1–2 (atoms directly bonded) and 1–3 (atoms bonded to the same atom) interactions are set to zero, and 1–4 interactions (atoms separated by two atoms) reduced by 50%.⁸³ A 10 Å cutoff is used. Rotamers with a total energy >10 kcal/mol (default) higher than the lowest energy rotamer of the same residue due to clashes with themselves or with the backbone are deleted. The ensemble now has an average of ≈30 rotamers/residue.

Step 2d: Rotamer Pruning by Side Chain Rotamer Packing

Using the remaining rotamers that do not have clashes the protein is packed 5000 times (default) to select positions that can form different low energy microstates before considering hydrogen positions or ionization states. Suboptimal packing is desired because the lowest energy rotamers here may not be the best when the system is complete and accurately analyzed. Energies are calculated with the standard AMBER force field for LJ and torsion interactions. A simple function attracts O and N, O and O, N and N atoms to mimic local electrostatic interactions:

$$E_{\text{hb}}=-10.0/d\text{Kcal}/\text{mol}$$ (1)

where d is the distance in Å. Adding this term to the LJ interactions yields an optimal heavy atom hydrogen bond distance of 2.9 Å with an energy minimum of − 3.5 kcal/mol. This function lacks the angular dependence of the hydrogen bond.

Each repacking starts from a random state with one heavy atom rotamer for each residue to form a microstate. For each residue, chosen in random order, the pool of rotamers is found with their energy within 2.5 kcal/mol of the lowest energy rotamer in the context of this microstate. One of these is randomly selected to modify the microstate structure and the process repeated until the rotamers of all residues are within the energy threshold. This produces one semioptimized packed structure, which will be used to determine the fate of rotamers. Rotamers of similar energy within this packed structure are all marked as acceptable. It is easy to generate similar rotamers on the protein surface. Therefore, when the experimental side chain is exposed with >50% solvent accessible surface, only rotamers within 0.5 kcal/mol (default) of the lowest energy structure are marked. If the side chain is buried, then all rotamers with energies not greater than 2.5 kcal/mol (default) from the minimum value in this packed structure are remembered as being selected. After the protein has been repacked 5000 times, rotamers that are marked in <5% (default) of the packed structures are deleted. Fewer than 10% of the heavy atom rotamers survive the packing and pruning step. In addition, the rotamers from the initial optimization (step 2a) are also kept. There are now an average of ≈10 rotamers/residue.

Step 2e: Adding Protons and Defining Ionization States

Protons are added to every remaining rotamer. Ionization state conformers of acidic and basic residue are created with different numbers of protons on appropriate atoms (Supp. Info. Table S1). Conformers are made with hydroxyl protons in each torsion minimum. For residues such as Asp and Glu, additional conformers have the proton on either of the two terminal oxygen atoms. Redox active groups have conformers added with the same number of atoms but labeled so they will have different charge distributions in the final structure. There are now an average of ≈15 conformers/residue.

Step 2f: Heavy Atom Relaxation

Rotamer pairs with acceptable LJ interactions may experience clashes when protons are added. Conformer pairs where the total LJ interaction is larger than 2 kcal/mol (default), while the heavy atom LJ interaction is smaller than 5 kcal/mol (default) are relaxed. Conformers with larger heavy atom clashes represent mutually exclusive states generated in different packed structures in step 2d and are preserved. Selected pairs of conformers are isolated and optimized using the steepest descent energy minimization^81,82 with fixed backbone. The force field includes full AMBER LJ and torsion energies. The electrostatic interactions are calculated with Coulomb’s Law using ε = 1 and charges from the residue topology files. SHAKE⁸⁴ fixes all bond lengths and bond angles. As the conformers are isolated constraints are used to keep the new positions close to the original. Only a short, 50 step (default) minimization is used with a femtosecond step (default). Following each step all velocities are reset to zero.^81,82 A harmonic restraint E = 0.5k(|x→−x→₀|−d)² is added to all heavy atoms, where k is a spring constant of 10 kcal/mol/Ų (default), x→ is the current position, x→₀ is the original position before any relaxation, d is the distance within which no penalty is applied (1 Å is default). For terminal hydroxyl groups, the torsion energy is increased 20-fold (default) at the start of minimization to keep the proton from moving over a torsion barrier, then linearly scaled back to the standard value during the first 25 steps (default), which is retained for the second half of the minimization routine. The conformer pairs are relaxed in random order. Since each conformer change is carried out in isolation from the protein, new clashes with other conformers can be introduced. After all conformers have been relaxed, the LJ energies are reevaluated and the clashes relaxed five times (default) working through the conformers in different random orders. When a conformer built from an experimental rotamer is relaxed, then both original and relaxed structures are retained. Otherwise the relaxed conformers replace the original one. After relaxation, additional conformers are generated from the relaxed conformers as needed to ensure each hydroxyl torsion minimum has a proton. There are now an average of ≈35 conformers/residue.

Step 2g: Hydroxyl Optimization

Additional conformers are made through optimizing hydroxyl positions. All backbone amides and side chains with any atom within 5 Å of the hydroxyl group are included. Each residue within this cluster of 3–5 residues is in a randomly chosen conformer. The hydroxyl groups for all residues in the cluster are optimized using the steepest decent minimization with heavy atoms fixed and the force field described above for heavy atom optimization without the position constraints and modified torsion energy. Each optimized conformation is saved. For each hydroxyl 100 (default) cluster conformer and ionization microstates are minimized. In the current implementation, the hydroxyl is then moved to positions at 30° (default) intervals to reduce the number of conformers. There are now an average of ≈50 conformers/residue.

Step 2h: Rotamer Pruning by Conformer Clustering

Groups that fall within a similarity threshold are viewed as being duplicates. The atom positions, and electrostatic and LJ interactions to conformers of other residues are compared for all conformers. If the biggest position difference between the same atoms from two side chain conformers at the same ionization state is >2 Å (default), these two side chain conformers are considered to be different and the other pruning steps are skipped. This prevents overpruning of conformers before more accurate energy terms are calculated, especially on the surface where the interactions with the protein accounted for here are small, whereas the difference in reaction field energy, calculated in step 3, can be significant. Then, an electrostatic interaction energy vector and a LJ interaction vector are calculated for each conformer. These measure the pairwise interaction of this conformer with the native conformers (in the ionized state for ionizable residues) of all other residues. The electrostatic energy is calculated with Coulomb’s Law at dielectric constant 6, and the LJ energy is calculated with the method described for step 2c. If all elements in electrostatic and LJ interaction vectors from two conformers differ by <1.5 kcal/mol (default), the conformers are viewed as too similar and one is removed. LJ interactions change rapidly for clashing conformers. Thus, LJ energies greater than 20 kcal/mol are not considered in deciding the uniqueness of conformers. Conformers derived from input coordinates will always be preferred to those built by MCCE. If both conformers are derived from a native conformer or both generated by MCCE, then a random choice is made. This reduces the number of conformers by ≈50%. After clustering, there are on average ≈20 conformers/residue with ≈50 conformers/ionizable residue; ≈15 conformers/polar residue, and ≈5 conformers/non-polar residue.

Step 2 provides a variety of means to generate conformers. A QUICK MCCE calculation makes only isosteric rotamers from the experimental side chain position then skips to add and optimize protons (steps b, e, and g). This has ≈2.5 conformers/residue and is about 50 times faster than a FULL calculation using default values in steps a–h. It takes about 1 h to carry out a QUICK calculation on hen egg white lysozyme (4LZT) on a single Intel^® Xeon^™ 2.66 GHz CPU. In addition, for large proteins with buried sites of interest it is possible to focus more conformer making in only a restricted area, while using only QUICK conformers for the rest of the protein.¹¹ As will be shown, many pK_as are not very different in QUICK and FULL simulations. However, it is useful to compare the results from different calculations with different conformer making strategies to find residues which are more sensitive to the degree of conformational flexibility.

Step 3: Preparing the Energy Look-Up Tables

The conformers are subjected to Monte Carlo sampling considering the solvation (reaction field) and torsion self-energies and the electrostatic and LJ pairwise interactions. Energy look-up table is prepared, allowing calculation of all microstate energies during Monte Carlo sampling starting with the same strategy used in MCCE1.⁴⁵ Thus, for M conformers, there are four M-dimensional vectors containing terms assumed to be independent of the selected conformers for other residues: the torsion energy (ΔG_torsion,i); the LJ interactions with all protein backbone atoms, and with appropriate atoms within the same conformer (ΔG_fixed,i); the electrostatic interactions with the backbone atoms (ΔG_bkbn,i); and the solvation energy of each conformer (ΔΔG_rxn,i). There are two symmetric M×M matrices for the conformer–conformer electrostatic and the LJ interactions.

The new energy term, ΔG_SAS = −γ•SAS, where γ = 0.06 kcal/mol/Ų, and SAS is the exposed surface area of the given conformer calculated when all other residues are in their input, experimental rotamer, is added in MCCE2. This represents favorable implicit van der Waals interactions between a conformer and the implicit solvent. The form and values is based on earlier studies comparing the solvent exposed surface area with the explicit van der Waals interactions between the protein and the solvent in molecular dynamics studies.⁷⁷

The electrostatic interactions are calculated with the Poisson-Boltzmann (PB) equation using multiple DelPhi runs integrated into MCCE.⁸⁵ DelPhi input and output has been modified to preassign atomic charges and radii and to make extensive use of unformatted IO (with thanks to Anthony Nicholls, OpenEye Scientific Software). This halves the time needed to create the energy look-up table for a protein with 2000 conformers. The protein dielectric constant is 4 (default) whereas the solvent is assigned 80 (default) with a salt concentration of 0.15 M (default). PARSE charges and radii are used for protein atoms.⁸⁶ The dielectric constants and salt concentration can be changed in the run control file, whereas charges and radii can be modified in the residue topology file. Focusing is carried out so that the final resolution is 2 grids/Å (default) or better using a 65³ grid (default).

The reaction field (solvation, self or Born) energy (ΔG_rxn) provides the favorable interaction of conformer charges and dipoles with water. For the calculation of the reaction field energy of residue A conformer i, only this conformer has atomic charges and all other conformers of residue A are deleted from the model (Fig. 1a, Table 1). All other residues contain only a conformer based on the rotamer found in the input PDB file, or the first rotamer made by the MCCE program if the side chain is missing. M DelPhi calculations yield the reaction field energy of each conformer. The change in reaction field energy, ΔΔG_rxn;Ar moving the conformer from solution to its position in the protein is:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn},A_i}=\mathrm{\Delta }{G}_{\text{rxn},A_i}-\mathrm{\Delta }{G}_{\text{rxn},A_i(\text{soln})}.$$ (2)

Figure 1.

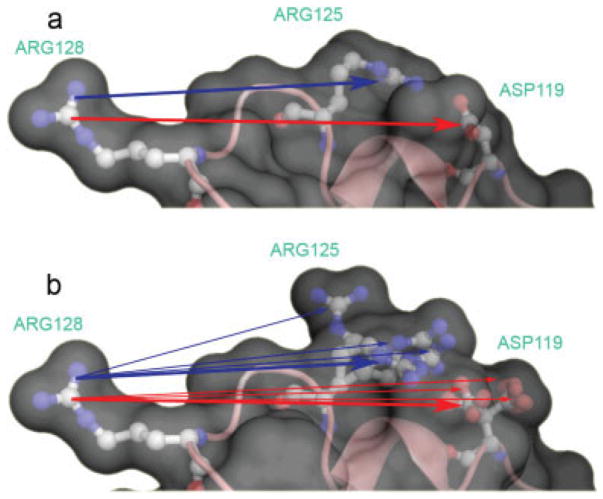
Fragment of lysozyme structure 4LZT. (a) Single conformation dielectric boundary used to calculate the reaction field energy ΔΔG_rxn; and the reference pairwise interactions $\mathrm{\Delta }{G}_{{\text{A}}_{\text{i}},{\text{B}}_{\text{j}}}^{\text{ES}}$ (bold lines) between the only conformer with partial charges (a conformer of Arg128 here) and the native conformer of all other residues; (b) Multiconformer dielectric boundary has more low dielectric boundary material so all pairwise interactions, $\mathrm{\Delta }{G}_{A_i,B_j}^M$ have larger absolute values than $\mathrm{\Delta }{G}_{A_i,B_j}^{\text{ES}}$. The raw pairwise interaction to each non-native conformer is corrected with eq. (6) to give $\mathrm{\Delta }{G}_{A_i:B_j}^C$.

Table 1.

The Conformers that Contribute to the Dielectric Boundary in Different Calculations.

Run type	Energy term	Conformer with chargea	Radii target residue	Radii other residues
Rxn field	ΔGrxn,Ai	Only Ai	Self-energy	Conf #1
MC	$\mathrm{\Delta }{G}_{A_i:B_j}^M$	Only Ai	All B	All
Pairwise	$\mathrm{\Delta }{G}_{B_j:A_i}^M$	Only Bj	All A	All
Exact SC	$\mathrm{\Delta }{G}_{A_i,B_j}^{\text{ES}}$	Only Ai	Only Bj	Conf #1
Pairwise	$\mathrm{\Delta }{G}_{B_j:A_i}^{\text{ES}}$	Only Bj	Only Ai	Conf #1

The default Conf #1 is the side chain rotamer in the initial input structure file. For residues with different ionization states this is a charged conformer. $\mathrm{\Delta }{G}_{A_i,B_j}^{\text{ES}}$ is calculated with the same boundary conditions as ΔG_rxn,Ai (Fig. 1). MC, multiconformation; SC, single conformation.

^aThe radii of all other conformers of this residue are set to zero.

ΔG_{rxn; Ai(soln)}, a standard value for each protonation and/or redox state is calculated with the internal dielectric constant matching ε_p to be used for the protein. Thus ΔG_rxn,Ai(soln) is larger in calculations run with ε_p of 4 than it is for ε_p 8. ΔG_rxn,A(soln) is the average DelPhi reaction field energy for ≈40 different conformers isolated from a protein. The standard deviation of ΔG_rxn,A(soln) for a group of conformations extracted from different protein structures is ≈3%.

The initial M×M conformer–conformer pairwise electrostatic interaction matrix is obtained by solving DelPhi M times. The raw multiconformation conformer-conformer pairwise interaction of residue A conformer i with residue B conformer j ( $\mathrm{\Delta }{G}_{A_i{B}_j}^M$) is calculated with only the atoms of A_i having charges; all other conformers of A are deleted from the model, but all other conformers of all other residues are present. Thus, there is more low dielectric material than in the calculations of the reaction field energy (Fig. 1b, Table 1). Entry A_i:B_j in the pairwise interaction matrix is^45,87:

$$\mathrm{\Delta }{G}_{A_i{B}_j}^M=\sum _{a=1}^{\text{atoms}{B}_j}{\mathrm{\Psi }}_{A_i{B}_j(a)}{q}_{B_j(a)}$$ (3)

where ψ_AiBj(a)is the electrostatic potential at atom a of conformer B_j from the charges on A_i q_Bj(a) is the partial charge on atom a in the appropriate conformer ionization state. The conformer–conformer interaction energy is given by the sum over all atoms in conformer B_j. Thus, one DelPhi calculation provides the interaction of A_i with all conformers of all residues. Interactions with other residue A conformers are set to zero. The pairwise interaction of conformer A_i with the protein backbone is obtained from the same DelPhi run summing the pairwise interaction over all atoms in the backbone:

$$\mathrm{\Delta }{G}_{\text{bkbn},A_i}=\sum _{a=1}^{\text{atomsbkbn}}{\mathrm{\Psi }}_{A_i\text{bkbn}(a)}{q}_{\text{bkbn}(a)}$$ (4)

The chain N and C termini are treated as separate, ionizable residues so are not included in ΔG_bkbn.

Correction of Errors in the Pairwise Interactions Due to the Changing Dielectric Boundary

MCCE^34,45 differs from standard single conformation continuum electrostatics (SCCE) calculations in that the dielectric boundary should be different in different microstates, with different conformers selected for each residue. Thus, accurate electrostatic interactions should use the microstate dielectric boundary. However, this is impractical given the time demands of a DelPhi calculation. Rather, the pairwise interactions of a conformer with all conformers of all other residues are efficiently, but less accurately determined in one DelPhi calculation containing the low dielectric material for all conformers (Fig. 1, Table 1). The influence of the incorrect boundary was determined by analysis of all pairwise interactions between fewer than 170 conformers in Barnase. The ≈28,000 exact, single conformation calculations( $\mathrm{\Delta }{G}_{A_i,B_j}^{\text{ES}}$) containing only A_i, B_j, and the single, native conformer of all other residues was compared with the standard, multicon-former calculations ( $\mathrm{\Delta }{G}_{A_i,B_j}^M$) containing A_i and all conformers of all other residues (Table 1). The standard calculation is found to overestimate charge–charge interactions by as much as a factor of 2 (Fig. 2). The error in charge–dipole interactions is smaller, whereas the short-range dipole–dipole interactions are very similar in the multiconformer and exact calculations (Fig. 2). In addition, in the standard calculations $\mathrm{\Delta }{G}_{A_i,B_j}^M$ need not equal $\mathrm{\Delta }{G}_{B_j,A_i}^M$ because the dielectric boundaries in the two calculations are different, while these are identical within the numerical accuracy of DelPhi in the exact calculations.

Figure 2.

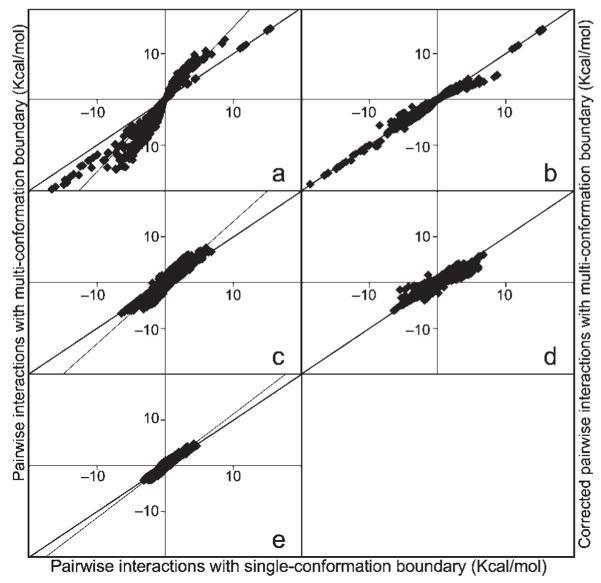
Comparison of pairwise interactions of 1200 conformers in Barnase (1A2P chain A) at ε_p of 4. ΔG^ES is calculated with only the interacting conformers present (Fig. 1a) whereas ΔG^M uses the standard multiconformation boundary conditions for calculating pairwise interactions (Fig. 1b, Table 1). $\mathrm{\Delta }{G}_{A_i,B_j}^M$ versus $\mathrm{\Delta }{G}_{A_i,B_j}^{\text{ES}}$ for (a) 1613 charge–charge and (c) 9679 charge–dipole interactions and (e) 16641 dipole–dipole interactions. Lines show slope 1 and best-fit lines through the points. $\mathrm{\Delta }{G}_{A_i:B_j}^C$ eq. (6) versus $\mathrm{\Delta }{G}_{A_i,B_j}^{\text{ES}}$ for (c) charge–charge and (c) charge–dipole interactions. Dipole–dipole interactions are generally small and no corrections are used. Line of slope 1 is shown.

The calculation used to determine the reaction field energy (Table 1, AFig. 1a) draws an exact, single conformer boundary to determine the pairwise interactions of the conformer of interest (_i) with the initial conformer of each other residue (B₁) ( $\mathrm{\Delta }{G}_{A_i{B}_j}^{\text{ES}}$) This energy can then be compared with the interactions between the same conformers in the standard multiconformation DelPhi calculation for A_i. Thus, of the M² calculations needed to accurately fill an M×M matrix with an exact single conformer boundary, M calculations are carried out in the standard cycle of MCCE DelPhi runs. A scaling factor c_AB compares the interactions in the two calculations:

$$c_{A_i{B}_1}=\mathrm{\Delta }{G}_{A_i{B}_1}^{\text{ES}}/\mathrm{\Delta }{G}_{A_i{B}_1}^M$$ (5)

The corrected pairwise interaction for any pair of conformers $\mathrm{\Delta }{G}_{A_i{B}_j}^C$ is the average value of the formally symmetric interactions from A_i to B_j and from B_j to A_i:

$$\begin{array}{l}\mathrm{\Delta }{G}_{A_i{B}_j}^C=\mathrm{\Delta }{G}_{B_j{A}_i}^C\\ =0.5\left[\mathrm{\Delta }{G}_{A_i{B}_j}^M\left(\mathrm{\Delta }{G}_{A_i{B}_1}^{\text{ES}}/\mathrm{\Delta }{G}_{A_i{B}_1}^M\right)+\mathrm{\Delta }{G}_{B_j{A}_i}^M\left(\mathrm{\Delta }{G}_{B_j:A_1}^{\text{ES}}/\mathrm{\Delta }{G}_{B_j{A}_1}^M\right)\right]\end{array}$$ (6)

The procedure to calculate $\mathrm{\Delta }{G}_{A_i{B}_j}^C$ fails if conformer A₁ and B_j or conformer B₁ and A_i are so close that charged atoms from the two residues are within the same grid in the DelPhi calculations. This is identified by the conformers having LJ interactions >50 kcal/mol. In this case only the c_Ai,B1 obtained between non-overlapping conformers is used for both $\mathrm{\Delta }{G}_{A_i:B_j}^C$ and $\mathrm{\Delta }{G}_{B_j:A_i}^C$. On the rare occasions when both conformer A₁ and B_j and conformer B₁ and A_i clash the averaged raw interactions $\mathrm{\Delta }{G}_{A_i:B_j}^M$ is divided by 1.5 for charge–charge interaction and by 1.3 for charge–dipole interactions. The factor 1.5 and 1.3 were determined from the exhaustive comparison of the Barnase $\mathrm{\Delta }{G}_{A_i:B_j}^M$ and $\mathrm{\Delta }{G}_{A_i:B_j}^{\text{ES}}$ (Fig. 2). This occurs in <0.1% of the interactions. Of the ≈28,000 charge–charge and charge–dipole interactions used to determine the best method with exact ( $\mathrm{\Delta }{G}_{B_j:A_i}^{\text{ES}}$) interactions 105 have interactions >5 kcal/mol. Of these large interaction 60% of $\mathrm{\Delta }{G}_{B_j:A_i}^M$ differ from $\mathrm{\Delta }{G}_{B_j:A_i}^{\text{ES}}$ by >25% and 32% have errors >50%. In contrast, only 2% of the corrected $\mathrm{\Delta }{G}_{B_j:A_i}^C$ differ from $\mathrm{\Delta }{G}_{B_j:A_i}^{\text{ES}}$ by >50%, 20% have errors >25%, whereas 37% still have errors of >10% after correction. Thus, although this correction scheme is not perfect, it represents a considerable improvement in accuracy with little increase in computation time, using 2N DelPhi runs to achieve an accuracy similar to that found for the M² exact calculations.

Step 4: Monte Carlo Sampling Under Defined External Conditions

The preselected conformers are subjected to Monte Carlo sampling to generate the Boltzmann distribution of conformers. One conformer of each residue makes up a microstate. For noncovalently bound groups such as waters or ions there is a conformer with no interactions with the protein and no loss in reaction field energy that represents an empty binding site, establishing a Grand Canonical Ensemble. Metropolis sampling is used to determine acceptance given the energy ΔG_x of microstate x^8,34,45,70:

$$\begin{array}{l}\mathrm{\Delta }{G}^x=\sum _{i=1}^M{\delta }_{x,i}\{[2.3m_i{k}_{b}T(pH-p{K}_{\text{sol},i})+n_{i}F(E_{\text{h}}-E_{\text{m}\text{sol},i})]\\ +(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn},i}+\mathrm{\Delta }{G}_{\text{bkbn},i}^{\text{CE}}+\mathrm{\Delta }{G}_{\text{bkbn},i}^{\text{LJ}}+\mathrm{\Delta }{G}_{\text{torsion}.i}+\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{SAS},i})\\ +\sum _{j=i+1}^M{\delta }_{x,j}[\mathrm{\Delta }{G}_{ij}^{\text{CE}}+\mathrm{\Delta }{G}_{ij}^{\text{LJ}}]\}\end{array}$$ (7)

M is the total number of conformers. δ_x(i) is 1 if conformer i is present in the microstate or 0 otherwise. n_i is the number of electrons transferred if redox active ligands are considered. F is the Faraday constant. m_i is 1 for bases, − 1 for acids, and 0 for neutral conformers. k_bT is 0.59 kcal/mol (0.43 ΔpK units) at 298 K, the default temperature. The pH and E_h describe the ability of the solvent to donate protons or electrons. The pK_a,sol,i and E_m,sol,i are the reference solution pK_a and E_m (electrochemical midpoint potential) of groups involved in acid/base or redox reactions. These are properties of the residue not the conformer.⁶ The second line of the equation describes the conformer self-energies, which are independent of the other conformers in the microstate. The third line gives the electrostatic (CE) and LJ pairwise interactions, which depend on the conformers selected in the microstate.

Entropy Correction

For a single heavy atom position there is one ionized conformer for the acidic and basic residues, whereas the proton can be removed from either His or Arg side chain nitrogen, and placed on either carboxyl oxygen (Supp. Info. Table S1). A carboxyl proton can also move around the oxygen to which it is bound in an appropriate torsion potential forming multiple alternative conformers. This imbalance between the numbers of ionized and neutral conformers artificially favors the neutral form in Monte Carlo sampling. The sampling entropy bias cannot be simply determined by the ratio of ionized and neutral input conformers because high-energy positions that are not accepted in Monte Carlo sampling do not contribute to the bias. The entropy is determined within Monte Carlo sampling:

$$\text{TS}=-1.36\sum _i{P}_i^{\prime }ln(P_i^{\prime })\text{Kcal}/\text{mol}$$ (8)

where $P_i^{\prime }$ is the renormalized occupancy of conformer i, assuming the total occupancy of the given ionization state is 1. $P_i^{\prime }=\frac{P_i}{{\displaystyle \sum _j}{P}_j}$, i and j run over the conformers in the same ionization state. All conformers of a residue within the same ionization state have the same entropy correction. Monte Carlo sampling is carried out with the entropy correction until it converges. This entropy correction term is found to range from 0 to ≈1.4 kcal/mol.

Monte Carlo Sampling

Each Monte Carlo step changes a residue or ligand ionization state and/or position. A Monte Carlo step first picks a residue then the conformer within that residue. Half the steps use multi-flip sampling.⁸⁸ Each residue has a list of other residues with which it interacts by >5.0 kcal/mol (default). When multiflip is triggered, residues in the big interaction list are randomly chosen to change conformer, together with the primary residue. The number of residues being flipped from the big interaction list is randomly chosen between 1 and a predefined number (2 by default) or the total number of residues in the big interaction list, whichever is smaller. This greatly aids convergence when the ionization states and/or position of several residues are interdependent.

One Monte Carlo sampling cycle is carried out in stages of annealing, initial sampling, conformer reduction, and equilibrium sampling. A random microstate is generated and annealed in 500×M (default, M is the total number of conformers) steps of Metropolis sampling.⁴⁵ Initial sampling is then carried out for 2000×M (default) steps. The conformer occupancies calculated at this stage are used to obtain the initial entropy correction values, but are not saved. Conformers that are never occupied are then removed from the sampling list and a longer 5000×M (default) stage of reduced, equilibrium sampling is initiated. At the end, the entropy eq. (8) is recalculated for ionized and neutral conformers of a residue and retained to start the annealing and initial sampling stages of the next cycle.

Six (default) independent Monte Carlo sampling cycles are carried out starting from new random states. The average conformer occupancies in equilibrium sampling from all sampling cycles provide the final output at each pH and E_h. In addition, the residue entropy correction, the standard deviation of conformer occupancy in the six Monte Carlo sampling cycles and the microstate energy every 5000 steps (default) are reported. Comparison of the average energy during the different equilibrium stages can indicate if the run has been trapped in a high-energy valley.

Independent Monte Carlo simulations are automatically carried out at 15 (default) different pHs (default) or E_hs providing the Boltzmann distribution of residue ionization and conformation with changing solution conditions. If a benchmarked residue of interest does not titrate in the default pH range, the pH range is expanded. The pK_a is calculated assuming a single site titration with a variable Hill coefficient (n) using the Henderson-Hasselbalch eq. (9) equation:

$$\langle {\text{Occ}}_{\text{ionized}}\rangle =\frac{{10}^{-mn(\text{pH}-\text{p}{K}_a)}}{1+{10}^{-mn(\text{pH}-\text{p}{K}_a)}}$$ (9)

in which m is − 1 for acid and 1 for base, representing the probability of the ionized form, A⁻ for an acid or BH⁺ for a base, being found. Shallow titrations, with n < 1, are the norm for intraprotein acid/base titrations.^34,89

Ionization states in proteins are sometimes found coupled to other groups, leading to a bimodal Henderson-Hasselbalch curve:

$$\langle {\text{Occ}}_{\text{ionized}}\rangle =\alpha \frac{{10}^{-m{n}_1(\text{pH}-\text{p}{K}_{\text{a},1})}}{1+{10}^{-m{n}_1(\text{pH}-\text{p}{K}_{\text{a},1})}}+(1-\alpha )\frac{{10}^{-m{n}_2(\text{pH}-\text{p}{K}_{\text{a},2})}}{1+{10}^{-m{n}_2(\text{pH}-\text{p}{K}_{\text{a},2})}}$$ (10)

where α and (1 − α) are the amplitude of each phase of the titration, pK_a,1, pK_a,2, n₁, and n₂ are the pK_a and n value for each titration.

The difference between χ² for one or two site titrations is compared, where χ² is:

$$x^2=\sum {(\langle {\text{Occ}}_{\text{ionized},\text{fitting}}\rangle -\langle {\text{Occ}}_{\text{ionized},\text{MCCE}}\rangle )}^2$$ (11)

Occ_ionized,MCCE is the MCCE-calculated occupancy and Occ_{ionized,fitting} is the theoretical occupancy from the best fit of this data to eq. (9) or (10). When the bimodal analysis decreases χ² by >0.01, the two pK_a fit is kept with the pK_a closer to the experimental value used for the benchmark analysis. Both pK_as are reported in supporting information Table S3.

Averaging the Results from Multiple Calculations for a Given Residue

Multiple PDB files are used for each protein. Some PDB structures include multiple models. Calculated pK_as are averaged among m models for each PDB structure and then averaged for n PDB files.

$$\langle \text{p}{K}_{\text{a}}\rangle =\frac{1}{n}\sum _{i=1}^n\left\{\frac{1}{m}\sum _{j=1}^m\text{p}{K}_{\text{a}}(i,j)\right\}$$ (12)

The standard deviation, σ, of each calculated pK_a is:

$$\sigma =\sqrt{{\sigma }^{{\text{o}}_2}+\frac{1}{n}\sum _{i=1}^n{\sigma }_i^2}$$ (13)

where σ_I is the standard deviation between the averaged pK_as for all models in a given PDB file, whereas σ⁰ is the standard deviation between the averaged pK_as in multiple, independent PDB files.

Analyzing the Energy Terms Contributing to a Calculated pK_a

A mean-field energy model is used for analysis of the energy components contributing to the pK_a shift of a residue. For each given conformer, the Boltzmann averaged mean-field energy is:

$$\begin{array}{l}\mathrm{\Delta }{G}_i^{\text{MFE}}=[2.3m_i{k}_{b}T(\text{pH}-\text{p}{K}_{\text{sol},i})+n_{i}F(E_{\text{h}}-E_{m\text{sol},i})]\\ +(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn},i}+\mathrm{\Delta }{G}_{\text{bkbn},i}^{\text{CE}}+\mathrm{\Delta }{G}_{\text{bkbn},i}^{\text{LJ}}+\mathrm{\Delta }{G}_{\text{torsion},i}+\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{SAS},i})\\ +\sum _{j\ne i}^M{\rho }_j[\mathrm{\Delta }{G}_{ij}^{\text{CE}}+\mathrm{\Delta }{G}_{ij}^{\text{LJ}}]\end{array}$$ (14)

This differs from eq. (7) in that δ_x,j is now replaced with ρ_j, which is the Boltzmann averaged occupancy found by Monte Carlo sampling. Therefore instead of summing over all occupied conformers in microstate x, here the Boltzman averaged interactions from all conformers are used. The Boltzmann averaged conformer energies are then used to obtain the mean field difference between ionized and neutral forms of an ionizable residue. For a residue with Nⁱ ionized conformers and Nⁿ neutral conformers:

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{ionization}}^{\text{MFE}}=\sum _{i,\text{ionized}}^{N^{\text{i}}}{\rho }_{i,\text{ionized}}^{\prime }•\mathrm{\Delta }{G}_{i,\text{ionized}}^{\text{MFE}}\\ -\sum _{i,\text{neutral}}^{N^{\text{n}}}{\rho }_{i,\text{neutral}}^{\prime }•\mathrm{\Delta }{G}_{i,\text{neutral}}^{\text{MFE}}\end{array}$$ (15)

here ρ′ is the renormalized occupancy of conformer i, assuming the total occupancy of the given ionization state is 1. MFE analysis is most accurate when performed at pH = pK_1/2, where both neutral and ionized conformers are present. Each energy component in eq. (14) can be calculated in a similar manner. For example, the averaged desolvation energy is:

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{rxn}}^{\text{MFE}}=\sum _{i,\text{ionized}}^{N^{\text{i}}}{\rho }_{i,\text{ionized}}^{\prime }•\mathrm{\Delta }{G}_{\text{rxn},i,\text{ionized}}\\ -\sum _{i,\text{neutral}}^{N^{\text{n}}}{\rho }_{i,\mathit{neutral}}^{\prime }•\mathrm{\Delta }{G}_{\text{rxn},i,\text{neutral}}\end{array}$$ (16)

Results

The pK_as for 36 proteins have been calculated with MCCE and compared with 340 measured values (Fig. 3). The smallest protein is the B₁ Domain of protein G, with 56 residues and the largest is the human DNA polymerase lambda lyase domain, with 324 residues. All substrates and crystal waters are removed except the heme in myoglobin. The removed substrates, including PO₄ and SO₄ groups, ADP and solvent exposed ions, are listed in supporting information Table S2. The experimental pK_a data are from NMR measurements, and the data set is largely based on earlier compilations from Stanton and Houk,⁴⁹ Edgcomb and Murphy,⁹⁰ Forsyth et al.,⁹¹ and Toseland et al.⁹² There are 1231 ionizable amino acids in these 36 proteins; with only 430 reported pK_as, representing only 35% of the ionizable residues in these well-studied proteins (Supp. Info. Table S3). Only 340 values are used here. Values are excluded where the reported pK_a is out of range of the measurements (57 residues); the residue assignments are ambiguous or controversial (8); the ionization changes of the residue of interest are coupled to protein denaturation (3); or where the pK_a is reported from a measurement of protein activity (2).

Figure 3.

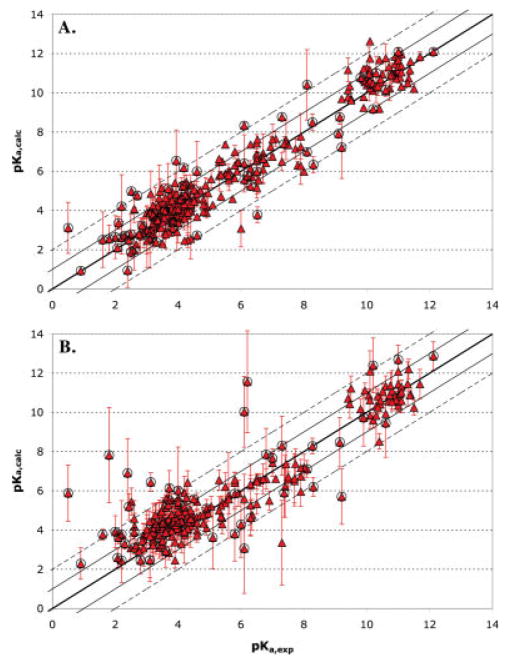
Comparison of calculated pKa values using FULL MCCE conformer flexibility with experimentally measured values. The error bars represent the standard deviation of the values for different structures. The thick central line is the ideal where pK_a (calc) = pK_a (expt); the solid line bracket errors <1 pH unit and the dashed lines errors <2 pH units. Circled points highlight residues buried in the protein with desolvation energies >2.04 kcal/mol (1.5 pH units) or with pK_as perturbed by >1.5 pH units from the solution value. (A) 305 averaged pK_as obtained starting with 86 structures obtained by X-ray crystallography of 33 proteins; (B) 265 pK_as obtained starting with 696 structures obtained by NMR methods of 24 proteins. The calculated and experimental pK_as are provided in supporting information Table S2.

Of the 36 proteins, 12 have only X-ray structures, 3 have only NMR structures, whereas 21 have both. Overall 114 different PDB files were considered. Only NMR structures (1JIC, 1SSO, and 1BBX) are used for Sso7d because the X-ray structure (1C8C) has a methylated N-terminal and highly disordered C-terminal. The protein structures are divided into three datasets to allow comparison of the results for structures derived by X-ray and NMR methods and an evaluation of the advantages of using multiple structures of a protein where available. The first set, which will be the most studied, includes one model of the 33 proteins with X-ray structures. If there are multiple available structures, the one with the highest resolution is used. The range of resolution of this group of PDB files is from 0.90 to 2.50 Å. This dataset includes 305 measured pK_as. The second data set includes all available X-ray structures. If there are multiple proteins in a single PDB file, each is extracted and calculated separately. On average, 2.6 structures are used for each protein. The resolution ranges from 0.90 to 3.00 Å. The third data set includes all NMR structures for 24 proteins. On average 29.0 models are used for each protein.

MCCE2 conformers are made and optimized. Previous studies have shown that alternative hydrogen positions and limited side chain conformers can improve calculated pK_as significantly.^{34,40,41,44,45} MCCE2 adds a more extensive side chain conformer search. Side chain positions are optimized by global packing as well as by local minimization. The 33 unique X-ray structures are used to show how the additions to MCCE2 changes the pK_a calculations at ε_p 4 (Table 2). Here, only one pK_a is calculated for each of 305 residues, providing a measure of the likelihood of obtaining a good pK_a prediction when only one structure is available. The different levels of calculations include SCCE, where one conformer is generated for each residue at one protonation state; isosteric conformer (QUICK) calculations, where isosteric conformers and torsion minima hydroxyl conformers are included; ROTAMER calculations, where heavy atom rotamers are generated around each rotatable bond and the optimized rotamer (FULL) calculations where local hydrogen bond optimization is added. QUICK and FULL are standard MCCE options. The pK_a titrations were fit to a monoprotic eq. (9) and a two-site bimodal model eq. (10). For 12 residues, the bimodal fitting decreases χ² by over 0.01 eq. (11). Here, the calculated pK_a is assigned to the value closer to the experimental value. Both results are noted in supporting information Table S3.

Table 2.

RMSD and Error Distribution of MCCE Calculations.

				Distribution of errors
	# pKas	RMSD	Avg erra	<0.5	0.5–1.0	1.0–1.5	1.5–2.0	>2.0
Part A: Errors as a function of the conformer selection methodology
FULL	305	0.90	−0.03	44.6%	31.1%	14.4%	7.2%	2.6%
Rotamer	305	1.02	0.00	43.3%	35.0%	12.7%	4.3%	4.7%
QUICK	305	1.34	0.27	40.3%	27.5%	16.4%	6.9%	8.9%
SCCE	305	2.23	0.41	41.3%	26.6%	11.8%	4.6%	15.7%
FULL εprot = 8	305	0.88	−0.07	41.6%	33.4%	16.1%	5.9%	3.0%
Errors as a function of MCCE corrections
FULL	305	0.90	−0.03	44.6%	31.1%	14.4%	7.2%	2.6%
w/o Boundary correction	305	1.47	0.50	33.4%	23.6%	17.7%	9.2%	16.1%
w/o Implicit van der Waals	305	0.93	0.06	47.2%	27.9%	14.4%	5.6%	4.9%
w/o Entropy correction	305	0.95	−0.32	44.6%	28.9%	15.1%	6.6%	4.9%
QUICK	305	1.34	0.27	40.3%	27.5%	16.4%	6.9%	8.9%
w/o Boundary correction	305	1.34	0.27	40.3%	27.5%	16.4%	6.9%	8.9%
w/o Implicit van der Waals	305	1.34	0.27	40.3%	27.5%	16.4%	6.9%	8.9%
w/o Entropy correction	305	1.34	0.08	38.0%	30.5%	15.4%	7.9%	8.2%
Part B: Errors for different residue types (standard FULL calculations, εp = 4)
Asp	81	1.05	−0.44	42.0%	30.9%	13.6%	8.6%	4.9%
Glu	94	0.73	0.08	55.3%	28.7%	9.6%	5.3%	1.1%
Tyr	14	0.83	0.23	28.6%	42.9%	28.6%	0.0%	0.0%
His	49	1.03	0.02	34.7%	22.4%	28.6%	14.3%	0.0%
Lys	53	0.78	0.27	47.2%	35.8%	11.3%	3.8%	1.9%
Ntr	4	1.41	0.22	0.0%	50.0%	0.0%	25.0%	25.0%
Ctr	10	0.91	−0.15	40.0%	50.0%	0.0%	0.0%	10.0%
Errors as a function of side chair burial and pairwise interaction with protein
Surface exposed residues (desolvation penalty <2 kcal/mol)
All	225	0.77	0.05	47.1%	33.8%	13.8%	4.0%	1.3%
|ΔG(prot)| <2 kcal/mol	171	0.72	0.00	50.9%	31.0%	14.6%	2.9%	0.6%
|ΔG(prot)| >2 kcal/mol	54	0.90	0.18	35.2%	42.6%	11.1%	7.4%	3.7%
Buried residues (desolvation penalty >2 kcal/mol)
All	80	1.20	−0.26	37.5%	23.8%	16.3%	16.3%	6.3%
|ΔG(prot)| <2 kcal/mol	21	1.47	−0.96	14.3%	33.3%	19.0%	19.0%	14.3%
|ΔG(prot)| >2 kcal/mol	59	1.09	−0.01	45.8%	20.3%	15.3%	15.3%	3.4%
Errors as a function of side chain secondary structure
All residues
Helix	107	0.86	0.14	49.5%	27.1%	15.0%	5.6%	2.8%
Strand	60	1.04	−0.27	38.3%	40.0%	10.0%	6.7%	5.0%
Loop	49	0.86	−0.06	46.9%	28.6%	12.2%	12.2%	0.0%
Other	76	0.84	−0.05	44.7%	27.6%	21.1%	6.6%	0.0%
Surface exposed residues (desolvation penalty <2 kcal/mol)
Helix	96	0.75	0.14	52.1%	28.1%	15.6%	3.1%	1.0%
Strand	26	0.57	−0.04	46.2%	50.0%	3.8%	0.0%	0.0%
Loop	35	0.70	0.06	48.6%	34.3%	14.3%	2.9%	0.0%
Other	58	0.82	−0.03	44.8%	31.0%	17.2%	6.9%	0.0%
Buried residues (desolvation penalty >2 kcal/mol)
Helix	11	1.50	0.17	27.3%	18.2%	9.1%	27.3%	18.2%
Strand	33	1.31	−0.45	30.3%	33.3%	15.2%	12.1%	9.1%
Loop	14	1.15	−0.34	42.9%	14.3%	7.1%	35.7%	0.0%
Other	18	0.92	−0.13	44.4%	16.7%	33.3%	5.6%	0.0%
Part C: Improving pKas by averaging calculations (standard FULL calculations, εp = 4)
Averaging 5 MCCE calculations for a 24 proteins
Single model	230	0.88	−0.06	47.0%	31.3%	13.0%	6.1%	2.6%
Average 5 models	230	0.86	−0.05	49.1%	30.0%	13.5%	4.8%	2.6%
Std <0.3	166	0.80	−0.01	51.8%	29.5%	12.0%	4.8%	1.8%
0.3 <Std <0.6	48	0.92	−0.21	43.8%	27.1%	20.8%	6.3%	2.1%
Std >0.6	16	1.38	−0.50	37.5%	37.5%	6.3%	6.3%	12.5%
Using multiple X-ray derived PDB files for a given protein
All values	832	0.90	−0.10	47.7%	29.3%	13.3%	6.6%	3.0%
Average calculations	305	0.87	−0.06	51.1%	26.6%	12.8%	6.9%	2.6%
Std <0.5	130	0.71	−0.07	59.2%	26.9%	9.2%	3.1%	1.5%
0.5 <std <1.0	65	0.66	−0.10	57.4%	23.5%	10.3%	4.4%	4.4%
std >1.0	24	1.11	−0.43	29.2%	37.5%	12.5%	12.5%	8.3%
NMR derived PDB files for a given protein
All values	7645	1.40	−0.47	40.9%	26.7%	14.0%	7.9%	10.4%
Average calculations	265	1.23	−0.52	41.6%	30.6%	13.1%	8.6%	6.1%

The protein dielectric constant (ε_prot) is 4 unless otherwise stated.

^aerr is m•(pK_a,calc − pK_a,exp), where m = −1 for acids, and 1 for bases. When err>0, MCCE overstabilizes the ionized form.

Both the RMSD between calculated and experimental pK_as, and the number of errors within a given range are used to assess the outcome (Table 2). The RMSD measures the global deviation between calculated and experimental data, and has been generally used to compare calculations using different methods. Recent pK_a benchmark studies yield RMSDs of ≈0.8–2.0 pH units, generally using similar benchmark data.^48,49,51 RMSD values are very sensitive to a few large errors. In contrast, reporting the distribution of errors provides the likelihood that calculations applied to any given structure will produce an erroneous pK_a for a particular residue.

The Improvements Provided by Different Rotamer Types

SCCE values provide a basis for comparison with other methods of calculation.^{34,40,55,93–97} SCCE calculations require that the protonation site for neutral His and hydroxyl protons placed on Ser, Thr, Tyr, and neutral acids be defined at the start of the simulation. In MCCE these proton positions are selected in the final Monte Carlo sampling. The current MCCE procedure does not provide a single optimized proton position during the rotamer making process. Instead, the QUICK calculations based on the isosteric conformer building (steps 2b, e, and h) is used. The most occupied hydroxyl positions in Monte Carlo sampling for Ser, Thr, and Tyr and the neutral His tautomer at pH 7 and the proton position for neutral Asp, Glu and C-termini when all acids are forced to be neutral and bases ionized are collected. All other protonated rotamers are removed from the protein structure for the energy calculations (step 3) and Monte Carlo sampling (step 4) to generate SCCE pK_as. This procedure is designed to mimic standard SCCE calculations, which places protons, optimized within the MCCE force field, to make the best hydrogen bonds assuming solution ionization states at pH 7.⁹⁸ The RMSD is 2.23 and 207 of the 305 pK_as (68%) have errors <1, whereas 15% have errors greater than 2 pH units.

The isosteric, QUICK runs are made using steps 2b, e, and h. There are no additional heavy atom rotamers, so the multiconformation routines add negligible low dielectric material to the protein boundary. These calculations include the protons found in the SCCE calculations but add additional hydroxyl protons, Asn, Gln termini and tautomeric neutral His conformers that remain in equilibrium with the protein as a function of pH. This increases the number of conformers by about two-fold over the SCCE calculations, with on average 2.5 conformers per residue. This type of conformational sampling has been suggested earlier to significantly improve the accuracy of pK_a calculations.^41,44 The QUICK runs show a much better RMSD of 1.13. Now 31% of the pK_as have errors <1, a negligible difference from the SCCE calculations. However, now only 8% have errors by greater than 2 pH units. The SCCE calculations are found to overstabilize the ionization state found at pH 7 where the hydrogen bond network is optimized. This generally pushes base pK_as up and acid pK_as down, in particular for residues with large interactions with the protein. For example, of 182 considered Asp, Glu, and C-termini, in the SCCE calculations 29 have calculated pK_as >2 pH units lower than the experimental values, with 19 pK_a calculated to be below 0. In the QUICK calculations, only three have errors greater than 2 pH units and only one calculated pK_a is below 0.

A set of ROTAMER calculations was made allowing heavy atoms to sample different positions using steps 2b–e and h in the rotamer building procedure. The number of conformers in these calculations increases by 13.5-fold from SCCE, with on average 16.7 conformers/residues. The additional heavy atom rotamers increase the amount of low dielectric material for each protein and as will be seen the boundary corrections become important (Fig. 1). With all MCCE2 corrections the RMSD decreases to 0.94. Now 78% of the residues have errors <1 pH unit and only 5% have errors greater than 2 pH units. There are 33 calculated pK_as with their errors reduced by over 1 pH unit compared with the QUICK calculations. For seven of them, the Monte Carlo selected position for the ionized conformer is more surface exposed than the input rotamer, reducing their desolvation penalty significantly (by >1.4 kcal/mol). Twenty of the selected conformers make significantly better interactions with the protein, whereas only five now make significantly less favorable interactions.

FULL calculations include steps 2a through h in the rotamer building process. In addition to rotamers generated around each rotatable bond, these calculations also optimize the starting structure to relax torsion and LJ clashes in the input structure given the Amber force field. It also allows hydroxyl protons to move out of torsion minima. The RMSD decreases to 0.90. There is a negligible difference in the number of residues where the error is already <1.5 pH units. However, now only 3% (8 of 305 residues) have errors greater than 2 pH units. In the FULL run, of the 57 residues where the reported pK_as are out of the bounds of the measurement (Supp. Info. Table S2), 56 calculated pK_as agree with the measured titration limit. Asp 27 in Turkey ovomucoid inhibitor has a calculated pK_a of 3.2, whereas the measured pK_a is below 2.2.

The optimization routines added moving from ROTAMER to FULL make quite small changes in the structure, but improve the pK_as of 40 residues by >0.5 pH units. This includes 17 residues with desolvation penalties <1.4 kcal/mol whereas the rest are more solvent exposed. Of the 40, 22 pK_as shift to stabilize the ionized form whereas the others find more stable neutral conformers. The stabilized ionized groups tend to have better pairwise interactions with the protein (15 of 22). For the 18 residues with more optimized neutral conformers, 8 improve their pairwise interactions with the protein by >0.7 kcal/mol, whereas the rest select conformers where both the solvation energy and protein interactions are slightly more favorable. In two cases, the optimized residue is shifted to a more buried position with better LJ interactions.

Analysis of Membrane Proteins

In the 305 residues used in the benchmark study only 80 have lost >2 kcal/mol of solvation energy. The transmembrane protein bacteriorhodopsin provides a group of deeply buried residues whose pK_as have been used to test computational methods.^37,99 An additional challenge for theory is that during the reaction large pK_a shifts are caused by small structural changes trapped in different crystal structure of intermediates. The pK_as of residues in bacteriorhodopsin trapped in the ground state (1C3W and 1C8R) and in the late M state (1C8S) were calculated within a membrane as described previously.¹¹ There are five buried ionizable residues whose pK_as are critical to the activity of this protein; the Shiff base, Asp 85 and 212 in a central proton pumping cluster and Glu 194 and 204 in the extracellular proton release cluster.

In MCCE calculations here, the retinal Schiff base and Asp 85 are fully coupled in the ground state. Between pH 5 and 11, RSB and Asp 85 are both 75% ionized. At low pH, Asp 85 becomes fully neutral with pK_a of 4 and at pH > 12, both RSB and Asp 85 become fully ionized. Asp 212 remains fully ionized. The pH values for changes in ionization are in good agreement with the experimental pK_as of 3 for Asp 85,¹⁰⁰ <1 for Asp 212¹⁰¹ and >12 for the Schiff base.^102,103 In the late M structure, the calculated RSB pK_a shifts down, with a bimodal pK_a at 6.0 and 8.5 and Asp 85 is fully neutral and Asp 212 ionized. Thus the proton from the RSB moves to Asp 85, consistent with experimental results for the M state.^101,104

In the extracellular proton release cluster, Glu 194 and 204 share a proton at neutral pH in the ground state, with 80% Glu 194 ionized and 20% Glu 204 ionized. The calculated cluster pK_a is 12 whereas the experimental value is 9.5.^105,106 Thus, the calculations overstabilize the binding of this proton. In the late M state calculations, Glu 194 is fully ionized and Glu 204 has bimodal pK_a of 5.3 and 8.1. The calculated pK_a agree with the measured value of 5.8¹⁰⁷ and the observed proton release in this intermediate.¹⁰⁸ Overall the calculations reproduce the measured pH and state dependence of site protonation, yielding results that are consistent with earlier MCCE calculations.¹¹

Comparison with Other Benchmark Studies

MCCE2 can be compared with the earlier published version.³⁴ The MCCE technique is a novel blend of CE and molecular mechanics force fields. The original versions used simple LJ parameters defined only by the element types. MCCE2 uses the standard Amber94 force field.⁸³ Amber has very small van der Waals repulsion for polar hydrogens, and this has proved to be important for MCCE to make good hydrogen bonds given the screening of the attractive electrostatic component by the continuum dielectric constant (data not shown). Earlier versions only added rotamers from the Dunbrack conformer library^109,110 without relaxation, few of which were acceptable. The current version provides far more extensive rotamer sampling and relaxation. The most serious problem with the MCCE technique is that the use of precalculated energy look-up tables means the protein contains too much low dielectric material when the electrostatic pairwise interactions are calculated. The earlier MCCE version used an ad hoc SOFT function to screen all interactions regardless of their position in the protein.³⁴ Without this the RMSD was 2.2 pH units, even worse than the FULL calculations without boundary corrections reported here (Table 2). The current boundary correction [eq. (6), Table 1] provides a more rational method to correct for the boundary artifact in MCCE. The implicit van der Waals interaction and entropy correction are also new in MCCE2.

In 2007 Stanton and Houk⁴⁹ selected 20 measured pK_as each for Asp, Glu, His, and Lys, to provide a benchmark dataset enriched with pK_as perturbed by >1 pH unit from the solution value. They compared the calculated values for eight different methods of pK_a calculation. This provides a good basis for comparing computational techniques. Two methods, MD/GB/TI³⁹ and PROPKA,⁵¹ were applied to all 80 pK_as and these are used for comparison here. Seven pK_as are treated separately in the analysis. These pK_as include two where the experimental pK_a is out of range of the measurements, three where the pK_a is coupled to acid dependent protein unfolding and two derived from activity measurements with bound substrate (Supp. Info. Table S3).

All 80 pK_as are calculated here using the same PDB structures reported by Stanton and Houk⁴⁹ (Supp. Info. Table S3). For the 73 vetted residues, the RMSD calculated by MCCE is 0.94, significantly better than the reported values of 1.24 with MD/GB/TI method and 1.40 with PROPKA. The slope of the benchmark line is 0.77 in MCCE, closer to the desired value of 1, which it is 0.64 and 0.62 for MD/GB/TI and PROPKA. A shallow slope indicates that the method moves the calculated pK_as closer to those found in solution. As most in situ pK_as are in fact close to those found in isolation, these methods move towards the correct answer by smoothing out interactions with the protein.³⁶ The MCCE R² of 0.53 is somewhat better than the 0.32 and 0.25 found for MD/GB/TI and PROPKA.

Including the pK_as of three Lys or His coupled to protein denaturation increases the MCCE RMSD to 1.46, with only modest increases in the values for MD/GB/TI (1.27) or PROPAK (1.45). The average error of these three residues is 5.5 in MCCE compared with 1.3 in MD/GB/TI and 2.3 in PROPKA. MCCE, limited by the need to fix the backbone, overstabilizes the neutral form, shifting the calculated pK_a down. The other programs overstablize the ionized state but by a smaller amount. In particular, in the MD based method,³⁹ the larger protein conformational and ionization changes can be coupled together, providing a more physically accurate picture of the process.

Corrections to the Energy Terms in MCCE2

The addition of explicit conformational degrees of freedom makes the pK_a calculations more accurate and provides additional information about changes in side chain position that may occur when groups in the protein change ionization state. MCCE2 also addresses several artifacts introduced by approximations used to reduce the cost of computation in the multiple conformation modeling.

Corrections to the Dielectric Boundary

As a surface protein side chain moves, the boundary between protein and water changes. The pairwise interactions between conformers should be calculated, dynamically within MC sampling, with the correct dielectric boundary for each microstate. In contrast, MCCE precalculates all pairwise interactions including all possible conformers in the protein (Fig. 1, Table 1).^34,45 The inflated boundary condition leads to the overestimate of electrostatic interactions, especially those on the protein surface (Fig. 2). Even creating a more accurate M×M matrix with M² DelPhi calculations for M total conformers, keeping only the two conformers of interest for two residues with an arbitrary selection of conformers of all other residues is not possible for the 2000–8000 conformers sampled for the proteins described here. In addition, MCCE only considers self-energy terms (torsion and reaction field) and pairwise interactions. The movement of a third residue can influence electrostatic interactions between other pairs of residues. Treating these higher order terms, while maintaining a technique where interaction energies are precalculated could require >N³ calculations. The limitation of MCCE to calculations with fixed backbone coordinates is also rooted in the decision to only treat self and pairwise interactions with pre-calculated energy look-up tables (see ref. 45 for a more complete discussion). A boundary correction is added to estimate the interaction of the correct single conformation boundary condition while keeping the calculation cost scaling between N and N² (Fig. 2).

The calculated RMSD shows the necessity for the boundary correction clearly (Table 2). The isosteric, QUICK run shows a significant improvement over the SCCE calculations even without including boundary corrections (Table 2). However, without the correction the addition of heavy atom rotamers does more harm than good. The RMSD increases to 1.42 and the number of residues with errors over 2 pK_a units is now even larger than in the SCCE calculations. The correction is especially important for residues near the surface that represent the majority of the sites studied here. The correction has only a small effect on larger or membrane embedded proteins.^11,33 Early versions of MCCE added an ad hoc SOFT function, weakening all strong interactions to achieve reasonable pK_as in smaller proteins.³⁴

As described in the Methods section, the boundary correction places a heavy reliance on the native conformer, since it is always one member of the pair selected for accurate pairwise calculation using eq. (6). The native rotamers are more likely to be selected in Monte Carlo sampling, minimizing the problems with this choice. Cases are found where a residue pK_a shifts significantly between a QUICK and FULL run, with significant occupancy of new rotamers. Here, additional improvement can be obtained for a small number of residues by substituting the selected rotamer into the input structure. This then becomes the privileged “native” rotamer. This procedure was carried out for all proteins and there were 4 pK_as changed by >0.5 pH unit (see Supp. Info. Table S3). The largest change is in Barnase (1A2P and 1B2X) where Asp 75 is buried by Arg 83 and 87. In MCCE calculations, both Args move to a more solvent exposed positions. Using the MCCE selected conformers for these Arg to define the default, input residue boundary conditions, the desolvation penalty for Asp 75 is reduced from 11 to 7 kcal/mol, meanwhile, the total interaction between Asp 75 and the two Args is 10 kcal/mol smaller. The Asp pK_a in a QUICK run is −2.5; in the FULL run the pK_a with the original Arg providing the default protein boundary the pK_a is –1.2; whereas using the Arg rotamers selected from a standard FULL run as the input positions moves the pK_a to 2.6. The experimental value is 3.

Nonelectrostatic Interactions with Implicit Solvent

Interactions between a side chain and the rest of the protein include the pairwise electrostatic energies, calculated by DelPhi and nonelectrostatic energies calculated with the AMBER LJ force field. Interactions with the implicit solvent include the favorable electrostatic, reaction field and add a new nonelectrostatic, implicit van der Waals term. The implicit van der Waals energy, based on earlier studies of Levy et al.⁷⁷ adds a favorable interaction of 60 cal/A² surface exposed for each conformer.

Adding the implicit van der Waals term does not change many pK_as significantly, leading to a small improvement of the RMSD from 0.93 to 0.90. Overall, 24 pK_as are improved by over 0.5 pH unit, whereas 15 increase their error by this much. However, the number of residues with errors greater than 2 pH units is halved. For 19 of 24 of the residues with better pK_as, the correction moves the outcome closer to the solution pK_a. Thus, the added energy stabilizes exposed conformers, especially when the competing, more buried conformer has very favorable explicit, LJ interactions with the protein. Although only 3 Lys show improved pK_as, now favored movements of large resides such as Lys and Arg improves the results for other sites. For example, in Chymotrypsin Inhibitor 2 (2CI2), the crystal structure conformation of Glu 26 and Lys 21 forms a salt bridge on the surface, which is always selected in Monte Carlo sampling when both residues are ionized. Without the implicit van der Waals energy, Lys 21 stays in the same conformation below the pK_a of Glu 26. Thus, alone the improved solvation energy for the exposed conformer is insufficient to compensate for the loss of explicit LJ interactions with the protein. Adding an implicit van der Waals attraction between the Lys and the solvent allows acceptance of a more exposed conformer when the Glu is protonated. This stabilizes the neutral Glu raising its pK_a from 0.3 to 2.6. The experimental value is 3.3. The freedom of movement of Arg 83 and 87 in Barnase described above in the section on the boundary correction is also dependent on the implicit van der Waals term.

Entropy Correction

MCCE pK_a calculations evaluate the relative probabilities of selecting a protonated or deprotonated conformer of a residue. MCCE starts with different numbers of neutral and ionized conformers for each residue. Each heavy atom rotamer generates 1 ionized and 2–5 neutral conformers (Supp. Info. Table S1). If they all had the same energy, this would lead to an error favoring the neutral form of 0.3 to 0.6 pH units. Each step of rotamer making, optimization and pruning modifies this imbalance. Following FULL rotamer making the average ionized: neutral conformer ratio is 1:10 for Asp and Glu, and 1:2 for Lys. The larger number of neutral conformers can artificially stabilize the neutral state. However, only low energy conformers that are accepted in Monte Carlo sampling contribute. The energy difference between neutral conformers is smaller than between ionized forms so more are accessible increasing the error. The entropy correction for each residue is evaluated within Monte Carlo sampling using eq. (8).

The entropy correction reduces the RMSD from 0.95 to 0.90 and the percentage of errors over 2 pH units from 4.9 to 2.6%. The entropy correction shifts all residues of the same type in the same direction favoring the state with fewer protons. The average errors of all residue types change by about 0.2–0.25 pH units, generally improving the Asp, Glu, His, and Tyr pK_as, while increasing the error for Lys slightly. Of the 41 pK_as that improve by >0.5 pH unit, 30 are Asp and Glu and the rest are mostly Tyr and His. Only 1 Lys pK_a improves here. There are 30 residues where the match with experiment worsen, 13 are Lys whereas the rest are evenly distributed between Asp, Glu and His. The implicit van der Waals correction actually decreases the impact of the entropy correction because now the surface exposed ionized conformers are more populated rebalancing the number of occupied neutral and ionized conformers. In addition, the degree of pruning affects the importance of this correction (step 2h). When more energetically similar neutral conformers are kept in the protein model the entropy correction becomes more significant.

The Importance of the Continuum Dielectric Constant Assigned to the Protein

The dielectric constant of a material describes implicitly the response of the material to changes in charge. Thus, it should affect the thermodynamics of protonation reactions measured by a pK_a. The dielectric constant assigned to the protein usually ranges from 4 to 20 in CE studies,^34–36 whereas 1 is used in Molecular Dynamics simulations. The higher the dielectric constant needed to get a good match with experimental values, the greater the uncertainty about the protein conformational changes hidden within the calculation.^14,15,36 MCCE methodology uses a mixture of explicit and implicit dielectric response, including explicit side chain conformational changes embedded in a protein with a dielectric constant of 4 and a solvent with a dielectric constant of 80. The degrees of freedom that remain in the implicit protein response include changes in the backbone conformation, in all atomic bond lengths and angles and the overall electronic polarization.

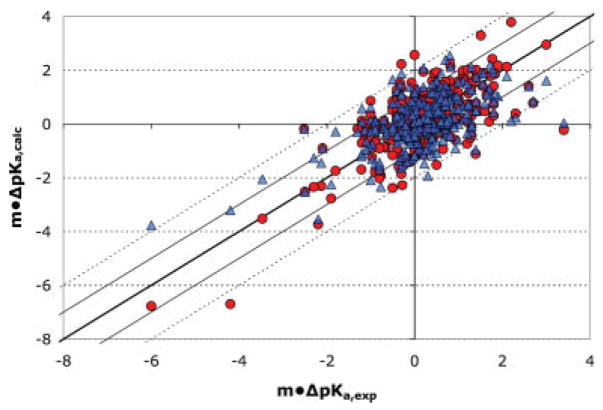
Calculations were compared with ε_p of 4 and 8. The solution reaction field energy is recalculated giving residues the same interior dielectric constant as the protein. In the benchmark data-set, 89.5% of the residues have an in situ experimental pK_a within <1.5 pH unit from their value in solution. Using the “null hypothesis”^35,36 where all residues are simply given their solution pK_a, the RMSD would be 0.97. The use of ε_p of 8 diminishes both the electrostatic interactions with the protein as well as the loss of reaction field energy, making all pK_as closer to their solution values, thus often improves the RMSD of pK_a calculations.^35,36 However, within MCCE the higher dielectric constant improves the RMSD little indicating the explicit conformational changes are capturing the local protein relaxation around charge changes (Fig. 2a). In addition, when the shift of the pK_as calculated at ε_p 4 and 8 are compared with experiments the slope with an ε_p 8 is 0.6 whereas it is 0.7 with an ε_p of 4. The steeper slope indicates the more shifted residues are calculated more accurately, whereas the shifts from solution pK_as are systematically underestimated with an ε_p of 8 (Fig. 4).

Figure 4.

Shifts in calculated experimental pK_as versus those calculated with a protein dielectric constant of 4 (●) or 8 (Δ). The dashed and dotted lines show errors of ±1 and ±2 pH units.

Improving Calculated pKas by Averaging

As the number of degrees of freedom MCCE explores increases, it can be harder to achieve convergence of the results. Convergence of both the initial selection of conformers and the final Monte Carlo sampling steps can be accessed. Because of the random procedure in rotamer packing, the sequence of local optimization, and rotamer clustering, the output structure will be different for each run with a different starting seed. Five independent MCCE calculations were carried out on the 24 structures with fewer than 170 residues providing 230 measured pK_as (Table 2, Part C). The average standard deviation of the 5 pK_as for the same residue is 0.2. Averaging multiple independent MCCE calculations improves the RMSD for this smaller dataset from 0.88 to 0.86. This is mostly due to better calculation of pK_as that started with modest errors. The group of residues with the largest standard deviation in multiple runs includes many of the residues with the largest errors, providing one way to identify problematic sites.

The convergence of the Monte Carlo sampling procedure was tested by comparing pK_as derived from a single multiconformation structure. In general, despite the large number of conformers, the sampled calculated pK_as show only small shifts. The maximum standard deviation for any pK_a is 0.06 and the average standard deviation is 0.01. The only significant instability is for residues with pK_as that are coupled together.¹⁰ As described previously^98,111 allowing closely coupled groups to change state in the same Monte Carlo sampling step allows the system to come to equilibrium more easily. The current version of MCCE can change the conformer of as many as three nearby residues in a single step. Coupled residues are identified by large n values and χ² when the analysis allows only a single pK_a eq. (9), which are improved by allowing two pK_a fit eq. (10). There are 12 residues from 6 proteins where a bimodal analysis is used. The analysis of proteins with residues with coupled ionization is improved by extending the Monte Carlo sampling from the default 5000 to 20,000×M (where M is the number of conformers). Thus, despite the large number of possible microstates available for sampling the Monte Carlo simulations are generally well converged.

The use of Multiple Structures

MCCE relies on a single backbone structure and each pK_a described up to this point has been calculated with a single X-ray structure. Earlier benchmark calculations have shown that side chain conformational sampling in MCCE reduces the dependence on the input structure.³⁴ However, when multiple experimental structural models are available the calculation can explore more backbone configurations.

There are 22 proteins with more than one available X-ray derived structure with 2.6 ± 1.9 structures/protein (Supp. Info. Table S2). The FULL calculations with only one structure for each protein has an RMSD of 0.90. The averaged pK_as of multiple structures reduces the RMSD to 0.84. Residues with errors >1.5 pH unit do not show much improvement with multiple X-ray structures. However, there are 3% more residues with errors <0.5 pH unit.

Twenty-four proteins with NMR structures were studied. The number of models for each ranges from 3 to 60. The RMSD for the individual pK_as from all NMR models is 1.40, compared with 0.90 using unique X-ray structures (Fig. 3, Table 2, Parts A and C). Averaging the pK_as has improves the accuracy of the calculation of NMR structures, reducing the RMSD to 1.23. Using individual NMR structures, 10.4% of all pK_as have errors over 2 pH units. On averaging, this number is reduced to 6.1%. Thus, even after averaging, the calculations starting from X-ray crystal structures provide significantly better pK_a values. This conclusion is different from that found in the earlier version of MCCE where the larger number of structures available in NMR dataset improved the pK_a values.³⁴

Distribution of Errors

A pK_a calculation program such as MCCE can be used to understand previously measured pK_as or E_ms within the context of the protein structure.^11,33,70,112 However, the more challenging job is to predict unknown pK_as in wild type or mutated structures. Calculating with one structure, only about 10% of the residues have errors greater than 1.5 pH units (30 of 305). To use MCCE in pK_a predication, it is useful to determine the characteristics of these residues.

Systematic Error

The errors for each residue type are not uniformly distributed. The average error is small for His and Glu, and there are too few NTR and CTR with measured pK_as to consider. However, Asp, Tyr, and Lys have pK_as that are ≈0.3 to 0.4 pH units too high stabilizing the protonated form (Table 2, Part B). The ionized Lys and neutral Tyr are overstabilized, which are the forms that are most likely to be found in the experimental protein structure. Thus, the protein may not be fully equilibrated around the neutral Lys or ionized Tyr in the MCCE calculations.

However, the calculations stabilize the neutral Asp, which is unlikely to be the form found in the crystal structure. The systematic errors for Asp are larger in the FULL then the isosteric QUICK calculations, which uses only the experimental side chain rotamer. There are several possible sources of error. The longer Glu finds more accessible surface exposed ionized conformers with the addition of the implicit van der Waals term, reducing the imbalance between occupied ionized and neutral conformers. The shorter Asp has less opportunity to move to the surface. This tends to reduce the acceptance of ionized conformers in the Monte Carlo sampling. Thus, the error could result from insufficient entropy correction. In addition, the short Asp often forms a hydrogen bond with its own backbone amide. This contact is quite sensitive to the balance of electrostatic and non-electrostatic force fields, so is not always maintained in the final selected structure. The ability to break this hydrogen bond in the FULL calculation also destabilizes the ionized residue.

Comparison of Surface and Buried Residues

Only 80 of 305 residues have a desolvation energy over 1.5 pH unit (2.04 kcal/mol). The RMSD for residues with a loss of reaction field energy >2.0 kcal/mol is 1.20 and for exposed residues is 0.77 (Table 2, Part B). MCCE achieves a reasonable level of accuracy for buried residues; with only 6.3% having errors greater than 2 pH units. The residues are divided into four groups noting their interactions with the protein and their loss of reaction field energy. There are no systematic errors in the exposed residues. However, it is noteworthy that the residues with large errors are enriched with residues that have a large desolvation penalty but little interaction with the protein. In general these calculations overstabilize the neutral form. Here, MCCE may overestimate the desolvation energy of residues near the surface or could miss a conformer which is more solvent exposed. These residues may be coupled to protein denaturation, as residues in this group generally have significant desolvation energies with small favorable interactions with the rest of the protein.

Comparison of Residues in Different Secondary Structures

The errors were assessed for residues in different secondary structures as defined by DSSP (Table 2, Part B). It might be expected that because MCCE maintains a rigid backbone the errors could correlate with secondary structure, favoring more rigid elements that would be less likely to change when residues change ionization state. Thus, the residues in a-helical structures have the smallest errors. Surprisingly resides in β-stands overpopulate the group of residues with large errors. However, this is likely to be due to 41% of the β-strand residues in the benchmark being classified as buried, whereas only 10% of the helical residues are. Loop structures are often the most uncertain elements in a protein structure. However, the amino acids in loop structures are not found to have larger errors in their calculated pK_as.

Conclusion

MCCE blends self and pairwise energies from Poisson-Boltzmann Continuum Electrostatics (CE). the Amber molecular mechanics force field and implicit van der Waals interactions with implicit solvent to calculate the energies of protein side chain position and ionization state. This, physics-based approach to pK_a calculations generates a reasonable match to experiment. Using only a single structure for each protein 75% of the pK_as have an error <1 pH unit with an overall RMSD of 0.90. Addition of isosteric conformers, that allow the protein to remake the hydrogen bond networks as the ionization states of surrounding residues change, significantly improves the calculations compared with standard Single Conformation CE calculations. However, with the proper corrections, addition of heavy atom rotamer flexibility provides increasing accuracy. The observation that the calculations are not improved when the protein dielectric constant is increased shows that the blend of energies used to calculate MCCE microstate energies gives a sufficiently accurate assessment of the relative energy of conformers with different position and/or charge. However, MCCE maintains a rigid backbone so it fails when the ionization changes are coupled to significant conformational changes such as those that accompany pH dependent denaturation.