Spectrally resolved bioluminescence tomography using the reciprocity approach

Abstract

Spectrally resolved bioluminescence optical tomography is an approach to recover images of, for example, Luciferase activity within a volume using multiwavelength emission data from internal bioluminescence sources. The underlying problem of uniqueness associated with nonspectrally resolved intensity-based bioluminescence tomography is demonstrated and it is shown that using a non-negative constraint inverse algorithm, an accurate solution for the source distribution can be calculated from the measured data. Reconstructed images of bioluminescence are presented using both simulated complex and heterogeneous small animal models as well as real multiwavelength data from a tissue-simulating phantom. The location of the internal bioluminescence source using experimental data is obtained with 0.5 mm accuracy and it is shown that small (2.5 mm diameter) sources of up to 12.5 mm deep, within a complex mouse model, can be resolved accurately using a single view data collection strategy. Finally, using the reciprocity approach for image reconstruction, a dramatic improvement in computational time is shown without loss to image accuracy with both experimental and simulated data, potentially reducing computing time from 402 to 3.75 h.

INTRODUCTION

Theoretical and instrumentation developments have led to the widespread implementation of bioluminescence imaging in cancer research, enabling a significant advance in the ability of investigators to track tumour cell growth and death in vivo.¹ Tumor metastases studies have been completed with luciferase imaging, showing tumor cell invasion, which otherwise could not be observed.² As these advanced imaging and prognostic measuring tools progress, it is important to seek improvements in imaging methodology, image reconstruction, and computational speed, in order to accurately visualize and quantify the bioluminescence signals in vivo in a linear and unbiased manner. These improvements allow gains in fundamental insight about tumor growth, regression, immune response, and the overall response to new therapies. Specifically it would be desirable to develop fast and accurate three-dimensional (3D) image recovery methods which provide anatomically accurate and spatially invariant volumetric images of bioluminescence activity in vivo. This study provides analysis of a new algorithm for bioluminescence tomography with robust accuracy and improved speed of computation.

Recent interest in modeling and reconstruction algorithms for bioluminescence tomography (BLT) has increased^{3, 4, 5} and led to the general consensus that nonspectrally resolved intensity-based BLT measurements result in a nonunique solution.^{6, 7} This specifically implies that using measurements of bioluminescence activity at a single wavelength can lead to multiple solutions of internal bioluminescence source distribution. However, the light emitted from bioluminescence sources, such as firefly Luciferase, is widely distributed over the band of wavelengths from 500 to 650 nm and above. When not attenuated, it produces a peak emission near 560 nm, but when detected from within an animal appears to have an “effective” peak emission closer to 600 nm with measurable light as much as 50 nm above and below this peak.¹ Using spectrally resolved detection schemes it is possible to measure the emission at the surface of the tissue in discrete steps of 10 nm ranging from 550 to 650 nm, although for deeper sources, strong optical absorption of tissue at the shorter wavelengths might preclude accurate measurements with adequate signal to noise.

To date, all reported reconstruction algorithms have either used a priori information to constrain the solution and keep the computation time low,^{5, 6} or analytical solutions which limit the problem to a homogenous tissue volume with regular shapes.^{4, 8} More specifically it has been shown that using a model based on homogeneous analytical solutions of photon propagation, the accuracy of the image reconstruction of bioluminescence sources decreases dramatically when the domain being imaged is heterogeneous.⁸ However, there have been theoretical proposals and experimental setups that aim to reconstruct not only the distribution of bioluminescence source, but also the underlying tissue absorption and scatter simultaneously.^{9, 10, 11} Additionally, it has been shown that using a single-perspective view, it is possible to reconstruct images of internal bioluminescence distribution with depth accuracy of less than 1 mm and a maximum of 20% error in reconstructed intensity.⁴ Methods have also been developed that incorporate multilevel adaptive finite element algorithms, whereby the discretized volume mesh is adaptively refined to improve both the robust performance and efficiency of the reconstruction algorithms and these have been shown to improve localization accuracy.¹²

There is a need to derive and construct a robust method that can accurately model light propagation in heterogeneous and complex tissue, using for example in this work, the finite element method (FEM). Additionally, reconstruction algorithms will need to be further advanced to overcome the need for spatial a priori information, by the use of spectral data, while at the same time reducing the computation time to provide accurate reconstructed images in reasonable time limit. This article demonstrates the development of a 3D algorithm used for multiwavelength 3D BLT image reconstruction using experimental and simulated data. The reciprocity approach, similar to that used in diffuse optical tomography¹³ (DOT) and fluorescence DOT,¹⁴ is presented and applied to the BLT source distribution problem. It is shown that accurate images can be obtained using a fast linear reconstruction algorithm without the use of a priori information.

THEORY

The forward model

Assuming that the photon propagation through tissue is dominated by scatter, the diffusion approximation (DA) to the radiative transport equation is widely accepted as being accurate to model transport of light through tissue.¹³ Assuming a continuous wave system, the DA is given as

$$-\nabla \cdot \kappa \left(r\right)\nabla \Phi \left(r\right)+{\mu }_a\left(r\right)\Phi \left(r\right)=B\left(r\right),$$ (1)

where B(r) is a bioluminescence source at location r, Φ(r) is the photon fluence rate, $\kappa =1∕3({\mu }_a+{\mu }_s^{\prime })$ is the diffusion coefficient, and μ_a and ${\mu }_s^{\prime }$ are absorption and reduced scattering (or transport scattering) coefficients, respectively.

The air-tissue boundary is an important aspect of accurate modeling of light propagation and is represented in this case by an index-mismatched type III condition, in which the fluence at the external boundary of the tissue exits but does not return.^{15, 16} The flux leaving the external boundary is equal to the fluence rate at the boundary weighted by a factor that accounts for the internal reflection of light back into the tissue

$$\Phi \left(\xi \right)+2A\widehat{\mathbf{n}}\cdot \kappa \left(\xi \right)\nabla \Phi \left(\xi \right)=0,$$ (2)

where ξ is a point on the external boundary and A depends upon the relative refractive index mismatch between the tissue domain and air derived from Fresnel’s law.

Linearity

The solution to Eq. 1 is linear with respect to its right-hand side, B(r). Therefore given multiple source distributions one can either calculate the fluence due to each source individually and then sum the solution, or calculate the fluence due to all source distributions simultaneously, as shown in Fig. 1. The fluence rate data Φ(r) can therefore be represented by an operator, which is linear in terms of the bioluminescence source, B(r). Thus, taking advantage of the linearity of the model, a set of independent basis solutions for the source can be created

$$B=\sum _{i=1}^N{a}_i{b}_i,$$ (3)

where the coefficients a_i are the weight functions for multiple unit sources b_i at each node i in the model containing a total number of nodes N. This structure can be represented in matrix form as B=ab.

Figure 1.

The top row shows three different bioluminescence sources plus their combination, while the bottom row shows the calculated fluence due to each source distribution.

The inverse model

Unknown bioluminescence distribution

Assuming that the underlying optical properties at appropriate wavelengths are known, the goal of the inverse problem is recovery of the unknown bioluminescence source at each point within the volume using measurements of bioluminescence light fluence from the tissue surface. This inversion can be achieved using a modified Levenberg–Tikhonov minimization

$$\Omega ={}_B{}^{\min }\Vert y-F\left[B\left(r\right)\right]\Vert ,$$ (4)

where y is the measured bioluminescence boundary data, and F[B(r)] is the calculated boundary data based on Eq. 1. Substituting the matrix expression of Eq. 3 into Eq. 4 and solving for the weight function coefficients, a, in a least squares manner, results in a single step linear expression

$$a=W^T{(W{W}^T+\alpha I)}^{-1}y,$$ (5)

where W is a sensitivity matrix containing the solution of Eq. 1 for all possible source positions N and y is the measured boundary flux. Here, α is a regularization parameter and I is the identity matrix. Although the Hessian matrix, WW^T, is invertible, the use of λ becomes necessary in the presence of noise in the data.

Unknown bioluminescence and optical property distribution

In the common case, where the underlying optical properties of the volume being imaged are unknown, Eq. 4 can be modified to

$$\Omega ={}_{\kappa ,{\mu }_a,B}{}^{\min }\Vert y-F[\kappa \left(r\right),{\mu }_a\left(r\right),B\left(r\right)]\Vert ,$$ (6)

where the solution must be optimized with respect to the optical properties as well as the unknown bioluminescence source distribution. This can be achieved using a two-step approach, whereby the unknown distribution of the optical properties can be calculated using a nonlinear spectral image reconstruction algorithm, as demonstrated for Fluorescence Imaging.¹⁷ Using this approach, once the problem has been optimized for the unknown optical properties at each wavelength, Eq. 5 is then used, as a single step optimization to solve for the unknown bioluminescence sources.

Uniqueness

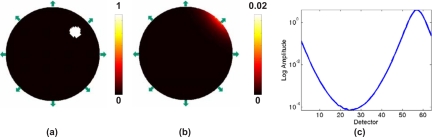
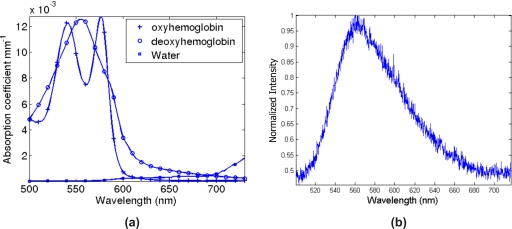
It has been shown theoretically and is generally accepted that the use of single wavelength bioluminescence data for source reconstruction is a nonunique problem.^{3, 7} Consider the example shown in Fig. 2, which is a two-dimensional (2D) circular model with background optical properties of μ_a=0.01 mm⁻¹ and ${\mu }_s^{\prime }=1.0{\mathrm{mm}}^{-1}$. Two different bioluminescence source distributions in this model produce identical boundary data for 64 equally spaced detectors on the external boundary, Fig. 2c. From this example, it is evident that using bioluminescence measurements at a single wavelength will lead to a nonunique problem and therefore multiple possible solutions of the bioluminescence source distribution. However, it has been shown that the use of multiwavelength data, measured from the same domain containing the same bioluminescence distribution, over a range of usable wavelengths can overcome this nonuniqueness issue,³ since the measured optical signal is a function of the underlying tissue spectral signature (due to chromophore and scattering parameters) as well as the spectral signature of the bioluminescence source emission, Fig. 3.

Figure 2.

(a) and (b) represent the circular 2D model with 64 detectors placed around the periphery (arrows with only 8 shown) with two different bioluminescence distributions, resulting in identical calculated boundary data as plotted in (c). The two lines of data are indistinguishable.

Figure 3.

The spectral response of (a), tissue absorption as a function of tissue chromophores and, (b), the measured Luciferase (bioluminescence) emission in a dilute sample.

Instead of using data from a single wavelength, multiwavelength BLT combines data sets over a range of usable wavelengths such that Eq. 5 becomes

$$a={\tilde{W}}^T{(\tilde{W}{\tilde{W}}^T+\alpha I)}^{-1}\tilde{y},$$ (7)

where $\tilde{W}=[W_{\lambda 1};W_{\lambda 2};W_{\lambda 3};\cdots ;W_{\lambda n}]$ is a matrix composed of cascaded weight matrices of all n wavelengths and $\tilde{y}=[y_{\lambda 1};y_{\lambda 2};y_{\lambda 3};\cdots ;y_{\lambda n}]$ contains the corresponding measured boundary data for each wavelength. The solution a, is then a vector corresponding to the number of unknowns (N) that define the bioluminescence source distribution.

The sensitivity matrix

The sensitivity matrices, W, in Eqs. 5, 7 are matrices that relate the change in measured boundary data, due to changes in bioluminescence source activity at each point within the domain

$$W_{j,i}=\left[\begin{array}{ccccc}{d}_{1,1}& d_{1,2}& d_{1,3}& \cdots & d_{1,i}\\ d_{2,1}& \ddots & & & \\ d_{3,1}& & \ddots & & \\ ⋮& & & \ddots & \\ d_{j,1}& d_{j,2}& d_{j,3}& \cdots & d_{j,i}\end{array}\right],$$ (8)

where W_j,i is the sensitivity at detector j due to a bioluminescence source at node i. Each element essentially is the detector reading d_j,i if node i alone was the only bioluminescence source within the domain.

Direct (perturbation) approach

The sensitivity matrix can be calculated using a direct approach, whereby the source intensity at each node of the model is perturbed by a small amount and the resulting boundary data are recorded. This process needs to be repeated for each node, at each wavelength to provide the full set of weight matrices required for image reconstruction as outlined above. The pseudo algorithm for the calculation of the weight matrices using this method can be stated as:

Repeat, for each wavelength λ

Repeat, for each nodeiwithin the model, wherei=1:N

Set the bioluminescence source,Bi=1

Solve Eq. 1 subject to boundary condition in Eq. 2 to obtain Φ(r)

Extract detector readingdjfor each detectorj

SetWji(λ)=dj.

Using this method, assuming a 2D model with 2000 nodes, 64 boundary measurements at 6 wavelengths, would equate to 12 000 (2000 nodes×6 wavelengths) forward model simulations.

Reciprocity approach

As derived and shown by Arridge et al.,¹⁸ the reciprocity principle can be stated as:

The measurement of flux at detector j that is due to a source at node i is equal to the measurement of the photon density at node i that is attributed to a source at detector j, provided that the source is created by the application of appropriate adjoint operator P

$$P_{ij}=-\kappa \widehat{n}\left({\zeta }_i\right)\cdot \nabla {\Phi }_i,$$ (9)

if boundary node ξ_j belongs to an element containing nodes on the external boundary, otherwise P_ij=0.

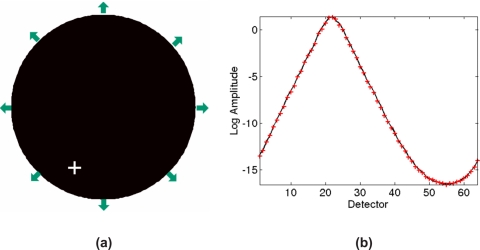
Consider the model shown in Fig. 4 which is a 2D heterogeneous model with varying optical properties. Using the basic principles of reciprocity, it can easily be shown that the detector reading at S2 [Fig. 4b] due to an external source at S1 is equal to a detector reading at S1 [Fig. 4c] when S2 is the source. The same principle can be extended to the bioluminescence problem as demonstrated in Fig. 5. In this case, a single bioluminescence source is modeled in the location as shown by the white cross in Fig. 5a and 64 boundary measurements are calculated, Fig. 5b. Additionally, using the reciprocity theorem, each detector is then modeled as a bioluminescence source and the corresponding photon density is calculated at the location of the original bioluminescence source and plotted. As evident, the calculated data are identical showing the validity of the reciprocity theorem, in this case, for a nonuniform model.

Figure 4.

Circular 2D model with (a) heterogeneous optical properties (μ_a shown in the color bar) with the corresponding internal fluence calculated for (b) source S1, and (c) source S2 [color bars show logarithm of the fluence in (b) and (c)].

Figure 5.

(a) Circular 2D model with the same optical properties as shown in Fig. 4, with 64 detectors placed around the periphery (arrows, only 8 shown) and one bioluminescence source (white cross), (b) fluence rate calculated at the 64 detectors due to the bioluminescence source (black solid line) as well as the fluence rate at the source location (white cross) when each detector on the periphery acts as a source (red cross).

Using the reciprocity approach, the weight matrices can be calculated for all nodes simultaneously, for each detector position, at each required wavelength. The pseudoalgorithm for the calculation of the weight matrices using this method can be stated as:

Repeat, for each wavelength λ

Repeat, for each detectorj

Set the “adjoint” bioluminescence source at the detector nodes=1

Solve Eq. 1 subject to boundary condition in Eq. 2 to obtain Φ(r)

SetWji(λ)=Φ(i).

Using this method, assuming a 2D model with 2000 nodes, 64 boundary measurements at 6 wavelengths, would equate to 384 (64 detectors×6 wavelengths) forward model simulations.

Non-negativity

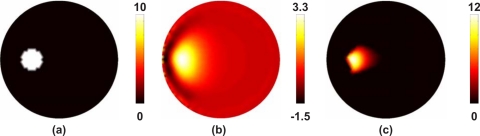
Image reconstruction in bioluminescence tomography using spectral data, as defined by Eq. 7, is a nonconstrained least squares solution to obtain the bioluminescence source distribution within a volume of interest. However, the nonconstrained least squares method does not ensure a unique solution to eliminate the reconstruction of negative sources within the medium. Consider, for example, the case presented in Fig. 6a, where a 2D model of soft tissue containing 20 μmol of blood at 75% oxygen saturation with 60% water fraction and scattering amplitude and power of 1 contains a 15 mm diameter bioluminescence source distribution. Boundary data using 64 equally distributed detectors at the external boundary were simulated using Eq. 1 for six wavelengths between 600 and 650 nm with 10 nm separation. Assuming correct knowledge of the background optical properties, images of bioluminescence were reconstructed using Eq. 7 without any constraints on the solution using a regularization factor of α=10⁻⁵×maximum of diagonal of the Hessian matrix (WW^T), Fig. 6b. As is evident, although the reconstructed images of the bioluminescence distribution appear qualitatively accurate, the distribution of the source strength is weak and contains negative solutions. Given that negative sources cannot physically exist, there is a need to apply non-negativity constraints to the least squares solution in Eq. 7.

Figure 6.

(a) Circular 2D model with spectral properties of 20 μmol blood content at 75% oxygen saturation of 60% water saturation, scattering amplitude and power of 1, and bioluminescence source distribution as shown. In (b) the reconstructed bioluminescence source are shown using 64 boundary measurements at 6 wavelengths without non-negativity constraints, and shown again produced with non-negativity constraints (c).

An iterative algorithm using the non-negativity least squares (NNLS) method as described by Lawson and Hanson¹⁹ has been implemented such that Eq. 7 now become

$$a={\tilde{W}}^T{(\tilde{W}{\tilde{W}}^T+\lambda I)}^{-1}\tilde{y},\text{subject}\text{to}\text{a}⩾0.$$ (10)

This algorithm, simply aims to minimize $\Vert \tilde{y}-a\tilde{W}\Vert$ subject to a⩾0. To demonstrate the effectiveness of the NNLS method, the same data used for image reconstruction shown in Fig. 6b was used with Eq. 10 to produce the image shown in Fig. 6c. Using the NNLS method, it is evident that the reconstructed solution is both quantitatively and qualitatively more accurate, as compared to the nonconstrained method, and is therefore essential for accurate image reconstruction in bioluminescence tomography.

PHANTOM STUDIES

A set of experimental data was used to demonstrate and validate the modeling and image reconstruction algorithms outlined above. Measurements were recorded for a single bioluminescence source placed within an otherwise uniform cylindrical phantom of 50.8 mm diameter and 50 mm height. The phantom was filled with a solution of 0.2% Intralipid and 0.2% oxygenated blood. The bioluminescent source was a 50:50 mixture of 165 microMolar ATP solution with Luciferase reagent solution solubolized in 1 ml distilled water (CLS II Kit, Roche Diagnostics, Inc.). The solution was held in a plastic cylinder of diameter 5 mm, placed 7 mm inside the edge of the phantom at the 3 o’clock position. Sixteen equally spaced measurements around the periphery were collected sequentially using a 1 mm silica fiber bundle leading to a single line of 200 μm fibers entering a spectrometer (Acton SpectraPro 2300i spectrometer with 300 l∕mm grating blazed at 750 nm wavelength) coupled to a cooled change coupled device (CCD) (Princeton Instruments Spec-10 XTE CCD). Integration time was 15 min per sample and a fresh sample was used for each detector location to avoid the effect of source decay. The measured spectrum of the bioluminescence source at each measurement point was then normalized using an un-attenuated measured emission spectrum from a dilute sample, Fig. 3b.

In order to image and calculate the spectral optical properties of the phantom, multiwavelength measurements at 661, 761, 785, 808, 826, and 849 nm were taken using a multiwavelength frequency domain instrumentation system²⁰ which collects amplitude and phase measurements of near-infrared light. Data were collected using 16 equally spaced fibers around the midpoint of the cylindrical phantom, giving rise to 480 (240 amplitude and 240 phase) measurements at each wavelength. Images of chromophore concentration (oxy and deoxy-hemoglobin, water content) and scattering properties (scatter amplitude and power) were reconstructed, Table 1, using a spectrally constrained reconstruction algorithm which calculates all parameters, simultaneously, using data at all wavelengths.²¹

Table 1.

Chromophore and scattering properties measured and calculated for the blood phantom used in experimental study, using spectral measurements between 661 and 849 nm.

Total hemoglobin	Oxygen saturation	Water content	Scatter amplitude	Scatter power
4.8 (μM)	96%	83%	0.154	1.89

An image of the bioluminescence source distribution was calculated using the methods outlined above. Specifically the measured and imaged concentration of chromophore and scattering properties were used to obtain the wavelength specific absorption and reduced scattering properties at 600, 610, 620, 630, and 640 nm. Using these parameters as background optical properties, an image of bioluminescence source distribution was calculated using Eq. 10, were the weight matrix for each wavelength is calculated using the reciprocity approach. The mesh used for image reconstruction was a cylindrical model of 50.8 mm diameter, 50 mm height consisting of 27 999 nodes corresponding to 145 835 linear tetrahedral elements, Fig. 7a. Although the Hessian matrix $\tilde{W}{\tilde{W}}^T$ in Eq. 10 is well conditioned and invertible, the use of α became necessary in the presence of noise in the data. In this work, α=10⁻⁵×maximum of the diagonal of the Hessian.

Figure 7.

(a) 3D cylindrical mesh used for image reconstruction using experimental data. In (b) the axial and (c) the coronal cross sections through the reconstructed bioluminescence source image.

SIMULATION STUDIES

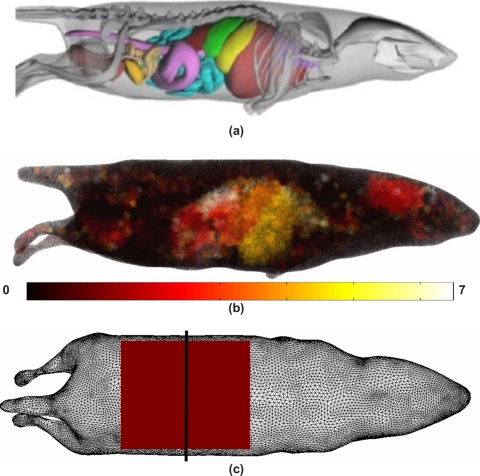
A 3D model of the MOBY mouse,²² Fig. 8a, was used to further investigate the efficiency and accuracy of the reciprocity approach in small animal imaging. Specifically, the MOBY mouse was used to generate a heterogeneous model of the small animal, containing seven distinct regions of varying optical properties [Fig. 8b and Table 2]. The 3D FEM forward model contained 80 917 nodes corresponding to 415 824 linear tetrahedral elements and a total of 750 detector positions (1 mm separation) were uniformly distributed in a grid along the top-most surface of the animal model, Fig. 8c.

Figure 8.

(a) Model of the MOBY mouse used to generate a (b) heterogeneous model based on seven regions (Table 2) and (c) the FEM mesh used to generate simulated data. The shaded square indicates the position of 750 detector reading on 1 mm grid separation, with the solid black line indicating the plane at which sources where modeled at varying depths.

Table 2.

The seven regions of anatomy used within the MOBY mouse model, Fig. 8, together with chromophore concentrations and scattering properties used. Both the scattering power and amplitude depend on the scattering center size and number density and may reflect variations in tissue composition due to different cellular, organelle, and structural sizes∕densities.

Region name (No.)	Total hemoglobin (mM)	Oxygen saturation (%)	Water concentration (%)	Scatter amplitude	Scatter power
Adipose (1)	0.0033	70	50	0.98	0.53
Bones (2)	0.049	80	15	1.4	1.47
Muscles (3)	0.07	80	50	0.14	2.82
Spleen∕liver (4)	0.3	75	70	0.45	1.05
Stomach (5)	0.01	70	80	0.97	0.97
Lungs (6)	0.15	85	85	1.7	0.53
Kidneys (7)	0.056	75	80	1.23	1.51

A number of single bioluminescence sources were placed within the heterogeneous mouse model, exactly at half distance plane within the measurement grid as shown in Fig. 8c. In each case, the sources (arbitrary strength of 10) were placed at depths of 15, 12.5, 10, 7.5, or 5 mm from the top surface of the model (as shown in Fig. 9) with a radius of 2.5 mm. Fluence due to the bioluminescence source throughout the model was calculated for each individual case at a total of six wavelengths, ranging from 600 to 650 nm in steps of 10 nm. For image reconstruction, boundary data (amplitude) were extracted from the calculated fluence, at the top-most surface of the model, as indicated in Fig. 8c. A mesh of the same model but different resolution consisting of 80 299 nodes corresponding to 414 960 linear tetrahedral elements was used to avoid the inverse crime. Images of the bioluminescence source distribution were reconstructed for each case (Fig. 9) using the methods described above, and data from a total of six wavelengths, ranging from 600 to 650 nm in steps of 10 nm. 1% randomly distributed noise was added to the amplitude data.

Figure 9.

Cross sectional images of the true and reconstructed bioluminescence source distribution for the MOBY model. Note the color bar scales at right vary with each reconstruction.

RESULTS

Cross sections of reconstructed 3D BLT images of the cylindrical phantom are shown in Figs. 7b, 7c. The use of multiwavelength data and the reciprocity approach, with the non-negativity constraint, has accurately estimated the size and location of the internal bioluminescence source at approximately 7.5 mm from the edge with a full width at half maximum of 8 mm, despite the relatively coarse spatial sampling of the emission spectrum. The computation time for each weight matrix was 42 s (2.6 s per each of 16 detectors) using a dual Xeon 3.4 GHz workstation with 8 GBytes RAM, leading to a total computation time of 210 s. As a comparison, calculating the weight matrices using the direct method, leads to approximately 73 000 s per weight matrix (2.6 s for each node), leading to a total computation time of approximately 101 h.

Using a simulated mouse model, images of single bioluminescence sources at varying depths from the tissue surface have been reconstructed using noise-added simulated data (Fig. 9). As is evident from the images, the size and location of the sources have been successfully reconstructed using the proposed reciprocity approach and the non-negativity constraint. The accuracy of the reconstructed source size, strength, and location appears dependent on the depth of the source. The source is reconstructed within 1 mm for both location and size for sources at depths of up to 12.5 mm, with the best quantitative accuracy seen for a depth of 10 mm. The reconstructed source location at 15 mm is 2.5 mm shallower than expected and exhibits a much weaker strength at only 15% of the true value. The computation time for each weight matrix for this model was 2250 s (3 s per each of 750 detectors) using a dual Xeon 3.4 GHz workstation with 8 GBytes RAM, leading to a total computation time of 13 500 s for all six wavelengths. As a comparison, calculating the weight matrices using the direct method takes approximately 241 000 s per weight matrix (3 s for each node of the mesh used for reconstruction), leading to a total computation time of approximately 402 h.

DISCUSSIONS

The principle of nonuniqueness in BLT has been shown using a simple 2D model (Fig. 2) demonstrating that there exist multiple solutions of internal bioluminescence sources that would give rise to identical measured boundary data. However, using spectral data at discrete wavelengths over the emission range of the bioluminescence source, it is shown that an accurate image of the internal source distribution can be recovered. However, given a set of boundary data, image reconstruction without appropriately applied constraints can lead to inaccurate and negative solutions (Fig. 6). It is shown that adapting the method of NNLS to the BLT problem, it is possible to set a lower and nonnegative bound to the calculated solutions. The applications of such constraints are critical in BLT to avoid recovering nonphysical negative source values. Although the NNLS algorithm used is an iterative algorithm, it is always guaranteed to converge to a solution.¹⁹

The concept of reciprocity, as defined and introduced in DOT by Arridge et al.,¹⁸ has been extended and adapted for BLT and shown to provide accurate solutions to the weight matrices used for image reconstruction. The use of the reciprocity approach has been shown to reduce the computation time of each weight matrix at each wavelength by reducing the matrix calculation from total number of unknowns to total number of measurements (Fig. 5). As an example, assuming a 3D model containing 30 000 unknowns and 1000 measurements at six discrete wavelengths, the total number of models that need to be solved for the computation of all weight matrices at all wavelengths can be reduced from 180 000 to 6000, without loss of accuracy.

The accuracy and speed of the proposed algorithm are demonstrated and validated in 3D using experimentally measured data and shown to reconstruct the location of an internal bioluminescence source within 0.5 mm accuracy. The reconstruction algorithm used is based on the NNLS and the reciprocity approach, and provided non-negative solutions at a reconstruction time of 210 s as compared to 101 h without the use of the reciprocity approach. The method has also been applied in a complex, nonhomogeneous mouse model (Fig. 8) further demonstrating the computational efficiency of the proposed algorithm and the capability of single-view imaging to recover bioluminescence sources at depths up to 15 mm (Fig. 9). The accuracy of the reconstructed source strength appears to be both a function of source depth and background optical properties. Previous studies have shown that using a single-view measurements from a homogeneous model, sources of up to 10 mm can be recovered with the accuracy decreasing for deeper sources.⁴ Another similar study has shown that although the location of sources can be recovered at 15 mm, the reconstructed source strength accuracy decreases for sources deeper than approximately 12 mm.⁸ The use of more appropriate and spatially varying regularization parameters may help improve the quantitative accuracy, as demonstrated in optical tomography.²³

CONCLUSIONS

In this work, the modeling and linear single step non-negativity constrained image reconstruction algorithm for spectral resolved BLT is presented which demonstrates unique BLT image recovery from experimental multiwavelength data. Multiwavelength emission is shown to provide a means of estimating the depth of a luminescence object, due to the wavelength dependent attenuation of tissue. Novel algorithms for the calculation of the weight matrices used in image reconstruction are presented, based on the reciprocity approach, and shown to provide solutions which are accurate compared to the conventionally used perturbation approach.

Images generated from both noisy simulated data and measured experimental data have been presented based on the defined models and algorithms. It is shown that in small animal imaging, the use of single view data collection geometries are able to provide reconstructed images that are accurate in depth recovery for objects within 12.5 mm of the tissue surface, whereas the source strength accuracy varies as a function of depth and background optical properties. However, it has already been demonstrated that the reconstructed images of bioluminescence are linear with respect to the original target source strength which is important when using the magnitude of the bioluminescence intensity to quantify physiological function, disease progression or response to intervention.³

Certain challenges remain which are the subject of further study, including the incorporation of more accurate numerical models based on the radiative transport equation^{24, 25} which are more accurate in small animal domains and near visible wavelengths. Although the application of the presented reciprocity theory should be valid regardless of the forward model, these should be validated, specifically when concerned with the implementation of appropriate boundary conditions that dictates the behavior of light propagation at the air∕tissue interface. Additionally, the design and improvement of instrumentation will allow the simultaneous detection of the bioluminescence spectrum with optimum signal to noise to allow faster data acquisition time. Although the discussion of the work presented here is limited to Luciferase, the presented theory and image reconstruction algorithm can be used for other light emitting sources.