Flickering Analysis of Erythrocyte Mechanical Properties: Dependence on Oxygenation Level, Cell Shape, and Hydration Level

Abstract

Erythrocytes (red blood cells) play an essential role in the respiratory functions of vertebrates, carrying oxygen from lungs to tissues and CO₂ from tissues to lungs. They are mechanically very soft, enabling circulation through small capillaries. The small thermally induced displacements of the membrane provide an important tool in the investigation of the mechanics of the cell membrane. However, despite numerous studies, uncertainties in the interpretation of the data, and in the values derived for the main parameters of cell mechanics, have rendered past conclusions from the fluctuation approach somewhat controversial. Here we revisit the experimental method and theoretical analysis of fluctuations, to adapt them to the case of cell contour fluctuations, which are readily observable experimentally. This enables direct measurements of membrane tension, of bending modulus, and of the viscosity of the cell cytoplasm. Of the various factors that influence the mechanical properties of the cell, we focus here on: 1), the level of oxygenation, as monitored by Raman spectrometry; 2), cell shape; and 3), the concentration of hemoglobin. The results show that, contrary to previous reports, there is no significant difference in cell tension and bending modulus between oxygenated and deoxygenated states, in line with the softness requirement for optimal circulatory flow in both states. On the other hand, tension and bending moduli of discocyte- and spherocyte-shaped cells differ markedly, in both the oxygenated and deoxygenated states. The tension in spherocytes is much higher, consistent with recent theoretical models that describe the transitions between red blood cell shapes as a function of membrane tension. Cell cytoplasmic viscosity is strongly influenced by the hydration state. The implications of these results to circulatory flow dynamics in physiological and pathological conditions are discussed.

Introduction

The mechanical properties of red blood cells (RBCs) are crucial to their function. Structurally, mammalian RBCs are organelle-free cells, full of hemoglobin, surrounded by a bilayer membrane with a thin cortical cytoskeleton. The lifespan of human RBCs is ∼120 days in the circulation (1). During this time, the cells have to survive repeated passages through capillaries narrower than any of the cell's dimensions. During this passage, they fold and squeeze in such a way as to maximize the cell area in contact with the endothelial wall, to optimize the gas exchange function. The mechanical properties that enable this extreme plasticity are therefore critical for RBC physiology. RBCs are particularly soft cells, with the ability to rapidly recover their original shape, even after large deformations. Various methods have been used to measure their mechanical properties; of particular importance in medical practice are erythrocytometers that measure deformation in flow. For research purposes, several single-cell techniques are currently in use, such as micropipette aspiration (2), stretching by optical tweezers (3–5), deformation in microfluidic channels (6), and analysis of shape flickering (7–11). RBCs are the experimental system of choice for the development of new technologies in this area. Ramser et al. (12) exemplify such advances with their combination of optical trapping and microfluidic dynamics allowing the micro-Raman signal to monitor the oxygenation cycle of RBCs in real time.

From the structural point of view, the membrane of the human red blood cell is a particularly simple system, composed of a thin (4–5 nm) lipid bilayer anchored by protein groups to a tenuous cytoskeleton of semiflexible spectrin filaments (1,9). The mesh size of the cytoskeleton is ∼60–80 nm (13). The lipid bilayer itself is a two-dimensional fluid; it has negligible shear elastic modulus and its mechanical response can be characterized by the bending modulus κ. In the absence of osmotic pressure across a simple closed bilayer (a vesicle), there can be an excess of membrane area relative to the volume, and in this situation there is no membrane tension. The composite cell membrane, however, is known from micropipette and tweezers experiments to have a finite shear elastic modulus μ, and can also be under tension. It is now well accepted that both of these properties arise from the spectrin filament network.

On observation under optical microscopy, RBCs are seen to flicker (14). Flickering of the red blood cell membrane has been known for a very long time, and was first analyzed quantitatively in a seminal article by Brochard and Lennon (7). This modulation of light is due to large shape fluctuations that lead to a dynamically evolving interference (phase contrast) in the transmitted field. This effect can be quantified and related to the cell mechanics. It has been proposed that flickering serves biological functions, for example enabling the cells to tune their adhesion to surfaces and thus control frictional resistance to flow (15). Flickering certainly is correlated to the cell mechanics, and in that sense, it is a valid and useful probe with which to measure the cell mechanical properties. Brochard and Lennon (7) investigated the energetics and hydrodynamics involved in membrane motion, and concluded that a purely physical interpretation of the flicker effect in terms of equilibrium mechanical properties was sufficient. They showed that the bending modulus of the membrane could be measured reliably. Their analysis assumed negligible tension and shear elasticity, and under these conditions they predicted that the power spectrum of fluctuations at each point in the membrane (away from the edge) should depend on the frequency ω as ω^−4/3, as observed by them. Their results imply that the large membrane fluctuations that are observed can be understood in terms of the thermal motion of a fluid bilayer, as derived more fully by Helfrich and Servuss (16). Using this model, the equilibrium amplitude of fluctuations can be related to the membrane bending modulus and tension.

In subsequent work, shape fluctuations have been investigated with increased sophistication, in order to attain a deeper understanding of cell mechanics (8,9,16–18) and of the underlying biochemical processes (11,19). Despite the fact that the experimental technique is widely available, and that there has been so much work on this system, there are surprisingly contradictory results. For example, although most investigators treat the fluctuations as thermal in origin (7–9,11,18), others suggested that the membrane motions might also be enhanced by nonequilibrium stress-relaxation events linked to membrane skeleton rupturing (19,20). Experiments by Tuvia et al. (21) supported the view that there are more than just thermal effects, claiming that extracellular fluid viscosity regulates membrane fluctuation amplitude, thereby implying a breakdown of the fluctuation dissipation theorem valid at equilibrium. They suggested that membrane fluctuations are driven by a metabolic driving force in addition to the thermal one. However, Evans et al. (11), performing similar experiments on a large number of cells, concluded that the membrane fluctuations are governed only by bending modulus, membrane tension, and cytosolic viscosity, with little or no dependence on the presence or absence of adenosine triphosphate.

In addition to the thermal versus nonthermal argument on the origin of fluctuations, there remain also disagreements over the precise relation between the measurements of RBC fluctuations and the underlying mechanical properties of the cell. Peterson and co-workers (22,23) showed that thickness fluctuation profiles depend on the relative importance of curvature modulus κ and shear modulus μ, and showed experimentally that μ was negligible, a result incompatible with the higher values of μ obtained from micropipette aspiration or optical tweezers (μ ≃ 6–9 × 10⁻⁶ J m⁻² (2,5)). The complex coupling between lipid bilayer and cortical cytoskeleton lies at the root of these controversial claims (24,25). Rochal and Lorman (25) proposed that when the quasi-three-dimensional nature of the complex membrane (phospholipid + polymer cytoskeletal mesh) is taken into account, the fluctuation amplitude becomes consistent with the cell shear moduli measured macroscopically. The work of Gov and Safran (20) and Gov et al. (24) also proposes models for the complex membrane, suggesting that membrane tension and membrane confinement effects should be taken into account. In recent work, Popescu et al. (10) used a new variation of microinterferometry, Hilbert phase microscopy, to investigate the mechanics of RBCs in three different shapes: discocytes, echinocytes, and spherocytes. That method too is sensitive to membrane curvature, i.e., deviations from an average flat surface, and is therefore a probe for the flickering phenomenon. They reported a nonvanishing tension on the RBC, which increases as cells transition from a discocytic to a spherical shape. Our results here confirm this trend. Interest in this tension is relevant because it appears unique to cell membranes and is absent in model membranes such as giant vesicles if they have enough excess area. However, a note of caution deserves attention here: the bending moduli reported in Popescu et al. (10) are approximately a factor-of-3 smaller than is commonly accepted (see (26) and references within). Reconciling the small deformation moduli from submicron fluctuations with larger scale deformations remains, at least in part, an unresolved problem.

Raman spectrometry has been widely used to probe the chemical composition and structural conformation of biological samples, relevant for the understanding of drug interactions and environmental influences in these complex dynamical systems (27–30). With the development of the micro-Raman apparatus, it became possible to probe samples at the single-cell level. Applied to RBCs, this should enable to resolve the distribution of chemical information within the cell population from detailed, nonaveraged information in single cells. Tuvia et al. (19) suggested that the physiological oxygenation-deoxygenation cycle provides a dynamic control of the bending deformability, which is directly linked to the amplitude of the fluctuations.

In this study, we combine the analysis of membrane flickering with the use of the micro-Raman technique to monitor the chemical change in the hemoglobin. We first proceed to outline how an advanced image-processing algorithm is used to extract both the bending modulus and tension values from a theoretical model of fluctuations. This allows us to provide a precise description of the changes in RBC shape and mechanics associated with changes in oxygenation and hydration state of the cells. The relevance of studying the hydration state of RBCs deserves clarification. The volume of the RBCs, and hence their hemoglobin concentration, varies with RBC age (31–33), and over a much wider margin in many pathological conditions (34). It has also been recently shown that mechanical properties and hydration state could be coupled (30). Tiffert et al. (35) have recently designed experimental conditions that allow the precise control of the hydration state of normal RBCs by reducing or increasing irreversibly the KCl content of the cells. We apply this method here to study the effects of cell volume and hemoglobin concentration on cell mechanics using our theoretical model of fluctuations.

Methods

Cell protocol

Oxygenation state

Blood was drawn from healthy volunteers after informed written consent. For all studies other than those on the effects of RBC hydration state, the following procedure was applied. Approximately 100 μL of blood obtained by a fingertip needle prick were diluted into phosphate-buffered saline containing acid citrate dextrose and 1 mg/mL bovine serum albumin (Sigma-Aldrich, St. Louis, MO) at pH 7.4 (10,11,19). The RBCs were washed three times by centrifugation and resuspension in the same buffer and finally suspended at ∼0.1% hematocrit in phosphate-buffered saline containing 1 mg/mL bovine serum albumin. Deoxygenated RBCs were obtained by adding sodium dithionite (Na₂S₂O₄; Sigma-Aldrich) to a final concentration of 2.5 mg/mL to an aliquot of this suspension (12,28). Raman spectroscopy showed that deoxygenation was complete after <1 min in these conditions.

Hydration state

To study the effects of RBC hydration (hemoglobin concentration) on cell mechanics we applied the method of Tiffert et al. (35) to control RBC volume. Briefly, the principle of the method is to allow RBCs to vary their KCl and osmotic water content by generating a transient increase in their K⁺ permeability. The protocol is described in detail in Supporting Material.

Micro-Raman analysis

Raman spectra of living RBCs were recorded on a Renishaw system-RM 1000 (Wotton-under-Edge, Gloucestershire, UK) using a 514-nm excitation line from a HeNe laser with 50× Zeiss objective (Carl Zeiss, Oberkochen, Germany). Power at the sample was ∼30 mW for a 1–2 μm laser spot size. Spectra were recorded between 1800 and 200 cm⁻¹ with a resolution of ∼1–2 cm⁻¹. The 520.5 cm⁻¹ band of the silicon wafer was used for the alignment and calibration of the instrument. For each spectrum, a laser exposure time of 10 s was selected and three scans were accumulated. The 12 sets of data were averaged and the statistical variance was calculated. A limitation of this study is that photodissociation causes damage to the cells after three scans at full power. Therefore, we could not measure the spectrum continuously while monitoring the same single cell. In future work we aim to optimize the micro-Raman setup to function at weaker powers ≤1 mW and at more benign wavelengths, with respect to photodissociation.

Sample chamber and video acquisition

Chambers for visualization were prepared by assembling a microscope slide and a coverslip, separated by a double layer of parafilm, giving a 200-μm-thick sample volume. The parafilm was shaped to create a space of ∼1 cm diameter. Small diametrically opposite apertures were used to load the cell suspension, which filled the volume by capillary forces, and these apertures were then sealed off with vacuum grease. The glass surfaces were dusted with a jet of compressed air, but otherwise untreated. The protein present in the buffer is expected to rapidly adsorb to the surfaces. In these conditions, erythrocytes sediment over time to the bottom, and stick very mildly to the glass, such that with optical tweezers it was possible to lift the cells off the glass (5).

The fluctuation videos were recorded using a 100× oil immersion objective, a 430-nm laser, and the fast resonant scanning option (8 kHz line-scanning frequency) in a confocal microscope (TCS SP5; Leica, Wetzlar, Germany). The frame rate was 27.7 frames/s. All measurements were done at room temperature (∼23°C). Due to the fast line scanning, neighboring pixels were acquired at most after 1.25 × 10⁻⁴ s, thus avoiding many of the complications due to finite exposure times (36). Approximately 2000 frames were captured for each cell, at 256 × 256 pixels. At this magnification the pixel size is 50 nm.

Contour detection

The contour of the cell membrane was detected by an algorithm developed in-house and coded as a C++ module called within MatLab (The MathWorks, Natick, MA). The essential steps are outlined in Fig. 1, and described in detail in Supporting Material. The result of this procedure is a set of 360 discrete radial positions of the cell boundary. The fluctuations h(θ_i(t)) for each time are defined as the deviation from the time-average of h at angle θ_i, as shown in Fig. 1 e. Each cell is measured over several thousand frames. The information from the whole image stack is analyzed to determine mechanical and dynamical parameters of the cell, as described below. Several cells are measured for each of the conditions studied here, as noted in Table 1, giving mean values and typical deviations.

Figure 1.

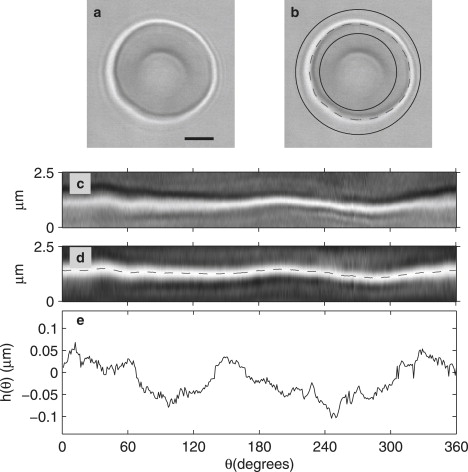
(a) RBCs in bright-field microscopy. Scale bar 2.5 μm (b) Contour of the RBC (dashed line), with inner and outer bounds used in image analysis (solid line). (c) The line profile array obtained at each radial section of panel b. (d) Effect of filtering the array in panel c with an optimized correlation kernel, and locus of maxima in the array (dashed line), which indicate the contour position. (e) Fluctuation amplitude h(θ) obtained as the difference between the instantaneous and time-average position of the contour at angle θ.

Table 1.

Summary of results of RBC static and dynamic moduli

Condition (No. cells in sample)		Values from static analysis			Values from dynamics
		Fitting for tension and bending		Fitting for bending only
		κ (10−20 J)	σ (10−7 N/m)	κ (10−20 J)	ηi (10−3 Pa s)
Oxy.	Discocyte (4)	26.7 ± 4.6	5.0 ± 1.7	32.0 ± 4.9	17.3 ± 7.5
	Spherocyte (11)	22.8 ± 4.2	12.1 ± 4.1	32.9 ± 4.1	34.3 ± 15.5
Deoxy.	Discocyte (4)	33.3 ± 10.4	4.4 ± 1.9	38.4 ± 10.4	14.8 ± 7.4
	Spherocyte (11)	23.6 ± 5.4	11.3 ± 2.8	33.7 ± 6.2	45.9 ± 15.1
Hydration	120 K (24)	18.4 ± 8.2	6.6 ± 1.4	23.7 ± 8.1	21.5 ± 14.0
	Control (19)	14.5 ± 2.9	6.4 ± 1.7	20.5 ± 3.2	23.6 ± 7.6
	50 K (17)	22.5 ± 5.5	6.6 ± 3.0	27.7 ± 4.8	42.8 ± 16.9
	3 K (12)	27.8 ± 10.7	13.6 ± 6.2	39.5 ± 12.1	953.2 ± 1376.5

Fits for tension (σ) and bending (κ) are for 3rd to 20th q_x mode, and fits for only κ are performed on 7th to 20th q_x mode. All values are mean ± SD.

Fluctuation amplitude analysis

Case of a simple bilayer

The spectrum of small fluctuations for quasi-flat (planar) membranes having tension and resistance to bending can be derived from the analysis of Helfrich and Servuss (16). The deviations from the plane depend on the position in the plane $\overrightarrow{x}$, and are described by the function $h\left(\overrightarrow{x}\right)$. The classical derivation of the fluctuation amplitude is reproduced in the Supporting Material. In a recent work, Pecreaux et al. (36) clarified how the analysis of analysis of planar fluctuations should be adapted to the case of experiments where the contour of closed objects is observed in microscopy. This work focused on giant vesicles, and pointed out several important technical issues (36), particularly the need to consider only the fluctuations of the cell in the plane of its equator. These contour fluctuations can be calculated by an inverse Fourier-transform over q_y of Eq. S4, obtaining the projection of the spectrum at y = 0 (36):

$$\langle h{\left(q_{\mathrm{x}},y=0\right)}^2\rangle =\frac{k_{\mathrm{B}}T}{L}\frac{1}{2\sigma }\left[\frac{1}{q_{\mathrm{x}}}-\frac{1}{\sqrt{\frac{\sigma }{\kappa }+q_{\mathrm{x}}^2}}\right]\text{.}$$ (1)

For equatorial contour fluctuation modes, mode n = 0 corresponds to q_x = 0. This mode is a change in the radius, i.e., an infinite wavelength fluctuation. Mode n = 1 corresponds to q_x = 2π/L = 1/R, has wavelength L, and can arise from cell (or vesicle) translation. Therefore modes n = 0 and n = 1 are not directly relevant for the study of membrane properties. Fig. S2 a shows that for modes n ≧ 3, Eq. 1 is a good representation of the spectrum: the mode amplitude given by the planar approximation of Eq. 1 and by the spherical model (see, e.g., (36)) are within 15% of each other. In general we have that q_x = 2πn/L = n/R and that the fluctuation wavelength is given by L/n.

Case of the red blood cell membrane

In previous work, the fluctuation spectrum of Eq. S4 was used to model the fluctuation behavior of the red blood cell membrane. However, this membrane is much more complex than a simple phospholipid bilayer. Recently it was proposed that the fluctuations of the RBC membrane could be considered as bilayer fluctuations, constrained by the spectrin skeleton. Specifically, Gov and Safran (20) and Gov et al. (24) proposed that the spectrin confinement would appear as a harmonic potential, and that the free energy functional of Eq. S1 should be modified with an additional term to account for this:

$$F=\underset{\mathrm{A}}{\int }d\overrightarrow{x}\left[\frac{1}{2}\gamma h^2+\frac{1}{2}\sigma {\left(\nabla h\right)}^2+\frac{1}{2}\kappa {\left({\nabla }^{2}h\right)}^2\right]\text{.}$$ (2)

Following the same steps as above, this leads to the fluctuation power spectrum:

$$\langle h_{\mathrm{q}}^2\rangle =\frac{k_{\mathrm{B}}T}{A}\frac{1}{\gamma +\sigma q^2+\kappa q^4}\text{.}$$ (3)

The presence of a solid boundary also gives rise to a confining term (37). Interestingly, the presence of a shear modulus (as opposed to a confining potential) would also lead to a similar formulation as that of Eq. 3, with γ replaced by the ratio of the shear modulus to the area of the surface μ/A. This does not follow from Eq. 2, but requires a calculation through spherical modes and the consideration of the continuous limit, as done in Peterson (38). We will keep the notation with γ as in Eq. 3, keeping in mind that this term can arise from either a confining potential or from the presence of a shear modulus.

The flickering spectrum form of Eq. 3 has been taken into account in recent work (10), but direct evidence for the confining potential is still lacking. This has not yet been investigated by the contour fluctuation method. To consider how the confining potential would manifest itself on the equatorial fluctuations, it is necessary to follow the treatment of Pecreaux et al. (36), but starting from Eq. 3 instead of Eq. S4. This gives the experimentally observable spectrum:

$$\langle h{\left(q_{\mathrm{x}},y=0\right)}^2\rangle ==\frac{k_{\mathrm{B}}T}{L}\sqrt{\frac{\mathit{\kappa }}{2\left({\sigma }^2-4\mathit{\kappa }\gamma \right)}}[\frac{1}{\sqrt{2\mathit{\kappa }{q}_{\mathrm{x}}^2+\sigma -\sqrt{{\sigma }^2-4\mathit{\kappa }\gamma }}}+-\frac{1}{\sqrt{2\mathit{\kappa }{q}_{\mathrm{x}}^2+\sigma +\sqrt{{\sigma }^2-4\mathit{\kappa }\gamma }}}]\text{.}$$ (4)

This somewhat complex analytical form hides what are actually very simple regimes: different terms dominate depending on the range of q vector, and on the relative magnitude of the membrane parameters. At very low q (large wavelength), the divergence of the fluctuation amplitude is cut off by the harmonic confinement, and the spectrum of Eq. 4 levels off. At intermediate values of q, there can be a regime where 〈h(q_x, y = 0)²〉 ∼ q⁻¹, if tension (σ) is nonnegligible. At large q, there is a bending-dominated regime where 〈h(q_x, y = 0)²〉 ∼ q⁻³. This is similar to the spectrum of simple bilayers (see Eq. 1), except for the small wavevector cutoff.

In the work where the original form of Eq. 3 was proposed and discussed (20), the comparison was made with experimental data in Zilker et al. (15). The constraining term γ appeared relevant for this data. However, the technique used in the experiments relied on quantifying the interference between light reflected by the glass substrate, and light reflected by the bottom of a cell sitting on the substrate. In that configuration, the flickering amplitude would be cut off at large wavelengths by the steric hindrance from the solid substrate. In our work, as can already be seen by inspection of the data in Fig. 2, we do not detect the presence of the confining potential. We use the form of the simpler power spectrum of Eq. 1 to fit our data, but we use the comparison with the full form of Eq. 4 to put an upper bound on the parameter γ.

Figure 2.

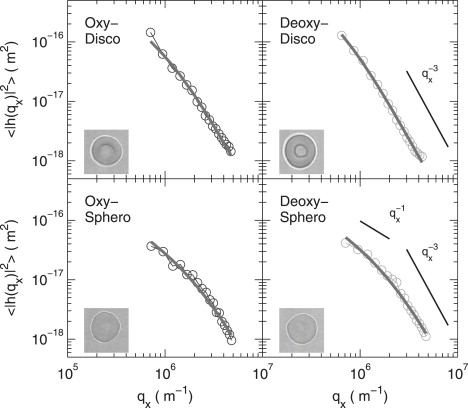
The mean-square amplitude of contour fluctuation modes versus the wave vector q_x, for the oxygenated and the deoxygenated state obtained by addition of Na₂S₂O₄. The solid lines correspond to the fit of the data using Eq. 1. Limiting behaviors are shown in bottom right, as discussed in the text. Each panel corresponds to the results of a single cell. Panels are divided by oxygenation state and cell shape, as marked. In this work we treated as spherocytes those cells of similar size to normal discocytes, but without the biconcave shape.

Data analysis of statics

Equation 1 can be directly compared to the Fourier-transform of the experimentally measured fluctuation profile h(θ). Equation 1 has limiting behaviors 〈h(q_x, y = 0)² 〉 ∼ q_x⁻¹ for modes dominated by membrane tension (σ ≫ κq_x²), and 〈h(q_x, y = 0)² 〉 ∼ q_x⁻³ for modes dominated by bending (σ ≪ κq_x²). These are highlighted in Fig. 2. The crossover between the two regimes clearly depends on the physical values of the two parameters, but also on the lengthscale. For sufficiently small wavelength fluctuations (large q) the bending modulus will always be the dominant constraint. We consider modes starting from the third mode of the spectrum (so that the approximation of planar membrane is valid), up to mode 20 where noise in the spectra due to limited resolution of the contour position becomes appreciable. The upper mode used for the fitting corresponds to q ≃ 10⁷ m⁻¹.

The bending modulus (κ) and the tension (σ) are obtained from the experimental data by fitting with Eq. 1, with σ and κ as the only fitting parameters. The fitted spectra are shown superposed on the data in Fig. 2. Above ∼q = 10⁶ m⁻¹, bending is the dominating restoring term. This is in agreement with previous work; for example, Zilker et al. (8) showed that the spectrum of erythrocyte flickering in the wave-vector regime 0.7 ≤ q ≤ 3 μm⁻¹ is dominated mainly by bending stiffness. The values of bending modulus are very close to previously reported values (18).

Dynamics of membrane fluctuations

Classical flickering in transmission or reflection

The dynamics of membrane motions has often been measured by probing the cell at a specific point, and measuring the fluctuation in the intensity of the transmitted (7) or reflected (15) beams. This approach has the advantage that the beam can be monitored at very high frequency (measurements in (7) are reported up to 100 Hz, but the approach can easily be extended to higher frequencies), and that there is little or no signal analysis to be done. In other words, the power spectrum of the fluctuating signal, which is readily calculated from the signal, is the final data. The simplicity of the measurement, however, is balanced by a difficulty of matching the results with the underlying membrane properties. This is because by probing at a single spatial point, the measurement is an integral over all the relaxation modes of the membrane, and the relaxation of different modes is driven by different parameters. A similar approach was followed recently in Evans et al. (11), where the frequency power spectrum of displacements of the contour points was measured, and then averaged over all angles.

Mode dynamics of continuous membranes

Significantly more information is contained in the dynamics of individual modes. We review here continuous membranes, and in the section below we show how this applies to contour modes. The time correlation of spatial modes of the membrane is defined as

$$C_{\overrightarrow{\mathrm{q}}}\left(t\right)={\langle h\left(\overrightarrow{q},t^{\prime }\right)h\left(\overrightarrow{q},t^{\prime }+t\right)\rangle }_{{\mathrm{t}}^{\prime }}\text{.}$$ (5)

The hydrodynamics that controls mode relaxation in two-dimensional membranes has been addressed in various articles, and we refer in particular to the literature (22,38). Combining the results predicted for a bending-modulus-dominated regime of RBC fluctuations (22,38) with the results related to giant vesicle fluctuations where the tension was taken into account (39,40), we expect that the time correlation function will be an exponential decay

$$C_{\overrightarrow{\mathrm{q}}}\left(t\right)=C\left(0\right)\exp \left(-t/{\tau }_{\overrightarrow{\mathrm{q}}}\right),$$ (6)

where the timescale ${\tau }_{\overrightarrow{\mathrm{q}}}$ is in general given by

$$\frac{1}{{\tau }_{\overrightarrow{\mathrm{q}}}}=\frac{2\mathit{\gamma }+\mathit{\sigma }{q}^2+\mathit{\kappa }{q}^4}{2\left({\mathit{\eta }}_{\mathrm{M}}/R^2+q{\mathit{\eta }}_{\text{int}}+q{\mathit{\eta }}_{\text{ext}}\right)}\text{.}$$ (7)

Note that this result follows from Eqs. 59 and 60 of Peterson (38), taking into account the typo in Eq. 60 reported in Peterson (22) and also an additional typo in Eq. 56, where η_M should be divided by a², carrying through to Eq. 60. This is consistent with the recent work of Kaizuka and Groves (37) that addressed two of the conditions described here.

In Eq. 7, η_M is the two-dimensional membrane viscosity, η_int and η_ext are the viscosities of the fluid on either side of the membrane, R is the radius of the cell membrane, and as before $q=\left|\overrightarrow{q}\right|$.

The two-dimensional phospholipid bilayers have viscosities η_M < 10⁻⁹Ns m⁻¹ for temperatures above room T (41). Therefore it can be seen that given R ≃ 4 μm, η_int ≃ 40 × 10⁻³ Pa s, and η_ext ≃ 1 × 10⁻³ Pa s, the cytoplasmic viscosity contributes the dominant term in the denominator of Eq. 7 at values of q ≃ 10⁶ m⁻¹. The numerator of Eq. 7 is dominated by whichever parameter (harmonic constraint, tension, or bending modulus) dominates the mean-square amplitude of fluctuations, at the observed wavevectors. With this analysis, the dynamic properties of the membrane can be accessed (e.g., cytoplasmic or membrane viscosities), in addition to the static properties that are independently estimated from the static mode spectrum.

Contour mode dynamics

Given that the contour can be readily identified, and that it is straightforward to measure the time correlation function of the amplitude of each contour mode, we show how this can be related to the result above. As far as we are aware, the effect of equatorial projection, which is intrinsic to the contour mode analysis, has not been discussed before for the case of mode dynamics.

Equation 7 gives the relaxation timescale of the modes of a two-dimensional flat membrane, as a function of the wavevector $\overrightarrow{q}$. We now need to reflect on two additional considerations: first, that the red blood cell is a closed object, i.e., the membrane is not flat; second, that we image the contour of the cell, and therefore probe only modes as a function of their mode component q_x.

Fig. S2 b shows that considering the membrane as planar continuous instead of spherical can lead to an error of ∼10% for the conditions relevant to the red blood cell. This error diminishes the higher the viscosity of the fluid. Due to the much greater simplicity of the analytical expressions for the planar case, and to the fact that 10% is much less than the standard error typical of our measurements, we choose to treat the data within this approximation.

A larger correction comes from the fact that we measure the dynamics of equatorial modes, on which the perpendicular modes are projected. This is the same effect that was addressed previously to relate the theoretical result for the static two-dimensional mode spectrum to the experimentally accessible contour mode spectrum. Here, in the case of mode dynamics, the theoretical result of Eq. 6 needs to be corrected by projection onto the equatorial contour to be compared to experiments. The observed contour time correlation function is the average over all the relaxations in the q_y modes that are perpendicular to the equatorial contour. Mathematically this is represented by

$${\tilde{C}}_{{\mathrm{q}}_{\mathrm{x}}}\left(t\right)={\langle h_{{\mathrm{q}}_{\mathrm{x}}}\left(t^{\prime }\right)h_{{\mathrm{q}}_{\mathrm{x}}}\left(t^{\prime }+t\right)\rangle }_{{\mathrm{t}}^{\prime }}=\frac{\int d{q}_{\mathrm{y}}\langle h_{\overrightarrow{\mathrm{q}}}^2\rangle \exp \left(-t/{\tau }_{\overrightarrow{\mathrm{q}}}\right)}{\int d{q}_{\mathrm{y}}\langle h_{\overrightarrow{\mathrm{q}}}^2\rangle },$$ (8)

where the denominator is the same integral that led from Eq. 3 to Eq. 4. The integral in the numerator of Eq. 8 does not have a closed form, and so the connection between the experimentally accessible ${\tilde{C}}_{{\mathrm{q}}_{\mathrm{x}}}\left(t\right)$ and the theoretically determined $C_{\overrightarrow{\mathrm{q}}}\left(t\right)$ must be established numerically. This point is discussed further in Supporting Material, where it is shown that the correlation function ${\tilde{C}}_{{\mathrm{q}}_{\mathrm{x}}}\left(t\right)$ is also a simple exponential decay, like $C_{\overrightarrow{\mathrm{q}}}\left(t\right)$, and that the experimentally observed decay time is ${\tilde{\tau }}_{{\mathrm{q}}_{\mathrm{x}}}\simeq 0.8{\tau }_{\overrightarrow{\mathrm{q}}}$. Having checked that this correction factor can be set to a constant value, we can fit the observed decay, obtaining ${\tilde{\mathit{\tau }}}_{{\mathrm{q}}_{\mathrm{x}}}$. Once the mechanical moduli of the membrane are known, the only parameter that affects ${\tilde{\mathit{\tau }}}_{{\mathrm{q}}_{\mathrm{x}}}$ is η_int. From ${\tilde{\mathit{\tau }}}_{{\mathrm{q}}_{\mathrm{x}}}$ (using the values of σ and κ obtained from the static spectrum of the same cell) we obtain the value of the internal viscosity of the cell, which is reported in Table 1. Existing methods to access cytoplasmic viscosity are much more complex; for example, infrared vibrational echo (42).

Raman spectrum

The Raman spectra show very clearly the change in deoxygenation state in each measured cell. Typical spectra are shown in Fig. S4. After addition of sodium dithionite, the 1640, 1589, and 1379 cm⁻¹ peaks in oxygenated RBC disappear and 1604, 1544, and 1355 cm⁻¹ peaks show up clearly, in agreement with previous results (28).

Results and Discussion

Oxygenation state of the cell

Fig. 2 shows that a discocyte-shaped RBC in both the oxygenated and deoxygenated states shows a q⁻³ negligible tension fluctuation spectrum, whereas a q⁻¹ scaling is clear at low q-values for a spherocyte in both the oxygenated and deoxygenated states. Looking at a relatively large sample of cells (≲40), we found that tension and bending depended on the shape, but not on the oxygenation state. Statistically, there was no significant difference in the averaged mechanical parameters between oxygenated and deoxygenated states, as shown in Table 1. The tension values of the discocyte shape in both oxygenated and deoxygenated states were remarkably lower than those of the spherocyte shape. The bending modulus was not significantly different between discocyte and spherocyte shapes. At high q, it is also possible to fit the spectrum ignoring the effect of tension, since the bending modulus dominates the mode amplitude. Values of κ obtained in this way are reported in Table 1.

The different tensions measured in the membranes of RBCs with different shapes were in broad qualitative agreement with the recent reported values (10). The morphological changes have been successfully modeled by considering the free energy contributions of both the bilayer and cytoskeleton (43). This work has shown that changing the relaxed area difference in the area-difference-elasticity model, combined with the elastic energy of the spectrin-based membrane-skeleton, drives the shape transition from a stomatocyte (negative area difference value) to the echinocyte (positive range of area difference), with all other parameters remaining constant. The authors discuss that an increase in tension can have a similar role. The increase in tension for the discocyte-spherocyte transition can be explained by changes in the spectrin cortical cytoskeleton anchored to the bilayer.

The good fit obtained with our data using the spectrum of Eq. 1 indicates that the confining parameter γ is playing a negligible role. Based on our results, summarized in Table 1, we can calculate an upper bound for γ. The spectrum of Eq. 4 reduces to the one we use, Eq. 1, in the limit of γ < σ²/(4κ) and γ < σq². Considering these limits, our experiments lead to bounds of γ < 2 × 10⁷ J/m⁴ and γ < 5 × 10⁵ J/m⁴. The first bound is compatible with the values obtained in Gov and Safran (20) (1–8 × 10⁷ J/m⁴), but the second bound is much smaller. Keeping in mind the discussion following Eq. 2, the limit on the parameter γ can also be considered as a limit on the membrane shear modulus. From γ = μ/A < 5 × 10⁵ J/m⁴ we obtain μ < 3 × 10⁻⁵ N m⁻¹. This is slightly larger than the shear moduli obtained from shear flow experiments (44) and pipette aspiration μ ∼ 6–9 × 10⁻⁶ N m⁻¹. In fact, it is clear from here that such values of shear modulus will not be apparent from the contour flickering experiment at modes ≥3, where tension and bending moduli dominate the response.

Tuvia et al. (19) reported that oxygenated RBCs are mechanically softer than deoxygenated ones, a result in agreement with recent observations based on small membrane fluctuations (45). The protocol in Tuvia et al. (19) differed from ours in that deoxygenation was implemented by bubbling N₂ or CO₂ gas in the cell suspension, and their conclusions were based on fluctuation measurements over a power spectrum in the frequency range 1.5–4 Hz, obtained with averaging by results from six or seven cells. In both previous studies (19,45) the reported effects were rather small, of ∼20% in the displacement power. Our results show a slightly lower viscosity for the oxygenated cells, which may, in part, explain the more pronounced fluctuation amplitudes seen for some frequencies in Tuvia et al. (19). The main conclusion from our data is that compared to the correlation between cell shape and cell stiffness, the effects attributable to the oxygenation state are very small.

From mode dynamics we can monitor the viscosity of the cell interior, as shown in Fig. 3. These values are summarized in Table 1 and are in good agreement with values measured by relaxation in micropipette and by other methods (42). The advantage of this analysis is that (at least in principle) it is very clear from the q-dependence which parameters dominate the statics and dynamics of fluctuations, and it is possible to extract the dominant moduli. Our data shows a clear increase in viscosity with deoxygenation and RBC dehydration (see Fig. 4), of obvious relevance to hemodynamics, particularly in diseased states with compromised blood rheology (46–50).

Figure 3.

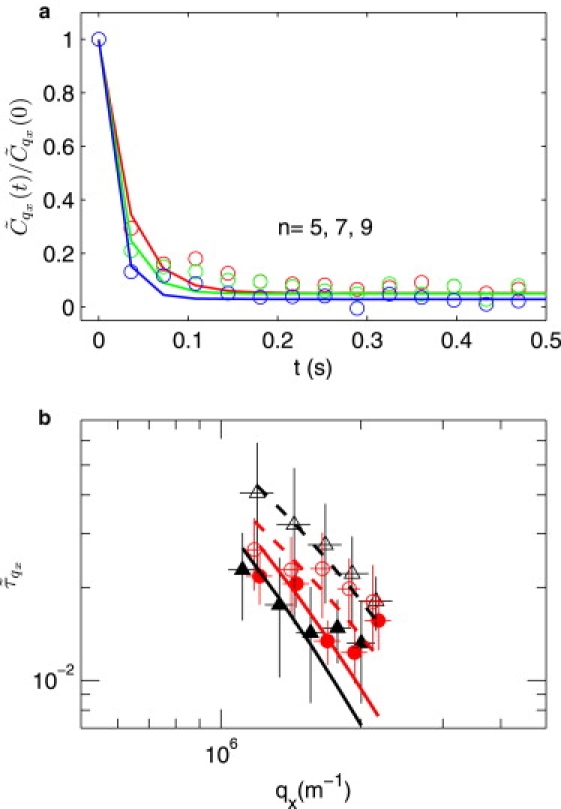
(a) Normalized autocorrelation function for ${\langle h_{{\mathrm{q}}_{\mathrm{x}}}^2\left(t^{\prime }\right)h_{{\mathrm{q}}_{\mathrm{x}}}^2\left(t^{\prime }+t\right)\rangle }_{\mathrm{t}}$, fitted with exponential function at each mode n = 5, 7, 9 for typical single cell data. (b) Relaxation time value (${\tau }_{{\mathrm{q}}_{\mathrm{x}}}$) versus q_x, modes from fifth to ninth. Fitting with ${\tilde{\tau }}_{{\mathrm{q}}_{\mathrm{x}}}=0.8·{\tau }_{\mathrm{q}}=0.8\left[2\left({\mathit{\eta }}_{\text{int}}+{\mathit{\eta }}_{\text{out}}\right)/\left(\mathit{\sigma }q+\mathit{\kappa }{q}^3\right)\right]$. ▴, deoxy-discocyte; ▵, deoxy-spherocyte; •, oxy-discocyte; ○, oxy-spherocyte.

Figure 4.

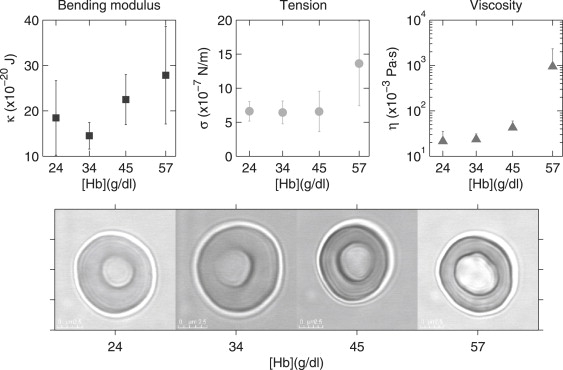
Mechanical properties and typical shapes of RBCs as a function of the Hemoglobin concentration. As discussed in the text, the hydration state is controlled by an incubation protocol in solutions of different KCl concentrations. Thirty-four grams/dL is the physiological concentration, and this is the control sample described in Methods. All values are mean ± SD.

Our results, and other previous work, also expose the large variability in the mechanical properties of RBCs. With a mean lifespan of ∼120 days in the circulation, the aging process of human RBCs is characterized by changes in metabolism, membrane transport, progressive densification, loss of membrane area, and increased stiffness (31–33,51,52). It may therefore be reasonably assumed that the observed variability is genuine and related to the age of the RBCs. Precise tests of this hypothesis, however, will require further measurements on age-segregated RBCs.

Hydration state of the cell

In many of the inherited hemoglobinopathies with high gene frequencies in malaria-endemic regions, the density distribution of RBCs is abnormal, with variable proportions of dense circulating cells. The most common of these are the thalassemias and sickle cell anemia (53–56). In all these instances, increased cell density was found associated with increased viscosity, with values well within the range observed here for the experimentally dehydrated RBCs (57,58).

At physiological conditions (∼[Hb] = 33.5 g/dL, or 21 mM in the units of McClain et al. (42)), reported viscosities inside erythrocytes are in the range 10–15 mPa s from micropipette relaxation (59,60), and 46 mPa s from recent infrared vibrational echo experiments (42).

In relation to sickle cells it should be emphasized that deoxygenation recruits ∼60–70% of the Hb into polymers, so the actual concentration of soluble tetramers is reduced. The hemodynamic effects reported for sickle cells are mainly due to the shape distortion generated by sickling and to the rigidity of the irreversibly sickled cells (47–49). The results in this article point to the additional effect of increased viscosity of the cytoplasm due to the increased concentration of pure Hb. This effect would apply at least partially to subpopulations of cells in people affected by thalassemia or sickle cell anemia.

Linear and nonlinear behavior

We showed here how flickering can be used as a probe for small (thermal, or possibly nonthermal (61)) fluctuations. These fluctuations are within the linear response regime of the cell, where the cell moduli do not depend on the amplitude of deformation. That for larger deformations the RBC is nonlinear was demonstrated by Fricke and Sackmann (17) who showed that the cells stiffen upon large deformation induced with electric fields. The dynamic response in such conditions was quite different from the simple exponential relaxation reported here. The large deformation response was interpreted in terms of microscopic effects on the cytoskeleton in Lee and Discher (62). In recent work, we reassessed the nonlinearity of RBC mechanics under large deformations (5) by stretching the cells with optical tweezers. These experiments showed that the cell cytoskeleton restructures in a nontrivial way at large deformations, under applied stress. The remaining open question concerns the bounds within which the RBCs exhibit a linear response. In this context, it will be important to understand if factors that play minor roles at small deformations (like the oxygenation state explored here, or adenosine triphosphate concentration explored recently by (11)) might play more important roles at large deformation, where the cytoskeleton is forced to rearrange.

Conclusions

We have adapted the existing theory on membrane fluctuations (both for the mean amplitude and for dynamics) to the case of boundary motion of a membrane with a tension and a bending modulus, as well as a confining potential. Using here human RBC from healthy donors as our experimental model, we measured membrane flickering in normal-volume cells and in cells with experimentally altered volumes, and also measured the effect of deoxygenation (by addition of sodium dithionite) on cell membrane properties. The oxygenation state of the cells was monitored by following the changes in micro-Raman spectra. The flickering analysis enabled us to measure the mechanical properties of RBC membranes in the oxygenated and deoxygenated states. The key results of our work are:

• 1.There is no significant difference in the mechanical parameters between oxygenated and deoxygenated states when comparing cells of the same shape. Cell shape is known to be strongly correlated to cell mechanics, and in recent work we showed higher stiffness and energy dissipation in large deformations of stomatocytes compared to discocytes cells (5).
• 2.The cell mechanical properties correlate with shape and hydration state, but contrary to earlier claims they appear to be largely independent of the oxygenation state of the cells. Previous work approached the comparison between effects of shape and oxygenation on cell mechanics by measurements on RBC populations, which precluded a proper assessment of the distinct contributions of shape and oxygenation state. Here we monitored the effects of both shape and oxygenation state on cell mechanics in single cells, allowing the separate assessment of the contribution of each of these two factors, and demonstrating that the oxygenation state per se is not correlated with cell fluctuation mechanics.
• 3.We have put an upper bound on the value of the shear modulus at the amplitude relevant to flickering, and to address the possible role of the cytoskeleton in confining the membrane motion.
• 4.We have presented an analysis of mode dynamics to measure cytoplasmic viscosity. This new method is much simpler and direct than existing alternatives for estimating local viscosity inside cells, and it can be applied to single cells.