Estimating dementia-free life expectancy for Parkinson's patients using Bayesian inference and microsimulation

Abstract

Interval-censored longitudinal data taken from a Norwegian study of individuals with Parkinson's disease are investigated with respect to the onset of dementia. Of interest are risk factors for dementia and the subdivision of total life expectancy (LE) into LE with and without dementia. To estimate LEs using extrapolation, a parametric continuous-time 3-state illness–death Markov model is presented in a Bayesian framework. The framework is well suited to allow for heterogeneity via random effects and to investigate additional computation using model parameters. In the estimation of LEs, microsimulation is used to take into account random effects. Intensities of moving between the states are allowed to change in a piecewise-constant fashion by linking them to age as a time-dependent covariate. Possible right censoring at the end of the follow-up can be incorporated. The model is applicable in many situations where individuals are followed over a long time period. In describing how a disease develops over time, the model can help to predict future need for health care.

1. INTRODUCTION

Many population studies now have longitudinal follow-up and mortality information that can be combined to investigate transitions between health and ill health prior to death. Multistate models can be used to describe these transitions when states reflect health status and a death state is included. In describing how a disease develops over time, the models can help to predict future need for health care. Examples of applications are studies where patients are followed after a surgical operation, studies where stages of a disease are monitored after an infection, and longitudinal epidemiological studies. Our research was initiated by a Norwegian study into dementia and survival among patients with Parkinson's disease (Buter and others, 2008). In this study, the health states are “no dementia, dementia, and death,” with the assumption that transitions from dementia to no dementia are not possible. Individuals with Parkinson's disease are more likely to develop dementia than individuals without the disease (see, e.g. de Lau and others, 2005). For individuals with Parkinson's disease, the onset of dementia is an important predictor of health and need for care.

This paper presents Bayesian inference for a continuous-time 3-state illness–death Markov model. The intensities of moving between the states are related to covariates and random effects. By including age as a time-dependent covariate, time dependency of intensities can be taken into account in a piecewise-constant fashion. Relaxing the assumption of constant intensities makes the model applicable in many situations where individuals are followed over a long time period. One way to make use of the random-effect structure is to model possible heterogeneity that is not captured by observed covariates. The model in this paper assumes that transition times are interval censored except for known death times. Right censoring at the end of follow-up can be incorporated.

In addition, we show how to apply the Markov model to estimate life expectancy (LE). Using a parametric model for the time-dependent intensities makes it possible to extrapolate the model beyond the follow-up time and to estimate how many years of total LE will be spent in a disease state and which risk factors are important. In the presence of a random-effect structure, microsimulation can be used to estimate LE.

For the Norwegian study, Buter and others (2008) fitted a 3-state fixed-effect model using maximum likelihood estimation. They presented LEs conditional on baseline state and used a nonparametric bootstrap to estimate the variance of the estimated LEs. The Bayesian approach makes it easy to incorporate random effects, and there is no need for an additional stage for the estimation of the distribution of LEs because the approach is well suited to investigate derived variables from posterior distributions of the model parameters. In addition to the LEs conditional on baseline state, we estimate marginal LEs that do not require a specified baseline state but instead require the distribution of the baseline state.

One of the first publications on Bayesian inference for continuous-time multistate models is Sharples (1993). In recent years, additional work has been presented by, for example, Welton and Ades (2005) and Pan and others (2007). Our work can be seen as an extension to the Bayesian inference in Pan and others (2007) in that we allow for time-dependent intensities and exact death times.

Laditka and Wolf (1998) used microsimulation to estimate active LE given a fixed-effect discrete-time Markov model. The variance of estimated LE, however, was not discussed. To estimate the variance of quantities that are derived by using microsimulation, first- and second-order uncertainty have to be distinguished (Halpern and others, 2000). We will show how this is handled in our setting.

An important aspect of the data that determine the model chosen is whether or not transition times are known. For Bayesian inference given a multistate model with known transition times, see Kneib and Hennerfeind (2008). In our setting, as is common in many studies, known transition times are not available except for the transition into the death state. The disease status of the individuals is observed at prescheduled interviews, and as a consequence, observations are interval censored. Our multistate model is defined using transition intensities, but the likelihood contributions of observed time intervals are defined using transition probabilities. In this way, we account for the interval censoring in line with frequentist multistate models (see, e.g. Kay, 1986).

The paper is organized as follows. Section 2 introduces the model, and Section 3 shows how to estimate LEs given the model with random effects. In Section 4, an extension of the model is presented to take right censoring into account. Section 5 discusses the application, and Section 6 concludes the paper.

2. MARKOV MODEL

The first-order Markov assumption in a multistate model implies that the probability of moving to another state only depends on the current state. Our 3-state Markov model assumes that there is no recovery from State 2 back to State 1 and that known transition times are only available for transitions into the death state. We regress intensities on age as a time-dependent covariate to model possible change in the intensities.

In the model, the time interval between 2 consecutive measurements is not fixed but is allowed to vary between and within individuals. Although the model is formulated for individually observed time intervals, the subscript denoting individuals will be suppressed in order to keep notation simple. Let t denote time since entry to the study. At time t ≥ 0, the state of an individual is x_t ∈ {1,2,3}. A transition at time t from State r to State s, r ≠ s, occurs with intensity q_rs(t), where q_rs(t) ≥ 0 for (r,s) ∈ {(1,2),(1,3),(2,3)} and q_rs(t) = 0 for (r,s) ∈ {(2,1),(3,1),(3,2)}. Intensities are regressed on covariates and random effects by the log-linear model

(2.1)

where v^⊤ denotes the transpose of vector v, β_rs = (β_0.rs,β_1.rs,…, β_p.rs)^⊤, z(t) = (1,z₁(t), …, z_p(t))^⊤, and random-effect parameter τ = (τ₁₂,τ₁₃,τ₂₃)^⊤ is multivariate normally distributed with mean zero and unknown covariance matrix Σ. The model is flexible to other random-effect structures as will be illustrated in the application.

The time dependency of the intensities is taken into account by a piecewise-constant approximation: intensities are assumed to be constant within individually observed time intervals but may vary between intervals. In our model, covariate vector z(t) is deterministic in the sense that we know its values at every time t ≥ 0. A typical example of this is the time-dependent covariate age. The constant intensities q_rs(t) for an observed interval (t, u] are defined using the covariate values midway, that is, at time (t + u)/2. In case observed time intervals are wide and/or the time dependency is strong, this approach can be fine-tuned by subdividing observed intervals in shorter intervals and assuming that intensities are constant within the shorter intervals (Van den Hout and Matthews, 2008), but this method is not required here.

The statistical model is defined using transition probabilities, that is, probabilities of moving between the states. Transition probabilities for an observed time interval (t,u] are given by the 3×3 matrix P(t, u) = exp[(u − t)Q(t)], where for t ≥ 0 we define

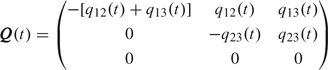(2.2)

and where exp[M] is defined for any square matrix M as the limit of the series ∑_{k = 0}^∞M^k/k!. The rs-entry P(t,u)[r,s] is given by ℙ(X_u = s|X_t = r). See, for example, Norris (1997) for details on time-continuous Markov chains with constant intensities. Matrix P(t, u) is available in closed form for the 3-state model without recovery.

Assume that an individual has observations at times t₁ = 0, t₂,…, t_M. Using the Markov assumption, the probability of the observed trajectory x_t1, x_t2,…, x_tM conditional on the first observation x_t1 is given by

(2.3)

where the conditioning on covariates and random effects is ignored in the notation. The contribution of this individual to the marginal likelihood is given by

(2.4)

where f is the density of the multivariate normal distribution with mean zero and covariance matrix Σ. To obtain the likelihood for the data, the individual contributions are taken together in a multiplication.

Given that the goal is Bayesian inference, we will use Markov chain Monte Carlo (MCMC) methods for approximating posterior distributions of model parameters. To do this, observed intervals (t₁, t₂],…, (t_{M − 1}, t_M] are modeled independently by using the multinomial distribution for the transitions to State X_{j + 1} given State X_j, j = 1,…,M − 1 (Pan and others, 2007).

Assume that the individual with observation times t₁ = 0,t₂,…,t_M has random-effect parameter vector τ. We recode States 1, 2, and 3 as (1,0,0), (0,1,0), and (0,0,1), respectively. Accordingly, we change the notation for the random variable that denotes the state from scalar X to vector X. For intervals (t_j, t_{j + 1}] that an individual survives, we assume that

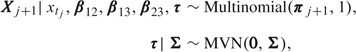where

(2.5)

for j ∈ {1, …, M − 1}.

In case an individual does not survive (t_{M − 1},t_M], we assume that

where

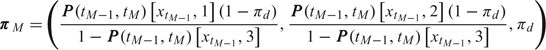(2.6)

given

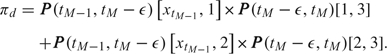(2.7)

This means that in case of death at t_M, we assume an unknown state just before death and then a transition into the death state within a small time interval ϵ (cf. Sharples, 1993). The probability of this event is denoted by π_d. Because of the ϵ-approximation of the exact death time in (2.7), 1 − π_d ≠ P(t_{M − 1}, t_M)[x_{tM − 1}, 1] + P(t_{M − 1}, t_M)[x_{tM − 1}, 2], hence the adjustment in (2.6) to ensure a proper distribution. Even though exact death times are known, we adhere to the ϵ-approximation. In maximum likelihood estimation, instantaneous intensities can be used, and in that case, the likelihood contribution of an observed death time would be P(t_{M − 1}, t_M)[x_{tM − 1}, 1]q₁₃(t) + P(t_{M − 1}, t_M)[x_{tM − 1}, 2]q₂₃(t) (see, e.g. Van den Hout and Matthews, 2009). In the Bayesian framework, we have to ensure that π_d is a probability, that is, 0 ≤ π_d ≤ 1, and we use the ϵ-approximation.

To estimate the total LE, the distribution of the state at baseline t₁ = 0 is needed. At baseline, the state is either State 1 or State 2. We propose to use the logistic regression model for the distribution of X₀ = X_t1. Defining θ = ℙ(X₀ = 2|z(0)), this model is given by logit(θ) = α^⊤z(0), where α = (α₁,…,α_p)^⊤. It follows that

For ease of exposition, we use the same covariate vector for the baseline distribution and for the intensities. This is not a necessary condition.

The following priors are used for the model parameters in the application. For the regression coefficients in the model for baseline state and the regression coefficients in the Markov model, we specify vague univariate normal distributions with mean zero and large variance. For the inverse of covariance matrix Σ, we specify a Wishart distribution. These choices will be illustrated in Section 5.

With both the distribution of the data and the prior distribution of the parameters specified, MCMC methods can be used to estimate the model. The models in this paper were programmed and run in OpenBUGS (Thomas and others, 2006). Output of OpenBUGS can be transported into R (R Development Core Team, 2008) using the R package coda (Plummer and others, 2006).

3. LES AND MICROSIMULATION

For the case without random effects, LE in State s ∈ {1,2} given initial state r ∈ {1, 2} is given by

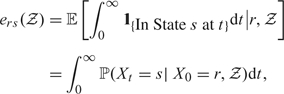(3.1)

where 𝒵 = {z(t)|t ≥ 0}. Expected LE in State s irrespective of the initial state (marginal LE) is given by

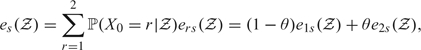(3.2)

where θ = ℙ(X₀ = 2|𝒵) is as defined in Section 2. Expected total LE is given by e_tot(𝒵) = e₁(𝒵) + e₂(𝒵). For applications of LEs given frequentists illness–death Markov models, see, for example, Izmirlian and others (2000) and Lièvre and others (2003).

Two methods can be used to estimate the posterior distribution of LEs. The first approximates the integral in (3.1) numerically, for example, by using the trapezoidal rule. The second is microsimulation where individual trajectories are simulated and corresponding individual survival is used to estimate LEs. Both methods can be applied within each MCMC run or after convergence using the posterior distribution of the model parameters. Straightforward numerical evaluation is possible if the covariate vector z(t) is deterministic in the sense that conditional on z(0), 𝒵 is completely specified. Microsimulation is more flexible in that it can also deal with random effects and with time-dependent covariates such as information about visited states. Microsimulation has been used in evaluating screening interventions (Cronin and others, 1998) and in cost-effectiveness modeling (Spiegelhalter and Best, 2003).

3.1. Using the trapezoidal rule

For each simulated parameter vector of the Markov model, the trapezoidal rule is applied to estimate e_rs(𝒵). Using the simulated parameter vectors of the baseline distribution, we derive the posteriors of marginal LEs and total LE.

It make sense to use one time grid for both the trapezoidal rule and the piecewise-constant model. Given time grid u₁ = 0,u₂,…, u_M, we approximate integrand ℙ(X_uj = s| X₀ = r, 𝒵) for all j ∈ {2,…, M}. To take into account the time dependency of the intensities, we use a piecewise-constant iterative method given by

(3.3)

We use 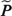(0, u_j) as an approximation for P(0, u_j). Whereas in the estimation of the model we use individually observed time intervals for the piecewise-constant intensities, in the estimation of the LEs we impose a time grid.

3.2. Using microsimulation

Let the time grid be given by u₁ = 0, u₂,…, u_M with time between equal to 1 year. Given a simulated parameter vector of the Markov model, a large number of trajectories through the states are simulated conditional on baseline state. If there is a random-effect structure, then random effects are simulated for each trajectory. If simulated states are denoted by their number, then individual survival in State 1 is estimated by the number of 1s in the simulated trajectory plus half a year. The half-year correction is to take into account that a transition to a next state can take place at any time in the year. Individual survival in State 2 is estimated by the number of 2s. A finer grid is of course possible, but the counting of the states has to be adjusted to the grid.

More formally, the nested simulation procedure above is as follows. Let ψ be the vector with the model parameters. First, values ψ_b, b = 1,…, B, are simulated from the posterior of ψ. Second, conditional on ψ_b, random effects τ_b^c, c = 1,…, C, are simulated. Next conditional on ψ_b and individual τ_b^c, a yearly trajectory is simulated and individual survival (generically denoted by L_b^c) is calculated. Sample mean 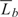_b and variance V_b are stored and are used to estimate first-order uncertainty 𝔼_ψ[V[L|ψ]] and second-order uncertainty V_ψ[𝔼[L|ψ]]. The former is the uncertainty caused by variability between individuals in the population, the latter is what we are after: uncertainty caused by model parameter uncertainty. The sum of these uncertainties is the total variance given by V[L] = 𝔼_ψ[V[L|ψ]] + V_ψ[𝔼[L|ψ]] (cf. Spiegelhalter and Best, 2003). In addition, we use the stored sample means to estimate 𝔼[L] = 𝔼_ψ[𝔼[L|ψ]].

O'Hagan and others (2007) discuss the choice of the number of simulations in the nested procedure, that is, B for the first level and C for the second level, and present a method to reduce the computational burden in case one is only interested in the mean and the variance of L. In case the goal is the posterior distribution of L, C has to be large. In the application, we used the method of O'Hagan and others (2007) to check whether the chosen C was large enough.

4. RIGHT CENSORING

Often in longitudinal data there will be right censoring. If death during follow-up is always observed, right censoring in our model means that if the state at the end of the study time is not observed, we still know that the individual is alive.

To take right censoring into account, we extend the model in Section 2. First, states are denoted by X^* and we code transition into the States 1, 2, 3, and the censored state by the vectors (1,0,0,0), (0,1,0,0), (0,0,1,0), and (0,0,0,1), respectively. The vectors are denoted by X^*. The 3 × 3 matrix P is computed as before. If the state at t_M is neither death nor right censored, we assume that

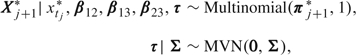where

for j = 1,…, M − 1. If the state at time t_M is the death state or a censored state, we assume that

where, in case of death, we define π_M* = (π_M, 0) where π_M is obtained by (2.6) after replacing the x_ts by x_t*s. In case of a censored state, we define π_M* = (0, 0, P(t_{M − 1}, t_M)[x_{tM − 1}*, 3], 1 − P(t_{M − 1}, t_M)[x_{tM − 1}*, 3]). By specifying the contribution to the likelihood as 1 − P(t_{M − 1}, t_M)[x_{tM − 1}*, 3], that is, by the probability of not dying within time interval (t_{M − 1}, t_M], we follow the literature on multistate model (see, e.g. Kay, 1986). Note that the contribution can be seen as P(T > C) when T is defined as time spent in the living states and C as the censoring time.

5. APPLICATION

5.1. Data

In a region with 220 000 inhabitants in Rogaland County, Norway, an attempt was made to recruit all individuals with recognized idiopathic Parkinson's disease. Parkinson's disease was diagnosed in 245 individuals. To avoid inclusion of individuals with dementia with Lewy bodies, 18 individuals with clinically significant cognitive impairment were excluded from the study. During follow-up, 3 individuals died before the first assessment, 7 were rediagnosed as not having Parkinson's disease, and 2 had schizophrenia, leaving n = 233 individuals eligible for the present study. The 233 individuals were followed from baseline 1993 up to 2005. For those individuals who did not die before 2005, interviews took place in 1993, 1997 and 2001–2005. There are 3 individuals with a censored last state. For further details, see Buter and others (2008).

In total, there were 897 observations (total number of interviews, censored states, and observed deaths), which means that there were 897 − n = 664 observed intervals. The number of individuals who died during study time is 187. Individuals with only one interview are also included. In the latter case, observations consist of the initial state and a time of death or the initial state and the censored state at the end of follow-up. The mean length of observed time intervals in years is 2.48 (median 1.48), and the mean number of interviews is 3.03 (median 2).

Table 1 presents observed frequencies in each state at follow-up times. Because of the progressive nature of dementia, a missing state can sometimes be derived from consecutively observed states. For series of states 1?1, 2?2, and 2?3, where the question mark denotes a missing state, we know the missing state. There are 10 individuals with intermediate missing states that cannot be derived in this way. These missing states are noted in the table as the 6 + 5 + 4 + 4 + 3 = 22 censored states during follow-up. Missing intermediate states is not a problem for the estimation of the model but might bias results if the missingness is substantial. Our piecewise-constant model assumes that intensities are not changing between the interviews but might change from interview to interview. Missing several interviews affects the piecewise-constant approximation to the continuous time dependency of the intensities. Since there are only 10 persons with missing intermediate interviews and only 2 of them with more than 1 consecutive interview missing, we assume that the bias is negligible.

Table 1.

Observed and rounded expected frequencies in each state at follow-up times in the Rogaland study, where (a + b) denotes a individuals previously in State 1 and b in State 2

State	Time in years
	Baseline	4	8	9	10	11	12
Observed
1	171	86	42	38	31	29	24
2	62	62(43 + 19)	54(25 + 29)	39(2 + 37)	28(2 + 26)	22(1 + 21)	19(5 + 14)
Dead		79(36 + 43)	53(20 + 33)	20(3 + 17)	18(5 + 13)	9(2 + 7)	8(0 + 8)
Censored		6	5	4	4	3	3
Expected given Model 1
1	171	91	46	35	32	26	24
2	62	66(42 + 22)	43(21 + 22)	47(5 + 42)	35(5 + 30)	26(4 + 22)	21(4 + 17)
Dead		78(38 + 40)	59(19 + 40)	13(1 + 12)	8(1 + 9)	7(1 + 6)	6(1 + 5)
Expected given Model 2
1	171	87	49	37	33	27	25
2	62	64(43 + 21)	44(19 + 25)	46(4 + 42)	35(4 + 31)	25(3 + 22)	21(3 + 18)
Dead		83(41 + 41)	55(18 + 37)	13(1 + 12)	9(1 + 8)	7(1 + 6)	5(1 + 4)

Frequencies of observed transitions between the states are given in Table 2. Note that there are no transitions from State 2 back to State 1. Three covariates will be used in the model: time-dependent age in years minus 77, sex as a dummy (0 ≡ men), and duration as the number of years the individual had Parkinson's disease before 1993 centered by subtracting 9 years. Before centering, minimum, mean, and maximum for age in years during follow-up are 36, 77.42, and 101, respectively. Minimum, mean, and maximum duration of Parkinson's disease in years are 1, 8.89, and 34, respectively. The time interval ϵ that is used to approximate exact transition times into the death state is fixed to be ϵ = 0.001 years. This value was chosen because it is small, and there is no individual in the data who dies within 0.001 years of their last interview.

Table 2.

Frequencies of observed transitions between the states in the Rogaland study

		To state		Death	Censored
		1	2
From state	1	250	78	66	3
	2	0	146	121	0

5.2. Models

Using t as the number of years since baseline, we specify 2 models. The models are the results of a model comparison that can be found in Section A of the supplementary material available at Biostatistics online. Fixed-effect Model 1 encompasses a model for the baseline state and one for the intensities and is given for individual i by

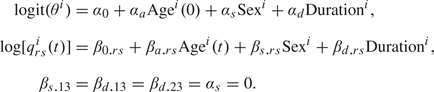Model 2 has the same model for the baseline and the same restrictions for the fixed effects. The model for the intensities, however, is extended with random effects and is given by

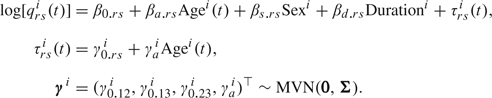Model 2 for the intensities is a slightly extended version of model (2.1). We include the random slope γ_aⁱ to allow τ_rsⁱ(t) to change over time.

For the fixed-effect regression coefficients in Models 1 and 2, we specified vague univariate normal distributions with mean zero and variance equal to 1000. For Model 2, a prior is needed for 4 × 4 covariance matrix Σ. Here we followed common practice and used a Wishart distribution to specify the prior of the precision matrix T = Σ ^{− 1}, that is, T ∼ W(R ^{− 1},4), where R is a 4 × 4 matrix. Since 𝔼[T] = 4R ^{− 1}, it follows that 4 ^{− 1}R can be seen as a prior guess at the order of magnitude of Σ.

Given a model, MCMC consisted of 2 chains with different starting values for α, β₁₂, β₁₃, and β₂₃. For both chains, the first 50 000 iterations were ignored (burn-in) and the additional 50 000 iterations were thinned and used to compute the posterior means, the 95% credible intervals, and the deviance information criterion (DIC, Spiegelhalter and others, 2002). For the models in this paper, the MCMC took about 2 h to run on a 2.59-GHz PC with dual core AMD microprocessor. Convergence of the chain was checked visually by plotting the chains, the autocorrelation, and the Gelman–Rubin convergence statistic, as modified by Brooks and Gelman (1998). Numerically, convergence was assessed by checking the Monte Carlo error. All these functions can be called within OpenBUGS. We used the DIC to compare models. The DIC comparison is based on trade-off between the fit of the data to the model and the complexity of the model. Models with smaller DIC are better supported by the data.

Both Models 1 and 2 have DIC = 4142. It makes sense in this case to choose Model 1 as it is the most parsimonious. However, we think that Model 2 is interesting as it includes random effects to capture possible heterogeneity not captured by the covariates and it allows random effects to change over time by regressing the effects on time-dependent age. To estimate LEs, we have to extrapolate the model beyond the follow-up of the survey. Assuming no heterogeneity beyond the covariates and no further change over time beyond the fixed effect of age might be too restrictive.

A sensitivity analysis with regard to the specification of priors was conducted. For the fixed effects, alternative univariate normal distributions were investigated with mean zero and variance equal to either 100 or 10000. For Model 2, alternative priors for the precision matrix T were considered. Denote the diagonal entries of R for the random intercepts r₁ and the diagonal entries for the random slopes r₂. The DICs varied slightly for specifications (r₁,r₂) = (1,0.001), (r₁,r₂) = (2,0.01), and (r₁,r₂) = (0.25,0.001), but we do not consider the variation to be significant. (For details, see Section B of the supplementary material available at Biostatistics online.)

5.3. Inference

Table 3 presents posterior means for the parameters in Models 1 and 2. For Model 2, we provide posterior means of σ_0.12 = Σ₁₁^1/2, σ_0.13 = Σ₂₂^1/2, σ_0.23 = Σ₃₃^1/2, and σ_a = Σ₄₄^1/2. There are differences in the posterior means of the covariate effects. Note that for Model 2, the means for the covariate effects are all larger than for Model 1. These differences and the posterior means of standard deviations of σ_0.12,σ_0.12,σ_0.23, and σ_a show that adding the random effects lead to a different description of the data.

Table 3.

Posterior means and DICs for Models 1 and 2 each including a Markov model and a logistic regression model for the baseline; 95% credible intervals in parentheses

		Model 1	Model 2
Markov model
Intercepts	β0.12	– 1.496(– 1.795, – 1.221)	– 1.394(– 1.772, – 1.015)
	β0.13	– 4.013(– 5.127, – 3.271)	– 4.342(– 5.716, – 3.420)
	β0.23	– 1.286(– 1.533, – 1.053)	– 1.288(– 1.574, – 1.009)
Age	βa.12	0.086(0.057, 0.115)	0.105(0.066, 0.152)
	βa.13	0.050(– 0.028, 0.147)	0.057(– 0.035, 0.167)
	βa.23	0.027(0.005, 0.054)	0.043(0.010, 0.079)
Sex	βs.12	– 0.571(– 0.970, – 0.174)	– 0.590(– 1.098, – 0.091)
	βs.13	0†	0†
	βs.23	– 0.361(– 0.682, – 0.038)	– 0.427(– 0.809, – 0.059)
Duration	βd.12	0.069 (0.027, 0.111)	0.080 (0.029, 0.136)
	βd.13	0†	0†
	βd.23	0†	0†
Random effect	σ0.12		0.650 (0.350, 1.111)
	σ0.13		0.748 (0.349, 1.583)
	σ0.23		0.436 (0.280, 0.653)
	σa		0.047 (0.030, 0.071)
Logistic regression model
Intercept	α0	– 0.914(– 1.255, – 0.584)	– 0.912(– 1.261, – 0.581)
Age	αa	0.166(0.112, 0.224)	0.165(0.112, 0.225)
Sex	αs	0†	0†
Duration	αd	0.047(– 0.009, 0.104)	0.047(– 0.008, 0.103)

^†Restricted to zero.

Both models show that for individuals with Parkinson's disease but without dementia, sex and the duration of the disease at baseline do not have an effect on the intensities for transitions to the death state. Further restriction, β_d.23 = 0 indicates that for individuals with Parkinson's disease and dementia, the history of the disease at baseline does not have an effect on the transition to the death state. The unrestricted regression coefficients show that all covariates are important for the onset of dementia and that given Parkinson's disease men are more likely to become demented than women of the same age and with the same history of the disease at baseline. Posterior means for the logistic regression model for the baseline state probability θ = ℙ(X₀ = 2|z(0)) show that with increasing age and more years of duration, it is more likely that the patient is demented. This concurs with our expectations.

The computation of the LEs was done using the posterior of the model parameters derived from MCMC after the burn-in. The time between h in the time grid for the LEs was 1 year. Table 4 presents the results. For Model 1 without random effects, we used both microsimulation and the trapezoidal rule in order to compare performance. For Model 2, we used microsimulation. To approximate LE given by (3.1), we impose a time that represents infinity conditional on specified age at baseline. This time is the time to assumed maximum age minus age at baseline. For maximum age, we choose 110 years old, which—for Parkinson's disease patients—seems reasonable. Microsimulation is computationally intensive. For B = C = 1000, the simulation took twice the time taken to estimate the model via MCMC. The estimation seems to be robust regarding the specification of the time between in the time grid. For h equal to 1/2 year, the results (not shown) are very similar.

Table 4.

Posterior means for LEs for men with 8 years of Parkinson's disease at baseline. Estimation for Models 1 and 2 with 95% credible intervals in parentheses

	Model 1		Model 2
	Trapezoidal rule (B = 1000)	Microsimulation (B = C = 1000)	Microsimulation (B = C = 1000)
Age 60 years
e11	8.7 (7.1, 10.4)	8.8 (7.0, 10.5)	9.4 (7.5, 11.5)
e12	3.5 (2.6, 4.5)	3.5 (2.6, 4.6)	3.7 (2.7, 5.0)
e22	5.0 (3.1, 7.0)	5.0 (3.1, 7.2)	6.3 (4.0, 8.7)
e1	8.5 (6.9, 10.1)	8.5 (6.8, 10.3)	9.2 (7.3, 11.3)
e2	3.6 (2.7, 4.6)	3.6 (2.6, 4.6)	3.8 (2.7, 5.0)
etot	12.0 (10.3, 13.8)	12.1 (10.2, 14.0)	13.0 (10.9, 15.1)
Age 70 years
e11	5.0 (4.1, 5.9)	5.0 (4.1, 6.0)	5.3 (4.2, 6.6)
e12	3.1 (2.5, 3.8)	3.1 (2.5, 3.9)	3.3 (2.5, 4.2)
e22	3.9 (3.0, 4.8)	3.9 (3.0, 4.9)	4.3 (3.2, 5.6)
e1	4.4 (3.6, 5.3)	4.4 (3.7, 5.4)	4.7 (3.7, 5.9)
e2	3.2 (2.6, 3.9)	3.2 (2.5, 4.0)	3.4 (2.6, 4.4)
etot	7.6 (6.7, 8.6)	7.7 (6.7, 8.7)	8.1 (6.9, 9.4)

Using the 1-way analysis of variance technique proposed by O'Hagan and others (2007), we checked results by comparing estimated standard errors. For C = 1000, there is indeed some consistent overestimation, but the bias is negligible for practical purposes. (For details, see Section C of the supplementary material available at Biostatistics online.)

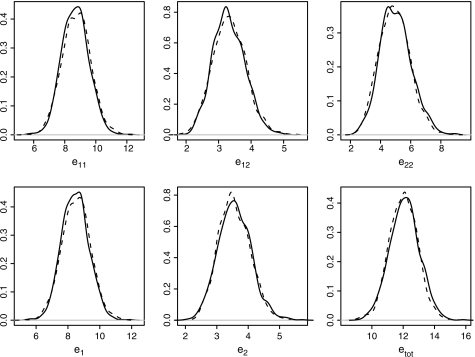
For Model 1, the posterior densities of the LEs for men aged 60 years at baseline with 8 years of Parkinson's disease at baseline are given in Figure 1. The dashed lines are the expectancies computed using the trapezoidal rule, and the solid lines are the expectancies computed using microsimulation. The results for the trapezoidal rule are a bit smoother. Overall, however, differences are minimal.

Fig. 1.

For Model 1, posterior distributions of the LEs for men aged 60 years at baseline with 8 years of Parkinson's disease at baseline (solid lines for microsimulation; dashed lines for trapezoidal rule).

For Model 2, credible intervals are wider. This is to be expected as there will be more variation due to the random effects. Posterior means for LEs for Model 2 are higher than the means for Model 1, especially for e₁₁ and e₁. This is not due to skewed distributions for Model 2. Median LEs (not shown) are very similar to the means reported in Table 4. Note that given a specific age at baseline, zero is the lower bound for the simulated LE, but there is no upper bound other than the assumed maximum age. The higher LEs for Model 2 are caused by simulated random effects that reflect more healthy individuals with relatively long lives. This trend may reflect the data where there is less information for the more healthy individuals who stay in State 1 during the whole follow-up.

Even though the 2 models yield different estimates, the differences are within bounds. Looking at the results for Models 1 and 2 for the LEs, it is interesting to note that the years spent with dementia irrespective of baseline state (e₂) do not differ much for the ages 60 and 70. Given that the extrapolation is largest for those aged 60 years, it is understandable that the 95% credible intervals are wider for those aged 60 years than for those aged 70 years.

5.4. Validation

Given the regular observation times in the Rogaland study, we can investigate some aspects of goodness of fit by comparing observed frequencies in each state with expected frequencies. The approach is inspired by the model assessment in the R package for multistate models msm (Jackson and others, 2003) but differs from msm in that it works with the observed covariate values at baseline. In principle, the setup makes it possible to use the Bayesian χ² test for goodness-of-fit as introduced by Johnson (2004). However, this χ² test relies on asymptotic properties that are not met in our situation. (For details see Section D of the supplementary material available at Biostatistics online.)

Observation times other than death take place at years t0, t1,…, t6 = 0, 4, 8, 9, 10, 12. Let n denote the number of individuals in the data and let Xti denote the state of individual i at time t. For State s ∈ {1, 2, censored}, define observed frequencies O[s, tj] = ∑i = 1n1{Xtji = s}, for j = 2,…, 6. Given the known death times, we define O[dead,tj] = ∑i = 1n1{∃t*[tj − 1 < t* < tj ∧ Xt*i = dead]}, for j = 2,…, 6. These frequencies are presented in Table 1. The table also shows the observed frequencies split according to the previously observed state. For example, 4 years after baseline, from the 62 individuals who are observed in State 2, 43 were observed in State 1 at baseline and 19 were observed in State 2 at baseline.

Observed frequencies can be compared with expected frequencies by defining table E[t] = ∑_{i = 1}ⁿPⁱ(t, 0), where Pⁱ(t, 0) is the matrix with the transition probabilities for individual i derived from a simulated model parameter vector (for Model 2, this includes the random effects). The individual transition matrices are approximated using the grid approach in (3.3), where the grid is given by t₀,t₁,…, t₆. In this approximation, the covariate values of individual i at baseline are used and the change of age at the grid points is taken into account.

For a visual inspection of goodness of fit, 1000 simulated values of the parameter vectors are used to computed 1000 times E[t]. For Models 1 and 2, the mean of the 1000 simulated tables is presented in Table 1 as the expected frequencies. In general, observed and expected frequencies are similar for both models. There is a deviation for State 2 in the later years in the sense that the number of individuals in State 2 is overestimated and the number of deaths underestimated. Although this is not a proper statistical test, Table 1 shows that Models 1 and 2 fit the data reasonably well.

6. DISCUSSION

LEs in health and ill health can be of importance for the planning of future health care. Survival is not only about total LE but also about whether or not remaining life time will be spent in good health. For longitudinal data, we have shown how transitions between health, ill health, and death can be modeled using the Bayesian framework. In addition, we have shown how to estimate the posterior densities of LEs in health and ill health. In many longitudinal studies, transition intensities will change over time and one way of taking this into account is to include age as a time-dependent covariate for the intensities.

The approach is illustrated using a 3-state model without recovery for Parkinson's patients where dementia represents ill health. BUGS was used for estimation with MCMC. The model in the paper can be extended to more complex models, for instance models with recovery from the ill health state or model with more states. When there is a closed-form expression for the matrix with the transition probabilities given the transition intensities, the standard functions in BUGS can be used to estimate the model. Another possibility is to disentangle the effect of baseline age and the effect of time by using q_rs(t) = exp[β_0.rs + β_t.rst + β_a.rs A g e(0) + ⋯], where Age(0) is age at the start of the study.

Interval censoring is an important feature of the data that we analyzed. If exact transition times had been available for transitions out of State 1, standard survival models might have been applied to estimate LE in State 1. The problem for an observed series of states such as 1113 is that we do not know whether the latent trajectory was via State 2 or directly from State 1 to State 3. We could right censor the series midway the last time interval as an approximation, but this leads to 100% censoring. For LE in State 2, standard survival models be sufficient, but it will only address part of our research question. Applying a multistate model seems to be best option as it formulates an overall model and makes it possible to borrow strength across the transitions, for example, via shared random effects such as the random slopes in the application.

The first-order Markov assumption that is often used in applications of multistate models is not always realistic. The model for the Parkinson's disease study uses the Markov assumption, and the informal assessment of goodness of fit shows that the model fits the data well. The use of age as a time-dependent covariate is crucial here. For example, time spent in the dementia state might have an effect on the risk of moving to the death state, but part of this is covered by the effect of changing age.

We have illustrated the use of microsimulation in the estimation of LEs when the regression model for the intensities includes random effects. Direct numerical approximation of the complex multidimensional integral that takes into account random effects and time-dependent age may often not be feasible. Microsimulation is an alternative that is intuitive and easy to implement. We think that microsimulation has potential for more complex multistate models. To estimate LEs, the multistate model is extrapolated beyond the follow-up of the study and this asks for special methods in case covariates are not deterministic. For example, given a 3-state illness–death model with recovery, it is possible to add the covariate “previously observed in State 2”. This covariate is not deterministic but can be used in a microsimulation where individual trajectories are simulated and the next state is simulated conditional on the history of previously simulated states.

FUNDING

Funding to pay the Open Access publication charges for this article was provided by the UK Medical Research Council Biostatistics Unit (U.1052.00.013).

SUPPLEMENTARY MATERIAL

Supplementary Material is available at http://www.biostatistics.oxfordjournals.org.