CELL SEGMENTATION USING HESSIAN-BASED DETECTION AND CONTOUR EVOLUTION WITH DIRECTIONAL DERIVATIVES

Abstract

The large amount of data produced by biological live cell imaging studies of cell behavior requires accurate automated cell segmentation algorithms for rapid, unbiased and reproducible scientific analysis. This paper presents a new approach to obtain precise boundaries of cells with complex shapes using ridge measures for initial detection and a modified geodesic active contour for curve evolution that exploits the halo effect present in phase-contrast microscopy. The level set contour evolution is controlled by a novel spatially adaptive stopping function based on the intensity profile perpendicular to the evolving front. The proposed approach is tested on human cancer cell images from LSDCAS and achieves high accuracy even in complex environments.

1. INTRODUCTION

Live cell imaging is emerging as an important tool in biomedical research. Nevertheless, there are few, if any, robust analysis systems capable of automatically extracting quantitative information from cell image streams. Large scale quantification of the dynamical behavior of cell populations in a variety of experimental systems would provide important capabilities for many areas of cell biology. In addition, such quantitative cellular data would be useful in many theoretical contexts. For example, high throughput-based drug discovery efforts would be more reliable if the timing and mechanism of cell death could be detected automatically, as existing methods for cell death determination are not mechanism-specific. Identification of abnormalities related to cell growth induced by anti-cancer treatments might lead to good indicators of undesirable side-effects in a candidate drug. Theoretical developments in the field of Cellular Biophysics have long been hampered by the lack of quantitative data at the level of a single cell. Phase-contrast microscopy is an ideal non-perturbing imaging technology for these studies examining long-term cell behaviors [1] since harmful side effects are minimized or avoided using fluorescent excitations which become toxic to cells over time. However, a necessary prerequisite for single-cell analysis frameworks using phase contrast microscopy imaging is the accurate and reliable detection of cell borders which is the focus of this paper.

In recent years, active contours have become popular for cell segmentation [2]. Geometric model of active contours [3] presents desirable properties such as the lack of need to reparameterize the curve and automatic handling of topology changes via level set implementation [4]. The major drawbacks of this approach is the leakage due to weak edges and stopping at local maximums in noisy images. While the region based active contours [5–7] overcome these drawbacks, they require a bimodal image model to discern background and foreground which is not applicable in higher resolution cell image acquisition. Figure 1 shows a typical phase contrast image of a cell. The white region surrounding the cell is the typical phase halo produced by the imaging process and proportional to the local thickness of the cell. A straight-forward implementation of [5] converges to the boundaries between phase halo and the rest of the image. Using various features in Chan and Vese formulation such as variance to discern cells from background [8] gives satisfactory results but the sharp phase halos contribute to the variance and may cause early stopping of curve evolution in certain cases. Similarly, edge stopping functions used in regular geodesic active contours, if initialized outside of the cells, respond to the outer edges of phase halos and cause early stopping which produces an inaccurate segmentation that includes the phase halo in the cell area. When the curve is initialized inside the cells, the texture inside the cell also causes premature stopping before the curve reaches to the boundary. Often phase halo is seen as a nuisance and is compensated by normalizing the image. While this produces a halo-free image, it also weakens the cell boundaries further, especially in the areas where cells are flattened. This leads to the leakage in the curve evolution. One remedy is to enforce a model on the cell shape such as [9], but it fails for cells with highly irregular shapes. Nuclei based initialization and segmentation [10, 11] is also not applicable to images such as in Figure 1.

Fig. 1.

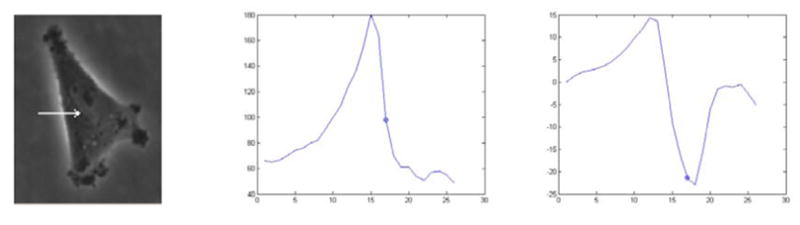
A sample cell image, its intensity profile at the marked direction, and the derivative of the directional profile. The actual cell boundary point is marked on the graphs.

To obtain an accurate segmentation, we propose an approach that exploits the phase halo effect instead of compensating it. The phase contrast microscopy imaging process produces a phase halo around the cell and as a result, the intensity profile in the perpendicular direction to the local cell boundary is similar; it passes from the brighter phase halo to the darker cell boundary at every boundary point. To exploit this observation, we propose to initialize the curve just outside the cell and the phase halo so that the initial curve resembles the final boundary in order to coincide the ideal boundary normal with the curve normal; and control the evolution of the curve by modifying the edge stopping function in such a way that the curve does not stop at the halo edge but at the actual cell boundary. By selecting at which edge in the local normal direction the curve stops, we effectively let the curve evolve through the halo and stop at the actual boundary. We also use a spatially adaptive force which slows the curve evolution in boundaries to prevent leakage. The rest of the paper is organized as following: section 2 explains the ridge measures we use to obtain a close initialization, section 3 presents the modified geodesic active contour, the experimental results are discussed in section 4 and conclusion is given in section 5.

2. HESSIAN-BASED CELL DETECTION

An initial curve that is close to the actual cell boundary is required to capture the desired characteristic of the local directional derivative as shown in Figure 1. Shape-based properties of the intensity surface are used to produce the initial coarse cell map. These properties are chosen because of their robustness to image contrast and intensity variations. In phase contrast microscopy images, the cell membrane boundaries and phase halos around the cells produce crest lines (ridges and valleys), and subcellular structures produce blob or ridge like patterns so the use of ridge detection methods are ideal for this purpose. Various ridge definitions can be found in the literature that lead to different detection methods. In curvature based detection, ridges can be defined as local extrema of principal curvatures [12, 13]. Principal curvatures and directions of a surface L correspond to the eigenvalues κ₁ ≥ … ≥ κ_n−1 and eigenvectors ξ₁ ≥ … ≥ ξ_n−1 of the shape operator matrix on the tangent space W:

$$W={\mathbf{I}}^{-1}\mathbf{II}={\left[\begin{array}{cc}{L}_x·L_x& L_x·L_y\\ L_x·L_y& L_y·L_y\end{array}\right]}^{-1}\left[\begin{array}{cc}{L}_{xx}·c& L_{xy}·c\\ L_{xy}·c& L_{yy}·c\end{array}\right]$$ (1)

where I and II are the first and second fundamental forms and c = (L_x × L_y)/(|L_x × L_y|) [12]. Since computation of principal curvatures is expensive, mean curvature $H=\frac{1}{2}({\kappa }_1+{\kappa }_2)=\frac{1}{2}\text{trace}(W)$ is often used [12,14] to classify surface patches (H < 0: peak, ridge, or saddle ridge; H = 0: flat or minimal surface; H > 0: pit, valley, or saddle valley).

The local extrema for real-valued functions can be generalized to vector spaces using the Hessian matrix [12]. A point x₀ is classified as maximum if ∇L(x₀) = 0 (critical point) and ℋ(L(x₀)) is negative definite (all eigenvalues λ_i < 0 ) where ℋ is the Hessian matrix:

$$\mathcal{\mathscr{H}}=\left[\begin{array}{cc}{L}_{xx}& L_{xy}\\ L_{xy}& L_{yy}\end{array}\right]$$ (2)

For critical points (∇L(x₀) = 0), with respect to the Taylor series expansion and curvature definitions, eigenvalues λ_i and eigenvectors υ_i of the Hessian matrix correspond to principal curvatures κ_i and principal directions ξ_i respectively [15]. Eigenvalues and eigenvectors of the Hessian matrix have been used in many medical image processing applications as a ridgeness measure [16,17]. Table 1 summarizes possible orientation patterns based on the value of the eigenvalues λ₁ and λ₂ of the Hessian matrix ℋ. Laplacian operator (Eq. 3) is a good approximation of the sign of the eigenvalues of the Hessian matrix. It returns positive values for intensity valleys, negative values for intensity ridges, and small absolute values in homogeneous regions with small noise.

Table 1.

Possible orientation patterns based on the eigenvalues ${\lambda }_{1,2}=\frac{1}{2}(L_{xx}+L_{yy}\pm \sqrt{{(L_{xx}-L_{yy})}^2+{(2L_{xy})}^2})$ (|λ₁| ≤ |λ₂|, H = high, L = low) [18].

λ1	λ2	orientation pattern
L	L	Flat or Noise no preferred direction
H−	L	Bright tubular structure
H+	L	Dark tubular structure
H−	H−	Bright blob-like structure
H+	H+	Dark blob-like structure

$$\mathrm{\Delta }(L)=\text{trace}(\mathcal{\mathscr{H}})=L_{xx}+L_{yy}={\lambda }_1+{\lambda }_2$$ (3)

Since we want to detect membrane boundaries, phase halos, and sub-cellular structures associated with cells (dark ridges, bright ridges and dark blobs respectively ), we use |λ₁(ℋ)|. Initial cell detection is done by thresholding |λ₁(ℋ)|. Threshold value T_r is chosen as 0.5σ where σ is standard deviation of λ₁(ℋ). Regions where |λ₁(ℋ)| > T_r are classified as cells. The obtained mask is further refined by morphological operations to make cell masks more compact, to remove spurious detections and to refine cell contours.

3. GEODESIC ACTIVE CONTOUR EVOLUTION CONTROLLED BY DIRECTIONAL DERIVATIVES

Ridges and blobs of the intensity surface are good initializations for cell detection, but obtained ridge/blob maps have spurious results or discontinuities. Morphological operations handle some of these problems but resulting cell masks are larger than the actual cells, particularly where the phase halos are thick, since these masks include the phase halos around the cells. To refine the initial cell detection, we propose a novel geodesic active contour segmentation with spatially adaptive force and controlled evolution using modified edge stopping function with directional derivatives. In level set based active contour methods, a curve is represented implicitly via a Lipschitz function ϕ by = {(x, y)|ϕ(x, y) = 0}, and the evolution of the curve is given by the zero-level curve of the function ϕ(t, x, y) [5]. We propose use of a modified version of the geodesic active contours [3]. In regular geodesic active contours [3] the level set function ϕ is evolved using the speed function,

$$\frac{\partial \varphi }{\partial t}=g(\nabla \mathbf{I})(F_c+\mathcal{K}(\varphi ))\mid \nabla \varphi \mid +\nabla \varphi ·\nabla g(\nabla \mathbf{I})$$ (4)

where F_c is a constant, 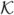is the curvature term (Eq. 5) and g(∇I) is the edge stopping function, a decreasing function of the image gradient which can be defined as in Eq. 6.

$$\mathcal{K}=\text{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)=\frac{{\varphi }_{xx}{\varphi }_y^2-2{\varphi }_x{\varphi }_y{\varphi }_{xy}+{\varphi }_{yy}{\varphi }_x^2}{{({\varphi }_x^2+{\varphi }_y^2)}^{\frac{3}{2}}}$$ (5)

$$g(\nabla \mathbf{I})=exp(-\mid \nabla G_{\sigma }(x,y)\ast \mathbf{I}(x,y)\mid )$$ (6)

The constant balloon force F_c pushes the curve inwards or outwards depending on its sign. The regularization term 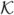ensures boundary smoothness and g(I) is used to stop the curve evolution at cell boundaries. The term ∇g·∇ϕ is used to increase the basin of attraction for evolving the curve to the boundaries of the objects. The geodesic active contours are more suitable for our application where intensity inside the cell boundaries is highly heterogeneous, and there is no clear difference between inside and outside intensity profiles so intensity thresholding or Chan-Vese type minimal variance models are not applicable. However, since they are designed to stop at edges, they suffer from: (1) early stopping on background or foreground edges, (2) contour leaking across weak boundaries, and (3) for our particular application, early stopping at outer edges of phase halos. To overcome the first problem, we use the ridge-based initialization that starts the contour from outside very close to the actual boundary. To reduce the effects of the second problem, we propose replacing the constant balloon force F_c in Eq. 4 with an intensity adaptive force F_A:

$$F_A(x,y)=c_1\mathbf{I}(x,y)$$ (7)

This intensity adaptive force increases speed of contraction on bright phase halos and reduces it on thin dark extensions and prevents leaking across weak edges. To handle the third problem, we propose a directional derivative controlled edge stopping function. Despite the problem it causes, the existence of phase halo increases the edge strength at cell boundaries which can be utilized. We propose a selective edge stopping function g_d (Eq. 10) controlled by the directional derivative, that lets the curve evolve through the outer halo edge and stop at the actual boundary edge. As shown in Figure 1, if initialized close to the actual boundary, the first light-to-dark edge encountered in the local perpendicular direction corresponds to the actual boundary. By choosing this transition as the stopping criterion we avoid the outer edge of phase halo. This stopping function is obtained as follows. Normal vector N⃗ to the evolving contour/surface can be determined directly from the level set function:

$$\overrightarrow{N}=-\frac{\nabla \varphi }{\mid \nabla \varphi \mid }$$ (8)

Edge profile is obtained using intensity derivative in the direction opposite to the contour normal (from outside to inside):

$${\mathbf{I}}_{-\overrightarrow{N}}=\frac{\nabla \varphi }{\mid \nabla \varphi \mid }·\nabla \mathbf{I}$$ (9)

Dark-to-light transitions produce positive response in I_−N⃗. We define the directional derivative controlled edge stopping function g_d as:

$$\begin{array}{l}{g}_d(\nabla \mathbf{I})=1-\text{H}(-{\mathbf{I}}_{-\overrightarrow{N}})(1-g(\nabla \mathbf{I}))\\ =1-\text{H}({\mathbf{I}}_{\overrightarrow{N}})(1-g(\nabla \mathbf{I}))\end{array}$$ (10)

where H is the heaviside step function:

$$\text{H}(x)=\{\begin{array}{ll}1\hfill & \text{if}x>0\hfill \\ 0\hfill & \text{elsewhere}\hfill \end{array}$$

This sets g_d to 1 at regions where there is a dark-to-light (background-to-halo) transition, and keeps regular edge stopping function everywhere else. Thus it lets the active contour evolve through dark-to-light edges and stop on light-to-dark edges.

4. EXPERIMENTAL RESULTS

Live cell image sequences were obtained using the Large Scale Digital Cell Analysis System (LSDCAS). LSDCAS is a research core facility at the Holden Comprehensive Cancer Center at the University of Iowa, and was developed to provide for non-perturbing live cell imaging capabilities [1,19]. LSDCAS images cell cultures under conditions identical to those used in routine biochemical and molecular investigations in biomedical research labs and is the only open-source complete live cell imaging solution available to the biomedical research community¹. For the cell images shown in this paper, WM793 human melanoma cells were grown on 25 cm² plastic flasks in minimal essential medium (GIBCO) supplemented with 10% fetal bovine serum and antibiotics. The inhomogeneous background is required to support proper cell growth but complicates reliable image analysis. The fields analyzed were chosen randomly from the T25 flask in which the cells are growing. These cells exhibit extensive pseudopodia and lammelapodia morphological structures that make accurate segmentation of thin structures very challenging for other techniques. The images were acquired using a Basler camera, with a 20× objective and pixel resolution of 0.67 × 0.59 microns/pixel. For details of the data acquisition and current analysis capabilities of LSDCAS, as well as cell culture environmental control, see [1].

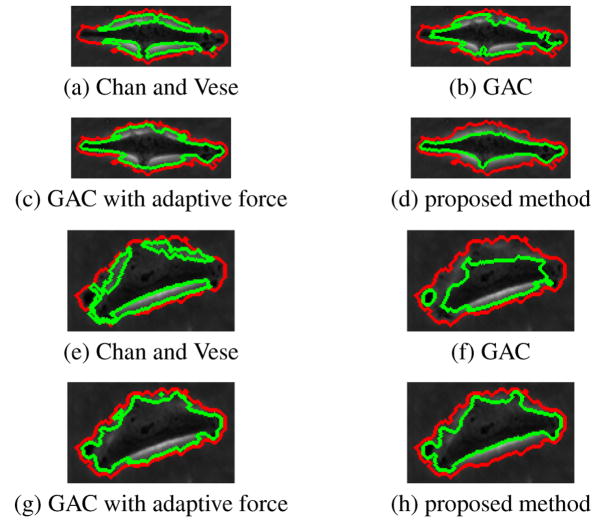
Figure 2 shows results of four methods on a sample frame. Figure 3 shows results of four methods on magnified cells. Red contour represents the ridge-based initialization as described before. For many cells, it produces a good approximation of the cell shape. Green contours represent the segmentation results. Chan and Vese method on intensity image, as expected, converges on phase halos. In an earlier study [8], the Chan and Vese method was applied to variance images rather than intensity to exploit the observation that cells have more texture than the background. For most of the cases good results were obtained in [8], but for some cases where image statistics vary significantly, the segmentation was poor. Geodesic active contour with fixed force and regular edge stopping function leaks through weak edges and is stopped by the strong phase halo edges. If the spatially adaptive force is applied, the contour tends to stop at weak edges most of the time as well as on strong halo edges. The proposed directional selective edge stopping function with spatially adaptive force obtains the desired result, it is stopped by weak halo-to-boundary edges, but evolves through the strong outer halo edges and converges to the desired boundary, producing a very tight cell segmentation. The proposed method is also tested on a different data set and similar results are obtained. This set was obtained with a lower magnification and image characteristics such as contrast and cell texture are different from the previous set. The proposed method in this paper also performs superior in that case. The results are not shown here due to limited space.

Fig. 2.

Segmentation of a frame from human melanoma data set.

Fig. 3.

Magnified contours of sample cells. Red: ridge-based initialization, green: final segmentation.

5. CONCLUSION

A new approach to obtain accurate cell boundaries in phase contrast microscopy is presented in this paper. The use of ridge and blob measures provides a robust initial detection that is utilized to calculate the directional derivatives that are perpendicular to the local image boundary to capture the desired intensity profile. The active contour is implemented with level set and its evolution is controlled by the directional derivative to stop it at the desired edges. This enables the active contour to pass through phase halo edges and stop at the actual cell boundary. Furthermore, the use of spatially adaptive force slows the evolution and prevents leakage at the boundaries. The approach is tested on cell images where the cells present highly irregular morphological structures and the method provides very robust performance. This approach can be extended to other domains (such as [20]) that require spatial or spatio-temporal segmentation of certain objects that fit a specific profile. Accurate cell segmentation using phase-contrast microscopy images will also enable the study of interacting populations of cells in addition to single cells. The precise segmentation of cells with complex morphology and cell border features will be essential for using high-throughput approaches to unravel the biochemical mechanisms of mitotic catastrophe – an important response pathway that leads to cell death in nearly all clinically important solid tumors [21].