Abstract
In many biomedical applications, researchers encounter semicontinuous data where data are either continuous or zero. When the data are collected over time the observations may be correlated. Analysis of this kind of longitudinal semicontinuous data is challenging due to the presence of strong skewness in the data. A flexible class of zero-inflated models in a longitudinal setting is developed. A Bayesian approach is used to analyze longitudinal data from an acupuncture clinical trial, in which the effects of active acupuncture, sham acupuncture and standard medical care is compared on chemotherapy-induced nausea in patients who were treated for advanced breast cancer. A spline model is introduced into the linear predictor of the model to explore the possibility of a nonlinear treatment effect. Possible serial correlation between successive observations is also accounted using the Brownian motion. Thus, the approach taken in this paper provides for a more flexible modeling framework and, with the use of WinBUGS, provides for a computationally simpler approach than direct maximum-likelihood. The Bayesian methodology is illustrated with the acupuncture clinical trial data.
1. Introduction
1.1. Statistical background
In many biomedical applications, a longitudinal response variable may have a continuous distribution with a large number of values clustered at zero. A longitudinal model with this type of response has been referred to as a two-part model by Lachenbruch (2002) and as a semicontinuous model by Olsen and Schafer (2001). Treating this kind of data using a normal distribution is not suitable since ignoring the many zeros, especially when a sizeable proportion of the data is zero, implies that the underlying parametric distributional assumptions will not be met. This type of data may also be positively skewed for the nonzero values. Thus, in a two-part model, zeros should be analyzed separately from the nonzero continuous data.
The two-part model which originated in econometrics (Heckman, 1976; Duan et al., 1983) is based on two equations. One equation (logistic model) is used to predict the probability of occurrence of a nonzero value, and a second equation (linear model) is used to predict the mean of nonzero values. Recently, Zhou and Tu (1999) and Tu and Zhou (1999) have proposed testing procedures for comparing different populations on the basis of a two-part model. More recently, Welsch and Zhou (2006) proposed methodology which allowed for flexible modeling of the continuous part of the data. However, a majority of the literature in this area is based on cross-sectional data whereby only a single observation is measured on each individual. Excess zeros may also occur with longitudinal data, and in this scenario the correlation among measurements on the same individual must be accounted for. Olsen and Schafer (2001) and Tooze et al. (2002) have extended a two-part regression model to include random effects in both the logistic and linear stages of the model to capture unexplained heterogeneity among individuals in a longitudinal data. Albert and Shen (2005) developed a longitudinal two-part model with both exchangeable random effect and a serial correlation. Lu et al. (2005) discuss an estimating equations approach for a two-part model with application to clustered data, and Li et al. (2005) introduced a measurement error model for semicontinuous longitudinal data. While a majority of these approaches are based on maximum-likelihood estimation, Zhang et al. (2006) developed a Bayesian two-part model to analyze health care data. Their two-part hierarchical model is composed of a hierarchical probit model and a hierarchical linear regression model, reflecting the hierarchical nature of their data (e.g., patients are nested within their primary care physician). Another Bayesian approach is developed by Robinson et al. (2006) who extended the two-part model to the case of charges of multiple services, using a log-linear model and a general multivariate lognormal model.
1.2. Motivating example
Our method is motivated from an interesting longitudinal clinical trial on acupuncture (Shen et al., 2000). Shen et al. (2000) presented the results of a clinical trial where daily emesis volume (measured in cubic centimeters per day) was collected longitudinally over a two-week period on breast cancer patients being treated with standard chemotherapy. All patients received chemotherapy (cyclophosphamide, cisplatin, and carmustine) during the first 4 days of follow-up. All patients were also given antiemetic agents (including prochlorperazine, lorazepam, and diphenhydramine) to reduce nausea. The purpose of the trial was to examine the effect of acupuncture on reducing emesis induced by the chemotherapy. Specifically, patients were randomized to either an active acupuncture, sham acupuncture, or no acupuncture group and followed longitudinally on daily emesis occurrences and volume. A total of 104 patients were randomized between three groups: (i) patients treated with standard chemotherapy only (34 patients), (ii) patients treated with sham acupuncture (33 patients), and (iii) patients treated with active acupuncture (37 patients). Further, acupuncture was given over the first 5 days of the treatment period. Patients randomized to the sham acupuncture received minimal needling acupuncture whereby needles were inserted minimally with no electrical stimulation at locations that were thought not to affect nausea. Patients receiving standard care received chemotherapy and medicine for nausea only. An important endpoint for this study was the daily measurement of the volume of emesis over a 14 day follow-up period. Interest was focused on comparing the longitudinal course of patients treated with sham acupuncture with that of patients treated with active acupuncture. There are a large number of days with zero emesis volume (Table 1). Albert and Shen (2005) used this dataset as motivation for a direct-likelihood approach for fitting two-part models for longitudinal data. Their model assumed a standard linear model for incorporating time effects on both the probability of a positive volume and the mean volume given a positive volume.
Table 1.
Number of zeros for each treatment
| Standard medical group (n = 34) | Sham acupuncture | Active (n = 33) acupuncture (n = 37) | |
|---|---|---|---|
| Day 1 | 6 | 6 | 14 |
| Day 2 | 11 | 13 | 29 |
| Day 3 | 9 | 12 | 27 |
| Day 4 | 3 | 2 | 5 |
| Day 5 | 6 | 14 | 27 |
| Day 6 | 13 | 20 | 19 |
| Day 7 | 18 | 13 | 19 |
| Day 8 | 18 | 13 | 23 |
| Day 9 | 17 | 17 | 19 |
| Day 10 | 21 | 18 | 24 |
| Day 11 | 23 | 18 | 22 |
| Day 12 | 20 | 21 | 23 |
| Day 13 | 21 | 23 | 30 |
| Day 14 | 22 | 21 | 29 |
There are a number of ways that the analysis presented in Albert and Shen (2005) can be improved.
First, the time effect is an important factor in this study which needs to be modeled explicitly. Albert and Shen (2005), considered dummy variables for each day as the time effect and then treatment effect is assumed to be constant over the first 5 days after randomization and constant over the remainder of the follow-up period (days 6 to 14). However, the piecewise constant assumption may be too restrictive. Fig. 1 shows the nonlinearity of the longitudinal trajectory of the mean emesis volume for patients over the weeks for each treatment. The figure suggests that the mean structure described by Albert and Shen (2005) may not adequately capture the dynamics of the treatment effects across time. A spline (Ruppert et al., 2003) model is introduced in both the logistic and linear predictor of the model to flexibly model the time effect. Further, to capture the nonlinear trajectory of the different treatments over time, we would be interested in fitting a separate mean curve for subjects receiving each treatment. Thus, apart from modeling the time effect using splines, we also model the treatment-by-time interaction nonparametrically. Second, computational efficiency is a continuing problem. Albert and Shen (2005) estimated the model parameters using the Monte Carlo EM, which is computationally intensive. Further, standard errors were estimated using the bootstrap, making inference particularly computational. In this paper we estimate the model parameter in a Bayesian paradigm using the freely available software WinBUGS (Spiegelhalter et al., 2005). This is in contrast to a likelihood approach, where Monte Carlo EM (see McCulloch (1997), for details) requires software development and is very computationally intensive. Apart from computational simplicity, Bayesian modeling gives some additional advantages due to its flexibility. It incorporates prior information and interval estimates for model parameters or functions of model parameters. It also allows for full parameter uncertainty, and Bayesian inference does not depend on asymptotic results Gelman et al. (2004).
Fig. 1.
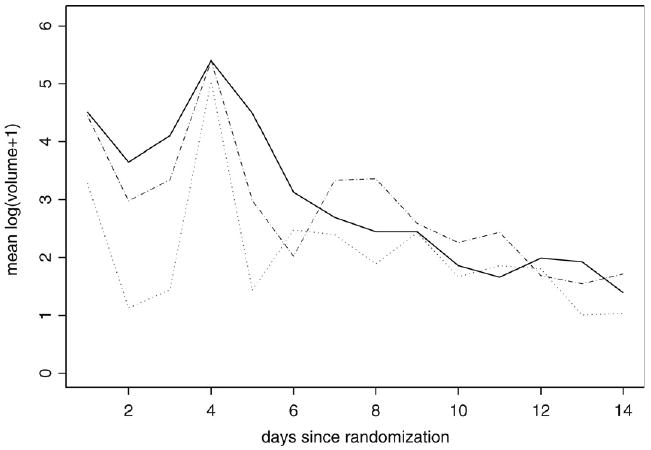
Mean.
In the next section we introduce a model which improves upon the existing model and discuss the parametric Bayesian method. In Section 3 we illustrate the application of the proposed method with an analysis of the acupuncture clinical trial data set. A discussion follows in Section 4.
2. Bayesian model for longitudinal two-part model
In this section a two-part model for semicontinuous longitudinal data is introduced. We develop our two-part model based on the model described by Albert and Shen (2005).
Let yij be the volume of emesis for subject i (i =, 2, …, n) at day j (j = 1, 2, …, m), where n is the total number of subjects and m is the total number of follow-up times. For the acupuncture clinical trial, n = 104 and m = 14. Let Rij be a random variable denoting the volume of daily emesis where,
| (1) |
with conditional probabilities
| (2) |
where θ1 is a vector of parameters.
Let Sij ≡ [yij|Rij = 1], denote the mean transformed positive emesis volume for the ith subject at jth week with p.d.f. f (sij|θ2) where f (sij) may be any distribution with yij > 0. As described by Albert and Shen (2005), positive volumes were log(Y + 1) transformed since the data were approximately normally distributed on this scale.
Stage one: We assume the following model for the two-part model:
| (3) |
| (4) |
The logistic regression (3) models the probability of a positive volume and the linear mixed model (4) models the mean transformed positive emesis volume. Here, βk (k = p, s) are qk vectors of regression coefficients and Xkij is the corresponding nm × qk design matrices. The nonparametric function of time fk(tij) is the spline model. In order to capture the nonlinear trajectory of the different treatments over time, we use an arbitrary smooth function (tij) to model interaction of treatment with time, in which a categorical factor (treatment) interacts with a continuous predictor (Coull et al., 2001; Durban et al., 2005; Ruppert et al., 2003). Here, ci ∈ {1, 2, …, L} represents the treatment group index corresponding to subject i, and are L different functions depending on the values of ci. Note that are the deviations of the treatment group from the overall curve. The random effects account for the unobserved heterogeneity among the subjects, and Z1ij, Z2ij are the corresponding design matrices of nm × p dimension. A random intercept in the logistic model allows some subjects to have a consistently high or low probability of a positive volume, while a random intercept in the lognormal part allows individuals to have a tendency to high or low mean volume given that they have a positive volume. To account for the serial correlation in the data (Albert and Shen, 2005), we include a stochastic process apart from the usual random effects to flexibly model the semicontinuous longitudinal data. Thus, the process Wij = (Wijp, Wijs)T is similar to the bivariate stochastic process model involving Brownian motion described by Sy et al. (1997). However, because the measurements in our data were taken on a fixed schedule, rather than irregularly as in the study data used by Sy et al. (1997), we instead use a bivariate random walk as the stochastic process in our model. This Brownian motion Wij models the local variation and departure from the polynomial trend, while the random effects bi account for the variability of the trend across the subjects. The measurement error eij is assumed to have a N (0, σ2) distribution.
Stage two: The second stage of the model (3–4) defines the distributional assumptions on the random subject effects vector bi and the bivariate stochastic process Wij. We assume a first-order random walk model (Zhou and Wakefield, 2006) for the stochastic process, with increments at time 0 are fixed at 0. Thus, we assume,
| (5) |
| (6) |
For the first time point we assume the increments to be zero, i.e., (Wi1p ≡ 0) and (Wi1s ≡ 0). Here, the Σw is multiplied by (tj − tj−1), so that observations closer in time are more likely to be similar. However, since we have equally spaced data, tj − tj−1 is a constant for our application.
We estimate the smooth functions by penalized splines. Thus, following Ruppert et al. (2003) we assume the linear spline estimator of the form
| (7) |
| (8) |
where zil = 1 if zil = l and 0 otherwise for l = 2, 3, …, L
and are knots for the k = p, s. The choice of the knots 's will be described in the data analysis section. We have assumed the same variance parameter for each curve, i.e., ; l = 2, 3, …, L, and that the random effects are independent from function to function, i.e., the curves are different but with the same amount of smoothing. In order for the fixed effects to be identified, we need to put constrains on , we assume . The specification of the treatment group curves is equivalent to for l = 1 and for treatment l = 2, …, L. This avoids the nonidentifiability of the slope and intercept parameters. A higher-degree spline may be used. However, the motivating application did not benefit from this extension.
There is no clear rule on how many knot points to include or where to locate them in the spline functions. More knots are needed in regions where the function is changing rapidly (Ruppert, 2002). Sometimes subject knowledge may be relevant in placing knots where a change in the shape of the curve is expected. Using too few knots or poorly sited knots means that the approximation to the curve will be degraded. By contrast, a spline using too many knots will be imprecise. Conceptually, the methodology described here does not depend on the location of knots. Eilers and Marx (2004) stated that “Equally spaced knots are always to be preferred.” In contrast, Ruppert et al. (2003) used quantile-spacing in all of their examples, though they did not make any categorical statement that quantile-spacing is always to be preferred. In the acupuncture application, we choose knots at equal spacings over the 14 day follow-up.
3. Prior specification
Let be the set of parameters for model (3–4). In the Bayesian framework we assume independent priors for these parameters. We assume conditionally conjugate priors, which lead to simpler updating schemes in the Markov chain sampling methodology. In particular, we assume a normal distribution for the location parameters. Specifically, we assume that ; k = p, s. Note that are assumed to be zero for identifiability and thus has no prior distribution. The variance parameters are assumed to have an inverse gamma prior distribution where, , and ; k = p, s. Here, IG(a, b) denotes an inverse gamma distribution with density proportional to exp(−b/x)/xa+1. Note that small values of a, b correspond to weak prior information. The variance–covariance matrices are assumed to follow an inverse Wishart prior distribution, where Σ ∼ IW (H, η0), Σw ∼ IW (G, η1), and where, Wishart(P−1, vb) denotes the Wishart distribution with vb degrees of freedom and scale matrix P−1.
The posterior mean of the mean response can be computed easily from the MCMC output using the above equation by:
where denotes the lth posterior sample of pij and μij.
3.1. Model selection
We compare the performances of various models using the model selection criteria based on Deviance Information Criterion (DIC) proposed by Spiegelhalter et al. (2002) and defined as
Here D (θ) = −2 log p(y|θ) is the deviance, is the average posterior deviance, is what Spiegelhalter et al. (2002) termed the “effective dimension”, and is an estimate of θ based on the data y. Recently, Celeux et al. (2006) have pointed out that the “effective dimension” pD can be negative in case of mixture of distributions. For models with mixtures, Celeux et al. (2006) suggested eight different modifications of the DIC. The model we propose utilizes mixture structures, and thus we choose DIC3 (based on terminology used in Celeux et al. (2006)), defined as
as our model comparison criterion. Note that the second term is simply based on the predictive distribution p(y|y) = Eθ[p(y|θ)|y]. The model with the smallest DIC is taken to be the best fitting model.
4. Example
We analyze the clinical trial data on acupuncture for treating chemotherapy-induced vomiting in patients being treated for advanced breast cancer (Shen et al., 2000; Albert and Shen, 2005). The only subject-specific covariate we consider is age. The data depict a large amount of serial correlation which diminishes and levels off with increasing distance between measurements (Albert and Shen, 2005). To account for this extra correlation, we consider the random walk increments described in (5) and (6).
Thus, we consider the following model for analyzing the data:
| (9) |
| (10) |
Since, knot spacing is not the main focus of this article we select knots among the existing values. We select the knots among the existing values, and they are equally spaced within the range [min(x), max(x)]. Thus we assume that there are 6 knots, and they are placed at time points 2, 4, 6, 8, 10, 12.
Our available data set is not large enough to allow part of it to be used for prior elicitation. Prior information based on expert opinion, even if available, is user specific. Hence, for our data set we choose the prior distributions to be weakly informative, while making sure that the models remain identifiable. For each β in the model we assume an N(0,1000) prior distribution. Similarly, for each α component we assume an N(0,1000) prior distribution. For the variance parameters we assume that IG(2.001, 1.001), resulting in a prior mean of 1 and prior variance of 1000. Each of the variance–covariance matrices Σ, ΣW is assumed to follow a IW (diag(1, 1), 3) prior distribution.
The posterior distributions are analytically intractable. We use a Gibbs sampler (Gelfand and Smith, 1990) to obtain samples from the posterior distribution. Thus, computations are done via Monte Carlo approximations using the Markov chain Monte Carlo (MCMC) methodology. The methods are implemented in the freely available software packages R (R Development Core Team, 2004), and WinBUGS (2005). Our code uses the R package R2WinBUGS (Sturtz et al., 2005) to execute WinBUGS while running a session in R. We ran a chain of 80 000 iterations with the first 30 000 discarded as burn-in. Convergence was assessed visually by monitoring the dynamic traces of Gibbs iterations and by computing the Gelman–Rubin (Brooks and Gelman, 1998) convergence statistic. The initial values for the fixed parameters were selected by starting with the prior mean and covering ±3 standard deviations. Inferences were insensitive to the choice of the initial values.
Table 2 contains the posterior means, posterior standard deviations, and 95% credible intervals for the parameters of interest. The covariate age has no significant effect on either the logistic regression or the linear regression. The large significant random intercept variance (Σ11) for the logistic part shows that after accounting for covariate differences among the subjects, some subjects have a greater probability of positive emesis volume than others. The positive random intercept variance (Σ22) shows that the subjects who are vomiting tend to have a larger mean transformed emesis volume than others. The correlation between the random intercepts of the model (Σ12) is positive, implying that the probability of positive volume and the mean emesis volume are correlated. The estimated Σw suggests that there is significant autocorrelation in both the occurrence of a nonzero emesis and the emesis volume given a positive volume. However, there was little cross-autocorrelation between the two components, since 95% credible intervals for included zero.
Table 2.
Parameter estimates
| Parametric model | ||||
|---|---|---|---|---|
| Parameter | Mean | SD | 95% CI | |
|
|
2.09 | 0.24 | (0.19, 2.31) | |
|
|
2.279 | 0.14 | (2.01, 3.16) | |
|
|
−7.34E−04 | 0.0033 | (−0.0072, 0.0057) | |
|
|
−0.0229 | 0.0135 | (−0.05, 0.001) | |
| Σ11 | 0.65 | 0.161 | (0.3843, 1.012) | |
| Σ12 | 0.17 | 0.028 | (−0.281, 0.661) | |
| Σ22 | 0.0402 | 0.0074 | (0.0278, 0.0569) | |
|
|
0.017 | 0.0085 | (0.0076, 0.0384) | |
|
|
0.0024 | 0.003 | (−0.0032,0.0103) | |
|
|
0.0116 | 0.0034 | (0.0067, 0.02) | |
| σ | 0.1337 | 0.007 | (0.1197, 0.1493) | |
Fig. 2 presents the mean profiles under our proposed model. The top panel shows the mean profile for the logistic model, and the lower panel shows the profile for the log-normal part. We focus on the logistic component (probability of a positive emesis volume), since this is where treatment differences appear. There is a sizeable effect of treatment on the probability of a positive emesis during the first five days after randomization (comparing the dashed and dotted lines), with the maximal treatment effect appearing at 4 days post randomization. Further, the treatment effect appears to be diminished after day 5, with the treatment effect disappearing by day 9. Since acupuncture was only provided over the first 5 days after randomization, the results suggest that active acupuncture may be beneficial over sham acupuncture while the acupuncture is given and for a few days after the cessation of acupuncture.
Fig. 2.
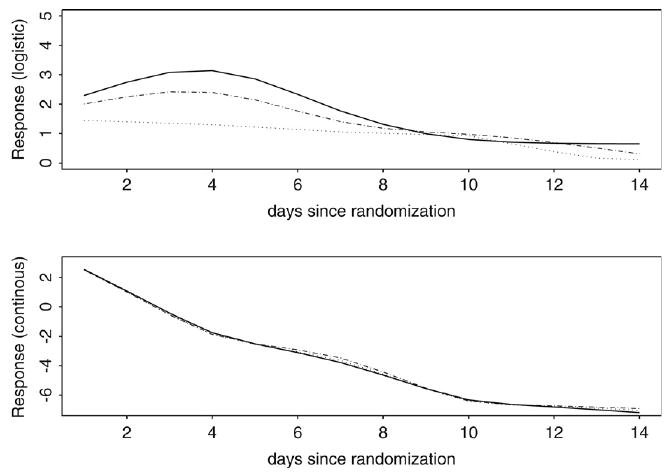
The top panel is a comparison of the logit transformed proportion of a positive volume over time across the three treatment arms of the acupuncture clinical trial. The lower panel compares the mean non-negative measurement over time across the treatment arms. “–” denotes the standard medical group; “.-.-” denotes the sham acupuncture group; “…” denotes the active acupuncture group.
Fig. 2 also shows the mean profile for the standard medical group (no acupuncture). A comparison of the sham acupuncture (dashed line) with the standard medical arm (solid line) is a measure of the placebo effect. As with the treatment effect, the placebo effect appears to be substantial over the first 5 days after randomization and to diminish after day 5.
To gain further insight into the differences between the treatments, especially between the sham acupuncture and acute acupuncture, we find the absolute difference between the nonparametric curves in the logistic model and the corresponding posterior probability. Let ga(t) and gs(t) be the two functions corresponding to acute acupuncture and sham acupuncture. We then define the difference between the function as
where tM1, tM2 are two boundary points of interest. Then the posterior probability that |Λ| > 0 can then be approximated as:
where Λl is the lth iterate in the Gibbs sampler. We can then calculate the posterior probability based on MCMC output.
We estimated the absolute difference between the active and sham acupuncture groups separately over 1–5 days and 6–14 days. The estimated absolute difference between the active and sham acupuncture groups during days 1–5 is 1.232 with the posterior probability of a nonzero treatment difference 0.92, and that during days 6–14 is 0.471 with a posterior probability 0.32. Thus, there is some evidence for an effect of treatment while acupuncture treatment is ongoing but very little evidence for a treatment effect once acupuncture treatment stops.
We compare among the following models using the DIC criteria as described in Section 3.1.
-
Model 2: Model without Brownian motion:
(11) (12) -
Model 3: Model without random effect :
(13) (14) -
Model 4: Model without spline :
(15) (16)
Model 4 is similar in spirit to the model of Albert and Shen (2005).
Table 3 reports the DIC values. It can be seen that the DIC for the two-part models was calculated separately for each part of the model as well as for the overall model. Overall, we see that our proposed model fits better than the other parametric random effect models.
Table 3.
DIC values
| Model 1 | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|
| DIClogistic | 1747.81 | 1937.1 | 1974.77 | 1912.7 |
| DIClog-normal | 689.72 | 762.5 | 749 | 694.1 |
| Overall DIC | 2437.53 | 2699.6 | 2723.77 | 2606.8 |
To assess the treatment effect, we also estimate the posterior mean of the mean response. Note that the mean response is given by
where and .
We compute the posterior mean response under each treatment arm at day 5 and 14. The estimated posterior mean responses at day 5 were 5.27, 4.91, and 4.69 for the standard medical, sham acupuncture and active acupuncture groups, respectively. The estimated posterior mean at day 14 were 3.62, 2.24, and 2.00 for the standard medical, sham acupuncture and active acupuncture groups, respectively. The estimated value shows the benefit of acupuncture during the 5 day treatment period. This result is in conformity with the previous findings in Albert and Shen (2005).
5. Discussion
This paper presented a parametric Bayesian approach for modeling longitudinal semicontinuous data. The approach allowed for flexible inference on the treatment effect over time using a penalized spline model, as well as the incorporation of serial correlation using a Brownian motion process. The approach is easily implemented in WinBugs (2005).
We used this methodology to analyze data from an acupuncture clinical trial. A goal of the trial was to compare daily emesis volume across a standard medical group, a sham acupuncture group, and an active acupuncture group, with the major focus on comparing the active and sham acupuncture groups to assess treatment effect. The results show some evidence that active acupuncture reduced emesis relative to sham acupuncture over the period in which acupuncture was administered. The treatment effect quickly diminished after acupuncture was stopped. The difference between the active and sham curves over days 1 to 5 was substantial under our model. Further, the posterior probability of the difference being greater than zero was 0.92. The difference was substantially reduced for the period between days 6 and 14. These results were similar to those reported by Albert and Shen (2005) in their likelihood analysis.
Albert and Shen (2005) presented a likelihood-based approach to this problem. A Monte Carlo EM procedure was used for parameter estimation to deal with the random effects with serial correlation. Unfortunately, this algorithm was very computationally intensive, requiring days of computation on a cluster of processors in order to make inference. Specifically, the approach took approximately one-week on a cluster of 50 processors. Using WinBugs, the Bayesian approach was much more computationally feasible than the maximum-likelihood approach, and it takes about 5 h to run the code on a PC(512 Mo RAM, 2.6 GHz CPU).
A few limitations of our methods must be emphasized. One major issue is the robustness of the distributional assumption. In the presented application, we assume a parametric normal distribution for the random effects. A broader class of distributions like the Dirichlet process may be a viable alternative. Another issue is the fixed knot points. A random knot points would be more flexible; however, such an approach would be numerically challenging in this framework.
References
- Albert PS, Shen J. Modelling longitudinal semicontinuous emesis volume data with serial correlation in an acupuncture clinical trial. Journal of the Royal Statistical Society: Series C. 2005;54:707–720. [Google Scholar]
- Brooks SP, Gelman A. General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics. 1998;9:262–285. [Google Scholar]
- Celeux G, Forbes F, Robert CP, Titterington DM. Deviance information criteria for missing data models. Bayesian Analysis. 2006;1:651–674. [Google Scholar]
- Coull BA, Ruppert D, Wand MP. Simple incorporation of interaction into additive models. Biometrics. 2001;57:539–545. doi: 10.1111/j.0006-341x.2001.00539.x. [DOI] [PubMed] [Google Scholar]
- Duan N, Manning WG, Morris CN, Newhouse JP. A comparison of alternative models for the demand for medical care. Journal of Business and Economic Statistics. 1983;1:115–126. [Google Scholar]
- Durban M, Harezlak J, Wand MP, Carroll R. Simple fitting of subject-specific curves for longitudinal data. Statistics in Medicine. 2005;24:1153–1167. doi: 10.1002/sim.1991. [DOI] [PubMed] [Google Scholar]
- Gelfand AE, Smith AFM. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association. 1990;85:398–409. [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin D. Bayesian Data Analysis. second. Chapman & Hall/CRC; 2004. [Google Scholar]
- Heckman JJ. The common structure of statistical models of truncation, sample selection, and limited dependent variables and a simple estimator of such model. Annals of Economic and Social Measurement. 1976;5:475–492. [Google Scholar]
- Lachenbruch PA. Analysis of data with excess zeros. Statistical Methods in Medical Research. 2002;11:297–302. doi: 10.1191/0962280202sm289ra. [DOI] [PubMed] [Google Scholar]
- Lu SE, Lin Y, Shih WJ. Analyzing excessive no changes in clinical trials with clustered data. Biometrics. 2005;60:257–267. doi: 10.1111/j.0006-341X.2004.00155.x. [DOI] [PubMed] [Google Scholar]
- McCulloch CE. Maximum-likelihood algorithms for generalized linear mixed models. Journal of the American Statistical Association. 1997;92:162–170. [Google Scholar]
- Olsen MK, Schafer JL. A two-part random-effects model for semicontinuous longitudinal data. Journal of the American Statistical Association. 2001;96:730–745. [Google Scholar]
- R Development Core Team. A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2004. [Google Scholar]
- Robinson JW, Zeger SL, Forrest CB. A hierarchical multivariate two-part model for profiling providers' effects on health care charges. Journal of the American Statistical Association. 2006;101:911–923. [Google Scholar]
- Ruppert D. Selecting the number of knots for penalized splines. Journal of Computational and Graphical Statistics. 2002;11:735–757. [Google Scholar]
- Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. Cambridge University; Cambridge: 2003. [Google Scholar]
- Shen J, Wenger N, Glaspy J, Hays R, Albert P, Choi C, Shekelle P. Electroacupuncture for control of myeloablative chemotherapy-induced emesis: A randomized controlled trial. Journal of the American medical Association. 2000;284:2755–2761. doi: 10.1001/jama.284.21.2755. [DOI] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit (with discussion) Journal of the Royal Statistical Society, B. 2002;64:583–639. [Google Scholar]
- Spiegelhalter D, Thomas A, Best N, Lunn D. MRC Biostatistics Unit Institute of Public Health and Department of Epidemiology & Public Health, Imperial College School of Medicine; 2005. WinBUGS User Manual, Version 1.4. Available at: http://www.mrc-bsu.cam.ac.uk/bugs. [Google Scholar]
- Sturtz S, Liggers U, Gelman A. R2WinBUGS: A package for running WinBUGS from R. Journal of Statistical Software. 2005;12:1–16. [Google Scholar]
- Sy JP, Taylor JMG, Cumberland WG. A stochastic model for the analysis of bivariate longitudinal AIDS data. Biometrics. 1997;53:542–555. [PubMed] [Google Scholar]
- Tooze JA, Grunwald GK, Jones RH. Analysis of repeated measures with clumping at zero. Statistical Methods in Medical Research. 2002;11:341–355. doi: 10.1191/0962280202sm291ra. [DOI] [PubMed] [Google Scholar]
- Tu W, Zhou XH. A Wald test comparing medical costs based on log-normal distributions with zero value costs. Statistics in Medicine. 1999;18:2749–2762. doi: 10.1002/(sici)1097-0258(19991030)18:20<2749::aid-sim195>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- Welsch A, Zhou XH. Estimating the retransformed mean in a heteroscedastic two-part model. Journal of Statistical Planning and Inference. 2006;36:860–880. [Google Scholar]
- Zhang M, Strawderman RL, Cowen ME, Wells MT. Bayesian inference for a two-part hierarchical model: An application to profiling providers in managed health care. Journal of the American Statistical Association. 2006;101:934–945. [Google Scholar]
- Zhou X, Tu W. Comparison of several different population means when their samples contain log-normal and possibly zero observations. Biometrics. 1999;55:645–651. doi: 10.1111/j.0006-341x.1999.00645.x. [DOI] [PubMed] [Google Scholar]
- Zhou C, Wakefield J. A Bayesian hierarchical mixture model for curve partitioning. Biometrics. 2006;62:515–526. doi: 10.1111/j.1541-0420.2005.00492.x. [DOI] [PubMed] [Google Scholar]


