ABSENCE SEIZURES AS RESETTING MECHANISMS OF BRAIN DYNAMICS

Abstract

To understand the increase in age-related incidence and frequency of absence seizures in the rat brain, we investigated the effect of these seizures on brain dynamics. This paper puts forward the hypothesis that age-related differences in the expression of absence seizures are associated with the ability of the seizures to reset brain dynamics.

1. INTRODUCTION

Epilepsy is one of the most common neurological disorders, second only to stroke, affecting about 0.8% of the world’s population [1]. Although epilepsy occurs in all age groups, the highest incidences are found in infants and the elderly. Absence epilepsy is a subtype of generalized epilepsy manifested by seizures characterized by brief periods of impaired consciousness (absence seizures). Human absence epileptic seizures are typically associated with bursts of generalized 3 Hz spike-wave discharges (SWDs) in the electroencephalogram (EEG). The usual duration is 3–10 sec, ranging up to a few minutes. The level of functioning during a SWD depends in part on the duration of the seizure, and the recovery from such episodes is usually fast, in the order of a few seconds.

Animal modeling of absence seizures has been conducted in numerous studies. The defining EEG events in rodents are 7–12 Hz generalized SWDs (Fig. 1) of variable duration with an abrupt onset and abrupt termination, which usually occurs during passive wakefulness or sleep [2, 3]. In the previous study [4], numerous spontaneous bilateral cortical 7–9 Hz spike-wave discharges were recorded in control and brain-lesioned animals spanning an age range from 2 to 30 months. As animals progress from mid-aged to aged periods, they can experience hundreds of absence seizures per day [5].

Fig. 1.

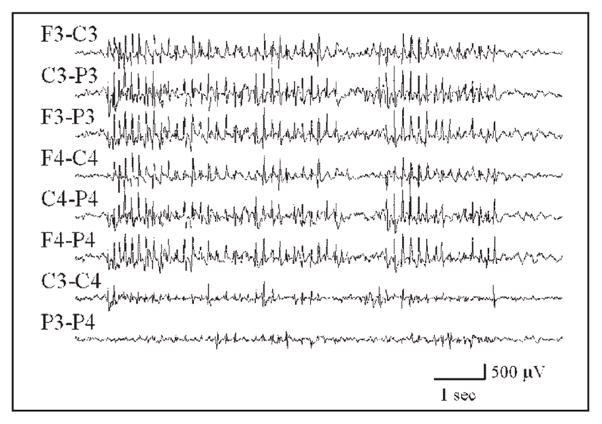
A sample of a generalized SWD recorded from a rat. The F3, C3, and P3 abbreviations refer to skull screw electrodes overlying left frontal, central, and parietal regions of the animal’s brain, respectively; F4, C4, and P4 refer to the brain areas on the right. An “F3-C3” label corresponds to an EEG channel produced by the output of one differential amplifier with inputs from the F3 and C3 electrodes.

A central feature of epilepsy is that it is characterized by seizures that are transient in nature and occur spontaneously in a recurrent fashion. Epilepsy has been described as a dynamical disease with pathological states characterized by the occurrence of abnormal dynamics [6]. From a dynamical perspective, a seizure may represent self-organizing behavior in which widespread cortical areas make an abrupt transition to an ordered state and reset to a normal state at the end of the seizure [7]. Nonlinear time-dependencies have also been reported in the pattern of seizure occurrence, which indicate that seizures do not occur randomly, but rather reflect determinism [8, 9].

In an effort to better understand the relationship between aging and the differential expression of SWDs, we studied the dynamical EEG properties of the epileptic brain. The concept of “brain dynamical resetting” may provide some insights into the mechanisms underlying increased seizure susceptibility of the aged brain. One way to quantify the effect of an event, e.g. a seizure, is to estimate how dynamical EEG properties change after the event. A nonlinear measure that is closely related to the rate at which information is produced, the short-term maximum Lyapunov exponent (STL_max), was utilized to extract a dynamical profile of the EEG signal over time for each recording channel. This measure has been found to be useful in capturing and predicting system (brain) dynamics associated with transitions into and out of epileptic seizures [10–15]. The overall goal of this study was to establish a clear relationship between changes in the dynamical EEG properties of the brain and differences in the age-related expression of SWDs.

2. STATE SPACE TOPOGRAPHY AND ANALYSIS OF iEEG

The state space portrait of a signal (time series) provides a visual representation of its evolution in a multidimensional space over time. Its characteristics reflect the original characteristics of the signal, and ultimately the system that generates the signal. The state space can be thought of as a collection of all possible states that a dynamical state visits during its evolution. In general, the state space is identified with a topological manifold. A p-dimensional state space is spanned by a set of p-dimensional “embedding vectors,” each of which defines a point in the state space, thus representing the instantaneous state of the system.

2.1. State Space Reconstruction

The theoretical basis for the relationship between a signal and its state space representation generated by earlier work [16, 17] was developed from the Whitney embedding theorem [18]. A state space portrait is created by treating each time-dependent variable of the system as a component of a vector in a multidimensional space. Each vector in the state space represents an instantaneous state of the system. These time-dependent vectors are plotted sequentially in the state space to represent the evolution of the state of the system over time. For many systems, this graphical mapping creates an object confined over time to a sub-region of the state space. The geometrical properties of these confined objects, called “attractors,” provide information about the global state of the system. The vector reconstruction is achieved as follows:

$$\overrightarrow{X}=\{x(t),x(t+\tau ),\dots ,x(t+(p-1)\tau )\},$$

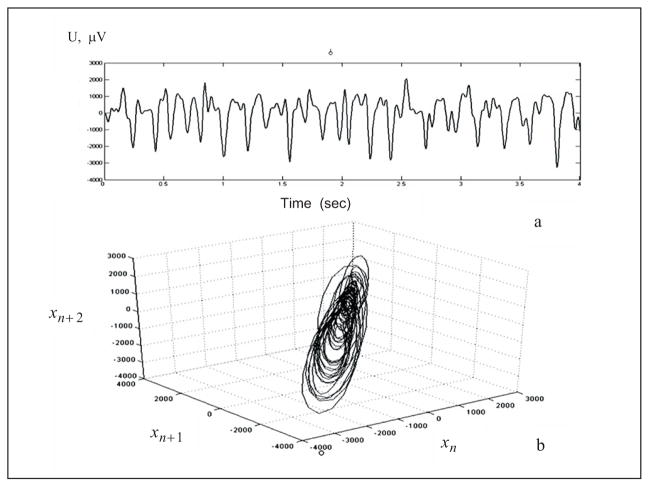
where x(t) is the value at time t; τ is a fixed time increment; and p is the embedding dimension. Every instantaneous state of the system is therefore represented by the vector X, which defines a point in the p-dimensional state space. The intracranial EEG (iEEG), being the output of a multidimensional system, has both spatial and temporal statistical properties. Components of the brain (neurons) are densely interconnected and there exists an inherent relation between the iEEG recorded from one site and the activity at other sites. This makes the iEEG a multivariate time series. The state space reconstruction of the iEEG signal in a three-dimensional state space (Fig. 2) was done using the method of delays [17].

Fig. 2.

(a) Ictal segment of a filtered iEEG recorded from the hippocampus of a rat, (b) Reconstructed iEEG segment in 3-D state space.

2.2. Embedding Parameters for iEEG Reconstruction

An accurate representation of the system in a state space depends upon making appropriate choices of the embedding dimension p and time delay τ. The choice of p for experimental data such as ours is not a straightforward issue. According to Takens [17], if d is the fractal dimension of the attractor in a state space, the embedding dimension p should be at least equal to 2d + 1 in order to correctly reconstruct the attractor. Therefore, one of the first steps in characterizing the properties of a system is to estimate the fractal dimension of the attractor. The dimension helps to determine the position of a point on the attractor to within a certain degree of accuracy. In addition, it provides a lower limit to the number of variables necessary to model the system.

To ensure that the ictal (seizure) dynamics were captured, we calculated the fractal dimension and the time delay from the iEEG recorded during the ictal period. For any attractor, the dimension can be estimated by looking at the manner in which the number of points within a sphere of radius r scales as the radius shrinks to zero. The geometric relevance of this observation is that the volume occupied by a sphere of radius r in the dimension d behaves as r^d. The correlation function or correlation integral C(r) measures the probability that two vectors on the attractor, selected at random, lie within a distance r of each other. This function of two variables is an invariant on the attractor, but it has become conventional to look only at the variation of this quantity when r is small. In that limit, it is assumed that

$$C(r)\approx r^d,$$

defining the generalized fractal dimension d when it exists. From the above equation, d can be estimated in the limiting case as

$$d=\underset{r\to 0}{lim}\frac{log[C(r)]}{log[r]}.$$

In practice, we need to compute C(r) for a range of small r over which we can argue that the function log [C(r)] is log[C(r)] linear in log[r] and then select the linear-like slope over the range. Figure 3 shows a plot of $\frac{dlog[C(r)]}{dlog[r]}$ versus log [r] for an ictal segment where C(r) denotes the correlation integral and r represents the attractor size. The curves correspond to different values of the embedding dimension (p = 6, 7, 8, and 9) and a time delay of 15 msec. The objective is to find a “middle” region in log [r] where the derivative (slope) is consistent. The figure illustrates the difficulties in establishing a clean, unsullied value of the correlation dimension for experimental data.

Fig. 3.

Derivative of the correlation function calculated for a rat iEEG ictal segment (2000 points) created from vector spaces of dimension p=6, 7, 8, and 9, with respect to ln (r). Consistency is observed in a broad range of ln (r) with slopes that lie in a range of values from 2 to 4.

Therefore, following the values used in human studies, we have used an embedding dimension p = 7 for the reconstruction of the phase space. This value of p may be too small for the construction of a state space that can reconstruct all interictal attractors of the brain, but it should be adequate for detection of the transition of the brain toward the ictal stage if the epileptic attractor is active in its space prior to the occurrence of the epileptic seizure.

The embedding delay parameter τ should be small enough to capture the shortest change (i.e., highest frequency component) present in the data, but should also be large enough to generate (with the method of delays) the maximum possible independence between the components of the vectors in the state space. These two conditions are usually addressed by selecting τ as the first minimum of the mutual information between the components of the vectors in the state space or as the first zero of the time-domain autocorrelation function of the data [19]. Theoretically, because the time span (p −1)× τ of each vector in the state space represents the duration of a state of the system, (p −1)× τ should be at most equal to the period of the maximum (or dominant) frequency component in the data. For example, a sine wave (or a limit cycle) has υ = 1, then a p = 2×1+1=3 is needed for the embedding, and (p −1)× τ should be equal to the period of the sine wave. Such a value of τ would then correspond to the Nyquist sampling of the sine wave in the time domain. In the case of the epileptic attractor, the highest frequency present is 70 Hz (the iEEG data are low-pass filtered at 70 Hz), which means that if p = 3, the maximum τ to be selected is about 7 msec. However, because the dominant frequency of the epileptic attractor (i.e., during the ictal period) in the animal iEEG was never more than 15 Hz, according to the above reasoning, the adequate value of τ for the reconstruction of the state space of the epileptic attractor with p = 7 is (7 −1)× τ = 67 msec, that is, τ should be about 11 msec [20].

2.3. Positive Lyapunov Exponent in the iEEG

The Lyapunov exponents of a system are a set of invariant geometric measures that describe the dynamical content of the system. In particular, they serve as a measure of the ease of predicting the future state of the system. Lyapunov exponents quantify the rate of divergence or convergence of two nearby initial points of a dynamical system, in a global sense. A positive Lyapunov exponent measures the average exponential divergence of two nearby trajectories, whereas a negative Lyapunov exponent measures exponential convergence of two nearby trajectories. A zero Lyapunov exponent indicates the temporal continuous nature of a flow. If a discrete nonlinear system is dissipative in nature, then a positive Lyapunov exponent quantifies a measure of chaos. Consequently, a system with positive exponents has positive entropy in that trajectories that are initially close together move apart over time. The more positive the Lyapunov exponents are, the faster they move apart. Similarly, for negative exponents, the trajectories move together in time. A system with both positive and negative Lyapunov exponents is said to be chaotic. Stated differently, Lyapunov exponents quantify the amount of linear stability or instability of an attractor or an asymptotically long orbit of a dynamical system.

Wolf et al. [21] proposed an algorithm for calculating the largest Lyapunov exponent. First, the state space reconstruction is made and the nearest neighbor is searched for one of the first embedding vectors. After the neighbor and the initial distance (l) are determined, the system is evolved forward for some fixed time (evolution time) and the new distance (l′) is calculated. This evolution is repeated, calculating the successive distances, until the separation is greater than a certain threshold. A new vector (replacement vector) is searched as close as possible to the first one, having approximately the same orientation of the first neighbor. The short term maximum Lyapunov exponent (STL_max) used in this study was estimated using the method proposed by Iasemidis et al. [23], which is a modification of Wolf’s algorithm. The measure was termed “short-term maximum Lyapunov exponent” to distinguish it from those used to study autonomous dynamical systems. Modification of Wolf’s algorithm was necessary to better estimate STL_max in small data segments that include transients, such as interictal spikes. The modification is primarily in the searching procedure for a replacement vector at each point of a fiducial trajectory.

The first step in the calculation of STL_max is to divide the iEEG signal recorded from each electrode (a one-dimensional time series) into sequential, non-overlapping segments of length 5.12 sec (1024 data points) and embed each segment in a 7-dimensional state space with a time delay τ = 3 (15 msec), using the method of delays. The computation of the largest Lyapunov exponent (L_max) involved the iterative selection of pairs of points on the state space portrait and the estimation of the convergence or divergence of their trajectory over time. More specifically, the largest Lyapunov exponent is defined as the average of local Lyapunov exponents L_ij in the state space, that is

$$L_{max}=\frac{1}{N}·\sum _N{L}_{ij},$$

where N is the necessary number of iterations for the convergence of the L_max estimated from a data segment of n points (n = N·Δt), and

$$L_{ij}=\frac{1}{\mathrm{\Delta }t}·{log}_2\frac{\mid X(t_i+\mathrm{\Delta }t)-X(t_j+\mathrm{\Delta }t)\mid }{\mid X(t_i)-Y(t_j)\mid },$$

where Δt is the evolution time allowed for δ₀ (x_ij) =| X (t_i) − X (t_j)|, the vector difference, to evolve to δ_κ(x_K) =|Y (t_i + Δt) − Y(t_j + Δt)|, the new vector difference, where Δt = k · dt and dt is the sampling period of the data u(t). If Δt is given in seconds, L_max is in bits/sec. Details of this method, including the selection of parameters for calculating STL_max, and a variation of L_max for nonstationary signals like iEEG, have been described previously by Iasemidis and colleagues [23, 24].

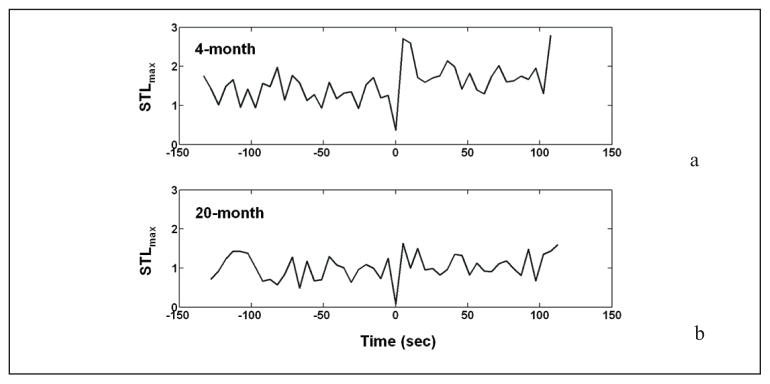
Figure 4 demonstrates the STL_max profile derived from a single bipolar EEG channel for a 4-month old animal and a 20-month old animal. The figure shows a drop in the STL_max value during the SWD (both at time 0), and a postictal increase in values compared to the average preictal value. Note that this postictal increase is more significant in the younger (4-month old) animal.

Fig. 4.

STL_max values estimated from a single bipolar channel of EEG from a 4-month (a) and 20-month (b) old animals, before, during, and following an absence seizure (SWD), each lasting approximately 5 sec. The estimation of the STL_max values was made by dividing the signal into non-overlapping segments of 5.12 sec each and using p = 7 msec and τ = 15 msec for the phase space reconstruction. The onset of the seizure, at time point 0, is associated with a drop in STL_max. In the immediate postictal period, STL_max has been reset to a value exceeding that of the preictal period. Note: STL_max values are reset to a higher average postictal value compared to the average preictal value in the 4-month old animal.

3. SEIZURES AS INTRINSIC MECHANISMS OF CONTROL

It has been postulated that seizures may be intrinsic mechanisms that serve to reset the brain from an abnormal state back to a more normal state [25, 26]. This theory suggested that epileptic brains, being chaotic nonlinear systems, repeatedly make abrupt transitions into and out of the ictal (ordered) state based on the following observations: (i) a positive Lyapunov exponent in the EEG; (ii) presence of nonlinearities in the ictal EEG; (iii) existence of spatiotemporal transitions (from chaos to order); and (iv) resetting of spatiotemporal dynamics by the seizure (to a more chaotic state). It follows intuitively that failure to sufficiently reset the brain by a seizure may increase the susceptibility of the epileptic brain to a subsequent seizure.

3.1. Resetting of Spatiotemporal Chaos: From Order to Chaos

A seizure can be characterized by a significant drop in the value of the Lyapunov exponent associated with it, thereby suggesting a sudden and brief transition to a highly ordered state. Following the seizure, these values are reset to a larger value compared with the immediate preictal values, suggesting that the seizure promotes the brain to revert to a normal functioning state that is more chaotic. The above observations constitute further support for the working model of dynamical state transitions underlying the evolution of epileptic seizures proposed in early literature [23–26]; this working model explained the temporal evolution of the maximum Lyapunov exponent in terms of a modified “cusp catastrophe model” [27–29] wherein a sudden bifurcation in system dynamics occurs when the system enters the local cusp of singularity of a folded surface S, due to a change in intrinsic parameters. A plausible hypothetical intrinsic feedback and resetting mechanism in the brain is shown in Fig. 5.

Fig. 5.

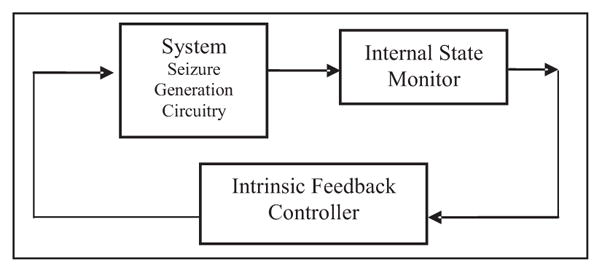
Conceptual schematic showing intrinsic brain feedback control responsible for seizure generation. Seizure expression is determined by an internal feedback control mechanism utilizing the brain state; the generator is activated until the normal state is reached (effective resetting) by the intrinsic controller.

3.2. Resetting and Age-Related Seizure Expression

In animal studies, several investigations using models of aging have shown an enhanced seizure susceptibility associated with older animals. We postulated that the functional anatomy of the brain changes as it ages resulting in global changes of brain operation that are reflected in part by a changed expression of SWDs. One approach to characterize these global changes is to employ dynamical measures of brain activity, which offers the possibility to understand how changes in the dynamics of neuronal networks could result in SWDs - sudden manifestations of paroxysmal widespread oscillations. To compare and contrast the dynamical EEG properties of 4- and 20-month old male rats as a means to delineate differences in age-related expression of SWDs, we estimated STL_max values to test for differences in peri-ictal (surrounding a seizure) dynamical properties of the EEG.

Four young adult (4-month old) and four aged (20-month old) male rats were included in the study. Fifty SWDs from each animal were used to estimate the dynamical properties during the peri-ictal period. We estimated the STL_max values for a 2-min EEG epoch recorded before and after each SWD using the algorithms described above. The values were computed for each EEG channel and averaged across electrodes to calculate overall pre-ictal, post-ictal, and difference (STL_{maxpost – ictal} − STL_{maxpre – ictal}) values for each SWD in each animal. A statistical comparison (by a nested two-way ANOVA test, where the random factor (rats) is nested within an animal group) of dynamical values during the pre-ictal period (2 min before a SWD) showed no significant difference between the 4- and 20-month old animals in STL_max values (p > 0.05). However, the same statistical test performed on post-ictal dynamical values (2 min after a SWD) revealed a significant difference between the two groups in STL_max values (p < 0.05). To compare how effective each SWD was in resetting the animal’s brain to a normal interictal state, we computed the difference between average pre-ictal and post-ictal dynamical values. The test of these “resetting” values suggested that the “resetting” was significantly more effective in the 4-month old cohort compared with the 20-month old cohort, evident from STL_max values (p < 0.05). Figure 6 illustrates the comparison of the differences between pre-ictal and post-ictal periods between animals in the two age groups.

Fig. 6.

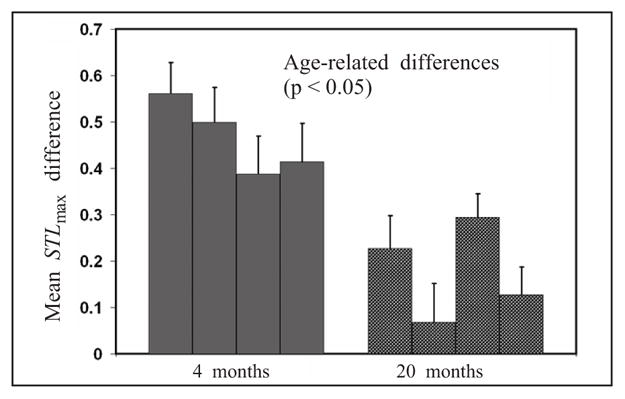
Age-related differences in resetting (difference between post-ictal and pre-ictal STL_max values) between young (4-month old) and aged (20-month old) animals.

4. CONCLUSION

As in human epilepsy, transitions from the interictal to the ictal state in the rat involve a transition from a chaotic (high STL_max) to a more ordered (lower values of STL_max) state. The transitions observed in the iEEG in human and rat temporal lobe epilepsy are consistent with early publications that introduced the concept of “dynamical diseases” [30–34]. This concept was introduced to explain how biological systems can make transitions between normal and pathophysiological states. Periodic state shifts observed in biological disorders, such as Cheyne–Stokes respiration, periodic hematopoiesis, and penicillin-induced neuronal spiking, were demonstrated to be similar to state transitions that occurred in certain mathematical models of low-dimensional nonlinear systems [31, 35].

The mean STL_max difference values (post seizure–pre seizure) were significantly different between 4-month old and 20-month old naive animals (4 months > 20 months; p < 0.05), which suggested that the age-related increase in SWD expression is associated with a decrease in seizure-related dynamical effect (resetting), as the animal ages. The results of this study suggest that the recovery of the brain back to its normal interictal state following SWDs was better in young adult animals compared with aged animals. This interpretation is supported by higher post-ictal dynamical values as well as a larger difference between post-ictal and pre-ictal dynamical values.

Mackey and Glass [30] speculated that certain periodic diseases arose because of a bifurcation in the behavior of a control system. Even in simple mathematical models of such systems, transitions between normal and pathological states, or between ordered and chaotic states, can result from small changes in the value of a control parameter [6, 30, 31, 33]. If dynamical diseases can be explained on this basis, then it may be possible to use this information to construct optimal therapeutic responses based on manipulation of a control parameter [33] or by external perturbations using techniques developed for the control of chaotic systems. Furthermore, models of coupled chaotic oscillators have given several insights into prediction of seizures and the resetting phenomenon [36]. Other studies modeling dynamical transition in nonlinear coupled map lattice systems have also shown similarities with the transitions in an epileptic brain [37]. Techniques applied for controlling chaos in dynamical systems, such as coupled map lattice systems, may also prove to be useful in controlling spatiotemporal chaos in the epileptic brain.