Changes in Performance Monitoring During Sensorimotor Adaptation

Abstract

Error detection and correction are essential components of motor skill learning. These processes have been well characterized in cognitive psychology using electroencephalography (EEG) to record an event-related potential (ERP) called error-related negativity (ERN). However, it is unclear whether this ERP component is sensitive to the magnitude of the error made in a sensorimotor adaptation task. In the present study, we tested the function of error-related activity in a visuomotor adaptation task. To examine whether error size is reflected in the ERP, two groups of participants adapted manual aiming movements to either a small (30°) or large (45°) rotation of the visual feedback display. Each participant's trials were sorted into large and small error trials using a median split to examine potential error magnitude waveform differences. We also examined these trial types at the early and late stages of adaptation. There were no group differences for the behavioral or neural measures; however, waveforms from large error trials were significantly different from small error trials. The waveforms also changed as a function of practice as early adaptation waveforms were larger than late adaptation waveforms. The observed ERP component reflected differences in error magnitude with the amount of activity corresponding to the size of the error. Movement monitoring potentials likely affected the frequency and time course of the waveform so that it did not resemble the typical ERN; however, error-related activity was still distinguishable. The present findings are discussed in terms of current theories of the ERN as well as skill acquisition.

INTRODUCTION

During skill acquisition, participants make much larger errors in the first few minutes of practice than even 20 min later with this change in performance commonly described through the power law of practice (cf. Newell and Rosenbloom 1981). Performance improves in a more incremental fashion on entering the middle stage of learning (Fitts and Posner 1967) and even more slowly later in learning (Fitts and Posner 1967; Karni and Sagi 1993; Karni et al. 1998; Puttemans et al. 2005). This division has also been described as a transition from a conscious mode, where strategies are utilized to enhance inexperienced performance, to an unconscious mode, where performance proceeds in an automatic fashion after learning has occurred [cf. control-based learning theory (COBALT)] (Willingham 1998). However, the separation of learning into distinct stages has been somewhat arbitrary in the literature, primarily reflecting the time course of the experiment at hand (Adams 1971; Fitts and Posner 1967; Karni et al. 1998; Puttemans et al. 2005; Schmidt 1976; Seidler et al. 2006; Willingham 1998). Focusing on the early and late stages has provided a useful framework for examining the sensorimotor adaptation process, given that the middle stage of learning is thought to be contaminated by components engaged during the early and late time points (Fitts and Posner 1967; Willingham 1998).

For over 100 years, visuomotor adaptation has been used as a model task to study how the CNS adapts to changes in the mapping between visual and motor representations (cf. Bock 1992; Seidler et al. 2006; von Helmholtz 1962; Welch et al. 1974). These studies typically involve reaching or throwing movements toward targets under normal and distorted visual feedback, with the largest off-target errors observed during the initial exposure to the altered mapping environment. Accuracy improves as the CNS adapts to the discrepant mapping (cf. Cunningham and Welch 1994), with adaptation scaling to the size of a previous error (Scheidt et al. 2001; Wolpert and Ghahramani 2000). Similarly, reinforcement learning theory proposes that the extent of learning is proportional to the magnitude of the predicted error (Barto 1994, 2003b; Sutton and Barto 1988). However, Fine and Thoroughman (2006, 2007) have demonstrated that, under certain task parameters, corrective actions are not related to error size.

Neuroimaging studies of sensorimotor adaptation have implicated several brain structures, including the anterior cingulate cortex (ACC), in the adaptation process (Anguera et al. 2007; Graydon et al. 2005; Miall et al. 2001; Seidler et al. 2006). However, it is not clear what role this structure plays during sensorimotor adaptation. It has been suggested that the ACC serves as an active monitoring system that reacts to the presence of conflict and/or performance errors in cognitive tasks (Botvinick et al. 1999; Carter et al. 1998; Gehring and Knight 2000; Gehring et al. 1993; Yeung et al. 2004). In particular, the ACC is believed to be the origin of a medial frontal negative event-related potential (ERP) component called the error-related negativity (ERN) (Debener et al. 2005; Holroyd et al. 2004; Miltner et al. 1997). This component peaks shortly following an incorrect response in speeded response tasks (Falkenstein et al. 1990; Gehring et al. 1993) and following the presentation of error feedback in reinforcement learning tasks (Badgaiyan and Posner 1998; Holroyd and Coles 2002; Miltner et al. 1997).

ERN studies have been very useful in providing insight into the cognitive and neural mechanisms involved in performance monitoring as well as the adjustment of flexible, goal-directed behavior. A recent computational model suggested that larger ERN amplitudes early in learning should be associated with a greater amount of overall learning as a function of avoiding maladaptive responses (Frank et al. 2005). This relates very well to the reinforcement learning theories of motor learning as they also suggest a correlation between the amount of learning and the predicted error between the actual and intended movement (Barto 1994, 1997, 2003; Sutton and Barto 1988; Wolpert and Ghahramani 2000). In fact, the reinforcement learning theory of the ERN (Holroyd and Coles 2002) suggests that ERN amplitude is magnified when participants are first learning a stimulus-response mapping, and this amplitude diminishes as the appropriate mapping is learned. It is not clear, however, whether the ERN scales with the size of motor errors in a similar fashion.

The ERN has been primarily studied using basic reaction time tasks [e.g., the Eriksen Flanker task (Eriksen and Eriksen 1971)] in which errors are binary in nature (present or absent). This is in direct contrast to errors in motor learning tasks (e.g., reaching or aiming movements, force production) where errors can extend over time, range in magnitude, and reflect mistakes in goal attainment and/or response execution. There has been a recent surge of studies examining performance monitoring via the ERN during motor tasks (de Bruijn et al. 2003; Contreras-Vidal and Kerick 2004; Krigolson and Holroyd 2006, 2007a,b); however, these studies have failed to characterize how this ERP component relates to error size.

These ERN studies of motor tasks have consistently shown a fronto-central negative-polarity potential associated with goal attainment errors (“high-level” errors) (as defined by Krigolson and Holroyd 2006). This activity resulted when participants incorrectly responded with the wrong hand or amount of force (cf. de Bruijn et al. 2003), failed to reach a designated target (Krigolson and Holroyd 2007a; Krigolson et al. 2008), or failed to avoid a barrier in a motor tracking task (Krigolson and Holroyd 2006, 2007b). These types of errors are binary in nature (“correct or incorrect”) with corrections not possible following a response. However, corrections are possible for response execution errors (“low-level” errors) (as defined by Krigolson and Holroyd 2006); for example, correcting an initially erroneous trajectory to reach a desired target (Contreras-Vidal and Kerick 2004; Krigolson and Holroyd 2007a; Krigolson et al. 2008) or avoid an oncoming barrier (Krigolson and Holroyd 2006, 2007b). For these types of errors, Krigolson and Holroyd (2006) observed parietal activity without medial-frontal/ERN activity. In light of these findings, Krigolson and Holroyd (2006) proposed a hierarchical error processing theory in which the frontal error system evaluates only high-level errors, whereas the posterior error system responds only to low-level errors. Such results suggest that the ACC may only be providing a binary (present or absent) high-level error signal rather than processing detailed information about the size of motor errors (see also Diedrichsen et al. 2005). Testing this hypothesis is critical to understanding the role that this neural process plays in motor learning and adaptation.

In the present study, we determined whether motor errors made during visuomotor adaptation elicit an ERP component the activity of which corresponds to the size of the motor error. Two groups of individuals performed a visuomotor adaptation task using a joystick, with each group exposed to a differing amount of feedback rotation. This design permitted us to test whether sensorimotor adaptation under more perturbed conditions would be associated with a greater amount of activity. We also examined this activity after separating trials into large and small error magnitudes relative to median performance for each participant at early and late adaptation. These approaches allowed us to evaluate whether errors of differing sizes would be reflected in the ERP. Thus we were able to test two mutually exclusive hypotheses: the error signal simply provides a binary alert that an error has occurred, without regard to the size of the error or the error signal is relative to the size of the error made.

METHODS

Participants

Nineteen women and 21 men between the ages of 18 and 27 yr [mean: 22.8 ± 3.5 yr] participated in the study. All participants were recruited from the University of Michigan student population and were paid for their participation. Each signed an IRB-approved informed consent form and a health history questionnaire prior to their participation. All participants were strongly right-handed (0.88 ± 0.06), as assessed by using the 20-item version of the Edinburgh Inventory (Oldfield 1971). They were randomly assigned to one of two perturbation groups: a 30° feedback rotation group (20 participants; 10 men) and a 45° feedback rotation group (20 participants; 11 men). A between-group design was used to examine potential ERP differences for perturbations of different magnitudes as previous work using these rotations has induced group differences (cf. Seidler et al. 2006). We avoided using a within-subject design as exposing participants to multiple perturbations has been shown to contaminate the adaptation experience with participants using their previous experience to progress through the adaptation period at a faster rate (Seidler 2004).

Apparatus and procedure

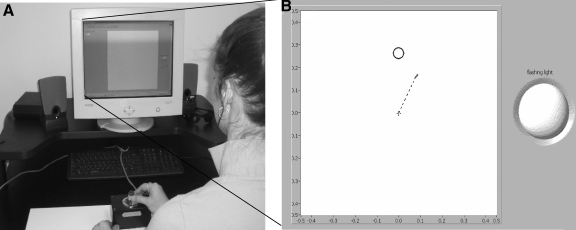
The stimuli were presented on a 15-in NEC (Tokyo, Japan) Multisync computer monitor at a viewing distance of 60 cm, which was used to provide real-time movement feedback. Participants moved a dual potentiometer joystick that was fixed to a table with Velcro, placed within arm's reach. They were instructed to hold the joystick with their thumb and index finger (see Fig. 1).

FIG. 1.

Experimental setup and initial endpoint error calculation. Participants viewed a computer screen from a distance of 60 cm with the joystick mounted via Velcro on the table in front of them (A). B: a screen shot of the computer screen during the task (including the flashing light for the photoreceptor). The dashed line drawn from the starting center point to the cursor illustrates a 30° perturbed trajectory during the early learning period when participants would aim the joystick directly toward the target.

The participants were instructed to use the joystick to position a cursor in a target circle on the screen. Targets (0.8 cm in diameter) appeared for 4 s in one of four locations: 4.8 cm to the right, left, above, or below the centrally located home position (0.8 cm in diameter). Participants were asked to move the cursor into the target circle as quickly (the velocity of the cursor was participant controlled) and accurately as possible and maintain the cursor within the circle until the target disappeared. On target disappearance, they were told to release the spring-loaded joystick handle, so that it would recenter for each subsequent trial. The next trial began 1 s later, resulting in an inter-trial interval (from 1 target presentation to the next) of 5 s.

The 30 and 45° rotation perturbations indicate a clockwise rotation of the cursor position about the central start location (cf. Cunningham and Welch 1994). When a participant in the 30° group moved toward a target at the top of the screen in the “12 o' clock” direction, they observed the cursor moving instead toward “1 o' clock” (see Fig. 1). Thus to reach a target in the 30° rotation condition, a participant would need to aim 30° counterclockwise of the target, or toward “11 o' clock.” Participants were not informed in advance as to whether the upcoming block was an adaptation or control block nor were they provided with any information about the applied rotations.

Participants performed 14 blocks (B) of the task (28 trials per block) with their right hand (see Table 1). Blocks 2–3 were considered to be the baseline (pre-test) stage for two reasons: the real-time feedback of the participants' movements was not altered during this period, and omitting the first block ensures that there was no task novelty effect present in the baseline measure. Blocks 4–5 were considered to be the early stage as these blocks encompassed the initial exposure to the visuomotor perturbation, and blocks 13–14 were the late stage. Both early and late stages were limited to having an equivalent number of blocks and trials to the baseline condition.

TABLE 1.

Condition by block for the visuomotor adaptation task

Block Number	Rotated Feedback	Condition
B1	NO	Practice
B2	NO	Baseline
B3	NO	Baseline
B4	30°/45°	Early adaptation
B5	30°/45°	Early adaptation
B6	30°/45°	Adaptation
B7	30°/45°	Adaptation
B8	30°/45°	Adaptation
B9	30°/45°	Adaptation
B10	30°/45°	Adaptation
B11	30°/45°	Adaptation
B12	30°/45°	Adaptation
B13	30°/45°	Late adaptation
B14	30°/45°	Late adaptation

B, block; 30°/45°, adaptation blocks with corresponding rotated feedback.

Electrophysiological acquisition parameters

The electroencephalogram (EEG) was recorded from 37 scalp electrode sites with sintered Ag/AgCl electrodes embedded in a nylon mesh cap (Easycap, Falk Minow Services). The electrode locations consisted of Fp1, Fp2, AFz, F7, F3, F1, Fz, F2, F4, F8, FT7, FC3, FC1, FCz, FC2, FC4, FT8, T7, C3, C1, Cz, C2, C4, T8, TP7, CP3, CPz, CP4, TP8, P7, P3, Pz, P4, P8, O1, Oz, and O2 (American Electroencephalographic Society 1991). EEG data were recorded with a left mastoid reference. An average mastoid reference was derived off-line using right mastoid data. The electrooculogram (EOG) was recorded from Ag/AgCl electrodes above and below the right eye, the naison, and external to the outer canthus of each eye. A ground electrode was placed on the forehead. Impedances were kept <10 kΩ. The EEG and EOG were amplified by SYNAMPS amplifiers (Neuroscan), recorded from 0.01 to 100 Hz (half-amplitude cutoff), and the data were digitized at 1,000 Hz. To time-lock the initiation of each trial to the EEG recordings, a flashing oval (3 cm in diameter) was activated for 5 ms on the appearance of each target circle with this flash captured by a photocell on the right side of the screen (see Fig. 1). The photocell channel data were acquired by the Neuroscan system in parallel with the EEG data to ensure that signal synchronization was achieved. To prevent this flashing from distracting the participants, the right side of the screen where the photocell was located was shielded from their view.

Behavioral data processing

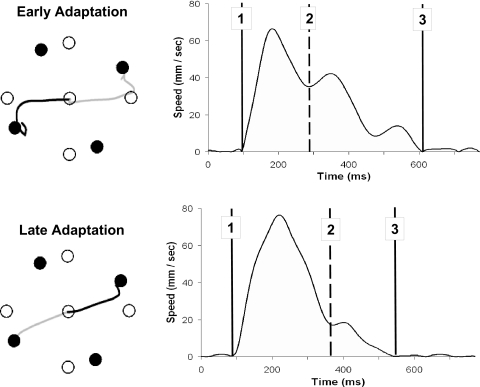
The x and y coordinates from the joystick were recorded at a rate of 100 Hz. We analyzed the joystick data off-line using custom Labview 6.1 software (National Instruments) to track behavioral changes with learning. We first filtered the data with a dual low-pass Butterworth digital filter (cf. Winter 1990), using a cutoff frequency of 10 Hz. The resultant joystick path was calculated by computing the square root of the sum of the squared x and y coordinate data at each time point. The tangential velocity profile was then calculated through differentiation. Movement onset and offset were computed through the application of Teasdale et al.'s (1993) optimal algorithm to the velocity profile for each movement. We used initial endpoint error (IEE), the distance from the end of the initial ballistic movement position to the target, to assess the extent of adaptation. This measure is calculated by finding the first time point of acceleration following the deceleration of the initial ballistic movement, which would reflect the phase of the movement associated with the initiation of the first corrective submovement (see Fig. 2 for illustration). We also calculated the corrective submovement distance (CSMD) traveled to assess whether there was a correlation between the IEE and corresponding corrective movement. The following temporal measures were also analyzed: reaction time (RT), primary submovement duration (PSD), and corrective duration time (CDT).

FIG. 2.

Spatial trajectories and corresponding velocity profiles (for each dark trajectory) during early and late adaptation. Top: a velocity profile from early adaptation under the 30° feedback rotation; bottom: a trial from the same subject during the late adaptation period. Point 1 is the movement onset, point 2 represents the initiation of the corrective phase [initial endpoint error (IEE)], and point 3 is the cursor's final endpoint position. ○, target location in visual space (including the center start position); •, the target locations in joystick space. The spatial trajectory is presented in joystick coordinates. Adaptation is evidenced by the straighter trajectories in the bottom comparison to the top.

We used a group × block × trial mixed model ANOVA to compare performance between the two groups. Significant interactions were followed up with simple contrasts. The Huynh-Feldt epsilon (Huynh and Feldt 1970) was evaluated to determine whether the repeated-measures data met the assumption of sphericity (Σ > 0.75). The trials for each stage were then pooled together, creating a block pair for each period (e.g., blocks 2 and 3 = block pair 1). In doing this, we were able to utilize a greater number of trials (56 trials per stage) in the EEG waveform averages; ≥46 trials went into each mean bin for the ERP analysis for each subject. Trials within each block pair for each participant were sorted using a median split of IEE values, resulting in large and small error trials.

EEG data reduction

After recording, the EEG data were digitally low-pass filtered with a half-amplitude cutoff point at 50 Hz (24 dB/octave roll-off) and reduced to a sampling rate of 200 Hz. Data were corrected for eye movement artifacts using the method designed by Gratton et al. (1983). Statistical analyses used data filtered at the 50-Hz cutoff, referenced to the average of the mastoid electrodes. EEG data were averaged off-line for epochs of 1,000 ms, using the photoreceptor flash time stamp as a starting point each trial. Each epoch was then time-locked to each participant's movement onset based on their RT and the time point when an initial corrective submovement began. For the RT time-locked waveforms, the baseline chosen was 200 ms prior to movement onset,1 while the IEE used a baseline 200 ms prior to the initiation of a corrective submovement. We quantified the ERP waveforms recorded using mean amplitude measures in three time windows: 200–400, 400–600, and 600–800 ms. While the 600- to 800-ms time window inclusion is much later than most studies examining response monitoring effects, the time course of error correction for a VMA task would typically require this long duration to ensure capturing a complete corrective submovement(s). Large and small error trials determined via the median split for each participant at each stage were then compared within each defined time window. We focused our statistical ERP analyses on activity recorded at the FCz electrode as previous ERN research has shown the greatest effect at this electrode. The data shown in the figures were generated using a 16-Hz low-pass Butterworth filter (Matlab 7.1; Mathworks, Natick, MA).

RESULTS

ERP data from two participants (1 in each group) were lost due to technical problems and were excluded from the analyses. Thus the behavioral results are presented for twenty participants in each group, while the ERP results are presented for nineteen participants in each group (10 males for each group).

Behavioral

INITIAL ENDPOINT ERROR AND CORRECTIVE SUBMOVEMENT DISTANCE.

Sample spatial trajectories for a single participant (under 30° rotation) are depicted in Fig. 2 at the early stages of adaptation (A) and the final adaptation block pair (B). Adaptation to the rotated feedback is seen in the less distorted trajectories employed in reaching the targets in B versus those in A.

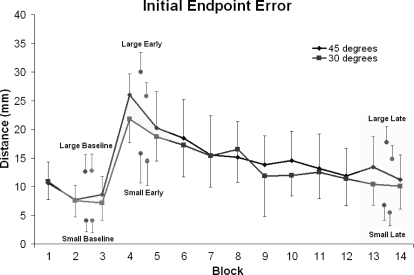
Figure 3 illustrates the performance for each group by block for IEE. Note that an IEE score of ≤4 mm (the radius of the target circle) indicates that the initial ballistic movement ended within the target circle; thus a corrective submovement was not required. However, participants still made corrections to movements that were inside the target circle to have the final endpoint as close to the center as possible. This design allowed for a comparison of across-error magnitudes without categorizing each trial in a binary fashion as “correct” versus “incorrect.” A repeated-measures ANOVA (RM ANOVA) with block (14) and trial (28) resulted in significant main effects for block [F(13,494) = 31.31, P < 0.0001, partial eta squared (η_p²) = 0.45], so follow-up tests were conducted. There was no difference between groups for the baseline block pair [B2–B3; F(1,38) = 0.51, P > 0.40, η_p² = 0.013], the early adaptation block pair [B4–B5; F(1,38) = 2.30, P > 0.10, η_p² = 0.06], or the late adaptation block pair [B13–B14; F(1,38) = 1.58, P = 0.22, η_p² = 0.04]. There were no group differences for any of the subsequent analyses that were performed; therefore we omitted the group variable from our analysis. The rotated feedback impaired accuracy of movements, as observed through performance differences between the baseline and early adaptation block pair [F(1,39) = 134.70, P < 0.0001, η_p² = 0.78]. Participants adapted to the rotated feedback as evidenced by the difference between the early block pair versus the late block pair [F(1,39) = 108.82, P < 0.0001, η_p² = 0.74]. The pooled late block pair was significantly different from the baseline block pair [F(1,39) = 13.33, P = 0.001, η_p² = 0.26], which reflects that performance did not reach baseline levels by the end of practice.

FIG. 3.

Group means and SDs for IEE are presented for each block of the experiment with the group pooled large/small error trial block pair indicated by a separate point within each respective stage (baseline, early, late). Blocks 1–3 were performed under nonperturbed conditions, whereas blocks 4–14 involved visual feedback of the cursor movement being rotated by 30°/ 45°. Adaptation is evidenced across blocks 4–14 as performance improved (e.g., mean block scores were closer to 0) with practice. There was no difference between perturbation groups at any stage.

Each group showed impaired movement accuracy when the rotation was first introduced during the early stage, followed by improvements in accuracy following practice at the late stage. As there were no differences in error magnitude between the two groups at these stages, we pooled their data and sorted it into large and small error trials based on a median split of the data for each block pair. Following the differentiation of each participant's trials using the median split into large and small error trials for all blocks, we observed a significant within group difference for IEE between large and small trial errors for each group [30°: F(2,119) = 42.34, P < 0.0001, η_p² = 0.54; 45°: F(2,119) = 39.27, P < 0.0001, η_p² = 0.51]. Consistent with previous between group analyses, there was no difference between groups for a group × block × error type ANOVA [F(1,38) = 0.54, P > 0.80, η_p² < 0.01; see Fig. 4]. There was a significant correlation between IEE and the corresponding CSMD traveled at each period (baseline: r = 0.39, early: r = 0.29, late: r = 0.48, r > 0.27 = P < 0.05).

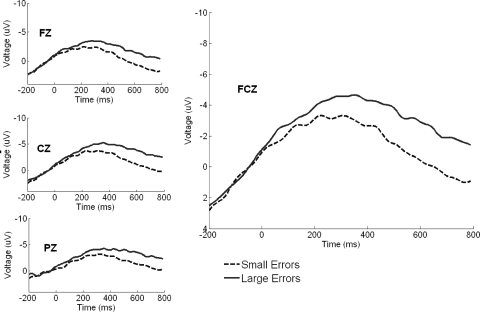
FIG. 4.

Large and small error trial waveforms time-locked to reaction time at selected central electrodes pooled across each stage, with activity at FCz highlighted. There was no difference between large and small error trial waveforms.

Temporal measures

The temporal performance variables (RT, PSD, and CDT) are presented in Table 2. At the early adaptation stage, both groups were equivalent for RT [F(1,38) = 0.05, P > 0.80, η_p² < 0.01] and PSD [F(1,38) = 2.41, P > 0.10, η_p² = 0.06]; however, there was a group difference for CDT [F(1,38) = 7.09, P < 0.05, η_p² = 0.16] with the 45° group taking more time correcting their initial movement. Initial exposure to the rotated feedback impaired both the accuracy of movements as well as the duration of the movement made, as the participants' RT [F(1,38) = 18.97, P < 0.0001, η_p² = 0.33], PSD [F(1,38) = 36.06, P < 0.0001, η_p² = 0.49], and CDT [F(1,38) = 14.85, P < 0.0001, η_p² = 0.28] were longer for the early block pair compared with baseline. There was no group difference here for RT [F(1,38) = 0.63, P > 0.40, η_p² = 0.02] or PSD [F(1,38) = 0.48, P > = 0.45, η_p² < 0.01], but there was for CDT [F(1,38) = 5.66, P < 0.05, η_p² = 0.13] as the 45° group took more time in implementing their corrections. The participants improved with practice as evidenced by the temporal improvements between the early and late block pair for RT [F(1,38) = 15.25, P < 0.0001, η_p² = 0.29], PSD [F(1,38) = 14.91, P < 0.0001, η_p² = 0.28], and CDT [F(1,38) = 15.29, P < 0.0001, η_p² = 0.29]. Again, a group difference was only apparent for CDT [F(1,38) = 8.12, P < 0.05, η_p² = 0.18].

TABLE 2.

Temporal measures by learning period

	Reaction Time, ms	Primary Submovement Duration, ms	Corrective Submovement Duration, ms
Baseline	286 ± 56	439 ± 72	339 ± 139
Early	388 ± 124	479 ± 73	442 ± 125
Late	345 ± 94	518 ± 100	348 ± 113

Values are means ± SD.

There was no group difference across the late stage as participants took an equivalent amount of time for RT [F(1,38) = 1.16, P > 0.25, η_p² = 0.03], PSD [F(1,38) = 0.14, P > 0.70, η_p² < 0.01], and CDT [F(1,38) = 1.91, P > 0.15, η_p² = 0.05]. The pooled late stage (B13–B14) showed a significant difference from the baseline blocks for PSD [F(1,38) = 81.38, P < 0.0001, η_p² = 0.68] but not for RT [F(1,38) = 3.06, P > 0.05, η_p² = 0.08] or CDT [F(1,38) = 0.35, P > 0.50, η_p² < 0.01]. Again, there was no group difference between these stages for RT [F(1,38) = 0.15, P > 0.70, η_p² < 0.01], PSD [F(1,38) = 0.03, P > 0.80, η_p² < 0.01], or CDT [F(1,38) = 2.72, P > 0.10, η_p² = 0.07].

Electrophysiological data

We chose to perform all ERP statistical analyses on activity recorded at the FCz electrode because this experiment was motivated by studies of the ERN, which is typically found at the 10–20 location FCz. We did not observe any differences between the two groups for any of the ERP comparisons that follow; therefore we omitted that variable from our analysis. A 2 (error magnitude, large vs. small) × 3 (stage: baseline, early, late) × 3 (time window: 200–400, 400–600, 600–800 ms) RM ANOVA of ERPs time-locked to movement onset failed to find a main effect of error magnitude [F (1,37) = 0.04, P > 0.80, η_p² < 0.01] or stage [F(2,74) = 0.37, P > 0.60, η_p² = 0.01] but did show a main effect of time window [F(2,74) = 56.70, P < 0.0001, η_p² = 0.61] and a time window × stage interaction [F(4,148) = 13.00, P < 0.0001, η_p² = 0.26]. Visual inspection of these data highlight these results as large and small error waveforms pooled across all adaptation periods did not differ (Fig. 4; see Table 3 for mean ERP amplitudes for each stage). These findings did not change when a prestimulus baseline (200-ms time window) was used instead (see Supplementary Materials,2 Fig. S1). Therefore we continued our analyses examining the time-locked ERP recordings at the onset of the corrective submovement.

TABLE 3.

RT and IEE time-locked ERP amplitudes

	Large Errors	Small Errors
RT time-locked
Baseline
200–400ms	−5.99 ± 0.75	−5.65 ± 0.72
400–600ms	−9.24 ± 0.75	−9.55 ± 0.77
600–800ms	−7.94 ± 0.68	−7.71 ± 0.81
Early
200–400ms	−3.63 ± 0.90	−3.57 ± 0.80
400–600ms	−8.54 ± 0.88	−8.58 ± 0.79
600–800ms	−9.26 ± 0.86	−10.42 ± 0.83
Late
200–400ms	−5.48 ± 0.71	−5.93 ± 0.68
400–600ms	−9.25 ± 0.87	−9.16 ± 0.83
600–800ms	−8.89 ± 0.93	−8.23 ± 0.86
IEE time-locked
Baseline
200–400ms	−3.89 ± 0.68	−2.99 ± 0.79
400–600ms	−2.36 ± 0.69	−1.03 ± 0.88
600–800ms	−0.25 ± 0.61	1.58 ± 0.86
Early
200–400ms	−6.40 ± 0.61	−5.62 ± 0.74
400–600ms	−7.01 ± 0.82	−5.54 ± 0.96
600–800ms	−5.79 ± 0.88	−4.25 ± 0.94
Late
200–400ms	−3.51 ± 0.59	−1.75 ± 0.68
400–600ms	−2.35 ± 0.80	0.32 ± 0.85
600–800ms	−0.88 ± 0.81	2.49 ± 0.82

Values are means±SE. RT, reaction time; ERP, event-related potential; IEE, initial endpoint error.

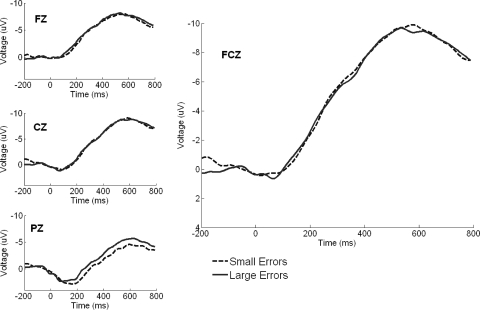
We were interested in determining whether the rotated feedback led to increased ERN amplitude by comparing the early adaptation stage relative to baseline, how ERN amplitude changed as adaptation progressed from the early to late stage, and whether, regardless of stage, errors of large magnitude produced greater ERN activity than small errors. A 2 (error magnitude, large vs. small) × 3 (stage: baseline, early, late) × 3 (time window: 200–400, 400–600, 600–800 ms) RM ANOVA resulted in a main effect of time window [F(2,74) = 47.65, P < 0.0001, η_p² = 0.56], a main effect of stage [F(2,74) = 28.08, P < 0.0001, η_p² = 0.43], a main effect of error magnitude [F(1,37) = 18.07 P < 0.0001, η_p² = 0.33], a time window × stage interaction [F(4,148) = 17.20, P < 0.0001, η_p² = 0.32], and a time window × error magnitude interaction [F(2,74) = 11.78, P < 0.0001, η_p² = 0.24]. High and low error waveforms pooled across all stages were significantly different when time-locked to the initiation of the corrective submovement (Fig. 5; see Table 3 for mean ERP amplitudes for each learning period). In the following text we explore these main effects and interactions using simple effects tests in the context of the issues described in the preceding text.

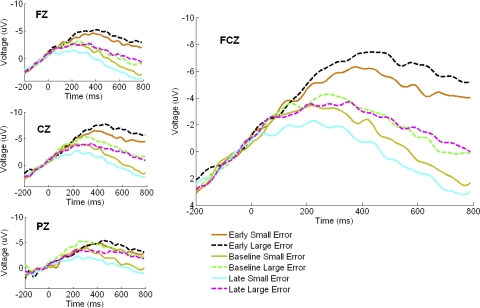
FIG. 5.

Large and small error trial waveforms time-locked to the initiation of the corrective submovement at selected central electrodes pooled across each stage with activity at FCz highlighted. Large error trials elicited significantly more activity vs. small error waveforms, reflecting a sensitivity to the size of the error experienced.

Overall error magnitude

The ANOVA comparing the pre test, early, and late stages showed a main effect of error magnitude[F(1,37) = 18.07, P < 0.0001, η_p² = 0.33] but no interaction between stage and error magnitude [F(2,74) = 1.57, P > 0.20, η_p² = 0.04; see Fig. 5]. The waveforms suggest that the difference between conditions grows throughout the epoch, which was confirmed by a time window by error magnitude interaction [F(2,74) = 11.78, P < 0.0001, η_p² = 0.24].

Early versus baseline

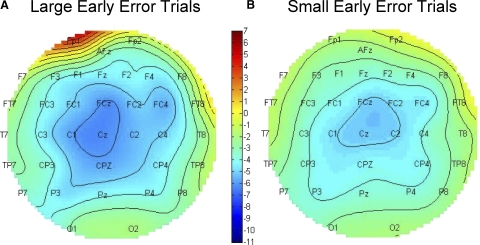
The waveforms in Fig. 6 suggest that the perturbation caused an increase in the ERP amplitude, seen as a difference in the ERP amplitude in the early adaptation versus baseline comparison. A repeated-measures ANOVA involving only the early and baseline waveforms showed a greater negativity in the early adaptation waveforms than in the baseline period, [F (1,37) = 52.39, P < 0.0001, η_p² = 0.59] and a time window × stage interaction [F(2,74) = 24.65, P < 0.0001, η_p² = 0.40]. Inspection of the waveforms suggests that the early versus baseline difference grows larger in the later time windows, and indeed a simple effects test showed that the difference was larger in the late time window than in the early one [F(1,37) = 34.43, P < 0.0001, η_p² = 0.48]. Topographic distribution of activity selective to large and small error magnitudes for early adaptation between 0 and 600 ms is shown in Fig. 7, illustrating a broad negativity encompassing the FCz electrode.

FIG. 6.

Large and small error trial waveforms time-locked to the initiation of the corrective submovement at selected central electrodes at each stage, with activity at FCz highlighted. Pooled early adaptation waveforms showed greater activity vs. pooled baseline or late adaptation waveforms, and early high and low error waveforms were distinct from one another.

FIG. 7.

Scalp plots for early adaptation. Mean scalp plot of all subjects between 100 and 600 ms after onset of the movement correction at the early stage. A: mean activity of large error trials; B: small error trials.

Progression of adaptation

The waveforms in Fig. 6 suggest that the negativity in the early stage was greater in amplitude than in the late stage. A repeated-measures ANOVA involving only the early and late waveforms confirmed a larger negativity in early than in late waveforms [F(1,37) = 40.75, P < 0.0001, η_p² = 0.52]. An interaction was also present between time window and stage [F(2,74) = 19.40, P < 0.0001, η_p² = 0.34], reflecting a shift toward positive polarity late in the epoch. There was also an error magnitude × time window interaction [F(2,74) = 7.56, P < 0.005, η_p² = 0.17]. Mean ERP amplitudes for each block pair across the entire adaptation period showed a significant linear fit [F(1,37) = 31.59, P < 0.0001, η_p² = 0.46]. A separate ANOVA comparing baseline and late waveforms failed to find a significant difference [F(1,37) = 0.517, P > 0.40, η_p² = 0.01]. A partial correlation controlling for the CSMD between IEE and mean ERP amplitude time-locked to the initiation of the corrective submovement was not significant at any stage (baseline: r = 0.15, early: r = 0.05, late: r = −0.13; r critical for P < 0.05, r > 0.32).

DISCUSSION

In the present study, we observed ERP waveforms associated with motor errors. While waveforms time-locked to movement onset did not distinguish between large and small errors, those time-locked to the onset of a corrective submovement did. There was a significant difference between these correction time-locked waveforms when all stages were collapsed, as well as distinctive waveforms at specific stages of the adaptation process. These findings support the idea that this signal is sensitive to differences in error magnitude and is modulated as a function of practice.

Large versus small errors: effects of error size

When all stages and time windows were collapsed, there was a significant difference between large and small error IEE time-locked waveforms. These results agree with reinforcement learning theories suggesting that the magnitude of the difference between the predicted and actual outcome is reflected by a corresponding amount of neural activity in the medial-frontal cortex (Barto 1994; Frank et al. 2005; Holroyd and Coles 2002). In addition, these findings are inconsistent with the proposed idea of neural activation being insensitive to error magnitude (Fine and Thoroughman 2006, 2007), although we cannot rule out the possibility of this being a condition-specific effect. Krigolson and Holroyd (2006, 2007a) and Krigolson et al. (2008) have demonstrated that while motor execution errors (low-level) do not elicit medial frontal activation, errors in goal attainment (high-level) do. The present findings demonstrate, however, that this is not the case. That is, we observed medial-frontal activity for low-level errors (correctable deviant trajectories). All errors in the present study were low level with a trial duration (4,000 ms) that provided participants more than enough time to initiate a movement, make corrections, and reach the target circle. With this methodological difference, comparing large errors in the present study to high-level errors found by Krigolson and Holroyd (2006, 2007a) and Krigolson et al. (2008) cannot be tested here. Similarly, this trial duration prevented the comparison with correct versus high-level endpoint-locked waveforms (cf. Krigolson and Holroyd 2006, 2007a) and Krigolson et al. (2008), as participants had accurately reached the target circle at this time. However, the present findings can be compared with their low-level errors as they are of the same nature (correctable trajectories) and show a similar CDT [471 ms (Krigolson and Holroyd 2007a) vs. 479 ms here].

There are other methodological differences which potentially explain the discrepancies between our findings and those of Krigolson and Holroyd (2006, 2007a) and Krigolson et al. (2008). In the present study, we specifically examined how error-related waveforms scaled with the size of errors, whereas Krigolson and Holroyd (2006, 2007a) and Krigolson et al. (2008) utilized the binary measure of reaching a target (Krigolson and Holroyd 2007a; Krigolson et al. 2008) or erroneously hitting a barrier during a tracking task (Krigolson and Holroyd 2006). However, we believe that both high- and low-level errors are present at each stage in our study, as discrepant trajectories led to difficulty in reaching the target. We suggest that the distinct, slow moving negative waveforms observed here reflect the ongoing evaluation and correction of the erroneous trajectory during the corrective submovement(s) following the initial ballistic movement.

Another key difference from the present study is that Krigolson and Holroyd (2006, 2007a) and Krigolson et al. (2008) did not allow participants to make corrective actions (they had no control over the cursor for part of the trial) on 50% of the trials in which they made a low-level trajectory error, forcing a high-level goal attainment error. Although participants did not report awareness of a loss of control, their overall strategy and corresponding neural activity may have changed for the task given the presence/absence of corrective submovements. It is common for participants to make one or more of these submovements during manual aiming tasks (see Fig. 2B) (also see Meyer et al. 1988). If, as our data suggest, medial-frontal activation does not appear to be solely tied to high-level errors, one would expect similar, if not greater, negativity during correctable trials as at least some of the submovements are imprecise (Meyer et al. 1988). In fact, Krigolson and Holroyd (2006) reported greater negativity for the correctable ERP compared with the uncorrectable condition. Furthermore, Krigolson and Holroyd (2007a) required the use of a difference waveform to isolate the ERN. It is not clear, however, that the peak in the difference waveform was caused by the ERN; the individual condition waveforms suggest that a positive-polarity peak on correct trials is a likely source of the apparent negative peak in the difference waveform.

Practice effects

There were significant changes in performance with practice with participants reducing errors from the early to late adaptation stage, and early adaptation waveforms being larger than baseline or late learning waveforms. This suggests that more error monitoring may have been occurring when performance was perturbed, and this monitoring led to more pronounced differences between these stages as time passed. Several fMRI studies have demonstrated differential involvement of the ACC depending on the stage of learning one is at (Bush et al. 1998; Jenkins et al. 1994; Raichle et al. 1994; Toni and Passingham 1999). In these studies, the ACC showed significant activation during the earliest stages of the task with a diminishing contribution as learning progressed. This pattern of activation at the ACC has also been observed with a visuomotor adaptation paradigm in an fMRI (Anguera et al. 2007) and ERP study (Contreras-Vidal and Kerick 2004).

Holroyd and Coles (2002; p. 694) suggested that the change in activity at the ACC as a function of practice reflects the “first indication that the consequences of an action are worse than expected.” These authors propose that activation originating from the ACC acts as a training signal that serves to adjust control of the motor system in subsequent trials. In the present study, this interpretation is supported by the waveform differences between large and small error magnitudes at early adaptation as a larger error would require a more robust training signal to adjust control in an effective manner. The present findings suggest that the signal does not reflect error size relative to the stage of adaptation but instead reflects the relative size of the error. While the present findings do show scaling across two points (large and small), a more precise understanding of this scaling would be facilitated by the inclusion of “medium-”sized errors into the analysis. We did not pursue this approach in the current study as it would have lead to an insufficient number of trials for each trial type (∼18 per block pair) for ERP averaging.

One could argue that the observed ERP varies with the magnitude of the movement to be initiated and not with the error committed, especially considering the observed influence of the MMP. This interpretation cannot be completely overlooked given the correlation between IEE and the corrective submovement distance at each stage. However, the partial correlation controlling for CSMD between IEE and ERP amplitude at each stage was not significant, suggesting that the ERP amplitude is not reflecting a greater distance to be traveled for a given error. This finding further supports the role of error monitoring processes in the observed ERP.

ERN and error processing

As the present study was motivated by the use of ERN to distinguish between error types during a visuomotor adaptation task, we will consider our results in the context of the three best known theories of response ERN production: error detection theory, reinforcement learning theory, and conflict monitoring theory. The error-detection theory proposes that the ERN reflects a process that compares motor system output (via an efferent copy of the movement command) to the best estimate of the correct response at the time of the ERN occurrence (Falkenstein et al. 1991a; Gehring et al. 1993). The ERN could then reflect the output of the comparison process (Coles et al. 2001; Falkenstein 1990), the comparison process itself (Falkenstein et al. 2000; Vidal et al. 2000), or a process that uses the error signal to prevent or correct the error, possibly through a strategic adjustment (Gehring et al. 1993; Holroyd and Coles 2002). The reinforcement-learning theory of the ERN (Holroyd and Coles 2002) suggests that ERN amplitude reflects a generic error processing system that incorporates both error-related feedback as well as an efference copy of the given motor command. This theory suggests that ERN amplitude is determined by a signal generated by the basal ganglia, which is then carried by the midbrain dopamine system to the ACC. Finally, the response-conflict monitoring theory proposes ERN amplitude reflects monitoring for conflict between incompatible responses (Botvinick et al. 2001; Yeung et al. 2004). Under this theory, the function of the ERN is to relay this information to neural regions involved in cognitive control, like the prefrontal cortex (Botvinick et al. 2001; Yeung et al. 2004).

In agreement with the error detection theory, greater negativity was associated with a greater disparity between the best estimate of a correct movement and the compared efferent copy. Similarly, larger performance errors (or larger prediction errors between the expected and actual outcome) corresponded with increased negativity, which would agree with reinforcement-learning theory. This would also be the case for the response conflict theory, as the competition between the initial response and the error correction would presumably lead to greater negativity for large error trials. Thus the present findings are consistent with each theory but do not clearly differentiate between them.

Interestingly, the medial frontal negativity recorded from a visuomotor adaptation ERP study attributed this activity to the acquisition and modification of an internal model of the visuomotor representation to the perturbed environment (Contreras-Vidal and Kerick 2004). Other ERN studies have also credited the medial frontal activity to the comparison of predicted and intended responses (Rodrguez-Fornells et al. 2002; Swick and Turken 2002), which is consistent with the role of feedback for internal model theory. We propose that the frontal–central negativity in the present study serves a performance monitoring function during the motor adaptation process (cf. Botvinick et al. 2001; Carter et al. 1998; Holroyd and Coles 2002). However, further research is warranted to isolate the role of the ERN and its potential involvement in the modification of the internal model of the task.

Do the waveforms reflect ERN activity?

Although the locus of the negativity in the present study cannot be completely attributed to the ACC, we have previously observed ACC activation in an fMRI study of this same task (Anguera et al. 2007). Likewise, the observed scalp distribution is similar to that of ERN, which previous studies have linked to the ACC (Carter et al. 1998; Herrmann et al. 2004; Miltner et al. 1997). While the present findings fit with each of the response-based theories of the ERN, they are also in line with a related component, the feedback-related negativity (FRN). FRN occurs following a feedback stimulus long after a given response (Badgaiyan and Posner 1998; Gehring and Willoughby 2002; Holroyd and Coles 2002; Miltner et al. 1997; Nieuwenhuis et al. 2004a) with greater amplitude following negative, unexpected feedback (Cohen et al. 2007; Hajcak et al. 2007; Holroyd et al. 2003; Potts et al. 2006).

The present findings would also agree with the FRN interpretation, as the unexpected change in mapping would correspond with greater negativity, while at late learning this change was more expected. However, recent studies suggest that this component covaries with outcome in a binary fashion (good or bad) without any gradation in outcome value (Hajcak et al. 2006; Holroyd et al. 2004, 2006; Nieuwenhuis et al. 2004b; Yeung and Sanfey 2004; but see Goyer et al. 2008). This is in contrast to the present findings, suggesting that this component may not play as prominent a role as the “classic” response-based ERN in this study. Nevertheless, although there is some similarity between the activity observed in the present study and the ERN, additional work is needed to determine whether they represent the same component or are instead two distinct ERP components.

One might question whether the pronounced, slow moving negative waveforms observed in the present study might be better explained by another component, as the shape and time course of the present waveforms do not resemble those of the ERN observed in more typical speeded button-press tasks. One possibility would be movement-monitoring potentials (MMPs) (Chiang et al. 2004; Grunewald-Zuberbier and Grunewald 1978; Slobounov et al. 1998, 2000, 2002), which are slow-moving negative potentials associated with preparation and execution of an action. The time course of this potential spans several seconds, with a rising negativity ∼1,500 ms before movement onset, and a much larger ERP amplitude than the ERN that can persist for well over 1,000 ms (cf. Chiang et al. 2004; Slobounov et al. 2000, 2002).

This component is readily observed during a force generation task (Slobounov et al. 2002) with a higher rate of force production corresponding with increased negativity and an EEG time series comparable to those observed in the present study. de Bruijn et al. (2003) also observed a force production negativity after response onset in differing conditions, which led to their conducting separate analyses for the high and low force ranges to separate out the potential contributions from a MMP. In doing so, they suggest that error monitoring processes can be dissociated from the MMP despite the potential interference of MMP activity. Like de Bruijn et al. (2003), we suggest that the negativity observed in the present study reflects not only a component of the MMP but also encompasses error-related ERP activity. Other ERP studies support this assertion, as a slowly rising negativity like the one observed here was associated with high-level errors from an incorrect response execution made during a force production task (de Bruijn et al. 2003), a continuous tracking task (Krigolson and Holroyd 2006, 2007b), and a computerized aiming task (Krigolson and Holroyd 2007a; Krigolson et al. 2008).

We hypothesize that the prolonged waveforms in the present study represent the on-line modification of the erroneous movement. The signal observed here remains on for an extended period of time, potentially providing for continuous modulation of the action as it is completed. Given the relatively lengthy duration of a trial in this study, it makes sense for the system to be in a state of readiness for a longer time to initiate a remedial action at any point between the initiation of the movement and its completion. These findings also suggest that the MMPs observed in other studies might serve a performance monitoring function. However, it should be noted that the MMP is typically isolated during “self-paced” initiation tasks, unlike the present task, suggesting that further investigation of the role of MMP warrants further investigation.

Conclusions

We found a differential ERP effect for errors of different magnitude (averaged across stage of adaptation). There was a significant difference between early adaptation waveforms versus baseline or late adaptation waveforms with early adaptation large and small error waveforms being distinct from their corresponding baseline and late adaptation waveforms. We propose that the medial frontal neural processes involved in sensorimotor adaptation interpret differences in error magnitude in a relative fashion with the amount of activity corresponding to the size of the error. While the waveforms observed are atypical compared with most ERN studies, it is plausible that they represent ERN-related activity involved in the sensorimotor adaptation process.

GRANTS

This work was supported by National Institute of Aging Grant AG-024106 to R. D. Seidler.