Abstract
Responses of neural units in two areas of the medial auditory belt (middle medial area [MM] and rostral medial area [RM]) were tested with tones, noise bursts, monkey calls (MC), and environmental sounds (ES) in microelectrode recordings from two alert rhesus monkeys. For comparison, recordings were also performed from two core areas (primary auditory area [A1] and rostral area [R]) of the auditory cortex. All four fields showed cochleotopic organization, with best (center) frequency [BF(c)] gradients running in opposite directions in A1 and MM than in R and RM. The medial belt was characterized by a stronger preference for band-pass noise than for pure tones found medially to the core areas. Response latencies were shorter for the two more posterior (middle) areas MM and A1 than for the two rostral areas R and RM, reaching values as low as 6 ms for high BF(c) in MM and A1, and strongly depended on BF(c). The medial belt areas exhibited a higher selectivity to all stimuli, in particular to noise bursts, than the core areas. An increased selectivity to tones and noise bursts was also found in the anterior fields; the opposite was true for highly temporally modulated ES. Analysis of the structure of neural responses revealed that neurons were driven by low-level acoustic features in all fields. Thus medial belt areas RM and MM have to be considered early stages of auditory cortical processing. The anteroposterior difference in temporal processing indices suggests that R and RM may belong to a different hierarchical level or a different computational network than A1 and MM.
INTRODUCTION
Pandya and Sanides (1973), based not only on cyto- and myeloarchitectonic properties but also on connectivity, proposed that the primary-like auditory koniocortex (or core) in the macaque is surrounded by belt areas. Although terminology differed in subsequent studies (most notably, medial belt was sometimes referred to as “root”), their results continued to demonstrate that the medial and lateral regions of the belt to some extent share thalamic and cortical connectivity and histochemical properties (Burton and Jones 1976; Cipolloni and Pandya 1989; Hackett et al. 1998; Mesulam and Pandya 1973; Pandya et al. 1994). According to these studies, medial and lateral belts are more similar to each other than to the core. In a model that is now widely adopted, the concentric core/belt structure has been refined and extended. It has been proposed that the macaque auditory cortex consists of three core (or primary-like) fields surrounded by a number of belt areas and of a parabelt region located lateral to the lateral part of the belt (Kaas and Hackett 2000).
Of the belt areas, the lateral belt has so far attracted the most attention, partly because it is relatively easily accessible for neurophysiological recordings. However, the lateral belt also appears to provide a clear step in hierarchical processing of auditory information, as suggested by its anatomical intermediate position between core and parabelt and between core and prefrontal areas (Hackett et al. 1998; Kaas and Hackett 2000; Rauschecker et al. 1997; Romanski et al. 1999a,b).
Most notably, it has been established that, in contrast to core neurons, cells in the lateral belt respond more vigorously to bursts of noise covering a restricted range of frequencies (band-pass noise [BPN]) than to pure (single-frequency) tones, suggesting that these neurons integrate auditory information over certain frequency bands (Rauschecker et al. 1995). Three lateral belt areas can be discerned whose boundaries are determined by reversal of cochleotopic gradients when tested with BPN bursts (Petkov et al. 2006; Rauschecker and Tian 2004; Rauschecker et al. 1995). Furthermore, the finding that the anterior lateral field (AL) shows enhanced selectivity for monkey calls, whereas caudal lateral belt (CL) neurons are relatively more selective to the spatial location of a sound source (Tian et al. 2001), provided support for the hypothesis of separate processing streams for sound identity (rostral “what” stream) and auditory space (caudal “where” stream) in the auditory cortex (Rauschecker and Tian 2000). The hypothesis was also supported by the anatomical finding that the caudal and rostral lateral belts are predominantly connected with, respectively, spatial and nonspatial domains of the prefrontal cortex (Romanski et al. 1999a,b) and by behavioral results of a lesion study (Harrington and Heffner 2003).
Given numerous similarities in connections and histochemistry between the medial and lateral belts, it is plausible that the neural response properties in these regions would also be more similar to each other than to the neural properties of the core. In particular, it can be predicted that the medial belt neurons would show a higher preference than neurons in core areas for intermediately complex (Rauschecker and Tian 2004; Tian and Rauschecker 2004) stimuli, such as BPN, similar to the lateral belt (Petkov et al. 2006; Rauschecker and Tian 2004; Rauschecker et al. 1995). Thus we expected to find an increased BPN preference medially to core areas and, if such a preference were found electrophysiologically, we would label these areas as the medial belt.
This prediction is based not only on the anatomical analogies with the lateral belt: Petkov et al. (2006) presented functional magnetic resonance imaging (fMRI) data suggestive of increased preference for BPN in all belt areas, including those located medially to core. However, the results from the medial belt were not as clear as those from the lateral belt and would benefit from electrophysiological confirmation, which has been lacking so far. Although a study by Lakatos et al. (2005) compared responses to tones and BPN bursts in core and belt areas, the authors did not distinguish individual fields within the combined posterior lateral and medial auditory belt; thus the significance of their findings for the determination of medial belt properties is unclear.
Because little information has been gathered on the medial belt compared with the lateral belt, it may not be surprising that it is not even clear how many medial belt fields exist in the macaque. Often four medial belt fields (rostrotemporal medial belt [RTM], rostral medial belt [RM], middle medial belt [MM], and caudal medial belt [CM]) are described (e.g., Petkov et al. 2006; Woods et al. 2006); another position is that there are just three of them (RTM, RM, and CM; e.g., Hackett et al. 1998; Smiley et al. 2007). According to the first view, MM lies medially to the auditory core's primary field A1. Anterior to these, RM is situated medially to the rostral core field R (previously also referred to as rostrolateral field [RL]; Merzenich and Brugge 1973), and further anterior lies RTM medially to the rostrotemporal field (RT). CM is located posterior to MM and posteromedial to A1 (Kaas and Hackett 2000). The “three-field” view considers MM and CM to be a single entity, called CM, which lies along the entire medial boundary of A1 and also posteromedial to it. Hackett et al. (1998) placed boundaries consistent with the existence of MM on their figure but avoided using the label, whereas Kaas and Hackett (2000) used the “MM” label in their figures, but stated that “connection patterns support the possibility of three to four medial belt areas.” In more recent papers, MM was explicitly mentioned and labeled (Hackett et al. 2007; Smiley et al. 2007), whereas at the same time it has been suggested that CM and MM should rather be considered a single area (Smiley et al. 2007). Similarly, the possible existence of area MM in the marmoset has been mentioned, but the area has not been distinguished from CM (de la Mothe et al. 2006a). Recanzone et al. (2000b) labeled the entire area along the medial and posterior border of rhesus primary auditory field as CM, whereas Woods et al. (2006) distinguished MM from CM.
Not much is known about basic response properties of the medial belt areas. Tonotopic gradients were reported in RM by Kosaki et al. (1997; using a different nomenclature) and in CM by Rauschecker et al. (1997). However, some of these recordings could actually have been from the caudal lateral area (CL). In another study, CM (including MM) was tested with tonal stimuli, yielding no clear tonotopic gradients (Recanzone et al. 2000a). More recently, Petkov et al. (2006) mapped responses to tones and BPN in macaque auditory cortex using fMRI, showing in most cases cochleotopic gradients in CM (in a direction consistent with Rauschecker et al. 1997) and RTM. Only in some cases were gradients in MM or RM demonstrated. Thus the existence of cochleotopic gradients in these areas needs to be confirmed (or disproved) using methods of higher spatial resolution, such as single-unit recordings. Demonstration of a cochleotopic gradient in area MM that is collinear with the gradient in A1 and discontinuous from the frequency organization in CM would also provide a final resolution to the question whether CM and MM are physiologically distinct areas.
Finally, the role of the medial areas in the proposed “what” and “where” streams needs to be elucidated. Although Recanzone et al. (2000a) reported that CM neurons predicted the behavioral performance in an auditory spatial task better than A1 neurons, consistent with the dual-stream hypothesis that attributes spatial processing to caudal fields, their definition of CM comprised the CM, MM, and CL of Kaas et al. (2000). In a more recent experiment, CL neurons were shown to display sharper spatial tuning than those in areas R, A1, and MM, but often sharper than those in CM as well (Woods et al. 2006). In the context of the “what” stream, it would be worthwhile to determine whether neurons in more anterior areas of the medial belt respond with a higher selectivity to natural sounds than cells in more posterior areas, similar to neurons in the lateral belt (Tian et al. 2001). This has not been investigated at all. Similarly, reports about neural response latencies in the medial belt are scarce and their results hard to reconcile (Lakatos et al. 2005; Recanzone et al. 2000b; also compare results from the marmoset in Kajikawa et al. 2005).
To examine response properties of neurons in the core and medial belt, we analyzed the cochleotopic organization, responses to BPN, pure tones (PT), and two classes of natural sounds, as well as response latencies in two alert rhesus monkeys. The results clearly support the existence of two cochleotopically organized medial belt areas, a rostromedial area (RM) and a middle medial area (MM), in addition to area CM and in parallel with core areas R and A1, respectively. Similarly to lateral belt, and consistent with our predictions and the results of Petkov et al. (2006), medial belt neurons prefer BPN bursts over PTs, indicating that the region is at a hierarchically higher level than core and its neurons integrate across certain frequency bands. On the other hand, response latencies in the middle medial belt are as short as those in A1. The lack of a pronounced selectivity for natural complex sounds and representation of low-level acoustic features also point to a relatively early processing stage of medial belt.
METHODS
Animals
Two male rhesus monkeys (S and L) were used. The animals had been trained previously on auditory go/no go differentiation and were used in other neural recording studies. They were implanted with round recording chambers (19-mm diameter; Crist Instruments, Hagerstown, MD) over the left auditory cortical areas, with the implant location confirmed by 3T MRI, with 1-mm3 voxel size. Monkeys were on water restriction to provide adequate drive for a fluid-rewarded task. All experiments were conducted in accordance with National Institutes of Health guidelines and approved by the Georgetown University Animal Care and Use Committee.
Stimuli and task
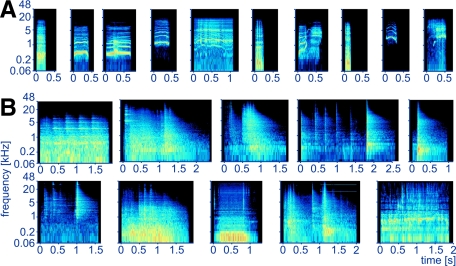
Monkeys were seated in a monkey chair (Crist Instruments) in a sound-attenuated chamber (IAC, Bronx, NY) measuring 2.6 × 2.6 × 2.0 m (W × L × H). Six classes of stimuli were used: pure tones (PT), 1/3-octave and 1-octave band-pass noise bursts (BPN), wideband noise bursts (WBN, white and pink), rhesus monkey calls (MC), and environmental sounds (ES). All PT, BPN, and WBN were 500 ms in duration. The 1/3-octave and 1-octave wide BPN were obtained by filtering pink noise with a band-pass fast Fourier transform (FFT) finite impulse response (FIR) filter (FFT size 24,000 points, Blackmann–Harris window). All noise bursts were generated once prior to the experiments and were therefore “frozen”; 20-ms-long linear on- and off-ramps were applied to PT, BPN, and WBN. The PT frequencies and BPN center frequencies spanned 125 Hz to 32 kHz with 1-octave spacing. MC were obtained from a digital library provided by M. Hauser (Hauser 1998). Ten exemplars (Fig. 1A; duration range, 151–1,071 ms) were resampled to 96 kHz and processed with filters, noise reduction, and the Frequency Space Editing tool (Audition 2.0; Adobe, San Jose, CA) to reduce background noise. Ten exemplars of ES were recorded in the monkeys' housing area and prep room and, because they were sounds of commonly occurring events, were highly familiar to the monkeys. They comprised noises produced when operating monkey cages, monkey chair, and monkey pole, moving a wheeled food container, turning on TV, operating a vacuum pump or a water faucet; the durations ranged between 961 and 2,614 ms (Fig. 1B). These stimuli were recorded with a Brüel & Kjær (Nærum, Denmark) 4133 1/2-in. condenser microphone, a Brüel & Kjær 2235 SPL meter (serving as a preamplifier), and an Audigy 2NX (Creative Technology, Singapore) sound card at 96 kHz/16 bit. Processing included gentle noise reduction and filtering, mainly to remove HVAC (heating, ventilating, and air conditioning) noise. ES stimuli and spectrograms of MC and ES are provided in Supplemental Figs. S1 and S2.1
FIG. 1.
Spectrograms of the natural stimuli used in the experiment. A: monkey calls (bark, coo1, coo2, coo3, girney, grunt, harmonic arch, pant threat, scream1, scream2). B: environmental sounds (middle row: cage [sound of monkey swinging], cage divider, cage lock open, monkey chair latch close, monkey chair latch open; bottom row: monkey pole latch, moving food container, vacuum pump, VCR and TV turning on, water running in sink). The frequency axis of the spectrograms has a logarithmic scale.
No attempt was made to equate the acoustic structure between ES and MC. Rather, based on the assumption that MC constituted complete and meaningful vocalizations, we selected ES to evoke (in human listeners) the perception of complete and meaningful acoustic events as well. This led to numerous differences between the two classes, which ultimately turned out to be responsible for observed differences in the preference indices or temporal structuring of responses (see discussion). That is, the ES were significantly longer than MC (mean: 1,817 vs. 466 ms); their spectra were more widely spread (as measured by power spectrum SD and coefficient of variation: mean 3,149 vs. 1,221 Hz and 1.72 vs. 0.83, respectively); they were noisier (mean harmonicity, i.e., ratio of periodic to aperiodic components, Boersma 1993: 1.7 vs. 9.6 dB); their intensity was more varied within each stimulus (mean SD of the intensity function: 7.6 vs. 2.8 dB); and their onset intensity was relatively lower (mean level difference between maximum intensity in the first 100 ms and the maximum intensity in the entire stimulus: −18.9 vs. −5.1 dB; P < 0.03 for all the above-cited comparisons, Mann–Whitney test). The power spectrum center of gravity did not differ between ES and MC (mean 2,515 vs. 1,757 Hz, P > 0.7). Measurements of stimulus parameters were done with Praat 4.3.27 (Paul Boersma, University of Amsterdam) on stimuli root-mean-squared (RMS)–matched in the digital domain.
In an attempt to match the loudness of the stimuli at the monkey's head location, the loudness was estimated by recording the stimuli played through the stimulus presentation system, filtering the recorded signal on the basis of a behaviorally determined Japanese macaque audiogram (Jackson et al. 1999), similar to the “A” filtering curve used in sound-level measurements for humans, and taking maximum RMS amplitude in a 200-ms-long sliding window. Out of numerous published macaque monkey audiograms we chose the one from Jackson et al. (1999) because it was obtained relatively recently in a lab with extensive experience in animal audiogram measurements, in free-field conditions (as in our experiment), and is complete. Many complete published rhesus monkey audiograms (Lonsbury-Martin and Martin 1981; Pfingst et al. 1975, 1978) were obtained using headphones. Therefore because of the influence of the head and pinnae on the sound field (Spezio et al. 2000), they would be appropriate only for matching loudness of stimuli presented via headphones. The only rhesus audiogram obtained in free field relatively recently (Bennett et al. 1983) is quite incomplete and thus is not suitable for constructing a filter for equalization purposes. Older rhesus free-field audiograms (Behar et al. 1965; Fujita and Elliott 1965) deviate from audiograms reported by Bennett et al. (1983) and Jackson et al. (1999) in an inconsistent way. Importantly, the incomplete free-field data from Bennett et al. (1983) agree better with the free-field Japanese macaque audiogram (Jackson et al. 1999) than with the headphone-based rhesus audiograms, especially in the 1- to 10-kHz range. On the other hand, a headphone-based cynomolgus macaque audiogram (Stebbins et al. 1966) agrees with the rhesus headphone-based audiograms. It thus seems that within the Macaca genus the shape of the audiogram is influenced more by the method of presentation (free-field vs. headphones) than by the actual species, which justifies our choice of a free-field Japanese macaque audiogram.
The 200-ms averaging window was chosen to approximate the rhesus monkey temporal integration function, which levels off around 200 ms (O'Connor et al. 1999). The stimulus presentation level was set to about 50 dB above threshold. Background noise, measured using the same filter, was nearly 30 dB below stimulus level.
Stimulus generation and processing were performed with Adobe Audition 1.0 or 2.0 at 96-kHz sampling frequency and 32-bit resolution. The stimuli were finally downsampled to 16 bit (using 0.7-bit dither and triangular probability distribution function, no noise shaping) and played using an Audiophile 192 (M-Audio, Irwindale, CA) sound card, PA4 attenuator (Tucker-Davis Technologies [TDT], Alachua, FL), SE 120 amplifier (Hafler, Tempe, AZ), and Reveal 6 loudspeaker (Tannoy, Coatbridge, UK). The speaker was located 1.7 m in front of the monkey. To minimize the influence of standing waves on the low-frequency response, we played white noise through the loudspeaker, recorded it back via the 4133 microphone placed on the monkey chair, examined the power spectrum, and iteratively adjusted the positions of loudspeaker and monkey chair until large variations of the low-frequency response were minimized.
The behavioral task was a go/no go auditory discrimination task: a bar-release response to an infrequent (∼14%) auditory target (a 500-ms “melody” consisting of four consecutive pure tones; Micheyl et al. 2005) was rewarded by a small amount of juice. The purpose of the task was to keep the animals at an approximately constant level of attention. A block consisting of 49 stimuli of interest and eight repetitions of the target was presented 10–13 times (in random order within each block presentation) to obtain reliable neural responses. A trial started with a 300-ms pretrial period, during which the animal had to keep its hand on the bar. The response window started with stimulus onset and continued 1 s beyond the end of the stimulus. Hits (responses to the target) were followed by a 1.5-s timeout to avoid contamination of the following trials by licking sounds; 2.5-s timeouts followed misses and false alarms and no timeout followed a correct rejection. The ITI varied randomly between 1.25 and 1.75 s.
Neural recordings
Single- and multi-unit recordings were obtained by advancing an epoxylite-insulated approximately 1-MΩ tungsten electrode (FHC, Bowdoin, ME) into the auditory cortex by means of a hydraulic micropositioner (Model 650; David Kopf, Tujunga, CA). A stainless steel guide tube was used to puncture the dura. A 1 × 1-mm spacing grid (Crist Instruments) provided a repeatable spatial reference for electrode location. The grid was oriented approximately parallel to the anteroposterior axis. The electrode signal was amplified (Model 1800; A-M Systems, Sequim, WA), filtered (PC1, TDT), and isolated with a window discriminator (SD1, TDT), with the aid of an oscilloscope and audio monitor. Spike time stamps were detected with close to 1-ms accuracy through a printer port with a custom-made program (see http://linc.georgetown.edu/fiodor) running on a Windows XP personal computer. The program also presented stimuli and controlled the behavioral task. Accurate timing of stimulus onset was achieved by combining the stimulus sound files with a square-wave marker into stereo files and timing the marker and spikes using the same port and procedure. When the auditory cortex was reached as determined by the recording depth and by the presence of a “silent” space above (corresponding to the lateral sulcus), we used the same stimuli as those used in the formal testing and/or natural sounds produced ad hoc (knocking, hissing, key jingling, clapping, etc.) to elicit auditory responses from neurons (whether identified by baseline activity or silent when not stimulated). Only auditory responsive units were recorded.
Neural data analysis
Neural responses were analyzed either in segments: “on” response (first 100 ms of stimulus duration), “sustained” response (starting from stimulus onset + 100 ms and ending at the stimulus end), and “off” response (200 ms beyond stimulus end); or as an “entire” response, for which “on,” “sustained,” and “off” responses were combined. The statistical significance of an “on,” “sustained,” or “off” response was determined by comparing average firing rate in the segment to the baseline firing rate obtained in 250 ms preceding the sound onset (Wilcoxon test, P ≤ 0.05).
Baseline activity (average activity in the 250 ms preceding the stimulus onset) was subtracted from further firing rate measures. Peak firing rate (PFR) was determined as the maximum firing rate in a sliding 40-ms window (1-ms step) along the response averaged across stimulus repetitions (Tian et al. 2001). Best frequency (BF, for PT) and best center frequency (BFc, for BPN) were determined for “on”, “sustained”, and “off” responses separately by fitting a quadratic function to the PFR–frequency curve at the frequency where the highest PFR occurred and the two neighboring frequencies on either side. If the highest PFR occurred at one of the outermost frequencies (0.125 or 32 kHz), that frequency was determined to be the BF(c) [BF(c) stands for “BF or BFc” or “BF and BFc combined”]. All calculations, including sound frequency and ratios of firing rates, were performed on log-transformed data. The reason for using the log transformation in the latter case was that spike ratios, when expressed on a linear scale, produce positively skewed distributions (e.g., Rauschecker and Tian 2004); thus log-transformation improves normality of the data. Units whose response at the highest PFR was not significant or not excitatory were not included in further calculations using BF(c).
Preference index (PI) within a class of stimuli was calculated as the proportion of stimuli in the class that elicited ≥50% of the PFR as the stimulus that produced the highest PFR. This measure is similar to a preference index used previously (Tian et al. 2001), but independent of the number of stimuli in the class. Another measure of selectivity was a variant of preference index based on a statistical comparison (Recanzone 2008; Romanski et al. 2005). We used the Recanzone (2008) variant, defining the t-test–based preference index (PIt) as the number of stimuli whose PFR were not significantly different (t-test with Bonferroni correction) from the PFR of the stimulus that evoked the highest PFR, divided by the number of stimuli in the class minus 1. In both cases low values (close to 0 for PI and starting from 0 for PIt) of the index indicate a high selectivity of a unit within the class, whereas high values (close to 1) mean low selectivity. The preference indices were always calculated within a stimulus class; thus they indicate how selective a neuron is, for example, to a 1/3-octave BPN in comparison to other 1/3-octave BPN.
To obtain an additional measure of neural selectivity, which also allows estimating the temporal accuracy of neural responses, we used a linear pattern discriminator (Recanzone 2008; Russ et al. 2008; Schnupp et al. 2006). For each unit and each stimulus class (PT, 1/3-oct BPN, 1-oct BPN, MC, and ES), a single spike train (trial) was selected from responses to one stimulus and binned with a certain window size, constituting the test peristimulus time histogram (PSTH). Next, stimulus PSTHs were constructed from the remaining trials (spike trains) of the same stimulus and from all trials of each of the other stimuli of the class. Then, the Euclidean distance between the test PSTH and each stimulus PSTH was computed and used to determine the discriminator's choice. If the distance between the test PSTH and the same stimulus PSTH was the smallest one, that is, the discriminator selected the same stimulus PSTH based on the test PSTH, the choice was considered correct. Alternatively, if the discriminator chose one of the other stimulus PSTHs based on the test PSTH, the choice was incorrect. This procedure was repeated for all other trials of the stimulus and then for all trials of the other stimuli. The percentage correct performance of the discriminator was the proportion of correct choices. For each neuron, this procedure was performed for different window sizes (2, 5, 10, 20, 50, 100, 200, 500, 1,000, and 2,000 ms) and for each stimulus class. Because stimulus durations appreciably differed, we submitted to the discriminator spike trains from stimulus onset to 500 ms beyond the end of the longest stimulus in the class, rounded up to the window boundary. Each neuron was characterized by the best discriminator performance (linear discriminator percent correct [LDPC]) value and by the best window (i.e., the window at which LDPC was achieved) for each stimulus class.
To estimate neural response latencies, PSTHs were created with a 1-ms bin from the “entire” response and smoothed with an exponential function yi = αxi + (1 − α)yi−1 (α = 0.3). Smoothing allowed estimation of the latency even if the first spike latency varied somewhat from trial to trial or if a recording was not very reliable and certain spikes were missed or noise was introduced. On the other hand, exponential smoothing (as opposed to, for example, Gaussian smoothing or rectangular/moving-average smoothing) is causal and thus cannot generate latencies shorter than the latency of the first spike. Latency of the response to a stimulus was defined as the time of the first bin in which the smoothed value exceeded the average smoothed firing rate from the 250 ms preceding the stimulus onset by ≥2SDs of that pretrial firing rate and remained above 2SD for ≥10 ms.
A unit's latency was estimated as the shortest of: 1) latency of the PT that elicited the highest “on” PFR of all PT, 2) latency of the 1/3-octave BPN that elicited the highest “on” PFR of all 1/3-octave BPN, 3) latency of the 1-octave BPN that elicited the highest “on” PFR of all 1-octave BPN, 4) latency of the stimulus that elicited the highest “on” PFR of all PT, BPN, pink noise, and white noise. This procedure also determined what value was used as BF(c) of the neuron when the relationship between latency and BF(c) was analyzed. Finally, 4 ms were subtracted from the calculated latency to account for the combined effect of the 1.7-m sound-travel distance (5 ms) minus a nearly 1-ms delay introduced by the spike processing path, mainly by the spike discriminator. PSTHs and raster plots in Fig. 2 and Fig. 6 were plotted without the 4-ms correction. MC and ES were not used for latency estimation because of their diverse onset envelope shapes.
FIG. 2.
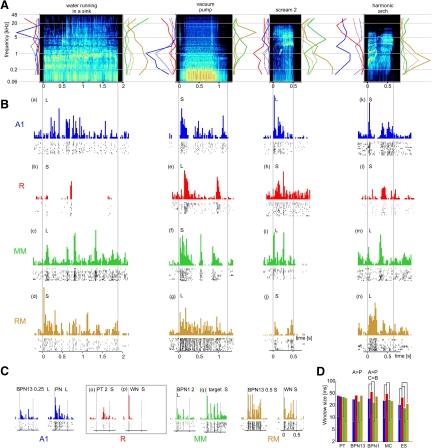
Determining the core/belt boundary. A: distribution of band-pass noise/pure tone (BPN/PT) ratio obtained from the neurons' sustained responses [BPN/PT(s)] in the recording area. Data smoothed with a 2-dimensional Gaussian kernel, σ = 1.5. Black line shows the core/medial belt boundary. Belt areas are located medially and are predominantly red/yellow; core areas are located laterally and are predominantly blue/green. Location of units whose responses are shown in C and D is marked with white letters. B: direction, strength, and significance of BPN/PT(s) gradients. Correlation coefficient of the ratio values with spatial locations of units projected onto an axis that was rotated 360° in 5° steps is shown as a black line. The gradient direction angle is the angle at which maximum correlation was found, the strength is the maximum r value, and the P value is determined by comparison with correlations obtained from scrambled data (shades of gray). See methods for details. The outer circle of the plot denotes r = 0.4. C: example response of a belt unit, showing sustained activity to BPN stimuli. D: example response of a core unit, showing no sustained activity to BPN stimuli. Vertical lines show stimulus start and end. Peristimulus time histograms (PSTHs) binned with 20 ms.
FIG. 6.
Temporal structure of neural responses. A: spectrograms of example environmental sounds and monkey calls. Line plots along each spectrogram's frequency axes show tuning profiles [rate-(center)frequency curves] of example units, whose responses to these sounds are shown below in B. Solid line, “on” tuning profile; dotted line, “sustained” tuning profile; line color indicates the cortical field in which the unit was found and matches the color of the unit's PSTHs in B. Tuning profiles averaged across PTs and BPNs. Plots normalized to maximum peak firing rate (PFR) produced by the unit in respective (“on” or “sustained”) response. B: PSTHs and raster plots obtained from example units in response to stimuli shown above in A. Each row contains examples from one cortical field: A1, R, MM, or RM. Individual monkeys are identified with letters L and S. Vertical lines show stimulus start and end. PSTHs binned with 20 ms. The PSTH ordinate shows spike count normalized to maximum spike count found for all stimuli in the unit. Individual responses are referenced using (a)–(q) labels when described in results. C: PSTHs and raster plots obtained from example units in response to tones, band-pass, and wide-band noise bursts. PT, pure tone; BPN13, 1/3-octave band-pass noise; BPN1, 1-octave band-pass noise; PN, pink noise; WN, white noise; target, behavioral target (4-tone “melody”; only 12 first sweeps out of 96 obtained are shown in the raster plot for the target). Numbers show stimulus (center) frequency of PT and BPN in kilohertz. Responses in gray rectangle come from the same unit. D: effect of stimulus class and cortical field on best discriminator window. Significant differences marked with “>” signs (main effects) or with lines joining bars (post hoc comparisons). A: anterior fields (R + RM); P: more posterior fields (A1 + MM); C: core (R + A1); B: medial belt (RM + MM).
We investigated whether neural responses of a unit to a class of stimuli (PT, noise [BPN and WBN combined], MC, and ES) exhibited temporal structure beyond the simple on/sustained/off pattern: PSTHs and raster plots of each unit were examined visually for the presence of such a structure. A stimulus class (PT, noise, MC, or ES) was determined to evoke temporally structured response in the unit if at least one member of the class evoked such a response. The criterion of at least one class member was used (instead of, for example, >50% of members) to avoid confounding effects of neural selectivity/tuning width.
The following novel way of determining quantitatively the direction of gradients of certain parameters was used. Gradient direction was determined for particular fields or for the whole recording area by finding the correlation coefficient of the parameter values with spatial locations of units projected onto an axis that was rotated 360° with a 5° step. The maximum correlation coefficient was the measure of the gradient strength and the rotation angle at which the maximum was found indicated the direction of the gradient. Because the largest correlation coefficient was chosen from 72 calculated coefficients, standard determination of the P value associated with the coefficient could not be used. Therefore the calculation was repeated 2,500 times in the same way, but with the parameter values randomly reassigned among the units' spatial locations. The number of maximum correlation coefficients obtained in this way that were higher or equal to the coefficient obtained from the original data was divided by 2,500 to obtain the P value. This method allows for a straightforward estimation of direction and strength of gradients such as tonotopic gradients within a cortical area. To our knowledge, a qualitative assessment of tonotopic gradient direction has rarely been used in neurophysiology of the auditory cortex. The methods used by Formisano et al. (2003) or Petkov et al. (2006) to analyze fMRI data serve a slightly different purpose and use different a priori assumptions; that is, they detect best frequency reversal (i.e., field boundaries) and need a predefined reference axis. Our method works within a cortical field or area (which needs to be predefined), detects linear gradients, and finds the gradient axis.
To determine whether responses to MC and ES are driven by the acoustic structure of the stimuli, we estimated the best frequency from neural responses to ES and MC. Each stimulus was split into 25 1/3-octave-wide bands with a FIR filter (order 16384, Hamming window). Center frequencies spanned 125 Hz to 32 kHz. The intensity profile of each band was determined by calculating the RMS value (expressed in dB) in 20-ms consecutive windows. Next, for each unit, neural responses to MC and ES were binned with 20-ms resolution after subtracting neural latency. The 20-ms window was chosen based on results from the linear pattern discriminator (see results). For each stimulus, the Pearson correlation coefficient was calculated between the binned neural response and each of the intensity profiles. The center frequency of the band whose intensity profile correlated best with the neural response was the BF estimate for the stimulus. Finally, after discarding results from stimuli for which the highest correlation coefficient was less than zero, the estimated BF for the neuron was determined to be the mean of all BF estimates in the stimulus class, calculated separately for monkey calls and environmental sounds. The resulting values were called BFMC and BFES, respectively.
If responses to MC and ES were driven by acoustic structure—i.e., if neurons behave like filters responding to frequencies in their frequency receptive fields—then BFMC and BFES should be correlated with BF and BFc. We addressed this question by calculating correlation coefficients of BFMC or BFES with BF(c) [the average of BF and BF(c) obtained from each BPN bandwith, from the “on” response] and by comparing the distribution of differences between BFMC (or BFES) and BF(c) with the distribution of differences between BFMC (or BFES) and BF(c) randomly shuffled among the units.
Determination of field boundaries
Two-dimensional (2D) distributions (within the recording area) of the average BPN/PT(s) ratio (ratio of the highest BPN-elicited PFR to the highest PT-elicited PFR in the “sustained” response) and average BF(c) were smoothed with a 2D Gaussian kernel [σ = 1 for BF(c); σ = 1.5 for BPN/PT ratio]. Nonrecorded grid locations (or empty locations because of nonsignificant responses) mostly around and sometimes within the recording area, which were neighbored by at least two locations for which data were available, were iteratively filled with the mean of the neighbors' values prior to smoothing until adequate coverage for smoothing was obtained. After smoothing, these fill-in data were removed from further calculations. Because the best (center) frequency gradients appeared to run roughly in the anteroposterior direction, anteroposterior profiles (recording grid rows) of the 2D BF(c) distribution were used to determine the boundary at the BF(c) reversal (Bendor and Wang 2008; Kosaki et al. 1997; Merzenich and Brugge 1973; Morel et al. 1993), which was estimated to lie between the grid location where the smallest BF(c) was found in that grid row and that of its two neighbors whose BF(c) was closer to the grid location with the smallest BF(c). A few obvious discontinuities in the resulting field designations were corrected arbitrarily.
RESULTS
In total, 231 units were recorded from 77 grid locations in monkey S and 190 units from 68 locations were recorded in monkey L.
Responses to band-pass noise (BPN) versus pure tone (PT)
The smoothed distribution of the ratio of maximum BPN-elicited PFR to maximum PT-elicited PFR in the “sustained” response (BPN/PT(s) ratio) in the recording area is presented in Fig. 2A. Figure 2B shows direction, strength, and significance of the BPN/PT(s) ratio calculated from raw (unsmoothed) data. The direction of the gradient was similar in both monkeys, with higher values located approximately medially and lower values located laterally. This confirmed our hypothesis of a higher preference for BPN than for PT in areas located medially to the core than in the core itself. For further analyses, recording locations with the average BPN/PT(s) ratio exceeding the mean of the maximum and minimum of the smoothed BPN/PT(s) ratio were labeled as medial belt areas and the remaining locations were labeled as core areas. The demarcated core/belt boundary is shown as a thick black line in Fig. 2A. The procedure yielded almost homogeneous core (lateral) and belt (medial) designations; a few obvious discontinuities in designations were corrected arbitrarily. In monkey L, for instance, three medial locations with small values of the BPN/PT(s) ratio [Fig. 2A; coordinates mediolateral (ML): −5; anteroposterior (AP): 0 to −2] were assigned to the medial belt. Using the median of the maximum and minimum smoothed BPN/PT(s) ratio instead of the mean did not change the field designation. Using the BPN/PT(o) ratio (calculated from the “on” response only) did not yield consistent results and could not be used for core/belt delineation (see Supplemental Fig. S3). However, the BPN/PT(o) ratio did appear to be related to BF (cf. Fig. 3). Median values for the BPN/PT(s) ratio were for the belt: 1.43 (L) and 1.73 (S), for the core: 1.26 (L) and 1.30 (S). In both monkeys significantly more neurons showed pure tone preference as demonstrated by the BPN/PT(s) ratio ≤1.0 in the core (L: 21/86 = 24.4%, S: 44/166 = 26.5%) than in the belt (L: 13/104 = 12.5% P = 0.038, S: 5/65 = 7.7%, P < 0.002, Fisher exact probability test). Examples of responses of a belt unit demonstrating a high BPN/PT(s) ratio and of a core unit with a low BPN/PT(s) ratio are shown in Fig. 2, C and D, respectively.
FIG. 3.
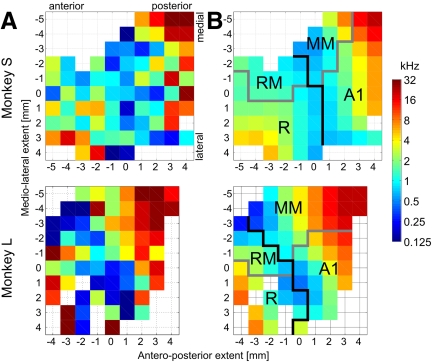
Best (center) frequency gradients and determination of the anteroposterior division of the recording area. A: average best (center) frequency at each recording location. Data from PT and BPN combined, “on” response only. B: smoothed data with the boundary between anterior and posterior areas shown in black; core/belt boundary is shown in gray. Core field designations: A1, primary auditory field; R, rostral field. Medial belt field designations: MM, middle medial belt; RM, rostral medial belt.
Cochleotopic organization
In both monkeys, the values of best (center) frequency for PT, 1/3-octave BPN, and 1-octave BPN were highly correlated (Pearson r >0.81–0.95). Therefore the values were pooled together across these stimulus classes and averaged distributions (Fig. 3) were used to determine the boundary between the anterior and posterior fields (black line on Fig. 3B). Based on the best (center) frequency reversal at low frequencies and the core/belt distinction, four fields were designated in each monkey: rostral (R) and primary auditory (A1) in the core and rostral medial (RM) and middle medial (MM) in the medial belt (Fig. 3B). The number of recorded units per field was in monkey L: R, 31; RM, 23; A1, 55; MM, 81; in monkey S: R, 74; RM, 31; A1, 92; MM, 34.
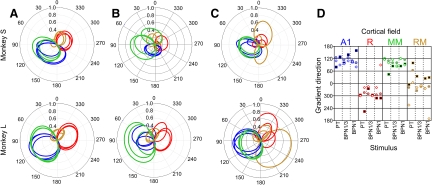
For fields A1, MM, and R, for each stimulus type, significant cochleotopy was found for the “on” responses (Table 1). The direction of cochleotopy was approximately opposite in the posterior fields (A1, MM) versus the anterior field R (Fig. 4A). The picture was somewhat less clear for “sustained” and “off” responses (Table 1 and Fig. 4, B and C), with significant cochleotopy detected in fields A1 and MM, but not for all stimuli or monkeys. Field RM might have been incompletely covered by the recording chambers (cf. Figs. 3 and 5B) and the smallest number of units was recorded there. In spite of this, the direction angle values determined for field RM clearly grouped closer to those of field R than to those of fields A1, in particular for BPN stimuli (Fig. 4D). This observation, together with the clear frequency reversal in the medial belt region (Fig. 3), shows that neurons in RM are arranged in a cochleotopic gradient as well, even though the strictly defined linear cochleotopic gradients did not reach statistical significance in this field (Table 1). In general, as shown in Fig. 4D, the direction of cochleotopy agreed between fields A1 and MM and was the opposite for field R (and RM) in both monkeys and most stimuli and response segments.
TABLE 1.
Cochleotopic gradients in the cortical fields
| Field | Stimulus | Monkey |
“On” Response |
“Sustained” Response
|
“Off” Response
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r | P | Angle, deg | r | P | Angle, deg | r | P | Angle, deg | |||
| A1 | PT | L | 0.712 | <0.0005 | 125 | 0.608 | 0.015 | 80 | 0.732 | <0.0005 | 110 |
| A1 | PT | S | 0.594 | <0.0005 | 125 | 0.290 | 0.125 | 130 | 0.601 | <0.0005 | 90 |
| A1 | BPN13 | L | 0.785 | <0.0005 | 115 | 0.435 | 0.103 | 100 | 0.714 | <0.0005 | 95 |
| A1 | BPN13 | S | 0.565 | <0.0005 | 125 | 0.337 | 0.036 | 140 | 0.498 | 0.008 | 110 |
| A1 | BPN1 | L | 0.708 | <0.0005 | 110 | 0.484 | 0.045 | 105 | 0.759 | <0.0005 | 105 |
| A1 | BPN1 | S | 0.547 | <0.0005 | 100 | 0.292 | 0.079 | 160 | 0.323 | 0.104 | 80 |
| R | PT | L | 0.581 | 0.008 | −60 | 0.506 | 0.367 | −55 | 0.403 | 0.320 | −60 |
| R | PT | S | 0.388 | 0.010 | −45 | 0.185 | 0.461 | −135 | 0.301 | 0.260 | −20 |
| R | BPN13 | L | 0.621 | 0.003 | −50 | 0.544 | 0.176 | −25 | 0.779 | 0.002 | −15 |
| R | BPN13 | S | 0.406 | 0.001 | −60 | 0.109 | 0.771 | −55 | 0.190 | 0.717 | −60 |
| R | BPN1 | L | 0.583 | 0.003 | −55 | 0.445 | 0.153 | −70 | 0.517 | 0.125 | −20 |
| R | BPN1 | S | 0.455 | 0.001 | −50 | 0.347 | 0.055 | −70 | 0.164 | 0.636 | 90 |
| MM | PT | L | 0.706 | <0.0005 | 120 | 0.458 | 0.068 | 120 | 0.537 | 0.005 | 115 |
| MM | PT | S | 0.480 | 0.025 | 110 | 0.509 | 0.220 | 45 | 0.548 | 0.063 | 100 |
| MM | BPN13 | L | 0.723 | <0.0005 | 100 | 0.802 | <0.0005 | 85 | 0.605 | <0.0005 | 115 |
| MM | BPN13 | S | 0.665 | <0.0005 | 100 | 0.565 | 0.012 | 85 | 0.522 | 0.116 | 85 |
| MM | BPN1 | L | 0.712 | <0.0005 | 120 | 0.692 | <0.0005 | 85 | 0.831 | 0.002 | 120 |
| MM | BPN1 | S | 0.542 | 0.004 | 115 | 0.678 | <0.0005 | 95 | 0.540 | 0.054 | 90 |
| RM | PT | L | 0.316 | 0.374 | −20 | 0.322 | 0.701 | −5 | 0.732 | 0.006 | −105 |
| RM | PT | S | 0.176 | 0.650 | 60 | 0.040 | 0.990 | 100 | 0.601 | 0.627 | 5 |
| RM | BPN13 | L | 0.234 | 0.598 | −35 | 0.147 | 0.882 | 35 | 0.714 | 0.517 | −20 |
| RM | BPN13 | S | 0.306 | 0.265 | −15 | 0.343 | 0.308 | −10 | 0.498 | 0.121 | −10 |
| RM | BPN1 | L | 0.332 | 0.302 | −25 | 0.246 | 0.679 | 25 | 0.759 | 0.281 | −25 |
| RM | BPN1 | S | 0.375 | 0.140 | −15 | 0.307 | 0.330 | 30 | 0.323 | 0.258 | −170 |
r, magnitude of gradient [maximum correlation coefficient between best (center) frequency and a rotated axis; see methods]; P, significance of the gradient (where bold entries are significant); Angle, angle of the gradient, i.e., angle at which maximum correlation was found. Values were calculated separately for each field (A1, R, MM, and RM), stimulus (PT, pure tone; BPN13, 1/3-octave band-pass noise; BPN1, 1-octave band-pass noise), and monkey (L and S).
FIG. 4.
Direction and magnitude of cochleotopic gradients in fields A1 (blue), R (red), MM (green), and RM (orange). A–C: polar plots of correlation coefficient of the best (center) frequency with a rotated axis (see methods for details) for “on” (A), “sustained” (B), and “off” (C) response. On each plot, 3 lines in the same color show data from PT, 1/3-octave BPN, and 1-octave BPN. D: angles of gradients for each field and stimulus. Within each stimulus column, the left-hand markers show data from monkey L; the right-hand markers show data from monkey S. Dark-filled squares, “on” response; light-filled circles, “sustained” response; open diamonds, “off” response. For detailed r, P, and angle values, see Table 1.
FIG. 5.
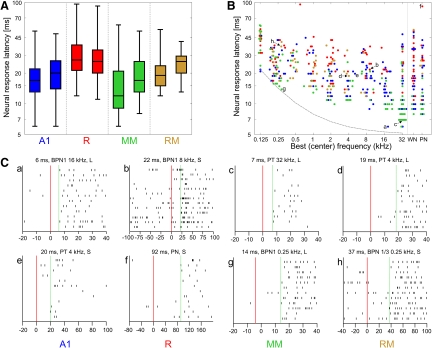
Neural response latencies. A: response latency distributions for each field and monkey. Boxes show the median and quartiles; whiskers show the range. For each field, data from monkey L are shown on the left, from monkey S on the right. B: relationship between response latency and unit's best (center) frequency [BF(c)], established for the stimulus bandwidth that provided the latency estimate; see methods. WN, white noise; PN, pink noise. Data from both monkeys pooled. Blue: field A1; red: field R; green: field MM; orange: field RM. Overlapping data points have been slightly scattered along the frequency axis to improve figure clarity. Correlation coefficients are provided in Table 2. Lowercase letters denote data points illustrated by raster plots in C. The gray dashed line shows the sum of cochlear travel time estimate (Anderson et al. 1971), one wave period, and a 5-ms constant delay; see discussion for details. C: spike raster plots obtained with the stimuli used to estimate latency of 8 example units, 2 for each field. Latency value, stimulus, and monkey designation are provided for each raster plot. Only relevant part of the neural response is shown; note different timescales. Red vertical line shows stimulus onset; green dashed line shows latency. These raster plots are corrected for sound travel time and window discriminator delay (see methods).
Response latencies
Distributions of response latencies in each field are shown in Fig. 5A. Clearly, shorter latencies were found in the (more posterior) middle areas A1 and MM (minimum latency per field and monkey: 6–8 ms) than in the anterior areas R and RM (minimum: 11–13 ms). Similar differences were observed for mean latencies (17.3–21.9 ms in A1 and MM; 22.0–31.9 in R and RM) and median latencies (12–20 and 19–27 ms, respectively). This effect was highly significant (ANOVA anterior–posterior × core-belt: monkey L: F(1,186) = 26.1, P < 10−6; monkey S: F(1,227) = 20.3, P < 10−4). Because neural latency was negatively correlated with BF(c) (see next paragraph) the result might have been confounded by possible underrepresentation in our sample of the anterior parts of areas R and RM containing neurons with high BF(c) (and, consequently, of short latencies; Fig. 3). Thus we additionally compared neural latencies between the anterior and middle (more posterior) areas using a t-test separately for low (<0.71 kHz), high (>5.66 kHz), and middle BF(c). In spite of the lower number of anterior neurons, the difference was still significant for high BF(c) (P < 10−4 for each monkey), even if only neurons with BF(c) higher than 11.31 kHz were taken into account (P < 0.005 for each monkey). It was also significant for middle BF(c) (P < 0.005 for each monkey), which should not be influenced by the underrepresentation of high BF(c). The difference did not reach significance for low BF(c) (P = 0.06, P = 0.14 for monkey L and S, respectively), but mean latency in A1 and MM was still numerically lower than that in RM and R. Thus the possible underrepresentation of high-BF(c) neurons in R and RM cannot account for the general effect; on the contrary, by increasing the fraction of low-BF(c) neurons it might have reduced its size as measured in our sample. Long-latency responses and scarcity of short-latency responses at middle and high BF(c) in areas R and RM are also clearly noticeable in Fig. 5B.
Response latencies were shorter for units with high BF(c) than in units with low BF(c) (Fig. 5B). This correlation was significant not only for all data pooled, but also for individual monkeys and fields; only in fields R of monkey L and RM of monkey S did the correlation not reach significance. However, its direction still matched that of the other fields (Table 2).
TABLE 2.
Correlation between neural latency and best (center) frequency
| Monkey | Field | r | P | n |
|---|---|---|---|---|
| L | A1 | −0.410 | 0.007 | 42 |
| S | A1 | −0.467 | <10−4 | 74 |
| L | R | −0.229 | 0.33 | 20 |
| S | R | −0.314 | 0.014 | 61 |
| L | MM | −0.743 | <10−13 | 72 |
| S | MM | −0.708 | <10−4 | 30 |
| L | RM | −0.623 | 0.0033 | 20 |
| S | RM | −0.364 | 0.0518 | 29 |
| Both pooled | All pooled | −0.562 | <10−29 | 348 |
r, Pearson correlation coefficient between log neural response latency and log best (center) frequency (calculated for the stimulus bandwidth that provided the latency estimate; see methods); P, significance of the correlation; n, number of units. Units for which latency was estimated based on pink or white noise were excluded.
Selectivity for pure tones and band-pass noise bursts
Three measures of selectivity for pure tones and band-pass noises were used: PI, PIt, and LDPC. The measures were evaluated separately and PI and PIt were analyzed separately for each response segment (“on,” “sustained,” and “entire”) with an ANOVA (stimulus class × core-belt × more anterior–more posterior fields) followed by one-sample or two-sample t-test with Bonferroni correction for post hoc comparisons. Detailed patterns of significant differences between the measures of selectivity to PT and BPN are shown in Supplemental Fig. S4.
In general, PI was the least discriminating measure, whereas more significant differences were found with PIt and LDPC. PI showed that for the “on” response, the selectivity decreased with the bandwidth, whereas for the “sustained” response, selectivity for PT was lower than that for both BPN bandwidths. Importantly, for the “sustained” response, neurons in the medial belt were significantly more selective to 1-octave BPN than to PT and the difference between PT and 1/3-octave BPN was close to significance (P = 0.0057; the Bonferroni-corrected threshold equivalent of 0.05 was 0.0056), but no differences were found in the core.
Analysis with PIt revealed that selectivity in the medial belt was in general higher than selectivity in the core in all response segments. In the “sustained” response, selectivity in the anterior fields R and RM was higher than that in the more posterior fields A1 and MM. Similar to what was found for PI, PIt-measured selectivity increased with the bandwidth in the “sustained” response. Although selectivity was higher to the BPN stimuli (both bandwidths) than that to PT stimuli in both the core and the medial belt, the difference in selectivity between 1/3-octave BPN and PT was much more pronounced (P values were 3 to 6 orders of magnitude smaller) in the belt than in the core. Also, selectivity for 1/3-octave BPN was consistently higher in the medial belt than that in the core for all response segments; a similar effect was seen for PT in the “on” response. The pattern obtained with the linear discriminator was essentially similar to results yielded by PIt analyses in the “on” and “sustained” (or “entire”) response segments, consistent with the fact that the linear discriminator analysis covered both the “on” and “sustained” segments.
In summary, we found response selectivity to 1) increase with bandwidth of the stimuli, 2) to be higher in the medial belt than in the core, and 3) to be particularly high in the belt for band-pass noise stimuli (1/3-octave BPN when measured with PIt or LDPC, 1-octave BPN when measured with PI). The “sustained” segment of the neural response appeared to be mainly responsible for these effects; also selectivity was higher in the anterior than that in the more posterior fields in the “sustained” response.
Selectivity for environmental sounds (ESs) and monkey calls (MCs)
The indices and methods used for the analysis of selectivity to MC and ES were identical with the analysis of selectivity to PT and BPN (see earlier text). Detailed patterns of significant differences between the measures of selectivity to MC and ES are shown in Supplemental Fig. S5.
PI analysis showed a higher selectivity for MC than that for ES in the “sustained” and “entire” responses. The opposite result was found using PI as well as PIt in the “on” response. A higher selectivity in general was detected with PIt in the medial belt than that in the core in the “sustained” and “entire” responses. Also, in the “entire” response segment, selectivity to MC was higher than selectivity to ES in the more anterior fields R and RM. Results from the linear discriminator supported the latter outcome: selectivity for ES was higher in the more posterior fields than that in the anterior ones. A higher general selectivity in the medial belt than that in the core was also confirmed. Additionally, selectivity to ES was clearly higher than selectivity to MC.
Temporal structure of neural responses
In numerous cases, neural responses to auditory stimuli showed a temporal structure beyond the simple “on”/“sustained”/“off” pattern (Fig. 6, B and C). Visual detection of temporal patterns from PSTHs and raster plots resulted in a finding that responses to ES were almost always temporally structured (95% of all units were determined to exhibit a structured response to at least one ES). Temporal structure was often detected in responses to MC (65.8%), less often in responses to noise (BPN or WBN, 34.9%), and very rarely in responses to PT (6.2%).
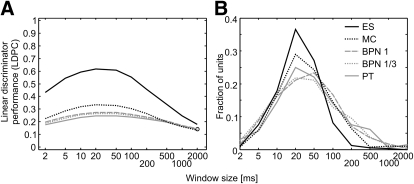
Additional confirmation of the temporal structuring of neural responses came from the results of the linear pattern discriminator. The average performance was the highest around 20–50 ms for each stimulus class and decreased for both shorter and longer windows (Fig. 7A), suggesting that neural responses to a stimulus were similar from trial to trial (i.e., structured) at this timescale. Only for few units was the best performance found at windows of ≤5 ms or ≥200 ms (Fig. 7B). The scarcity of long best windows was particularly apparent for monkey calls and even more for environmental sounds, as indicated by virtually no units with best performance of ≥200 ms (ES) or ≥500 ms (MC), in contrast to pure tones and band-pass noise bursts. Also, the discriminator, which relies on the temporal information in the neural response, performed best for ES, followed by MC and then by other classes. The temporal structure of responses differed significantly across cortical fields: for 1-octave BPN, MC, and ES, the best discriminator window was longer in R than that in the other fields (Fig. 6D).
FIG. 7.
Performance of the linear pattern discriminator for 5 stimulus classes: ES, environmental sounds; MC, monkey calls; BPN1, 1-octave noise bursts; BPN13, 1/3-octave noise bursts; PT, pure tones. A: effect of analysis window on the average performance (proportion correct) of the discriminator. Chance level is 0.111 for PT and BPN and 0.1 for MC and ES. B: distribution of the best window, i.e., the window at which the discriminator performed best for each stimulus.
Very often, the structured neural response patterns could be explained as corresponding to the spectrotemporal structure of the stimulus; in other words, they followed the envelope of the frequency band to which the neuron was tuned. In the following text, we provide examples of such a correspondence.
Two peaks in the response of a high-frequency-tuned R unit to the “vacuum pump” stimulus matched two high-frequency clicks in the stimulus [see (e) on Fig. 6B]. The periodic structure of an RM unit response to the same sound seemed to match the periodicity exhibited by the stimulus at the unit's BF(c) of about 8 kHz (g). The second peak in the response of an approximately 4-kHz-tuned MM unit to “scream 2” coincided with the onset of a powerful high-frequency burst (i), whereas an R unit, tuned to about 1 kHz, responded to the onset of the FM component preceding the burst (h); this onset occurred close to 1 kHz. The late peaks of the neural response of a low-frequency-tuned RM unit coincided with the low-frequency components of the “scream 2” stimulus occurring roughly in the last 150 ms (j). An RM unit tuned to about 0.5 kHz responded with a burst of activity during the first approximately 200 ms of the “harmonic arch” stimulus, which corresponded to the timing of the first call segment, whose fundamental frequency was well within the unit's response area (n), whereas an R unit's burst of activity seemed to match the middle call segment (l). Although the fundamental frequency of the segment was about 3.5–5.5 kHz and lay close to the border of the unit's tuning range, the frequency range of the first overtone (only faintly visible on the spectrogram) was close to the unit's BF(c) of 13–14 kHz. A broadly tuned A1 unit responded (besides the onset peak) to the third segment of the call and the maximum of energy of the segment at 2.7 kHz matched a prominent peak in the unit's tuning curve (k). Finally, the response of an MM unit to the behavioral target (a four-tone “melody”) clearly showed onset responses to each component tone [see (q), Fig. 6C].
In some cases, however, a clear-cut correspondence between the temporal structure of neural response and the sound's spectrotemporal structure (as visible in the spectrograms) was less obvious. For example, the patterning of A1 [see (a), Fig. 6B], MM (c), and RM (d) unit responses to “water running in sink” evoked the fine-grained structure of the stimulus, but exact matching of components could not be found. The single peak of activity of the R unit shown in Fig. 6B could also not be explained in a straightforward manner (b). The response of an MM unit to “harmonic arch” showed a clear burst attributable to the second component of the call in the absence of frequency tuning that would explain it (m). Conversely, the prominent peak in the middle of an MM unit response to “vacuum pump” did not match any evident acoustic event (f), whether at the unit's BF or elsewhere. Structured responses were sometimes found for stimuli with less pronounced temporal structure, such as band-pass and wide-band noise bursts (Fig. 6C).
Only very rarely did we find structured responses to tone bursts, which have no apparent temporal structure whatsoever. An example of such a response is shown in Fig. 6C, (o). The response of the same unit to white noise is shown in (p) to demonstrate that the unit's latency was not responsible for the effect seen with PT. It is likely that these occasionally found “structured” PT responses were more unusual cases of on/sustained/off responses. In case (o), the response appears to be a rebound from an inhibitory “on” response. Similarly, cases where no clear correspondence between the structure for neural response and the spectrogram was detected likely resulted from similar interactions of inhibitory and excitatory responses and/or from responses to acoustic features that could not be visually discerned in the spectrograms.
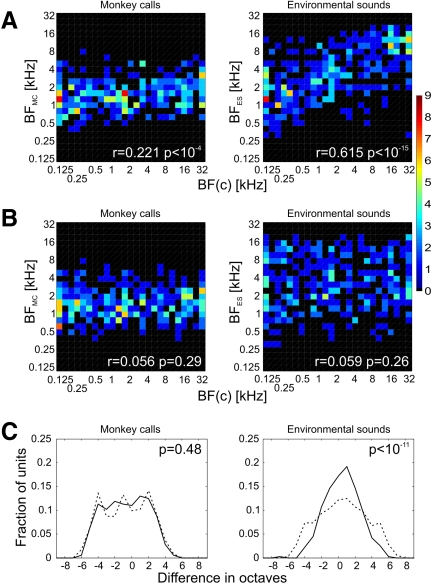
Nevertheless, cases of clear correspondence between the acoustic pattern of the stimulus and the temporal structure of the neural response together with an increasing proportion of temporally structured responses and improving performance of the linear discriminator with increasing acoustic complexity of stimuli (PT to BPN and WBN to MC to ES) show that neurons were typically sensitive to temporal features of the acoustic structure of the stimuli. This notion is strongly supported by the comparison of BF(c) with BF estimated from responses to monkey calls and environmental sounds (BFMC and BFES). BFMC was rather weakly, but very significantly, correlated with BF(c) and for BFES the correlation was quite strong and extremely significant (Fig. 8A). As expected, no correlation of either BFMC or BFES with BF(c) randomly shuffled among units was found (Fig. 8B). Also, the difference between BFES and BF(c) was significantly less widespread than the difference between BFES and shuffled BF(c) [the SD was 2.08 octaves for the BFES–BF(c) distribution and 2.90 octaves for the randomized data distribution; Fig. 8C]. The respective SD values for BFMC, 2.57 and 2.70, did not differ significantly. These results show that a substantial portion of the neurons' activity was driven by low-level acoustic features, i.e., by the amplitude envelope within the neuron's receptive field; this behavior was demonstrable most clearly for environmental sounds, but less so for monkey calls.
FIG. 8.
Comparison of best frequency calculated from responses to monkey calls (BFMC) and environmental sounds (BFES) with best (center) frequency [BF(c)] obtained from “on” responses to PT and BPN bursts. Left column: monkey calls; right column: environmental sounds. A: correlation of BFMC/BFES with BF(c). Color scale represents number of units. B: correlation of BFMC/BFES with BF(c) shuffled among the units. C: distributions of differences between BFMC/BFES and BF(c) (solid line) and between BFMC/BFES and shuffled BF(c) (dashed line). P values calculated with the F-test.
DISCUSSION
Band-pass preference: medial belt versus lateral belt versus core
In this study we recorded from the supratemporal plane in two alert rhesus monkeys. Our results show that units located medially in our recording area prefer band-pass noise bursts over pure tones to a greater degree than those located more laterally. This finding mirrors one reported previously for the comparison of lateral belt and core areas (Rauschecker and Tian 2004; Rauschecker et al. 1995). Therefore we conclude that the present recordings stem from medial belt and core areas, respectively, and the preference for band-pass noise versus pure tones can be used as a distinguishing feature between belt and core areas in general.
There are, however, several differences between our findings and the results of Rauschecker and Tian (2004). First, the band-pass noise preference in the lateral belt was established using the “entire” response of units measured from stimulus onset to offset, whereas in the present experiment only the sustained portion of the response contributed to the mediolateral difference. The “on” response, which typically dominated the response, did not show a mediolateral differentiation. Second, Rauschecker and Tian (2004) reported that close to 15% of units in the lateral belt and almost 60% of units in A1 preferred pure tones over noise, compared with about 10% from the medial belt and nearly 25% from the core in the present data set. Thus both the magnitude of the difference appeared to be smaller and the tendency to prefer noise over tone was stronger in the present experiment.
Three factors may account for these differences. First, sampling of fewer bandwidths than those used in the study by Rauschecker and Tian (2004) might have underestimated BPN preference, if we missed the preferred bandwidth more frequently. However, the overall greater proportion of noise-preferring units found in the present study rules out this explanation. Second, responses in the experiment reported by Rauschecker and Tian (2004) might have been influenced by anesthesia, which was not used in the present study. Both in A1 and the lateral belt of awake marmosets, responses to preferred and nonpreferred stimuli were mainly differentiated by the sustained response, whereas the onset transient was not very specific (Wang et al. 2005). Third, properties of the medial belt may intrinsically differ from the properties of the lateral belt. The pattern of thalamocortical connections supports this explanation: area CM, but not its lateral belt counterpart (CL), receives part of its input from the ventral nucleus of the medial geniculate body—that is, the nucleus that provides the dominant input to the auditory core (Burton and Jones 1976; Hackett et al. 2007; Mesulam and Pandya 1973; Molinari et al. 1995; Morel et al. 1993), possibly contributing to more “corelike” properties in the medial belt compared with lateral belt. Also, Petkov et al. (2006), using fMRI in anesthetized animals, showed a less clear preference for band-pass noise over tones in much of the medial compared with the lateral belt, supporting a genuine difference between medial and lateral belt areas.
Using different selectivity measures we found that in the medial belt, selectivity tended to be higher for band-pass noise bursts than that for pure tones. This result is expected given that BPNs elicit higher firing rates in medial belt neurons than in core neurons, thus increasing the firing rate difference between stimuli at best frequency and those outside the receptive field.
Results from the use of a preference index (PI), as defined previously (Tian et al. 2001), suggested that selectivity in the medial belt was highest for 1-octave BPN. By contrast, two other measures (PIt and LDPC) demonstrated the most clearly elevated selectivity for 1/3-octave BPN. Rauschecker and Tian (2004) used a greater variety of BPN bandwidths than those used in the present study and were thus able to show that the percentage of neurons in the lateral belt preferring 1-octave BPN was relatively low and more neurons preferred 1/3-octave BPN.
In summary, then, it appears that the preference for BPN stimuli is overall somewhat milder in the medial belt than that in the lateral belt. In the present experiment, the difference was clear enough to separate belt from core. The ultimate comparison, however, must be left to future experiments that record from medial and lateral belts in the same animals at the same state of alertness.
Cochleotopic organization
In both core areas and in the middle medial belt area (MM) we detected a pronounced cochleotopic organization when analyzing “on” responses. The data for “sustained” and “off” responses, as well as for rostromedial (RM) belt overall, were less clear. Most significantly, the consistent and tight distributions of gradient angles (Fig. 4D) suggest that cochleotopy is an important organizing principle for all four fields and all three response segments. It thus seems that the difficulty in demonstrating cochleotopic gradients in RM and MM encountered by Petkov et al. (2006) was due to limits of the fMRI method when applied to relatively small areas, rather than to a lack of such gradients.
At first glance it may appear contradictory that the “on” response produced more significant gradients than the “sustained” response, whereas the “sustained” response is more precisely tuned to stimulus properties (Wang et al. 2005; the present study). However, relatively sparse sampling of the frequency space (in 1-octave steps) might have caused some of the finely tuned “sustained” responses to be missed, whereas more broadly tuned “on” responses were more often covered. It is noteworthy that in both monkeys' area MM, gradients calculated from the “sustained” response were significant for both band-pass noise bandwidths, but not for pure tones, providing further support for the notion of a medial belt preference for processing spectrally complex stimuli.
The direction of the cochleotopic gradients in the medial belt fields RM and MM was collinear with the direction of the adjacent core fields R and A1, respectively, and a frequency reversal was found at the RM/MM boundary. This result is consistent with predictions from the work of Kaas, Hackett, and colleagues (e.g., Hackett et al. 1998), with tendencies observed in fMRI data (Petkov et al. 2006), with data obtained in parallel lateral belt fields AL and ML (Petkov et al. 2006; Rauschecker and Tian 2004; Rauschecker et al. 1995), and with previous results from the core fields (e.g., Kosaki et al. 1997; Pfingst and O'Connor 1981; Rauschecker et al. 1997; Recanzone et al. 2000b). Our recording area did not extend much beyond the MM/CM boundary in the caudal direction; thus we were not able to demonstrate another best (center) frequency gradient reversal at that boundary. However, best (center) frequencies as high as 16–32 kHz were found in the posterior part of MM in both monkeys, collinear with a similar representation in A1. This means that a complete representation of the cochlea is present in MM, which defines MM as a separate area from CM and settles previous disputes.
In a comparison of the size of medial belt areas in individual monkeys from the present study as well as prior anatomical studies (e.g., Smiley et al. 2007), individual differences between animals are apparent. This may in part arise from variations in the location of recording chambers, probably more medial in monkey L and more lateral in monkey S. Also, the method used to determine borders between fields in our study was based on a smoothed distribution of an indirect parameter (the ratio of BPN-evoked to PT-evoked firing rate in the sustained response), which limits spatial resolution, and may have led to placing the boundaries somewhat differently than a histochemical study would do. The seemingly rather large size of field MM in one of our monkeys could even be due to the existence of a “medial parabelt” region, continuous with one of the auditory regions in the insula, which we have not attempted to investigate in the present study.
Neural response latencies
ABSOLUTE VALUES.
We have demonstrated neural response latencies as low as 6 ms in the rhesus auditory cortex. This result matches one reported by Lakatos et al. (2005) using multiunit activity and median values obtained in our experiment are also consistent with those reported by Kajikawa et al. (2005) for the marmoset. Recanzone et al. (2000b) found considerably higher latencies (field mean: ≥32.4 ms). Similarly high mean and median latencies were reported recently in the marmoset (Bendor and Wang 2008). Values of the shortest latencies were not reported explicitly in that study, but examination of their figures suggests very short latencies in A1. In cat A1, mean latency values were found to be even shorter than those in the present study, but the shortest individual latencies were slightly longer when measured for single units and similarly short as in our data when measured for multiunits (Mendelson et al. 1997). Given the various methods of latency estimation and the possible technical issues of proper relative timing of the stimulus and neural response, our results agree quite well with other experimenters' data. The general conclusion is that stimulus information can reach certain cortical fields in as little as a few milliseconds.
DIFFERENCES BETWEEN FIELDS.
Probably more interesting than absolute latency values are the relative differences in latency values between cortical fields because they may hint at processing hierarchies in the auditory cortex. We did not find a consistent difference in response latencies between core and medial belt areas. There was, however, a tendency for area MM to exhibit particularly short latencies: in both monkeys, mean and median latencies were shorter in MM than those in other areas. A similar result was found in the marmoset: latencies in A1 were significantly longer than those in a region medial to it, which the authors termed CM (Kajikawa et al. 2005; this would be called MM in rhesus by us and other authors). On the other hand, in rhesus monkeys, latencies in CM were reported to be slightly longer than those in A1 by Recanzone (2000b); here, the area labeled as CM encompassed MM, CM, and CL according to Kaas and Hackett (2000) and our terminology. Lakatos et al. (2005) also found shorter latencies in the auditory belt than those in A1. However, data from the posterior lateral and medial belt areas were combined in that study and latencies in the belt were short only when measured with broadband noise, whereas pure tones evoked multiunit responses with latencies longer than those in A1. Rauschecker et al. (1997) demonstrated that responses to tones, but not to complex stimuli, in area CM (and possibly including CL in current terminology) depended on the integrity of area A1. This is consistent with the posterior belt areas receiving substantial serial input from A1 (de la Mothe et al. 2006a; Smiley et al. 2007) and with data showing longer pure-tone latencies in the belt than those in A1 (Lakatos et al. 2005; Recanzone et al. 2000b), but not for broadband noise (Lakatos et al. 2005). Of interest are also results from Kajikawa et al. (2005) and the present study, which show that responses to tones may occur in the medial belt with latencies as short as (or shorter than) those in A1 [see Fig. 5, B and C, e.g., example (c)]. This suggests that a population of neurons in the medial and/or caudal belt may receive early information about pure tones in parallel to the pathway via A1, possibly via direct thalamic input. It is noteworthy in this context that the caudomedial belt receives a strong input from the magnocellular/medial nucleus of the medial geniculate body (de la Mothe et al. 2006b; Hackett et al. 2007), which, in turn, has been shown in certain species to exhibit very short response latencies (Anderson et al. 2006) and to receive direct connections from the dorsal cochlear nucleus (Anderson et al. 2006; Malmierca et al. 2002; Strominger et al. 1977). Whether the same connectivity exists in the rhesus monkey remains to be determined, but it would support a faster direct route, possibly based on a separate population of neurons, in the posterodorsal auditory stream of primates (Rauschecker and Scott 2009).
A clear latency difference was found across the A1/R and MM/RM boundaries, with (more posterior) middle fields A1 and MM showing shorter latencies. A similar difference between A1 and R was reported by other authors (Bendor and Wang 2008; Pfingst and O'Connor 1981; Recanzone et al. 2000b). Although R and A1 are substantially interconnected (Cipolloni and Pandya 1989; de la Mothe et al. 2006a; Jones et al. 1995; Morel et al. 1993), it is unlikely that this latency difference reflects a processing hierarchy from A1 to R: lesion of A1 did not influence responses in R (Rauschecker et al. 1997). Based on the segregation of connections from anterior and posterior subdivisions of the dorsal MGB nucleus to the caudal and rostral medial belt in the marmoset, as well as relative segregation of connections between R and RM from connections between A1 and CM (again including the area termed “MM” in the present paper), de la Mothe et al. (2006b) proposed that the posterior auditory cortex, including CM (and A1), and the anterior auditory cortex, including RM and R, formed two separate pathways. Similar tendencies may be observed in macaques in thalamic connectivity (Hackett et al. 2007; Molinari et al. 1995) and in corticocortical connections (Jones et al. 1995; Smiley et al. 2007). The proposition of de la Mothe et al. (2006b) clearly evokes the two pathways proposed earlier (e.g., Romanski et al. 1999a,b) based on connections between lateral belt and prefrontal cortex. Thus the difference in response latencies between A1 and MM on one side and R and RM on the other side might reflect different input to the posterior and anterior pathways in the auditory cortex. It is noteworthy that shorter response latencies (compared with anterior areas) were also found in the posterior areas of human auditory cortex using magnetoencephalographic techniques (Ahveninen et al. 2006).
RELATIONSHIP TO BEST FREQUENCY.
Response latencies were inversely correlated with the units' best (center) frequency, whereas the shortest latencies of units with BF(c) of 16–32 kHz were as short as 6 ms, latencies of units with BF(c) around 0.25 and 0.125 kHz exceeded 12 and 20 ms, respectively. Thus the shortest latency difference reached about 15 ms over the investigated frequency range. It is likely that it could be even larger if the full macaque hearing range down to around 30–40 Hz had been tested (Jackson et al. 1999). A similar frequency–latency dependence has previously been observed in the auditory cortex of rhesus and marmoset monkeys (Bendor and Wang 2008; Lakatos et al. 2005), cats (Mendelson et al. 1997), and humans (Roberts et al. 2000; Salajegheh et al. 2004), whereas others did not find it (Kajikawa et al. 2005). A delay of activity evoked in the auditory nerve by low-frequency tones relative to high-frequency tones is generated in the cochlea by the fairly slow travel of the basilar membrane displacement from the base to the apex of the cochlea (e.g., Anderson et al. 1971; Ren 2002; Robles and Ruggero 2001). Cochlear travel times are shorter, however, by a factor of approximately two or more than delays found at the cortical level in the present experiment (Anderson et al. 1971; Carney and Yin 1988; Donaldson and Ruth 1992; Kim and Molnar 1979; Ruggero and Rich 1987). Therefore a mechanism central to the cochlea must contribute to the latency differences observed in the cortex (Greenberg et al. 1998; Mendelson et al. 1997). When the duration of one wave period is added to the cochlear travel time [calculated using the formula t = 1.95f−0.725 obtained by Anderson et al. (1971) from measurements in the squirrel monkey], the resulting delay versus frequency function fits well with the shortest latencies found in the present experiment for low and high frequencies, with a slight deviation at intermediate frequencies (Fig. 5B). The difference between the function and the actual latencies at low and high frequencies is about 5 ms. Thus it may be speculated that the latency difference at the cortical level results from a combination of three factors: cochlear travel time, the time required to resolve the frequency from temporal information (which would be related to the duration of wave period), and a constant nearly 5-ms delay due to processing and synaptic delays throughout the auditory pathway. That the frequency-dependent latency delay cannot be entirely explained by the cochlear traveling wave has also been claimed by other authors based on the time discrepancy between the two processes (Greenberg et al. 1998), on incongruity of the auditory nerve delay function with the distribution of characteristic frequencies along the basilar membrane in certain species (Köppl 1997), and on the occurrence of the cortical latency delay for stimuli that evoke a pitch percept, but are devoid of any frequency structure at the level of the basilar membrane (Chait et al. 2006).
Linear pattern discriminator analysis
Using the linear pattern discriminator provided us with two general findings: 1) using temporal structure of neural response allowed for moderately good discrimination (62% for ES, 33% for MC, and 25–27% for PT and BPN) of stimuli based on individual unit responses and 2) the temporal window that provides the most information for such discrimination is 20–50 ms.
The latter result seems to fit pretty well to the values already published in the literature for auditory cortical processing. Schnupp et al. (2006) in their study of coding of ferret calls in ferret A1 showed that mutual information for their “highly informative” units reached the maximum at 10–20 ms and declined above 40 ms and below 5 ms. Russ et al. (2008) presented mutual information values obtained from recordings of responses to monkey calls in macaque ventral prefrontal cortex and the anterior superior temporal gyrus, which peaked roughly around 20 ms, and decreased for longer and shorter windows. Classifiers used by Malone et al. (2007) achieved the best performance at a 5- to 10-ms window; in this study, sinusoidally modulated tones were used as stimuli and recordings were obtained in macaque A1. Finally, Averbeck and Romanski (2006), using linear discriminant analysis to examine responses in the ventrolateral prefrontal cortex to monkey vocalizations, found the best window to be 60 ms.
As we demonstrated that units from which we recorded respond to amplitude modulations within their receptive fields, data showing synchronization limits of cortical neurons are also relevant. Malone et al. (2007) and Bendor and Wang (2008) have shown that only very few neurons synchronize to sinusoidally amplitude-modulated tones beyond modulation frequency of about 100 Hz (equivalent to 10 ms) in rhesus A1 and marmoset core fields, respectively. A similar limit was found by Oshurkova et al. (2008) in rhesus A1 and CM with click trains.
Currently, we are unable to reconcile our results and the data cited earlier with results provided by Russ et al. (2008) and Recanzone (2008), who presented much higher discriminator performance (∼80–90% for monkey calls) and much shorter best window (2 ms) using an identical classifier as we did. On the other hand, as mentioned earlier, Russ et al. (2008) found the highest amount of mutual information being carried in responses to monkey calls at about 20 ms. This issue needs further scrutiny.
Complex stimuli: monkey calls and environmental sounds
One of the important results supporting the existence of separate processing streams for stimulus identity (“what”) and stimulus location (“where”) in the auditory cortex of the rhesus monkey was the demonstration that neurons in the anterior lateral belt (AL) were more selective to monkey calls than were neurons in the middle (ML) or caudal lateral belt (CL), whereas CL cells were more selective for spatial location than those in ML or AL (Tian et al. 2001). The biggest differences were between AL and CL, whereas ML was in between. In the present study, we tested the sampled cortical fields for selectivity to stimulus identity, using five classes of sounds: pure tones (PT), band-pass noise bursts (BPN) of two bandwidths, monkey calls (MC), and environmental sounds (ES). We found no difference between rostral areas (R and RM) and middle areas (A1 and MM) in any measure of response selectivity for MC. This could mean that a rostrocaudal gradient for identity processing of complex sounds (such as MC) is absent in the medial belt or that finding the gradient requires a direct comparison between the two extremes (RM and CM), which was not possible in the present study. Still, increased selectivity (measured with PIt) to PT and BPN was found in the “sustained” response in the anterior fields R and RM compared with A1 and MM.
A result that might be indirectly associated with the existence of dual-stream gradients in early auditory cortical areas is the aforementioned latency difference between R + RM and A1 + MM, suggesting that they may belong to separate processing pathways. It has been suggested that rapid processing by the posterior/dorsal “where” pathway provides coarse information (a “primal sketch”) about auditory stimuli and their source locations, facilitating the later perception of auditory objects by the slower anterior/ventral “what” pathway (Ahveninen et al. 2006).
Interestingly, selectivity to ES (measured with the linear discriminator, which takes temporal information into account) was actually lower in the anterior fields than that in the middle areas A1 and MM. ES were relatively noisy but exhibited rapid and deep amplitude modulations. Thus representation of this sound class likely depends on temporal information. Indeed, the linear discriminator in general performed particularly well for ES (Fig. 7A). Furthermore, only for ES almost no neurons showed a long (≥200 ms) best discriminator window (Fig. 7B). On the other hand, we found that the linear discriminator best window size was larger in field R than that in the other fields and latencies were longer in R and RM than those in A1 and MM, suggesting that the anterior areas operate on a slower temporal scale than the middle areas (cf. Bendor and Wang 2008). Consequently, they are less suitable for representing ES.
The preference indices for natural stimuli differed between stimulus classes. ES preference index (PI) was higher than the MC PI for the “entire” and “sustained” responses, indicating a higher selectivity for monkey calls than that for environmental sounds in the tested areas, which might suggest cortical specialization for processing conspecific vocalization in this region. However, the direction of the difference was exactly the opposite for the “on” response. This observation, together with an examination of the stimulus acoustic structure in spectrograms (Fig. 1) and of their measured parameters (see methods), led to a simpler explanation. Spectra of ES were relatively widespread, their intensity typically varied more during the stimulus, and they had more abrupt component peaks, which drove prominent neural responses in the “sustained” component. This resulted in a relatively uniform “sustained” PFR across all ES and consecutively high PI values. MC showed less intensity variation and their spectra were more compact. Thus they evoked “sustained” responses that depended on the frequency content of the stimulus and frequency tuning of the neuron and that varied across stimuli, leading to lower PI values. This reasoning is additionally confirmed by the observation that almost all ES but only two thirds of MC drove responses that were temporally structured beyond the simple “on”/“sustained”/“off” pattern. On the other hand, MC onset intensity was usually close to the entire stimulus intensity, whereas ES onset intensity typically varied between stimuli, causing a higher variation in neural response magnitude at the onset in ES than in MC, and lower PI values for the “on” response.
A selectivity difference between ES and MC was also found with LDPC, but in this case selectivity was higher for ES than for MC. Again, this can be explained by the sensitivity of the linear discriminator to temporally modulated neural responses elicited by ES with their modulated acoustic structure. Thus the differences in selectivity measures between ES and MC appear to be due to their particular acoustic structure and are not an indication of preference of the recorded areas for any of these two stimulus classes.
Finally, an increased selectivity for both classes of natural sounds was detected in the medial belt compared with the core, suggesting a role of spectral integration in the processing of these sounds.
Temporal structure of neural responses
We often observed temporal structure in the neural response, which was more complex than a simple “on”/“sustained”/“off” pattern (Fig. 6). The prevalence of the neural response structure ranged from very high (95%) for ES, which were characterized by temporally complex acoustic (mainly intensity) structure easily seen in the spectrograms and confirmed by stimulus measurements, to almost nonexistent (6%) in pure tone bursts whose acoustic parameters do not change in time. In between the two classes, MC with relative acoustic complexity (though less than ES) elicited structured responses almost twice as often as the frozen (prerecorded; see methods) noise. Although a correspondence between the structure of a neural response with the acoustic structure of a stimulus could not be always established, the percentage of units exhibiting temporal structure in different stimulus classes and between-class differences of performance of the linear pattern discriminator (which uses temporal structure of responses) suggest that acoustic structure was the main underlying cause for neural response patterning.
Moreover, we were able to use the correlation method to infer units' best frequency from responses to ES and MC. These BFES and BFMC were correlated with BF(c) obtained with PT and BPN (Fig. 8), which is a direct indication that the responses were driven by amplitude modulations within unit's receptive field.
BFES values were correlated much more strongly with BF(c) than with BFMC. Figure 8A shows that BFMC values were never high (≳8 kHz) or low (≲0.4 kHz). A similar, though not as strict (∼0.25 to 20 kHz), limitation appears to affect BFES. We interpret this as an effect of limited frequency range of the natural stimuli: obviously, if a neuron's best frequency is 250 Hz, it cannot be accurately inferred from stimuli that have little acoustic energy <500 Hz. Therefore MC, with their less widespread spectra than those of ES, provided a poorer BF estimate. In addition, MC exhibited less intensity variation than did ES; this hampered the BF extraction method based on correlation of intensity with neural responses, both directly and because neural responses driven by MC were probably less varied.
Taken together, the structure observed in neural responses appears to reflect normal “on,” “sustained,” and possibly “off” responses to stimulus components, instead of any kind of temporally structured neural code. That the neural responses followed the acoustic structure of stimuli closely indicates that the neurons in the areas from which we recorded generally represent low-level features of stimuli, rather than integrated auditory objects.
As mentioned earlier, for 1-octave BPN, MC, and ES stimuli, the best window of linear discriminator was longer in R than that in the other fields. This result, together with the longer latencies in areas R and RM than those in A1 and MM, indicates that temporal processing windows increase in the anterior direction and agrees with a recent report in the marmoset (Bendor and Wang 2008).
Summary
Our results support the conclusion that a rostromedial area (RM) and a middle medial area (MM) exist in the medial belt, in addition to area CM and in parallel with core areas R and A1, respectively. Like the lateral belt, the medial belt seems to be at a hierarchically higher level than the core because its neurons show a greater preference for intermediately complex sounds (band-pass noise bursts) over pure tones, as well as a higher selectivity for different stimulus classes. On the other hand, many characteristics are shared across the core/medial belt boundary, such as similar response latencies, representation of low-level acoustic features of stimuli, or lack of a pronounced selectivity for natural complex sounds or of variance thereof between fields. Thus RM and MM constitute a part of the early cortical processing network.
Areas RM and MM show cochleotopic organization collinear with neighboring core areas R and A1 and with lateral belt areas AL and ML. Both in the core and medial belt, neural latencies are shorter for high-frequency stimuli than those for low-frequency sounds and this difference is generated at lower levels of the auditory system, in addition to a delay generated in the cochlea. Neurons in field R operate on a slower temporal scale than that in the other areas. Response latencies differ between A1 and MM on the one hand and R and RM on the other hand. Together with connectivity data reported by other authors, this suggests that anterior (R + RM) and middle (A1 + MM) areas may belong to separate computational networks or pathways. It will be interesting to see where caudal areas (CL + CM) stand in this continuum. Our data fit in and extend the model proposed recently—i.e., that the temporal integration window increases in the anterior direction from A1—whereas the spectral integration window gets bigger laterally from the core; our results provide further evidence that the spectral integration window also increases medially from the core.
GRANTS
This work was supported by National Institute of Neurological Disorders and Stroke Grant R01-NS-052494 to J. P. Rauschecker.
Supplementary Material
Acknowledgments
We thank C. Silver for assistance with surgeries and animal care and Drs. Stanley T. Fricke and John VanMeter for help with the MRI scans.
Footnotes
The online version of this article contains supplemental data.
REFERENCES
- Ahveninen et al. 2006.Ahveninen J, Jääskeläinen IP, Raij T, Bonmassar G, Devore S, Hämäläinen M, Levänen S, Lin FH, Sams M, Shinn-Cunningham BG, Witzel T, Belliveau JW. Task-modulated “what” and “where” pathways in human auditory cortex. Proc Natl Acad Sci USA 103: 14608–14613, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson et al. 1971.Anderson DJ, Rose JE, Hind JE, Brugge JF. Temporal position of discharges in single auditory nerve fibers within the cycle of a sine-wave stimulus: frequency and intensity effects. J Acoust Soc Am 49: 1131–1139, 1971. [DOI] [PubMed] [Google Scholar]
- Anderson et al. 2006.Anderson LA, Malmierca MS, Wallace MN, Palmer AR. Evidence for a direct, short latency projection from the dorsal cochlear nucleus to the auditory thalamus in the guinea pig. Eur J Neurosci 24: 491–498, 2006. [DOI] [PubMed] [Google Scholar]
- Averbeck and Romanski 2006.Averbeck BB, Romanski LM. Probabilistic encoding of vocalizations in macaque ventral lateral prefrontal cortex. J Neurosci 26: 11023–11033, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behar et al. 1965.Behar I, Cronholm JN, Loeb M. Auditory sensitivity of the rhesus monkey. J Comp Physiol Psychol 59: 426–428, 1965. [DOI] [PubMed] [Google Scholar]
- Bendor and Wang 2008.Bendor D, Wang X. Neural response properties of primary, rostral, and rostrotemporal core fields in the auditory cortex of marmoset monkeys. J Neurophysiol 100: 888–906, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett et al. 1983.Bennett CL, Davis RT, Miller JM. Demonstration of presbycusis across repeated measures in a nonhuman primate species. Behav Neurosci 97: 602–607, 1983. [DOI] [PubMed] [Google Scholar]
- Boersma 1993.Boersma P. Accurate short-term analysis of the fundamental frequency and the harmonics-to-noise ratio of a sampled sound. IFA Proc 17: 97–110, 1993. [Google Scholar]
- Burton and Jones 1976.Burton H, Jones EG. The posterior thalamic region and its cortical projection in New World and Old World monkeys. J Comp Neurol 168: 249–301, 1976. [DOI] [PubMed] [Google Scholar]
- Carney and Yin 1988.Carney LH, Yin TC. Temporal coding of resonances by low-frequency auditory nerve fibers: single-fiber responses and a population model. J Neurophysiol 60: 1653–1677, 1988. [DOI] [PubMed] [Google Scholar]
- Chait et al. 2006.Chait M, Poeppel D, Simon JZ. Neural response correlates of detection of monaurally and binaurally created pitches in humans. Cereb Cortex 16: 835–848, 2006. [DOI] [PubMed] [Google Scholar]
- Cipolloni and Pandya 1989.Cipolloni PB, Pandya DN. Connection analysis of the ipsilateral and contralateral afferent neurons of the superior temporal region in the rhesus monkey. J Comp Neurol 281: 567–585, 1989. [DOI] [PubMed] [Google Scholar]
- de la Mothe et al. 2006a.de la Mothe LA, Blumell S, Kajikawa Y, Hackett TA. Cortical connections of the auditory cortex in marmoset monkeys: core and medial belt regions. J Comp Neurol 496: 27–71, 2006a. [DOI] [PubMed] [Google Scholar]
- de la Mothe et al. 2006b.de la Mothe LA, Blumell S, Kajikawa Y, Hackett TA. Thalamic connections of the auditory cortex in marmoset monkeys: core and medial belt regions. J Comp Neurol 496: 72–96, 2006b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donaldson and Ruth 1993.Donaldson GS, Ruth RA. Derived band auditory brain-stem response estimates of traveling wave velocity in humans. I: Normal-hearing subjects. J Acoust Soc Am 93: 940–951, 1993. [DOI] [PubMed] [Google Scholar]
- Formisano et al. 2003.Formisano E, Kim DS, Di Salle F, van de Moortele PF, Ugurbil K, Goebel R. Mirror-symmetric tonotopic maps in human primary auditory cortex. Neuron 40: 859–869, 2003. [DOI] [PubMed] [Google Scholar]
- Fujita and Elliott 1965.Fujita S, Elliott DN. Thresholds of audition for three species of monkey. J Acoust Soc Am 37: 139–144, 1965. [DOI] [PubMed] [Google Scholar]
- Greenberg et al. 1998.Greenberg S, Poeppel D, Roberts T. A space–time theory of pitch and timbre based on cortical expansion of the cochlear traveling wave delay. In: Psychophysical and Physiological Advances in Hearing, edited by Palmer A, Summerfield Q, Rees A, Meddis R. London: Whurr, 1998, p. 293–300.
- Hackett et al. 2007.Hackett TA, de la Mothe LA, Ulbert I, Karmos G, Smiley J, Schroeder CE. Multisensory convergence in auditory cortex, II. Thalamocortical connections of the caudal superior temporal plane. J Comp Neurol 502: 924–952, 2007. [DOI] [PubMed] [Google Scholar]
- Hackett et al. 1998.Hackett TA, Stepniewska I, Kaas JH. Subdivisions of auditory cortex and ipsilateral cortical connections of the parabelt auditory cortex in macaque monkeys. J Comp Neurol 394: 475–495, 1998. [DOI] [PubMed] [Google Scholar]
- Harrington and Heffner 2003.Harrington IA, Heffner HE. A behavioral investigation of “separate processing streams” within macaque auditory cortex. Assoc Res Otolaryngol Abstr 25: 456, 2003. [Google Scholar]
- Hauser 1998.Hauser MD. Functional referents and acoustic similarity: field playback experiments with rhesus monkeys. Anim Behav 55: 1647–1658, 1998. [DOI] [PubMed] [Google Scholar]
- Jackson et al. 1999.Jackson LL, Heffner RS, Heffner HE. Free-field audiogram of the Japanese macaque (Macaca fuscata). J Acoust Soc Am 106: 3017–3023, 1999. [DOI] [PubMed] [Google Scholar]
- Johnson 1980.Johnson DH. The relationship between spike rate and synchrony in responses of auditory-nerve fibers to single tones. J Acoust Soc Am 68: 1115–1122, 1980. [DOI] [PubMed] [Google Scholar]
- Jones et al. 1995.Jones EG, Dell'Anna ME, Molinari M, Rausell E, Hashikawa T. Subdivisions of macaque monkey auditory cortex revealed by calcium-binding protein immunoreactivity. J Comp Neurol 362: 153–170, 1995. [DOI] [PubMed] [Google Scholar]
- Kaas and Hackett 2000.Kaas JH, Hackett TA. Subdivisions of auditory cortex and processing streams in primates. Proc Natl Acad Sci USA 97: 11793–11799, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kajikawa et al. 2005.Kajikawa Y, de la Mothe L, Blumell S, Hackett TA. A comparison of neuron response properties in areas A1 and CM of the marmoset monkey auditory cortex: tones and broadband noise. J Neurophysiol 93: 22–34, 2005. [DOI] [PubMed] [Google Scholar]
- Kim and Molnar 1979.Kim DO, Molnar CE. A population study of cochlear nerve fibers: comparison of spatial distributions of average-rate and phase-locking measures of responses to single tones. J Neurophysiol 42: 16–30, 1979. [DOI] [PubMed] [Google Scholar]
- Köppl 1997.Köppl C. Phase locking to high frequencies in the auditory nerve and cochlear nucleus magnocellularis of the barn owl, Tyto alba. J Neurosci 17: 3312–3321, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosaki et al. 1997.Kosaki H, Hashikawa T, He J, Jones EG. Tonotopic organization of auditory cortical fields delineated by parvalbumin immunoreactivity in macaque monkeys. J Comp Neurol 386: 304–316, 1997. [PubMed] [Google Scholar]
- Lakatos et al. 2005.Lakatos P, Pincze Z, Fu K-MG, Javitt DC, Karmos G, Schroeder CE. Timing of pure tone and noise-evoked responses in macaque auditory cortex. Neuroreport 16: 933–937, 2005. [DOI] [PubMed] [Google Scholar]
- Lonsbury-Martin and Martin 1981.Lonsbury-Martin BL, Martin GK. Effects of moderately intense sound on auditory sensitivity in rhesus monkeys: behavioral and neural observations. J Neurophysiol 46: 563–586, 1981. [DOI] [PubMed] [Google Scholar]
- Malmierca et al. 2002.Malmierca MS, Merchán MA, Henkel CK, Oliver DL. Direct projections from the cochlear nuclear complex to auditory thalamus in the rat. J Neurosci 22: 10891–10897, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone et al. 2007.Malone BJ, Scott BH, Semple MN. Dynamic amplitude coding in the auditory cortex of awake rhesus macaques. J Neurophysiol 98: 1451–1474, 2007. [DOI] [PubMed] [Google Scholar]
- Mendelson et al. 1997.Mendelson JR, Schreiner CE, Sutter ML. Functional topography of cat primary auditory cortex: response latencies. J Comp Physiol A Sens Neural Behav Physiol 181: 615–633, 1997. [DOI] [PubMed] [Google Scholar]
- Merzenich and Brugge 1973.Merzenich MM, Brugge JF. Representation of the cochlear partition on the superior temporal plane of the macaque monkey. Brain Res 50: 275–296, 1973. [DOI] [PubMed] [Google Scholar]
- Mesulam and Pandya 1973.Mesulam M-M, Pandya DN. The projections of the medial geniculate complex within the sylvian fissure of the rhesus monkey. Brain Res 60: 315–333, 1973. [DOI] [PubMed] [Google Scholar]
- Micheyl et al. 2005.Micheyl C, Tian B, Carlyon RP, Rauschecker JP. Perceptual organization of tone sequences in the auditory cortex of awake macaques. Neuron 48: 139–148, 2005. [DOI] [PubMed] [Google Scholar]
- Molinari et al. 1995.Molinari M, Dell'Anna ME, Rausell E, Leggio MG, Hashikawa T, Jones EG. Auditory thalamocortical pathways defined in monkeys by calcium-binding protein immunoreactivity. J Comp Neurol 362: 171–194, 1995. [DOI] [PubMed] [Google Scholar]
- Morel et al. 1993.Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol 335: 437–459, 1993. [DOI] [PubMed] [Google Scholar]
- O'Connor et al. 1999.O'Connor KN, Barruel P, Hajalilou R, Sutter ML. Auditory temporal integration in the rhesus macaque (Macaca mulatta). J Acoust Soc Am 106: 954–965, 1999. [DOI] [PubMed] [Google Scholar]
- Oshurkova et al. 2008.Oshurkova E, Scheich H, Brosch M. Click train encoding in primary and non-primary auditory cortex of anesthetized macaque monkeys. Neuroscience 153: 1289–1299, 2008. [DOI] [PubMed] [Google Scholar]
- Pandya et al. 1994.Pandya DN, Rosene DL, Doolittle AM. Corticothalamic connections of auditory-related areas of the temporal lobe in the rhesus monkey. J Comp Neurol 345: 447–471, 1994. [DOI] [PubMed] [Google Scholar]
- Pandya and Sanides 1973.Pandya DN, Sanides F. Architectonic parcellation of the temporal operculum in rhesus monkey and its projection pattern. Z Anat Entwicklungsgesch 139: 127–161, 1973. [DOI] [PubMed] [Google Scholar]
- Petkov et al. 2006.Petkov CI, Kayser C, Augath M, Logothetis NK. Functional imaging reveals numerous fields in the monkey auditory cortex. PLoS Biol 4: 1213–1226, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfingst et al. 1975.Pfingst BE, Hienz R, Miller J. Reaction-time procedure for measurement of hearing. II. Threshold functions. J Acoust Soc Am 57: 431–436, 1975. [DOI] [PubMed] [Google Scholar]
- Pfingst et al. 1978.Pfingst BE, Laycock J, Flammino F, Lonsbury-Martin B, Martin G. Pure tone thresholds for the rhesus monkey. Hear Res 1: 43–47, 1978. [DOI] [PubMed] [Google Scholar]
- Pfingst and O'Connor 1981.Pfingst BE, O'Connor TA. Characteristics of neurons in auditory cortex of monkeys performing a simple auditory task. J Neurophysiol 45: 16–34, 1981. [DOI] [PubMed] [Google Scholar]
- Rauschecker and Scott 2009.Rauschecker JP, Scott SK. Maps and streams in the auditory cortex: nonhuman primates illuminate humans speech processing. Nat Neurosci 12: 718–724, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauschecker and Tian 2000.Rauschecker JP, Tian B. Mechanisms and streams for processing of “what” and “where” in auditory cortex. Proc Natl Acad Sci USA 97: 11800–11806, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauschecker and Tian 2004.Rauschecker JP, Tian B. Processing of band-passed noise in the lateral auditory belt cortex of the rhesus monkey. J Neurophysiol 91: 2578–2589, 2004. [DOI] [PubMed] [Google Scholar]
- Rauschecker et al. 1995.Rauschecker JP, Tian B, Hauser M. Processing of complex sounds in the macaque nonprimary auditory cortex. Science 268: 111–114, 1995. [DOI] [PubMed] [Google Scholar]
- Rauschecker et al. 1997.Rauschecker JP, Tian B, Pons T, Mishkin M. Serial and parallel processing in rhesus monkey auditory cortex. J Comp Neurol 382: 89–103, 1997. [PubMed] [Google Scholar]
- Recanzone 2008.Recanzone GH. Representation of con-specific vocalizations in the core and belt areas of the auditory cortex in the alert macaque monkey. J Neurosci 28: 13184–13193, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recanzone et al. 2000b.Recanzone GH, Guard DC, Phan ML. Frequency and intensity response properties of single neurons in the auditory cortex of the behaving macaque monkeys. J Neurophysiol 83: 2315–2331, 2000b. [DOI] [PubMed] [Google Scholar]
- Recanzone et al. 2000a.Recanzone GH, Guard DC, Phan ML, Su TK. Correlation between the activity of single auditory cortical neurons and sound-localization behavior in the macaque monkey. J Neurophysiol 83: 2723–2739, 2000a. [DOI] [PubMed] [Google Scholar]
- Ren 2002.Ren T. Longitudinal pattern of basilar membrane vibration in the sensitive cochlea. Proc Natl Acad Sci USA 99: 17101–17106, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts et al. 2000.Roberts TP, Ferrari P, Stufflebeam SM, Poeppel D. Latency of the auditory evoked neuromagnetic field components: stimulus dependence and insights toward perception. J Clin Neurophysiol 17: 114–129, 2000. [DOI] [PubMed] [Google Scholar]
- Robles and Ruggero 2001.Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev 81: 1305–1352, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romanski et al. 2005.Romanski LM, Averbeck BB, Diltz M. Neural representation of vocalizations in the primate ventrolateral prefrontal cortex. J Neurophysiol 93: 734–747, 2005. [DOI] [PubMed] [Google Scholar]
- Romanski et al. 1999a.Romanski LM, Bates JF, Goldman-Rakic PS. Auditory belt and parabelt projections to the prefrontal cortex in the rhesus monkey. J Comp Neurol 403: 141–157, 1999a. [DOI] [PubMed] [Google Scholar]
- Romanski et al. 1999b.Romanski LM, Tian B, Fritz J, Mishkin M, Goldman-Rakic PS, Rauschecker JP. Dual streams of auditory afferents target multiple domains in the primate prefrontal cortex. Nat Neurosci 2: 1131–1136, 1999b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose et al. 1967.Rose JE, Brugge JF, Anderson DJ, Hind JE. Phase-locked response to low-frequency tones in single auditory nerve fibers of the squirrel monkey. J Neurophysiol 30: 769–793, 1967. [DOI] [PubMed] [Google Scholar]
- Ruggero and Rich 1987.Ruggero MA, Rich NC. Timing of spike initiation in cochlear afferents: dependence on site of innervation. J Neurophysiol 58: 379–403, 1987. [DOI] [PubMed] [Google Scholar]
- Russ et al. 2008.Russ BE, Ackelson AL, Baker AE, Cohen YE. Coding of auditory-stimulus identity in the auditory non-spatial processing stream. J Neurophysiol 99: 87–95, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salajegheh et al. 2004.Salajegheh A, Link A, Elster C, Burghoff M, Sander T, Trahms L, Poeppel D. Systematic latency variation of the auditory evoked M100: from average to single-trial data, Neuroimage 23: 288–295, 2004. [DOI] [PubMed] [Google Scholar]
- Schnupp et al. 2006.Schnupp JWH, Hall TM, Kokelar RF, Ahmed B. Plasticity of temporal pattern codes for vocalization stimuli in primary auditory cortex. J Neurosci 26: 4785–4795, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smiley et al. 2007.Smiley JF, Hackett TA, Ulbert I, Karmas G, Lakatos P, Javitt DC, Schroeder CE. Multisensory convergence in auditory cortex, I. Cortical connections of the caudal superior temporal plane in macaque monkeys. J Comp Neurol 502: 894–923, 2007. [DOI] [PubMed] [Google Scholar]
- Spezio et al. 2000.Spezio ML, Keller CH, Marrocco RT, Takhashi TT. Head-related transfer functions of the rhesus monkey. Hear Res 144: 73–88, 2000. [DOI] [PubMed] [Google Scholar]
- Stebbins et al. 1966.Stebbins WC, Green S, Miller FL. Auditory sensitivity of the monkey. Science 153: 1646–1647, 1966. [DOI] [PubMed] [Google Scholar]
- Strominger et al. 1977.Strominger NL, Nelson LR, Dougherty WJ. Second order auditory pathways in the chimpanzee. J Comp Neurol 172: 349–365, 1977. [DOI] [PubMed] [Google Scholar]
- Tian and Rauschecker 2004.Tian B, Rauschecker JP. Processing of frequency-modulated sounds in the lateral auditory belt cortex of the rhesus monkey. J Neurophysiol 92: 2993–3013, 2004. [DOI] [PubMed] [Google Scholar]
- Tian et al. 2001.Tian B, Reser D, Durham A, Kustov A, Rauschecker JP. Functional specialization in rhesus monkey auditory cortex. Science 292: 290–293, 2001. [DOI] [PubMed] [Google Scholar]
- Wang et al. 2005.Wang X, Lu T, Snider RK, Liang L. Sustained firing in auditory cortex evoked by preferred stimuli. Nature 435: 341–346, 2005. [DOI] [PubMed] [Google Scholar]
- Woods et al. 2006.Woods TM, Lopez SE, Long JH, Rahman JE, Recanzone GH. Effects of stimulus azimuth and intensity on the single-neuron activity in the auditory cortex of the alert macaque monkey. J Neurophysiol 96: 3323–3337, 2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.