Abstract
The classical view of the space of protein structures is that it is populated by a discrete set of protein folds. For proteins up to 200 residues long, by using structural alignments and building upon ideas of the completeness and continuity of structure space, we show that nearly any structure is significantly related to any other using a transitive set of no more than 7 intermediate structurally related proteins. This result holds for all structures in the Protein Data Bank, even when structural relationships between evolutionary related proteins (as detected by threading or functional analyses) are excluded. A similar picture holds for an artificial library of compact, hydrogen-bonded, homopolypeptide structures. The 3 sets share the global connectivity features of random graphs, in which the local connectivity of each node (i.e., the number of neighboring structures per protein) is preserved. This high connectivity supports the continuous view of single-domain protein structure space. More importantly, these results do not depend on evolution, rather just on the physics of protein structures. The fact that evolutionary divergence need not be invoked to explain the continuous nature of protein structure space has implications for how the universe of protein structures might have originated, and how function should be transferred between proteins of similar structure.
Keywords: completeness of fold space, connectivity of protein structure space, graph representation of protein structural relationships, evolution of protein folds, protein structure alignments
Traditionally, on the basis of all-against-all structure comparisons of the Protein Data Bank (PDB) (1), for single-domain proteins, protein structure space is viewed as a discrete collection of folds (2–4), wherein a fold is defined as a particular spatial arrangement of α-helical and/or β-sheet secondary structures (5). This forms the basis of the Structural Classification of Proteins (SCOP) (6) and Class/Architecture/Topology//Homologous superfamily (CATH) (2) structural databases. SCOP aims to provide the structural and evolutionary relationships between proteins with a classification protocol that strongly exploits evolutionary relationships. CATH is more structure-based and proceeds from secondary structure class to architecture to topology to homologous superfamilies (5). In CATH, structural alignments are done by using the sequential structure alignment program (7), a powerful approach for identifying highly significant relationships between structures but one that encounters difficulty in detecting more subtle structural similarities. Thus, it will implicitly enforce a more discretized picture of protein structure space.
In practice, such idealized classifications encounter many problems, including their ambiguity, often manifest in the difficulty that automated fold assignment approaches have in classifying 2 subtly different folds. In the extreme, if protein structure space were truly disjoint, this would imply that the library of contemporary folds evolved independently, as there would be no connecting bridges between different folds. Alternatively, analogous protein folds can emerge by subtle rearrangements of the protein core (8). This could provide an underlying mechanism for the Big Bang theory of protein folds (9, 10).
Early support for the continuity of protein structure space at least for approximately 130-residue-long substructures that transgress fold type came from Shindyalov and Bourne (11). Similarly, Harrison et al. concluded that fold space is a continuum for some topology types in the β or α/β secondary structure class (12). Yang and Honig (13) also detected structural similarities between different folds in SCOP (14). Consistent with these ideas, recent protein structure comparison studies suggest the alternative view that protein structure space is continuous, in the sense that “there are meaningful structural relationships between proteins that are classified very differently” (15), with many structural intermediates (16). However, protein structure space could be piece-wise continuous, with the space of α-helical, β-proteins, and α/β proteins disjoint from each other. This view is supported by the work of Kim et al., who found that protein structures associated with each type of secondary structure emerge from a common center (4), with sparse intervening regions that possibly arise because certain folds are unstable. Alternatively, this sparseness could arise because of the insensitivity of the structure comparison algorithms used (4) or because the library of solved structures is not yet complete.
To compare a pair of protein structures, a structural alignment is done to identify their “optimal” structural similarity. In practice, structure alignment algorithms employ different structure similarity metrics and approaches to identify this “best” structural alignment (17–23). Especially when 2 proteins have subtle structural similarities, different comparison metrics will capture different structural features (24). One widely used structure comparison metric is the TM-score whose range is 0–1, with 1.0 indicating structurally identical proteins (25). The average TM-score of the best structural alignment between randomly related structures is 0.30, with a SD of 0.01 (16). The TM-score offers the advantage that, unlike many other metrics (26), the statistical significance of an alignment for a given TM-score is protein length-independent and no rigid distance cutoffs are introduced so that more subtle structural similarities can be detected. The TM-align structure alignment algorithm (25, 27), used later in this article, uses the TM-score, but any sensitive structural alignment algorithm could be used in the analysis that follows.
The continuity of fold space does not require that the library of solved protein structures in the current PDB be complete. Is there a limited, but large repertoire of single-domain topologies such that, at some point, the likelihood of discovering a new protein structure would be minimal? Or is protein fold space essentially infinite? Kihara and Skolnick (28) demonstrated for single-domain proteins that the PDB is likely already complete; however, this conclusion is not true for multi-domain proteins or multimeric protein structures. More recently, it was shown that, by analyzing randomly generated 100- and 200-residue compact conformations of generic homopolypeptides in simplified and all-atom protein models, all have similar folds in the PDB, and conversely, all compact, single-domain protein structures in the PDB have structural matches to the set of compact homopolypeptide structures (16). Thus, both sets are quite likely complete, with the protein fold universe arising from compact conformations of hydrogen-bonded, secondary structures. As side chains are represented by Cβs in both protein models, these results suggest that the observed protein folds are insensitive to chain packing details. Sequence specificity enters in fine-tuning the structure and stabilizing a given fold with respect to alternatives.
In this article, we further explore the issues of the continuity and completeness of protein fold space. We adopt and extend the view of continuity described by Kolodny et al. (15), according to which one can “navigate” fold space to link 2 arbitrarily selected structures, following a path of statistically significant similar structures. We show for proteins up to 200 residues long that nearly any protein structure can be related to any other protein structure using a transitive set of no more than 7 intermediate structurally related proteins. Thus, protein structure space is almost completely connected; viz. when fold space is conceived as a graph, a giant sub-graph exists wherein every protein pair is structurally connected. Although one cause of the connectivity and continuity of fold space is the process of fold evolution (9, 29), we show that this condition is not necessary by excluding structural relationships between proteins that have an evolutionary relationship as identified by threading and/or that share a common fold/function. More importantly, we show that the library of randomly generated, compact hydrogen bonded, homopolypeptide structures whose secondary structures match those in the PDB is also extremely connected. As the latter set of proteins have no evolutionary relationship whatsoever, this implies that the continuity of fold space is a fundamental property of protein structures and protein physics, which is then exploited during the course of protein evolution.
Results
Structural Relationships in the PDB.
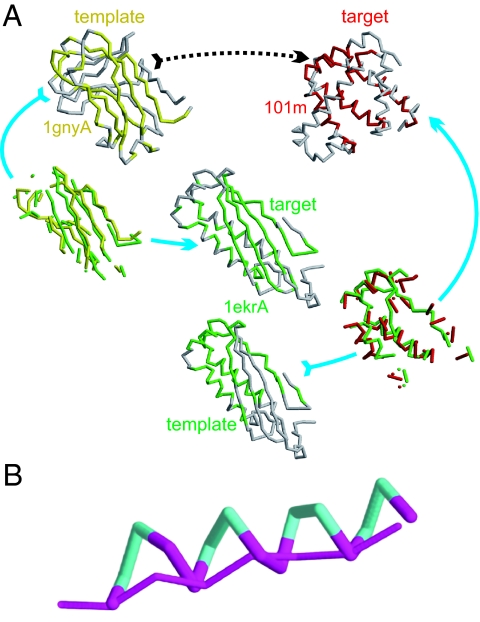
All-against-all structural alignments of compact proteins containing 40 to 300 residues that cover the PDB at no greater than 35% pair-wise sequence identity—the PDB300 set—were done. We consider here the PDB300holo subset of proteins whose functions are either known or can confidently be predicted, so as to be able to exclude proteins with apparent functional relationships from the analysis (30). Proteins 200 to 300 residues long can act as bridges between proteins no greater than 200 residues long—PDB200holo—but their exclusion leaves the results essentially unchanged. To compare a pair of protein structures, a structural alignment is done to identify their “closest” structural similarity as assessed by a structure comparison metric. We define the template as the structure of the protein being aligned to the protein structure of interest, the target. We use the TM-score to compare structures (25); any protein pair with a TM-score greater than 0.40 is structurally related [e.g., Fig. 1A; 1gnyA (template)→1ekrA (target)].
Fig. 1.
(A) Structural relationship between an all β-protein template (pdbid: 1gnyA) and an all α-protein target (pdbid: 101m) obtained through transitive alignments involving one α+β intermediate protein (pdbid:1ekrA). Gray represents unaligned regions; Yellow represents aligned region in 1gnyA; green represents aligned region in 1ekrA; Red represents aligned region in 101m. The TM-score(1gnyA→101m) is 0.31, the TM-score(1gnyA→1ekrA) is 0.43, and the TM-score(1ekrA→101m) is 0.41. The structural alignment between the template 1ekrA and the target 101m shows a β-strand from 1ekrA aligned to an α-helix from 101m (aligned secondary structural elements, Right). (B) Structural alignment of a β-strand to an α-helix.
At a finer-grained level, what happens when a helical protein is aligned to a β-protein? As in Fig. 1B, when a single helix is aligned to a β-strand, the β-strand aligns parallel to the principal axis of the helix, with half the helical residues omitted on average. As geometric objects, the aligned coordinates will be quite close in space. In this manner, the spatial proximity of secondary structural elements is maintained even when proteins of different secondary structure class are aligned. Because the TM-score depends on the number of aligned residues and half the helical residues are unaligned whereas all β-strand residues are aligned, for the single helix and β-strand considered here, the TM-score (helix→β) = 0.5 TM-score (β→helix). This effect introduces a subtle secondary structure dependence of the connectivity of protein space, with the set of helical proteins being most highly connected, followed by β-proteins, followed by mixed α/β proteins (see Discussion).
A further illustration as to how one can connect 2 apparently disparate protein structures of different secondary structure types is shown in Fig. 1A, in which we link the structure of the β-protein 1gynA to the helical protein 101m [TM-score(1gnyA→101m) = 0.31] via an intermediate mixed α and β containing protein structure: 1gynA→1ekrA→101m. The TM-score (1gynA→1ekrA) is 0.43 and that of 1ekrA→101m is 0.41. Among other features, this gives the partly unaligned gray helix in 101m (Fig. 1A Upper Right). There are a sufficient number of aligned residues so that the 2 proteins (1ekrA and 101m) bear a significant structural relationship to each other. Thus, we have a transitive walk in structure space from a β- to a helical protein.
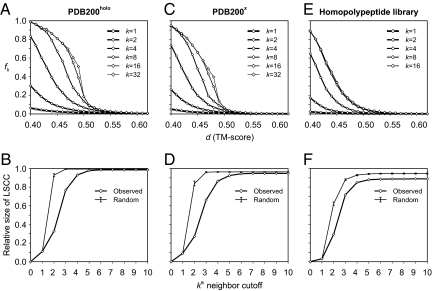
For template protein B aligned to target protein A, if the TM-score(B→A) ≥ d, then template B is a first neighbor of target protein A in structure space, at a TM-score cutoff d. If target and template structures A and B, and B and C, but not A and C, satisfy this criterion, then C is a second neighbor of A, with a transitive relationship C→B→A. More generally, template X is a kth neighbor of target Y if the length of the shortest path from X to Y is k. In Fig. 2A, the mean fraction of proteins, fk, in PDB200holo that are no more than k = first, second, fourth, eighth, 16th, and 32nd neighbors to another protein are shown versus d. The converged value of fk(k → ∞) is fmax. As shown in Fig. 2A (thick line), at d = 0.40, fk≥8 = fmax = 98.5%; i.e., nearly all proteins are no more than eighth structural neighbors. In fact, fk=4 = 83.2%, indicating that the majority of proteins are just fourth structural neighbors at most.
Fig. 2.
Mean fraction of proteins in PDB200holo (A), PDB200x (C), and the homopolypeptide library (E) that are no more than kth neighbors (fk), whose first neighbors have a TM-score ≥ d. Relative size of the LSCC in PDB200holo (B), PDB200x (D), and the homopolypeptide library (F), as a function of the kth neighbor cutoff, at d = 0.40. The thick line with diamonds corresponds to the values in the original set; the thin line indicates the median values obtained from 2,000 randomly generated digraphs with the same number of nodes and first-order local connectivity per node as in the original set (error bars indicate the minimum and maximum values from the 2,000 random graphs).
From Fig. 2B, the fraction of proteins in the largest strongly connected component [LSCC; the largest sub-graph of a directed graph, where a path exists from every vertex in the sub-graph to every other vertex in the sub-graph, i.e., every pair of vertices is connected in both directions; see supporting information (SI) Fig. S1], is S = 0.986. Here, the LSCC at a given kth cutoff includes the largest subset of proteins such that every possible pair of proteins in the subset are no more than kth neighbors to each other, with k ≠ 0. Thus, for k = 1, the LSCC comprises the maximal subset of proteins where the TM-score(A→B) ≥ d and the TM-score(B→A) ≥ d for every pair of proteins A and B that are members of the subset (i.e., the largest clique in the corresponding digraph). This figure clearly shows that protein structure space is almost completely connected (i.e., most proteins belong to the LSCC) and is continuous (15) in that one can link 2 arbitrarily selected structures, following a path of statistically significant similar structures. The results are very close to what happens when random digraphs with the same distribution of first neighbors are generated (Fig. 2B, thin line; S = 0.992).
At the transition midpoint of fmax, d = 0.49, and the strongly connected members are no more than 32nd neighbors, with a significant fraction of structure pairs (0.44) ≤16th neighbors. As protein structures are highly similar at this TM-score threshold (their structural alignment Z-score is 19), this further reinforces the conclusion that protein structure space is globally continuous and highly inter-linked. However, as d increases further, we recover the traditional discrete view of protein structure space (31).
Similar results are shown in Fig. S2. When the full PDB300 structures up to 300 residues is used, at d = 0.4, then fmax = 0.95 and the transition midpoint moves to d = 0.515. Thus, the results are remarkably insensitive to protein length or the size of the database used, with the transition midpoint occurring at a d well above the regime where statistically significant structural similarities are found.
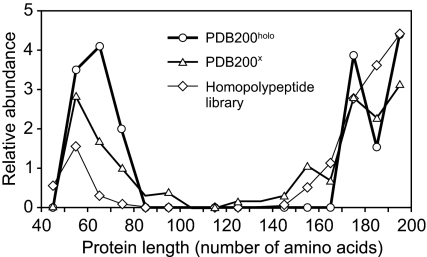
Fig. 3 shows the length distribution of proteins in PDB200holo not belonging to the LSCC; these proteins are either very small or very large. Because the TM-score is not commutative, there are large proteins aligned to the smallest proteins, but it takes at least second neighbors of intermediate length for a small protein to be aligned to a large protein. In practice, a tiny subset of the smallest proteins are not acceptable templates for the largest proteins. Moreover, just because of their size, some large proteins fail to have a sufficient number of neighbors to belong to the LSCC. They are effective templates for the smaller proteins, but do not have many structures aligned to them with a TM-score ≥ d. As the strongly connected component requires reciprocity, they are excluded. Which protein folds that are not part of the LSCC is somewhat anecdotal; when the entire PDB300 is used, all proteins excluded from the LSCC for PDB200holo become part of the LSCC.
Fig. 3.
Length distribution of proteins not belonging to the LSCC at d = 0.40 relative to all proteins in the PDB200holo set, the PDB200x set, and the homopolypeptide library. Relative abundance is the fraction of the total number of proteins excluded from the LSCC that fall in a given interval of protein length divided by the fraction of the total number of proteins in the set in the same protein length interval.
In Fig. 2C, for PDB200x, i.e., PDB200holo where functional relationships as detected by threading (32) and FINDSITE (30) are excluded, we plot the fraction of proteins that are no more than k = first, second, fourth, 16th, and 32nd neighbors as a function of the TM-score cutoff d. The goal here is to remove evolutionary relationships between proteins so that, as far as is practical, the underlying structural relationships are explored. At d = 0.4, fk≥8 = fmax = 0.947, with approximately 74% of proteins no more than fourth neighbors (fk=4 = 0.737). The transition midpoint shifts to a TM-score of 0.47 from 0.49 for PDB200holo. Fig. 2D shows for PDB200x (thick line), at d = 0.40, the fraction of proteins in the LSCC as a function of the kth neighbor cutoff. For k ≥ 8, S = 0.947, i.e., a rather minor diminution in the size of the LSCC compared with PDB200holo. The thin line shows the random digraph results given the same distribution of first neighbors for each protein as in PDB200x. Again, the asymptotic behavior is essentially indistinguishable from a random digraph (S = 0.965). However, real protein structures see the entire subspace at a larger number of neighbors than for the corresponding randomly generated graph; this is a result of a protein length effect that is entirely ignored in the random digraph. As in PDB200holo, those proteins excluded from the LSCC lie at the extremes of protein size; see Fig. 3. Thus, even when we try our best to remove evolutionary relationships between proteins, protein structure space is still almost completely connected.
We then considered the subset of PDB200x comprised only of proteins of identical secondary structure class. Interestingly, for structurally significant alignments among the 229 helical proteins, at d = 0.4, S is 0.952, while f1 is 0.172. For structural alignments among the 209 purely β-proteins, at d = 0.4, S is 0.874, while f1 is 0.174. Finally, for structural alignments among the 388 mixed motif proteins, at d = 0.4, S is 0.895, while f1 is 0.087. The lower f1 for αβ proteins reflects the TM-score reduction effect discussed earlier, when helices are aligned to β-strands, resulting in a smaller average number of neighbor structures. Nevertheless, in all 3 cases, the majority of structures within a given class belong to the LSCC. The fact that S is considerably larger for helical proteins than β-proteins reflects the fact that helices are longer than strands, so the average number of secondary structural elements in a helical protein of a given length is less than for β-proteins. Thus, the space of helical structures is effectively more compact (33). Interestingly, the distributions of the length of the shortest path k, linking protein pairs of identical secondary structure class are remarkably similar to those for protein pairs of different secondary structure classes (Fig. S3), indicating that if k would be used as a metric of protein similarity, protein structure space would be less segregated by secondary structure class than previously reported (4).
Structure Space of Compact, Sticky Homopolypeptides.
Despite our best efforts in PDB200x to remove evolutionary relationships among proteins to expose the purely structural characteristics of protein fold space, we still cannot guarantee that all such relationships have been excised. Previously, by examining the relationship between a randomly generated set of compact sticky, hydrogen-bonded homopolypeptides and real proteins, we demonstrated that all such structures were in the PDB and that the converse was also true (16). This suggested that the PDB is likely complete and that the completeness arises from the packing of hydrogen-bonded, compact arrangements of secondary structural elements, and nothing more. Here, in a similar spirit, for a set of polyvaline homopolypeptides, each with the same secondary structure assignment per amino acid position as one of the members of PDB300holo, we further explore the nature of the structure space of the library of folds generated by TASSER in the ab initio limit (33).
A number of interesting results were found. Using the original hydrogen bond scheme of TASSER (33), for β-sheet-containing proteins, protein structure space was not highly connected. We did find that, for the subspace of helical proteins, at d = 0.4, all helical protein structures are no more than eighth neighbors and the subspace of helical structures is almost completely connected. Examination of β-strand containing proteins above approximately 100 residues revealed that they failed to form hydrogen-bonded sheets, an effect exacerbated with increasing length. This is an echo of our previous work (16), where we showed that, if the hydrogen bonding is turned off, most generated compact structures are not in the PDB. Thus, we concluded that hydrogen bonding is necessary to generate protein-like structures. Without well formed β-sheets, there are many more geometric arrangements of the strands, and as a consequence, the resulting structure space is not so well connected.
Using the improved hydrogen bond scheme described in Methods (Fig. 2E), for the homopolypeptide structures, we plot fk as a function of d. The transition midpoint is at d = 0.435. When d = 0.40, fmax is 0.888 and S is 0.887. As in the case of real proteins, the space of homopolypeptide structures is extremely connected. Consistent with Fig. 2E, at d = 0.4, Fig. 2F shows that all members of the LSCC are no more than eighth structural neighbors. Interestingly, the random digraph with the same distribution of first neighbors for each node has a somewhat larger size of the LSCC (S = 0.946).
Focusing on the subset of helical proteins, we find that at d = 0.40 nearly every protein is no more than an eighth neighbor, with f1 equal to 0.18 (essentially, the same as in PDB200x), and S equal to 0.991. The transition midpoint occurs at d = 0.49. In contrast, for the structural subspace comprised only of β-proteins, at d = 0.40, f1 is 0.019 and S is 0.518, with all proteins in the LSCC no more than 16th neighbors. For the structural subspace of αβ proteins, at d = 0.40, f1 is 0.011 and S is 0.404, again with all proteins in the LSCC no more than 16th neighbors. The qualitative trends are the same as in PDB200x, but the nonhelical structural subspaces are more diffuse in the homopolypeptide library.
The most striking difference between the homopolypeptide structural library and the real PDB wherein detectible evolutionary relationships are excluded is in the size of the LSCC. This is a consequence of the difference in the average fraction of structures that are first neighbors, with an f1 of 0.024 compared with 0.051 for real proteins. Note that, for the homopolypeptide structure library, if we consider the top 2 and 5 clusters for each pattern of secondary structure, f1 values are 0.027 and 0.025, respectively. Thus, f1 is quite insensitive to the size of the homopolypeptide structural library. To reproduce the qualitative behavior of the size of the LSCC in real PDB structures, we need to include the top 8 clusters per secondary structure arrangement; that is, the structure space covered by the homopolypeptide library is less connected than that of PDB200x.
If we randomly delete connections in PDB200x so that f1 is 0.024 as in the homopolypeptide structural library, then the size of the LSCC is S = 0.881 at d = 0.4, i.e., essentially the same as in the homopolypeptide library, where S is 0.887 at d = 0.4. In other words, for the size of the LSCC, the real PDB200holo set excluding detectible functional relationships, i.e., PDB200x, behaves the same as the homopolypeptide structure library. The size of the LSCC is also comparable for the random digraphs that preserve the first-order local connectivity, with S = 0.965 for the random digraphs corresponding to the first neighbor depleted PDB200x and S = 0.946 for random digraphs corresponding to the homopolypeptide library. That is, the continuity of protein structure space is largely a generic property of randomly connected nodes that reflects the intrinsic structural similarities of proteins.
Discussion
This study builds on previous work that strongly suggested that the library of folds of compact single-domain proteins found in the PDB is already likely complete and that the set of protein structures arises from the packing of compact, hydrogen-bonded secondary structural elements (16). This does not require that protein structure space be continuous in the sense defined by Kolodny et al. (15), which is unrelated to the mathematical concept of graph continuity, nor that it be highly connected (e.g., if the LSCC were small in the real PDB library, then the set of randomly generated homopolypeptide structures corresponding to them would also have a very small LSCC). Here, we further argue that protein structure space is nearly completely connected, whereby essentially all protein structures can be linked from an arbitrary starting structure using a transitive set of 7 structurally related neighbors or less. The fact that protein structure space is almost completely connected suggests a means by which the observed universe of protein folds as generated by evolution (9, 10) could have arisen. During evolution, sequences that adopt any arbitrary fold that is at least marginally stable can give rise to sequences whose structures eventually filled all of fold space. Our homopolypeptide structure library results suggest that there are many ways that this could happen, and nature took advantage of at least one scenario.
Further support for the view that the high connectivity of fold space is an intrinsic structural property of proteins emerges from the fact that the size of the LSCC of real single-domain proteins in the PDB and the homopolypeptide structure library are quite consistent with the properties of a random directed graph (whose nodes represent structures) with the same number of nodes and first neighbors per node. The major difference between the space of real protein structures and homopolypeptide structures is that, in the latter, there are fewer first neighbors, the number of which is essential for dictating the size of the LSCC. Whether this reflects the residual influence of evolution or is caused by inadequacies in the potential used to fold the homopolypeptides is uncertain at this time.
Our results further emphasize the importance of hydrogen bonding. In an earlier report (16), we showed that, if hydrogen bonding were removed, the library of compact homopolypeptide structures do not resemble PDB structures. Rather, the average TM-score of the closest related homopolypeptide structure corresponds to the mean value of the best structural alignment of a pair of randomly related structures. Here, we show that it is the inclusion of a reasonable H-bond scheme that restricts the conformational space of the compact homopolypeptides so that their structural space has a large LSCC. In other words, hydrogen bonding acts at the level of individual protein structures as well as dictating the size and connectivity of the structural space of single domain proteins. Thus, the ability to reproduce the features of the structure space of real proteins can be another design criterion used to optimize the hydrogen bond potential used to fold proteins.
This work augments and supports the idea that fold space is discrete at high structural similarity and continuous at lower but still significant structural similarity (31). Moreover, we show that most protein pairs are separated by just 3 structural neighbors or less, irrespective of their secondary structure class. There are other biological ramifications of this study as well. Considerable effort has been expended over the years in the development of fold classification schemes that study the interrelationships of protein structures, not only because they might provide functional insights but also because they are of fundamental interest (5, 34). The fact that one need not invoke evolution to explain the structural interrelationships of almost all protein structures provides potentially important insights into how structure space is globally organized. Furthermore, because such interrelationships arise in the homopolypeptide library, wherein proteins with similar structures are not evolutionary related, care must be exercised in transferring function on the basis of structural similarity alone, without additional local structure and sequence-based filters. Thus, this analysis provides a foundation for the study of the interplay of evolution and protein physics on the nature of protein structure space.
Methods
The PDB300 Set.
The PDB300 set is a representative set of 5,906 compact PDB proteins with pair-wise sequence identity no greater than 35% and containing between 40 and 300 residues; many are in a ligand-free state. As our goal is to understand their underlying structural relationships, we wish to remove all detectible evolutionary relations between protein pairs. We therefore constructed the subset of PDB300, in a procedure detailed later, for which we had observed/predicted binding sites and associated binding ligands, the PDB300holo set comprised of 1,932 proteins. The subset of 1,186 proteins whose length is no greater than 200 residues is the PDB200holo set.
Detection of Distant Evolutionary Relationships Among Proteins.
For a given protein in PDB300holo, we thread against the entire structural template library using PROSPECTOR_3.5 (32) and exclude structural relationships between all protein partners whose z-score is 4 or higher. As PROSPECTOR_3.5 is driven by a strong sequence profile component, it can detect distant evolutionary relationships among proteins. To detect even more evolutionary distant pairs of proteins, we examined proteins of similar structure that share at least one common binding site and which are predicted to bind a correlated set of ligands using FINDSITE (30). The set of structural relationships after these exclusions is the PDB300x set. PDB200x is defined analogously from PDB200holo. Additional details are in the SI Appendix.
TM-Score and the Structural Alignment Program TM-Align.
The TM-score between the structure of template protein B with respect to target protein A, of lengths NB and NA respectively, is:
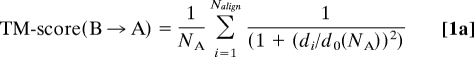 |
where Nalign is the number of aligned residues, di is the distance between the ith pair of aligned residues (1 ≤ i ≤ Nalign) and do(NA) is the average distance between a pair of residues in a randomly related structure pair (25). For unequal-length protein pairs, from Eq. 1a, TM-score(B→A)≠ TM-score(A→B), i.e., the TM-score is non-symmetric. To perform structural alignments, we employ an improved version of TM-align, fr-TM-align (27).
Calculation of kth Neighbors in Protein Structure Space.
For a given TM-score value of the structural similarity cutoff d, the mean fraction of structures that are kth neighbors, fk, and the fraction of proteins that are part of the LSCC, S, are calculated using a standard-depth first algorithm from graph theory (35). The implementation details are in the SI Appendix.
Random Directed Digraphs.
We represent the network of structural relationships between protein pairs as a 2-colored directed graph or digraph, whose nodes are protein structures and whose edges have a direction. The number of template proteins aligned to protein i is the in-degree and the number of proteins that protein i is aligned to is the out-degree of i. Each node can have one of 2 possible colors that correspond to small proteins (up to 200 residues) or large proteins (200–300 residues) that act as structural bridges. Random digraphs are generated by a procedure described in the SI Text that conserves the number of nodes, their colors, and first-order local connectivity. Fig. S1 illustrates how we represent structural relationships between proteins in a graph.
Polyvaline Simulations.
For each protein in the PDB300holo library, we extract its secondary structure (helix, strand, and coil) and transfer this bias to a polyvaline sequence of the same length. For helices, we use the highly accurate helix extraction subroutine in TM-align (25). For strands, we use the high-accuracy strand assignment algorithm our group described earlier (36). Residues assigned as helices are unchanged during the simulation, whereas strands and loops/turns experience a conformational bias and can dissolve and reform simulation. Folding is done using the ab initio version of TASSER (33), with modifications to the hydrogen bond potential described in the SI Text. The resulting structures are clustered and the structural properties of the space comprised of the top 8 clusters per secondary structure arrangement in PDB300holo are reported.
Supplementary Material
Acknowledgments.
This work was supported by grants GM-44835 and GM-37408 of the Division of General Medical Sciences of the National Institutes of Health. We thank Dr. Jose Borreguero for suggesting threading to remove evolutionary relationships between proteins and Dr. Shashi Pandit and Jake Boggan for useful discussions.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0907683106/DCSupplemental.
References
- 1.Berman H, Henrick K, Nakamura H, Markley JL. The worldwide Protein Data Bank (wwPDB): ensuring a single, uniform archive of PDB data. Nucleic Acids Res. 2007;35:D301–303. doi: 10.1093/nar/gkl971. Database issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Orengo CA, et al. CATH–a hierarchic classification of protein domain structures. Structure. 1997;5:1093–1108. doi: 10.1016/s0969-2126(97)00260-8. [DOI] [PubMed] [Google Scholar]
- 3.Holm L, Sander C. New structure–novel fold? Structure. 1997;5:165–171. doi: 10.1016/s0969-2126(97)00176-7. [DOI] [PubMed] [Google Scholar]
- 4.Hou J, Jun SR, Zhang C, Kim SH. Global mapping of the protein structure space and application in structure-based inference of protein function. Proc Natl Acad Sci USA. 2005;102:3651–3656. doi: 10.1073/pnas.0409772102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Greene LH, et al. The CATH domain structure database: new protocols and classification levels give a more comprehensive resource for exploring evolution. Nucleic Acids Res. 2007;35:D291–D297. doi: 10.1093/nar/gkl959. database issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Andreeva A, et al. SCOP database in 2004: refinements integrate structure and sequence family data. Nucleic Acids Res. 2004;32:D226–D229. doi: 10.1093/nar/gkh039. database issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Taylor WR, Orengo CA. Protein structure alignment. J Mol Biol. 1989;208:1–22. doi: 10.1016/0022-2836(89)90084-3. [DOI] [PubMed] [Google Scholar]
- 8.Ding F, Dokholyan NV. Emergence of protein fold families through rational design. PLoS Comput Biol. 2006;2:e85. doi: 10.1371/journal.pcbi.0020085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dokholyan NV, Shakhnovich B, Shakhnovich EI. Expanding protein universe and its origin from the biological Big Bang. Proc Natl Acad Sci USA. 2002;99:14132–14136. doi: 10.1073/pnas.202497999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zeldovich KB, Chen P, Shakhnovich BE, Shakhnovich EI. A first-principles model of early evolution: emergence of gene families, species, and preferred protein folds. PLoS Comput Biol. 2007;3:e139. doi: 10.1371/journal.pcbi.0030139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shindyalov IN, Bourne PE. An alternative view of protein fold space. Proteins. 2000;38:247–260. [PubMed] [Google Scholar]
- 12.Harrison A, Pearl F, Mott R, Thornton J, Orengo C. Quantifying the similarities within fold space. J Mol Biol. 2002;323:909–926. doi: 10.1016/s0022-2836(02)00992-0. [DOI] [PubMed] [Google Scholar]
- 13.Yang AS, Honig B. An integrated approach to the analysis and modeling of protein sequences and structures. I. Protein structural alignment and a quantitative measure for protein structural distance. J Mol Biol. 2000;301:665–678. doi: 10.1006/jmbi.2000.3973. [DOI] [PubMed] [Google Scholar]
- 14.Lo Conte L, Brenner SE, Hubbard TJ, Chothia C, Murzin AG. SCOP database in 2002: refinements accommodate structural genomics. Nucleic Acids Res. 2002;30:264–267. doi: 10.1093/nar/30.1.264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kolodny R, Petrey D, Honig B. Protein structure comparison: implications for the nature of ‘fold space’, and structure and function prediction. Curr Opin Struct Biol. 2006;16:393–398. doi: 10.1016/j.sbi.2006.04.007. [DOI] [PubMed] [Google Scholar]
- 16.Zhang Y, Hubner IA, Arakaki AK, Shakhnovich E, Skolnick J. On the origin and highly likely completeness of single-domain protein structures. Proc Natl Acad Sci USA. 2006;103:2605–2610. doi: 10.1073/pnas.0509379103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Grindley HM, Artymiuk PJ, Rice DW, Willett P. Identification of tertiary structure resemblance in proteins using a maximal common subgraph isomorphism algorithm. J Mol Biol. 1993;229:707–721. doi: 10.1006/jmbi.1993.1074. [DOI] [PubMed] [Google Scholar]
- 18.Bachar O, Fischer D, Nussinov R, Wolfson H. A computer vision based technique for 3-D sequence-independent structural comparison of proteins. Protein Eng. 1993;6:279–288. doi: 10.1093/protein/6.3.279. [DOI] [PubMed] [Google Scholar]
- 19.Holm L, Sander C. Dali: a network tool for protein structure comparison. Trends Biochem Sci. 1995;20:478–480. doi: 10.1016/s0968-0004(00)89105-7. [DOI] [PubMed] [Google Scholar]
- 20.Gerstein M, Levitt M. Using iterative dynamic programming to obtain accurate pairwise and multiple alignments of protein structures. Proc Int Conf Intell Syst Mol Biol. 1996;4:59–67. [PubMed] [Google Scholar]
- 21.May AC. Pairwise iterative superposition of distantly related proteins and assessment of the significance of 3-D structural similarity. Protein Eng. 1996;9:1093–1101. doi: 10.1093/protein/9.12.1093. [DOI] [PubMed] [Google Scholar]
- 22.Shindyalov IN, Bourne PE. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng. 1998;11:739–747. doi: 10.1093/protein/11.9.739. [DOI] [PubMed] [Google Scholar]
- 23.Chew LP, Kedem K. Finding the consensus shape for a protein family. Algorithmica. 2004;38:115–129. [Google Scholar]
- 24.Godzik A. The structural alignment between two proteins: is there a unique answer? Protein Sci. 1996;5:1325–1338. doi: 10.1002/pro.5560050711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang Y, Skolnick J. TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 2005;33:2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zemla A, Venclovas , Moult J, Fidelis K. Processing and evaluation of predictions in CASP4. Proteins Suppl. 2001;5:13–21. doi: 10.1002/prot.10052. [DOI] [PubMed] [Google Scholar]
- 27.Pandit SB, Skolnick J. Fr-TM-align: a new protein structural alignment method based on fragment alignments and the TM-score. BMC Bioinformatics. 2008;9:531. doi: 10.1186/1471-2105-9-531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kihara D, Skolnick J. The PDB is a Covering Set of Small Protein Structures. J Mol Biol. 2003;334:793–802. doi: 10.1016/j.jmb.2003.10.027. [DOI] [PubMed] [Google Scholar]
- 29.Roessler CG, et al. Transitive homology-guided structural studies lead to discovery of Cro proteins with 40% sequence identity but different folds. Proc Natl Acad Sci USA. 2008;105:2343–2348. doi: 10.1073/pnas.0711589105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brylinski M, Skolnick J. A threading-based method (FINDSITE) for ligand-binding site prediction and functional annotation. Proc Natl Acad Sci USA. 2008;105:129–134. doi: 10.1073/pnas.0707684105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pascual-Garcia A, Abia D, Ortiz AR, Bastolla U. Cross-over between discrete and continuous protein structure space: insights into automatic classification and networks of protein structures. PLoS Comput Biol. 2009;5:e1000331. doi: 10.1371/journal.pcbi.1000331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lee SY, Skolnick J. Benchmarking of TASSER_2.0: an improved protein structure prediction algorithm with more accurate predicted contact restraints. Biophys J. 2008;95:1956–1964. doi: 10.1529/biophysj.108.129759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Borreguero JM, Skolnick J. Benchmarking of TASSER in the ab initio limit. Proteins. 2007;68:48–56. doi: 10.1002/prot.21392. [DOI] [PubMed] [Google Scholar]
- 34.Andreeva A, et al. Data growth and its impact on the SCOP database: new developments. Nucleic Acids Res. 2008;36:D419–D425. doi: 10.1093/nar/gkm993. database issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Floyd RW. Algorithm-97 - shortest path. Commun ACM. 1962;5:345–345. [Google Scholar]
- 36.Kolinski A, Skolnick J, Godzik A, Hu WP. A method for the prediction of surface “U”-turns and transglobular connections in small proteins. Proteins. 1997;27:290–308. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.