Abstract
Protein fold classification often assumes that similarity in primary, secondary, or tertiary structure signifies a common evolutionary origin. However, when similarity is not obvious, it is sometimes difficult to conclude that particular proteins are completely unrelated. Clearly, a set of organizing principles that is independent of traditional classification could be valuable in linking different structural motifs and identifying common ancestry from seemingly disparate folds. Here, a four-dimensional ensemble-based energetic space spanned by a diverse set of proteins was defined and its characteristics were contrasted with those of Cartesian coordinate space. Eigenvector decomposition of this energetic space revealed the dominant physical processes contributing to the more or less stable regions of a protein. Unexpectedly, those processes were identical for proteins with different secondary structure content and were also identical among different amino-acid types. The implications of these results are twofold. First, it indicates that excited conformational states comprising the protein native state ensemble, largely invisible upon inspection of the high-resolution structure, are the major determinant of the energetic space. Second, it suggests that folds dissimilar in sequence or structure could nonetheless be energetically similar if their respective excited conformational states are considered, one example of which was observed in the N-terminal region of the Arc repressor switch mutant. Taken together, these results provide a surface area-based framework for understanding folds in energetic terms, a framework that may eventually yield a means of identifying common ancestry among structurally dissimilar proteins.
Introduction
The most common means of representing a protein is with a crystallographic or nuclear magnetic resonance structure (1). Although extremely useful, such a representation is incomplete in that it does not account for the experimental observation that folded proteins are actually ensembles of interconverting conformational states (2–4). Despite this reality, it remains a difficult problem to apply such knowledge in a practical way to questions of protein structure, function, stability, or the organization of fold space. Indeed, most progress in structural biology to date has been achieved without explicit consideration of the dynamic nature of protein structure.
This work is motivated by the hypothesis that ensemble-derived thermodynamic information can provide significant insight into these fundamental questions. Such a hypothesis is supported by the success of our own ensemble-based treatment of proteins, known as COREX/BEST (5), in capturing a broad spectrum of biophysical and functional observations, ranging from the identification of long range allosteric effects (6,7), the identification of the effects of fluctuations on binding affinity (8), the prediction of functional residues (9), the prediction of hydrogen exchange protection factor patterns (10), to the recapitulation of the effects of pH (11) and temperature (12,13) on the ensemble.
The ability to unify the description of these diverse phenomena within a single framework suggests that the COREX/BEST representation of proteins provides a set of organizing principles that allow structure, function, and stability to be quantitatively linked through the energetics of the ensemble. Indeed, using ensemble-based thermodynamic descriptors, our lab has empirically identified a general set of thermodynamic environments in proteins (14), which could be used successfully in fold recognition experiments (15,16). Understanding the physical and mathematical underpinnings for that result is one focus of this work.
Another more important focus concerns understanding of the natural origins of protein architecture. In the absence of complete knowledge of the physical and evolutionary mechanisms underlying protein fold space, much has been learned from provisional organization of fold space relying on similarities in primary sequence and secondary or tertiary structure (17–21). However, one drawback to provisional organization is that, in the absence of sequence or structure similarity, it is unclear whether a particular pair of proteins possesses an evolutionary relationship. It is possible that such cases reflect more on the current technological limits of sequence and structure comparison than on the absence of common ancestry. Indeed, many exceptions to similarity-based organization of fold space exist: it has long been known that the structure of some sequences is context-dependent (22), that folds may be similar in the absence of detectable sequence similarity (23), and that folds may even be different in the presence of substantial sequence similarity (24). Clearly, new metrics, possibly independent of sequence and structure similarity, would be of great value in increasing the limits of remote homology detection and elucidating the natural organization of protein fold space.
As a step toward understanding the effectiveness of thermodynamic environments in fold recognition, and, more generally, toward understanding the energetic basis of the organization of protein fold space, a novel representation of a protein as a multidimensional structure composed of thermodynamic environments was explored. By applying principal components analysis to the energetic space, the principal axes of energetic variation within the database of structures were identified. This revealed the independent mechanisms that combine to determine the stability of different states in the ensemble, and thus different regions of each protein. Interestingly, these mechanisms turn out to be independent of both secondary structure class and amino-acid type. Because the resultant eigenstates correspond to the underlying framework for a thermodynamic representation of protein fold space, to our knowledge they provide a novel means of energetically assessing the similarity of proteins with different sequences and structures.
Methods
Thermodynamic environment space of proteins defined from native state ensembles
Previously, we described the COREX/BEST algorithm (5,10,25), which generates a conformational ensemble for a protein using the high-resolution structure as a template. This algorithm has been vetted in both retrospective validation (8,11,12,26) and prediction (10), and thus provides a reasonable representation of the ensemble. For this work, a COREX/BEST analysis was performed on each member of a database of 120 diverse human proteins (15,27) (Table S1 in the Supporting Material) using the default parameters as described in the Supporting Material. Secondary structure was assigned using STRIDE (28).
Although potentially many thermodynamic quantities may be computed from a COREX/BEST ensemble, analysis here was restricted to four, in agreement with those employed in previous work (14–16): stability (ΔG), apolar enthalpy of solvation (ΔHap), polar enthalpy of solvation (ΔHpol), and conformational entropy (TΔSconf). These values were computed as residue-specific descriptors averaged over the native state ensemble, providing a quantitative report of the energetics experienced by each position j in the protein:
| (1) |
| (2) |
| (3) |
| (4) |
In Eqs. 1–4, [ΔG]j, [ΔHap]j, [ΔHpol]j, and [TΔSconf]j were the residue-specific thermodynamic descriptors for the native state ensemble at position j, Pi was the Boltzmann-weighted probability of a particular microstate i in the entire ensemble, and or were the respective probabilities in the folded or unfolded subensembles of a microstate i or k containing residue j in either a folded or unfolded conformation. Additional details concerning the calculations of these Boltzmann-weighted probabilities are given in the Supporting Material.
Distance calculations in three-dimensional Cartesian space and four-dimensional thermodynamic environment space
Distances between sequential α-carbon atoms j and j + 1 in both Cartesian (Eq. 5) and thermodynamic environment space (Eq. 6) were calculated as follows:
| (5) |
| (6) |
In Eq. 5, (xj, yj, zj) denotes coordinates of α-carbon atom j in the Protein Data Bank file. In Eq. 6, (ΔGj, ΔHap,j, ΔHpol,j TΔSconf,j) denotes thermodynamic parameters of residue j as given by Eqs. 1–4. Units of Euclidean distances were in Ångstroms; units of thermodynamic distances were in kcal/mol at 25°C. Distances were computed between all sequential residues within each of the 120 proteins in the dataset described above, and the distributions of these distances were normalized such that the area of each distribution was 1.
Principal component analysis (PCA) of thermodynamic environment space
Principal component analysis (PCA) was performed using the R function princomp (http://www.r-project.org) on the four-dimensional energetic data computed from the 120 native state ensembles of the protein database. This procedure is described in more detail in the Supporting Material.
Results
Energetic environments and thermodynamic structure of a protein
We define the thermodynamic structure of a protein as its vector set of points given by Eqs. 1–4. This novel four-dimensional thermodynamic structure is analogous to the three-dimensional Cartesian coordinate-based structure, but instead exists in thermodynamic space. Examples of protein structures in both traditional three-dimensional coordinate space as well as in thermodynamic space are displayed in Fig. 1. It is important to note that the attributes of thermodynamic structures in thermodynamic space differ with respect to those of crystal structures in Cartesian space. For example, two residues within a typical structure cannot occupy the same place at the same time due to excluded volume constraints; however, residues in a thermodynamic structure can, and often did. Also, two α-carbon residues in sequence (i.e., a virtual CA-CA bond) are almost always 3.8 ± 0.1 Å apart in typical structures (Fig. 2 A). In contrast, two sequential atoms can have very large energetic jumps in thermodynamic space (Fig. 2 B).
Figure 1.
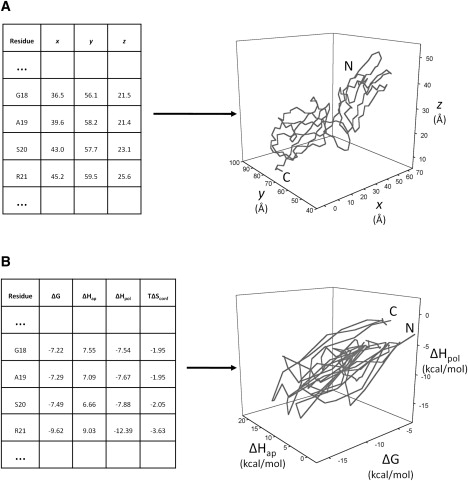
Comparison of conventional protein structure with thermodynamically defined protein structure. (A) A table (left) containing a subset of the three-dimensional Cartesian coordinates for the human mucosal addressin cell adhesion molecule 1 (PDB id 1gsmA) and its corresponding structural image (right). Positions of α-carbon atoms in Cartesian space are joined by virtual bonds, and N- and C-termini are marked. (B) A table containing a subset of the native state ensemble's four-dimensional thermodynamic coordinates for the same protein. Only the first three dimensions of these coordinates are plotted to visually approximate the protein's thermodynamic structure. Characteristics of the thermodynamic protein structure are graphically different from those of the conventional structure.
Figure 2.
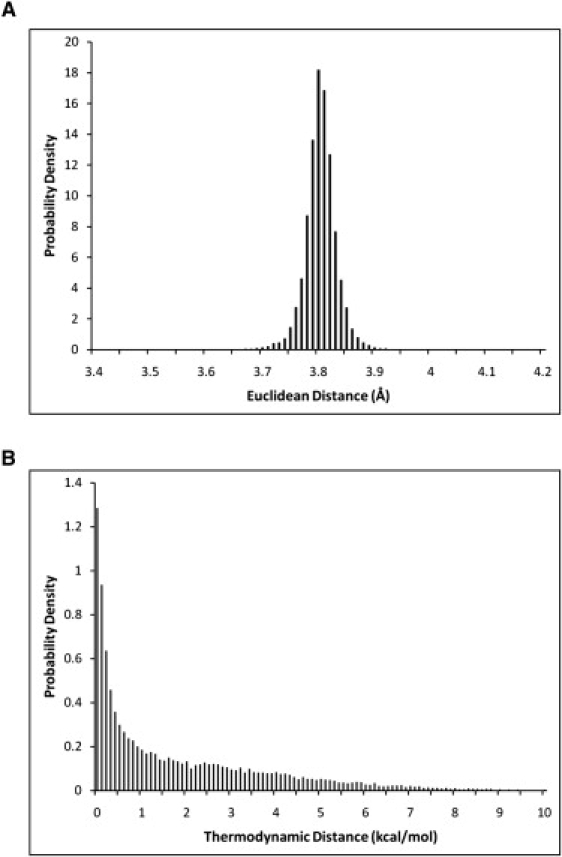
Comparison of Euclidean protein distances between sequential residues with thermodynamically defined distances. (A) Histogram of the probability density of sequential α-carbon CA-CA virtual bond distances (Eq. 5) for the 120 proteins in the thermodynamic database. Note that >99% of these distances are tightly clustered at 3.8 ± 0.1 Å. (B) Histogram of four-dimensional energetic distances (Eq. 6) between sequential residues. Note that the distribution of energetic distances is markedly broadened by comparison.
As described in Methods, residue-specific descriptors were computed for a large database of 120 diverse human proteins using default COREX/BEST parameters (15,27). In earlier work, these 17,484 position-specific energetic values were statistically clustered, and subjected to fold recognition experiments based on the propensities of different amino acids to appear within each cluster (14–16,27,29). The success of the fold recognition experiments indicated that the entire descriptor space could be meaningfully represented by a small number of clusters, which we termed thermodynamic environments (TEs). Here we investigated the physical principles underlying the TE space. Shown in Fig. 3 is a three-dimensional representation of TE space with the fourth (entropy) dimension presented by color. Two significant observations can be made from these data. First, the data assume an arrowhead shape, indicating physical limitations to the boundaries of the TE space. Second, the entropy axis (color) is correlated to the other three axes, and thus not independent. In fact, significant correlation in all of the parameters exists, motivating principal component analysis.
Figure 3.
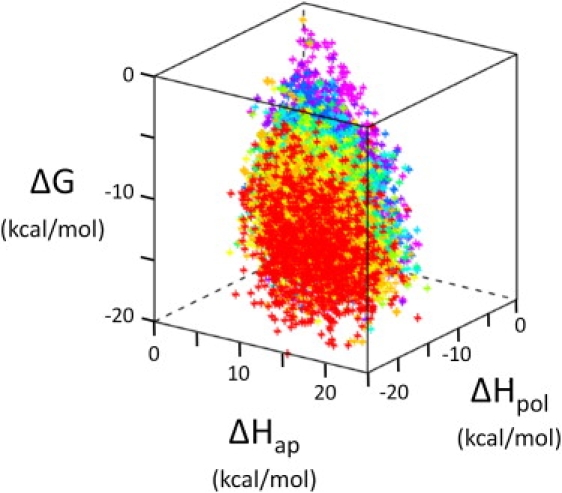
Thermodynamic environments space of 120 diverse human proteins. Energetic values from the native state ensembles of 120 proteins, 17,484 residues total, are plotted. The conformational entropy value is indicated by color, red for the lowest conformational entropies, and violet for the highest. These data assume an arrowhead shape and span the physical limits of thermodynamic environments space. The segregation of entropy colors suggests latent organization of this space, organization subsequently revealed by PCA.
Organization of TE space revealed by PCA is independent of primary and secondary structure
Because the original thermodynamic axes were correlated, change along one axis necessarily implied a change along all other correlated axes, hindering analysis of the underlying mechanism behind the organization of the TE space. To address this issue, we employed PCA. Eigenvectors and eigenvalues from the TE space of human proteins are displayed in Table 1. The first three principal components explain 99.2% of the variance of the original data, with a sharp decrease in the magnitude of the eigenvalues. This indicates that the data are substantially linearly related and supported the use of PCA as a valid analytical technique. The proportion of variance explained by each eigenvector is 75.2%, 22.0%, 2.6%, and ∼0.1% for principal components 1–4, respectively. Thus, principal component 1 alone explains the majority of variance of the original energetic data.
Table 1.
Principal components of the thermodynamic database of 17,484 residues from 120 human proteins
| PC1 | PC2 | PC3 | PC4 | Average∗ | |
|---|---|---|---|---|---|
| [ΔG] | −0.55 | 0.15 | 0.59 | −0.57 | −8.13 |
| [ΔHap] | 0.65 | 0.69 | 0.22 | −0.23 | 9.52 |
| [ΔHpol] | −0.51 | 0.70 | −0.23 | 0.44 | −11.72 |
| [TΔSconf] | −0.09 | 0.11 | −0.74 | −0.66 | −4.56 |
| Eigenvalue | 24.07 | 7.04 | 0.85 | 0.02 |
Average value of the thermodynamic quantity given in column 1, in kcal/mol.
To assess the possible differential contributions of secondary structure elements and individual amino-acid types to the principal components obtained from the complete TE space, subsets of the complete space were also analyzed. Eigenvectors and eigenvalues were found to be essentially unchanged with respect to secondary structure class or amino-acid type (Fig. 4 and Table S2).
Figure 4.
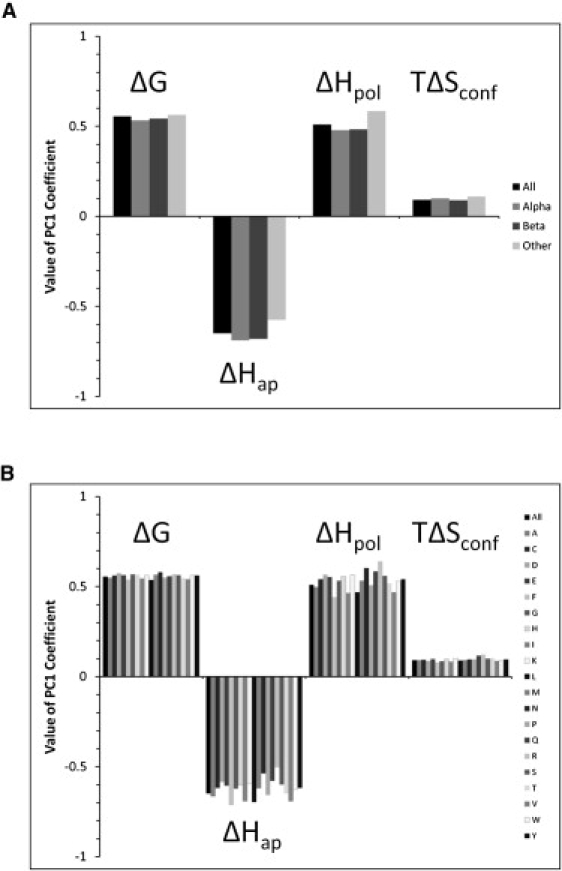
Principal components are independent of primary and secondary structure. (A) Values of each coefficient of the first principal component for secondary structure subsets of the entire thermodynamic descriptor dataset. Subsets were extracted based on STRIDE (28) secondary structure assignment (helix = H, G, I; strand = E, B, b; and coil = T, C). (B) Values of each coefficient of the first principal component for amino-acid type subsets of the entire thermodynamic descriptor dataset. Eigenvectors and eigenvalues were highly similar among all subsets. In both panels, the term “All” indicates results from the entire thermodynamic descriptor dataset of 17,484 residues, also given in the first column of Table 1.
Because the principal components decomposition of TE space is independent of primary or secondary structure, it implies that changing a protein's sequence or structure is possible without necessarily changing its energetic profile. In other words, the results of Fig. 4 suggest that multiple sequences or secondary structures could be tolerated by a single native state ensemble. If this hypothesis is true, a novel mechanism for evolutionary fold change can be inferred: fold change can proceed through an incremental change to the ancestral sequence or structure with minimum change to the new fold's thermodynamic profile (i.e., its sequence of position-specific energetic values). This hypothesis is developed in more detail in the Discussion.
Relationship between principal components of TE space, protein energetics, and solvent-accessible surface area
As described in Methods, a change in location parallel to the first principal axis corresponds to a change in the four energetic parameters. For example, a change of +1.0 unit exactly incident with principal component 1 equals changes of −0.55 kcal/mol along [ΔG], 0.65 kcal/mol along [ΔHap], −0.51 kcal/mol along [ΔHpol], and −0.09 kcal/mol along [TΔSconf]. To arrive at the structural basis of each axis, we correlated energetic changes along principal components axes with the ensemble-average changes in solvent-accessible surface area (ΔASA) from the unfolding events for a particular residue. This transformation was possible because the energy function used in the COREX/BEST algorithm was parameterized in terms of ΔASA (10,25), as detailed in the Supporting Material. The enthalpy component of the COREX/BEST energy function, for example, given by Eq. 7, can be rearranged to express changes in apolar and polar surface area in terms of changes in apolar and polar enthalpy, Eqs. 8 and 9, respectively:
| (7) |
| (8) |
| (9) |
In Eqs. 8 and 9, ΔHap(25) and ΔHpol (25) refer to the apolar and polar terms of Eq. 7; aH and bH are the temperature-independent coefficients of −8.44 and 31.4 cal × mol−1 × Å−2, respectively; and aCp and bCp are 0.45 and −0.26 K−1 × cal × mol−1 × Å−2, respectively (10).
This conversion of enthalpy to surface area is quantitatively displayed in Table 2. This table provides estimates of the quantity and type of surface area exposure necessary, on average, for a given energetic change in the folding of an arbitrary globular protein. Note that this is a valid transformation because the phenomenological effect of surface area exposure relative to energy is additive (30,31). Analogous, albeit redundant, equations can be derived to express ΔASA in terms of solvation entropy or conformational entropy. In the case of conformational entropy, it was found that changes in conformational entropy in the absence of surface area changes are rare and minor in magnitude when they do occur in our database. Note for example that PC3, containing conformational entropy as the dominant contributor, accounts for an insignificant fraction of the variance, thus justifying its exclusion from the analysis.
Table 2.
Correspondence between one-unit changes along principal component axes and changes in average solvent-accessible surface areas for a folded to unfolded transition in the native state ensemble
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| 〈ΔASAap〉 (× 103 Å2) | −0.027 | −0.028 | −0.009 | −0.009 |
| 〈ΔASApol〉 (× 103 Å2) | −0.013 | +0.017 | −0.006 | −0.011 |
| 〈ΔASAap〉 / 〈ΔASApol〉 | 2.15: 1 | −1.64: 1 | 1.66: 1 | 0.86: 1 |
Interpretation of thermodynamic environment space in terms of solvent-accessible surface area
Inspection of Table 2 reveals that the first principal component represents the increase (or decrease) in the ensemble-averaged amount of total ASA associated with unfolding. For PC1, a change of +1.0 units requires the simultaneous changes of −27 Å2 of apolar surface and −13 Å2 of polar surface. (Note that negative values indicate a larger amount of solvent-accessible surface area in the unfolded subensemble than in the folded subensemble.)
Tables 1 and 2 also reveal the relationship between surface area changes and stability: a protein can be stabilized (a negative change in [ΔG] of −0.55 kcal/mol) by exposing both apolar and polar surface areas in an ∼2:1 ratio. Residues with higher values of PC1 are stabilized because their unfolded subensembles exhibit a lower probability due to the exposure of large amounts of surface area at the ratio of 2:1, apolar/polar. Note that this ratio includes areas of complementary exposure as well as the area of direct unfolding. Complementary surface area exposure results from the fact that although residue j may always be folded in Fj (or unfolded in NFj), other residues can be newly exposed due to unfolding of the segment containing residue j. Fig. 5 shows the total ensemble-averaged surface area exposed (ΔASAap+ΔASApol) at each residue position as a function of PC1; clearly the magnitude of surface area exposure is strongly correlated with position along PC1. Thus, the most dominant local unfolding events in the native state ensemble for this database of proteins involve surface area exposure at a 2:1 apolar/polar ratio.
Figure 5.
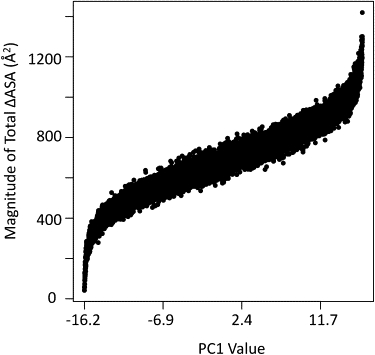
Correlation between change in total solvent-accessible surface area and PC1. Each of the 17,484 points represents values from one residue in the thermodynamic database of 120 proteins. The x axis indicates the value of the first principal component. The y axis indicates the total change in average solvent-exposed surface area (ΔASAap + ΔASApol) for each residue in the ensemble simulated folded to unfolded transition. As discussed in the text, a correlation is evident between PC1 value and solvent-exposed surface area, highlighting the biophysical interpretation of PC1 in terms of area.
In contrast to PC1, changes in PC2 reflect changes in the type of surface area exposed: the apolar and polar values in Table 2 have opposite sign. For a +1.0 unit change along PC2, the folded to unfolded ΔASA values are −0.028 and +0.017 Å2 for apolar and polar, respectively. Such a change slightly destabilizes a particular state by an average of ∼+0.15 kcal/mol. Also, in contrast to PC1, this change exposes less apolar surface area while exposing more polar surface area. In summary, PC2 is more directly related to the type of surface area exposed rather than the quantity, and combinations of PC1 and PC2 can account for all possibilities of type and amount of exposure.
ASA coefficients in Table 2 for a +1.0 unit change along PC3 are much smaller than those of PCs 1 or 2, indicating that the major energetic component of PC3 is not due to surface area exposure. The conformational entropy change for PC3 is three-to-five times larger than for PC1 or PC2. Thus, a small change in ASA with larger changes in entropy and stability characterize PC3. Finally, the amount of variance explained by PC4 is insignificant in value and can be considered rank-one noise. PCA thus reduced the thermodynamic environment space from four ensemble-averaged dimensions (i.e., [ΔG], [ΔHap], [ΔHpol], and [TΔSconf]) to three orthogonal components (i.e., PC1, PC2, and PC3), simplifying thermodynamic environments space.
Understanding the structural basis of TE space through investigation of extreme principal component values
To determine how the structures of proteins are related to the thermodynamic environments, the structural and energetic properties of residues at the extremes of each PC were contrasted. For PC1, two such residues are Ile156 from 1jhjA and Pro79 from 1i71A (Table 3 and Fig. 6). Their differences in ensemble-weighted average accessible surface areas upon unfolding of these positions were computed from the differences between their apolar and polar enthalpies, resulting in 1030 and 348 Å2 of buried apolar and polar areas, respectively. This indicates that Pro79 is 16.5 kcal/mol less stable than Ile156. In other words, the most probable states in the 1jhjA native state ensemble containing Ile156 unfolded expose a Boltzmann average of almost 1400 Å2 of additional surface, 75% of which is apolar, as compared to the most probable states in the 1i71A ensemble. Thus, the probability of being in an unfolded state is lower for Ile156 due to its large amount of buried apolar surface area, and this position can thus be considered stable (Fig. 6 A). On the contrary, the probability of being in an unfolded state is higher for Pro79 due to its large amount of solvent exposure, and thus this position can be considered unstable (Fig. 6 B).
Table 3.
Extreme values observed along the first three principal component directions in the thermodynamic database
| Direction | PDB ID | Residue | [ΔG]∗ | [ΔHap] | [ΔHpol] | [TΔSconf] |
|---|---|---|---|---|---|---|
| PC1 + | 1jhjA | Ile156 | −15.2 | 25.1 | −15.5 | −7.1 |
| PC1 − | 1i71A | Pro79 | 1.3 | 0.2 | −1.4 | −2.3 |
| PC2 + | 1ifrA | Arg471 | −14.1 | 7.8 | −22.6 | −6.5 |
| PC2 − | 1gsmA | Leu180 | −6.8 | 15.5 | −5.1 | −4.1 |
| PC3 + | 1a17A | Ile63 | −11.1 | 7.8 | −10.2 | −0.4 |
| PC3 − | 2ilkA | Ile147 | −6.3 | 12.8 | −14.1 | −9.5 |
Units of all thermodynamic quantities in kcal/mol.
Figure 6.
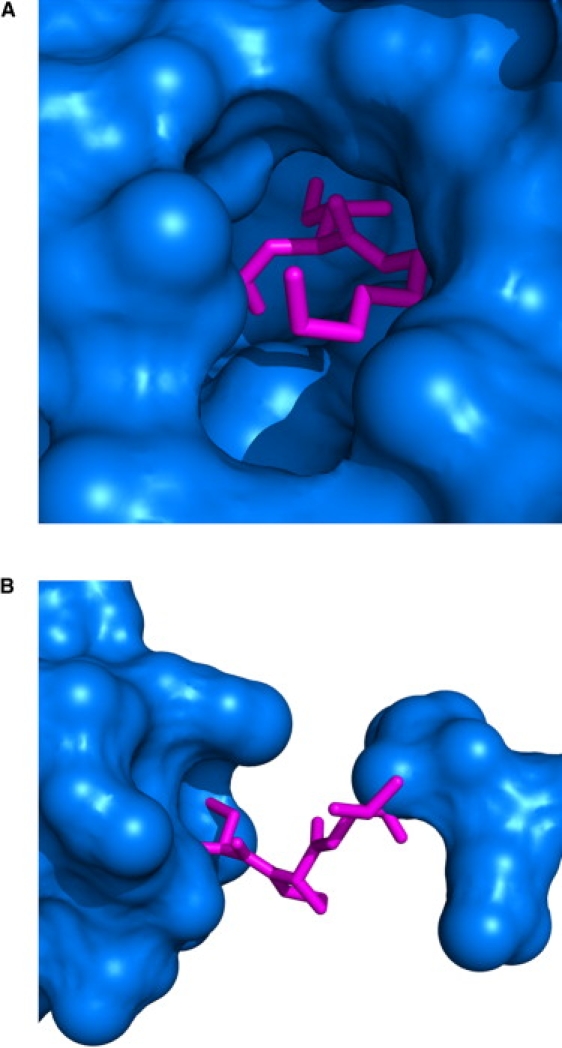
Structural microenvironments of residues exhibiting extreme positions along PC1. (A) Ile156 (PDB id 1jhjA), near a maximum value of PC1, and its immediate unfolding neighbors are displayed as pink-colored sticks. Note that removal of these residues (i.e., upon unfolding) would result in a large amount of newly exposed solvent-accessible surface area; water could potentially fill the entire cavity left by the removal. (B) Residue Pro79 (PDB id 1i71A) and its unfolding neighbors near the smallest PC1 value. Note that no cavity would be left upon unfolding of these residues.
Similarly, two residues exhibiting extreme values of PC2 were chosen, Arg471 from 1ifrA and Leu180 from 1gsmA (Table 3 and Fig. 7). Although both residues appear mostly buried, the large differences in [ΔHap] and [ΔHpol] between the residues indicates a large difference in the type of surface area exposed upon unfolding. This large difference in apolar surface area between Arg471 and Leu180 is 321 Å2 of increased exposure, reflecting the dominance of polar (red) surface area in Fig. 7 A. The polar change is a similarly large, but opposite in sign, −433 Å2, reflecting the dominance of apolar (blue) surface area in Fig. 7 B.
Figure 7.
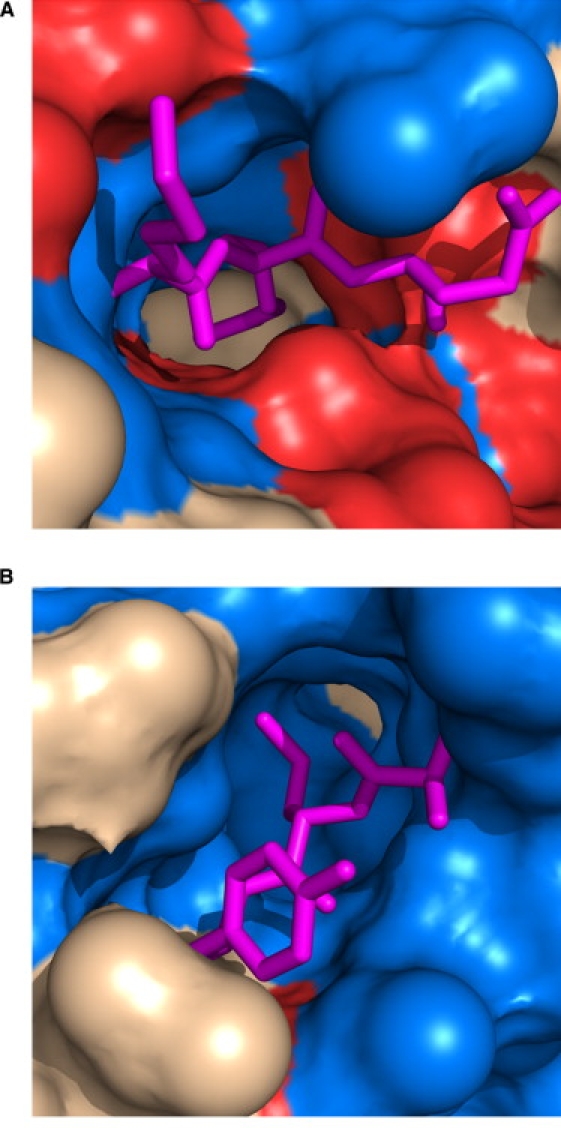
Structural microenvironments of residues exhibiting extreme positions along PC2. (A) Arg471 (PDB id 1ifrA), near a maximum value of PC2, and its immediate unfolding neighbors are shown as pink sticks. A large amount of polar surface area (colored red) surrounds these residues. (B) Leu180 (PDB id 1gsmA), near a minimum in PC2, and its unfolding neighbors are shown as pink sticks. Note the surrounding surface area is almost completely apolar (blue). In both panels, gray area corresponds to surface that is neither highly apolar nor highly polar. Polar area is defined as residue types R, K, H, E, D, N, Q, T, S, and C, and apolar area is defined as residue types A, G, V, I, L, F, and M.
Discussion
A large body of work has demonstrated that the native state of a protein is most accurately described not as a single crystal structure, but rather as an ensemble of interconverting states in equilibrium with that structure (2–4). These conformational fluctuations within the ensemble are known to be important for protein function, stability, and evolution (32–34). However, detailed information about the ensemble is often impossible to obtain by experiment or by computational analysis of single crystal structures. Our model of the native state ensemble, COREX/BEST, developed over the past decade (5,10,25), provides such information about the equilibrium conformational fluctuations of proteins in terms of energetics. COREX/BEST represents an improvement over a single crystal structure because it can reproduce many different experimental observables of proteins (6–13). This article provides a concise description of this energetic information through construction and investigation of a thermodynamic environment space. Future work will use these results to develop improved tools for protein structure analysis tasks and fold recognition (27,35).
Principal component analysis was employed to organize and simplify the thermodynamic environment space of proteins. Notably, the three physical processes revealed by PCs 1–3 were independent of secondary structure elements or amino-acid content, as demonstrated in Fig. 4. The reason for this independence is that the native state of a protein can be defined independently of its secondary structure elements or amino-acid content. Therefore, the local energetics of the same protein, depending only on the equilibrium between the native and denatured states and not their structural identities, can also be independent of primary and secondary structure.
Importantly, this equilibrium is not apparent from inspection of the crystal structure, as it depends on the unfolding of multiple residues in the form of partially disordered states. Consideration of all partially disordered states, comprising the native state ensemble, provides additional information about this equilibrium, in effect averaging the energetic contributions of each residue position with those of neighboring positions. Therefore, considerable similarity may exist between sequence segments in two different proteins when the equilibria of those segments are compared, even though those segments may be structurally quite different when folded. In other words, differences between the static structures of two proteins may belie similarities in the thermodynamic stabilities of those same static structures. The central hypothesis proposed in this work is that these thermodynamic similarities between proteins, perhaps contradictory to similarities between their crystal structures, have evolutionary relevance.
One implication of this hypothesis is that energetic similarities between secondary structure elements of different type may mediate the evolution of new folds from existing ones. Secondary structure is mentioned specifically because evolutionary mechanisms of fold change are thought to include localized changes to secondary structure elements (36,37). This hypothesis, schematically outlined in Fig. 8, could thus be considered a novel thermodynamic explanation of this accepted evolutionary mechanism.
Figure 8.
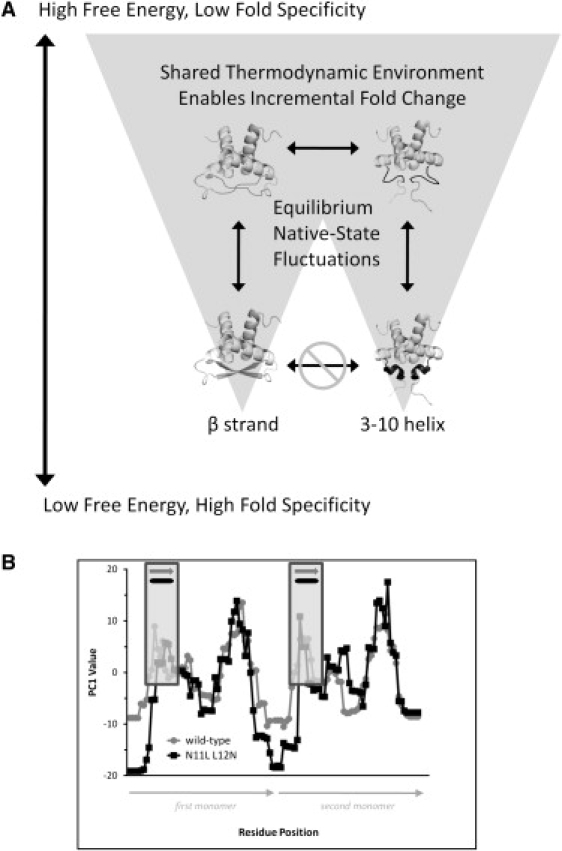
Schematic illustration of incremental fold change resulting from energetic equivalence. (A) A highly simplified energy landscape with two dominant wells is displayed. In this scenario, evolution of different secondary structures, and different folds, is mediated by moderately excited conformational states accessed by local equilibrium fluctuations. Direct evolutionary changes of entire secondary structure elements, absent the sequence changes, are forbidden, as indicated by the lowest horizontal double arrow. However, the structure of a particular protein may gradually morph, mechanistically driven by changes in secondary structure elements caused by random mutation of amino-acid sequence. Each change is tolerated because energetic properties (thermodynamic environments) of both the original and new secondary structure elements are similar in the context of the entire protein. The experimentally observed case of the Arc repressor homodimer switch mutant is consistent with this scenario. Ground states of wild-type Arc protein (39) and mutant N11L L12N (40) are shown: the wild-type forms β-structure at the N-terminal region of the chain (dark shaded) whereas the mutant forms 3-10 helical structure in the same region (solid). (B) Despite the different secondary structure elements observed in the wild-type (dark shaded) and mutant (solid) proteins, the energetic properties of these elements (vertical boxed regions), as well as of the entire proteins, were similar as computed by the COREX/BEST algorithm. The PDB codes 1bdt, chains A and B, and 1nla, chains A and B, were used for these calculations, with window size of 5, minimum window size of 4, entropy weighting of 0.750, and simulated temperature of 25.0°C. Plotted are the values of the first principal component (Table 1) of each protein as a function of residue position in the homodimer.
This mechanism is possibly observed in vitro in the case of the Arc repressor protein homodimer (38) (Fig. 8 A). Two proteins with different secondary structure elements (in a specific region), exemplified in the figure by wild-type Arc and the switch mutant N11L L12N, undergo equilibrium fluctuations resulting from similar thermodynamic environments in these elements. The similar thermodynamic environments, captured by the COREX/BEST algorithm (Fig. 8 B, boxed regions), are places where localized structural change can occur with minimum disruption to the rest of the fold, because of the similar energetic properties of the ancestral and changed structures. Over time, many localized changes could gradually result in a different fold, possibly with a residual energetic similarity to its ancestor. Unknown at present is the degree to which the evolutionary distance between two proteins is reflected in their degree of energetic similarity, as quantified by the energetic principal components. This latter hypothesis is currently being investigated in more detail through the COREX/BEST analysis of large numbers of proteins with known evolutionary relationships (data not shown).
Conclusion
Principal component analysis was used to gain insight into the organization of thermodynamic environment space of proteins, and it was discovered that protein energetics, as described by three principal components, are independent of primary and secondary structure. In addition to the implications for fold classification, these results clearly illuminate the biophysical origin of thermodynamic environments in terms of solvent-exposed surface area. The first principal axis in TE space is highly correlated to the magnitude (in total surface area) of the local unfolding event. In contrast, PC2 is most directly related to the type, not the quantity, of surface area unfolded. PC3 is related to stability changes mediated by conformational entropy instead of surface area. The importance of these results is twofold. First, similarities in thermodynamic environment space, often hidden by tertiary structure, yet quantified by these principal energetic components, can provide a novel metric for comparison of proteins, even those with dissimilar folds. Second and equally as important, these results provide a quantitative thermodynamic basis for how new and structurally dissimilar folds can arise from an existing fold.
Supporting Material
Two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01153-9.
Supporting Material
Acknowledgments
The authors thank two anonymous reviewers for constructive comments that greatly improved the clarity of the original manuscript.
This work was supported by the National Institutes of Health (grant No. R01-GM63747) and the Robert A. Welch Foundation (grant No. H-1461).
Footnotes
Jason Vertrees' present address is Department of Computer Science, Dartmouth College, 6211 Sudikoff Laboratory, Room 252, Hanover, NH 03755.
References
- 1.Berman H.M., Westbrook J., Feng Z., Gilliland G., Bhat T.N. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Henzler-Wildman K., Kern D. Dynamic personalities of proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 3.Igumenova T.I., Frederick K.K., Wand A.J. Characterization of the fast dynamics of protein amino acid side chains using NMR relaxation in solution. Chem. Rev. 2006;106:1672–1699. doi: 10.1021/cr040422h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mittermaier A., Kay L.E. New tools provide new insights in NMR studies of protein dynamics. Science. 2006;312:224–228. doi: 10.1126/science.1124964. [DOI] [PubMed] [Google Scholar]
- 5.Vertrees J., Barritt P., Whitten S., Hilser V.J. COREX/BEST server: a web browser-based program that calculates regional stability variations within protein structures. Bioinformatics. 2005;21:3318–3319. doi: 10.1093/bioinformatics/bti520. [DOI] [PubMed] [Google Scholar]
- 6.Sayar K., Ugur O., Liu T., Hilser V.J., Onaran O. Exploring allosteric coupling in the α-subunit of heterotrimeric G proteins using evolutionary and ensemble-based approaches. BMC Struct. Biol. 2008;8:23. doi: 10.1186/1472-6807-8-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu T., Whitten S.T., Hilser V.J. Ensemble-based signatures of energy propagation in proteins: a new view of an old phenomenon. Proteins. 2006;62:728–738. doi: 10.1002/prot.20749. [DOI] [PubMed] [Google Scholar]
- 8.Pan H., Lee J.C., Hilser V.J. Binding sites in Escherichia coli dihydrofolate reductase communicate by modulating the conformational ensemble. Proc. Natl. Acad. Sci. USA. 2000;97:12020–12025. doi: 10.1073/pnas.220240297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu T., Whitten S.T., Hilser V.J. Functional residues serve a dominant role in mediating the cooperativity of the protein ensemble. Proc. Natl. Acad. Sci. USA. 2007;104:4347–4352. doi: 10.1073/pnas.0607132104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hilser V.J., Freire E. Structure-based calculation of the equilibrium folding pathway of proteins. Correlation with hydrogen exchange protection factors. J. Mol. Biol. 1996;262:756–772. doi: 10.1006/jmbi.1996.0550. [DOI] [PubMed] [Google Scholar]
- 11.Whitten S.T., Garcia-Moreno E.B., Hilser V.J. Local conformational fluctuations can modulate the coupling between proton binding and global structural transitions in proteins. Proc. Natl. Acad. Sci. USA. 2005;102:4282–4287. doi: 10.1073/pnas.0407499102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Babu C.R., Hilser V.J., Wand A.J. Direct access to the cooperative substructure of proteins and the protein ensemble via cold denaturation. Nat. Struct. Mol. Biol. 2004;11:352–357. doi: 10.1038/nsmb739. [DOI] [PubMed] [Google Scholar]
- 13.Whitten S.T., Kurtz A.J., Pometun M.S., Wand A.J., Hilser V.J. Revealing the nature of the native state ensemble through cold denaturation. Biochemistry. 2006;45:10163–10174. doi: 10.1021/bi060855+. [DOI] [PubMed] [Google Scholar]
- 14.Wrabl J.O., Larson S.A., Hilser V.J. Thermodynamic environments in proteins: fundamental determinants of fold specificity. Protein Sci. 2002;11:1945–1957. doi: 10.1110/ps.0203202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Larson S.A., Hilser V.J. Analysis of the “thermodynamic information content” of a Homo sapiens structural database reveals hierarchical thermodynamic organization. Protein Sci. 2004;13:1787–1801. doi: 10.1110/ps.04706204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang S., Gu J., Larson S.A., Whitten S.T., Hilser V.J. Denatured-state energy landscapes of a protein structural database reveal the energetic determinants of a framework model for folding. J. Mol. Biol. 2008;381:1184–1201. doi: 10.1016/j.jmb.2008.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Andreeva A., Howorth D., Chandonia J.M., Brenner S.E., Hubbard T.J. Data growth and its impact on the SCOP database: new developments. Nucleic Acids Res. 2008;36:D419–D425. doi: 10.1093/nar/gkm993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Greene L.H., Lewis T.E., Addou S., Cuff A., Dallman T. The CATH domain structure database: new protocols and classification levels give a more comprehensive resource for exploring evolution. Nucleic Acids Res. 2007;35:D291–D297. doi: 10.1093/nar/gkl959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Finn R.D., Tate J., Mistry J., Coggill P.C., Sammut S.J. The Pfam protein families database. Nucleic Acids Res. 2008;36:D281–D288. doi: 10.1093/nar/gkm960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tatusov R.L., Fedorova N.D., Jackson J.D., Jacobs A.R., Kiryutin B. The COG database: an updated version includes eukaryotes. BMC Bioinformatics. 2003;4:41. doi: 10.1186/1471-2105-4-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kriventseva E.V., Fleischmann W., Zdobnov E.M., Apweiler R. CluSTr: a database of clusters of SWISS-PROT+TrEMBL proteins. Nucleic Acids Res. 2001;29:33–36. doi: 10.1093/nar/29.1.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Minor D.L., Kim P.S. Context-dependent secondary structure formation of a designed protein sequence. Nature. 1996;380:730–734. doi: 10.1038/380730a0. [DOI] [PubMed] [Google Scholar]
- 23.Kinch L.N., Grishin N.V. Expanding the nitrogen regulatory protein superfamily: homology detection at below random sequence identity. Proteins. 2002;48:75–84. doi: 10.1002/prot.10110. [DOI] [PubMed] [Google Scholar]
- 24.Alexander P.A., He Y., Chen Y., Orban J., Bryan P.N. The design and characterization of two proteins with 88% sequence identity but different structure and function. Proc. Natl. Acad. Sci. USA. 2007;104:11963–11968. doi: 10.1073/pnas.0700922104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hilser V.J., Garcia-Moreno E.B., Oas T.G., Kapp G., Whitten S.T. A statistical thermodynamic model of the protein ensemble. Chem. Rev. 2006;106:1545–1558. doi: 10.1021/cr040423+. [DOI] [PubMed] [Google Scholar]
- 26.Wooll J.O., Wrabl J.O., Hilser V.J. Ensemble modulation as an origin of denaturant-independent hydrogen exchange in proteins. J. Mol. Biol. 2000;301:247–256. doi: 10.1006/jmbi.2000.3889. [DOI] [PubMed] [Google Scholar]
- 27.Vertrees J. University of Texas Medical Branch; Galveston, TX: 2008. A Thermodynamic Definition of Protein Folds. Department of Biochemistry and Molecular Biology. [Google Scholar]
- 28.Frishman D., Argos P. Knowledge-based protein secondary structure assignment. Proteins. 1995;23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- 29.Wrabl J.O., Larson S.A., Hilser V.J. Thermodynamic propensities of amino acids in the native state ensemble: implications for fold recognition. Protein Sci. 2001;10:1032–1045. doi: 10.1110/ps.01601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Freire E., Murphy K.P. Molecular basis of co-operativity in protein folding. J. Mol. Biol. 1991;222:687–698. doi: 10.1016/0022-2836(91)90505-z. [DOI] [PubMed] [Google Scholar]
- 31.Xie D., Freire E. Structure-based prediction of protein folding intermediates. J. Mol. Biol. 1994;242:62–80. doi: 10.1006/jmbi.1994.1557. [DOI] [PubMed] [Google Scholar]
- 32.Eisenmesser E.Z., Millet O., Labeikovsky W., Korzhnev D.M., Wolf-Watz M. Intrinsic dynamics of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 33.Lee A.L., Wand A.J. Microscopic origins of entropy, heat capacity and the glass transition in proteins. Nature. 2001;411:501–504. doi: 10.1038/35078119. [DOI] [PubMed] [Google Scholar]
- 34.Tokuriki N., Tawfik D.S. Protein dynamism and evolvability. Science. 2009;324:203–207. doi: 10.1126/science.1169375. [DOI] [PubMed] [Google Scholar]
- 35.Vertrees J., Wrabl J.O., Hilser V.J. Energetic profiling of protein folds. Methods Enzymol. 2009;455:299–327. doi: 10.1016/S0076-6879(08)04211-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Grishin N.V. Fold change in evolution of protein structures. J. Struct. Biol. 2001;134:167–185. doi: 10.1006/jsbi.2001.4335. [DOI] [PubMed] [Google Scholar]
- 37.Van Dorn L.O., Newlove T., Chang S., Ingram W.M., Cordes M.H. Relationship between sequence determinants of stability for two natural homologous proteins with different folds. Biochemistry. 2006;45:10542–10553. doi: 10.1021/bi060853p. [DOI] [PubMed] [Google Scholar]
- 38.Cordes M.H., Walsh N.P., McKnight C.J., Sauer R.T. Evolution of a protein fold in vitro. Science. 1999;284:325–328. doi: 10.1126/science.284.5412.325. [DOI] [PubMed] [Google Scholar]
- 39.Schildbach J.F., Karzai A.W., Raumann B.E., Sauer R.T. Origins of DNA-binding specificity: role of protein contacts with the DNA backbone. Proc. Natl. Acad. Sci. USA. 1999;96:811–817. doi: 10.1073/pnas.96.3.811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cordes M.H., Walsh N.P., McKnight C.J., Sauer R.T. Solution structure of switch Arc, a mutant with 3(10) helices replacing a wild-type β-ribbon. J. Mol. Biol. 2003;326:899–909. doi: 10.1016/s0022-2836(02)01425-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


