The Control of the Controller: Molecular Mechanisms for Robust Perfect Adaptation and Temperature Compensation

Abstract

Organisms have the property to adapt to a changing environment and keep certain components within a cell regulated at the same level (homeostasis). “Perfect adaptation” describes an organism's response to an external stepwise perturbation by regulating some of its variables/components precisely to their original preperturbation values. Numerous examples of perfect adaptation/homeostasis have been found, as for example, in bacterial chemotaxis, photoreceptor responses, MAP kinase activities, or in metal-ion homeostasis. Two concepts have evolved to explain how perfect adaptation may be understood: In one approach (robust perfect adaptation), the adaptation is a network property, which is mostly, but not entirely, independent of rate constant values; in the other approach (nonrobust perfect adaptation), a fine-tuning of rate constant values is needed. Here we identify two classes of robust molecular homeostatic mechanisms, which compensate for environmental variations in a controlled variable's inflow or outflow fluxes, and allow for the presence of robust temperature compensation. These two classes of homeostatic mechanisms arise due to the fact that concentrations must have positive values. We show that the concept of integral control (or integral feedback), which leads to robust homeostasis, is associated with a control species that has to work under zero-order flux conditions and does not necessarily require the presence of a physico-chemical feedback structure. There are interesting links between the two identified classes of homeostatic mechanisms and molecular mechanisms found in mammalian iron and calcium homeostasis, indicating that homeostatic mechanisms may underlie similar molecular control structures.

Introduction

Many physiologically important compounds are under tight homeostatic regulation, where internal concentrations are adapted (1) at certain levels, despite environmental disturbances. Two concepts have developed to understand homeostasis: one is related to the intrinsic properties of the network showing that the adaptation response is independent of (most but not all) rate constant values (referred to here as robust (2–4) adaptation/homeostasis), whereas the other concept looks at the homeostasis due to a fine-tuning between rate constants. Perfect adaptation describes an organism's response to an external stepwise perturbation by regulating some of its variables/components precisely to their original preperturbation values. Perfect adaptation has been found, for example, in bacterial chemotaxis (5–8), photoreceptor responses (9), and MAP-kinase regulation (10–12). In this respect, perfect adaptation and homeostasis are closely related and in the following, we look at homeostasis as a perfectly adapted process.

Robust perfect adaptation/homeostasis of a perturbed system can be related to the concept of integral control (13) or integral feedback (14). In this type of control mechanism, the error between the value of the system output (controlled variable, CV) and its setpoint is integrated, and the integral value is fed to the input of the process (the so-called manipulated variable, MV), which results in a robust adaptation of the system output to the setpoint (Fig. 1). Recently, El-Samad et al. (15) have shown that calcium homeostasis under hypocalcemia conditions can be described on the basis of an integral feedback approach, where the error between the calcium setpoint and the actual calcium level is related to the activity of the parathyroid hormone (PTH), an important hormone in calcium regulation.

Figure 1.

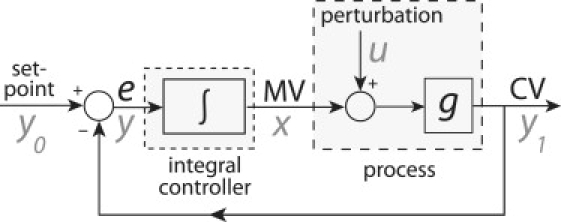
Scheme of integral control/feedback of a perturbed system, where the system output is perfectly adapted to the setpoint (i.e., the error e is robustly controlled to zero). MV and CV are the manipulated and controlled variables, respectively. Symbols in gray denote the notation for integral feedback by Yi et al. (14).

However, the molecular mechanisms behind error-sensing processes are little understood. To investigate the relationship between the integral control/feedback concept and its reaction kinetic realization, we provide here a kinetic analysis. We show that robust perfect adaptation (homeostasis) is associated with a control species working under zero-order flux conditions while acting on another control species in the way of a “control of the controller”. There is an interesting and close analogy between the mechanisms shown here and mechanisms found in mammalian iron and calcium homeostasis, indicating that other homeostatic mechanisms may underlie similar control structures.

Computational methods

Rate equations were solved numerically by using the FORTRAN subroutine LSODE (Livermore Solver of Ordinary Differential Equations) (16) and MATLAB (www.mathworks.com). To make notations simpler, concentrations are denoted by their names without square brackets.

Results

Molecular representation of integral control

Fig. 2 a shows a simple scheme where a homeostatic-regulated intermediate A is being synthesized, transformed, and degraded. Rate constant k_pert indicates an environmental perturbation, such as a sudden increase in A. To avoid possible cell damage by excess of A, A has to be homeostatically regulated. A way to achieve this is to use an A-induced enzyme, E_adapt, which clears the cell for excess A. To make the homeostasis perfect, i.e., A adapts always to the same A_set value, the rate in the formation of E_adapt has to be proportional to the difference (i.e., the error) between A and its setpoint, A_set, as indicated by the following equations and shown in Fig. 2, a and b:

$$\frac{dA}{dt}=k_{\text{synth}}+k_{\text{pert}}-\frac{V_{\text{max}}^{E_{\text{tr}}}A}{K_{\mathrm{M}}^{E_{\text{tr}}}+A}-\frac{V_{\text{max}}^{E_{\text{adapt}}}A}{K_{\mathrm{M}}^{E_{\text{adapt}}}+A},$$ (1)

$$\frac{d{E}_{\text{adapt}}}{dt}=k_{\text{adapt}}\left(A-A_{\text{set}}\right)\text{.}$$ (2)

Figure 2.

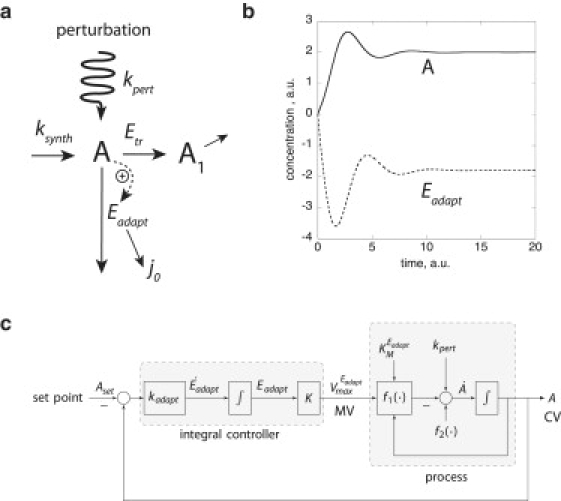
(a) Reaction scheme of system with rate Eqs. 1 and 2. Species A is formed by a zero-order process with rate constant k_synth and then transformed to the product A₁. Rate constant k_pert is related to a perturbing process (wavy line), which increases the level of A. To remove excess A, A is forming enzyme species E_adapt, which removes A with the flux $V_{\text{max}}^{E_{\text{adapt}}}A/\left(K_{\mathrm{M}}^{E_{\text{adapt}}}+A\right)$ (indicated by the vertical arrow). To get robust adaptation in A independent of k_pert, E_adapt is removed through a zero-order flux j₀ = k_adaptA_set. (b) Calculation showing that negative E_adapt concentrations may arise when A_set is regarded as a fixed setpoint. Initial concentrations of A and E_adapt are zero; k_adapt = 5, k_pert = k_synth = 0.5, $V_{\text{max}}^{E_{\text{adapt}}}=1$, $K_{\mathrm{M}}^{E_{\text{adapt}}}$ = 1, $V_{\text{max}}^{E_{\text{tr}}}$ = 110, $K_{\mathrm{M}}^{E_{\text{tr}}}$ = 100, and A_set = 2. Concentration and timescales are in arbitrary units (a.u.). (c) Scheme of the adaptive process shown in panel a containing the setpoint A_set, the integral controller and the process units. The controlled variable (CV) is A. Eqs. 1 and 2 are written as dA/dt = f₂(·) – f₁(·) + k_pert, dE_adapt/dt = k_adapt(A – A_set), respectively, with $f_1(·)=V_{\text{max}}^{E_{\text{adapt}}}A/\left(K_{\mathrm{M}}^{E_{\text{adapt}}}+A\right)$, $f_2(·)=k_{\text{synth}}-V_{\text{max}}^{E_{\text{tr}}}A/\left(K_{\mathrm{M}}^{E_{\text{tr}}}+A\right)$, and $V_{\text{max}}^{E_{\text{adapt}}}$ = K · E_adapt. K is the turnover number for E_adapt, i.e., $K=k_{\text{cat}}^{E_{\text{adapt}}}$. MV: manipulated variable.

However, writing the rate of formation of E_adapt in proportion to the error (A – A_set) (Eqs. 1 and 2, and Fig. 2 c) does still lack a molecular understanding of how the setpoint A_set is determined. In addition, treating the setpoint A_set as a fixed parameter can lead to the problem that, for certain parameter values, concentrations in E_adapt may become negative (Fig. 2 b).

To avoid negative concentrations, the zero-order term in Eq. 2, j₀ = k_adaptA_set, has to be replaced in a kinetically plausible way. A possibility is the removal of E_adapt by an additional controller/enzymatic species (E_set) working at zero-order conditions. In this case, the set-value A_set is then determined by E_set's maximum velocity, $V_{\text{max}}^{E_{\text{set}}}$, divided by the A-induced influx rate, which generates E_adapt (Eq. 3). Fig. 3 shows two representations of this mechanism with robust perfect adaptation/homeostasis in A avoiding any negative concentrations. In Fig. 3 a, a fully expanded Michaelis-Menten mechanism is shown, whereas in Fig. 3 b the mechanism is formulated in terms of steady-state or rapid equilibrium assumptions for the individual enzymatic steps. The kinetic equations with rate constants are given in the Appendix. For both cases, the setpoint in A is given by

$$A_{\text{set}}=\frac{{\text{V}}_{\text{max}}^{E_{\text{set}}}}{k_{\text{adapt}}}=\frac{k_{\text{cat}}^{E_{\text{set}}}{E}_{\text{set}}^{\text{tot}}}{k_{\text{adapt}}},$$ (3)

where $E_{\text{set}}^{\text{tot}}$ is the total concentration of enzyme E_set. Keeping A_set fixed, the mechanism shows robust homeostasis in A even when rate constants of the three enzymatic pathways (Fig. 3 a) are varied by over six orders of magnitude! Fig. 4 shows the A-homeostasis for the scheme shown in Fig. 3 a, using several perturbing and initial conditions (for details, see Appendix and Fig. 3 legend). Fig. 4 a shows the homeostasis in A when k_pert is increased from 0.0 to 1.0 a.u. In Fig. 4 b, a large positive excursion in A is observed when k_pert is increased from 1.0 to 1 × 10³ a.u., which is accompanied by an increased relaxation time in A for reaching A_set. Negative excursions in A are observed when k_pert is decreased. This is illustrated in Fig. 4 c when k_pert is decreased from 1.0 to 1 × 10⁻³ a.u.

Figure 3.

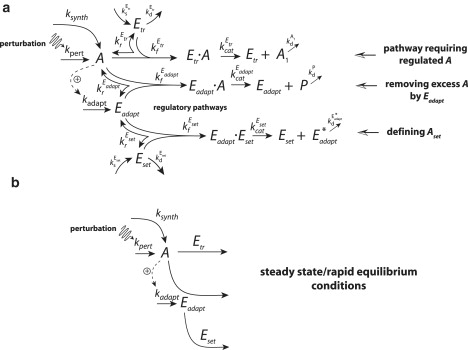
To avoid negative concentrations in E_adapt, j₀ (Fig. 2a) is represented as an enzymatic zero-order process. (a) Fully expanded Michaelis-Menten mechanism. The rate equations together with rate constants are shown in the Appendix. To obtain robust homeostasis in A, E_set removes active E_adapt into an inactive form E_adapt^∗ under zero-order conditions with A_set given by Eq. 3. (b) Same mechanism as in panel a, but formulating the Michaelis-Menten mechanism under steady-state/rapid equilibrium conditions. Rate equations are given in the Appendix. A zip-archive containing MATLAB and Berkeley Madonna versions of the model shown in Fig. 3 A with instructions and annotation available in the Supporting Material.

Figure 4.

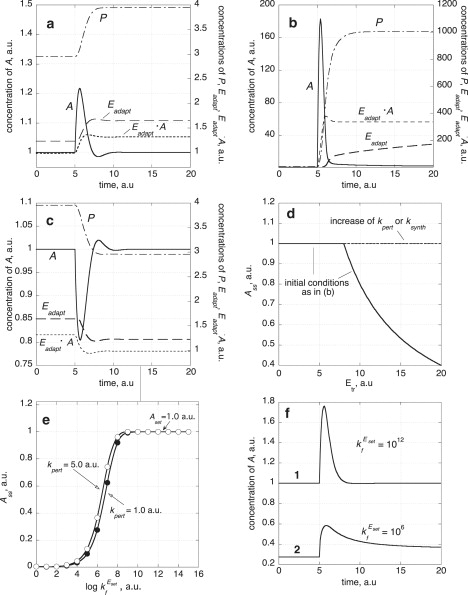
Robust perfect adaptation in A with A_set = 1.0. (a) Model described in Fig. 3a with rate constants as given in the Appendix. At t = 5.0 time units, k_pert is increased from 0.0 to 1.0. (b) Initial conditions as given in the Appendix with k_pert = 1.0. At t = 5.0 time units, k_pert is increased from 1.0 to 10³ a.u. (c) Initial conditions as in panel b. At t = 5.0 time units, k_pert is decreased from 1.0 to 10⁻³ a.u. (d) Same initial conditions as in panel b, but E_tr is successively increased leading eventually to the breakdown in homeostasis indicated by the decreasing A_ss values. This breakdown can be opposed to a certain degree by increasing the values of k_pert or k_synth. In the figure, k_pert or k_synth were increased from their original values 1.0 and 3.0 to 10.0 and 12.0, respectively, thereby extending the homeostasis to larger E_tr values (dashed line). However, at higher E_tr concentrations the homeostasis fails again with decreasing A_ss values (data not shown). (e) Calculated A_ss values for varying $\log k_{\mathrm{f}}^{E_{\text{set}}}$ with k_synth = 3.0 a.u. and k_pert = 1.0 a.u. (solid circles), or with k_synth = 3.0 a.u. and k_pert = 5.0 a.u. (open circles). For $k_{\mathrm{f}}^{E_{\text{set}}}$ < 10⁹ a.u., perfect homeostasis in A is lost (indicated by the condition that A_ss < A_set), because for decreasing $k_{\mathrm{f}}^{E_{\text{set}}}$ the $K_{\mathrm{M}}^{E_{\text{set}}}=\left(k_{\text{cat}}^{E_{\text{set}}}+k_{\mathrm{r}}^{E_{\text{set}}}\right)/k_{\mathrm{f}}^{E_{\text{set}}}$ associated with the removal of E_adapt by E_set increases, which eventually leads to the loss of the zero-order kinetics in the E_adapt degradation. (f) Time profiles in A with two different $k_{\mathrm{f}}^{E_{\text{set}}}$ values. At t = 5.0 time units, k_pert is increased from 1.0 to 5.0 a.u. 1 = Perfect homeostasis in A for $k_{\mathrm{f}}^{E_{\text{set}}}$ = 10¹² a.u.; 2 = Loss of perfect homeostasis in A when $k_{\mathrm{f}}^{E_{\text{set}}}$ = 10⁶ a.u., which is due to the loss of zero-order kinetics in the degradation of E_adapt.

However, due to the introduction of enzymatic zero-order kinetics (for avoiding negative concentrations in E_adapt), both mechanisms in Fig. 3 show homeostasis only for perturbations, which result in increased or moderate decreased levels in A. When a perturbation removes A too quickly, then the homeostasis in A breaks down. We therefore call this type of homeostatic control for inflow-homeostatic control. In Fig. 4 d such a breakdown in A-homeostasis is illustrated by the A steady-state level (A_ss) in relation to the (total) concentration of the A-removing enzyme E_tr. When the removal rate in A becomes greater than the total production rate (k_synth + k_pert), A_ss decreases below A_set and homeostasis in A is lost. This type of homeostatic failure can be avoided by using controllers, which specifically address the removal of A (outflow-homeostasis). A mechanism for calcium homeostasis under outflow conditions (hypocalcemia) was recently suggested by El-Samad et al. (15), but in this mechanism, the problem of zero-order fluxes and their association with negative concentrations was not addressed. Specific examples of other inflow and outflow homeostatic mechanisms are discussed below. Fig. 4 e illustrates the breakdown in A-homeostasis when the kinetics in the removal of E_adapt by E_set is no longer zero-order. For sufficiently large $k_{\mathrm{f}}^{E_{\text{set}}}$ values, the $K_{\mathrm{M}}^{E_{\text{set}}}$ becomes much lower than E_adapt, ensuring zero-order kinetics in the removal of E_adapt and leading to A_ss values which are equal to A_set. For lower $k_{\mathrm{f}}^{E_{\text{set}}}$ values, the $K_{\mathrm{M}}^{E_{\text{set}}}$ increases and the zero-order kinetics in the removal of E_adapt are eventually lost leading to A_ss values lower than A_set and to the loss in the homeostasis of A. As shown in Fig. 4 e, the A_ss values under non-zero-order conditions also depend on k_pert. In Fig. 4 f, two A-time profiles are shown for two perturbations, one applied for zero-order conditions ($k_{\mathrm{f}}^{E_{\text{set}}}={10}^{12}$, upper curve), and the other for non-zero-order conditions ($k_{\mathrm{f}}^{E_{\text{set}}}={10}^6$, lower curve). In both cases, k_pert is increased from 1.0 to 5.0 a.u. at t = 5.0 a.u. Clearly, zero-order kinetics in the removal of E_adapt is required to ensure robust homeostasis in A.

Robust perfect temperature compensation

Temperature is an important environmental parameter, which influences each reaction step in a reaction kinetic network. Van 't Hoff's rule states that the velocity of a chemical or biochemical process increases generally by a factor between 2 and 3 (the so-called Q₁₀) when the temperature is increased by 10°C. A Q₁₀ of 2 corresponds to an activation energy of ∼50 kJ/mol (17). In general, the concentration of a chemical component, a flux within a kinetic network, or the period length of an oscillatory network, can show temperature compensation/adaptation near a given reference temperature, T_ref, when the following balancing equation, here written for the concentration in A, is satisfied (18–21):

$$\frac{d\text{ln}A}{dT}=\frac{1}{R{T}^2}\sum _{\mathrm{i}}{C}_{k_{\mathrm{i}}}^{\mathrm{A}}{E}_{\mathrm{i}}\text{.}$$ (4)

Here $C_{k_{\mathrm{i}}}^A=\frac{\partial \text{ln}A}{\partial \text{ln}{k}_{\mathrm{i}}}$ is the control coefficient (22,23) describing how sensitive concentration A is with respect to variations to the network's rate constants k_i. The values R, T, and E_i describe the gas constant, the temperature (in Kelvin), and activation energy (in J/mol) of the process indexed by i, respectively. The balancing equation (Eq. 4) requires a fine-tuning between the control coefficients and activation energies. In general, the resulting temperature compensation in A is not robust, i.e., temperature compensation is only observed within a local region around T_ref (see, for example, (24)). Considering the network in Fig. 3, we have 21 rate constants with associated activation energies, and in general, temperature compensation in A is given by Eq. 4 including all 21 terms.

However, this situation changes dramatically when one assumes that E_adapt is removed by E_set under saturating (zero-order kinetics) conditions and that E_set's turnover is negligible compared to the other fluxes associated with E_set. In this case, most of the control coefficients become zero, except for two, which are related to the rate constants k_adapt and $k_{\text{cat}}^{E_{\text{set}}}$. Together with the concentration of E_set, k_adapt and $k_{\text{cat}}^{E_{\text{set}}}$ define the setpoint for A (Eq. 3). Due to the concentration summation theorem (22,25,26),

$$\sum _{\mathrm{i}}{C}_{k_{\mathrm{i}}}^{\mathrm{A}}=0\text{.}$$ (5)

$C_{k_{\text{adapt}}}^{\mathrm{A}}$ and $C_{k_{\text{cat}}^{E_{\text{set}}}}^{\mathrm{A}}$ have the same magnitude but opposite signs. This indicates that the network can show robust temperature compensation in the level of A when the activation energies for k_adapt and $k_{\text{cat}}^{E_{\text{set}}}$ are equal. In fact, when all activation energies are equal, say each reaction step has an activation energy E_a, then all concentrations of the reaction intermediates in the network, I_j, become robust perfectly adapted, as seen by Eq. 6:

$$\frac{d\text{ln}{I}_{\mathrm{j}}}{dT}=\frac{1}{R{T}^2}\sum _{\mathrm{i}}{C}_{k_{\mathrm{i}}}^{I_{\mathrm{j}}}{E}_{\mathrm{a}}=\frac{E_{\mathrm{a}}}{R{T}^2}\sum _{\mathrm{i}}{C}_{k_{\mathrm{i}}}^{I_{\mathrm{j}}}=0\text{.}$$ (6)

Fig. 5, a and b, shows this situation for 5°C and 100°C. When activation energies are different (except for the activation energies of k_adapt and $k_{\text{cat}}^{E_{\text{set}}}$), then only A shows robust temperature compensation, whereas the concentrations of the other intermediates are no longer invariant. This is indicated in Fig. 5, c and d, for temperature changes between 5°C and 100°C.

Figure 5.

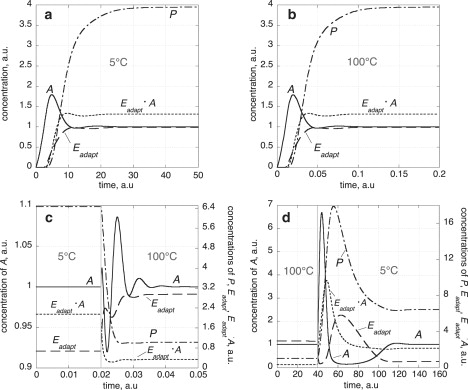
Robust perfect temperature compensation of the model described in Fig. 3a. Rate constants (Appendix) refer to 25°C with A_set = 1. (a) All activation energies are 50 kJ/mol and temperature is 5°C. (b) All activation energies are 50 kJ/mol and temperature is 100°C. Please note the much shorter timescale compared to panel a needed for the system to approach the same steady state. (c) Activation energies are as given in the Appendix. The system is initially at its steady state at 5°C. At 0.02 time units, the temperature is changed to 100°C showing perfect homeostasis only in A. (d) Activation energies as in panel c. The system is initially at its steady state at 100°C. At 40.0 time units the temperature is changed to 5°C showing perfect homeostasis only in A.

Discussion

Zero-order kinetics, integral feedback, and homeostatic breakdown

Integral feedback (14) or integral control (13) is a concept from control theory assuring that the output (the CV, Fig. 1) of a perturbed process is kept at a certain setpoint by integrating the associated error e such that e approaches zero (Fig. 1).

To keep the level of A homeostatic-regulated by integral control/feedback, the rate of formation of an additional species (E_adapt) has to be linked to the error, integrated, and then fed into the production rate of A. Integrated A is subtracted from A_set and the error e is recalculated (Fig. 2 c). Essential for this approach is the definition of the error e through Eq. 2, which provides the actual condition that A approaches A_set when the system's steady state is reached. Critically in this respect is the kinetic interpretation of the term k_adaptA_set. To avoid unrealistic situations such as negative concentrations (Fig. 2 b), the zero-order flux needs to be put into a proper mechanistic perspective. To achieve this, the mechanism shown in Fig. 3 includes an additional enzymatic species (E_set) leading to zero-order degradation/inactivation in E_adapt. This step is essential to obtain robust homeostasis. It requires that the level of E_set is kept constant and that the ratio between k_adapt and $k_{\text{cat}}^{E_{\text{set}}}$ remains unchanged. The latter condition is similar to that found by Levchenko and Iglesias for a model of eukaryotic chemotaxis (27) and a model by Ingalls et al. for a fast excitation-slow inhibition mechanism (Fig. 12.7 in (28)), where activation and inhibition steps are simultaneously activated by a common environmental signal. It may be noted that such a control is, principally, still based on balancing. In our model (Fig. 3 a), the balancing between 21 components has been effectively reduced to three parameters, as indicated by Eq. 3.

Interestingly, the kinetic restriction that concentrations must be positive leads to the breakdown of homeostasis for the mechanism in Fig. 3 at high removal/outflow rates in A. Whereas the homeostasis in Fig. 2 is robust for both high inflow and high outflow rates in A (leading sometimes to unrealistic negative concentrations in E_adapt), the chemically realistic mechanism shown in Fig. 3 works only for (high) inflow and moderate outflow rates in A. To address the situation of A-homeostasis at higher outflow rates (outflow-homeostasis), another homeostatic mechanism is necessary. Fig. 6 shows four motifs of homeostatic control mechanisms, two addressing inflow-homeostasis (Fig. 6, a and b) and two addressing outflow-homeostasis (Fig. 6, c and d). Each of these mechanisms work properly when the perturbing inflow and outflow conditions in A match their appropriate working conditions, but will fail otherwise, i.e., when total outflow in A becomes too large for an inflow-homeostatic controller or when total inflow in A becomes too large in an outflow-homeostatic controller. Thus, biochemical homeostasis will, in general, require at least two types of mechanisms, i.e., one addressing inflow-homeostasis and another addressing outflow-homeostasis.

Figure 6.

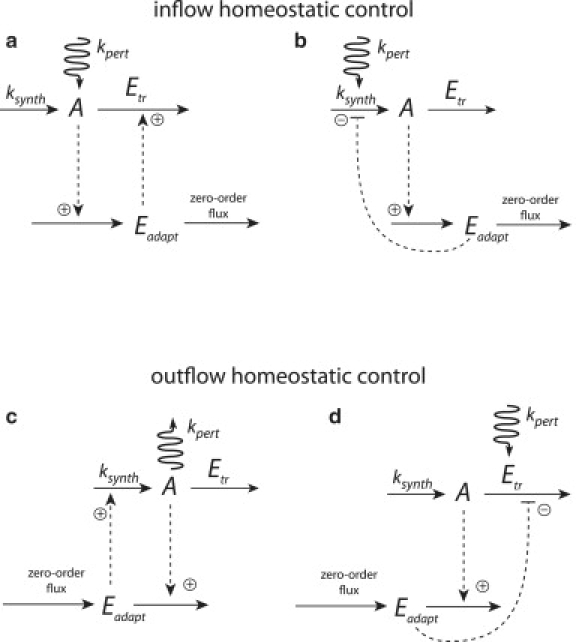
Homeostatic control motifs. Due to the kinetic restriction that concentrations need to be positive, two classes of homeostatic controllers arise: 1), inflow homeostatic controllers leading to homeostasis in the concentration of A for increasing (and moderate decreasing) perturbations in A (panels a and b); and 2), outflow homeostatic controllers leading to homeostasis in A for decreasing (and moderate increasing) perturbations in A (panels c and d). Rate equations with example parameter values are given in the Appendix. Note that many of the parameter values may be changed within certain limits (besides changing k_pert) without affecting the homeostasis. (a) Schematic representation of the two (inflow) homeostatic models shown in Fig. 3. Robust homeostasis is due to the zero-order kinetic removal of E_adapt. (b) Inflow homeostatic model where E_adapt inhibits the inflow of A through k_synth. To maintain homeostasis the perturbation needs to be applied to the same reaction channel as k_synth. The integral feedback is due to the zero-order removal of E_adapt and is not related to the physico-chemical negative feedback from E_adapt to (k_synth + k_pert). (c) Outflow homeostatic controller by removing E_adapt through A. (d) Outflow homeostatic controller by inhibiting E_tr through E_adapt. Similar to panel b, homeostasis is obtained when the perturbation increases the outflow of A through the same reaction channel that is used by enzyme E_tr.

Fig. 6 a shows an outline of the inflow-control mechanisms described in Fig. 3. The inflow-control mechanism in Fig. 6 b shows a related scheme suggested by Yi et al., including a zero order reaction step (14), where instead of the increased removal of A the formation of A is inhibited by a molecular feedback loop.

Fig. 6 c shows an outflow-homeostatic mechanisms closely related to the scheme by El-Samad et al. (15), but avoiding negative concentrations, as shown in their Fig. 8. In our Fig. 6 d, outflow homeostatic control is achieved by inhibiting the outflow of A through E_adapt. In the Appendix we show kinetic representations of these four mechanisms.

Robust perfect adaptation can be related to the concept of integral control or integral feedback (13,14), which involves a negative feedback in the control-theoretic formulation of the system as indicated in Fig. 1 or Fig. 2 c. Although some schemes, as in Fig. 6, b and d, or in the literature (14,29), contain molecular feedback inhibitions (molecular negative feedbacks), the presence of robust perfect adaptation, i.e., the behavior of a control-theoretic negative feedback, does not necessarily require molecular negative feedbacks. An example of robust perfect adaptation with integral feedback behavior but without molecular feedback loops is given by a consecutive reaction such as → A → B →, where B (or the flux forming B) can show robust perfect adaptation for any stepwise change in the rate constant forming intermediate B (11,30,31), as long as A is formed by zero-order kinetics. Thus, the essential part to get robust homeostasis in the mechanisms shown in Fig. 6, and as illustrated in Fig. 4, e and f, is the presence of the zero-order kinetic term (i.e., “control of the controller”).

Possible regulation points in homeostatic mechanisms

Iron homeostasis

Iron is an essential element for all mammalian cells, but gets toxic when in excess. Special transport and regulatory processes are therefore needed to ensure iron homeostasis within the organism as a whole as well as in individual cells (32). Ferroportin (33) and hepcidin (34) have been suggested to be two key players in iron homeostasis. Ferroportin is an iron exporter, which transports iron from cells such as macrophages or intestinal or liver cells into the blood plasma. Hepcidin, a liver-produced hormone, is a negative regulator of iron absorption with antimicrobial properties, which itself is under homeostatic regulation. An interesting regulatory aspect, which relates to the models in Fig. 3, is that hepcidin binds to ferroportin and leads to its degradation in a similar way as E_set removes E_adapt. Considering the interaction between ferroportin and hepcidin, the mechanism in Fig. 3 suggests that under iron inflow conditions, hepcidin may serve as a setpoint controller for cell-internal iron concentrations with ferroportin having the role as E_adapt, i.e., removing iron (A) out of the cell. The binding between ferroportin (E_adapt) and hepcidin (E_set), which leads to the degradation of ferroportin (E_adapt) (34), may thus provide a mechanism of how hepcidin acts as a “control of the controller” and leads to potential robust homeostasis. Hepcidin works at concentrations as low as 10 nM (34) and can efficiently reduce upregulated ferroportin levels when iron influx into the cell is high (35). It is not known whether the removal of ferroportin by hepcidin at normal iron concentrations is a zero-order process.

Calcium homeostasis

Fig. 7 shows a scheme of calcium homeostasis in humans. Calcitonin (CT), parathyroid hormone (PTH), and the active form of vitamin D (calcitriol) are important (but not the only) factors involved in the regulation of Ca²⁺ and bone metabolism (36). PTH increases bone resorption and plasma Ca²⁺ levels. Calcitriol increases intestinal Ca²⁺ absorption, bone resorption, and plasma Ca²⁺. Calcitonin (CT) decreases bone resorption and plasma Ca²⁺. CaSR denotes the calcium-sensing receptor in the nephron, which appears to mediate effects of hypercalcemia on calcium excretion (37). In case of low calcium levels or when the outflow of calcium needs to be compensated for, an outflow-control mechanism like that indicated in Fig. 6 c may come into play. The mechanism is similar to that suggested by El-Samad et al. (15) for hypocalcemia. In this mechanism, E_adapt plays the role of PTH. The level of PTH is decreased by increased calcium levels. Robust calcium homeostasis is obtained due to a zero kinetic formation rate of E_adapt (PTH) and its downregulation by calcium. In the case of high calcium levels, an inflow-control mechanism like that shown in Fig. 6 a appears to be operative. High calcium (A) levels activate CT and CaSR, which are responsible for the removal of plasma calcium by transporting it into the bone and/or by excretion through the urine. Homeostatic control may be achieved by zero-order kinetic inactivation of CT and/or CaSR.

Figure 7.

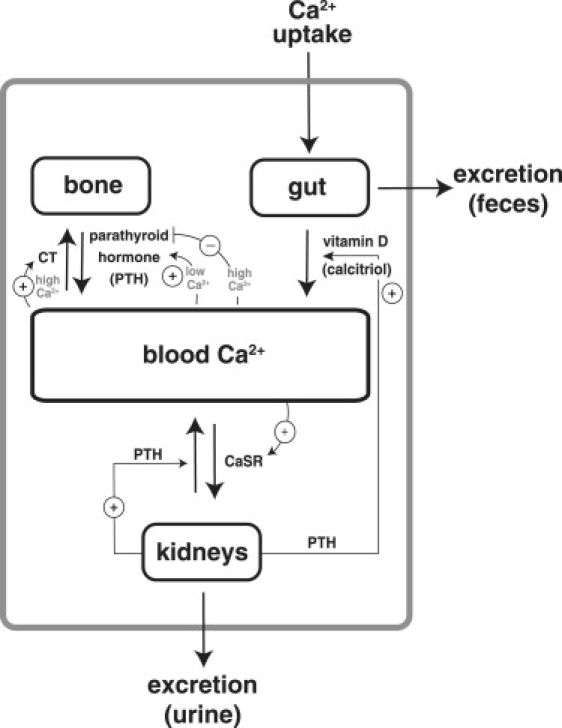
Schematic representation of blood calcium homeostasis in humans. Important regulators are parathyroid hormone (PTH), calcitonin (CT), vitamin D, and the calcium-sensing receptor in the nephron. For a discussion of how these regulators may participate in inflow- and outflow mechanisms, see main text.

Robust temperature compensation

It is interesting that the occurrence of robust (activation-energy-independent) temperature compensation for a certain intermediate is closely associated with a robust homeostatic control of that intermediate. This indicates that calcium, iron, and other homeostatic mechanisms may be capable of showing temperature compensation. Unfortunately, there have been few studies in this direction. Herrera et al. (38) studied the temperature dependence of calcium homeostasis in rat pachytene spermatocytes and rat round spermatids in suspension without external calcium concentration. The pachytene spermatocytes showed practically unchanged calcium levels at 10 nmol/L when the temperature was varied (increased) between 16°C and 33°C. Above 33°C, the internal calcium levels quickly increased, reaching levels at 120 nmol/L at 40°C. In the rat round spermatids, the internal calcium levels did not show any temperature compensation, but a monotonic increase from 30 nmol/L to ∼150 nmol/L was observed when the temperature was varied from 5°C to 40°C. Interestingly, the temperature compensation in the calcium homeostasis in the pachytene spermatocytes appears to be due to a balance between two opposing reactions, i.e., between uptake and leakage to and from the cell's internal calcium stores, with determined activation energies of 62 kJ/mol and 55 kJ/mol, respectively.

Although robust homeostatic and adaptation mechanisms appear to be attractive concepts, it is still unclear to what extent temperature compensation (of oscillatory or nonoscillatory processes) is due to a balancing between individual reaction steps (18,21) or due to mechanisms as outlined in Fig. 5, where the balancing is reduced to a few parameters (39). Characteristic to all physiological and chemical temperature compensated systems (20,24,38,40–48) is that the compensation mechanism operates at a local (for the organism) important temperature range and not globally over the whole temperature range such as shown in Fig. 5. However, this does not necessarily invalidate homeostatic control structures as those shown in Figs. 3 and 6. The controllers (for example, E_adapt and E_set) have to be seen in the context of the dynamics of the whole cell and the whole organism (2), a systems (biology) perspective (49–51), where the controllers themselves are controlled and influenced by factors important for other cellular purposes.

Appendix

Rate equations, rate constants, and activation energies for the mechanism in Fig. 3a.

Rate equations

$$\frac{dA}{dt}=k_{\text{pert}}+k_{\text{synth}}-k_{\mathrm{f}}^{E_{\text{tr}}}A{E}_{\text{tr}}-k_{\mathrm{f}}^{E_{\text{adapt}}}A{E}_{\text{adapt}}+k_{\mathrm{r}}^{E_{\text{adapt}}}\left(E_{\text{adapt}}·A\right)+k_{\mathrm{r}}^{E_{\text{tr}}}\left(E_{\text{tr}}·A\right)$$ (7)

$$\frac{d{E}_{\text{adapt}}}{dt}=k_{\text{adapt}}A-k_{\mathrm{f}}^{E_{\text{adapt}}}A{E}_{\text{adapt}}+\left(k_{\text{cat}}^{E_{\text{adapt}}}+k_{\mathrm{r}}^{E_{\text{adapt}}}\right)\left(E_{\text{adapt}}·A\right)-k_{\mathrm{f}}^{E_{\text{set}}}{E}_{\text{set}}{E}_{\text{adapt}}+k_{\mathrm{r}}^{E_{\text{set}}}\left(E_{\text{adapt}}·E_{\text{set}}\right),$$ (8)

$$\frac{d\left(E_{\text{adapt}}·A\right)}{dt}=k_{\mathrm{f}}^{E_{\text{adapt}}}A{E}_{\text{adapt}}-\left(k_{\text{cat}}^{E_{\text{adapt}}}+k_{\mathrm{r}}^{E_{\text{adapt}}}\right)\left(E_{\text{adapt}}·A\right),$$ (9)

$$\frac{dP}{dt}=k_{\text{cat}}^{E_{\text{adapt}}}\left(E_{\text{adapt}}·A\right)-k_{\mathrm{d}}^{\mathrm{P}}P,$$ (10)

$$\frac{d{E}_{\text{set}}}{dt}=k_{\text{s}}^{E_{\text{set}}}-k_{\mathrm{f}}^{E_{\text{set}}}{E}_{\text{set}}{E}_{\text{adapt}}+\left(k_{\mathrm{r}}^{E_{\text{set}}}+k_{\text{cat}}^{E_{\text{set}}}\right)\left(E_{\text{adapt}}·E_{\text{set}}\right)-k_{\mathrm{d}}^{E_{\text{set}}}{E}_{\text{set}},$$ (11)

$$\frac{d\left(E_{\text{adapt}}·E_{\text{set}}\right)}{dt}=k_{\mathrm{f}}^{E_{\text{set}}}{E}_{\text{set}}{E}_{\text{adapt}}-\left(k_{\mathrm{r}}^{E_{\text{set}}}+k_{\text{cat}}^{E_{\text{set}}}\right)\left(E_{\text{adapt}}·E_{\text{set}}\right),$$ (12)

$$\frac{d{E}_{\text{adapt}}^{\ast }}{dt}=k_{\text{cat}}^{E_{\text{set}}}\left(E_{\text{adapt}}·E_{\text{set}}\right)-k_{\mathrm{d}}^{E_{\text{adapt}}^{\ast }}{E}_{\text{adapt}}^{\ast },$$ (13)

$$\frac{d{E}_{\text{tr}}}{dt}=k_{\text{s}}^{E_{\text{tr}}}-k_{\mathrm{d}}^{E_{\text{tr}}}{E}_{\text{tr}}-k_{\mathrm{f}}^{E_{\text{tr}}}A{E}_{\text{tr}}+\left(k_{\mathrm{r}}^{E_{\text{tr}}}+k_{\text{cat}}^{E_{\text{tr}}}\right)\left(E_{\text{tr}}·A\right),$$ (14)

$$\frac{d\left(E_{\text{tr}}·A\right)}{dt}=k_{\mathrm{f}}^{E_{\text{tr}}}A{E}_{\text{tr}}-\left(k_{\mathrm{r}}^{E_{\text{tr}}}+k_{\text{cat}}^{E_{\text{tr}}}\right)\left(E_{\text{tr}}·A\right),$$ (15)

$$\frac{d{A}_1}{dt}=k_{\text{cat}}^{E_{\text{tr}}}\left(E_{\text{tr}}·A\right)-k_{\mathrm{d}}^{A_{\text{1}}}{A}_1\text{.}$$ (16)

Rate constants with activation energies

The following rate constants and activation energies (given in parenthesis) have been used unless otherwise stated in the text. Rate constant values refer to 25°C. The Arrhenius equation k_i = A_i·exp(−E_i/(RT)) has been used to calculate the rate constant k_i at other temperatures (A_i: preexponential factor, assumed to be temperature-independent; E_i, activation energy; R, gas constant; and T, temperature in Kelvin). All rate constants are given in arbitrary units (a.u.):

$$k_{\text{pert}}\ge 0\left(70\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{f}}^{{\mathit{E}}_{\text{adapt}}}=4.0\left(50\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{r}}^{{\mathit{E}}_{\text{adapt}}}=2.0\left(40\mathrm{kJ}/\text{mol}\right);$$

$$k_{\text{cat}}^{{\mathit{E}}_{\text{adapt}}}=3.0\left(80\mathrm{kJ}/\text{mol}\right);$$

$$k_{\text{adapt}}=3.0\left(90\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{d}}^{\mathrm{P}}=1.0\left(80\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{s}}^{E_{\text{set}}}=1.0e-13\left(70\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{d}}^{E_{\text{set}}}=1.0e-7\left(50\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{f}}^{E_{\text{set}}}=1.0e+11\left(70\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{r}}^{E_{\text{set}}}=1.0e+7\left(60\mathrm{kJ}/\text{mol}\right);$$

$$k_{\text{cat}}^{E_{\text{set}}}=6.0e+6\left(90\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{d}}^{E_{\text{adapt}}^{\ast }}=1.0\left(30\mathrm{kJ}/\text{mol}\right);$$

$$k_{\text{synth}}=3.0\left(40\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{f}}^{E_{\text{tr}}}=1.0\left(50\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{r}}^{E_{\text{tr}}}=5.0\left(60\mathrm{kJ}/\text{mol}\right);$$

$$k_{\text{cat}}^{E_{\text{tr}}}=5.0\left(50\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{d}}^{A_{\text{1}}}=1.0\left(40\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{s}}^{E_{\text{tr}}}=1.0\left(50\mathrm{kJ}/\text{mol}\right);$$

$$k_{\mathrm{d}}^{E_{\text{tr}}}=10.0\left(70\mathrm{kJ}/\text{mol}\right)\text{.}$$

Rate equations for the mechanism in Fig. 3b/Fig. 6a

$$\frac{dA}{dt}=k_{\text{pert}}+k_{\text{synth}}-\frac{V_{\text{max}}^{E_{\text{adapt}}}A}{K_{\mathrm{M}}^{E_{\text{adapt}}}+A}-\frac{V_{\text{max}}^{E_{\text{tr}}}A}{K_{\mathrm{M}}^{E_{\text{tr}}}+A},$$ (17)

$$\frac{d{E}_{\text{adapt}}}{dt}=k_{\text{adapt}}A-\frac{V_{\text{max}}^{E_{\text{set}}}{E}_{\text{adapt}}}{K_{\mathrm{M}}^{E_{\text{set}}}+E_{\text{adapt}}}\text{.}$$ (18)

The following rate constants and initial concentrations give perfect homeostasis with A_set = 1.0, k_synth = 1.0, and k_pert ≥ 0: $k_{\text{cat}}^{E_{\text{adapt}}}$ = 1.0; $K_{\mathrm{M}}^{E_{\text{adapt}}}$ = 2.0; k_adapt = 3.0; $k_{\text{cat}}^{E_{\text{set}}}$ = 6.0e+6; $K_{\mathrm{M}}^{E_{\text{set}}}$ = 1.0e−6; $k_{\text{cat}}^{E_{\text{tr}}}$ = 0.01; and $K_{\mathrm{M}}^{E_{\text{tr}}}$ = 5.0, where $V_{\text{max}}^{E_{\text{adapt}}}=k_{\text{cat}}^{E_{\text{adapt}}}·E_{\text{adapt}}^{\text{tot}}$; $V_{\text{max}}^{E_{\text{tr}}}=k_{\text{cat}}^{E_{\text{tr}}}·E_{\text{tr}}^{\text{tot}}$; and $V_{\text{max}}^{E_{\text{set}}}=k_{\text{cat}}^{E_{\text{set}}}·E_{\text{set}}^{\text{tot}}$.

Initial concentrations: A = 1.0; E_adapt = 0.01; $E_{\text{set}}^{\text{tot}}$ = 5.0e−7; and $E_{\text{tr}}^{\text{tot}}$ = 0.1. Concentrations of $E_{\text{tr}}^{\text{tot}}$ and $E_{\text{set}}^{\text{tot}}$ are kept constant.

Rate equations for the mechanism in Fig. 6b

$$\frac{dA}{dt}=\frac{\left(k_{\text{synth}}+k_{\text{pert}}\right)}{\left(K_{\mathrm{I}}^{E_{\text{adapt}}}+E_{\text{adapt}}\right)}-\frac{V_{\text{max}}^{E_{\text{tr}}}A}{\left(K_{\mathrm{M}}^{E_{\text{tr}}}+A\right)}\text{,}$$ (19)

$$\frac{d{E}_{\text{adapt}}}{dt}=k_{\text{adapt}}A-\frac{V_{\text{max}}^{E_{\text{set}}}{E}_{\text{adapt}}}{\left(K_{\mathrm{M}}^{E_{\text{set}}}+E_{\text{adapt}}\right)}\text{.}$$ (20)

The following rate constants with zero initial concentrations (both a.u.) give perfect homeostasis in A with A_set = 1.0, when varying k_pert (≥0): k_synth = 10.0; $K_{\mathrm{I}}^{E_{\text{adapt}}}$ = 0.1; $V_{\text{max}}^{E_{\text{tr}}}$ = 40; $K_{\mathrm{M}}^{E_{\text{tr}}}$ = 1.0; k_adapt = 1.0; $V_{\text{max}}^{E_{\text{set}}}$ = 1.0; and $K_{\mathrm{M}}^{E_{\text{set}}}$ = 1.0e−6.

Rate equations for the mechanism in Fig. 6c

$$\frac{dA}{dt}=k_{\text{synth}}+k{E}_{\text{adapt}}-k_{\text{pert}}A-\frac{V_{\text{max}}^{E_{\text{tr}}}A}{\left(K_{\mathrm{M}}^{E_{\text{tr}}}+A\right)},$$ (21)

$$\frac{d{E}_{\text{adapt}}}{dt}=j_0-\frac{V_{\text{max}}^{E_{\text{set}}}{E}_{\text{adapt}}A}{\left(K_{\mathrm{M}}^{E_{\text{set}}}+E_{\text{adapt}}\right)}\text{.}$$ (22)

The following rate constants with zero initial concentrations (both a.u.) give perfect homeostasis in A with A_set = 1.0 when varying k_pert (≥0.1): k_synth = 1.0; k = 1.0; and $V_{\text{max}}^{E_{\text{tr}}}$ = 1; $K_{\mathrm{M}}^{E_{\text{tr}}}$ = 0.1; zero-order flux j₀ = 1.0; $V_{\text{max}}^{E_{\text{set}}}$ = 1.0; and $K_{\mathrm{M}}^{E_{\text{set}}}$ = 1.0e−6.

Rate equations for the mechanism in Fig. 6d

$$\frac{dA}{dt}=k_{\text{synth}}-\frac{\left(V_{\text{max}}^{E_{\text{tr}}}+k_{\text{pert}}\right)A}{\left(K_{\mathrm{M}}^{E_{\text{tr}}}+A\right)\left(K_{\mathrm{I}}^{E_{\text{adapt}}}+E_{\text{adapt}}\right)},$$ (23)

$$\frac{d{E}_{\text{adapt}}}{dt}=j_0-\frac{V_{\text{max}}^{E_{\text{set}}}{E}_{\text{adapt}}A}{\left(K_{\mathrm{M}}^{E_{\text{set}}}+E_{\text{adapt}}\right)}\text{.}$$ (24)

The following rate constants with zero initial concentrations (both a.u.) give perfect homeostasis in A with A_set = 1.0 when varying k_pert (≥0): k_synth = 1.0; $V_{\text{max}}^{E_{\text{tr}}}$ = 10; $K_{\mathrm{M}}^{E_{\text{tr}}}$ = 1.0; and $K_{\mathrm{I}}^{E_{\text{adapt}}}$ = 1.0; zero-order flux j₀ = 1.0; $V_{\text{max}}^{E_{\text{set}}}$ = 1.0; and $K_{\mathrm{M}}^{E_{\text{set}}}$ = 1.0e−6.

Supporting Material

Supporting Material files are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01166-7.