Sarcomere Mechanics in Capillary Endothelial Cells

Abstract

Tension generation in endothelial cells of the aorta, spleen, and eye occurs in actin stress fibers, and is necessary for normal cell function. Sarcomeres are the tension-generating units of actin stress fibers in endothelial cells. How sarcomeres generate and maintain tension in stress fibers is not well understood. Using femtosecond laser ablation, we severed living stress fibers and measured sarcomere contraction under zero tension. The length of the sarcomere decreased in two phases: an instantaneous initial response, followed by a slower change in length attributed to myosin activity. The latter phase ceased abruptly after a minimum sarcomere length was reached, suggesting a rigid resistance that prevents further contraction. Furthermore, severed, contracted stress fibers did not relax when treated with myosin inhibitors, indicating that contracted stress fibers do not store elastic potential energy. These novel measurements combined with modeling suggest that myosin-generated forces in adjacent sarcomeres are directly in balance, and argue against sarcomere models with springlike elements in parallel with myosin contractile elements. We propose a new model for tension generation in the sarcomere, which provides a mechanistic interpretation for our observations and previous observations of inhomogeneous sarcomere contraction and apparent stress fiber viscoelastic behavior.

Introduction

Tension generation inside cells and its transmission to the extracellular matrix at cell-matrix adhesions enables cells to adhere, spread, migrate, and maintain tissue form. Tension is generated in vascular endothelial cells by actomyosin stress fibers. While stress fibers are found in various cell types cultured in vitro, stress fibers in vivo are observed in endothelium of intact tissues such as the aorta (1), the spleen (2), and the eye (3). Tension in stress fibers promotes strong adhesion between endothelial cells and the basement membrane (2). This adhesion allows endothelial cells to resist blood flow-induced mechanical stresses including cyclic strain, hydrostatic pressure, and shear flow (1–6). Endothelial cells respond to applied mechanical stresses by changing their orientation in both tissue (4,5) and culture (6–9), which depends on remodeling of stress fibers (6). Thus, stress fibers are necessary for resisting and sensing mechanical stresses in vascular endothelial cells. Stress fiber tension is also greatly altered in tumor endothelial cells, which have an aberrant response to mechanical stresses (10). Stress fiber tension is implicated in abnormal endothelial response to altered hemodynamic forces that cause atherosclerotic plaques at vascular bifurcations (11). Owing to their key importance as a contractile structure that enables normal endothelial cell function, there is considerable recent interest in understanding the mechanical properties of stress fibers (12–15). However, it has remained a fundamental challenge to measure these properties in the context of a living, functioning cell.

Stress fibers are composed of repeating units termed sarcomeres after the analogous muscle structures (16–21). Using electron microscopy, Cramer et al. confirmed the sarcomeric microstructure of stress fibers in nonmotile PtK2 cells by showing that they contain actin filaments of alternating polarity along the entire length of the fiber (22). Tension is generated in the sarcomere by walking of bipolar myosin heads in opposite directions, resulting in contraction of the sarcomere ((2,23,24) and see Fig. 1 A for a schematic). Neighboring sarcomeres are connected by dense bodies containing α-actinin, filamin, and VASP (Fig. 1 B). Physical coupling between stress fibers and focal adhesions allows transfer of the tension to the substrate (25).

Figure 1.

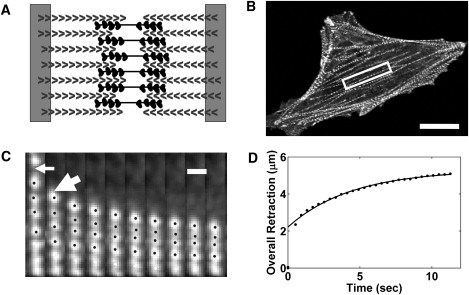
Sarcomeres contract in a severed fiber. (A) Schematic showing the structure of a sarcomere with dense bodies of actin-bundling proteins such as α-actinin marking the ends and polymerization-competent ends of actin filaments pointing inwards joined by bipolar myosin filaments. (B) An epifluorescence micrograph illustrating the punctate staining of EGFP-α-actinin in dense bodies of bovine capillary endothelial cell stress fibers (scale bar, 20 μm). (C) A kymograph showing the results for one-half of a severed fiber cut at the thin arrow. Notice that sarcomeres contract and that the contraction is not uniform in every sarcomere (thick arrow). (Scale bar, 1.4 μm; time between frames is 840 ms.) (D) The distance the severed edge moves follows an exponential form; the solid line is a least-squares regression fit of the retraction model (Eq. 11) to the data.

Recently proposed mechanical models for stress fiber sarcomeres (14,15) assume that velocity-dependent myosin contraction operates in parallel with an elastic element, analogous to the Kelvin-Voigt model (spring-and-dashpot in parallel) for viscoelasticity. A feature of these models is that expanded or compressed elastic elements partially balance the tension and account for the distribution of sarcomere sizes (14,15). These mechanical models have been used to explain the experimental observation of Peterson et al. (26) that sarcomeres contract near focal adhesions on activation of myosin light chain kinase (14,15). However, to date, no direct experimental evidence has been offered to test current mechanical models of stress fiber sarcomeres.

Although the majority of experimental data on stress fiber mechanics is from in vitro experiments of extracted stress fibers (12,27), a recent study used a femtosecond laser to sever individual stress fibers, allowing the first in vivo measurements of stress fiber mechanics (13). Cutting the fiber caused the severed ends to retract (see Fig. 1 C for an example). The retraction of the fiber exhibited an exponential relaxation characteristic of that following tension loss in a Kelvin-Voigt element (13), with a relaxation time constant of ∼6 s. Myosin inhibition completely eliminated retraction in severed stress fibers (13). Although this work pioneered a new approach to measure mechanics of stress fibers in living cells, it did not provide a mechanistic explanation for the observed mechanical response. For example, the molecular origin of the apparent viscosity of the fiber is unknown, and it is unclear whether the observed lack of retraction under myosin inhibition can be explained by existing sarcomere models. To explain this viscoelastic retraction of the severed ends, a recent model represented the stress fiber as a tensegrity structure containing tensed and compressed elements (28). However, this model did not involve a sarcomeric description of the stress fiber.

In this study, we used femtosecond laser ablation to sever individual fibers and directly measured sarcomere contraction by tracking the position of α-actinin-labeled dense bodies in the severed fiber. The lengths of individual sarcomeres decreased in two phases: an instantaneous initial decrease, followed by a linear contraction at constant speed. The latter phase, interpreted as active myosin-mediated contraction, ceased abruptly after a minimum sarcomere length was achieved. The linear response suggests that there is no increase in resisting force (for example, due to a spring element) during contraction. In addition, subsequent inhibition of myosin after severing and contraction yielded no elastic recovery, suggesting that elastic potential energy is not stored in the contracted fiber. Together, these observations argue against models that have elastic elements in parallel with myosin contractile elements. Based on these findings, we propose a new and simpler mechanical model for the sarcomere in which stress fiber tension is determined only by myosin contraction in series with a stiff elastic element. The fundamental difference between this model and previous models is that all tension in the stationary stress fiber is borne entirely by the myosin contractile elements in each sarcomere, with no apparent elastic element existing in parallel with the myosin contractile element.

Materials and Methods

Cell culture and transfection

Bovine capillary endothelial (BCE) cells were used at passages 11–14 and were maintained at 37°C in humidified 10% CO₂. The BCE cells were cultured on tissue culture dishes in complete medium consisting of low-glucose Dulbecco's modified Eagle's medium (Mediatech, Manassas, VA) supplemented with 10% donor bovine serum (Gibco, Billings, MT), 1% 1 M HEPES (Mediatech), and glutamine (0.292 mg/mL)/penicillin (100 U/mL)/streptomycin (100 g/mL) (Sigma, St. Louis, MO). This culture method was described previously in Chen et al. (29).

For experiments, cells were transiently transfected with EGFP-α-actinin plasmid (kindly provided by Prof. Carol Otey) or EGFP-actin using the Effectene (Qiagen, Valencia, CA) reagent. Previous studies have shown that the fusion construct is functional and localizes with the endogenous protein (30). Cells were transfected for 6 h in a 12-well cell culture dish. After 24 h the cells were trypsinized (Gibco) and plated sparsely on glass bottom dishes (MatTek, Ashland, TX). For imaging experiments, the media was changed to a CO₂-independent media as described previously (31).

Laser ablation

For laser ablation experiments, an inverted Axiovert 200M laser scanning confocal microscope (LSM 510 NLO; Zeiss, Thornwood, NY) was used with a 63×, 1.4-NA Plan-Apochromat oil immersion lens (Zeiss). To image GFP-α-actinin, the 488-nm laser line with the power attenuated to 9% and the appropriate GFP bandpass filter was used. Single stress fiber ablation was done with a Ti:Sapphire laser at 100% transmission (Chameleon XR; Coherent, Santa Clara, CA) as previously described (13). The Ti:Sapphire laser was focused through the objective and scanned a thin, ∼0.14-μm, rectangle orthogonally crossing the width of the stress fiber for 5–10 iterations. A wavelength of 790 nm was used with a laser-head power of 1.5 W, pulse duration of 140 fs, and repetition rate of 90 MHz. After ablation, confocal scans as described previously were collected using LSM 510 4.2 software (Zeiss) at 100–1000 ms/frame to capture the kinetics of sarcomere contraction.

For myosin inhibition, BCE cells were treated with 50 μM blebbistatin for ∼30 min after stress fibers were severed and allowed to reach steady state. Confocal images were taken to determine whether stress fibers were able to lengthen or relax after myosin poisoning. For all blebbistatin experiments, exposure to the 488-nm laser was minimized to prevent photoinactivation or phototoxicity.

Image correlation

To measure the change in length of the sarcomeres during stress fiber retraction, an image-correlation-based tracking method was developed in MATLAB 7.2 (The MathWorks, Natick, MA) to determine the positions of GFP-α-actinin labeled dense bodies to subpixel accuracy. Image sequences from the Zeiss software were exported to ImageJ (National Institutes of Health, Bethesda, MA) for image processing; images were rotated to make the stress fibers vertical and then smoothed to remove noise. MATLAB was used for contrast stretching (MATLAB function strechlim) on the image sequences before analysis.

The image correlation-based method works as described previously in the literature (32,33). Briefly, a kernel was chosen containing the GFP-α-actinin-labeled dense body from the image at time t, which was used for a correlation calculation (MATLAB function normxcorr2) with an image at time t+Δt. The relative spatial offset between images t and t+Δt was then calculated from the peak position of the correlation matrix. A paraboloid was fit to the correlation function around the peak to achieve subpixel accuracy for the offset. To assign positions to the feature through time, an intensity-weighted centroid calculation was done on the first frame to provide initial conditions to be updated by offsets from the correlation calculations. To minimize any error due to changes in the dense body shape, averaged positions were found by correlating each image with every other image and averaging the result. Tracking a simulated particle indicated that the error was minimal, <1%, for the spatial offsets.

Parameter estimation

The sarcomere lengths measured at n data points during contraction was fit with the four parameter model by minimizing the sum of the square of the residuals (MATLAB function fminsearch) to estimate the parameter set,

$$\underset{¯}{p}\equiv {\left[\begin{array}{cccc}\delta & x_{\min }& x_{\mathrm{c}}& V\end{array}\right]}^{\mathrm{T}}\text{.}$$

In the case where no sustained linear decrease in length was observed and a line could not be fit, a two-parameter model was fit to the data with parameter set,

$$\underset{¯}{p}\equiv {\left[\begin{array}{cc}\delta & x_{\min }\end{array}\right]}^{\mathrm{T}}\text{.}$$

To determine the uncertainty and correlation in the parameter estimates, the variance-covariance matrix was found for each data set.

To calculate the variance-covariance matrix, the n × 4 Jacobean matrix, $\underline{\underline{F}}$ was constructed where

$$F_{\mathrm{i},\mathrm{j}}\equiv \partial x\left(t_{\mathrm{i}}\right)/\partial p_{\mathrm{j}}\text{.}$$

This was used to calculate the variance-covariance of the parameters, according to this formula

$$\underline{\underline{C_{\mathrm{p}}}}=\left(\frac{1}{n-4}\sum _{\mathrm{i}=1}^n{\mathit{\varepsilon }}_{\mathrm{i}}^2\right){\left[{\underline{\underline{F}}}^{\mathrm{T}}\underline{\underline{F}}\right]}^{-1},$$ (1)

where ${\mathit{\varepsilon }}_{\mathrm{i}}\equiv y_{\mathrm{i}}-x\left(t_{\mathrm{i}}\right)$ are the residuals. The parameter variances, s_i, lie along the diagonal of $\underline{\underline{C_{\mathrm{p}}}}$ and were used to calculate a weighted mean and standard deviation,

$$\hat{p}=\sum _{\mathrm{i}=1}^n{w}_{\mathrm{i}}{p}_{\mathrm{i}},$$ (2)

$$\sqrt{s^2}=\sqrt{\frac{\sum _{\mathrm{i}=1}^n{w}_{\mathrm{i}}{\left({\overline{x}}_{\mathrm{j}}-\hat{x}\right)}^2}{1-\sum _{\mathrm{j}=1}^n{w}_{\mathrm{j}}^2}},$$ (3)

where the weighting factor was calculated using the parameter variances calculated from Eq. 3 and the form

$$w_{\mathrm{i}}=\frac{1/s_{\mathrm{i}}^2}{\sum _{\mathrm{j}=1}^{n}1/s_{\mathrm{j}}^2}\text{.}$$

Results and Discussion

Sarcomeres contract in the severed stress fiber

To measure sarcomere contraction in living BCEs, we expressed GFP-α-actinin, which labels stress fibers at junctions of neighboring sarcomeres (Fig. 1 B). Next, we severed individual stress fibers in living cells using a recently developed femtosecond laser ablation technique (13). A key feature of femtosecond laser ablation is that it minimizes collateral damage outside the ablated spot (34). On severing a stress fiber, individual sarcomere units in the fiber contracted (see kymograph in Fig. 1 C). The severed end appeared to retract exponentially with time (Fig. 1 D), consistent with a previous study by Kumar et al. (13). Thus, the net retraction of the severed edge corresponded to the contractions of individual sarcomeres as measured by the distance between α-actinin-labeled dense bodies.

Although the severed edge of the cut fiber appeared to retract exponentially, the contraction of individual sarcomeres was quite variable but shared qualitatively similar nonexponential behavior. As shown in Fig. 2 A, the contraction of individual sarcomeres from their initial length, x_initial, to their final contracted length, x_min, occurred in two distinct phases. First, a nearly-instantaneous contraction occurred of distance δ ∼ 0.1 μm, which was followed by a slower contraction over a variable distance of x_c ∼ 0–0.4 μm at nearly-constant speed. After the linear phase, the contraction ceased abruptly and the sarcomere remained constant at the final length x_min for the duration of the experiment. Noting this consistent behavior, all sarcomere contraction trajectories were fit by least-squares regression to the following piecewise linear model,

$$x\left(t\right)=\{\begin{array}{cc}{x}_{\min }+x_{\mathrm{c}}+\delta \equiv x_{\text{initial}}& \text{for}t=0\\ x_{\min }+x_{\mathrm{c}}-Vt& \text{for}0<t<x_{\mathrm{c}}/V\\ x_{\min }& \text{for}t\ge x_{\mathrm{c}}/V\end{array}\text{.}$$ (4)

The fit allowed us to estimate the sarcomere contraction parameters V, δ, x_c, and x_min. The characteristic time for the transition from linear contraction to steady state was calculated as x_c/V. For all analyzed sarcomeres from different stress fibers, normalized contraction (x – x_min)/x_c was plotted against Vt/x_c excluding initial sarcomere lengths (Fig. 2 B). As seen in Fig. 2 B, there is a clear linear trend followed by a stationary noncontracting phase in the pooled, normalized contraction data.

Figure 2.

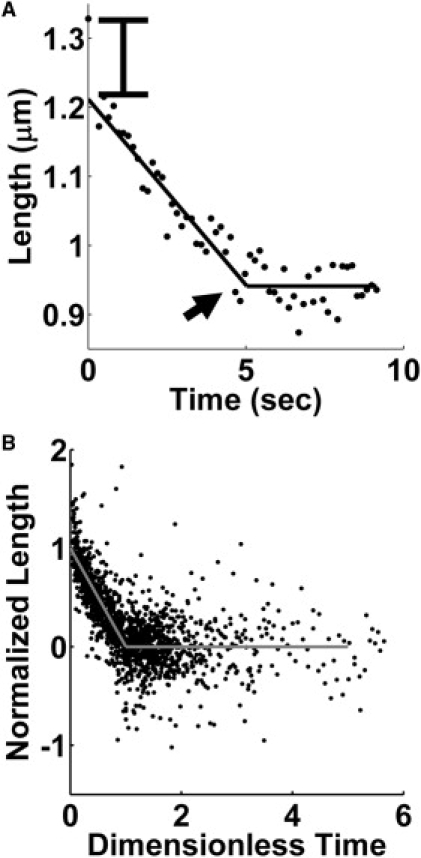
Time-dependent length change of a sarcomere. (A) Representative example of sarcomere length change in a severed fiber. The contraction occurs in two distinct phases: first, a quick initial drop (marked on plot) followed by sustained contraction at nearly constant speed. After some time, the sarcomere reaches a steady-state length (arrow) and remains there for the remainder of the experiment. (B) Pooled data from contraction of 28 sarcomeres in 18 cells was normalized and plotted together, excluding initial sarcomere lengths (see text for details). A clear linear trend is visible in the normalized data.

The initial and final lengths (x_initial and x_min, respectively) were approximately Gaussian distributions, with means and standard deviations, 1.21 μm ± 0.31 μm and 0.97 μm ± 0.32 μm, respectively. Shown in Fig. 3 are the distributions of contraction distances. The distribution of the initial contraction distance δ was approximately symmetric, with a mean and standard deviation of 0.085 μm ± 0.059 μm (Fig. 3 A). The linear contraction distance was approximately exponentially distributed, with mean and standard deviation of 0.19 μm ± 0.087 μm (Fig. 3 B). The net contraction had a mean and standard deviation of 0.28 μm ± 0.11 μm. (Fig. 3 C) For sarcomeres with a significant linear contraction regime, (x_c > 0.1), the fit to Eq. 4 yielded the velocity V of the slower contraction phase. The mean and standard deviation of the contraction velocities was found to be 0.0099 μm/s ± 0.010 μm/s.

Figure 3.

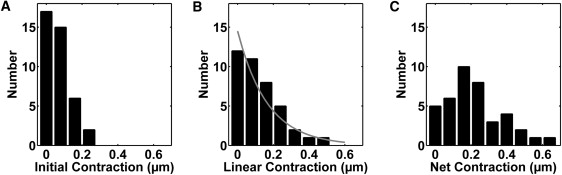
Histograms of sarcomere contraction parameters. (A) The distribution of the initial contraction of sarcomeres appears symmetric with a mean and standard deviation of 0.10 μm ± 0.06 μm (N = 40 sarcomeres, 18 cells). (B) Interestingly, the distribution of the linear contraction appears to be approximately exponential (shaded curve is drawn for visualization) with a mean and standard deviation of 0.15 μm ± 09 μm (N = 28 sarcomeres, 18 cells). (C) The distribution of the net contraction appears to be a shifted exponential with a mean and standard deviation of 0.26 μm ± 0.11 μm (N = 40 sarcomeres, 18 cells).

Potential energy is not stored in severed stress fibers

To confirm that stress fiber retraction is myosin-dependent, we severed stress fibers in cells pretreated with blebbistatin for 30 min. As shown in Fig. 4 A, stress fibers in cells treated with blebbistatin retracted insignificantly compared to nontreated cells (see Fig. 4 B). This confirms the results as reported by Kumar et al. (13) that retraction in the severed fiber is myosin-dependent.

Figure 4.

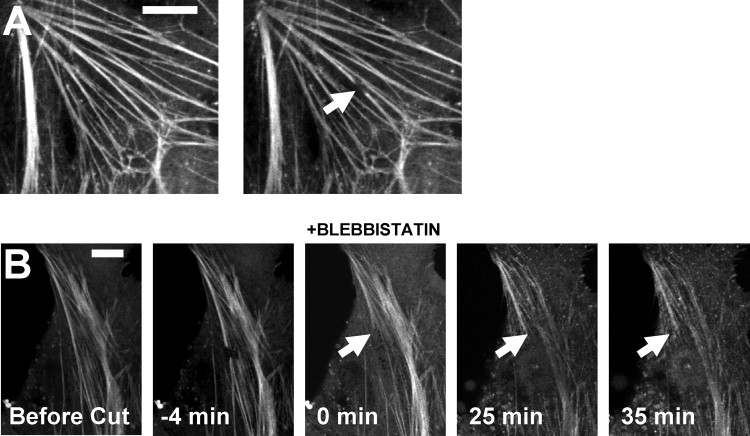
Potential energy is not stored in a severed stress fiber. (A) A stress fiber severed in a cell treated with 50-μM blebbistain retracted minimally (∼1 μm in 20 s), indicating that myosin activity is responsible for the stress fiber retraction (scale bar, 10 μm). (B) A cut stress fiber that is allowed to reach steady state (marked by arrow) before myosin poisoning does not recover its length after blebbistatin treatment for several minutes. This indicates that potential energy was not stored in the contracted fiber. (Scale bar, 10 μm.)

To determine the extent to which the sarcomere contraction could be reversed, we quantified recovery of sarcomere length upon inhibition of myosin. Stress fibers were severed and sarcomeres were allowed to contract to a new steady state. Next, myosin activity was poisoned by treatment with blebbistatin (Fig. 4 B). The severed fiber length was determined after myosin inhibition and compared with the severed fiber length before inhibition. As seen in Fig. 4 B, there was no visible lengthening of the contracted stress fiber several minutes time after blebbistatin treatment (see Fig. S1 in the Supporting Material for another example). These results show that there is no elastic energy stored in the contracted sarcomeres that can be recovered upon inhibition of myosin contraction. This finding argues against the presence of an elastic element in parallel with myosin force generation. This finding is also in agreement with the results of Katoh et al. (27), who showed that isolated stress fibers cannot relax after contracting in a myosin-dependent fashion.

A mechanical model for the sarcomere

The behavior of contracting sarcomeres after loss of tension, i.e., a near-instantaneous initial retraction followed by slower linear contraction until a minimum length is reached, can be explained with the simple mechanical model shown in Fig. 5. In this model, an elastic element is in series with a myosin contractile element. After severing, the sarcomere initially relaxes elastically, followed by slower myosin-mediated contraction at a constant speed V, which is likely limited by the maximum (unhindered) myosin motor velocity. The abrupt cessation of contraction suggests that either a strong resistance to further contraction is suddenly encountered, which could reflect a rigid steric barrier, or that myosin motors have reached a limiting minimum distance from the dense bodies where the motors can no longer walk on actin filaments.

Figure 5.

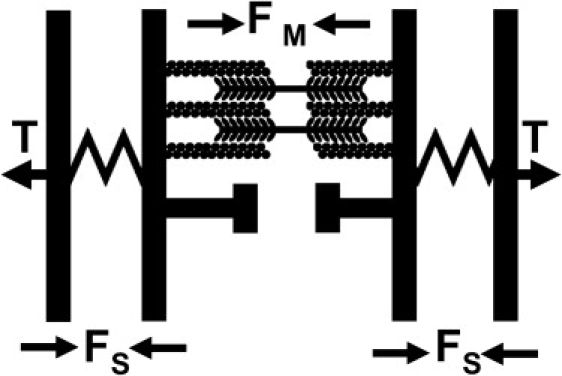
Proposed mechanical model for the sarcomere. The tension, T, in the stress fiber is only determined by myosin forces, F_M, in series with a stiff elastic element, F_S. An impenetrable barrier prevents further sarcomere contraction at some minimum sarcomere length.

Because myosin motors are sensitive to load, the uniform speed of the contraction phase suggests that elastic forces do not increase (and are not relieved) during contraction. This observation, combined with the observation that elastic energy is not stored in contracted stress fibers, suggests that there is no elastic element in parallel with the contractile element, contrary to other recent models for stress fiber sarcomere mechanics (14,15).

Based on the model in Fig. 5, V corresponds to the zero-load working velocity of myosin motors in living stress fibers. The mean velocity of myosin walking is found to be 0.0099 μm/s (in vitro measurements of myosin velocity are in the range of 0.14 μm/s (35)). Although this speed may be limited by the maximum speed of the ensemble of myosin motors, we cannot rule out other sources of internal friction within the sarcomere operating in parallel with myosin motors. However, the near-instantaneous initial retraction argues against a significant external viscous drag limiting the rate of contraction after severing. In addition, any internal or external viscous drag does not alter the main conclusions of the model: that spring elements do not contribute to the force balance in the stress fiber; and that there are internal barriers present that limit contraction under zero tension.

Based on the exponential distribution of contraction distances x_c reported in Fig. 3 B, the most probable state of a sarcomere after the initial instantaneous contraction is at its minimum length. This surprising conclusion again argues against models that invoke tensile or compressive elastic elements within the sarcomere to position the sarcomere length at some optimal value.

A key question remains: How does the observed exponential distribution of contraction distances arise in a steady-state stress fiber? One possibility is that the tension in the stress fiber fluctuates in way that results in this distribution in lengths, as demonstrated by the following model.

If tension is balanced by myosin contractile forces only, and the tension-velocity relation is linear, then the contraction velocity has the form

$$v\equiv d{x}_{\mathrm{c}}/dt=V\left(T/T_{\max }-1\right),$$ (5)

where V is the maximum myosin contraction speed at zero tension, as obtained from the sarcomere contraction measurements, and T_max is the fiber tension required to stall contraction. Assume that the mean tension in the stress fiber, $\overline{T}$, is less than the stall tension for myosin contraction in the sarcomere, such that the sarcomeres tend to contract, thus decreasing x_c, with an effective drift velocity

$$\overline{v}=V(\overline{T}/T_{\max }-1)<0\text{.}$$ (6)

However, fluctuations in the instantaneous T could lead to transient increases in x_c, analogous to diffusion. The effective diffusion coefficient D for x_c arising from fluctuations in T, is given by

$$D={\left(\frac{V}{T_{\max }}\right)}^2\underset{0}{\overset{\mathrm{\infty }}{\int }}C\left(\tau \right)d\tau ,$$ (7)

where $C\left(\tau \right)\equiv \overline{T\left(t+\tau \right)T\left(t\right)}-{\overline{T}}^2$ is the autocorrelation function for the fluctuations. Under these assumptions, the distance x_c is governed by a diffusion process with constant drift toward an impenetrable barrier (x_c ≥ 0), for which the stationary probability density p(x_c) has the exponential form

$$p\left(x_{\mathrm{c}}\right)=\frac{\overline{v}}{D}\exp \left(-\overline{v}{x}_{\mathrm{c}}/D\right)\text{.}$$ (8)

Therefore, this model predicts an exponential distribution in x_c as observed experimentally, and the mean value of x_c is equal to $D/V\left(1-\overline{T}/T_{\max }\right)$.

In addition to explaining the distribution of contraction distances, the above model provides an alternative mechanical explanation for the observation that stimulation of myosin contraction of sarcomeres at a cell boundary by calyculin-A (26) causes shortening of the stimulated sarcomeres and a corresponding lengthening of distal sarcomeres. The increase in myosin activity causes an overall increase in the stress fiber tension $\overline{T}$, and an overall increase in T. However, a greater stimulation of peripheral sarcomeres leads to a corresponding increase in their value of T_max. In this interpretation, the calyculin-A treatment decreases the ratio $\overline{T}/T_{\max }$ and hence the mean of x_c in peripheral sarcomeres, while increasing this ratio in distal sarcomeres. This can cause the observed distribution of sarcomere lengths in cells treated with calyculin-A.

Insight into the mechanics of stress fibers

A key prediction of the proposed model is that, after the initial elastic retraction, sarcomere tension is entirely balanced by myosin contraction, without invoking elastic elements in parallel or a dependence of tension on sarcomere length. Removal of tension causes linear contraction against zero external resistance until the minimum distance is reached. Because the dynamics of individual sarcomeres in the linear retraction model differs from the stress fiber end retraction as a whole, a question arises as to whether this linear retraction model is consistent with the exponential retraction curves reported here (Fig. 1 D) and by Kumar et al. (13).

In fact, an approximately exponential retraction of the severed fiber end does arise from the linear contraction of multiple sarcomeres in series, if contraction distances x_c come from an exponential distribution, as we found in our measurements (Fig. 3 B). The measurements suggest that x_c has a probability density that can be approximated as an exponential density, such that

$$p\left(x_{\mathrm{c}}\right)d{x}_{\mathrm{c}}={\Delta }^{-1}{e}^{-x_{\mathrm{c}}/\Delta }d{x}_{\mathrm{c}}$$ (9)

is the probability of a contraction distance between x_c and x_c + dx_c, and Δ is the mean contraction distance ($\Delta =D/V\left(1-\overline{T}/T_{\max }\right)$ in the above model. From Eq. 4, the time-dependent mean sarcomere length is thus exponential, given by

$$\langle x\left(t\right)\rangle =x_{\min }+\underset{\text{Vt}}{\overset{\mathrm{\infty }}{\int }}\left(x_{\mathrm{c}}-Vt\right)p\left(x_{\mathrm{c}}\right)d{x}_{\mathrm{c}}=x_{\min }+\Delta e^{-\text{Vt}/\Delta }\text{.}$$ (10)

For a stress fiber consisting of N sarcomeres, the mean initial length is $L_0=N\left[\delta +x_{\min }+\Delta \right]$. Following cutting and the initial elastic retraction, the mean time-dependent length is $L\left(t\right)=N\left[x_{\min }+\Delta e^{-\text{Vt}/\Delta }\right]$, such that relative retraction length is

$$R\left(t\right)\equiv \frac{L_0-L\left(t\right)}{L_0-L_{\min }}=\frac{\delta +\Delta \left(1-e^{-\text{Vt}/\Delta }\right)}{\delta +\Delta }\text{.}$$ (11)

The solid line in Fig. 1 D is a least-squares regression fit of Eq. 11 to these data, illustrating the good agreement of the exponential model, with initial retraction, to the stress fiber retraction data. If the initial retraction δ happens to be small relative to Δ, then this equation becomes ∼$R\left(t\right)\cong \left(1-e^{-\text{Vt}/\Delta }\right)$, consistent with the exponential distribution reported by Kumar et al. (13). Therefore, there is no inconsistency between the linear contraction model and the apparent exponential retraction curves of the severed ends of the stress fiber.

In summary, we have performed the first measurements of sarcomere contraction in stress fibers formed by living endothelial cells. Our results suggest that tension in the fiber is established entirely by myosin activity, and is not influenced by spring elements as is currently believed. Taken together, our experiments and analysis shed new light into the behavior of living sarcomeres and suggest a new model for stress fiber sarcomere mechanics. Future avenues of investigation will need to identify molecular players that contribute to the stiffness of sarcomeres and determine the barrier position.