Importance of Contact Persistence in Denatured State Loop Formation: Kinetic Insights into Sequence Effects on Nucleation Early in Folding

Abstract

Protein folding is dependent on the formation and persistence of simple loops early in folding. Ease of loop formation and persistence is believed to be dependent on the steric interactions of the residues involved in loop formation. We have previously investigated this factor in the denatured state of iso-1-cytochrome c using a five amino acid insert in front of a unique histidine in the N-terminal region of the protein. Previously, we reported that the apparent pK_a of loop formation for the most flexible (all Gly) and least flexible (all Ala) insert were within error the same. We evaluate whether this observation is due to differences in the persistence of loop contacts or due to effects of local sequence sterics and main chain hydration on the persistence length of the chain. We also test whether sequence order affects loop formation. Here we report kinetic results coupled to further mutagenesis of the insert to discern between these possibilities.

We find that the amino acid, glycine versus alanine, next to the loop forming histidine has a dominant effect on loop kinetics and equilibria. A glycine in this position speeds loop breakage relative to alanine resulting in less stable loops. At high % Gly in the insert, rates of loop formation and breakage exactly compensate leading to a leveling out in loop stability. Loop formation rates also increase with glycine content, inconsistent with poly-Gly segments being more extended than previously suspected due to main chain hydration or local sterics. Unlike loop breakage rates, loop formation rates are insensitive to local sequence. Together these observations suggest that contact persistence plays a more important role in defining the folding code than rates of loop formation.

Introduction

The denatured state of a protein is the starting point for folding a protein to its native structure which confers its function. Early studies on denatured proteins indicated that disordered polypeptides had properties consistent with a random coil.¹ However, it is now widely accepted that protein denatured states contain non-random structure.^2,3 Non-random structure results in part from the intrinsic bias of the polypeptide chain toward extended structures such as the polyproline II helix.^2,4,5 Structural data, particularly from NMR studies of denatured proteins, and computational studies demonstrate the presence of persistent secondary structure and hydrophobic clusters under denaturing conditions.^6–13 Thermodynamic approaches to characterizing protein denatured states also show strong deviations from the properties expected for a random coil.^14–16 For example, ionic interactions within residual structures can stabilize protein denatured states by 1 to 4 kcal/mol.^14,16–22 These non-random electrostatic interactions have been shown to influence the kinetics of protein folding.^17,22 Although, in other cases, mutations which destabilize residual native-like structure have no effect on folding rates.²³ Thus, non-random structure in the denatured state of a protein can clearly influence the folding process, but does not always do so. Still, stable residual structures present in the denatured state ensemble have the potential to dictate early nucleation events, which in turn guide the denatured polypeptide down the ‘folding funnel’, limiting the “walk across conformational space” towards a thermodynamic minimum. In so doing, non-random structures can greatly increase protein folding efficiency,²⁴ thereby satisfying Levinthal’s Paradox. Unfortunately, the question of how this increased efficiency is accomplished is still not fully understood.

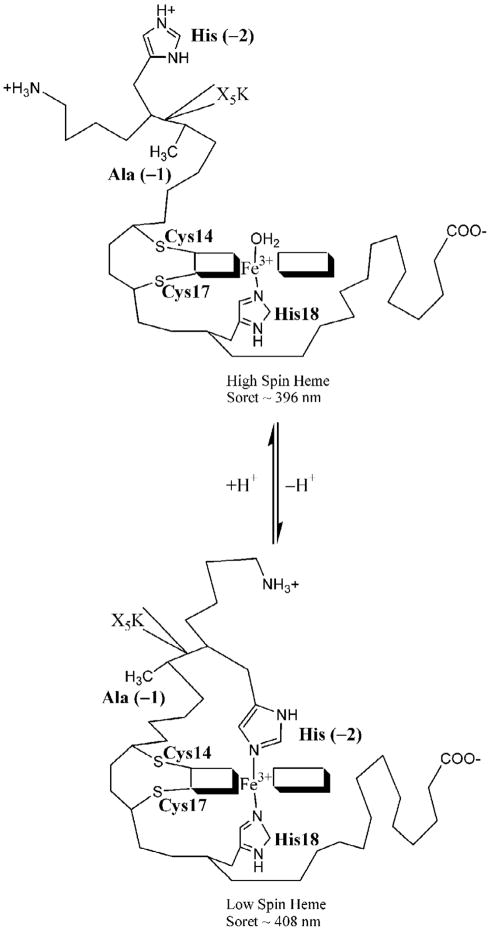
To probe the conformational constraints which act on a denatured protein, we have developed methods to measure the equilibria and kinetics of formation of simple polypeptide loops under denaturing conditions.^14,15 Loop formation is of great interest because contact between two monomers along a polypeptide chain is the most primitive type of structure which forms during protein folding.^25,26 We use variants of the c-type cytochrome, yeast iso-1-cytochrome c, that have been engineered to contain only a single histidine besides the native heme ligand, His 18. Histidines on the N-terminal side of the heme attachment site (Cys 14, Cys 17 and His 18) will form a loop which includes residues between the engineered histidine and Cys 14 (Figure 1). Histidines on the C-terminal side of the heme attachment site will form a loop between His 18 and the engineered histidine. A simple pH titration allows evaluation of the stability of a given histidine-heme loop, providing an apparent pK_a, pK_a(obs). Since a higher proton concentration is required to break a more stable loop, a lower pK_a(obs) indicates a more stable loop. Thus, the relative stabilities of different loops can be evaluated easily. We have used this method to evaluate the conformational properties of a denatured protein^14,15 including the scaling properties of a polypeptide chain,²⁷ the effect of varying denaturing conditions on loop formation,²⁸ the effects of local excluded volume on loop formation,²⁹ and most recently the effects of sequence composition on loop formation.³⁰

Figure 1.

Schematic representation of denatured state His-heme ligation from the N-terminal side of the heme of iso-1-cytochrome c. Ala/Gly inserts were made following a histidine substituted in place of Lys(-2) for the NH5A and GlyX variants. Ala(-1) terminates each insert sequence.

Studies on the kinetics of loop formation using synthetic peptides have provided key insights into the effects of sequence composition on the conformational constraints that limit the rate of loop formation in a disordered polypeptide.^25,26 Except for glycine and proline the effects of sequence composition are minimal.^26,31,32 However, intramolecular hydrogen bonds from Thr, Ser, and Gln side chains may stiffen the polypeptide backbone.^31,33–35

To examine the effects of sequence composition on equilibrium loop formation in the denatured state, we inserted the sequence AAAAAK in between a histidine at position −2 (K(−2)H) of yeast iso-1-cytochrome c (Figure 1; we use the horse cytochrome c numbering, thus the 5 amino acids preceding Gly 1 of yeast iso-1-cytochrome c are designated −5 to −1).30 Under denaturing conditions, His(−2)-heme binding forms a 22 residue loop. In our previous study, we progressively changed each of the alanines in this insert into a glycine, producing a set of 22 residue loops where the percent glycine within the loop varied from 9% to 32%. Polymer theories predict that the average end-to-end distance of a chain of a fixed length (n = 22 in our case) will decrease as glycine content increases.^4,36 Therefore, the probability of closing a loop should increase with increased glycine content, for a loop of fixed length. In fact, we observed an identical pK_a(obs) for equilibrium loop formation in 3 M gdnHCl for the all alanine insert (NH5A variant) and the all glycine insert (Gly5 variant). The decrease in Flory’s characteristic ratio, C_n, for the 22-residues contained in the loop for the Gly5 variant relative to the NH5A variant predicted a decrease in the pK_a(obs) of ~0.4.

In the present work we test three hypotheses that could explain the lack of a decrease in the equilibrium pK_a(obs) with increased glycine content for the Gly5 variant relative to the NH5A variant. The first hypothesis is that increased glycine content leads to faster rates of loop breakage counterbalancing the faster rates of loop formation expected for the more flexible glycine sequence. We have measured rates of loop breakage to test this hypothesis.

The second hypothesis is based on NMR studies on short poly-glycine peptides which indicate that the persistence length of glycine is greater than previously thought.³⁷ In this study, it was suggested that the greater than expected persistence length of poly-glycine stretches was either due to local sequence effects or to peptide backbone hydration. The latter is not accounted for in early polymer models. In our previous study, the pK_a(obs) decreased as the first two alanines were inserted and then increased as the remaining glycines were added. The glycines were inserted contiguous to each other in this study. This observation raised the possibility that a critical threshold of contiguous glycines is necessary to extend the backbone through local sequence or hydration effects. Similarly, in the NMR studies on poly-Gly peptides, the residual dipolar coupling for a peptide with the sequence Ac-YES-G₆-ATD was very different from that of a peptide with the sequence Ac-YGEGSGAGTGDG, where the stretch of contiguous glycines is broken up. Thus, to test the effect of local sequence/hydration on the conformational properties of glycine rich polypeptide segments, we have prepared variants with the same glycine content as in the original study, but with a decrease in the number of contiguous glycine residues.

The third hypothesis is that local sequence dominates early in folding when the overall structure of a protein is largely disordered. The work of Robinson et al.³⁸ suggested that equilibrium stability of loops or linkers between two subunits of a protein is primarily dependent on sequence composition rather than specific sequence. In particular, a balance between adequate versus too much flexibility was essential for optimal stability of the domain interface. This investigation tests whether those findings are applicable to nucleating structures such as simple loops in the denatured state or if they are only applicable to the large contact interfaces of subunits or subdomains. In particular, we test whether the amino acid – glycine versus alanine – next to the histidine involved in loop formation has a dominant impact on loop dynamics. In our previous study, variants with 1 to 3 glycines in the 5 amino acid insert in front of the histidine had an alanine next to the histidine, whereas the inserts with 4 and 5 glycines had a glycine next to the histidine (Table 1).

Table 1.

Variant nomenclature and sequence composition of insert

% Gly in Insert	Previous Variants	New Variants
0	NH5A (HAAAAAK)	--
20	Gly1 (HAAGAAK)	Gly1v2 (HGAAAAK)
40	Gly2 (HAGGAAK)	--
60	Gly3 (HAGGGAK)	Gly3v2 (HGAGAGK)
80	Gly4 (HGGGGAK)	Gly4v2 (HGGAGGK)
		Gly4v3 (HAGGGGK)
100	Gly5 (HGGGGGK)	--

Results

Design of new poly-Ala/Gly variants

The previous set of poly-Ala/Gly inserts was made by progressively replacing the five alanines in the NH5A variant with glycine working from the center of the insert outwards (Table 1).³⁰ In this set of variants, all of the glycines were contiguous and the amino acid next to His (−2) was Ala in some cases and Gly in others.

To test the role of local sequence or backbone hydration in extending the main chain of poly-Gly sequences, we have prepared two new variants where the number of contiguous glycines is decreased, Gly3v2 and Gly4v2 (Table 1). In Gly3v2, the three glycines are now separated by alanines in the 5 amino acid insert. In Gly4v2, the sole alanine is now placed in the center of the insert, so each run of glycines is only two amino acids in length. We note that the kinetic experiments on the His-heme loops will also test the degree of extension of the poly-Gly inserts. If hydration or local sequence sterics extend the main chain of the poly-Gly inserts to the level of the poly-Ala insert (or greater as indicated in ref. 37), then the forward rate constant for loop formation, k_f, should not be significantly increased when alanines are replaced by contiguous glycines and k_f should be sensitive to whether or not the glycines are contiguous.

We also made several variants that test whether the amino acid next to His (−2) on the C-terminal side (i.e., within the loop) – Ala versus Gly – affects His-heme loop formation (Table 1). The Gly1v2 variant places the sole Gly in the insert next to His (−2) for comparison with the Gly1 variant which has Ala next to His (−2). The Gly4v3 variant places the sole Ala in the insert next to His (−2), for comparison with the Gly4 variant which has Gly next to His(−2).

Global stability of new GlyX variants

The global stability of all new variants was measured by guanidine hydrochloride (gdnHCl) denaturation monitored by circular dichroism spectroscopy. Table 2 contains the stability data for these variants. All new variants have higher global stability ranging from about 0.3 to 0.8 kcal/mol more than their previous counterparts (previous variants all had ΔG^o′_u(H₂O) ~ 2 kcal/mol).³⁰ Specifically, the largest change is observed for Gly1v2 (2.70 kcal/mol) compared to Gly1 (1.87 kcal/mol) while the smallest is Gly4v3 (2.25 kcal/mol) compared to Gly4 (2.02 kcal/mol). In our previous work, the decrease in stability of all variants relative to a variant with the five alanine insert but Lys(−2) instead of His(−2) (NK5A, ΔG^o′_u(H₂O) ~ 4 kcal/mol)³⁰ could be attributed completely to stabilization of the denatured state by His-heme loop formation. For the new variants, the dominant effect on stability relative to the NK5A variant is still the very stable His-heme denatured state loop. The differences in the stability of variants with the same number of glycines in some cases are consistent with changes in denatured state loop stability and in other cases are not. Thus, some of the changes in protein stability may reflect effects on the native state.

Table 2.

Thermodynamic parameters for gdnHCl induced unfolding of iso-1-cytochrome c variants at pH 7.0 and 25 °C

Iso-1-cytochrome c variant	ΔGo′u(H2O) (kcal/mol)a	m-value (kcal/mol×M)a	Midpoint Cm (M)a
Gly1v2	2.70 ± 0.07	5.52 ± 0.25	0.49 ± 0.03
Gly3v2	2.33 ± 0.24	5.19 ± 0.64	0.45 ± 0.07
Gly4v2	2.34 ± 0.16	5.42 ± 0.46	0.43 ± 0.05
Gly4v3	2.25 ± 0.09	5.23 ± 0.08	0.43 ± 0.02

^aValues reported are based on an average of 3 separate experiments. The reported error is the standard deviation.

The denaturation midpoints, C_m, are all less than 0.5, confirming that these variants are fully denatured in 3 M gdnHCl, the experimental conditions used for denatured state loop formation.

Equilibrium loop formation in the denatured state

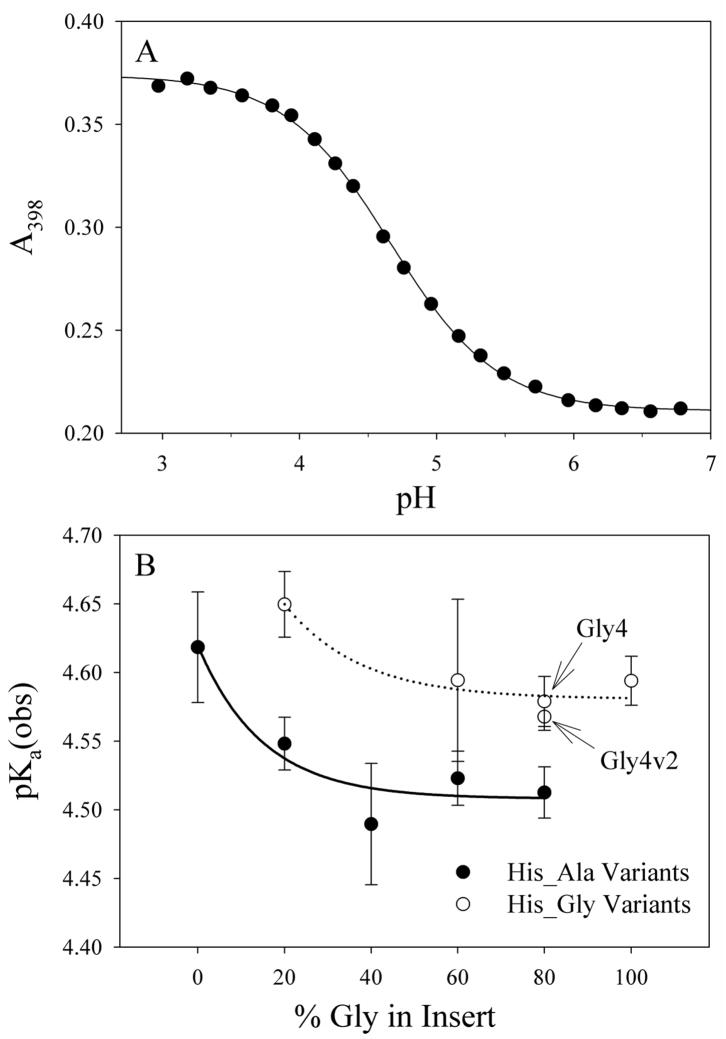
The stabilities of the His-heme loops under denaturing conditions (3 M gdnHCl) were measured for all new variants. Figure 2A represents a typical titration curve for equilibrium loop formation. The thermodynamic parameters from the equilibrium loop formation experiments are presented in Table 3. Proton transfer numbers (n-values) are at or near the expected value of 1 based on a one proton process as depicted in Figure 1. In Figure 2B, the data are segregated based on whether Ala (His_Ala variants) or Gly (His_Gly variants) is next to the histidine involved in loop formation. In all cases, the pK_a(obs) is higher when Gly is the residue next to the histidine (and within the loop formed by histidine binding to the heme). This result indicates that increased chain flexibility immediately next to the histidine disfavors loop formation. Thus, the equilibrium data indicate that sequence immediately adjacent to the histidine that forms the loop (and within the loop) is important for loop stability.

Figure 2.

(A) A representative pH titration curve monitoring His-heme ligation in 3 M gdnHCl, 5 mM sodium phosphate, 15 mM NaCl, 1.0 mM EDTA. Data are for the Gly3v2 variant and were acquired at room temperature, 22 ± 1°C. The solid curve is a fit of the data to a modified form of the Henderson-Hasselbalch equation. The parameters from the fit, pK_a(obs) and the number of protons, n, coupled to loop formation are reported in Table 3. (B) Graph of pK_a(obs) versus % Gly in Insert. Data are segregated based on whether Gly follows His, His_Gly variants (○), or Ala follows His, His_Ala variants (●). The solid and dotted curves in panel B are meant to guide the eye and have no physical significance.

Table 3.

Thermodynamic parameters for denatured state loop formation at 22 ± 1 °C in 3 M gdnHCl for variants of iso-1-cytochrome c

Iso-1-cytochrome c variant	pKa(obs)a	na,b
Gly1v2	4.65 ± 0.02	1.02 ± 0.10
Gly3v2	4.59 ± 0.06	1.09 ± 0.05
Gly4v2	4.57 ± 0.01	1.01 ± 0.01
Gly4v3	4.51 ± 0.02	1.03 ± 0.01

^aValues reported are based on an average of 3 separate experiments. The reported error is the standard deviation.

^bn is the apparent number of protons linked to breakage of the His-heme loop.

Furthermore, the apparent pK_a(obs) of the Gly4 variant with 4 contiguous glycines is the same as that for the Gly4v2 variant with two sets of two contiguous glycines (Figure 2B). As seen in Table 1, these variants both have Gly next to the His involved in His-heme loop formation, controlling for the local sequence effect of the residue next to the histidine. Thus, the data for the Gly4 and Gly4v2 variants do not support unusual extension of the backbone due to contiguous glycines. Variants Gly3 and Gly3v2 were also designed to probe backbone hydration due to contiguous glycines. However, given the clear segregation of the pK_a(obs) data for His_Ala versus the His_Gly variants, the difference in the pK_a(obs) for these two variants is more likely due to the Gly3 variant having Ala next to His(−2) and Gly3v2 having Gly next to His(−2) (Figure 2B).

Interestingly, for both the His_Ala and His_Gly series of variants, increased glycine content in the insert initially confers greater loop stability (Figure 2B). However, above approximately 40% glycine in the insert, loop stability levels out. This trend is more pronounced for the His_Ala series than the His_Gly series.

Measurement of loop breakage kinetics

In previous studies,³⁹ we have shown that loop formation and breakage kinetics are consistent with a model involving a rapid protonation equilibrium (of histidine) followed by His-heme loop formation. This model predicts that k_obs has the pH dependence given by Eq 1,

$$k_{\mathit{obs}}=k_b+k_f\left(\frac{K_a({\mathit{HisH}}^{+})}{[H^{+}]+K_a({\mathit{HisH}}^{+})}\right)$$ (1)

where K_a(HisH⁺) is the ionization constant of the histidine involved in loop formation and k_f and k_b are the rate constants for loop formation and loop breakage respectively. Thus, if pH < pK_a(HisH⁺), k_b can be obtained. Table 4 summarizes the kinetic parameters from loop breakage for both new, as well as previously designed variants. We measured k_obs using downward pH jumps to both pH 3.5 and 3.0. The k_obs values are uniformly about 10% lower at pH 3.0 versus pH 3.5, consistent with the smaller contribution expected from k_f at lower pH (Eq 1). Thus, we use the k_obs values at pH 3.0 for k_b.

Table 4.

Kinetic parameters for denatured state loop breakage and loop formation at 25 °C in 3 M gdnHCl for variants of iso-1-cytochrome c

Variant	Loop Breakagea		Loop Formationa,b
	kobs, s−1 (pH 3.50)	kobs, s−1 (pH 3.00)	kf, s−1
His_Ala Variantsc
NH5A	100.5 ± 1.0	93.0 ± 0.2	8910 ± 830
Gly1	91.6 ± 1.8	83.1 ± 1.9	9360 ± 470
Gly2	87.4 ± 0.9	76.8 ± 0.7	9900 ± 1000
Gly3	92.1 ± 1.3	81.6 ± 1.0	9740 ± 460
Gly4v3	94.9 ± 3.0	87.2 ± 1.0	10670 ± 470
His_Gly Variantsd
Gly1v2	110.3 ± 3.6	101.8 ± 2.3	9080 ± 540
Gly3v2	109.5 ± 3.9	96.7 ± 3.1	9790 ± 1370
Gly4v2	114.0 ± 2.5	100.8 ± 3.8	10860 ± 480
Gly4	116.2 ± 2.2	107.0 ± 1.8	11230 ± 500
Gly5	122.0 ± 2.3	111.4 ± 1.3	11300 ± 480

^aThe errors reported for k_obs are the standard deviations of the mean and those for k_f are from standard propagation of errors.

^bLoop closure rate constants are beyond the limitation of our SX-20 stopped-flow apparatus. Thus, these values were extracted using pK_loop obtained as described in the text. k_f was calculated as k_f = k_b× K_loop = k_b× 10^−pK_loop, using k_obs for loop breakage at pH 3.00 for k_b.

^cVariants where the amino acid on the C-terminal side of the His which forms the loop with the heme is an alanine.

^dVariants where the amino acid on the C-terminal side of the His which forms the loop with the heme is a glycine.

Loop formation rates are much faster than the dead time of stopped-flow instrumentation.³⁹ Expression in E. coli also leads to a free N-terminal amino group which is likely to interfere with the kinetics of histidine-heme binding in the critical region near the pK_a of histidine (see Eq 1).^30,40 Thus, these rate constants were calculated by extracting the pK_loop (pK for loop formation with a fully deprotonated His) from the apparent pK_a(obs), using Eq 2.

$${pK}_a(\mathit{obs})={pK}_a({\mathit{HisH}}^{+})+{pK}_{\mathit{loop}}$$ (2)

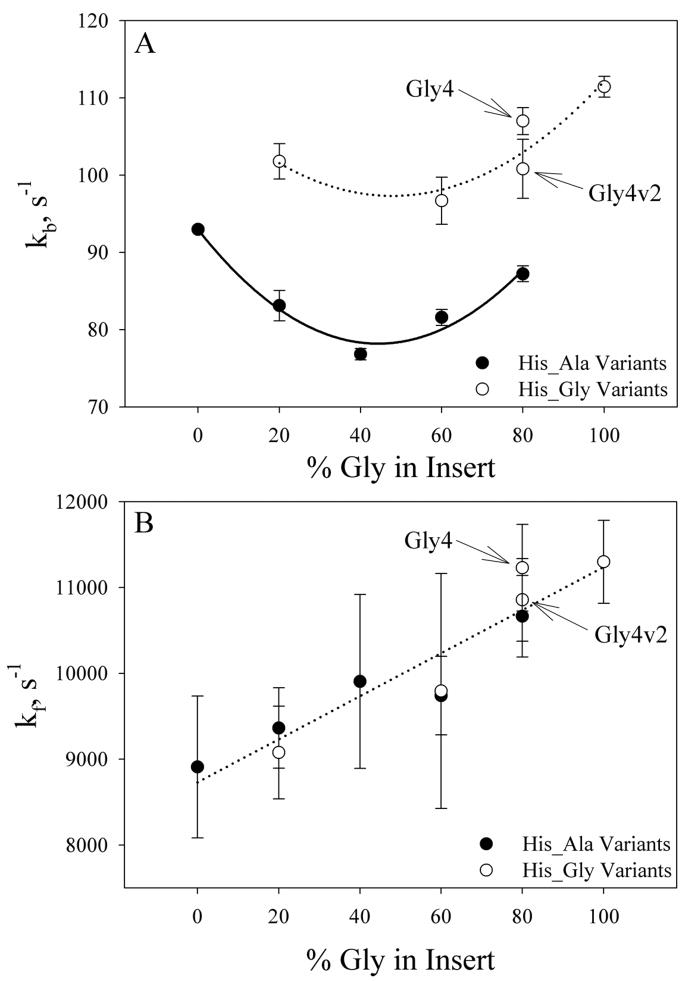
This equation is a reasonable approximation if pK_a(obs) is at least one unit less than pK_a(HisH⁺). Since pK_a(HisH⁺) equals 6.6 ± 0.1 in 3 M gdnHCl,²⁸ the approximation is reasonable for the data presented here (Table 3, Fig. 2). pK_loop was then used in conjunction with the loop breakage rate constants, k_b, to extract loop formation rate constants (Table 4). Figures 3A and 3B show loop breakage and loop formation rate constants, respectively, segregated based on the amino acid immediately adjacent to the histidine involved in loop closure. It is evident that loop breakage is faster if glycine is next to histidine. We note that with pK_a(His) = 6.6 ± 0.1, Eq 1 indicates that the contribution of k_f to k_obs at pH 3 is about 2 to 3 s⁻¹. Thus, equating k_obs to k_b at this pH is a reasonable assumption.

Figure 3.

(A) Loop breakage rate constants, k_b, at 25 °C in 3 M gdnHCl plotted as a function of % Gly in Insert and grouped based on whether Gly follows His, His_Gly variants (○) or Ala follows His, His_Ala variants (●). The dotted and solid lines are meant to guide the eye and have no physical significance. (B) Loop formation rate constants, k_f, at 25 °C in 3 M gdnHCl plotted as a function of % Gly in Insert and grouped based on local sequence, His_Gly variants (○) or His_Ala variants (●), as in part A. The dotted line is meant to guide the eye and has no physical significance.

Figure 3A shows a decrease in loop breakage rate constants for inserts with low glycine content. For the His_Ala variants, the decreasing trend is more pronounced, reaching a minimum at 40% glycine content in the insert. Above this glycine content there is a significant increase in loop breakage rate constants. The trend is similar for the His_Gly variants, except the decrease in k_b is less pronounced at low glycine percentage with a minimum at 40% glycine content, as well. Furthermore, k_b does not increase significantly until >60% glycine content in the insert, for the His_Gly variants. A comparison of the kinetics data for the Gly4 and Gly4v2 variants (Table 1, Fig. 3A) suggests that the number of contiguous glycine residues adjacent to the histidine has a small but significant effect on k_b, as well.

Figure 3B shows that k_f increases modestly with increasing glycine content in the insert for both His_Ala and His_Gly combinations. While the propagated errors for variants that differ by one glycine clearly overlap, the NH5A and the Gly5 variants have significantly different values of k_f. In contrast to k_b, k_f depends within error, only on glycine content and not on the specific sequence.

Discussion

Does hydration or local sequence sterics make polyGly segments unexpectedly extended?

If local sequence sterics or backbone hydration, due to contiguous glycines, results in polypeptide chain extension in the denatured state, then the denatured state of our GlyX variants should be more expanded than expected.³⁷ If this is true, one might expect glycine percent in our insert to have a minimal effect on k_f. However, we observe a 25 ± 15% increase in k_f going from 0% (NH5A, k_f = 8910 ± 830 s⁻¹) to 100% (Gly5, k_f = 11,300 ± 480 s⁻¹) glycine in our insert. Also, if hydration or local sequence sterics cause poly-Gly segments to be extended, one might expect slower loop formation for contiguous versus non-contiguous glycines in the insert. Our observation, that Gly3 (9740 ± 460 s⁻¹) and Gly3v2 (9790 ± 1370 s⁻¹) variants have similar values for k_f, suggests otherwise. Similarly, the values of k_f are within error the same for the Gly4 variant (11230±500 s⁻¹) which has 4 contiguous glycines and Gly4v2 (10860±480 s⁻¹), which has the four glycines separated into two groups of two contiguous glycines by an alanine.

Thus, we see no clear evidence that hydration or local sequence sterics of poly-Gly segments causes such sequences to be as extended or more extended than poly-Ala segments.³⁷ Rather, as with previously published experimental and computational studies, the polyglycine stretches in our variants appear to be flexible enough to cause compaction of the denatured state permitting more rapid loop formation.^41,42

Effect of the sequence immediately adjacent to histidine on loop dynamics

Our data indicate that the amino acid adjacent to the histidine involved in His-heme loop formation has a significant effect on loop equilibria and breakage rates. In our equilibrium data (Figure 2B), the stability is uniformly lower (i.e., higher pK_a(obs)) for loops with a glycine next to the His which forms the loop than for those loops with an Ala next to the His which forms the loop. Comparison of loop formation rate constants, k_f, and loop breakage rate constants, k_b, (Figure 3) shows that the effect on equilibrium loop stability of the amino acid within the loop that is next to the histidine can be attributed primarily to k_b. The loop breakage rate constants, k_b, for the His_Gly variants are clearly larger than those of the His_Ala variants. The rate constants for loop formation, k_f, on the other hand are not sensitive to the amino acid next to the histidine (Figure 3B). Since glycine is more flexible than alanine, it is likely that the faster breakage rates for the Gly_His variants versus the His_Ala variants are due to lower main chain rotational barriers for glycine compared to alanine.³² The greater main chain flexibility of glycine residues likely allows the histidine ligand to swing away from the heme iron faster after the His-heme bond breaks than when alanine is next to the histidine. Although the effect is subtle, the enhanced flexibility effect seems to extend beyond the residue next to the His involved in loop formation. k_b for Gly4 (107.0 ± 1.8 s⁻¹, 3^rd residue from the His is Gly) is slightly faster than that of Gly4v2 (100.8 ± 3.8 s⁻¹, 3^rd residue from the His is Ala).

Sequence composition effects on the loop formation rate constant, k_f

As glycine content in a polypeptide chain increases, Flory’s characteristic ratio for an infinite chain, C_n(∞), decreases from a value of ~9 for alanine (and most other amino acids except proline) to ~2 for pure glycine.⁴³ C_n(∞) initially decreases rapidly as % Gly increases, dropping from 9 to 4 as % Gly increases from 0 to 30. The change is much more gradual above 30% Gly. As C_n(∞) decreases, the random coil is expected to be more compact and the rate of contact between two monomers separated by a given number of residues should increase. Thus, the increase in the rate of contact formation should be most pronounced as % Gly content increases from 0% to 30%. We note that Flory’s evaluation of the effect of % Gly on the characteristic ratio assumes that glycine is uniformly distributed through the chain. As discussed below, our variants do not satisfy this requirement and thus our results can be expected to deviate from Flory’s theory.

Kiefhaber and coworkers,^26,31,32 observed that poly(Ser) peptides (% Gly = 0, C_n(∞) = 9) have about 2- to 3-fold slower contact rates compared to poly(Gly-Ser) peptides (% Gly = 50, C_n(∞) = 3) for loop sizes ranging from 3 to 12 residues. For a set of peptides with a single Gly in the middle of a poly(Ser) chain ranging from 4 (% Gly = 25) to 12 residues (% Gly = 8.3), the rate constant for first contact of the loop ends (k_c in the terminology of Kiefhaber) moved progressively from near coincidence with the k_c versus loop size curve observed for poly(Gly-Ser) to coincidence with that for poly(Ser). While a % Gly series at a single loop size was not done in this study, the results suggest that a progressive decrease in k_c should be observed as % Gly decreases at a single loop size.

There are several key differences between our system and that of Kiefhaber and co-workers. First, His-heme loop formation is reaction limited not diffusion limited,^39,44 Thus, our values of k_f do not provide a measure of k_c. The magnitude of k_f does still scale with the end-to-end distance distribution of the chain and thus will reflect compaction of the chain due to increased chain flexibility. Second, the characteristic ratio, C_n, varies considerably with chain length for short chain lengths and the chain length at which it approaches C_n(∞) varies considerably with % Gly.⁴³ For poly(Ala), C_n reaches 90% of C_n(∞) at a chain length of 64 whereas C_n reaches 90% of C_n(∞) at a chain length of ~16 for poly(Gly-Ala) (% Gly = 50). Thus, C_n is not the same for the equivalent % Gly for our 22-residue loop and for Kiefhaber’s data for the chain lengths where poly(Gly-Ser) and poly(Ser) can be compared (chains of 3 to 12 residues). Finally, our insert is placed near the N-terminus of iso-1-cytochrome c in a segment of the protein with irregular and dynamic structure that can readily accept inserts.⁴⁵ Thus, unlike Kiefhaber’s system the glycines are not evenly distributed throughout the sequence. The 22 residue loop we study here is attached to the heme at Cys 14 and there are glycines in the natural sequence at positions 1 and 6. With the six amino acid insert, the Histidine is at position -8 (horse numbering) and the insert runs from positions -3 to -7. Flory’s theoretical treatment assumes an even (random) distribution of glycines, whereas in our system as we increase % Gly, the glycine content becomes skewed toward the N-terminus of our 22 residue loop. Thus, as discussed above, the % Gly dependence of k_f, for the set of variants we discuss in this work, is expected to deviate from the predictions of Flory’s theoretical treatment.

We do observe a modest increase in k_f as the glycine content increases (Figure 3B, Table 4). As noted earlier, k_f increases by 25 ± 15% in going from the NH5A variant (% Gly = 9) to the Gly5 variant (% Gly = 32). We expect that the uneven distribution of glycine residues in our 22-residue loop will affect the magnitude of the change in k_f, the question is by how much. Using Flory’s results on the effects of % Gly and chain length on C_n, we can estimate C_n at a chain length of 22, C_n(22), for a chain with an even distribution of glycines.⁴³ For the NH5A variant C_n(22) ~ 5.5 and for the Gly5 variant C_n(22) ~ 3.5. Using the Jacobson-Stockmayer equation,^36,46 we estimated in our previous report,³⁰ that this change in C_n(22) would lead to a decrease in the pK_a(obs) of 0.41 units which corresponds to an increase by a factor of ~2.6 in the equilibrium constant for loop formation. If we make the simplifying assumption that k_b is independent of sequence composition for a non-interacting random coil, then k_f should increase by a factor of ~2.6 for the Gly5 variant versus the NH5A variant. If we account for the observed changes in k_b (Table 4), an increase in k_f by a factor of ~3.1 would be expected. Thus, an even distribution of glycines would be expected to cause a 250 to 300% increase in k_f. Instead, we observe a 25 ± 15% increase in k_f. The skewed distribution of glycines in our insert clearly dampens the decrease in the end-to-end distance distribution of the Gly5 variant relative to the NH5A variant compared to what would be expected for an even distribution of glycine in the loop. Since Flory’s treatment of polypeptides assumes theta solvent condition, some of the deviation of our results from the predictions of Flory’s theory may result from 3 M gdnHCl not being a theta solvent for the denatured state of our protein.

Sequence composition effects on the loop breakage rate constant, k_b

The most notable observation in these data is the degree to which k_b varies. There is a factor of 1.45 difference between the largest and the smallest k_b (pH 3.00 data in Table 4). This variation is larger than that for k_f, indicating that k_b is more important in controlling the loop formation equilibrium.

As noted above, k_b is larger for the His_Gly than for the His_Ala series of variants. There is a reasonably constant factor of 1.20 ± 0.03 increase in k_b for the His_Gly versus the His_Ala variants for all values of % Gly in the insert (Figure 3A). This ~20% increase in k_b is likely due to lower rotational barriers about the main chain of glycine, as discussed earlier. However, the unusual dependence of k_b on % Gly in the insert indicates that there is more to the effect of glycine on chain dynamics than main chain rotational barriers. In both the His_Ala and His_Gly series of variants, k_b initially decreases. This observation is counter to what might be expected if glycine acted only to increase conformational space and the rate at which it is explored (rotational barriers).³² The initial decrease in k_b also argues against nucleation of α-helical structure when histidine binds to the heme as seen in several peptide model systems,^47–49 since glycine is a helix breaker.⁵⁰ The observed decrease in k_b for the first two Ala→Gly replacements suggests that the conformational flexibility of glycine allows the polypeptide chain to relax to a more stable conformer (perhaps allowing better interactions with the heme) than is possible with the all Ala insert. It is also possible that the first two glycines relieve strain in the loop, thus slowing loop breakage.

The increase in k_b for inserts with more than two glycines might be attributable to the increased rate of exploration of conformational space overtaking the effects of reduced loop strain or of conformational relaxation of the closed loop form of the chain to conformations with better stabilization by van der Waals interactions. It is also possible that decrease in the net stabilization possible by van der Waals interactions in the closed loop for the small glycine side chain versus the larger alanine side chain contributes to the increase in k_b as the number of glycines in the insert increases.

Compensation between k_f and k_b

In Figure 2B for both the His_Gly and the His_Ala variants, the pK_a(obs) decreases initially, but as the number of glycines in the insert increases above 2, pK_a(obs) levels out. The data in Figure 3 shows that both k_b and k_f are increasing as the pK_a(obs) levels out. Thus, at higher % Gly in the insert, the increases in k_f and k_b exactly compensate for each other such that the equilibrium for loop formation remains unchanged. For the range of overall percent glycine within the 22-residue loops studied here (9 to 32 %), this observation is inconsistent with the predictions of the Jacobson-Stockmayer equation.^36,46 This leveling out in pK_a(obs) is not expected to occur until above 30% glycine content. This inconsistency is likely due to the skewed distribution of glycines in our insert.

However, our observation of this compensation between k_f and k_b points out an interesting aspect of the effects of increased polypeptide chain flexibility (decreased C_n) on the probability of loop formation as given by the Jacobson-Stockmayer equation. As the chain becomes more flexible, initially, compaction of the chain dimension increases the probability of loop formation for a given loop size. However, it appears that as conformational space increases with increased glycine content, the time that any given contact can persist diminishes due to the proliferation of nearby conformations where the contact is broken. Compaction and diminished persistence appear to compensate nearly exactly at high flexibilities. Thus, the advantage conferred by increased glycine content for rapid formation of contacts and compaction of a polypeptide so that it can fold, saturates rapidly due to decreased contact persistence.

Guiding the initial stages of folding

The observation that loop breakage rates play a dominant role in modulating loop equilibria is consistent with our previous results on the kinetics of His-heme loop formation for a set of His-heme loops in the denatured state of iso-1-cytochrome c ranging in size from 16 to 83 amino acids.³⁹ We found that loop breakage rates varied by a factor of 5 and were primarily responsible for the deviations from random coil behavior for equilibrium loop formation in the denatured state in 3 M gdnHCl.

Rates of loop formation are sensitive to sequence composition, but appear to be insensitive to sequence order (Figure 3B). This observation argues that the speed at which contacts form is unimportant to the “folding code”. Rather what appears to be important to the “folding code” is whether a contact persists once it forms. Thus, the key to the “folding code” may be in understanding how local sequence order modulates rates of breakage of contacts as a protein folds.

From the perspective of a folding funnel, it is likely that many contacts form and break rapidly near the lip of the funnel. Early in folding, it will be the contacts with a greater tendency to persist that will begin the descent down the funnel. Experimental data for poly(Ser) or poly(Gly-Ser) peptides indicate that loops ranging in size from 3 to 11 residues form on a 5 to 25 ns timescales. Protein folding at its fastest occurs on an ~1 μs time scale.^51,52 Thus, simple loop formation is not what limits folding efficiency. Our data indicate that the key to efficiency and specificity of folding is in the relative persistence of early contacts. The idea that the folding of a protein involves forward and backward reactions (i.e., reversible equilibria) is not new. It has been clearly established in the misligation equilibria of cytochrome c,⁵³ the observation of equilibration between compact and extended forms of denatured iso-1-cytochrome c during folding,⁵⁴ and most recently in the observation of “backtracking” during the folding of interleukin-1β.⁵⁵ Thus, in considering a speed limit for folding, it is not just the forward rates but also backward rates of structure formation that must be considered, even for primitives structures such as loops.¹⁵

Conclusion

Using poly-Ala/Gly inserts near the N-terminus of iso-1-cytochrome c, we observe significant effects of local sequence on the kinetics and equilibria of loop formation. In particular the amino acid – Ala versus Gly – next to the histidine which forms the loop has a large effect on loop equilibria. The rate of loop breakage appears to play a dominant role in this effect. Our data indicate that increasing glycine content – even when skewed to one end of the residues involved in loop formation – increases the rate of loop formation. This observed increase in k_f does not provide support to the possibility that the main chain of poly-Gly sequences is more extended than previously thought due to backbone hydration or local sterics. Unlike rates of loop breakage, rates of loop formation are insensitive to local sequence effects. This observation suggests that the key to deciphering the “folding code” may lie in defining which of the contacts that can form actually persist, rather than in trying to discern what factors control how fast these contacts form.

Materials and Methods

Mutagenesis methods

All variants were made using the unique restriction site elimination method⁵⁶ as previously described.⁵⁷ The Gly1v2 variant was made using single-stranded pBTR1 vector DNA⁵⁸ carrying the NH5A variant of iso-1-cytochrome c as the template and the following primer: 5′-d(CAGCAGCAGCACCGTGGAATTCAG)-3′. The Gly3v2, Gly4v2 and Gly4v3 variants were made using single-stranded pBTR1 vector DNA carrying the Gly5 variant of iso-1-cytochrome c as the template and the following primers: 5′-d(GCCTTACCTGCACCAGCACCGTGGA)-3′, 5′-d(CTTACCGCCAGCGCCACCGTG)-3′ and 5′-d(GCCACCGCCAGCGTGGAATTCA)-3′, respectively. The EcoRV⁻ selection primer, 5′-d(GTGCCACCTGACGTCTAAGAAACC)-3′ was used together with each of these mutagenic primers in the mutagenesis reactions. It converts a unique EcoRV restriction site in the pBTR1 vector carrying the Gly5 and NH5A variants into an Aat2 restriction site.

Expression and purification of protein variants

Iso-1-cytochrome c mutant genes were expressed from BL21-DE3 Escherichia coli cells (Novagen) using the pBTR1 vector (provided by Grant Mauk at the University of British Columbia)^58,59 as previously described using standard protocols from our laboratory.^30,39 This vector co-expresses heme lyase to allow covalent attachment of heme to iso-1-cytochrome c in the cytoplasm of E. coli. Typical yields ranged from 30 – 45 mg per liter of culture, depending on the variant. As discussed previously,³⁰ cleavage of the protein near the N-terminus was minimized through diligent and rapid protein workups with sufficient protease inhibitor (3 mM PMSF) present in cell lysates. Cleavage is likely due to trace amounts of redox active metals.⁶⁰ It was effectively neutralized by adding 1.0 mM EDTA to all buffers used in protein isolation and purification.³⁰ Ultrafiltration devices were also pre-washed with EDTA-containing buffers before use. An Applied Biosystems Voyager–DE^™ PRO Biospectrometry Workstation MALDI-TOF instrument was used to verify the integrity of the isolated as well as purified iso-1-cytochrome c variants. The possibility of a metalloprotease co-eluting with the HPLC purified protein can likely be ruled out since rapid processing by ultrafiltration down to ~200 uL after HPLC purification also seems to arrest the cleavage process.

Proteins were oxidized with potassium ferricyanide just prior to each experiment and separated from the oxidizing agent by sephadex G-25 chromatography. The sephadex G-25 resin was equilibrated to a buffer appropriate to the experiment. All buffers used for experiments contained 1.0 mM EDTA. All proteins were analyzed by MALDI-TOF mass spectrometry, as described above, prior to and after each experiment to verify the integrity of the protein. If more than 10% degradation of the protein was observed, the experimental data were discarded and the experiment repeated with freshly purified protein.

Protein stability measurements

The stability of all variants was monitored at 25 °C as a function of gdnHCl concentration using an Applied Photophysics Chirascan circular dichroism spectrometer coupled to a Hamilton MICROLAB 500 Titrator using methods described previously.⁶¹ Data were acquired at pH 7.0 in the presence of 20 mM Tris, 40 mM NaCl as buffer with 1.0 mM EDTA to minimize protein cleavage. The data were fitted to a linear free energy relationship, as described previously,^27,62 to extract the free energy of unfolding in the absence of denaturant, ΔG^o′_u(H₂O), and the m-value. At low gdnHCl concentrations, slight increases in ellipticity at 222 nm have been observed possibly due to specific Cl⁻ binding.^63,64 The ellipticity subsequently levels off before the unfolding transition. Thus, a constant native state baseline has been used here as previously described.^27,62 Reported parameters are the average and standard deviation of three independent trials.

Equilibrium loop formation in the denatured state

Equilibrium loop formation in the denatured state (3 M gdnHCl, 5 mM Na₂HPO₄, 15 mM NaCl with 1.0 mM EDTA) was monitored through pH titrations using a Beckman DU800 UV-Vis spectrophotometer. All titrations were done at 3 μM protein concentration and at room temperature, 22 ± 1 °C. Spectra from 350 to 450 nm were acquired at each pH. Titration procedures have been described previously.²⁸ Data at 398 nm versus pH were fit to a modified form of the Henderson-Hasselbalch equation allowing extraction of the apparent pK_a for loop formation, pK_a(obs), and the number of protons, n, involved in the process. Reported parameters are the average and standard deviation of three independent trials.

pH dependent stopped-flow kinetic measurements

In order to monitor the breakage of the His-heme bond in the denatured state for all variants, stopped flow mixing methods were used (Applied Photophysics SX-20 spectrometer). Reaction progress was monitored by absorbance spectroscopy at 398 nm to observe the Soret band shift resulting from His-heme bond breakage.²⁸ All data were collected at 25 °C. For pH dependent His-heme bond breakage reactions, the 10 mm pathlength of the 20 μL flow cell was used. The final reaction mixture was obtained from 1:1 mixing of 6 μM protein, 3 M gdnHCl, 10 mM MES pH 6.2, 1.0 mM EDTA with 3 M gdnHCl, 100 mM glycine buffer containing 1.0 mM EDTA to achieve the desired ending pH of 3.0 or 3.5. All kinetics experiments were done the same day each variant was HPLC purified. This minimized the N-terminal cleavage of sensitive variants in the lower pH starting buffer (pH 6.2). Final reaction pH was determined by collecting the product of the mixing reaction and immediately measuring pH. Using the method of reduction of 2,6-dichlorophenolindophenol,⁶⁵ a 0.7 ms dead time was determined for the 20 μL flow cell under our mixing conditions. Loop breakage rate constants were obtained by adjusting the stop time to the dead time of the instrument and then removing data up to the first 3 ms to deal with an instrumental glitch. All data were fit to a single exponential rise to maximum equation. Double exponential fits were attempted but did not significantly improve the fit to the data.