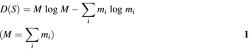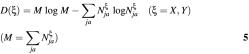Splice site prediction with quadratic discriminant analysis using diversity measure

Abstract

Based on the conservation of nucleotides at splicing sites and the features of base composition and base correlation around these sites we use the method of increment of diversity combined with quadratic discriminant analysis (IDQD) to study the dependence structure of splicing sites and predict the exons/introns and their boundaries for four model genomes: Caenorhabditis elegans, Arabidopsis thaliana, Drosophila melanogaster and human. The comparison of compositional features between two sequences and the comparison of base dependencies at adjacent or non-adjacent positions of two sequences can be integrated automatically in the increment of diversity (ID). Eight feature variables around a potential splice site are defined in terms of ID. They are integrated in a single formal framework given by IDQD. In our calculations 7 (8) base region around the donor (acceptor) sites have been considered in studying the conservation of nucleotides and sequences of 48 bp on either side of splice sites have been used in studying the compositional and base-correlating features. The windows are enlarged to 16 (donor), 29 (acceptor) and 80 bp (either side) to improve the prediction for human splice sites. The prediction capability of the present method is comparable with the leading splice site detector—GeneSplicer.

INTRODUCTION

The more comprehensive and accurate initial computational analysis performed for new genomic sequences, the less time-consuming and costly experimental work will have to be done to determine their functions. Several complex systems for predicting gene structure have been developed in recent years. The gene sequence often includes non-coding regions, called introns that are removed from the primary transcript during RNA splicing. The precise removal of introns from mRNA precursors is defined mainly by the highly conserved sequences near the ends of introns. Analysis shows that the overwhelming majority of splice sites contain conserved dinucleotides GT-AG: they start with the GT consensus dinucleotide (at the 5′ boundary) called a donor site and end with the AG consensus dinucleotide (at the 3′ boundary) called an acceptor site. And the other major group includes GC-AG pairs and a small number of other non-canonical splice sites.

The donor and acceptor splice signals are probably the most critical signals for accurate exon prediction. However, the splice signal alone is not enough for exon/intron boundary determination since many false splice sites are incorrectly predicted. To eliminate false positives and find missing true splice sites other information is needed. In fact, there are different compositional features between exons and introns (1,2). The standard method computes the probabilities of the bases in each position of junction region as if they were independent of adjacent bases (3). Most previous probabilistic models have assumed either independence between positions, e.g. the weight matrix method (WMM) model or dependencies between adjacent positions only, e.g. the weight array method (WAM) model (4,5). Inspired by the observation of apparent consensus at donor and acceptor sites researchers also proposed to make prediction using neural networks and Markov models (6,7). However, further studies showed that there are strong dependencies between non-adjacent as well as adjacent position around splice sites. Especially in donor sites almost three out of four of all base pairs exhibit significant dependence (8). The difficulty is further complicated by the limitation of high-quality data set. It was indicated that a training set of several hundred is not enough to estimate the transition parameters of high-order Markov models (9). To solve the problem, several new algorithms such as the maximal dependence decomposition method (MDD) (10), the Bayes network model (11) and the maximum entropy modeling combined with Bahadur expansion (9), etc., were proposed to improve the prediction. The latter two attempted to module splicing sites with pairwise correlations. Employing a combination of MDD and Markov modeling techniques, GeneSplicer introduced a new computational tool for detecting splice sites in eukaryotic mRNA (12). The comparison of GeneSplicer to other splice site predictors, such as NetPlantGene (13), NetGene2 (6,13), HSPL (14,15), NNSplice (16), GENIO (17,18), SpliceView (19), etc., indicates that GeneSplicer performs comparably with the best predictors for both human and Arabidopsis data.

Due to complex dependencies existing among most base pairs in splicing sites, and de facto impossibility of obtaining a large enough high-quality data set at the present stage, the accurate splice site determination is still a difficult problem and the development of new methods or improvement of existing methods is continuing to be expected (9,20).

Current gene prediction programs are sophisticated systems that integrate many different methods for identifying elements of genes. The widely used and recognized approach for genome annotation consists of employing first, homology method, also called ‘extrinsic methods’ or ‘similarity measure’, and secondly, ab initio recognition of gene elements, also called ‘intrinsic methods’ (21,22). In addition, two different types of information are currently used to locate genes in a genomic sequence. (i) Content sensors are measures that try to classify a DNA region into types, e.g. coding versus non-coding by use of statistical information. Many coding measures have been published (23,24). (ii) Signal sensors are measures that try to detect the presence of the conserved or functional sites specific to a gene (21,25). The combination of the above methods and information will achieve valuable improvements in prediction accuracy. In fact, any successful program for gene identification contains two important aspects: one is the type of information used by the program, and the other is the algorithm that is employed to combine that information into a coherent prediction.

In this article we shall introduce a new prediction model based on diversity measure that can synthesize different types of information, the splicing signals and the compositional and base-correlating features of exons and introns, and employ two types of method, intrinsic and extrinsic, automatically and simultaneously in a simple and unified approach. The diversity measure was first introduced and employed in biogeography (26,27). Recently, it was also applied in the recognition of protein structural class (28,29) and the combination of classifiers to improve the performance since the measure quantifies the dependence between classifiers (30). In the study of biogeography, the geographical distribution of species (the absolute frequencies of the species in different locations) forms a source of diversity. The more diverse the distribution is, the larger the diversity measure. To compare the distribution of two species one defines the increment of diversity (ID) by the difference of the total diversity measure of two systems and the diversity measure of the mixed system. It can be proved that the higher the similarity of two sources, the smaller the ID. So, the increment of diversity of two sources is essentially a measure of their similarity level. Here, we generalize the diversity increment method and combine it with the quadratic discriminant analysis (31) (called IDQD, increment of diversity combined with quadratic discriminant analysis) to identify and predict the splice sites. The comparison of compositional features and the base dependencies at adjacent or non-adjacent positions of two sequences (for example, one sequence before exon/intron boundary and one sequence after exon/intron boundary, or one standard set of exons or introns and another set of sequence whose property is to be predicted, etc.) can be integrated automatically in the diversity increment. Simultaneously, since in defining diversity increment a standard set of exons or introns is introduced and another sequence to be predicted is compared with the standard set, the method has followed the extrinsic as well as the intrinsic approach. Therefore, different kinds of sequence information and two types of methods have been integrated in a single formal framework, they are easy to implement and interpret. We will use 3000 genes in four model organisms to train and test the new system, namely Caenorhabditis elegans, Arabidopsis thaliana, Drosophila melanogaster and human. The method can be applied also to the detection of non-canonical sites but this work is dealing mainly with canonical ones.

MATERIALS AND METHODS

Gene collections

We used the Exon-Intron Database (32) to collect confirmed genes in several model genomes that include C.elegans, A.thaliana, D.melanogaster and human. The original data were taken from http://mcb.harvard.edu/gilbert/EID on December 27, 2002. Only fully annotated genes with experimental supporting evidence are collected. To decrease the possible errors in the data, we removed genes with unknown bases, genes containing a partial coding DNA sequence (CDS), genes whose total length of all coding sequences is not 3-multiple and genes with sequence overlapping to others. We also removed all genes with non-canonical (non GT/AG) splicing. After removing above entries, we have 185 genes of C.elegans, 749 genes of A.thaliana, 1196 genes of D.melanogaster and 1231 genes of human. Genes in each species are divided in 10% groups and a jack-knife procedure (10-fold cross-validation test, i.e. nine in ten groups for training and the other for test) will be done. The numbers of genes, exons and introns for each species are shown in Supplementary Material.

Definitions

Let m_i the absolute frequency of the i-th category. There are t categories corresponding to a space (called category space) of t dimension. Set S: {m_i | i = 1, …, t} the source of diversity and

the measure of diversity, which is a function of source S (26,27).

In general, for two sources of diversity in the same space of t dimension, X: {n₁, n₂, …, n_t} and S: {m₁, m₂, …, m_t}, the increment of diversity is defined by

ID(X,S) = D(X + S) – D(X) – D(S) 2

where D(X + S) is the measure of diversity of the mixed source X + S: {n₁ + m₁, n₂ + m₂, …, n_t + m_t}. Note that ID is a function of two sources. It can be proved that the increment of diversity satisfies

0 ≤ ID(X,S) ≤ D(N,M) 3

where D(N,M) is the maximum of ID(X,S),

D(N,M) = (N + M)log(N + M) – Nlog N – MlogM 4

(M = Σm_i, N = Σn_i).

Suppose that we shall distinguish with exons and introns. For the purpose of predicting a property of sequence S we should compare S with a standard set, which consists of sequences with property having been known. By calculating the number of four bases in three codon positions (or ideal codon positions) for all exons and introns we deduce two standard sources of diversity, X: {N_ja^X | j = 1,2,3; a = A,C,G,T} for exons and Y: {N_ja^Y | j = 1,2,3; a = A,C,G,T} for introns. Two standard measures of diversity [D(X) and D(Y)] corresponding to two standard sources of diversity can be deduced by use of similar equations as Equation 1, namely

Suppose that S is a DNA sequence the class of which is to be predicted. It also defines a source of diversity S in the same category space as X or Y and has a measure of diversity D(S). The increment of diversity for two sources of diversity S and X (or Y) is

ID(ξ,S) = D(ξ + S) – D(ξ) – D(S) (ξ = X,Y) 6

If

ID(λ,S) = Min{ID(X,S), ID(Y,S)} 7

then the sequence S is predicted to be in the class λ.

The measure and the increment of diversity described above (Equations 5 and 6) are defined based on the diversity source in the category space of 12 dimensions, three codon positions and four bases. The increment of diversity will be denoted as ID {3 × 4} (the notation in curved bracket after ID gives the dimension of category space for the corresponding diversity source). It can be generalized to several other forms in its application to gene recognition and splicing selection. Its possible generalizations are:

(i) ID {m × 4} (the increment of diversity for consensus sequences). In intron/exon boundary there is a conservative segment of length m. The frequencies of four bases occurred in the s-th site of all m-long sequences, N_sa (s = 1, …, m; a = A,G,C,T), form a diversity source. The measure of diversity is

Accordingly, the increment of diversity ID {m × 4} is defined.

(ii) ID {C₂^m × 4²}. The diversity source is composed of frequencies of 16 kinds of base-pair correlation occurred in m(m-1)/2 double-sites in all m-long sequences.

(iii) ID {C₃^m × 4³}. The diversity source is composed of frequencies of 64 base-triplets occurred in m(m-1)(m-2)/3! tri-sites in all m-long sequences.

(iv) ID {4³}. The diversity source is composed of the frequency of 64 codons or 64 triplets in a given DNA segment.

There are several types of information currently used to locate genes in a genomic sequence—the intrinsic content sensors, the extrinsic content sensors and the signal sensors, etc. (20,21). The privilege of the diversity measure method is the synthesis of different types of information in a single approach. ID {3 × 4} is useful in studying base composition in three codon positions and ID {4³} useful in studying base composition and correlation in triplet, they are suitable for using content sensors in gene prediction; ID {m × 4}, ID {C₂^m × 4²} and ID {C₃^m × 4³} are the increment of diversity for consensus sequences, they are suitable for using signal sensors in boundary determination. Moreover, since the diversity source is defined for some standard set composed of sequences of a given class the corresponding ID method implies a similarity based approach. In combining above diversity measures and increments through IDQD (31) one can differentiate between exons and introns and find their boundaries.

IDQD of splice sites by using increment of diversity

The information used in exon/intron identification is mainly extracted from two classes of diversity source. The first class source is built from base composition, pairwise correlation and triplet correlation at seven sites in donor consensus sequence (namely, XGTXXXX), and eight sites in acceptor consensus sequence (namely, XXXXXXAG). They describe the base conservation near splice sites. The second class source is built from triplet frequency in L₁-base-long sequence before exon/intron or intron/exon boundary (including AG in intron/exon boundary, called L₁ sequence) and that in L₂-base-long sequence after exon/intron or intron/exon boundary (including GT in exon/intron boundary, called L₂ sequence). L₁ = L₂ = 48 will be taken in the following calculation. They describe the compositional and base-correlating feature in a sequence around splice site. The first class increment of diversity includes ID {m × 4}, ID {C₂^m × 4²} and ID {C₃^m × 4³} with m = 5 for donor case and m = 6 for acceptor case. The second class increment of diversity includes ID{4³} in different combinations of the standard source of diversity and the diversity source of DNA sequence to be predicted. (ID{3 × 4} instead of ID{4³} has been used in our calculation. But the latter is better, so we will confine ourselves in ID{4³}.) Plainly saying, in our algorithm for exon/intron identification (IDQD) eight feature variables around a potential splice site are defined by eight increments of diversity ID₁ to ID₈. They are listed in Table 1. For example, the first variable ID₁ is the increment of diversity of ID{m × 4} type, which is defined by two sources, a diversity source constructed from the consensus sequence with potential splice site (GT or AG) and a standard source of diversity constructed from all consensus sequences of true (donor or acceptor) splice sites in training set. The quantity can be calculated by use of Equation 6 where the diversity measure is deduced from Equation 8.

Table 1. Eight increments of diversity used in exon/intron identification.

ID notation	ID type	Source of information	ID defined by two sources
			First source	Second source
ID1	ID {m × 4}	7 or 8 bases around splice site	Potential splice site region	All true splice site region
ID2	ID {C2m × 42}	7 or 8 bases around splice site	Potential splice site region	All true splice site region
ID3	ID {C3m × 43}	7 or 8 bases around splice site	Potential splice site region	All true splice site region
ID4	ID{43}	48 bases before potential and true boundary	Potential splice site region (L1 sequence)	All true splice site region (L1 sequences)
ID5	ID{43}	48 bases before potential and after true boundary	Potential splice site region (L1 sequence)	All true splice site region (L2 sequences)
ID6	ID{43}	48 bases after potential and before true boundary	Potential splice site region (L2 sequence)	All true splice site region (L1 sequences)
ID7	ID{43}	48 bases after potential and true boundary	Potential splice site region (L2 sequence)	All true splice site region (L2 sequences)
ID8	ID{43}	48 bases before and after potential boundary	Potential splice site region (L1 sequence)	Potential splice site region (L2 sequence)

The definitions for eight IDs are shown in the table. The second column gives the ID type. The third column gives the location of the source of information that is necessary for defining ID. As a rule, each ID is defined by two diversity sources (Equation 2 of the text). The last two columns indicate two sources where ‘potential splice site region’ refers to a sequence to be identified and ‘all true splice region’ refers to all sequences (exons or introns) in standard set.

Since there are eight feature variables for a sample to be identified, each potential splice site is then characterized by a vector of eight dimensions, corresponding one-to-one to the eight variables (ID₁ to ID₈) defined above. We compute the vector values for all the potential splice sites in the training set, and divide in two groups: true and false splice sites. Next, given a problem (or a test) of splice site, we apply IDQD to classify it as a true or false splice site, according to its vector values. The increment of diversity (ID_j, j = 1, …, 8) averaged over true group or false group in training set is denoted by µ₁ and µ₂, respectively. The corresponding covariance in true group or false group is represented by 8 × 8 matrix Σ₁ or Σ₂, respectively. For a potential splice site to be identified, the increment of diversity is denoted by X. Following IDQD (28), the discriminant function that differentiates with the potential site X belonging to true group or false group is given by

where p and q denote numbers of samples in the true and false group respectively and |Σ| is the determinant of matrix Σ. Due to the mutual independence among these eight variables we have not found the singularity of matrix Σ. So there is no problem in calculating Equation 9. δ_i is the squared Mahalanobis distance between X and µ_iwith respect to Σ_i. In the common use of IDQD the threshold of ξ is 0; that is, the discriminating rule assigns X to true group if ξ >0. The decision rule is simply based on the comparison of posteriori probabilities of two groups for given X. However, in present case the 5′ splice site and 3′ splice site should match each other to make a correct exon/intron identification. We lose the optimal condition ξ >0 introduced for 5′ splice site or 3′ splice site alone. Let the threshold of ξ being ξ_D for donor and ξ_A for acceptor, that is, the potential 5′ splice site is assigned to the donor candidate group if ξ > ξ_D, and the potential 3′ splice site is assigned to the acceptor candidate group if ξ > ξ_A. Then from the matching between these two groups in a gene we determine the splice sites. Both parameters ξ_D and ξ_A are computed from the training set. In the jack-knife procedure, the 10-fold cross-validation test will be done and the optimal values ξ_D and ξ_A will be chosen through the comparison of fitted values in 10 computations (see Supplementary Material).

RESULTS

The prediction accuracy for the splice sites of genes in training set and testing set are estimated by two approaches. In the first approach (on the exon basis), we compute the number of exons whose boundaries are both predicted correctly, denoted by N₁, and the number of exons whose only one boundary is predicted correctly, denoted by N₂. The number of observed exons is denoted by N_exon and the number of predicted exons by N_pre-exon. We define sensitivity and specificity as follows

Sn = (2N₁ + N₂)/2N_exon

Sp = (2N₁ + N₂)/2N_pre-exon. 10

In the second approach (on the nucleotide basis), we check the assignment of each base to exon or intron one by one. For a nucleotide in exon or intron, if the assignment is true we denote it as E_t or O_t; otherwise, E_f or O_f. The percentages of nucleotides predicted correctly in exon and intron are

Ac(e) = (number of E_t) / (number of E_t + number of E_f)

Ac(o) = (number of O_t) / (number of O_t + number of O_f),

respectively. The percentage of nucleotides predicted correctly in whole genes is

Ac(all) = (number of E_t + number of O_t) / (number of E_t + number of E_f + number of O_t + number of O_f). 11

The prediction sensitivity, specificity and accuracy are dependent on parameter ξ_D and ξ_A. They are computed from the maximization of the prediction accuracy in training set. The optimal values are: (ξ_D, ξ_A) = (–10,–4) for C.elegans, (–5,–5) for A.thaliana, (–3,–5) for D.melanogaster and (–4,–1) for human (see Supplementary Material).

Given the values of parameter ξ_D and ξ_A as above the prediction results for C.elegans, A.thaliana, D.melanogaster and human in 10-fold cross validation are shown in Table 2. The average sensitivity, specificity and accuracy are shown in third to seventh columns of the table and their standard deviations given in brackets. For comparison the sensitivity, specificity and accuracy are also calculated in setting ξ_D = ξ_A = 0 and the results are listed in the lower half of the table.

Table 2. The accuracy of prediction for splice sites in 10-fold cross validation.

Species	(ξD ξA)	Sn (%)	Sp (%)	Ac(e) (%)	Ac(o) (%)	Ac(all) (%)
C.elegans	(–10,–4)	94.6(1.32)	96.6(0.88)	97.4(2.28)	96.7(1.87)	96.9(1.82)
A.thaliana	(–5,–5)	92.6(0.96)	94.8(0.71)	97.8(0.93)	97.6(0.96)	97.7(0.65)
D.melanogaster	(–3,–5)	95.4(1.16)	97.6(0.63)	96.9(1.75)	96.6(2.82)	96.8(1.70)
Human	(–4,–1)	86.8(0.75)	89.6(1.68)	91.0(1.50)	94.3(0.93)	93.8(0.95)
C.elegans	(0,0)	88.5(2.30)	97.7(0.98)	95.8(1.62)	95.0(2.39)	95.3(1.51)
A.thaliana	(0,0)	86.3(0.89)	96.0(0.67)	94.8(1.03)	94.0(1.85)	94.5(1.23)
D.melanogaster	(0,0)	92.3(1.75)	98.1(0.52)	94.4(2.38)	94.9(2.38)	94.6(2.08)
Human	(0,0)	82.4(1.06)	91.9(1.21)	89.0(1.44)	94.2(0.83)	93.4(0.87)

The average and deviation (in parentheses) for each accuracy parameter in 10 computations in 10-fold cross validation are listed. In the upper half of the table the parameters (ξ_D ξ_A) are computed from training set and in the lower half they are assumed to be 0.

To compare our approach with current splice site detector—GeneSplicer, we use a 3-fold cross-validation in all above data to estimate the splice site detection accuracy following the method given in (12). The data set includes all sequences containing the consensus GT or AG dinucleotide. The set is randomly divided into three disjointed subsets and the numbers of gene, true and false donor and true and false acceptor present in the data are shown in Supplementary Material. Here ‘false’ splice site means a sequence containing the consensus GT or AG dinucleotide that was not annotated as a splice site. For a given subset in the partition, we use all data outside the subset to train and then test the program on the data in the subset. The reported accuracy represents the average of the accuracies computed on all three subsets. As in (12), for a given false negative rate (the percentage of true sites missed) we calculate the false positives as a measure to estimate the prediction accuracy. In this estimation of prediction accuracy the matching between donor and acceptor has not been considered. So, in calculating the false positives we use IDQD by setting ξ_D = ξ_A = 0 to distinguish between true and false. The results for C.elegans, A.thaliana, D.melanogaster and human are given in Table 3. The prediction for A.thaliana and human by use of GeneSplicer was made before and the results were published in (12). For comparison they are also listed in brackets in the table. (Note that the false negative rate has been set to be the same in two works and the comparison should be carried out for false positives.)

Table 3. False negative and false positive rates for acceptor and donor site detection in four species.

	True sites missed	False positives (%)
	(%)	C.elegans	A.thaliana	D.melanogaster	Human
Acceptor site (ag) detection	3	1.69	6.65(11.7)	1.70	4.52(9.3)
	5	0.72	2.89(4.9)	0.79	2.26(5.8)
	7	0.29	1.92(3.3)	0.48	1.46(4.7)
	8	0.26	1.65(2.9)	0.42	1.22(4.3)
	10	0.14	1.25(2.4)	0.33	0.92(3.7)
	15	0.05	0.74(1.6)	0.22	0.49(2.6)
	20	0.02	0.54(1.1)	0.13	0.30(1.9)
	30	0.02	0.31(0.7)	0.07	–
	40	–	–	–	0.09(0.8)
Donor site (gt) detection	3	5.59	3.93(4.7)	2.09	10.07(14.7)
	5	3.36	2.37(2.8)	0.93	7.00(6.4)
	7	2.47	1.69(1.9)	0.61	5.28(4.8)
	8	2.08	1.52(1.7)	0.55	4.86(4.1)
	10	1.36	1.27(1.4)	0.40	3.97(3.5)
	15	0.72	0.83(0.9)	0.29	2.44(2.5)
	20	0.51	0.61(0.6)	0.19	1.57(1.8)
	30	0.23	0.37(0.4)	0.09	–
	40	–	–	–	0.31(0.7)

For C.elegans the data include 953 donor and 953 acceptor sites, 51 624 false donors and 36 642 false acceptors; for A.thaliana 3533 donors and 3533 acceptors, 141 850 false donors and 91 525 false acceptors; for D.melanogaster 2526 donors and 2526 acceptors, 229 344 false donors and 118 631 false acceptors; for human 5604 donors and 5604 acceptors, 765 291 false donors and 511 333 false acceptors. For a given false negative rate (the percentage of true sites missed) the false positives are calculated. The values in parentheses are taken from (12) for comparison.

To generalize our method to non-canonical splice site prediction we collected 103 genes containing non-standard splicing for human, 65 for D.melanogaster, 143 for A.thaliana and 22 for C.elegans, called non-standard set (32). Considering GT/AG and GC/AG consensus sequences as the potential splice sites, using the same method given above and the same parameters obtained from previous training set we identify the splice sites (GT/AG type and GC/AG type only, other types of non-canonical splicing not considered) in non-standard set. The results are: accuracy Ac(all) on nucleotide basis, 93.6% for human, 88.2% for D.melanogaster, 93.4% for A.thaliana and 97.8% for C.elegans; sensitivity Sn on exon basis, 71.9% for human, 67.6% for D.melanogaster, 76.9% for A.thaliana and 80.1% for C.elegans; and specificity Sp on exon basis, 74.7% for human, 72.4% for D.melanogaster, 79.5% for A.thaliana and 81.5% for C.elegans.

In the above IDQD algorithm, seven sites in donor consensus sequence, eight sites in acceptor consensus sequence and 48-base-long L₁ and L₂ sequences around splice sites are studied. If the widths of window are enlarged, namely, enlarged to 16 sites around donor, 29 sites around acceptor and 80-base-long L₁ and L₂ sequences, then the prediction capability will be further improved. [These width values are comparable with those adopted in (12).] To lessen the labor we applied the same algorithm but 2-fold cross validation to human case. By utilizing information stored in sequences in the enlarged windows we obtain the prediction accuracy as follows: sensitivity Sn = 90.7%, specificity Sp = 95.4%, accuracy on nucleotide basis Ac(all) = 92.3%. In above statistics the best-fit parameters are calculated from the training set, ξ_D = –9, ξ_A= –2. If ξ_D = –4, ξ_A = –1 are taken (as in previous smaller window case), then the prediction accuracy changes to Sn = 88.3%, Sp = 96.3%, Ac(all) = 91.4%.

DISCUSSION

Based on the conservation of nucleotides and the feature of base composition and base correlation around splice sites GT/AG, we applied the method of increment of diversity combined with IDQD to the prediction of gene structure and identification of exon/intron boundaries for four model species. In the method, only two parameters ξ_D and ξ_A are introduced and need to be decided for a given species. We have studied the dependence of prediction sensitivity, specificity and accuracy on the choice of ξ_D and ξ_A. In the range of ξ_D from 0 to –10 and ξ_A from 0 to –5 (for human ξ_A from 0 to –3) the prediction sensitivity changes about 4–7 points, specificity changes about 1–11 points and the prediction accuracy Ac(all) about 2–3 points. For human the accuracy parameters decrease rapidly as ξ_A < –3. We also found that these accuracy parameters could not increase as ξ_D and ξ_A further changed (up to –15 for ξ_D and –10 for ξ_A). By calculating the average of Sn and Sp, (Sn + Sp)/2, and Ac(all) in the test set and comparing the best-fit values of ξ_D and ξ_A in 10 computations we obtain the optimal values for these two parameters in four species (see Supplementary Material). Using these values as input we obtain the prediction accuracy for test set Sn = 94.6%, Sp = 96.6% and Ac(all) = 96.9% for C.elegans; Sn = 92.6%, Sp = 94.8%, Ac(all) = 97.7% for A.thaliana; and Sn = 95.4%, Sp = 97.6%, Ac(all) = 96.8% for D.melanogaster. For human, we obtain Sn = 86.8%, Sp = 89.6% and Ac(all) = 93.8% (lower than other three species).

The above results are obtained in 10-fold cross validation. However, the reported accuracy does not much depend on the design of the test. We have made the same calculations in 2-fold cross validation. The results of prediction sensitivity, specificity and accuracy are in full agreement with those in 10-fold cross validation (differences lower than 1–2 points for most cases). So, in using enlarged window to improve the prediction we are restricted to the 2-fold cross validation. Utilizing the information in the enlarged window and making the 2-fold calculation for human we obtain the prediction sensitivity, specificity and accuracy all higher than 90%.

From Table 2 we also find that even in ξ_D = ξ_A = 0 case, in the non-parametric discrimination, the prediction accuracies are not low. This indicates the efficiency of the IDQD method. However, introduction of adjustable parameters ξ_D and ξ_A would increase prediction accuracy Ac(all) by 1–3 points and sensitivity Sn by 3–6 points.

The prediction capability of a splice site detector can be estimated by different methods. Apart from the method we proposed in the article one may calculate the false positives for a given false negative rate, since under given false negative rate (missing a given number of true splice sites as the threshold) the false positive rates of a splice site detector reflect its prediction capability. The lower the false positive rate, the higher the prediction accuracy. Pertea et al. introduced the GeneSplicer, a leading detector, to predict the splice site for A.thaliana and human (12). By setting the false negative rate to be the same as other detectors and then comparing the differences in false positives, GeneSplicer reported fewer falsely predicted sites in many cases. By use of the same method we calculated the false positive rate under given false negative rate and compare our algorithm with GeneSplicer. For A.thaliana, 15 in 16 cases the false positive rate obtained from IDQD is lower than that deduced from GeneSplicer. For human, the number is 12 in 16. Moreover, the score is counted based on non-parametric discrimination. In fact, introduction of parameters ξ_D and ξ_A in IDQD would further increase prediction accuracy Ac(all) and sensitivity Sn. Thus, the prediction capability of the present IDQD method is comparable with the leading splice site detector—GeneSplicer.

Using the false positive rates as an index of the prediction capability, from Table 3 we find the prediction capability of IDQD for 3′ splice sites (acceptor) generally higher than 5′ splice sites (donor). But for A.thaliana, the donor prediction seems better than acceptor on average. For acceptor, the order of prediction capacity from high to low is: C.elegans first, then D.melanogaster, human and A.thaliana. For acceptor, the order is: D.melanogaster first, then A.thaliana, C.elegans and human.

Most splice site prediction methods published previously have not been applied to cases with non-canonical (non-GT/AG type) splicing. However, in principle, the non-canonical splicing sites can be predicted by IDQD method. We have reported the preliminary results of non-canonical splice site prediction with a considerable accuracy. If all non-canonical splice sites in non-standard set in addition to GC/AG type are considered, we expect the prediction accuracy will be further increased.

Bernaola-Galvin et al. used Jensen-Shannon divergence to find the border between coding and non-coding in a DNA sequence (33). The divergence is defined by the entropic difference between the total sequence and its two segments. This is an ‘entropic segmentation method’ as they stated. However, the ID defined in our paper is related to the difference between the entropy sum of a sequence and a standard set of coding sequences (exons) or non-coding sequences (introns) and the entropy of the mixed system. So, the ID is essentially a measure of entropy increase as a sequence merged to a standard source. Two methods are different in their application though both they start from the Shannon entropy. In fact, the information contained in a single DNA sequence is not enough to make a differentiation between exons and introns of that sequence. Following our experience, it is possible probably to differentiate between coding and intergenic segments in prokaryotic and the yeast genome by only using the information of a single sequence (24), but it is impossible to differentiate between exons and introns and find their borders in a genome of higher organism without reference to homology comparison or similarity measure. The advantage of the ID method is the utilization of content measure, signal measure and similarity measure synthetically in a simple and unified approach. From a theoretical point of view the source of diversity is essentially an informational source and thus the ID is a quantity based on the comparison of two informational sources. One knows that the mutual information is such a quantity that describes how to extract information regarding b from source a if the conditional probability p(b|a) is known. But, different from mutual information, ID describes other relations between two informational sources. So, the use of ID provides new possibilities for investigators.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.