On Estimating Diagnostic Accuracy From Studies With Multiple Raters and Partial Gold Standard Evaluation

Abstract

We are often interested in estimating sensitivity and specificity of a group of raters or a set of new diagnostic tests in situations in which gold standard evaluation is expensive or invasive. Numerous authors have proposed latent modeling approaches for estimating diagnostic error without a gold standard. Albert and Dodd showed that, when modeling without a gold standard, estimates of diagnostic error can be biased when the dependence structure between tests is misspecified. In addition, they showed that choosing between different models for this dependence structure is difficult in most practical situations. While these results caution against using these latent class models, the difficulties of obtaining gold standard verification remain a practical reality. We extend two classes of models to provide a compromise that collects gold standard information on a subset of subjects but incorporates information from both the verified and nonverified subjects during estimation. We examine the robustness of diagnostic error estimation with this approach and show that choosing between competing models is easier in this context. In our analytic work and simulations, we consider situations in which verification is completely at random as well as settings in which the probability of verification depends on the actual test results. We apply our methodological work to a study designed to estimate the diagnostic error of digital radiography for gastric cancer.

1. Introduction

Diagnostic and screening tests are important tools of modern clinical decision making. These tests help to diagnose illness to initiate treatment (e.g., a throat culture for streptococcal infection) or to identify individuals requiring more extensive follow-up (e.g., mammography screening for breast cancer). Estimation of sensitivity and specificity, measures of diagnostic accuracy, requires knowledge of the true disease state, which is assessed by a gold or reference standard. (Throughout, we use both “gold standard” and “reference standard” to mean the accepted standard for diagnosis.) Gold standard evaluation may be expensive, time consuming, or unethical to perform on all subjects and is commonly difficult to obtain in clinical studies. Latent class models offer a tempting alternative because assessment of the true status is not necessary. However, it has been shown that latent class models for estimating diagnostic error and prevalence may be problematic in many practical situations (Albert and Dodd 2004). Specifically, they showed that, with a small number of tests, estimates of diagnostic error were biased under a misspecified dependence structure, yet in many practical situations it was nearly impossible to distinguish between models based on the observed data. The lack of robustness of these models is problematic; however, the limitations of obtaining gold standard are a practical reality and reasonable alternatives are desirable.

Although it may be difficult to obtain the gold standard on all subjects, in many cases, it may be feasible to obtain gold standard information on a fraction of subjects (partial gold standard evaluation). In radiological studies, for example, gold standard evaluation usually requires multiple radiologists simultaneously examining images and clinical information. This may be an infeasible proposition for many studies to collect the gold standard on all subjects. However, it may be feasible to obtain gold standard information on a fraction of study subjects. Thus, methodological approaches that incorporate partial gold standard information may be an attractive alternative to latent class modeling.

Our application is a medical imaging study to compare conventional and digital radiography for diagnosing gastric cancer (Iinuma et al. 2000). In this study six radiologists evaluated 225 images on either conventional (n = 112) or digital (n = 113) radiography, to compare the sensitivity and specificity across techniques and radiologists. A gold standard evaluation was obtained from three independent radiologists simultaneously reviewing clinical information along with all imaging data to provide a reference truth evaluation of the image. Specifically, these radiologists reviewed clinical information such as patient characteristics, chief symptoms, purposes of the examination, endoscopic features, and histologic findings in biopsy specimens. This time-consuming consensus review was done on all 225 images, although this may not be feasible in larger studies or in other studies with more limited resources. Rater-specific as well as overall sensitivity and specificity were estimated by treating the consensus review by the three independent radiologists as gold standard truth. Our methodological development will focus on the data from this study.

Although our primary example is in radiology, the problem occurs more generally in medicine. For example, similar problems exist for the evaluation of biomarkers in which one wishes to compare the diagnostic accuracy of a series of tests, where a gold standard exists, but is very expensive. See, for example, Van Dyck et al. (2004), in which a set of tests for herpes simplex virus type 2 (HSV-2) was compared, but only a subset of samples was verified with the reference standard Western blot.

In this article we extend two classes of models, originally proposed for modeling diagnostic error on multiple tests without a gold standard (Albert and Dodd 2004), to the situation of estimating diagnostic error for a partially verified design. We examine the robustness of these models to the assumed dependence structure between tests. In particular, we examine bias and model selection using asymptotic results and simulation studies. We examine whether observing gold standard information on a small percentage of cases improves the lack of robustness to assumptions on the dependence between tests found when modeling without a gold standard. In Section 2 we describe our approach, which considers various models for the dependence between tests. In Section 3 we fit the various classes of models to the gastric cancer dataset and show that the results are quite different when we use the reference standard evaluation or when we model without a gold standard. In Section 4 we investigate the asymptotic bias from misspecifying the dependence structure under full as well as partial reference sample evaluation. Simulations examining the finite sample properties of partial reference sample verification are described in Section 5. We illustrate the effect of partial reference sample verification using the gastric cancer dataset in Section 6. A discussion follows in Section 7 in which we make general recommendations.

2. Models

Let Y_i = (Y_1i, Y_i2, …, Y_iJ)′ be dichotomous test results for individual i, i = 1, 2, 3, …, I, with Y_ij denoting the result from the j th of J tests. We denote by d_i the true unobserved disease status for patient i and by v_i an indicator of whether the ith patient is verified by a reference standard (v_i = 1 if verified and v_i = 0 otherwise). When a patient is verified, the contribution to the likelihood is L_i = P(v_i = 1|Y_i) P(Y_i|d_i) P(d_i). Similarly, when a patient is not verified, the contribution is $L_i=P(v_i=0|{\text{Y}}_i){\sum }_{l=0}^{1}P({\text{Y}}_i|d_i=l)P(d_i=l)$. In a general form, if the verification mechanism is fixed by design (i.e., is not estimated from the data) and does not share parameters with the probability of disease P(d_i) or the diagnostic accuracy P(Y_i|d_i), then the contribution of the ith patient to the likelihood (L_i) is proportional to

$$L_i\propto [P({\text{Y}}_i|d_i)P{(d_i)]}^{v_i}{\left[\sum _{l=0}^{1}P({\text{Y}}_i|d_i=l)P(d_i=l)\right]}^{1-v_i},$$ (1)

where P(d_i = 1) is the disease prevalence, which will be denoted by P_d.

There are three types of verification processes. First, consider verification that is completely at random, which occurs if the verification process is a simple random sample chosen independently from the test results Y_i. The proportion of individuals verified is denoted by r, where r = P(v_i = 1). Second, consider verification in which the probability of verification depends on Y_i, which we denote as r_Yi = P(v_i = 1|Y_i). Of particular interest is when the probability of verification depends on the number of positive tests, $r_s=P(v_i=1|{\sum }_{j=1}^J{y}_{ij})$, s = 1, 2, …, J. This type of verification has been referred to as verification biased sampling (Pepe 2003). An important special case, called extreme verification biased sampling, occurs when the gold standard test is obtained only on test-positive subjects because it requires an invasive procedure such as surgery, which is unethical to perform on all subjects if the experimental tests Y_i are negative. Various authors have proposed models for analyzing the results of two tests under extreme biased sampling (Walter 1999; Hoenig, Hanumara, and Heisey 2002; van der Merwe and Maritz 2002). The third type of verification occurs when the probability of verification depends on the true disease status, which is only known for those patients verified, denoted by r_di = P(v_i = 1|d_i). This so-called, nonignorable verification has been discussed by various authors, including Kosinski and Barnhart (2003) and Baker (1995). We focus only on the first two types of verification processes.

We consider two different ways to specify P(Y_i|d_i) that were originally developed for estimating diagnostic error without a gold standard. The Gaussian random effects and finite mixture models, which both have attractive features, are very different formulations for describing conditional dependence between tests. The Gaussian random effects (GRE) model (Qu, Tan, and Kutner 1996) introduces dependence across tests by assuming that (Y_ij|d_i, b_i) are independent Bernoulli with proportion given by Φ(β_jdi + σ_dib_i), where the random variables b_i are standard normal and Φ is the cumulative distribution function of a standard normal distribution. Under this model, $P({\text{Y}}_i|d_i)=\int \{{\prod }_{j=1}^{J}P(Y_{ij}|d_i,b)\}\phi (b)db$, where φ(b) is the standard normal density. Under the GRE model, the sensitivity and specificity of the j th test is given by $\Phi ({\beta }_{j1}/\sqrt{1+{\sigma }_1^2})$ and $1-\Phi ({\beta }_{j0}/\sqrt{1+{\sigma }_0^2})$, respectively. A substantially different model for incorporating dependence is the finite mixture (FM) model (Albert et al. 2001; Albert and Dodd 2004) in which some individuals who are truly positive are always classified as positive by any test whereas others are subject to diagnostic error. Similarly, some truly negative subjects are always classified as negative by any test whereas others are subject to diagnostic error. Let l_idi be an indicator of whether the ith subject, given disease status d_i, is always classified correctly, so that l_i1 = 1 when a true positive subject is always positive and l_i0 = 1 when a truly negative is always rated negative. Further, define η₀ = P(l_i0 = 1) and η₁ = P(l_i1 = 1). Test results Y_ij, given d_i and l_idi, are independent Bernoulli with probability

$$P\left(Y_{ij}=1|d_i,l_{i{d}_i}\right)=\{\begin{array}{cc}1\hfill & \text{if}{d}_i=1\text{and}{l}_{i1}=1\hfill \\ 0\hfill & \text{if}{d}_i=0\text{and}{l}_{i0}=1\hfill \\ {\omega }_j(1)\hfill & \text{if}{d}_i=1\text{and}{l}_{i1}=0\hfill \\ 1-{\omega }_j(0)\hfill & \text{if}{d}_i=0\text{and}{l}_{i0}=0,\hfill \end{array}$$ (2)

where ω_j(d_i) is the probability of the j th test making a correct diagnosis when the individual is subject to diagnostic error (l_i1 = 0 or l_i0 = 0). Under the finite mixture model, the sensitivity and specificity of the j th test are η₁ + (1 − η₁)ω_j(1) and η₀ + (1 − η₀)ω_j(0), respectively. Under both the GRE and the FM models, estimates of a common sensitivity and specificity across J tests can be obtained by assuming β_0l = β_1l = ⋯ = β_Jl = β₁ and ω₁(l) = ω₂(l) = ⋯ = ω_J(l) = ω(l) for l = 0, 1.

Depending on the application, the FM or the GRE model may better describe the dependence structure between tests. Both models need to be compared with a simple alternative, which is nested within both of these conditional dependence models. The conditional independence (CI) model, which assumes the tests are independent given the true disease status, provides such an alternative. The GRE model reduces to the CI model when σ₀ = σ₁ = 0, whereas the FM model reduces to the CI model when η₀ = η₁ = 0.

For each of the models, estimation is based on maximizing $L={\prod }_{i=1}^I{L}_i$, where L_i is given by (1). Standard errors can be estimated with the bootstrap (Efron and Tibshirani 1993).

3. Analysis of Gastric Cancer Data

We estimate the prevalence, sensitivity, and specificity of digital radiography for gastric cancer using the likelihood in (1) and the GRE, FM, and CI models, under both complete and no verification. Table 1 shows the overall estimates of prevalence, sensitivity, and specificity for digital radiography with the consensus measurements as a gold standard and with no gold standard. Estimates were obtained by assuming a common sensitivity and specificity across the six raters and were derived under the CI model, as well as the GRE and FM models. Bootstrap standard errors are also presented under each model. Interestingly, under complete verification, overall estimates of prevalence, sensitivity, and specificity, as well as their bootstrap standard errors, were nearly identical across the three classes of models. In addition, these estimates were identical to estimates obtained by Iinuma et al. (2000) using generalized estimating equations (Liang and Zeger 1986), a procedure known to be insensitive to assumptions on the dependence structure between tests. These results suggest that estimates of prevalence, sensitivity, and specificity are insensitive to the dependence structure between tests under complete verification. When no gold standard information is incorporated, estimates of prevalence and diagnostic error differ across models for the dependence between tests. This is consistent with results by Albert and Dodd (2004) who showed that diagnostic error estimation may be sensitive to assumptions on the dependence between tests when no verification is performed.

Table 1.

Estimation of overall prevalence, sensitivity, and specificity for digital radiography using no gold standard (GS) and with the consensus rating as the gold standard

Estimator	Model	GS	No GS
Pd	CI	.24(.04)*	.18(.04)
	GRE	.24(.04)	.16(.10)
	FM	.24(.04)	.17(.04)
SENS	CI	.75(.06)	.89(.05)
	GRE	.75(.06)	.92(.19)
	FM	.75(.06)	.91(.05)
SPEC	CI	.91(.01)	.89(.02)
	GRE	.91(.01)	.88(.03)
	FM	.91(.01)	.90(.02)

NOTE: Models were fit under the conditional independence (CI), finite mixture (FM), and Gaussian random effects (GRE) models using Iinuma et al.'s data.

^*Standard errors were estimated using a bootstrap with 1,000 bootstrap samples.

By the likelihood principle, we compare models based on a comparison of the likelihood values. Using the gold standard, the log-likelihoods were −314.63, −300.36, and −305.45, for the CI, GRE, and FM models, respectively (there are three, five, and five parameters for each model, respectively). We compared the GRE and FM models with the CI model using a likelihood ratio test because the CI model is nested within both of these conditional dependence models. Because the parameters that characterize the conditional dependence are on the boundary (σ₀ = σ₁ = 0 for the GRE model and η₀ = η₁ = 0 for the FM model) under the null hypothesis corresponding to a CI model, the standard likelihood ratio theory is inappropriate (Self and Liang 1987). We conducted a simulation study to obtain the reference distribution under the null hypothesis by simulating 10,000 datasets under the estimated CI model and evaluating the likelihood ratio test of σ₀ = σ₁ and η₀ = η₁ = 0 corresponding to the GRE model and FM models. Based on the observed log-likelihoods and the simulated reference distribution, we reject the independence model in favor of the GRE and FM models (P < .001 for both models). Further, parameter estimates characterizing the conditional dependence under both conditional dependence models are sizable. For the GRE model, σ̂₀ = 1.1 and σ̂₁ = .37, and for the FM model η̂₀ = .31 and η̂₁ = .38, respectively. A comparison of the two nonnested GRE and FM models can be made by directly comparing the two log-likelihoods because both models have the same number of parameters. Under complete gold standard evaluation, this comparison clearly favors the GRE model.

For the no gold standard case, the log-likelihoods for the CI, GRE, and FM models were −283.19, −280.16, and −280.30, respectively. Consistent with Albert and Dodd (2004), these results suggest that, although it is easy to distinguish between conditional dependence and a conditional independence model (likelihood ratio tests computed as described previously for complete verification showed evidence for conditional dependence; P values for the comparisons of the GRE and FM models relative to the CI model were .009 and .016, respectively), it may be difficult to choose between the two models for conditional dependence with no gold standard.

Table 2 shows rater-specific estimates of sensitivity and specificity, along with prevalence, for models that incorporate the gold standard information and those that do not. As with the overall estimates of sensitivity and specificity, individual rater estimates are nearly identical across models for the dependence between tests as well as to the rater-specific estimates presented in Iinuma et al. (2000). In contrast, estimates obtained using no gold standard information were highly model dependent and were very different from those estimates that used the gold standard information.

Table 2.

Estimation of prevalence and rater-specific sensitivity and specificity for digital radiography with no gold standard (GS) and with the consensus rating as the gold standard

	Estimator		CI		GRE		FM
Rater			GS	No GS	GS	No GS	GS	No GS
	Pd	Est	.24	.18	.24	.22	.24	.22
		SE	(.04)b	(.04)	(.04)	(.07)	(.04)	(.07)
1	SENS	Est	.67	.88	.66	.77	.67	.78
		SE	(.09)	(.11)	(.09)	(.16)	(.09)	(.11)
	SPEC	Est	.99	.99	.99	1.00	.99	1.00
		SE	(.01)	(.01)	(.01)	(.01)	(.01)	(.01)
2	SENS	Est	.78	.89	.77	.80	.78	.81
		SE	(.08)	(.07)	(.08)	(.14)	(.08)	(.08)
	SPEC	Est	.87	.85	.87	.86	.87	.86
		SE	(.04)	(.04)	(.04)	(.05)	(.04)	(.04)
3	SENS	Est	.52	.68	.51	.57	.52	.57
		SE	(.10)	(.13)	(.10)	(.14)	(.10)	(.13)
	SPEC	Est	.99	.99	.99	.97	.99	.99
		SE	(.01)	(.01)	(.01)	(.01)	(.01)	(.01)
4	SENS	Est	.81	1.00	.82	.92	.81	1.00
		SE	(.07)	(.05)	(.07)	(.14)	(.08)	(.01)
	SPEC	Est	.97	.95	.97	1.00	.97	.99
		SE	(.02)	(.03)	(.02)	(.03)	(.02)	(.03)
5	SENS	Est	.85	1.0	.86	.92	.85	.92
		SE	(.07)	(.05)	(.07)	(.14)	(.07)	(.04)
	SPEC	Est	.72	.71	.72	.72	.72	.72
		SE	(.05)	(.05)	(.05)	(.06)	(.05)	(.05)
6	SENS	Est	.89	.94	.88	.84	.89	.85
		SE	(.06)	(.07)	(.07)	(.09)	(.06)	(.06)
	SPEC	Est	.90	.85	.89	.86	.90	.86
		SE	(.03)	(.04)	(.03)	(.05)	(.03)	(.04)

NOTE: Models were fit under the conditional independence (CI), finite mixture (FM), and Gaussian random effects (GRE) models^a using Iinuma et al.'s data.

^aThere are 13 (2J + 1) parameters for the CI model and 15 (2J + 3) parameters for the FM and GRE models.

^bStandard errors were estimated using a bootstrap with 1,000 bootstrap samples.

Thus, modeling approaches with complete verification appear to be more robust against misspecification of the dependence structure between tests, whereas approaches with no verification appear to lack robustness. A natural question is how the statistical properties of the estimation improve with an increasing proportion of gold standard evaluation. This will be the primary focus of this article. We discuss asymptotic and simulation results before returning to this example and varying the amount of verification. We focus on comparing the GRE and FM models because it was shown in Albert and Dodd (2004) that it is difficult to distinguish between these rather different models with no gold standard evaluation.

4. Asymptotic Results

We examined the asymptotic bias when the dependence structure is misspecified as a function of the proportion of samples receiving gold standard evaluation. For simplicity, we examined this bias for the case when interest focuses on estimating a common sensitivity and specificity across raters (denoted as SENS and SPEC, respectively). We examined both verification that is completely at random and verification biased sampling. The misspecified maximum likelihood estimator for the model parameters, denoted by θ̂*, converges to the value θ*, where

$${\theta }^{\ast }=\underset{\theta }{\text{arg}\text{max}}{E}_T[\text{log}L({\text{Y}}_i,\theta )],$$ (3)

and log L(Y_i, θ) is the individual contribution to the log-likelihood under the assumed model and the expectation is taken under the true model T. The notation

$$E_T(\text{log}{L}_M)=E_T[\text{log}L({\text{Y}}_i,\theta )]{|}_{\theta ={\theta }^{\ast }}$$ (4)

denotes the expectation (taken under the true model T) of an individual's contribution to the log-likelihood under the assumed model M when evaluated at θ*. Sensitivity and specificity are model-dependent functional forms of the model parameters, SENS* = g₁(θ*) and SPEC* = g₂(θ*), where g₁ and g₂ relate model parameters to sensitivity and specificity. Estimators of sensitivity and specificity converge to SENS* and SPEC* under misspecified models. Expressions for an individual's contribution to the expected log-likelihood under the correct and misspecified models are provided in Appendix A. Asymptotic bias for sensitivity and specificity is defined as SENS* ′ SENS and SPEC* ′ SPEC, respectively.

First, we examined the case of completely at random verification (i.e., r_s = r for all s = 1, 2, …, J). We initially examined the asymptotic bias of estimators of sensitivity and specificity when we falsely assumed a GRE model and when the true model was an FM model, as well as when we falsely assumed an FM model and the true model was a GRE model. This reciprocal misspecification with the FM and GRE models is an extreme type of misspecification because the two models are so different.

Table 3 shows the results for various proportions of completely at random verification for five tests and a presumed constant sensitivity and specificity, with the true model being the FM model and the misspecified model being the GRE model. When we have no gold standard information (r = 0), there is serious bias under a misspecified dependence structure and the expected individual contribution to the log-likelihood under the correctly specified model is nearly identical (to more than six digits) to the expected log-likelihood under the correctly specified model, which is consistent with results reported in Albert and Dodd (2004). Thus, with no gold standard reference and with five tests, estimates of diagnostic error may be biased under a misspecified dependence structure, yet it may be very difficult to distinguish between models in most situations. As little as 2% gold standard verification (r = .02) reduces the bias considerably, and the expected log-likelihoods are no longer nearly identical, making it simpler to distinguish between models. With 20% verification, the bias is small. For complete verification (r = 1), marginal quantities such as sensitivity and specificity are nearly unbiased under a misspecified dependence structure. This is consistent with work by Tan, Qu, and Rao (1999) and Heagerty and Kurland (2001) who showed for clustered binary data that marginal quantities (which sensitivity, specificity, and prevalence are) are robust to misspecification of the dependence structure. The large differences in expected log-likelihoods suggest that it will be relatively simple to distinguish between models.

Table 3.

Large-sample robustness of the assumed Gaussian random effects (GRE) model to the true dependence structure between tests given by the finite mixture (FM) model

r	η1	Estimator (misspecified model)			Expected log-likelihood*
		$P_d^{\ast }$	SENS*	SPEC*	EFM[log LFM]	EFM[log LGRE]
0	.2	.41	.45	.92	−2.24106	−2.24106
.02		.21	.71	.90	−2.24327	−2.24374
.2		.20	.74	.90	−2.26317	−2.26454
1		.20	.75	.90	−2.35160	−2.35410
0	.5	.15	.77	.86	−2.10467	−2.10476
.02		.16	.75	.87	−2.10796	−2.10973
.20		.18	.76	.89	−2.13749	−2.14648
1		.20	.76	.90	−2.26875	−2.28668

NOTE: Verification is independent of Y_i, and r denotes the proportion of random samples verified [i.e., P(V_i = 1) = r]. The true model is an FM model with η₀ = .2, P_d = .20, SENS = .75, and SPEC = .9 for differing r and η₁ and with J = 5. Asymptotic bias for sensitivity and specificity is SENS^* ′ SENS and SPEC^* ′ SPEC, respectively.

^*Expected individual contribution to the log-likelihood.

Table 4 shows asymptotic bias with five tests when the true model is the GRE model and the misspecified model is the FM model. As in Table 3, there is substantial asymptotic bias under the misspecified model when there is no gold standard evaluation. In addition, the expected log-likelihood for the misspecified model is nearly identical to the expected log-likelihood for the correctly specified model, again showing the difficulty in choosing between competing models with no gold standard information with few tests. Similar to the results in Table 3, estimates of prevalence, sensitivity, and specificity are asymptotically unbiased under the misspecified model when there is complete gold standard evaluation (r = 1). Unlike the results in Table 3, a larger percentage of verification (about 50%) is necessary to achieve approximate unbiasedness. In both cases, however, a small percentage of verification results in different expected log-likelihoods under the true and misspecified models, suggesting that it is simpler to choose between competing models with even a small percentage of gold standard verification.

Table 4.

Large-sample robustness of the assumed finite mixture (FM) model to the true dependence structure between tests given by the Gaussian random effects (GRE) model

r	σ1	Estimator (misspecified model)			Expected log-likelihood*
		$P_d^{\ast }$	SENS*	SPEC*	EGRE[log LGRE]	EGRE[log LFM]
0	1.5	.22	.84	.94	−1.74339	−1.74339
.2		.21	.82	.93	−1.78383	−1.81920
.5		.20	.78	.91	−1.86950	−1.91198
1		.20	.75	.90	−1.99560	−2.05440
0	3	.22	.86	.95	−1.61806	−1.61806
.2		.21	.82	.93	−1.67106	−1.70415
.5		.20	.76	.90	−1.75057	−1.79748
1		.20	.75	.90	−1.88307	−1.95351

NOTE: Verification is independent of Y_i and r denotes the proportion of random samples verified [i.e., P(V_i = 1) = r]. The true model is a GRE model with P_d = .2, SENS = .75, SPEC = .9, σ₀ = 1.5, and J = 5 for differing r.

^*Expected individual contribution to the log-likelihood.

Tables 3 and 4 provide an assessment of asymptotic bias under reciprocal model misspecification for both the FM and the GRE models when the sensitivity and specificity are .75 and .9, respectively. We also examined the relative asymptotic bias for a wide range of sensitivity and specificity (a grid ranging from values of .65 to .95 for both sensitivity and specificity) corresponding to the cases specified in these tables for r = .5. Figure 1 shows the results corresponding to the models and parameters described in Table 4 when σ₁ = 3. Over the wide range of sensitivity and specificity, the maximum relative percent bias was 2.8% for sensitivity and 5.1% for specificity. Other scenarios provided similar results with all percent biases being less than 6% over the grid (data not shown).

Figure 1.

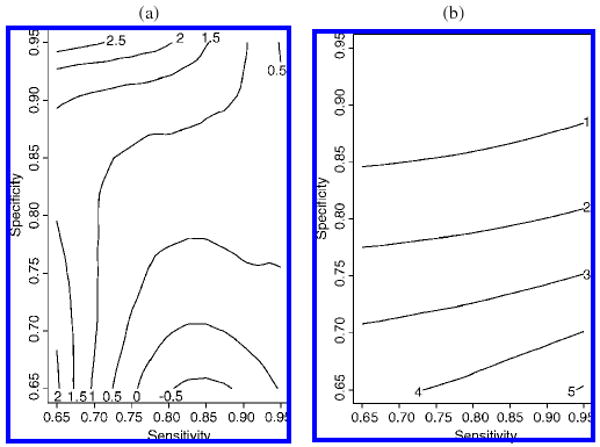
Contour plot of relative asymptotic bias in sensitivity and specificity for 50% completely at random verification when the true model is a GRE model with P_d = .20, σ₀ = 1.5, σ₁ = 3, and J = 5. Relative asymptotic bias of sensitivity and specificity is defined as (SENS* ′ SENS)/SENS (a) and (SPEC* ′ SPEC)/SPEC (b), respectively. The contour plot was generated for sensitivities and specificities over an equally spaced grid ranging from .65 to .95 with 400 points.

We examined asymptotic bias of the FM and GRE models under alternative dependence structures. Specifically, we examined the asymptotic bias when the true conditional dependence structure P(Y_i|d_i) is a Bahadur model (Bahadur 1961), a log-linear model (Cox 1972), and a Beta-binomial model, where a description of each of these models is provided in Appendix B. All three alternative models were formulated so they had the same number of parameters as the GRE and FM models. For the Bahadur model, we considered the special case of only pairwise conditional dependence between tests (i.e., all interactions of order 3 and higher are set to 0). For example, the conditional distribution of Y_i|d_i is $P({\text{Y}}_i|d_i=1)=\{{\prod }_{j=1}^J\text{SEN}{S}^{Y_{ij}}{(1-\text{SENS})}^{1-Y_{ij}}\}(1+{\sum }_{j<k}{\rho }_1{e}_{ij}{e}_{ik})$, where $e_{ij}=Y_{ij}-\text{SENS}/\sqrt{\text{SENS}(1-\text{SENS})}$ and ρ₁ = E[e_ije_ik|d_i = 1] for all j ≠ k for any i. As in Tables 3 and 4 for reciprocal model misspecification, we evaluated the asymptotic bias of sensitivity and specificity for an increasing fraction r of completely at random verification under a GRE and FM model when the true model was the Bahadur model. For five tests (J = 5), SENS = SPEC = .75, and P_d = .20, sensitivity and specificity were nearly asymptotically unbiased under both the GRE and the FM models with 20% completely random verification. For example, under a GRE model, SENS* = .50, .63, .72, .74, and .75 for r = 0, .02, .2, .5, and 1. Under an FM model, SENS* = .61, .73, .78, .76, and .75 for the same values of r.

For all three alternative models, we examined the bias in sensitivity and specificity of the GRE and FM models with 50% completely random verification over a wide range of sensitivity and specificity values (identical to the grid described for Fig. 1) for a prevalence of .20. Table 5 shows that the maximum relative asymptotic bias was less than 7% for both sensitivity and specificity for all three alternative models. Thus, estimates of diagnostic error appear to be quite robust with 50% completely random verification. When prevalence was very low or very high (e.g., below 5% or above 95%), there was more substantial bias under certain model misspecification with 50% completely random verification. For example, for a prevalence of .05 when the true model was the log-linear model, there was a maximum bias of 10% under a GRE model (as compared to a maximum bias of 4.3% for a prevalence of .20). However, unlike when there is no gold standard evaluation (r = 0), it is much easier to identify the better fitting model using likelihood and other criteria for model assessment. Further, for a rare disease, completely random verification would not generally be recommended due to efficiency considerations.

Table 5.

Range in relative asymptotic bias for the GRE and FM models when the true conditional dependence structure is (i) a Bahadur model with all correlations of order 3 and higher equal to 0, (ii) a log-linear model with a three-way interaction, and (iii) a beta-binomial model

True model	Estimator	GRE	FM
Bahadur modela	SENS	−2.8–.19%	−.83–4.4%
	SPEC	−.75–.18%	−.40–1.6%
Log-linear modelb	SENS	0–4.3%	0–7.0%
	SPEC	−.20–1.3%	0–3.7%
Beta-binomial modelc	SENS	−.13–0%	.17–4.3%
	SPEC	−.07–.05%	.14–3.8%

NOTE: The range is over a range of sensitivities and specificities between .65 and .95. The range in relative bias is for P_d = .20, J = 5, and for 50% completely random verification (r = .5).

^aBahadur model with two-way correlations of .20 and all correlations of order 3 and higher equal to 0.

^bLog-linear model with log P(Y_i|d_i) = β_di + .5I + Δ, where I is an indicator that is equal to 1 if at least three or more of the Y_ij's are equal to 1 and where Δ is a normalizing constant so that P(Y_i|d_i) sum to 1 over all possible Y_i. The parameters β_di were chosen to correspond to the different values of sensitivity and specificity.

^cP(Y_i|d_i) followed beta-binomial distributions with β = .4 (for both d_i = 0 or 1) and α varied corresponding to the desired sensitivity or specificity.

Although random verification is of concern in our application, we also consider verification biased sampling because it is so common. We examine asymptotic properties under a misspecified dependence structure with verification biased sampling. Table 6 shows asymptotic bias and expected log-likelihoods for the situation in which a random sample of cases among those who test positive on at least one of the five tests is verified (e.g., extreme verification biased sampling) and where the true model is the FM model and the misspecified model is the GRE model. Interestingly, these results suggest that, in some cases, an increase in the proportion verified can result in an increase in bias under the misspecified model. For example, when η₁ = .5 and η₀ = .2, the estimator of sensitivity is only slightly asymptotically biased (SENS* = .77) with no gold standard evaluation (r_s = 0 for s = 0, 1, 2, …, 5) and substantially biased (SENS* = .57) under complete verification of any case with positive tests (r₀ = 0 and r_s = 1 for s = 1, 2, …, 5). This result is consistent with our simulation results, which are presented in the next section. This problem occurs more generally under a wide range of verification biased sampling. For example, situations where one oversamples discrepant cases can result in bias under model misspecification. Bias can also increase with an increasing proportion of verification of discrepant cases. As an illustration, under completely random verification, when the true model is the FM model as described in Table 3 with η₁ = .5, the sensitivity converges to SENS* = .76 and is nearly unbiased when r = .2. When we oversample discrepant cases r₀ = r₅ = .20 and r_s = .4 for s = 1, 2, 3, 4, estimates of sensitivity are more asymptotically biased (SENS* = .73). The asymptotic bias is increased further (SENS* = .71) when r_s, s = 2, 3, 4, is changed from .4 to 1. We found similar results when the true model was the GRE model and the misspecified model was the FM model (data not shown).

Table 6.

Large-sample robustness of the assumed Gaussian random effects model (GRE) when the true dependence structure between tests is a finite mixture (FM) model

r	η1	Estimator (misspecified model)			Expected log-likelihood*
		$P_d^{\ast }$	SENS*	SPEC*	EFM[log LFM]	EFM[log LGRE]
0	.2	.41	.45	.92	−2.24106	−2.24106
.02		.22	.70	.90	−2.24359	−2.24319
.2		.20	.73	.90	−2.26357	−2.26241
1		.20	.75	.90	−2.34997	−2.34782
0	.5	.15	.77	.86	−2.10467	−2.10476
.02		.16	.74	.87	−2.10903	−2.10758
.20		.25	.57	.88	−2.13865	−2.13370
1		.26	.57	.89	−2.25944	−2.24983

NOTE: Verification is restricted to those patients who screen positive on at least one test, and r is the proportion of samples who are verified at random from those patients [i.e., $P(V_i=1|{\sum }_{j=1}^J{y}_{ij}=s)=0$ if s = 0 and r otherwise]. The true model is an FM model with η₀ = .2, P_d = .2, SENS = .75 and SPEC = .9 for differing r and η₁ and with J = 5.

^*Expected individual contribution to the log-likelihood.

In the next section we examine the finite sample results for both robustness and efficiency when we observe partial gold standard information.

5. Finite Sample Results

We examine bias, variability, and model selection of the different models using simulation studies. Table 7 shows the effect of model misspecification on estimates of prevalence, sensitivity, and specificity when the true model is an FM model and we fit the misspecified GRE model. Results are shown for sample sizes of I = 100 and I = 1,000 and for various proportions of random verification r. Similar to simulations in Albert and Dodd (2004), we found that when r = 0 estimates of sensitivity, specificity, and prevalence are biased under a misspecified model, and it is difficult to distinguish between models based on likelihood comparisons. In addition, estimates under the misspecified GRE model are substantially more variable than estimates under the correctly specified FM model. However, with only a small percentage of samples verified, estimation of sensitivity, specificity, and prevalence has improved statistical properties. Table 7 shows that bias is substantially reduced when only 5% of cases are verified. With as little as 20% random verification, estimates of sensitivity, specificity, and prevalence are nearly unbiased under model misspecification. In addition, variance estimates are very similar under the misspecified model relative to the correctly specified model. Under complete verification (r = 1), there is essentially no effect to misspecifying the dependence structure. The table suggests that there are other advantages to measuring the gold standard test on at least a fraction of samples or individuals. First, there is a large payoff in efficiency. For sensitivity, under the correct FM model with I = 1,000, the efficiency gain relative to no gold standard information (r = 0) is 46%, 276%, and 640% for 5%, 20%, and 100% gold standard evaluation (these calculations were based on variance estimates computed to the fourth decimal place, whereas the standard errors in Table 7 are only presented to the second decimal place). This decrease in variance is even more sizable under the misspecified GRE model. Second, it becomes increasingly easier to distinguish between models for the dependence structure with increasing r. In Table 7 we show the percentage of times the correctly specified FM model is chosen to be superior than the misspecified GRE based on the criterion of a separation of likelihoods greater than 1. With five tests (J = 5) and a sample size of I = 1,000, the correctly specified FM was declared to be superior in 12% of the cases when there was no gold standard tests. The ability to choose the correct model increased dramatically with even a small fraction of gold standard evaluation. With only 5%, 20%, and 100% verification, the correct model was identified in 45%, 64%, and 79% of the cases.

Table 7.

Simulations with a common sensitivity and specificity

I	r	FM model average estimate			GRE model average estimate			% (log LFM ≫ log LGRE)*
		Pd	SENS	SPEC	Pd	SENS	SPEC
100	0	.20 (.05)	.75 (.10)	.90 (.03)	.25 (.13)	.64 (.18)	.88 (.04)	2
	.05	.20 (.05)	.76 (.09)	.90 (.02)	.19 (.09)	.74 (.13)	.88 (.04)	7
	.10	.20 (.05)	.75 (.09)	.90 (.02)	.19 (.07)	.75 (.11)	.89 (.03)	10
	.20	.20 (.04)	.75 (.07)	.90 (.02)	.20 (.05)	.75 (.08)	.90 (.02)	12
	.50	.20 (.04)	.75 (.06)	.90 (.02)	.20 (.04)	.75 (.06)	.90 (.02)	16
	1	.20 (.04)	.75 (.05)	.90 (.02)	.20 (.04)	.75 (.05)	.90 (.02)	19
1,000	0	.19 (.02)	.75 (.04)	.90 (.01)	.32 (.12)	.57 (.16)	.91 (.02)	12
	.05	.19 (.02)	.75 (.03)	.90 (.01)	.20 (.03)	.73 (.05)	.90 (.01)	45
	.10	.20 (.02)	.75 (.03)	.90 (.01)	.20 (.02)	.74 (.03)	.90 (.01)	55
	.20	.20 (.01)	.75 (.02)	.90 (.01)	.20 (.02)	.74 (.03)	.90 (.01)	64
	.50	.20 (.01)	.75 (.02)	.90 (.01)	.20 (.01)	.75 (.02)	.90 (.01)	75
	1	.20 (.01)	.75 (.02)	.90 (.01)	.20 (.01)	.75 (.02)	.90 (.01)	79

NOTE: Data were simulated under the finite mixture (FM) model with P_d = .2, η₀ = η₁ = .2, SENS = .75, SPEC = .90, and J = 5. Results are based on 1,000 simulations. Mean parameter estimate and standard errors are presented in ( ).

^*Proportion of realizations where the log-likelihood under the FM model is more than 1 larger than the log-likelihood under the misspecified GRE model.

Table 8 shows the effect of model misspecification on estimates of sensitivity and specificity when the true model is a GRE model and the misspecified model is the FM model. As with the asymptotic results in this situation, a random sample of more than 20% reference standard evaluation is needed to get approximately unbiased estimates under the misspecified model. However, unlike when r = 0, where it is difficult to choose the correct model (by the criterion that the log-likelihood for the GRE model was larger than the log-likelihood for the FM model by more than 1), we can choose between the GRE and FM models with high probability when r = .2.

Table 8.

Simulations with a common sensitivity and specificity

r	FM model average estimate			GRE model average estimate			% (log LGRE ≫ log LFM)*
	Pd	SENS	SPEC	Pd	SENS	SPEC
0	.24 (.03)	.84 (.04)	.95 (.01)	.20 (.06)	.73 (.18)	.88 (.06)	0
.2	.22 (.01)	.81 (.04)	.92 (.01)	.20 (.02)	.75 (.04)	.90 (.01)	100
.5	.21 (.01)	.78 (.03)	.91 (.01)	.20 (.02)	.75 (.03)	.90 (.01)	100
.8	.21 (.01)	.76 (.03)	.90 (.01)	.20 (.01)	.75 (.03)	.90 (.01)	100
1	.20 (.01)	.75 (.02)	.90 (.01)	.20 (.01)	.75 (.02)	.90 (.01)	100

NOTE: Data were simulated under the Gaussian random effects (GRE) model with P_d = .2, σ₀ = σ₁ = 1.5, SENS = .75, SPEC = .90, I = 1,000, and J = 5. Results are based on 1,000 simulations.

^*Proportion of realizations where the log-likelihood under the GRE model is more than 1 larger than the log-likelihood under the misspecified FM model.

We also examined the robustness of the GRE and FM models when the true dependence structure is governed by a Bahadur model. Specifically, we simulated data with the conditional dependence structure [P(Y_i|d_i)] given by a Bahadur model with pairwise correlation of .2 and all three and higher way correlations equal to 0. Further, data were simulated corresponding to SENS = SPEC = .75, P_d = .20, I = 1,000, and J = 5. For r = 0, there was substantial bias under the misspecified GRE and FM models. In this case, the average sensitivity and specificity were .52 (SE = .09) and .68 (SE = .05) under the GRE model and .65 (SE = .06) and .87 (SE = .04) under the FM model. In addition, it was difficult to distinguish between the correctly specified Bahadur model and the GRE or FM model. For example, the misspecified FM model had a larger likelihood than the correctly specified Bahadur model in 40% of the simulated realizations. Both the GRE and the FM models resulted in nearly unbiased estimates of sensitivity and specificity for r = .20. The average estimates of sensitivity and specificity were .73 (.03) and .74 (.01) for the GRE model and .77 (.03) and .77 (.01) for the FM model when r = .2. Also, the likelihood for the correctly specified model was larger than the likelihood of the FM and GRE models in more than 99% of the simulated realizations. Thus, with only 20% completely random verification, both the GRE and the FM models are robust to model misspecification, and it is relatively easy to distinguish between models.

Table 9 shows simulation results for the case of four raters under a correctly specified FM model and a misspecified GRE model. Estimates of sensitivity and specificity, which are seriously biased with no gold standard evaluation, are nearly unbiased under the misspecified model with 20% random verification. As in Table 7, this table illustrates the pay-off in efficiency with at least some partial gold standard evaluation under both the correct and the misspecified models. This table also shows the percentage of realizations where the FM model has a larger likelihood than the GRE model. Unlike with no gold standard evaluation, the FM model is almost always correctly identified with 20% verification. In addition, unlike with r = 0, models with 20% verification result in the correct ordering of sensitivity and specificity almost all of the time. We also performed simulations for the case of four raters when the true model is a GRE model and the misspecified model is the FM model. Under the misspecified FM model, bias is substantially reduced for r = .20 as compared to r = 0. Furthermore, estimates of sensitivity, specificity, and prevalence computed under the FM model were nearly unbiased for r = .5 (data not shown).

Table 9.

Simulations with four tests with rater-specific sensitivity and specificity

			Average estimate
			r = 0		r = .20		r = 1
Test	Estimator	Truth	FM	GRE	FM	GRE	FM	GRE
1	SENS	.80	.80 (.08)	.64 (.23)	.80 (.03)	.79 (.03)	.80 (.02)	.80 (.02)
	SPEC	.95	.95 (.03)	.79 (.11)	.95 (.01)	.94 (.02)	.95 (.01)	.95 (.01)
2	SENS	.85	.85 (.06)	.72 (.20)	.85 (.02)	.84 (.02)	.85 (.02)	.85 (.02)
	SPEC	.90	.90 (.05)	.72 (.10)	.90 (.02)	.89 (.02)	.90 (.01)	.90 (.01)
3	SENS	.90	.90 (.05)	.77 (.19)	.90 (.02)	.89 (.02)	.90 (.01)	.90 (.01)
	SPEC	.85	.85 (.06)	.68 (.11)	.85 (.02)	.84 (.02)	.85 (.012	.85 (.02)
4	SENS	.95	.95 (.03)	.79 (.21)	.95 (.01)	.94 (.02)	.95 (.01)	.95 (.01)
	SPEC	.80	.80 (.08)	.64 (.13)	.80 (.02)	.79 (.02)	.80 (.02)	.80 (.02)
	Pd	.50	.50 (.07)	.50 (.22)	.50 (.02)	.50 (.02)	.50 (.02)	.50 (.02)
% log LFM > log LGRE			.63		.95		.97
% order preserved SENS			.85	.74	.96	.95	.98	.98
% order preserved SPEC			.86	.65	.96	.95	.98	.98

NOTE: Data were simulated under the finite mixture (FM) model with P_d = .5, η₀ = η₁ = .5, with SENS = .80, .85, .90, and .95 and SPEC = .95, .90, .85, and .80 for the four tests. Results are based on 1,000 simulations.

Next, we examine verification biased sampling. Our asymptotic results show that estimates of diagnostic error and prevalence can be biased when we oversample discrepant cases under a misspecified model, which was in contrast to results with random verification. We conducted simulations to examine this further. We examine bias in sensitivity, specificity, and prevalence estimates from a GRE model when the FM model is the correct model. We simulated under an FM model with J = 5, I = 100, η₀ = .20, η₁ = .50, P_d = .20, SENS = .75, and SPEC = .90 (same parameters as in rows 5–8 in Table 3) and fit both the correctly specified FM and the misspecified GRE models. When all individuals with at least one positive value were verified (r_s = 1 for s = 1, 2, …, 5 and r₀ = 0), we had sizable bias under the misspecified model. Average estimates of prevalence, sensitivity, and specificity were .27 (SE = .08), .61 (SE = .13), and .89 (SE = .02) under the misspecified GRE model and .20 (.04), .75 (.07), and .90 (.02) under the correct model.

Under the correctly specified model, oversampling discrepant cases may improve the precision of our estimates. Thus, an interesting question is whether the increase in efficiency from oversampling discrepant cases is worth the potential of serious bias under a misspecified model. We conducted a simulation where we simulated under a finite mixture model and fit the correctly specified FM model and the misspecified GRE model both under completely random verification and under a verification process where we oversampled discrepant cases. We simulated data with J = 5, I = 1,000, P_d = .2, η₁ = .5, η₀ = .2, SENS = .75, and SPEC = .90. We oversampled by obtaining a gold standard result on 40% of discrepant cases and only 5% of cases where Y_i are all concordant. For the completely at random verification cases, we chose 21% verification to correspond to the overall proportion of verification in the oversampling cases. Figure 2 shows the distribution of sensitivity estimates for each of the four scenarios. The figure shows that there is an efficiency gain in estimating sensitivity by oversampling discrepant cases. Specifically, there is a 28% efficiency gain in oversampling as compared to completely random verification. In addition, the figure demonstrates the robustness of sensitivity estimates to model misspecification under completely random verification and the lack of robustness under oversampling. In this particular case, the pay-off in efficiency with oversampling under the correct model is small relative to the potential for bias due to model misspecification. Furthermore, the correct model was definitely selected more often under completely random verification than under oversampling. The FM model had a likelihood greater than 1 more than the GRE model in over 99.5% and 54% of the simulations under completely random verification and under the mechanism that oversamples discrepant cases, respectively.

Figure 2.

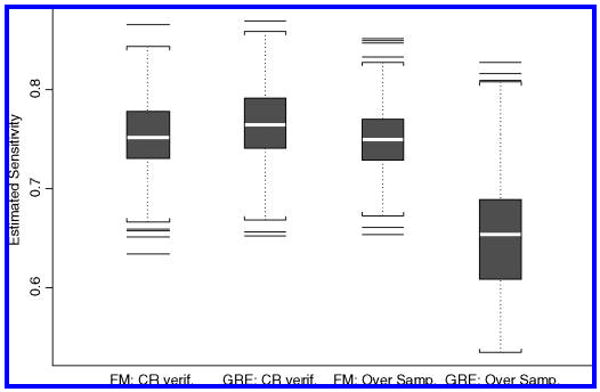
Distribution of estimates of sensitivity using the FM and GRE model under completely random (CR) verification as well as under oversampling. Data were simulated under an FM model with J = 5, I = 1,000, SENS = .75, SPEC = .90, P_d = .2, η₁ = .5, and η₀ = .2. One thousand simulated realizations were obtained.

6. Gastric Cancer Example Continued

Next, we return to the gastric cancer dataset and use only partial gold standard evaluation. Our initial focus is on examining verification that is completely at random. We evaluated designs with different probabilities of verification (r). To capture the variability associated with different amounts of verified sampling, we resample data with replacement and incorporate the reference standard on a given image with probability r. Table 10 shows results for an assumed common and for an assumed rater-specific sensitivity and specificity for r ranging from .1 to .8. In each situation, we fit both the FM and the GRE models. A comparison of these results with those presented for complete verification and for no gold standard evaluation (Tables 1 and 2) is most revealing. The results suggest that the common as well as the rater-specific estimates for r = .50 are close to those presented for complete verification. In addition, the results for r = .2, although not very close to those presented for the complete verification case, are substantially closer than those estimated with the latent class models under r = 0 (Table 2).

Table 10.

Estimation of overall and rater-specific sensitivity and specificity as well as prevalence for digital radiography using partial verification designs

Rater	Estimator	r = .10		r = .20		r = .50		r = .80
		FM	GRE	FM	GRE	FM	GRE	FM	GRE
Overall	Pd	.21 (.05)	.22 (.07)	.22 (.05)	.23 (.06)	.23 (.04)	.24 (.05)	.24 (.04)	.24 (.04)
	SENS	.84 (.08)	.80 (.14)	.82 (.08)	.78 (.11)	.78 (.07)	.76 (.07)	.76 (.06)	.76 (.06)
	SPEC	.90 (.02)	.89 (.02)	.90 (.02)	.90 (.02)	.91 (.02)	.90 (.02)	.91 (.01)	.91 (.01)
	Pd	.20 (.05)	.23 (.06)	.21 (.05)	.22 (.05)	.23 (.04)	.23 (.04)	.24 (.04)	.24 (.04)
1	SENS	.81 (.13)	.75 (.16)	.76 (.13)	.72 (.15)	.71 (.11)	.69 (.11)	.68 (.10)	.67 (.10)
	SPEC	.99 (.01)	1.00 (.01)	.99 (.01)	1.00 (.01)	.99 (.01)	.99 (.01)	.99 (.01)	.99 (.01)
2	SENS	.85 (.09)	.76 (.13)	.83 (.09)	.76 (.12)	.80 (.09)	.76 (.10)	.79 (.08)	.77 (.09)
	SPEC	.86 (.04)	.86 (.05)	.87 (.04)	.86 (.05)	.87 (.04)	.87 (.04)	.97 (.04)	.87 (.04)
3	SENS	.62 (.13)	.55 (.14)	.57 (.14)	.53 (.14)	.54 (.11)	.52 (.11)	.52 (.11)	.51 (.11)
	SPEC	.99 (.01)	.99 (.01)	.99 (.01)	.99 (.01)	.99 (.011	.99 (.01)	.99 (.01)	.99 (.01)
4	SENS	.96 (.07)	.90 (.14)	.93 (.08)	.88 (.13)	.87 (.09)	.85 (.10)	.83 (.08)	.83 (.08)
	SPEC	.97 (.03)	.98 (.03)	.97 (.03)	.98 (.03)	.97 (.02)	.97 (.02)	.97 (.02)	.97 (.02)
5	SENS	.95 (.07)	.87 (.12)	.92 (.08)	.86 (.11)	.88 (.08)	.86 (.09)	.86 (.06)	.85 (.08)
	SPEC	.72 (.05)	.72 (.06)	.72 (.05)	.72 (.05)	.72 (.05)	.72 (.05)	.72 (.05)	.72 (.05)
6	SENS	.91 (.08)	.82 (.13)	.90 (.08)	.83 (.11)	.88 (.07)	.85 (.09)	.89 (.06)	.87 (.07)
	SPEC	.86 (.04)	.86 (.05)	.87 (.04)	.87 (.05)	.88 (.04)	.88 (.04)	.89 (.03)	.88 (.04)

NOTE: Individuals were resampled with replacement to obtain a resampled dataset of 113 patients. Verification was done completely at random with probability r. One thousand resampled datasets were obtained and means (SE) across these datasets are presented. Both the GRE and the FM models were used for estimation.

We also examined extreme bias verification. Specifically, we evaluated a design whereby we verified all images in which at least one of the six radiologists rated the image positive for gastric cancer (52% of images were declared positive by at least one radiologist). As with random verification, we constructed datasets by resampling images with replacement and incorporating reference standard information whenever a positive image for any radiologist was recorded. For a common sensitivity and specificity, estimates of sensitivity, specificity, and prevalence were .78 (SE = .05), .90 (.01), and .23 (.04) for the FM model and .72 (.11), .90 (.02), and .23 (.06) for the GRE model, respectively. There was greater discrepancy between the estimates across the two models under extreme verification bias than for a comparable proportion verified under a completely random verification mechanism (r = .50 in Table 10). Large differences between the FM and the GRE models for rater-specific estimates were also found (data not shown). These results, along with the analytic and simulation results, demonstrate less robustness under verification biased sampling.

7. Discussion

It has been shown in previous work that estimates of diagnostic error and prevalence are biased under a misspecified model for the dependence between tests and that, with only a small number of tests, it is difficult to distinguish between models for the dependence structure using likelihood and other model diagnostics (Albert and Dodd 2004). Under complete verification, results on generalized linear mixed models would suggest that the estimation of marginal quantities (which prevalence, sensitivity, and specificity are) are insensitive to misspecification of the dependence between tests (Tan et al. 1999; Heagerty and Kurland 2001). Our results confirm this. Furthermore, we showed that it is much simpler to distinguish between models with complete verification. A natural question is whether gold standard verification on even a small percentage of cases improves the statistical properties of estimators of sensitivity, specificity, and prevalence. We examined both whether observing partial verification lessens the bias when the dependence structure is misspecified and whether one is able to more easily distinguish between different models for the dependence structure between tests. For the situation where verification is independent of the test results Y_i, gold standard evaluation on even a small percentage of cases greatly lowers the bias for estimating prevalence, sensitivity, and specificity under a misspecified model. In addition, identifying the correct model for the dependence structure using likelihood comparisons becomes much easier with even a small percentage of gold standard evaluation. Although there are advantages to performing the gold standard test on as many individuals as possible, this is not often possible due to limited resources. Our results suggest that between 20% and 50% gold standard evaluation results in large improvements in robustness, efficiency, and the ability to choose between competing models over no gold standard information. If the gold standard test is expensive, performing the gold standard test on more than 50% of patients may not be costeffective.

We also examined situations in which the probability of verification depends on observed test results (i.e., verification biased sampling). An important special case of verification biased sampling is extreme verification biased sampling where individuals who test negative on all tests do not receive gold standard evaluation. Such verification sampling occurs in situations where the gold standard is invasive (e.g., surgical biopsy) and it is considered unethical to subject a patient to the invasive test when there is little evidence for disease. Unlike for a single test where sensitivity, specificity, and prevalence are not identifiable under extreme verification bias sampling (Begg and Greenes 1983; Pepe 2003), these quantities are identifiable with multiple tests and an assumed model for the dependence between these tests. However, unlike the case where verification is completely at random, estimates of sensitivity, specificity, and prevalence may not be robust to misspecification of the dependence between tests with a large fraction of verification.

A gold standard can be defined in various ways depending on the scientific interest. The gold standard test could be a laboratory test, a consensus evaluation of an image, or an assessment of clinical disease. The nature of the gold standard will determine how diagnostic accuracy is interpreted. In the gastric cancer study, the gold standard was a consensus assessment (across three radiologists) of all available clinical information, including imaging data. All suspect gastric cancers were confirmed with biopsies, while patients who were negative had limited follow-up of two months to see if gastric cancer symptoms developed. A longer follow-up would have been ideal in assuring that these negative cases did not develop gastric cancer.

Other types of verification biased sampling schemes may be employed to improve efficiency. For example, our simulation results show that oversampling discrepant cases can result in improved efficiency over sampling completely at random. Our results further show that, although oversampling discrepant cases can improve efficiency, such a strategy loses the attractive feature of decreasing bias with an increasing proportion of verification found for a completely random verification mechanism. In addition, our results suggest that, for a comparable proportion of verification, choosing the correct model for the dependence between tests is more difficult for a verification process in which we oversample discrepant cases as compared with completely random verification.

Irwig et al. (1994) and Tosteson, Titus-Ernstoff, Baron, and Karagas (1994) considered optimal design strategies for the case of a single diagnostic test. Optimal design for multiple correlated tests is an area for future research. However, the choice of an optimal design will depend heavily on assumed models and parameter values for the dependence between tests. For this reason, we question the practicality of developing an optimal design in this situation.

A common criticism of latent class models for estimating sensitivity, specificity, and prevalence without a gold standard is that, without a gold standard, it is difficult to conceptualize sensitivity and specificity (Alonzo and Pepe 1999). Partial verification lessens the problem of conceptualizing the truth because a gold standard test needs to be defined and evaluated on at least a fraction of the cases.

The different models presented for analyzing partial verification data use a latent class structure for observations that do not have gold standard evaluation. In contrast with the full latent class modeling used when there is no gold standard evaluation, the semilatent class approach is more conceptually appealing, more robust under verification completely at random, and allows for model comparisons using likelihoods with only small number of tests.

Appendix A: Expected Individual Contribution to the Log–Likelihood Under a Correct and Misspecified Model

This is evaluated under the assumption of a common sensitivity and specificity across J tests, where the number of positive tests S is a sufficient statistic. Denote by Z_SD an indicator of whether the individual is verified, has S of J positive tests, and is verified with disease status D. Let X_S be an indicator for an individual not being verified and having S positive tests. Denote by T the true model and M the assumed model. The expected (under T) log-likelihood of the assumed model M is

$$\begin{array}{l}{E}_T\left[\text{log}L\left({\text{Y}}_i,{\theta }_M\right)\right]\hfill \\ =\sum _{d=0}^1\sum _{s=0}^J{E}_T\left[Z_{sd}\right]\text{log}\left[P_M(S=s|D=d)P_M(D=d)\right]\hfill \\ +\sum _{s=0}^J{E}_T\left[X_s\right]\text{log}[P_M(S=s|D=0)P_M(D=0)\hfill \\ +P_M(S=s|D=1)P_M(D=1)]+C_v,\hfill \end{array}$$ (A.1)

where P_M(S|D) and P_T(S|D) are the conditional distributions for the sum of J binary tests from the assumed and true models, respectively. Additionally, P_M(D) and P_T(D) are the probabilities of disease under the assumed and true models, respectively, and C_v is a constant corresponding to the verification process. Denote by r_s = P(V_i|S = s) the probability of verification for a particular observed sum s. The expected values E_T [Z_sd] and E_T[X_s] can be expressed as

$$E_T[Z_{sd}]=r_{s}P(S=s|D=d)P(D=d)$$ (A.2)

and

$$\begin{array}{l}{E}_T[X_s]=(1-r_s)[P(S=s|D=1)P(D=1)+P(S=s|D=0)P(D=0)].\hfill \end{array}$$ (A.3)

Appendix B: Alternative Models for the Conditional Dependence between Tests

Bahadur Model

Let π_ij be the probability of a positive response conditional on d_i for the j th test on the ith subject. Let $e_{ij}=Y_{ij}-{\pi }_{ij}/\sqrt{{\pi }_{ij}(1-{\pi }_{ij})}$ and let ρ_ijk = E[e_ije_ik|d_i], ρ_ijkl = E[e_ije_ike_il|d_i], ⋯, ρ_ijkl…_J = E[e_ije_ike_il…e_iJ|d_i]. The probability distribution can be expressed as $f({\text{Y}}_i|d_i)=g({\text{Y}}_i|d_i){\prod }_{j=1}^J{\pi }_{ij}^{Y_{ij}}{(1-{\pi }_{ij})}^{1-y_{ij}}$, where g(Y_i|d_i) = 1 + Σ_j<kρ_ijke_ije_ik + Σ_j<k<lρ_ijkle_ije_ike_il + ⋯ + ρ_ijkl…_Je_ije_ik × e_il ⋯ e_iJ.

Log-Linear Model

The probability distribution can be expressed as $f({\text{Y}}_i|d_i)=\text{exp}({\sum }_{j=1}^J{\theta }_j{Y}_{ij}+{\sum }_{j<k}{\theta }_{jk}{Y}_{ij}{Y}_{ik}+\cdots +{\theta }_{jk\cdots J}{Y}_{ij}{Y}_{ik}\cdots Y_{iJ}+\Delta )$, where Δ is a normalization factor so that f (y_i|d_i) sum to 1 over all values of y_i, and where θ's depend on d_i.

Beta-Binomial Model

This distribution assumes that the probability of a positive test (conditional on d_i) is common across the J tests. The probability distribution is P(Y_i|d_i) = B(S + α, J − S + β)/B(α, β), where $S={\sum }_{j=1}^J{y}_{ij}$, and the two parameters α and β depend on d_i.