The Semiquinone-Iron Complex of Photosystem II: Structural Insights from ESR and Theoretical Simulation; Evidence that the Native Ligand to the Non-Heme Iron Is Carbonate

Abstract

The semiquinone-iron complex of photosystem II was studied using electron spin resonance (ESR) spectroscopy and density functional theory calculations. Two forms of the signal were investigated: 1), the native g ∼ 1.9 form; and 2), the g ∼ 1.84 form, which is well known in purple bacterial reaction centers and occurs in photosystem II when treated with formate. The g ∼ 1.9 form shows low- and high-field edges at g ∼ 3.5 and g < 0.8, respectively, and resembles the g ∼ 1.84 form in terms of shape and width. Both types of ESR signal were simulated using the theoretical approach used previously for the BRC complex, a spin Hamiltonian formalism in which the semiquinone radical magnetically interacts (J ∼ 1 cm⁻¹) with the nearby high-spin Fe²⁺. The two forms of ESR signal differ mainly by an axis rotation of the exchange coupling tensor (J) relative to the zero-field tensor (D) and a small increase in the zero-field parameter D (∼6 cm⁻¹). Density functional theory calculations were conducted on model semiquinone-iron systems to identify the physical nature of these changes. The replacement of formate (or glutamate in the bacterial reaction centers) by bicarbonate did not result in changes in the coupling environment. However, when carbonate (CO₃²⁻) was used instead of bicarbonate, the exchange and zero-field tensors did show changes that matched those obtained from the spectral simulations. This indicates that 1), the doubly charged carbonate ion is responsible for the g ∼ 1.9 form of the semiquinone-iron signal; and 2), carbonate, rather than bicarbonate, is the ligand to the iron.

Introduction

Photosystem II (PS II), a pigment-protein complex of plants, algae, and cyanobacteria, is responsible for the oxidation of water and reduction of plastoquinone in oxygenic photosynthesis. The PS II core is composed of 10 membrane-spanning helices provided by the D1 and D2 polypeptides. These bind all redox active centers involved in charge separation and water oxidation.

Photoexcitation of the primary electron donor P680, a chlorophyll complex located near the lumenal membrane interface, initiates the transfer of an electron to the neighboring pheophytin_a (pheo_D1). From there, the electron is rapidly passed to the primary plastoquinone (Q_A) on the stromal side (for a recent review, see Diner and Rappaport (1)). Q_A is a tightly bound species that undergoes a one-electron reduction, forming a semiquinone (Q_A⁻), as shown in Scheme 1 (2).

Scheme 1.

Acceptor-side electron transfer pathways in PS II and BRC: the two-electron gate (2).

Electrons leave PS II via the secondary plastoquinone acceptor (Q_B), the mobile electron acceptor of PS II. Q_A⁻ reduces Q_B first to a semiquinone (Q_B⁻) and then to a quinol (Q_BH₂) after a second photochemical turnover (2). This two-electron gate mechanism was discovered in PS II (3,4) and later in purple bacterial reaction centers (BRC) (5,6). The secondary quinone (Q_B) and quinol (Q_BH₂) bind weakly (dissociation constants of ∼1–2 mM (2,7)), in contrast to the semiquinone (Q_B⁻), which has a dissociation constant (∼0.5 μM) 2000 times less than that of the quinol. The relative stability of the bound semiquinone is thought to arise from coulombic interactions with the surrounding protein/metal environment and H-bonding to residues in the Q_B pocket. The mechanism of electron transfer through the two quinones and the structure of their sites are similar in PS II and BRC (2,8–10).

In the BRC, the electron transfer between Q_A⁻ and Q_B (Scheme 1, K_AB(1)) is limited by a conformational gating process rather than by the driving force (11). The subsequent electron transfer step from Q_A⁻ to Q_B⁻ (K_AB(2)) appears to be rate-limited by the uptake of a proton (12). After a second protonation, the Q_BH₂ exchanges with a quinone from the pool in the membrane, completing the two-electron reaction cycle (for reviews, see (2,12)).

In PS II, Q_A and Q_B are positioned on either side of a non-heme iron center (Fe²⁺), which is within ∼7.5 Å of either quinone (center to center). The Fe²⁺ adopts a near-octahedral ligand geometry (9,10,13,14). Four coordination sites are provided by histidine residues, two from D1 (H215 and H272) and two from D2 (H214 and H268). An exogenous bidentate bicarbonate fills the remaining two coordination sites (15). In BRCs, a homologous quinone-iron complex is present (8,16) with an almost identical geometry, a six-coordinate Fe²⁺ center, with four histidine ligands (provided by the L and M subunits, the bacterial D1/D2 analogs). The remaining coordination site is, however, occupied by a glutamate residue of the M subunit (M234 in Rhodobacter sphaeroides) rather than the exchangeable bicarbonate. In the BRC, the H subunit encloses the quinone-iron complex, isolating it from the external environment (8,16). In PS II, there is no corresponding H subunit.

The role of the non-heme iron in BRC and PS II is not fully understood. In BRCs, other divalent transition metal ions (Mn²⁺, Co²⁺, Ni²⁺, and Cu²⁺), and even Zn²⁺, can replace the iron and show identical electron transfer rates, i.e., 1/k_AB = ∼150 μs⁻¹ (17). Indeed, it has been found that Mn²⁺ is naturally present in some strains (18). In a similar way, metal-free BRCs have been shown to be functional, with the observed rate of electron transfer between Q_A and Q_B approximately half that of the native system (17). These studies suggest that the Fe²⁺ center has a marginal role in electron transfer between Q_A and Q_B in BRCs.

In contrast to the BRC, electron transfer in PS II is more strongly influenced by changes at the non-heme iron site. The relative “openness” of the Fe²⁺ center in PS II allows the exogenous bicarbonate ligand to be displaced by various other small molecules including: formate, cyanide, nitric oxide, etc. (see (2) and references therein). The electron transfer rate between Q_A and Q_B is often significantly reduced in these ligand-perturbed systems.

The “bicarbonate effect”—an enhanced electron transfer rate between Q_A and Q_B seen when the non-heme iron binds bicarbonate—is a topic of substantial interest in PS II research. Experiments show that electron transfer between Q_A and Q_B slows after the second actinic flash in samples where bicarbonate has been exchanged (formate-treated, etc.) (19). As the second electron transfer step (Scheme 1) requires protonation of the Q_B, it has been proposed that bicarbonate facilitates this process. It is unclear whether bicarbonate donates protons to Q_B (either directly or via a protein side-chain network) or influences protonation events by modifying the pK_a environment of the Q_B protein scaffold (see (20) and references therein).

The electron-spin resonance (ESR) spectrum of the semiquinone (Q_A⁻ or Q_B⁻) observed in BRCs appears as a broad resonance with a turning point at g ∼ 1.84 (21–27). It has been simulated using the spin Hamiltonian formalism, where the semiquinone, Q⁻, interacts magnetically with an Fe²⁺ center (28). The ground manifold of the semiquinone-iron system is composed of five Kramer's doublets. The ESR spectrum (between 5 and 20 K) is dominated by the two lowest-spin-allowed transitions; the transitions within the two lowest doublets (with doublet separation ∼3 K).

The ESR spectrum of the native Q_A⁻ semiquinone iron signal observed in PS II is similar, but not identical, to that seen in BRCs: a very broad resonance, with a turning point at g ∼ 1.9 (29,30). A broad positive feature has also been identified at g ∼ 1.7 and since it is only resolved at low temperatures (<10 K), it has been assigned to the lowest spin-allowed transition (30). Treatment of PS II with formate suppresses the g ∼ 1.9 signal. Instead, a g ∼ 1.84 signal is observed that has a line shape and width nearly identical to those of the semiquinone iron signal observed in BRCs (31). A similar, but weaker, signal at g ∼ 1.84 is seen in PS II in the absence of exogenous carboxylic acid ligands under certain circumstance (e.g., (2,29,32).).

Here, we use the basic theoretical model established by Butler et al. (28) to describe the semiquinone iron signal in BRCs to model the corresponding signal in native PS II. A specific simulation package was written to calculate the theoretical absorbance ESR spectra at different temperatures. These results were compared to density functional theory (DFT) calculations of model semiquinone-iron complexes. New insights were obtained into the nature and role of the exchangeable ligand to the non-heme iron in PS II.

Material and Methods

Sample preparation

PS II core complexes from spinach were made according to the method of Smith et al. (33). The cores had an activity of ∼2500–4000 μmol O₂/mg chl/h and were stored at 1–3 mg chl/mL in 400 mM sucrose, 20 mM NaCl, 20 mM MgCl₂, and 0.3g/L dodecyl maltocide, pH 6.5, at −88°C until use.

EPR measurements

PS II core samples (1–2 mg/mL chl) were treated with either 5 mM sodium formate or 5 mM sodium bicarbonate to generate either the g ∼ 1.84 or the g ∼ 1.9 form of the semiquinone iron signal, respectively. EPR sample loading was performed under dim green illumination followed by >10 min dark adaptation at 4°C before freezing to 200 K (CO₂ (dry ice)/ethanol) and subsequently 77 K (LN₂). Samples were used immediately or within 24 h of transfer to the quartz EPR tube. Samples at 4°C were pumped using a rotary pump for 1–2 min. The EPR tube was then filled with Ar gas to minimize O₂ signals.

To generate the semiquinone iron signal, samples were illuminated with a 125-W halogen lamp. The beam was focused to a 20-mm-diameter spot directly onto the front grate of the EPR cavity after passing through a water filter (path length 10cm) and an interference filter centered at 690 nm with spectral width 10 nm.

ESR measurements were performed on a Bruker ESP300E spectrometer with an Oxford ESR9 liquid helium flow cryostat using a gold-chromel thermocouple directly below the sample position.

Spectral simulations were performed numerically from a Hamiltonian (10 × 10 matrix) using Scilab-4.4.1, an open source vector-based linear algebra package (www.scilab.org). A complete description of the EPR simulations can be found in the Supporting Material.

DFT calculations were performed using Gaussian 03 (34). The B3LYP hybrid density functional theory (35) was used, combined with the basis set of Wachters (36), augmented with additional f functions (37) for the iron, and the D95(d,p) basis set of Dunning (38) for all other atoms. The total spin multiplicity of the system in the high and low spin configurations was 6 and 4, respectively. The zero-field parameters (D and E) were calculated using the ORCA package. The coupled-perturbed methodology was used for the spin-orbit coupling component.

Results

Q_A⁻-Fe²⁺ resonance in PS II

Fig. 1 shows the derivative ESR semiquinone-iron signals observed in our PS II core complex preparation. Characteristic of these signals are turning points in the g ∼ 1.8–1.9 region. As a consequence, semiquinone signals are identified by the position of this spectral feature. In native BRC, the turning point is at g ∼ 1.84, whereas in PS II it is at g ∼ 1.9.

Figure 1.

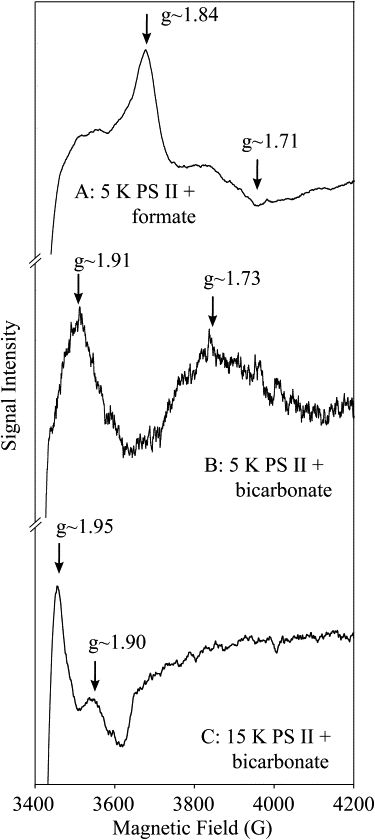
Derivative ESR spectra of the semiquinone-iron observed in PS II. (A) g ∼ 1.84 Q_A⁻-Fe²⁺ signal (5 K) seen in formate-treated PS II (similar to BRC (28)). (B) g ∼ 1.9 Q_A⁻-Fe²⁺ signal (5 K) seen in bicarbonate-treated PS II. (C) g ∼ 1.9 Q_A⁻-Fe²⁺ signal (15 K) seen in bicarbonate-treated PS II.

The g ∼ 1.9 signal was photoinduced by illumination with visible light for ∼10 min at cryogenic temperatures (5–20 K). The Cyt_b559 was fully oxidized before illumination. The oxidized electron donor (D⁺) for the system appears as a narrow (10–15 G p-p), featureless radical centered at g ∼ 2.0 that is assigned to an admixture of chlorophyll (chl⁺) and carotenoid (car⁺) radicals (39).

The g ∼ 1.9 signal observed in this PS II core complex preparation is similar to that seen from PS II membranes (29,30) and cyanobacterial sources (40). Two pseudoderivative features were resolved at 5 K, at g ∼ 1.9 and g ∼ 1.7 (Fig. 1 B). At higher temperatures (15 K), the latter is lost, whereas the former narrows (Fig. 1 C) (30).

When treated with formate, the PS II core complexes exhibited a semiquinone-iron signal similar to that observed in BRCs, as seen previously in PS II membranes (30,31) (Fig. 1 A). Formate is believed to bind to the non-heme iron, displacing the bicarbonate ligand (see Introduction (30,31)).

Absorption ESR spectra of the Q_A⁻-Fe²⁺ resonance in PS II

Fig. 2 displays the ESR absorption spectra of the semiquinone-iron seen in PS II at 5 and 15 K. The absorption spectrum of the g ∼ 1.9 signal was generated by integration of data presented in Fig. 1, B and C. It is experimentally difficult to resolve such a broad ESR signal, since the baseline is inherently variable over large field ranges. To minimize this problem, the g ∼ 1.9 semiquinone-iron signal was generated by direct illumination of the sample in the cavity at 5 K, This avoided movement of the sample. The difference between a spectrum taken during (or after) the 5 K illumination and a spectrum taken immediately before illumination effectively eliminated baseline features and yielded a well-defined semiquinone-iron signal. This also canceled Cyt_b559^OX signals, tyrosyl radical (Y_D^•), etc. Even with these measures, a baseline correction had to be subtracted to remove a signal offset. Consequently, there is a degree of uncertainty in the position of the high-field edge of the signal (Fig. 2, dashed curve).

Figure 2.

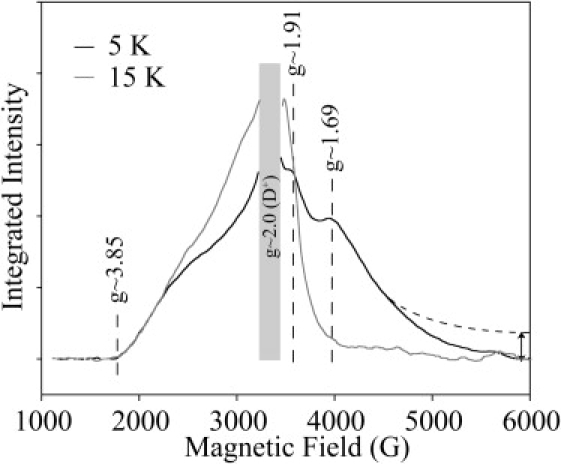
Absorption ESR spectra of the g ∼ 1.9 semiquinone-iron signal observed in PS II at 5 K (black trace) and 15 K (gray trace). Spectra scaled to account for Curie temperature dependence (i.e., 15 K spectrum × 3). The radical region around g = 2 (gray column) is dominated by light-induced radicals (D⁺) and has been omitted for clarity.

A comparison of the absorbance spectra measured in PS II and BRCs highlights the similarities of these signals. Butler et al. (28) demonstrated that the g ∼ 1.84 semiquinone-iron signal extends to low field (g ∼ 6). The same is true for the g ∼ 1.9 signal of PS II, with the signal extending to g ∼ 3.5. This spectrum is the first to show the low-field edge of the g ∼ 1.9 signal. Interestingly, although the absorbance spectrum of the g ∼ 1.84 signal exhibits one maximum at g ∼ 1.84, the g ∼ 1.9 spectrum has two local maxima at g ∼ 1.9 and g ∼ 1.7 (Fig. 2).

The absorbance line shape of the g ∼ 1.9 signal was strongly temperature-dependent. The high-field component of the spectrum (g < 1.9) was evident only at low temperatures (5 K), whereas the low-field component remained virtually unchanged over the 5–20 K region. This behavior is similar to that observed in BRCs (28).

Modeling and analysis: spin Hamiltonian formalism

A description of the non-heme iron (S = 2) and semiquinone, Q_A⁻ (S = 1/2) system requires 10 basis vectors. These are expressed in terms of three quantum numbers,

$$|S,m,s\rangle ,$$

where S is the total spin of the ground iron manifold (S = 2), m is the iron magnetic sublevel (m = −S, −S + 1, ……, S − 1, S) and s is the semiquinone sublevel (s = −1/2, 1/2).

The spin Hamiltonian for the Q_A⁻-Fe²⁺ system, including zero field (D, E), Zeeman (g_Fe, g_Q), and anisotropic exchange (J) is

$$H=D\left[\right(S_{\text{FeZ}}^2-1/3S_{\text{Fe}}(S_{\text{Fe}}+1)+(E/D)(S_{\text{FeX}}^2-S_{\text{FeY}}^2)]+\beta H\cdot {\mathrm{g}}_{\text{Fe}}\cdot S_{\text{Fe}}+g_{\mathrm{Q}}\beta H\cdot S-S_{\text{Fe}}\cdot J\cdot S_{\mathrm{Q}}\text{.}$$ (1)

Subsequent calculations assume the zero-field, Zeeman-iron, and exchange tensors to be colinear and g_Q to be scalar as in Butler et al. (28).

Computational simulation of the semiquinone-iron signals

The program used to simulate the system using the above Hamiltonian (Eq. 1) is described in sections S1–S8 of the Supporting Material. It outputs the ESR spectrum for transitions within the three lowest doublets. It also reproduces the g ∼ 1.84 spectrum of Butler et al. (28). The g ∼ 1.84 simulation presented here was significantly improved by inclusion of transitions involving the second excited doublet. It has the effect of breaking the symmetry of the simulation in the g ∼ 1.8 region (see Fig. 3 below). No further attempt was made to improve the BRC spectral simulation. Nevertheless, it is likely that an increase in the exchange coupling along the y axis may improve the simulation of the low-field edge.

Figure 3.

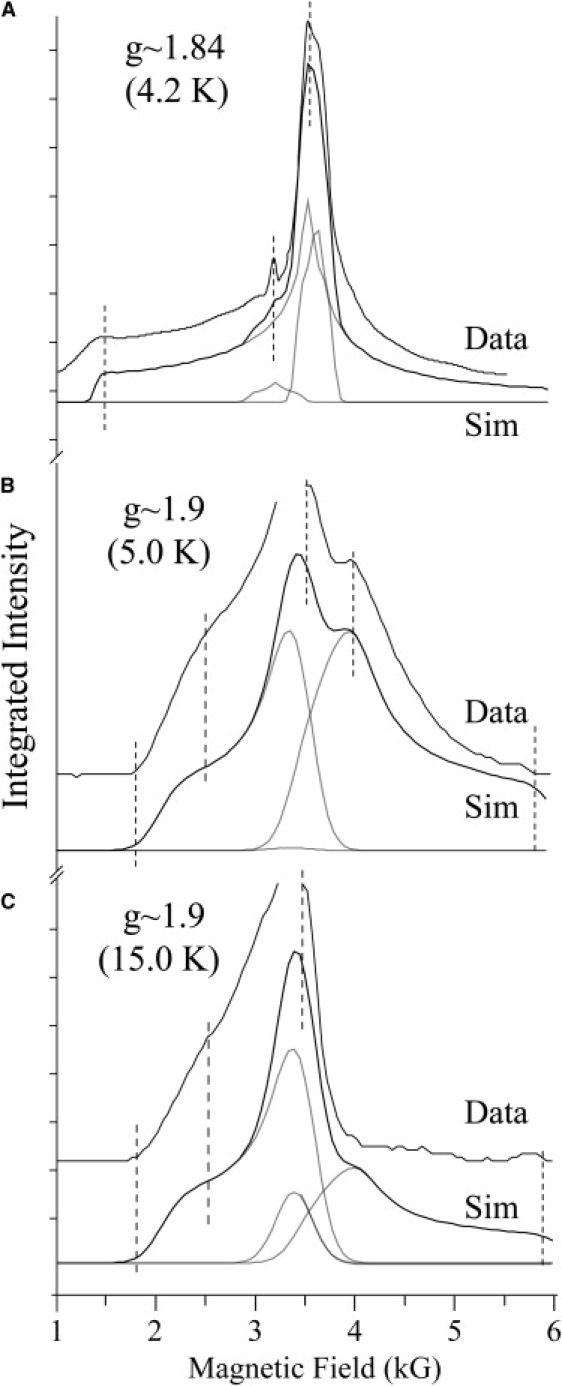
Simulation of the semiquinone-iron using the spin Hamiltonian formalism: comparison of experimental and theoretical results. Parameter values are as in Table 1. (A) g ∼ 1.84 (BRC + o-phenanthroline, taken from Butler et al. (28)). (B) g ∼ 1.9 (PS II) at 5 K. (C) g ∼ 1.9 (PS II) at 15 K. Free radical region omitted in B and C. Black lines, total simulation; gray lines, doublet transitions.

The iron-quinone sites of PS II and BRC are very similar (8–10,13,14,16). The mean iron-quinone distance is nominally the same (8,13,14,16). The ligand field of the iron is nearly identical (8,13,14,16). As a consequence, it is expected that the zero-field and exchange-coupling parameters for the g ∼ 1.9 semiquinone-iron signal are likely to be very similar to those for the g ∼ 1.8 signal. Within this framework, a simulation of the g ∼ 1.9 signal could be readily obtained. The numerical simulation of the g ∼ 1.9 signal (Fig. 2) is shown in Fig. 3. The optimized parameters are given in Table 1 (together with those for the g ∼ 1.84 simulation). The model quantitatively fits the spectral data at two temperatures. The simulation models well the low-field edge and dominant turning points of the g ∼ 1.9 spectrum. It deviates on the high-field edge, overestimating the signal intensity in this region. As this region is the most difficult to measure experimentally due to baseline effects in the CW spectra, this may reflect deficiencies in the data rather than the theoretical model. It is interesting that the g ∼ 1.9 position describes the intersection point of the ground and first (and second) excited-state doublets. This explains in part the unusual temperature dependence in this region, as observed earlier (30,41).

Table 1.

Optimized parameter set for simulation of semiquinone-iron signals

	g ∼ 1.84 (K, BRC) (28)	g ∼ 1.9 (K, PS II)∗
Jx	−0.13	−0.90
Jy	−0.58	−0.50
Jz	−0.58	−0.10
JISO∗	−0.43	−0.52
D	7.6	15.0
E/D	0.25	0.27
Width (FWHM)	160 (G)	600 (G)

Semiquinone-iron signals used are those shown in Fig. 3.

^∗g_Fe tensor values are as in Butler et al. (28).

The simulation parameters for the g ∼ 1.9 and g ∼ 1.84 signals differ in two respects: 1), the simulation of the g ∼ 1.9 signal requires a significant increase in the magnitude of the zero-field splitting of the iron (D) (by ∼10 K (∼6 cm⁻¹) relative to the g ∼ 1.84 value); and 2), apparent rotation of the exchange tensor relative to the fine-structure tensor (see Fig. S2 and Fig. S3). The exchange coupling tensor, J, for the g ∼ 1.9 semiquinone-iron signal has its largest component along J_x and smallest along J_z. The opposite is observed for the BRC (see Butler et al. (28)). The largest coupling component here is along J_z and the smallest along J_x. This suggests that the two signals differ by a rotation of the exchange tensor of ∼90° relative to the fine-structure tensor, within the tensor geometries implicitly assumed in the simulation formalism (collinear tensors, see above). In a more general sense, it is shown in Fig. S9 that a significant reorientation of the exchange tensor relative to the fine-structure tensor (as compared to the g ∼ 1.84 signal) is required to resolve the characteristic two-maxima pattern seen for the g ∼ 1.9 signal. The increase in the zero-field splitting (D) alone does not significantly alter the spectral pattern in the g ∼ 1.7–2.0 region. It is also noted that the anisotropy of the g-tensor of the iron had little influence on the line shape of the simulations of either the g ∼ 1.84 or g ∼ 1.9 signals. The line widths used for either simulation (g ∼ 1.84 or g ∼ 1.9) were assumed to be isotropic. The simulations shown in Fig. 3 are also consistent with the known orientation dependence of the two semiquinone iron signals (42) (Fig. S10).

Modeling and analysis: density functional theory

DFT calculations on model semiquinone-iron complexes were carried out on fragment geometries based on the respective crystal structures of PS II and BRC. Partial optimization of the geometry of each complex was conducted. All atoms were frozen except for hydrogen and the atoms of the fifth (nonhistidine) ligand to the Fe²⁺. The spin densities, coupling tensors, and zero-field parameters presented were calculated from these partially optimized geometries.

Five complexes were examined, which differed primarily in the nonhistidine ligation to the Fe²⁺ center:

• 1.BRC (ubiquinone) with glutamate as the Fe²⁺ ligand
• 2.BRC (ubiquinone) with formate as the Fe²⁺ ligand
• 3.PS II (plastoquinone) with formate as the Fe²⁺ ligand
• 4.PS II (plastoquinone) with bicarbonate as the Fe²⁺ ligand
• 5.PS II (plastoquinone) with carbonate as the Fe²⁺ ligand

In these structures, the native glutamic acid side chain was modeled by propanoic acid, whereas the quinones included the isoprenoid side chain up to the C5 atom.

These complexes represent the semiquinone-iron systems where either the g ∼ 1.84 or g ∼ 1.9 is expected to be observed. The BRC + glutamate and PS II + formate should exhibit a g ∼ 1.84 signal, whereas the PS II + carbonate/bicarbonate would be expected to show a g ∼ 1.9 signal. The BRC + formate complex is a hypothetical state (since glutamate cannot be displaced experimentally) that is expected to show a g ∼ 1.84 signal, similar to that from the native glutamate ligand.

General remarks on the DFT calculation results

DFT calculations did not identify any large changes in the electron density distribution or in the coupling between the five model complexes described above. For all complexes, the unpaired spin (S = 1/2) of the semiquinone was localized on its conjugated ring. In a similar way, the spin density of the Fe²⁺ was shown to be localized predominantly on the metal center. Partial optimization of the quinone-iron geometry showed that the coordination of the ligand (bicarbonate, formate, glutamate, etc.) was bidentate. Previous experimental results have demonstrated this to be the case for bicarbonate in PS II (15) and glutamate in BRC (43).

Exchange coupling

The exchange coupling for the system can be determined using the equation (44)

$$J=-\frac{E_{\text{HS}}-E_{\text{LS}}}{S_{\text{HS}}(S_{\text{HS}}+1)-S_{\text{LS}}(S_{\text{LS}}+1)},$$ (2)

where HS and LS refer to high-spin and low-spin configurations, respectively. Computational estimates for the exchange coupling between the semiquinone and the iron (based on Gaussian03-derived total energies) were small in all modeled systems. For the BRC models, J values of −0.35 cm⁻¹ (−0.5 K) were predicted, whereas for PS II models, J values of −0.4 cm⁻¹ (−0.6 K) for carbonate and −0.7 cm⁻¹ (−1 K) for bicarbonate and formate were found (Table 2). These values were within the tolerance of the computational methods employed (for systems of this size, ∼100 atoms). Thus, computational estimates provide only an upper limit of the extent of exchange coupling. Isotropic exchange (J) couplings determined from ESR simulation (Table 2) are all ∼0.5 K in magnitude (0.35 cm⁻¹).

Table 2.

DFT estimates of the exchange coupling, hyperfine, and zero-field tensors of the semiquinone and the Fe²⁺ center

	S2HS	S2LS	EHS (cm−1)	ELS (cm−1)	JISO (cm−1)	Fe2+ hyperfine (10−4 cm−1)			Zero-field parameters
						x	y	z	D (cm−1)	E/D
BRC + glutamate∗	8.75	3.78	−806599620	−806599622	−0.34	−9.1	14.4	−5.3	−3.0 (5.3)	0.22
BRC + formate∗	8.75	3.78	−780708648	−780708650	−0.37	−9.2	14.4	−5.2	−3.2 (5.5)	0.20
PS II + formate∗	8.75	3.78	−755589365	−755589369	−0.70	−9.5	14.1	−4.5	−3.1 (5.4)	0.24
PS II + bicarbonate∗	8.75	3.80	−755465371	−755465374	−0.70	−8.9	14.2	−5.3	−2.9 (5.2)	0.21
PS II + carbonate∗	8.75	3.78	−739070237	−739070240	−0.43	−5.1	13.0	−8.0	3.0 (11.3)	0.28
PS II + carbonate†	8.75	3.78	−739070237	−739070240	−0.43	−5.1	13.0	−8.0	10.5	0.28

Numbers in parentheses (D values) are corrected assuming an offset of 8.3 cm⁻¹.

^∗High spin (ferromagnetic coupling) (HS).

^†Low spin (antiferromagnetic coupling) (LS).

Zero-field parameters

An attempt was made to calculate the zero-field spin-spin (fine-structure) tensor using ORCA. However, this proved challenging due to difficulties with wave-function convergence for most models. The source of this problem was the requirement that the semiquinone be antiferromagnetically (low-spin) coupled to the iron. If, instead, the semiquinone-iron coupling was assumed to be ferromagnetic (high-spin), no convergence problems were encountered. Thus, as a starting point, we calculated the D and E parameters for all models assuming ferromagnetic coupling (Table 2). By comparing these values with experimental values for the BRC + glutamate (45), it was observed that the calculated DFT value for D was offset by −8.3 cm⁻¹. Corrected D values, which take into account this offset, are also given in Table 2.

To ensure that subtraction of a fixed offset from our calculated D values was valid, we made further attempts to solve the model complexes for which antiferromagnetic coupling was assumed. This was achieved for one model system, PS II + carbonate. The DFT estimate of the D value for this system was 10.5 cm⁻¹. This value is offset 7.5 cm⁻¹ from the equivalent ferromagnetically coupled estimate. This offset is approximately the same as that between the DFT-calculated value for ferromagnetically coupled BRC + glutamate and the experimental result, i.e., 8.3 cm⁻¹.

It is clear that the corrected D and E values obtained for all model systems are very similar, except in the case of the carbonate ligand system, where the D value increased by ∼6 cm⁻¹, i.e., from ∼5.3 to 11.3 cm⁻¹. This is approximately the same difference in D as determined from the simulation of g ∼ 1.84 and g ∼ 1.9 ESR signals, where the D value increased by ∼5 cm⁻¹ (∼7.5 K) upon moving from the g ∼ 1.84 and g ∼ 1.9 ESR signals.

As an aside, it is worth noting that the DFT calculation for the antiferromagnetically coupled PS II + carbonate complex reproduces exactly (within the limits for both the DFT calculation and ESR simulation) the D value of 10.5 cm⁻¹ (15 K) from the ESR simulation.

Hyperfine/zero-field tensor orientations

A description of the coupling environment for all five model complexes could be made from examining the anisotropic hyperfine tensor and zero-field tensor orientations of the Fe²⁺. The hyperfine tensors are shown in Table 2. The largest tensor component is in the membrane plane, roughly connecting the semiquinone to the iron. It is assigned to the y direction. Its exact position varies with different systems (Fig. 4). The other two components align such that they are perpendicular to a vector connecting the iron and quinone centers.

Figure 4.

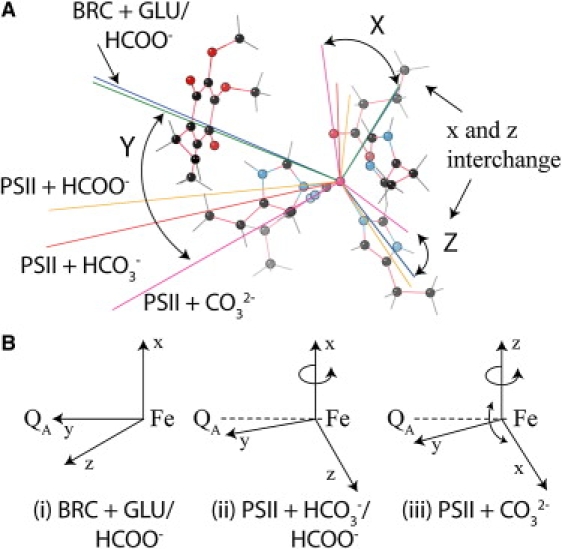
Orientation of the Fe²⁺ hyperfine tensor for the semiquinone-iron geometry seen in BRC/ PS II. (A) Hyperfine tensors are color-coded green for BRC + glutamate; blue for BRC + formate; orange for PS II + formate; red for PS II + bicarbonate; and pink for PS II + carbonate. (B) A simple representation of the rotation of the hyperfine tensor in the various ligand systems.

The two complexes based on the BRC (glutamate/formate) have a near-identical hyperfine tensor orientation. Tensor components along the three principle axes are very similar (within 3%). On shifting to the PS II system (+ formate), the hyperfine tensor rotates ∼30° in the yz plane. Note that the hyperfine-tensor orientation (x, y, z principle directions) need not be the same as the exchange/zero-field tensor estimated from the EPR simulation.

There was surprisingly little change observed in either the orientation or magnitude of the hyperfine tensor in the PS II + bicarbonate complex as compared with that in the PS II + formate complex. Tensor values seen along the three principal axes show modest variation (within 15%) and still nominally retain the same spatial orientation (within 10%).

A notable change in the Fe²⁺ hyperfine tensor could, however, be induced by deprotonating the bicarbonate ligand. Compared to the BRC, the hyperfine tensor principal directions rotate as seen in PS II (+ formate or bicarbonate), i.e., the hyperfine tensor rotates ∼45° in the yz plane. However, in addition, the tensor principal values now interchange along the x and z axes. This behavior is qualitatively similar to the change in the exchange tensor orientation relative to the fine-structure tensor as inferred from the ESR simulations discussed above (Fig. 4).

The orientation of the zero-field tensor for the five quinone-iron complexes follows a trend analogous to that seen for the hyperfine tensor of the iron (Fig. 4). For both BRC and PS II, where the fifth ligand is glutamate, formate, or bicarbonate, the largest tensor component (in absolute magnitude and assigned to D_z) is directed toward the Q_A⁻. For BRC (+ glutamate or formate), the D_y direction bisects the fifth ligand, whereas D_x is directed toward the axial histidine, defining a plane characterized by lower tensor values (in absolute magnitude). As seen for the hyperfine tensor, the orientation of the zero-field tensor does not dramatically change between BRC and PS II. In PS II (+ formate or bicarbonate), the D_x/D_y plane still contains axial histidines and the fifth ligand, but now D_x points to the axial histidine and D_y is directed toward one of the binding oxygens, rather than the carbon of the carboxyl group. In contrast, for PSII (+ carbonate), D_z is now the smallest tensor component (in absolute magnitude) and is rotated into the membrane plane, pointing toward one of the axial histidines. The D_x/D_y plane still contains the fifth ligand (CO₃²⁻), but it now also contains the equatorial histidines with the D_x and D_y components directed toward binding nitrogens of the histidines. As with the analysis of the hyperfine tensor above, the apparent interchange of the principal values of the zero-field tensor for PS II (+ carbonate), as compared to all other model systems, is qualitatively similar to the change inferred from the ESR simulations discussed above. Here, it was shown that the exchange tensor reorientates relative to the fine-structure tensor for the g ∼ 1.9 signal as compared to the g ∼ 1.84 signal.

Discussion

Comparison of DFT results to ESR spectrum simulations

Although the ESR simulations of the g ∼ 1.84 and g ∼ 1.9 forms of the semiquinone-iron signal suggested that there was no dramatic difference between them in overall coupling within the complex, they did highlight interesting variations in the exchange and zero-field tensor parameters. A rotation of the relative orientations of the exchange and zero-field tensors was observed, as well as an increase in the D value (by up to 10 K). It is significant that when the computational results were compared among model complexes in which the g ∼ 1.84 or g ∼ 1.9 forms should be observed, viz. g ∼ 1.84 (BRC + glutamate and PS II + formate (28,30,31)) or g ∼ 1.9 (PS II + bicarbonate (28,30,31)), no analogous changes were seen. The coupling environment (as inferred from the hyperfine tensor of the iron and orientation of the fine-structure tensor) is similar in all complexes as is the zero-field splitting of the Fe²⁺ center. Only when the Fe ligand was changed from bicarbonate to carbonate did the hyperfine and zero-field tensors significantly change. This effect is seen experimentally among the g ∼ 1.84 and g ∼ 1.9 systems in that the spectral simulations indicate that they differ by a rotation of the exchange coupling tensor (J) relative to the fine-structure tensor. In a similar way, the zero-field parameter D increased by ∼6 cm⁻¹. This comparative analysis of the semiquinone-iron complex suggests that the native exogenous ligand in PS II is actually carbonate.

The binding pocket of the bicarbonate/carbonate ligand contains residues that are hydrophobic, or potentially positively charged. These include D1-Leu²³³, D1-Val²¹⁹, D2-Asn²³⁰, D2-Thr²³¹, D2-Phe²³², D2-Arg²³³, D2-Ala²³⁴, D2-Pro²³⁷, and D2-Lys²⁶⁴ (13,14,46). Of these, the lysine residue (D2-K²⁶⁴) most likely interacts directly with the bicarbonate/carbonate ligand. The ɛ-amino group of the lysine is within 4 Å of the oxygen of the carbonate (see Fig. 5). The carbonate ligand could be stabilized by forming a hydrogen bond/salt bridge to this residue. This residue has not been previously assigned a role in carbonate/bicarbonate electron transfer kinetics. However, it has been demonstrated that mutation of this residue leads to a 40-fold drop in bicarbonate binding affinity (47).

Figure 5.

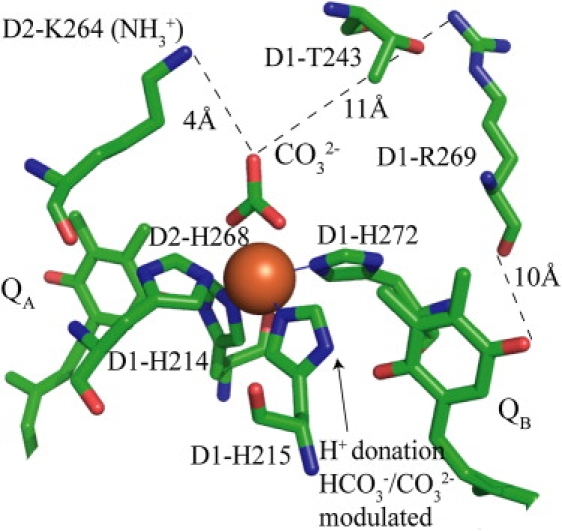
The quinone-iron complex of PS II. Residues in the immediate vicinity of the carbonate ligand to the non-heme iron (Loll et al. (14)).

pH dependence

Early pH-dependent measurements support the assignment of CO₃²⁻ as the native ligand of functionally intact PS II. Rutherford and Zimmerman (29) noted that the g ∼ 1.84 form of the semiquinone-iron signal could be generated in a large fraction of Mn-depleted PS II centers without the addition of formate, by lowering the pH (to ∼6.0). In a similar way, they found that the g ∼ 1.9 semiquinone-iron signal was best resolved at relatively high pH (∼8.0).

At the lower pH, bicarbonate (HCO₃⁻) is the more likely protonation state, whereas at higher pH, the equilibrium progressively shifts to carbonate (CO₃²⁻). The DFT calculations presented above suggest that changing the ligand from bicarbonate to carbonate significantly alters the inferred exchange tensor orientation. This rotation is qualitatively similar to the change that occurs on shifting between the g ∼ 1.84 and g ∼ 1.9 forms as estimated from ESR simulations.

To be observed in the pH range in which PS II is generally studied, this effect would require a large lowering of the pK_a,2 of the bicarbonate bound to the iron center.

$${\mathrm{HCO}}_3^{-}+{\mathrm{HO}}^{-}\stackrel{\mathrm{p}{\mathrm{K}}_{\mathrm{a},2}}{\to }{\mathrm{CO}}_3^{2-}+{\mathrm{H}}_2\mathrm{O}\text{.}$$ (3)

In aqueous solution, pK_a2 is ∼10.33 (48), excluding any significant CO₃²⁻ concentration in solution over the pH range used here (pH 6–8). However, the pK_a,2 of the Fe²⁺-ligated species presumably would be lowered due to the Lewis acidity of the metal ion. In a similar way, the effect of the positively charged hydrophobic residue in close proximity (K²⁶⁴) could alter the acid base properties of the bicarbonate/carbonate.

Mechanistic role of bicarbonate: protonation of the reduced Q_B

Bicarbonate has been proposed to be involved in 1), the protonation step(s) of the reduced Q_B; and 2), the stabilization of the structure of the quinone-iron complex ((20) and references therein).

Electron transfer between Q_A and Q_B dramatically slows after the second actinic flash in PS II, when bicarbonate has been exchanged (formate-treated, etc. (reviewed in (19))). As the second electron-transfer step (see Introduction and Scheme 1) requires protonation of the reduced forms of Q_B, it has been proposed that bicarbonate somehow facilitates this process (20). The mechanism for this effect is as yet unclear; however, the proposal that bicarbonate is the proton donor for Q_B is consistent with its known acid/base properties. The pK_a of CO₂ solvation is ∼6.3.

$${\mathrm{CO}}_2+{\mathrm{H}}_2\mathrm{O}\stackrel{}{\to }{\mathrm{H}}_2{\mathrm{CO}}_3\stackrel{\mathrm{p}{\mathrm{K}}_{\mathrm{a}}}{\to }{\mathrm{HCO}}_3^{-}+{\mathrm{H}}^{+}\text{.}$$ (4)

For fully functional PS II embedded in the thylakoid membrane, the functional pH environment for quinone reduction and proton uptake is ∼7.8, the pH of the stroma. The inhibitory action of formate (49,50) is then easily rationalized, as its pK_a (∼3.8) makes it fully deprotonated under conditions of normal PS II operation.

This study requires a reappraisal of such explanations. As the native ligand to the Fe²⁺ is a carbonate ion rather than bicarbonate, the ligand cannot act as the terminal H⁺ donor to Q_B. The earlier suggestions for the role of bicarbonate in protonation of Q_B involved bicarbonate picking up a proton and passing it on to the reduced quinone (20). This involved the carbonic acid/bicarbonate couple. In the context of the results presented here, we suggest that carbonate could play a similar role, except that the bicarbonate/carbonate couple would be involved. In such a model, bicarbonate could form transiently during the Q_A⁻-to-Q_B⁻ electron transfer step.

An alternative explanation is that the function of carbonate in protonation is indirect. It could modulate protonation reactions by changing the pK_a values of residues in the vicinity of the Q_B site, consequently promoting proton transfer ((20) and references therein). The influence of carbonate should be most dramatic on residues that make up the coordination sphere of the non-heme iron. The D1-H²¹⁵ residue (Fig. 5) is a candidate for such a bicarbonate/carbonate pK_a modulation, although the precise mechanism is as yet unclear. The second NH group of its imidazole ring is within 3 Å of one of the O atoms of quinone Q_B, allowing it to be a potential proton donor. The presence/absence of carbonate could conceivably influence the acid/base properties of this residue, facilitating proton transfer. This result is compatible with a recent Fourier transform infrared study (51). Here, it was shown that the binding of the exogenous carbonate ligand was associated with the presence of the NH mode of the D1-H²¹⁵ residue.

Supporting Material

Ten supporting information subsections with additional text, figures, equations, and code are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01204-1.