Elbow Flexibility of the kt38 RNA Kink-Turn Motif Investigated by Free-Energy Molecular Dynamics Simulations

Abstract

Kink-turns (K-turns) are common structural motifs that can introduce sharp kinks into double-stranded RNA, and have been proposed to mediate large-scale motions in the ribosome. K-turns consist of a bulge loop region flanked by trans sugar-Hoogsteen G:A pairs, and the sharp kink conformation is stabilized by A-minor interactions (adenine contacting a G:C basepair in the minor groove). Umbrella-sampling molecular dynamics simulations were used to disrupt an A-minor interaction in the ribosomal kt38 turn and to calculate the associated free-energy change. Coupling of umbrella sampling with replica exchanges between neighboring umbrella-sampling intervals could further improve the convergence of the free-energy calculations. The simulations revealed a coupled A-minor disruption and global opening of the K-turn motif, and allowed us to characterize several intermediate A-minor conformations. The calculated free-energy profile indicated a meta-stable, semi-open structure of slightly higher free energy (∼1 kcal mol⁻¹), separated by a small free-energy barrier (∼1.5 kcal mol⁻¹) from the closed (highly kinked) form. Both K-turn states are stabilized by distinct variants of the A-minor interaction. Further opening of the K-turn structure required significantly larger free-energy changes. The semi-open form had a reduced kink angle compatible with experimental data on K-turn solution structures, and opening was coupled to a continuous global unwinding of the K-turn motif. The range of free-energy changes associated with kt38 opening and unwinding are compatible with the idea that K-turns may facilitate biologically relevant motions during large-scale ribosome dynamics.

Introduction

Recurrent structural motifs that stabilize RNA tertiary structures were recently discovered in the analysis of crystal structures of large RNA-containing biomolecules (1–6). One of the most abundant motifs that mediate RNA tertiary interactions is the A-minor interaction (2), which involves the N1-C2-N3 edge of an adenine inserted into the RNA minor groove. A-minor interactions stabilize contacts between RNA helices and between loops and helices, as well as the conformation of kink (K)-turn motifs (4). K-turn motifs are characterized by a sharp bend (∼120°, included angle of ∼60°, also frequently called a “V-type” structure) of the phosphodiester backbone between a canonical helix (Watson-Crick basepairs, C-stem) and a helix that contains noncanonical (typically Hoogsteen) basepairs (termed the NC-stem). The tip of the “V” structure forms a short asymmetric loop that comprises nominally unpaired nucleotides between the two flanking rigid stems. K-turns have been found in conserved regions of ribosomal (r)RNA and messenger (m)RNA of archaea, prokarya, and eukarya (4–6). Most of the K-turn motifs serve as protein recognition sites and are probably involved in protein-assisted RNA folding (2,5,7). However, some K-turns may also act as passive molecular elbows that mediate long-range intra- and intermolecular motions in the ribosome during the elongation cycle or ribosome folding (8–10). Further, it has been suggested that K-turns specify distal targeting in neurons (11). Fluorescence resonance energy transfer solution experiments (12) indicate that K-turns are highly flexible and exhibit a dynamic equilibrium between a tightly kinked conformation and a more open unfolded structure similar to a simple bulged loop.

Molecular dynamics (MD) simulations allow the characterization of molecular motions in biomolecules on the nanosecond timescale at atomic resolution. The MD approach has already been applied to many RNA-containing molecules (13–15). It has been used to characterize the flexibility of RNA, as well as hydration and ion binding (14–19). The dynamics of structures as large as a complete ribosome have been investigated in the nanosecond time regime (20). In combination with advanced sampling methods, it has also been used to study folding of RNA (21,22) and DNA (23) hairpins. Folding of such motifs has also been studied using low-resolution RNA models (24). MD simulation studies on several K-turn structures (8–10) indicated a significant mobility of the angle between the two rigid stems corresponding to alternative K-turn substates. All the arrangements identified by earlier simulations (8–10) are likely fine substates corresponding to the tightly kinked topology identified by solution experiments. The simulations are too short to achieve any spontaneous unfolding of the K-turns and thus characterize the internal flexibility of the K-turns relevant to their functional (folded) geometries. The biological significance of these findings is that K-turn motifs could mediate large-scale hinge-like motions during both protein synthesis and the assembly of ribonucleoproteins.

Experimental data on isolated K-turn structures indicate that they can indeed undergo global conformational changes upon metal ion association or protein binding (12,25,26). K-turn flexibility may be contributing to tRNA translocation between the A-, P-, and E-sites at the interface between the small and large ribosomal subunits during protein synthesis, or to the dynamics of the L7/L12 stalk during its interactions with incoming tRNA and elongation factors. For instance, the long helical segment known as the acceptor (A)-site finger (H38 of the large ribosomal subunit) contains an elbow segment at its base, which is formed by a K-turn in archaea. Cryo-electron microscopy shows that the intersubunit bridge B1a located at the tip of the tRNA A-site finger moves up and down during the global ratchet-like rotation of the ribosomal machinery (27,28). This allows for a coordinated translocation of tRNA from the A- to the P-site because the A-site finger is positioned between the A- and P-sites in such a way as to permit the passage of tRNA (29,30). It has been suggested that such large-scale coordination during elongation is provided by the elbow flexibility of the K-turn kt38 located near the base of the A-site finger (8). It has also been suggested that the A-site finger can act as a gate in regulating access of the tRNA from the A-site to the P-site in a coordinated movement with 5S rRNA (9). To date, biochemical studies have not provided a definite characterization of the biochemical role of the A-site finger, which reflects the complexity of the ribosome (31,32). However, in general, investigators agree that the A-site finger is involved in fine tuning of the ribosome function and is dynamical. It may be acting, among other functions, as an attenuator of translocation, or it may be involved in ribosome folding (32).

Of interest, kt38 is present in archaea but is not conserved in bacteria or eukarya (6). Nevertheless, MD simulations (J. Sponer, unpublished results) reveal that the RNA building blocks that replace kt38 in bacteria have elbow-like flexibilities very similar to those of kt38. Further, kt38 is structurally similar to the conserved kt42, and both K-turns show similar behavior in unrestraint MD simulations (9). The tertiary fold of the kt38 motif is stabilized by two A-minor interactions. During MD simulations of kt38, the A-minor interactions remained stable but the global dynamics of the K-turn appeared to be directly regulated by local variation of the second A-minor interaction (9). A conformational search on kt38 in which the orientation of the stems was stochastically modified (10) pointed to a bimodal distribution between two kinked conformations. It was predicted that the more-open structures would be separated from the closed kinked form by an energy barrier. This barrier was estimated at >10 kcal mol⁻¹ (10), without accounting for an explicit representation of the solvent or for full conformational freedom of the flanking stems.

Of the four types of A-minor interactions that have been identified in experimental RNA structures (2), two have been found to serve as the second A-minor interactions in K-turn motifs (9). The two motif types differ in the position of the ribose O2′ atom and base N3 atom of the adenine residue relative to the ribose O2′ atoms in the basepair of the receptor helix. The type I A-minor interaction involves direct trans sugar-edge/sugar-edge (SE/SE) and cis SE/SE base-base interactions, and is defined by both the O2′ and N3 of the adenine residue at the minor groove of the receptor helix (observed in K-turns kt42, kt7, and kt94/99). A variant that is referred to as a water-inserted type I A-minor interaction has also been found to be important in stabilizing some K-turns (kt7, kt23, and kt38), and involves insertion of a water molecule to mediate the cis SE/SE hydrogen bonds. In simulations, both kt38 and kt42 reveal dynamic oscillations between direct and water-mediated A-minor I topologies (9). The second A-minor interaction found in some K-turns (kt15, kt46, kt58, and ktU4), termed type 0, involves a lateral shift of the adenine residue that brings its N3 atom outside the O2′ of the opposing strand in the receptor helix.

In this study we analyzed both the A-minor fine structure and free-energy costs for disruption of the motif and the associated conformational changes in the kt38 structure. MD umbrella-sampling calculations of K-turn opening/closing motion were performed using the disruption/formation of the A-minor interaction as a reaction coordinate. The results indicate a nearly bimodal free-energy curve for kt38 elbow motion, with a semi-open state of slightly higher free energy compared to the fully kinked state. Several variants of the A-minor interaction were observed during the K-turn opening/closing simulations, some of which are new (to our knowledge) or have already been observed experimentally in other K-turn structures. Of interest, the simulations suggest a coupling of global angular kt38 motion and a relative helical orientation (twist) of the flanking stem regions. A similar effect was recently characterized in gel electrophoresis experiments on a related K-turn motif (12). More generally, this study confirms a possible role of K-turn elbow flexibility in coordinating large-scale motion in the ribosome.

Materials and Methods

kt38 RNA oligomer

The starting conformation of the K-turn kt38 was taken from the x-ray structure of the 50S subunit of Haloaricula marismortui (1) (residues 934–942 and 1024–1036 of the 23S ribosomal RNA, Protein Data Bank entry: 1JJ2 (1)). The kt38 K-turn motif contains 22 nucleotides from which four nominally unpaired nucleotides form a tightly bent loop (kink element) linking two paired helical stems, referred to as elements C (canonical basepairs) and NC (noncanonical basepairs). The NC-stem comprises two trans Hoogsteen SE basepairs (A939/G1031 and A1032/G938) that are involved in A-minor tertiary interactions between C- and NC-stems, stabilizing the global structure (Fig. 1). The first A-minor interaction involves the trans SE/SE A939/G1027 basepairing (for the sake of simplicity, we refer to this interaction as “A-minor” throughout this work, although the strict definition of an A-minor interaction requires the presence of a complete Watson-Crick basepair as a receptor for the adenine). The position of the adenine residue in the NC-stem is conserved in all K-turn motifs reported so far. The second A-minor interaction involves both the trans SE/SE A1032/G940 and the cis SE/SE A1032/C1026 basepairing (Fig. 1).

Figure 1.

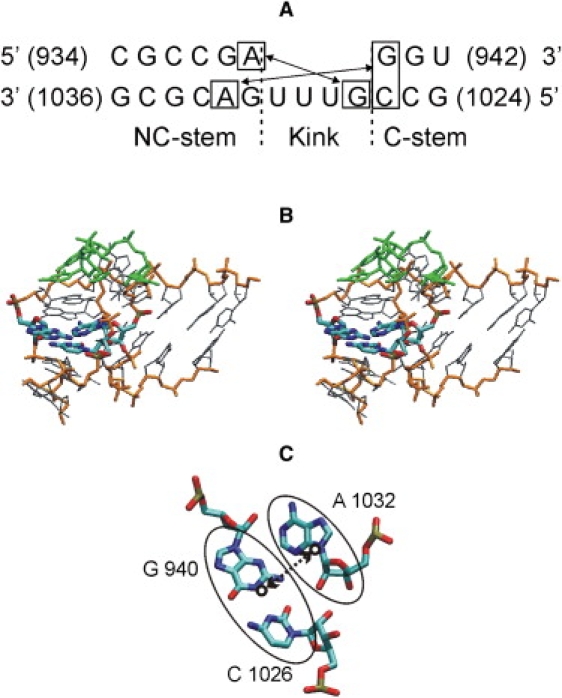
(A) Sequence, basepairing, and A-minor interactions of the kt38 structure (Protein Data Bank entry: 1JJ2 (1)). Numbering is given with respect to the 23S rRNA of Haloaricula marismortui. The first A-minor interaction (critical for K-turn stability) is indicated by the shorter double arrow; the second A-minor interaction (the longer double arrow) is formed by adenine from the intrastem A:G basepair interacting with a G:C basepair in the RNA minor groove of the other stem. The A-minor interactions stabilize a V-shaped geometry of the C (canonical paired)-stem and the NC (noncanonical paired)-stem flanking element K. (B) Stereo view of the three-dimensional structure of kt38. The three nucleotides forming the second A-minor interaction are indicated as bold sticks (atom color code) and the central loop nucleotides are in green (backbone in orange/gray). (C) Stick model of the second A-minor interaction (atom color code). The atoms that determine the centers of mass and the reaction coordinate distance used during the umbrella-sampling free-energy simulations are encircled (thin ellipses around A1032 and G940:C1026). The distance between the centers of mass (circles at the center of the ellipses) is indicated by a double arrow (dotted line).

Umbrella-sampling approach

The umbrella coordinate was defined as the distance between the center of mass of the nucleoside A1032 and the pair of nucleosides G940 and C1026. Umbrella sampling consists of a series of simulation “windows” for steadily increasing or decreasing values of the reaction coordinate δ. The reaction coordinate was modified in 1 Å steps between adjacent windows and restrained to a window-specific reference value using an harmonic biasing potential v_i(δ) = k (δ − δ_ref)² with a force constant k = 2.0 kcal mol⁻¹Å⁻². As δ ∼ 6 Å corresponds to the crystal structure, and δ ∼ 13 Å corresponds to a quasilinear RNA helix, the range of δ-values for the umbrella sampling was chosen to be 6–13 Å.

Umbrella sampling was also carried out by means of the replica-exchange umbrella sampling (REUS) (33,34) method. The latter was used because of a significant hysteresis between free-energy pathways obtained by conventional forward and backward umbrella sampling, as discussed in the Results section. REUS (33,34) is an enhanced sampling technique that consists of frequent swaps of conformations between adjacent replicas i and j (every pair i, j is tested in turn) according to an exchange probability that satisfies the detailed balance. This exchange criterion takes the form of an equation of microreversibility and takes into account the probability density of conformations in the two replicas i, j (i.e., Boltzmann factors based on the biased potential energy function of replica i and replica j). The periodic exchanges can significantly improve the sampling in each window because conformations trapped in a low-energy region of the conformational landscape easily diffuse to neighboring replicas that are under the control of a different umbrella potential. The alternative replicas provide an enhanced variety of conformations, accessible to every replica in the limit of a large number of exchanges between the replicas (long-time limit). Details of the Hamiltonian replica-exchange method and its application for free-energy calculations (REUS) can be found elsewhere (33–35). Replica exchanges were attempted every 2 ps (1000 attempted exchanges during 2 ns of data gathering), and traveling of structures through all replica runs was observed.

Simulation details

The starting conformation was neutralized by 20 Na⁺ counterions and solvated with 8408 TIP3P water molecules within a truncated octahedral box using periodic boundary conditions. Long-range electrostatic interactions were treated using the particle mesh Ewald method (36) with a 9 Å direct space sum cutoff. Simulations were performed at constant temperature and pressure using the Berendsen algorithm (37). Bond lengths involving hydrogen atoms were constrained using SHAKE (38), and the equations of motion were integrated using the Verlet algorithm with a 2 fs time step. MD simulations were performed using the sander module of Amber 8.0 (39) with the most recent force field developed for nucleic acids (parmbsc0 (40)). The solvent and counterions were first relaxed by energy minimization (2000 steps) and then allowed to equilibrate around a harmonically restrained kt38 structure during three simulations of 0.2 ns at constant pressure and simulation temperatures of 100 K, 200 K, and 300 K, respectively. The kt38 oligomer was then relaxed by progressively decreasing the harmonic restraints applied to each atom from 15 to 0 kcal mol⁻¹ Å⁻² over a total period of 1.2 ns at constant volume and temperature.

Further equilibration of 0.2 ns was carried out in each window and the structure obtained at the end of this sampling was used as a starting point for the subsequent window. Production runs (umbrella sampling and REUS) were then performed in parallel using the final structure of each equilibration step and the same force constant of k = 2.0 kcal mol⁻¹ Å⁻² in each umbrella-sampling window. MD simulations in each independent window were carried out for 2 ns. Both backward (the same protocol for equilibration in each window, but starting from the final conformation obtained in the forward sampling window at δ = 13 Å) and extended (an additional 2 ns forward per window) simulations were carried out to better assess the convergence of the sampling. The weighted histogram analysis method (41) was used to calculate the potential of mean force (PMF) or free energy along the reaction coordinate δ. Helical and global parameters were calculated using Curves (42,43).

Results and Discussion

Free-energy change of kt38 elbow motion and A-minor disruption

The PMF for the kt38 opening was calculated using umbrella sampling by gradually increasing the distance δ between geometric centers of A1032 and the G940:C1026 basepair of the second A-minor interaction (Fig. 2). Free-energy simulations were performed in both the forward direction (starting from the equilibrated experimental kt38 structure) and, as a control, the backward direction (starting from the final structure of the forward simulation after reequilibration). To further improve the sampling quality and convergence, the REUS method of using umbrella sampling coupled with replica exchanges between neighboring umbrella-sampling windows was also used (backward control REUS simulation restricted to δ = 6–9.5 Å).

Figure 2.

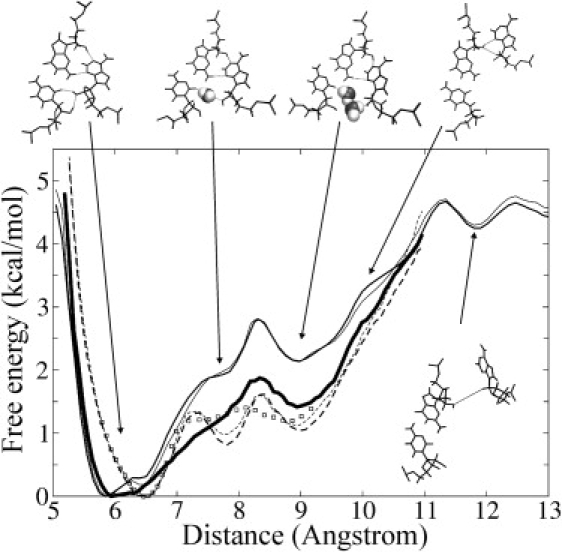
Calculated PMF for the opening of the kt38 K-turn motif along the reaction coordinate δ. The reaction coordinate δ corresponds to the distance between the geometric center of the adenine (A1032) and the guanine (G940):cytosine (C1026) basepair of the second A-minor interaction. Thin lines correspond to PMFs calculated in the forward (full line) and backward (dashed line) simulations, respectively. Hair lines correspond to a data-gathering time of 1 ns per umbrella-sampling interval. Thin lines indicate the same simulations but extended to 2 ns per interval. The bold line is the PMF obtained by using the REUS method with starting conformations in each window as obtained after the forward (full line) or backward (open squares) umbrella-sampling production runs. Representative simulation snapshots of the second A-minor interaction (G940:C1026 basepair and A1032) for each phase of the umbrella-sampling simulation are shown as stick models (inserted water molecules in van der Waals representation). The third and fourth conformations represent semi-open structures, and the last stick model corresponds to a fully open kt38 structure.

In each simulation the calculated global free-energy minimum was close to the experimental highly kinked kt38 structure with a reaction coordinate distance δ of 6–6.5 Å. In addition, a second local energy minima at δ = 9 Å was observed that corresponded to a semi-open conformation. In the semi-open state, the direct second A-minor interactions were disrupted, but the global geometry of the structure had not reached a fully open state (see below). A comparison of the forward and backward umbrella-sampling simulations revealed a free-energy hysteresis, with the calculated free energies shifted to lower values by ∼1 kcal mol⁻¹ around δ = 7–11 Å in the backward simulation. When conformation exchanges were allowed between the umbrella windows according to the REUS formalism (Fig. 2, bold line), the forward and backward PMF curves showed a much smaller hysteresis effect, indicating better convergence. Two secondary minima from the backward simulation were found; however, when REUS was applied to the starting conformations, for each window, obtained after the backward equilibration phase, these two local minima merged into a broad plateau (from δ = 7 to δ = 9 Å). Thus, with the REUS enhanced sampling technique, the PMF results from forward and backward simulations are in agreement for predicting a meta-stable conformation (secondary minimum) at δ ∼ 9 Å for kt38, characterized by a free-energy difference of ∼1 kcal mol⁻¹ and a small barrier with respect to the closed form of ∼1.5 kcal mol⁻¹ (Fig. 2). The intermediate A-minor conformations contain water molecules inserted between A1032 and the G:C basepair. Similar A-minor states with inserted water molecules have been described in previous unrestrained K-turn MD simulation studies (9,10). Further opening of the kt38 structure (i.e., δ > 11Å) resulted in a disruption of all stabilizing tertiary interactions (a complete loss of A-minor interaction) and a free-energy level of ∼4 kcal mol⁻¹ higher than the folded motif. This corresponds to globally almost colinear arrangements of the kink stem helices. Details of the molecular interactions that characterize the successive kt38 substates are described in the following sections.

Global deformability of kt38

The phosphodiester backbone root mean-square deviation (RMSD; see Fig. S1 in the Supporting Material) based on heavy atoms with respect to the initial conformation revealed consecutive shifts in the range of 1–5 Å during the umbrella-sampling simulations. One can distinguish four different RMSD levels corresponding to δ < 7 Å (global minima), 7 Å < δ < 8 Å (saddle region), 8 Å < δ < 10 Å (local minimum, semi-open state), and δ > 10 Å (plateau regime, fully open state). These states closely resemble the different A-minor states identified in the previous paragraph. The amplitude of RMSD fluctuations increased from one regime to the next. RMSD fluctuations were >1 Å on the plateau, which indicates a significantly increased flexibility of the open kt38 structures compared to the closed highly kinked form.

Global kink and twist deformations associated with different regimes of the PMF curves are illustrated in Fig. S2. The kink angle between the two flanking stems remained close to 100° for the closed conformation (see error bars), whereas the semi-open geometry corresponded to an average value of 125°. As indicated in the previous paragraph, although the second A-minor interactions are already disrupted in the semi-open state, a further opening of the kt structure is still possible. The average interstem kink angle in the fully open geometry was 150°. For the semi-open and open conformations, much higher fluctuations of the kink angle were observed with standard deviations of ∼25° and 50°, respectively. Very good agreement was observed between averages obtained from the forward, backward, and REUS production sampling for each regime.

The simulation studies predict that the opening motion of kt38 is correlated with a twist rotation of the two flanking stems (Fig. S2, lower panels, and Fig. 3). The calculated average interstem twist angle is −50° for the closed conformation, −75° for the semi-open conformation, and ∼ −100° for the open conformation in kt38. The correlation coefficient with the global kink angle extracted from Fig. 3 is −0.87. Note that larger global twist fluctuations were also observed for more open K-turn structures. This increase was, however, less pronounced than for the kink angle fluctuations. Of interest, recent gel electrophoresis studies of the kt7 motif in RNA constructs that contained a second kinked RNA motif also indicated a significant twist change upon K-turn formation (12). The kt7 motif is similar to the kt38 element and undergoes a metal ion-induced transition between open and closed forms with an associated change in bending direction of ∼75° (12), in qualitative agreement with the above calculated twist change upon transition from the closed to the semi-open kink turn state. Obviously, the experiment does not provide a direct atomistic structural insight, so we cannot quantitatively compare the structures seen in simulations with those present in the experiment. Thus, the meaning of “open” and “closed” may differ between the experiment and theory.

Figure 3.

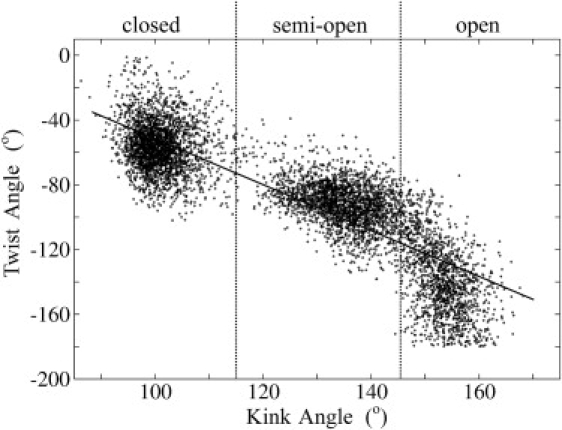
Correlation of the interstem kink and twist angles calculated using Curves (42,43). Data points were recorded every 2 ps during umbrella-sampling simulations. The kink/twist correlation is also indicated by the least-square fitted line.

Dynamics of the second tertiary A-minor interaction reveals three local substates engineering the hinge-like motion of kt38: type I, type 0, and disrupted

The global dynamics of kt38 is correlated with the local variability of its second A-minor interaction linking the C- and NC-stems (9). Upon opening of the K-turn, the A-minor interaction undergoes a transition to a number of conformational variants (Fig. 2), including conformations that involve one or two water molecules partially filling the space between A1032 and the G940/C1026 basepair. The type I A-minor interaction in the kinked structure includes the trans SE/SE A1032/G940 and the cis SE/SE A1032/C1026 pairing in accordance with the classification of Nissen et al. (2) and Leontis and Westhof (44). In the closed state of kt38 in our free-energy simulations (δ = 6–6.5 Å), both the N3 and O2′ atoms of A1032 are inside the minor groove of the receptor helix formed by the G940:C1026 basepair (Fig. 4 A, left panel), and thus correspond to a type I A-minor interaction. Both interactions between A1032 (N3 and N5) and G940 (O4 and O2′, respectively) and between A1032 (O2′) and C1026 (O2′ and O2 simultaneously) are hydrogen-bonded. The representative snapshots of structural motifs in kt38 shown in Fig. 4 are close to average structures from umbrella-sampling windows representing the closed, semi-open, and fully open forms. Since the center-of-mass distance restraint within one umbrella-sampling window allows only narrow distance changes (∼1 Å), the A-minor interaction structures shown in Fig. 4 and Fig. S1 show structural fluctuations of similar order.

Figure 4.

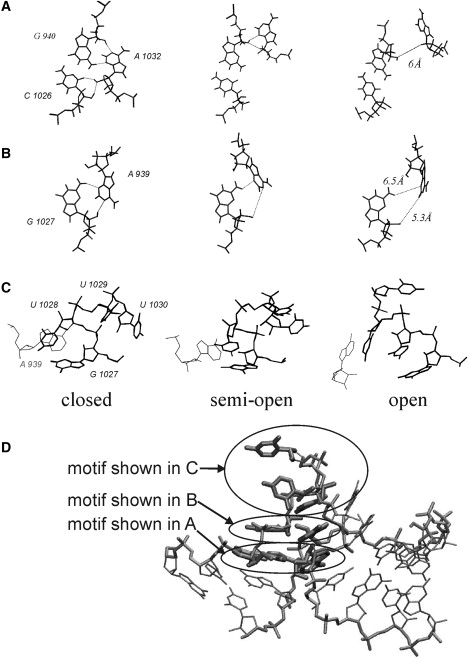
Structural motifs characterizing the closed, semi-open, and open conformations of the kt38 K-turn structure. Some key hydrogen-bond donor-acceptor distances are included as dotted lines. (A) Second A-minor interaction of kt38, from left to right: A-minor type I cis SE/SE A/C, A-minor type 0, and disruption of the second A-minor interaction. (B) Representative snapshots of the first A-minor interaction during kt38 opening. (C) Central loop (element K) between C- and NC-stems (A939 is shown as a thin line). From left to right: U1028 stacks on A939, U1028 alternatively stacks on A939 and U1027, and in the open conformation U1029 inserts into the central cavity, inducing stable stacking between A939, U1029, A1028, and G1027, respectively. The location of the structural motifs (shown in A–C) within the kt38 structure are indicated in D (encircled).

At the saddle point (δ = 8 Å, ΔG = 1.5 kcal mol⁻¹), opening the A-minor interaction induces an increase of the distance between A1032 and C1026, i.e., these two nucleotides lose their direct hydrogen bonds. The disruption of the A-minor interaction does not occur simultaneously for all hydrogen bonds; rather, it occurs in a stepwise fashion involving a translational shift as well as a rotation of the A1032 relative to the G940:C1026 basepair. The free-energy saddle is indeed associated with a second A-minor type I water inserted cis SE/SE A/C basepair, as also observed in unrestrained MD simulations (9,10). We observed both the insertion of one out-of-plane water molecule mediating hydrogen bonds between A(O2′) and C(O2), and the insertion of two water molecules mediating hydrogen bonds between A(O2′) and C(O2)/C(O2′) (termed “semiopen and open states” by Razga et al. (9), who used a different terminology from the one used here). We observed multiple water molecule exchange events at this site and very frequently an absence of such water molecule-mediating H-bonds, i.e., no interaction between A1032 and C1026. A possible interpretation is that the loss of entropy associated with the water-inserted A-minor type I variant is relatively high and is the reason for the peak in the free-energy surface (∼1.5 kcal mol⁻¹) corresponding to the semiclosed state. Note that the A-minor I interaction can still be considered as well paired, because its main stabilization comes from the trans SE/SE A1032/G940 basepair, which remains well bound upon water insertion into the A/C basepair.

In the semi-open conformation of kt38 (local energy minima at δ = 9 Å), the distance between A1032 and G940/C1026 basepairs further increases. This induces a transition of the second A-minor interaction to a weakly bound structure, known as an A-minor type 0 interaction illustrated in Fig. 4 (upper middle panel) (2,45). Type 0 is characterized by a lateral shift of the A1032 with respect to the G/C receptor minor groove: the N3 of A1032 is located outside of the G940:C1026 minor groove, but it can still form a hydrogen bond with the ribose of G940. The local lateral shift when going to a type 0 variant in the second A-minor interaction is a major reason for the global untwisting of the structure. During the simulations this tertiary interaction is disrupted in the fully open substate (onset of plateau; Fig. 4, upper right), in agreement with previously reported conformational search results (10). The first A-minor interaction in the kt38 motif involves a trans SE/SE G1027/A939 basepairing interaction. In contrast to the second A-minor interaction, this interaction was not completely disrupted throughout the induced kt38 opening (Fig. 4 B). A significant change was a progressive inclination of A939 with respect to G1027 upon kt38 opening (Fig. S3).

Rearrangement of nominally unpaired nucleotides

The long strand of the interstem loop (termed element K) contains four nominally unpaired nucleotides (G1027, U1028, U1029, and U1030). G1027 has been described as part of the first A-minor interaction. The aromatic base of U1028 remained stacked inside the motif during all stages of the simulations. In the closed state, U1028 is approximately in the plane of G1027, with which it forms a side-by-side cis Hoogsteen SE pair (Fig. 4 C, left panel). In the semi-open state, U1028 stacked preferentially on G1027 (Fig. 4 C, middle) and this was favored by the lateral shift of A939 (NC-stem) with respect to the C-stem.

Global opening of the kt38 motif induced the extension of a free space below the phosphodiester backbone containing unpaired and bulged-out nucleotides (i.e., element K; Fig. 1). This cavity was absent in the closed conformation because of the sharp kink in element K. During the smooth elbow dynamics, wherein δ < 11 Å, the cavity was accommodated by a lateral shift between the C- and NC-stems (see above). At δ = 11 Å, the larger cavity was filled by either solvent molecules or partial stacking of U1028 between G1027 and A939 (Fig. 4 C, middle). For δ > 11 Å, the U1029 base inserted into the cavity and stabilized the stacking of U1028 on top of G1027 (Fig. 4 C, right panel). U1030 remained looped-out in all simulations. In the most extended form of kt38 (δ = 13 Å), most of the bulge loop bases (with the exception of U1030) remained in an intrahelical stacked conformation (Fig. 5). It is possible that further opening could result in a looped-out conformation for all bulge bases; however, the current reaction coordinate may not be appropriate to achieve a complete colinear arrangement of the stem helices. Most of the backbone conformational changes that accompanied the transition of kt38 to a fully open form were localized to the U1027 and U1030 bulge nucleotides (Fig. 5).

Figure 5.

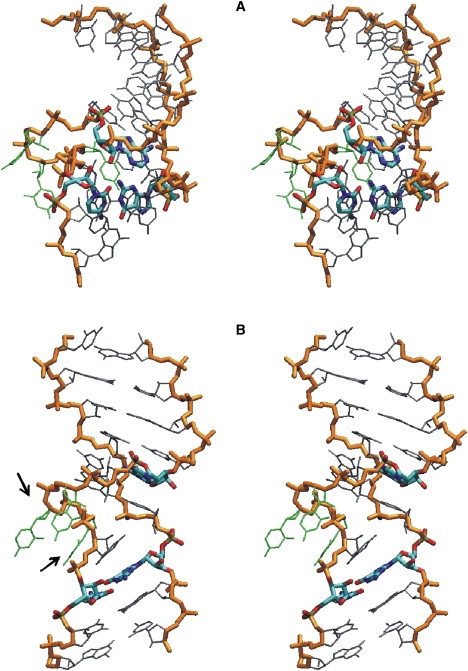
Comparison of a snapshot from a simulation of the initial closed kt38 structure at a reaction coordinate distance δ = 6 Å (stereo view in A) and a snapshot from the simulation window with δ = 13 Å corresponding to a fully open geometry (stereo view in B). The nucleic acid backbone (orange/gray) and the nucleotides forming the second A-minor interaction (color-coded) are indicated in bold sticks. Loop nucleotides are in green. The central loop (element K) in the open state contains a single completely bulged-out nucleotide (U1030). The two nucleotides with the largest associated changes in backbone structure upon K-turn opening are indicated by arrows in B.

It has been shown experimentally that kt structures can undergo open–closed transitions in the presence of divalent Mg²⁺ ions (12). Our simulations were performed in the presence of monovalent cations (Na⁺). However, the location of ions in the closed versus open forms, respectively, may give insight into the mechanism of cation-dependent conformational changes in the kt38 motif. In the case of the closed kt38 conformation, two cation-binding sites with ion residence times of >1 ns were identified (Fig. 6). The same ion-binding sites (ion contact atoms belonging to nucleotides C1033, G1034, C937, and G1034) were previously reported and characterized in detail in an MD simulation study of the kt38 motif (10). Of interest, these stable ion-binding sites with long residence times disappeared in the fully open form. This result is qualitatively compatible with the experimental finding of a specific stabilization of the closed kt structure by cations (12), which potentially could be mediated by stable cation-binding sites with a long associated residence time.

Figure 6.

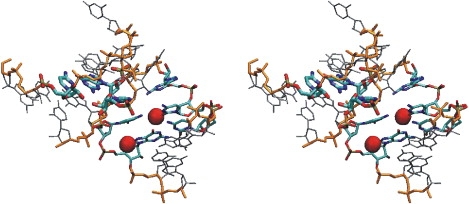
Location of two binding sites for sodium ions (red/gray spheres) with a long associated residence time (>1 ns) during the simulation of the closed kt38 structure (reaction coordinate distance δ = 6 Å). The second A-minor interaction (atom color code) and the backbone (orange/gray) are in bold stick representation. Bases C936, C937, G938, C1033, and G1034, which contact the ions at the two binding sites, are also atom-color coded (thin sticks).

Conclusions

Kt38 is a stem-elbow-stem-like ribosomal RNA motif with contacts between its stems mediated by two tertiary interactions: the first A-minor-like basepair interaction between A939 and G1027 is followed, farther away from the apex of the elbow, by a second A-minor type I interaction between A1032 and G940:C1026 canonical basepair (Figs. 1 and 4).

Umbrella-sampling simulations on kt38 using the opening (or closing) of the A-minor I interaction as a reaction coordinate were used to study the free-energy change associated with K-turn opening and to characterize associated structural changes. In the case of kt38, the elbow motion within the closed geometry region involved free-energy changes of ∼1.5 kcal mol⁻¹, which supports the notion that the closed form involves only a small energy barrier. The relatively small calculated free-energy change (∼3 RT, where R is the gas constant, and T is the temperature) may trigger biologically relevant motions during large-scale ribosome dynamics and protein synthesis. It was demonstrated that coupling of umbrella-sampling simulations with a Hamiltonian replica-exchange methodology significantly improved the convergence of calculated free energies and resulted in a closer match of forward and backward simulations compared to “standard” umbrella sampling.

Replica-exchange MD simulations (using temperature as the replica coordinate) have been used to study the folding of RNA and DNA motifs (22,23) on longer timescales than those required for the REUS simulations presented here (33,34). In the former type of simulations, a much broader range of conformations must be sampled. The kt structures in two neighboring replicas differ by ∼1 Å in the center-of-mass reaction coordinate distance and otherwise preserve most of the secondary and tertiary structure arrangement. In addition, the global mobility within each window is restricted to a relatively narrow distance regime around the preset reaction coordinate distance. The restricted mobility within each umbrella-sampling window contributes to the convergence of the calculated PMF within 1–2 ns per simulation window. It needs to be emphasized that even with the application of the REUS technique, we cannot exclude the possibility that transitions to relevant kt substates separated by high-energy barriers that may require much longer simulation timescales might be overlooked.

The simulations revealed a dynamic equilibrium between a fully paired type I A-minor interaction and several additional type I A-minor substates, with one or more inserted water molecules characterizing the “saddle point” regime of sampled conformations. The small calculated free-energy difference is consistent with the frequent sampling of K-turn states with inserted water molecules during unrestrained MD simulations (10). Coarse-grained models of RNA have been used to simulate large-scale conformational transitions in RNA (e.g., folding of hairpins) (24). Although such models are helpful for understanding the principles of RNA folding, it is unlikely that such approaches could cover the detailed substates of the kt motifs observed in our simulations. However, the calculated free-energy profiles could be used to parameterize effective energy functions for coarse-grained RNA models.

Further along the opening path, the simulations locate a meta-stable semi-open conformation with a shift of the second A-minor interaction from the tightly bound type I to the weakly bound type 0 arrangement. In addition to the local conformational changes, the simulations indicated a global change in bending and twist of the C-stem with respect to the NC-stem correlated with the opening of the kt38 structure and controlled by the conformation of the A-minor I interaction motif. The molecular origin of the bending and twist motion is due at least in part to the shift induced locally in the second A-minor interaction from type I to type 0. It has been reported for the related kt7 element that, in solution (in the absence of Mg²⁺ ions), the motif adopts an open conformation with a bend angle representing that of a three- or four-base bulge structure (12). A three-base bulge in RNA adopts a bending angle of ∼130° ((46), in the current nomenclature where 180° corresponds to no bending). Such global geometry closely matches what we define as “semi-open” in this study, whereas the fully open form that requires higher free-energy changes (∼4 kcal mol⁻¹) approaches a global geometry with a smaller residual overall bending. The latter form is characterized by a complete disruption of the second A-minor I interaction.

In our simulation study, the semi-open state is predicted to be of slightly higher free energy than the closed, highly kinked state. In contrast, experiments on a related kt7 motif indicate that in free solution, kt7 prefers a form that matches our proposed semi-open structure (12). It is important to keep in mind that the experimental system differs from the simulation system in that the former contains longer negatively charged RNA stem regions. Such negatively charged stem regions may add a significant electrostatic repulsion of the stem helices. This electrostatic contribution can shift the free-energy profile such that the semi-open form is more favorable at low salt concentrations (because of the larger distance and smaller repulsion of the stem regions). In turn, at high salt concentration or in the presence of divalent cations, which are known to very efficiently neutralize the negative phosphate charges in RNA, the highly kinked K-turn form (closed form) becomes the most stable structure. Hence, the conditions of our simulation study resemble experimental conditions in which the RNA stem charges are completely neutralized (simply absent in the simulations). In addition, stable cation binding with long residence times was found for the closed kt38 structure but not for the semi-open and fully open structures. It is possible that the occupation of such ion-binding sites by divalent cations (Mg²⁺) adds a specific stabilization of the closed form compared to open kt structures. Nevertheless, the relatively small calculated free-energy changes for K-turn opening/closing support the idea that K-turn motifs can act as flexible elements to mediate global changes of helical stem elements in large RNA-containing molecules, possibly triggered by ion or protein binding. Given the range of geometries with fully paired and partially water-mediated A-minor interactions, it appears that kt38 is able to move over small barriers by adapting to the conformational preferences of the surrounding ribosomal elements.

Supporting Material

Three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01295-8.