The Folding Free Energy Surface of HIV-1 Protease: Insights into the Thermodynamic Basis for Resistance to Inhibitors

Abstract

Spontaneous mutations at numerous sites distant from the active site of HIV-1 protease enable resistance to inhibitors while retaining enzymatic activity. As a benchmark for probing the effects of these mutations on the conformational adaptability of this dimeric β-barrel protein, the folding free energy surface of a pseudo wild-type variant, HIV-PR*, was determined by a combination of equilibrium and kinetic experiments on the urea-induced unfolding/refolding reactions. The equilibrium unfolding reaction was well-described by a two-state model involving only the native dimeric form and the unfolded monomer. The global analysis of the kinetic folding mechanism reveals the presence of a fully-folded monomeric intermediate that associates to form the native dimeric structure. Independent analysis of a stable monomeric version of the protease demonstrated that a small amplitude fluorescence phase in refolding and unfolding, not included in the global analysis of the dimeric protein, reflects the presence of a transient intermediate in the monomer folding reaction. The partially-folded and fully-folded monomers are only marginally stable with respect to the unfolded state, and the dimerization reaction provides a modest driving force at micromolar concentrations of protein. The thermodynamic properties of this system are such that mutations can readily shift the equilibrium from the dimeric native state towards weakly-folded states that have a lower affinity for inhibitors, but that could be induced to bind to their target proteolytic sites. Presumably, subsequent secondary mutations increase the stability of the native dimeric state in these variants and, thereby, optimize the catalytic properties of the resistant HIV-1 protease.

Human Immunodeficiency Virus (HIV), the viral infection that causes AIDS, has come to the forefront as a global public health crisis since the initial identification of this disease twenty-five years ago.^1,2 HIV-1 protease, the protein responsible for viral maturation through multiple cleavages of the Gag and Gag-Pol polyproteins, has been a therapeutic target in the treatment of AIDS for a number of years.³ Structure-based drug design guided the development of the first generation of HIV-1 protease inhibitors.⁴ Though these inhibitors initially showed great promise, the high frequency of mutations in the viral genome resulted in multiple HIV-1 protease variants that maintain activity yet are drug-resistant.⁵ The presence of both active site and non-active site mutations in these variants⁶ suggests that the retention of activity for the non-active site variants may arise from an altered free energy landscape that provides access to alternative HIV-1 protease conformations.⁷ The proposal that differential perturbations in the conformational ensemble of protease may be responsible for resistance is consistent with the concepts of applying protein folding landscape theory to ligand binding.⁸

Proteolytic enzymes, in general, have been shown to function through conformational selection,⁹ and molecular dynamics simulations have postulated that the catalytic power of HIV-1 protease reflects mechanical fluctuations of the whole protein.¹⁰ Crystal structures detailing a crucial “intermediate” conformation of the HIV-1 protease active-site flap tips during substrate binding confirm the role of conformational changes in drug resistance.¹¹ Moreover, calculations of the reaction path between two alternate HIV-1 protease conformations have shown that the small free energy difference between the closed and open conformations of the active site would allow even conservative mutations to influence the activity of the enzyme.¹² However, a comprehensive quantitative experimental assessment of the folding free energy surface for the HIV-1 protease, required to test the conformational adaptability hypothesis for drug resistance,^13,14 has been lacking.

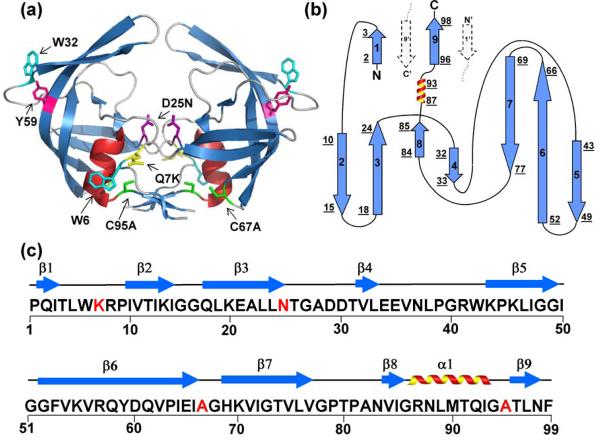
HIV-1 protease is a homodimer with 99 residues per subunit (Figure 1a), and each subunit is comprised of nine β-strands and one α-helix. β-strands two through eight are involved in the formation of a jelly-roll β-barrel topology within each subunit. The dimeric interface is comprised of an anti-parallel β-sheet formed by the interdigitation of the N- and C-terminal β-strands in each subunit (Figure 1b) and by an interlocking and symmetric pair of threonines, Thr26, in the active site.¹⁵ The active site and the Asp25 required for proteolysis are nested beneath the flap tips and span the subunit interface. Trp6 and Trp42, providing intrinsic FL probes of the folding reaction, are located at the subunit interface and the base of the active-site flap tips, respectively. NMR studies of HIV-1 protease variants have shown that mutations at or near the interface shift the monomer-dimer equilibrium to favor the folded but inactive monomeric form.^16-18 Deletion of the C-terminal β-strand of HIV-1 protease, providing the two central elements in the four-stranded β-sheet at the interface (Figure 1b), also produces a folded monomer in solution.¹⁷ This monomer construct is disordered at the N- and C-termini and at the flap tips from residues 48 to 54. As a result, the active site becomes solvent-exposed.¹⁷

Figure 1.

Structure, topology and sequence of HIV-PR. (a) The crystal structure of unliganded, homodimer, D25N HIV-1 (1TW7) protease shows two β-barrel subunits with a dimerization interface comprised primarily of an anti-parallel β-sheet formed from the interdigitation of the N- and C- termini of each subunit. The flaps (residues 43-56) at the top of each barrel are in an “open position” with respect to each other. Mutated residues in the wild-type HIV-1 protease and FL chromophores are shown in stick model representation and are indicated in one subunit of the structure by residue number: Q7K (yellow), D25N (purple), C67A and C95A (green); intrinsic chromophores are indicated by Tyr59 (magenta) and Trp6 and Trp42 (cyan). (b) The topology map of one subunit has a jelly-roll β-barrel topology. β-strands are indicated with arrows, the α-helix is represented by a coil, and loop regions are displayed with lines. Strands are numbered successively, and the underlined numbers correspond to the N- and C-terminal residues of each secondary structural element. Dashed arrows indicate the N- and C- terminal β-strands from the interacting subunit. (c) The amino acid sequence of the HIV-1 protease variant used for these studies. Highlighted in red are the sites that were mutated to create the protease variant used in these studies, Q7K/D25N/C67A/C95A. The 9 β-strands and single α-helical secondary structural elements are indicated above the sequence.

Several previous investigations have examined the thermodynamic and kinetic folding properties of HIV-1 protease under a variety of conditions and using a variety of techniques, including urea denaturation,¹⁹ inhibitor-binding assays,²⁰ sedimentation equilibrium studies,²¹ differential scanning calorimetry,²² NMR,^23,24 and off-lattice Gō-model simulations.²⁵ Although each of these studies has clarified complementary aspects of the thermodynamic and kinetic properties of HIV-1 protease, none has provided a quantitative and comprehensive view of its folding free energy surface.

A battery of equilibrium and kinetic experiments, combined with a global analysis of these data, have been employed to determine the folding mechanism and the folding free energy surface for an inactive but well-folded variant of dimeric HIV protease. The thermodynamic properties of the native dimer and the monomeric folding intermediate support the conformational adaptability hypothesis for the development of resistance to inhibitors for HIV-1 protease.

Results

An inactive variant of HIV-1 protease (HIV-PR*), containing the mutational background Q7K/D25N/C67A/C95A (Figure 1c), was used for these folding studies. Q7K decreases autoproteolysis in active protease variants^26,27 and was a mutation that existed in the background of the plasmid. D25N eliminates HIV-PR activity,^13,28 ensuring thermodynamic reversibility that would be compromised by auto-proteolytic degradation. The C67A and C95A replacements also enhance the reversibility of the system by eliminating cysteine oxidation, including aberrant disulfide bond formation.

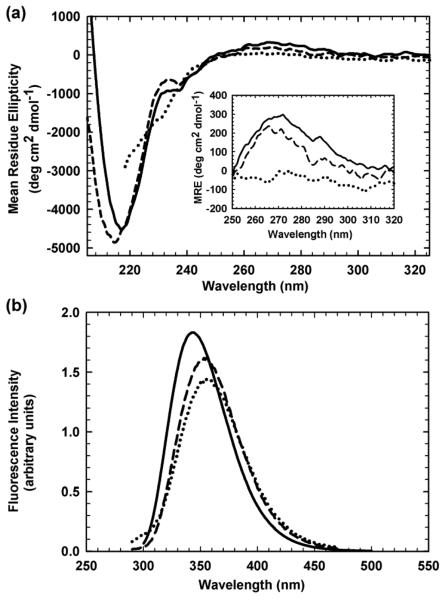
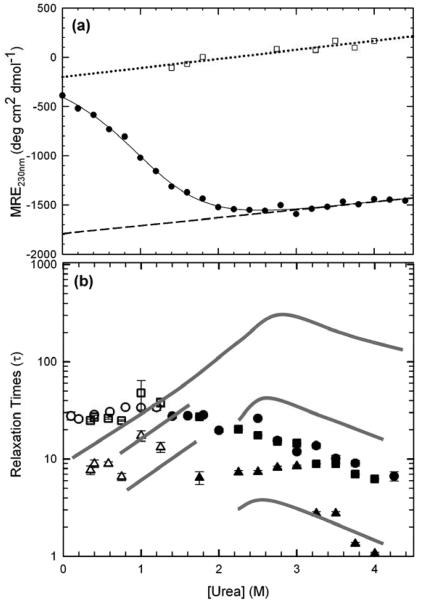
The secondary structure of HIV-PR* was monitored by far-UV CD spectroscopy. A mean residue ellipticity of −4500 deg cm² dmol⁻¹ was observed at the 218 nm minimum (Figure 2a), a characteristic CD band for β-sheet proteins.²⁹ The local maximum at 230 nm may reflect exciton coupling³⁰ between Trp42 and Tyr59 (A. Kundu & C. R. Matthews, unpublished data), and the broad positive band in the near-UV CD between 260 and 285 nm, with a maximum at 270 nm, reflects specific tertiary structure arising from chiral packing of aromatic side chains (Figure 2a, inset). Upon unfolding in 6 M urea, the absence of these three features in the resulting spectrum (Figure 2a) is consistent with a random coil-like structure. The two intrinsic tryptophan residues in each subunit of HIV-PR*, Trp6 and Trp42 (Figure 1a), provided FL probes of tertiary and quaternary structure accompanying denaturation. Native HIV-PR* exhibits a maximum emission peak at 347 nm upon excitation at 295 nm (Figure 2b); unfolding in 6 M urea yields a decrease in intensity and a shift in the maximum of the emission peak to 353 nm as the tryptophans are increasingly exposed to solvent.

Figure 2.

CD and FL spectral characteristics of HIV-PR* and mHIV-PR*. (a) CD spectra and (b) FL emission spectra of HIV-PR*, residues 1-99, (solid lines) and mHIV-PR*, residues 1-95, (dashed lines). The CD and FL spectra of unfolded HIV-PR* and mHIV-PR* in 6 M urea (dotted lines) are coincident. Protein concentration was 5 μM in terms of monomer, and the buffer conditions were 100 μM sodium phosphate, pH 6.0, and 0.2 mM EDTA at 25 °C. The near-UV CD spectra of HIV-PR* (30 μM), mHIV-PR* (8 μM), and unfolded HIV-PR* in 6 M urea are shown as an inset in Figure 2a.

Thermodynamic Folding Properties of HIV-PR*

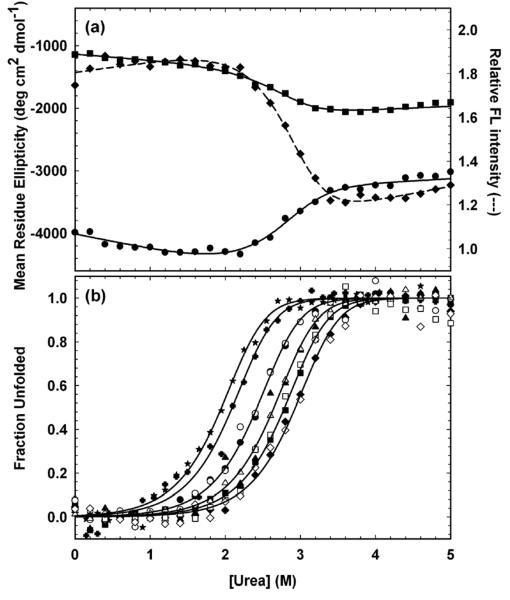
The HIV-PR* equilibrium unfolding reaction was monitored as a function of the urea concentration at pH 6.0 and 25 °C. The titrations were performed across a protein concentration range of 0.5 μM to 60 μM and monitored with both CD and FL spectroscopy to compare the disruption of secondary, tertiary and quaternary structure during denaturation. Unless otherwise noted, protein concentrations refer to the concentration expressed in terms of monomeric protease. Sigmoidal transitions for CD at 220 nm and 230 nm and FL at 350 nm, spanning the range from ∼2 M urea to ∼3.5 M urea, were well-described by a simple two-state model, 2U ⇆ N₂ (Figure 3a). The coincidence of the normalized CD and FL curves at the same protein concentration (Figure 3b) demonstrates the high cooperativity of the reaction, and the coincidence of the unfolding and refolding CD titration curves (FigureS1 in Supplementary Material) ensures that the reversibility of the urea denaturation process is greater than 95%. Thermodynamic parameters extracted from fits of these individual data sets agreed within error, with an average free energy of folding in the absence of urea, ΔG°(H₂O), of −13.0 ± 1.0 kcal (mol dimer)⁻¹ and a dependence of ΔG° on the urea concentration, the m value, of 2.5 ± 0.5 kcal (mol dimer)⁻¹ M⁻¹.

Figure 3.

Equilibrium folding properties of HIV-PR*. (a) Equilibrium unfolding monitored by CD at 220 nm (circles) and at 230 nm (squares) and by FL at 350 nm (diamonds) at 30 μM HIVPR*. Lines represent local fits to the two-state model, 2U ⇆ N₂. Protein concentration in monomer units was 30 μM. (b) Fraction unfolded protein (F_app) plots of the SVD vectors extracted from equilibrium unfolding CD (open symbols) and FL (filled symbols) spectra fit globally to the two-state model, 2U ⇆ N₂. Protein concentrations, expressed in terms of monomer, are 0.5 μM (stars), 1 μM (crosses), 5 μM (circles), 15 μM (triangles), 30 μM (squares), and 60 μM (diamonds). Buffer conditions are described in the caption to Figure 2.

The accuracy of these results was enhanced and the validity of the model tested by singular value decomposition (SVD) analysis of the CD and FL data collected on the same samples and at four different protein concentrations, ranging from 5-60 μM.³¹ In addition, FL data were also collected at 0.5 and 1 μM; the inherently weak CD signal for HIV-1 protease precluded the collection of reliable CD data at concentrations below 4 μM. SVD data reductions for each set of CD or FL spectra for a particular protein concentration were performed separately. In all cases, two SVD vectors were considered significant based on the degree of randomness, the autocorrelation, and the singular values for a given vector. A total of twenty SVD vectors, from six different protein concentration titrations, were fit globally to the above two-state equilibrium model. The fraction apparent plot of the combined CD and FL fits (Figure 3b) displays the increase in the transition midpoint with protein concentration expected for a dimeric system.³² The global analysis yielded a ΔG°(H₂O) of −14.23 ± 0.23 kcal (mol dimer)⁻¹ and an m value of 2.89 ± 0.08 kcal (mol dimer)⁻¹ M⁻¹ (Table S1 in Supplementary Material). These values are in excellent agreement with previous studies of active protease stability, −14 kcal (mol dimer)⁻¹ at pH 6.0¹⁹ and −14.9 kcal (mol dimer)⁻¹ at pH 5.5.²² The amino acid replacements required to produce HIV-PR* have no discernable effect on the thermodynamic properties of HIV-1 protease.

Kinetic Folding Properties of HIV-PR*

The thermodynamic properties of HIV-PR* provide a quantitative assessment of the stability of HIV-PR*, presuming the validity of the two-state model for folding under equilibrium conditions. Kinetic studies of the folding mechanism offer a valuable complement by enabling a partitioning of the global free energy change into possible individual steps for a more complex mechanism that could involve folding intermediates. The kinetic analysis of folding also permits the assessment of the transient populations of such intermediates during refolding and unfolding reactions. The existence of a stable monomeric variant, mHIV-PR*,^17,33 provides an obvious candidate for a folding intermediate that might be expected to appear during the folding of HIV-PR*. The kinetic folding properties of HIV-PR* were assessed by a comprehensive analysis of the unfolding and refolding reactions at a series of urea and protein concentrations using both CD and FL spectroscopy. Representative unfolding and refolding traces by CD and FL can be found in Supplementary Material (Figure S2).

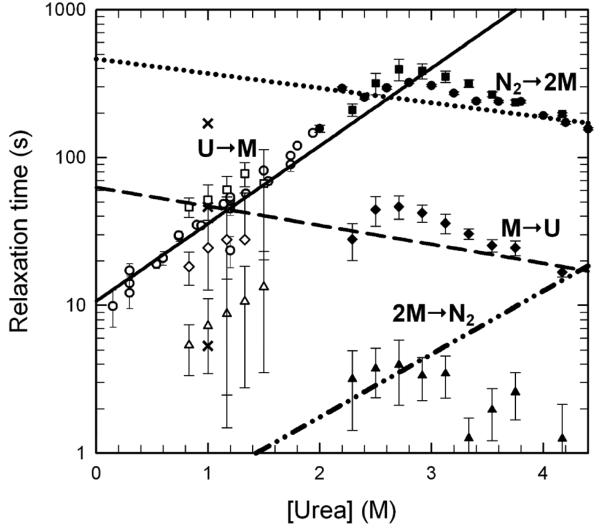
The unfolding kinetics monitored by CD at 230 nm are well-described by a single, slow kinetic phase. The estimated ellipticity at the beginning of the unfolding reaction agrees well with the estimated ellipticity of the native state under identical conditions (Figure S2), precluding any undetected phases within the dead time of these manual-mixing experiments, ∼10 s. The refolding kinetics were largely well-described by a single slow exponential phase whose relaxation time merged smoothly with that for the unfolding reaction in the transition region (Figure 4). A faster phase of small amplitude was also detected for refolding jumps to less than 1.0 M urea, but the limitations of the S/N of the CD technique and the dead time of manual mixing methods did not allow for an accurate assessment of its properties. As will be shown below, refolding phases in this time range become apparent by FL spectroscopy. A semi-log plot of the relaxation times extracted from these fits shows a chevron shape (Figure 4) with a maximum near 3 M urea. Contrary to what might be expected for a rate-limiting bimolecular reaction in a simple two-state folding mechanism, 2U ⇆ N₂, the refolding relaxation time was independent of the protein concentration over the range from 1 μM to 12 μM (data not shown). Either dimerization has occurred within the manual-mixing dead time without the development of significant secondary structure or the bimolecular association step is rate-limited by a prior unimolecular monomer folding reaction. The unfolding reaction is also independent of the protein concentration (data not shown).

Figure 4.

The chevron analysis of HIV-PR* folding kinetics and its comparison with the relaxation times calculated from the microscopic rate constants (τ=1/k) obtained from the global fit. All symbols are open for refolding and closed for unfolding at a final protein concentration of 4 μM, with the exception of a refolding jump to 1.0 M urea at a final protein concentration of 100 nM (×). Manual-mixing kinetic traces observed by CD at 230 nm displayed single exponential behavior for both unfolding and refolding (circles). Stopped-flow kinetic traces monitored by FL at >320 nm, with λ_exc = 280 nm, were fit to three exponentials in both refolding and unfolding: τ_s in squares, τ_i in diamonds, and τ_f in triangles. The lines represent the inverse of the microscopic rate constants as obtained from the global fits. The rate-limiting refolding step (solid line) corresponds to the U → M transition. The rate-limiting unfolding step (dotted line) corresponds to the N₂ → 2M dissociation rate. The intermediate unfolding step (dashed line) correlates with the M → U unfolding rate. The line for the association step, 2M → N₂ (dotted and dashed line) is shown as a pseudo-first order approximation calculated at a final protein concentration of 4 μM. Because of the oversimplification of using a pseudo first-order approximation, the bimolecular association rate at 4 μM protein does not overlay with the τ_i phase as expected. Buffer conditions are described in the caption to Figure 2.

To help resolve this mechanistic ambiguity, the refolding and unfolding reactions of HIV-PR* were also monitored by FL spectroscopy. The enhanced signal-to-noise enables analysis at lower protein concentrations where the second-order association reaction might become rate-limiting. In addition, the focus of the FL method on a pair of chromophores, Trp6 near the dimer interface and Trp42 on the exterior of the β-barrel (Figure 1a), might reveal local conformational changes that are too subtle to be detected by CD spectroscopy.

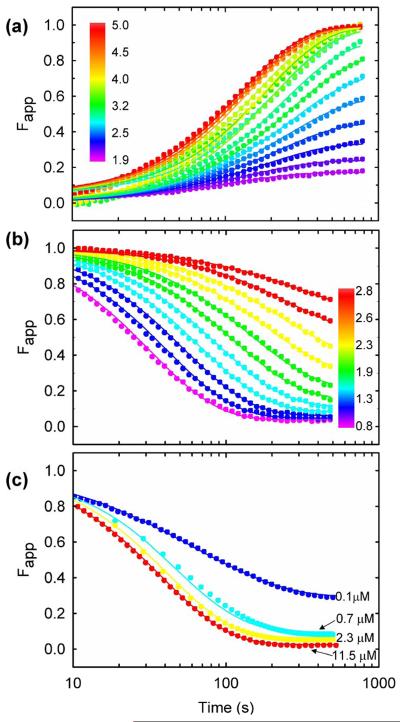
Stopped-flow FL measurement of the urea-induced unfolding (Figure 5a) and refolding (Figure 5b) reactions yielded complex responses, some of which were not detected by CD spectroscopy. Fits of these data to a multi-exponential function produced three apparent exponentials for both reactions: the slow, τ_s, phase whose relaxation time is very similar to that for the sole CD phase, an intermediate, τ_i, phase and a fast, τ_f, phase. The three unfolding phases decrease in intensity (Figure 5a) and accelerate with increasing urea concentration (Figure 4). At 4.2 M urea, the relative amplitudes are 85%, 12%, and 3%, respectively (data not shown). All three refolding phases increase in intensity (Figure 5b) and accelerate with decreasing urea concentration (Figure 4). At 0.8 M urea, the relative amplitudes are 82%, 15% and 3%, respectively (data not shown). The small amplitudes of the τ_i and τ_f phases and the order-of-magnitude range for the three relaxation times result in rather large uncertainties in the relaxation times for the intermediate and fast refolding phases (Figure 4).

Figure 5.

Global analysis of HIV-PR* folding kinetics monitored by SF-FL. Representative fits of the data to the 2U ⇆ 2M ⇆ N₂ model are shown. (a) Unfolding kinetics between 1.9 M and 5.0 M urea at 4 μM protease. (b) Refolding kinetics between 0.8 M and 2.8 M urea at 4 μM protease. (c) Refolding kinetics to 1.0 M urea at increasing protein concentrations. The signals are normalized to the extrapolated values for the native (y_N) and unfolded (y_U) protein, F_app(t)=(y(t)-y_N)/(y_U-y_N). Buffer conditions are described in the caption to Figure 2.

To probe the possibility that the faster responses detected by FL spectroscopy reflect the bimolecular association reaction, HIV-PR* was refolded at a series of protein concentrations. Although the slow, τ_s, and fast, τ_f, phases are independent of protein concentration, the relaxation time of the intermediate, τ_i, phase increases with decreasing protein concentration and approaches the relaxation time of the τ_s phase at 1 μM protein concentration (Figure S3 in Supplementary Material). The correspondence between the τ_i refolding phase and the bimolecular reaction was confirmed by examining the refolding reaction at 100 nM protein concentration. Under these conditions where the bimolecular reaction becomes rate-limiting, the slowest phase in refolding now occurs with a relaxation time of ∼200 s at 1 M urea (Figure 4 and Figure S3 in Supplementary Material) and has a relative FL amplitude of 55%. The τ_s phase persists with a relaxation time of 50 s, and the τ_f phase has a relaxation time of 8 s, very similar to their respective relaxation times at higher protein concentrations (Figure 4). Thus, the bimolecular reaction contributes primarily to the τ_i refolding phase detected by FL spectroscopy.

Global Analysis

The simplest kinetic model consistent with the main features of the observable kinetics is where U represents an apparent unstructured monomer, M is a folded monomer and N₂ is the dimeric native state. The asterisk (*) in Scheme 1 denotes that the unimolecular rate constants k*_f and k*_u are defined with respect to a dimeric reference state (see Methods and Materials for details). The first-order monomer folding reaction is rate-limiting at protein concentrations above 1 μM, and the second-order association reaction becomes rate-limiting below 1 μM. The capability of this three-state kinetic model to describe the FL data was tested using a non-linear least squares fitting algorithm that simultaneously fit 96 kinetic traces. Both protein and urea concentration dimensions were included in the fit to provide a comprehensive test of the mechanism. A description of this procedure can be found in Materials and Methods. Although three kinetic phases in unfolding and refolding imply a minimum of four species, the very small amplitude of the fast phases in unfolding and refolding, ∼3%, made it difficult to reliably discriminate the validity of the three-state model from several four-state models that include additional monomeric or dimeric intermediates. Thus, a three-state model was used to fit the kinetic FL data. An independent study of a stable monomeric variant, mHIV-PR* (created by deleting the C-terminal four amino acids¹⁷), demonstrated that the minor fast phases correspond to folding and unfolding reactions within each subunit (see below).

Scheme 1.

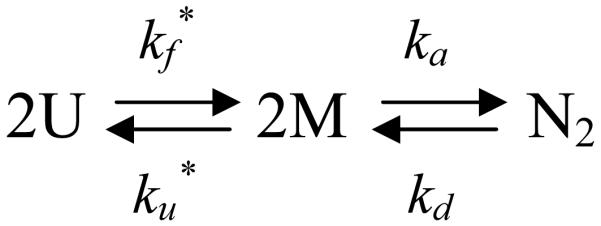
The three-state model provided an excellent description of the unfolding (Figure 5a) and refolding (Figure 5b) FL data over the 100 ms to 500 s time range and over the 100 nM to 11.5 μM protein concentration range (Figure 5c). Using a pseudo first-order approximation for the predicted bimolecular reaction at 4 μM protein (Materials and Methods), the relaxation times corresponding to the microscopic rate constants in Scheme 1 are shown as a function of denaturant concentration in Figure 4. The τ_s phase in refolding, detected both by CD and FL spectroscopy, corresponds to the unimolecular monomer folding reaction. Calculation of the microscopic rate constant for the association reaction at 4 μM protease concentration, using a pseudo-first order approximation, predicts a relaxation time far faster than the τ_i refolding phase. This effect has been observed previously for dimeric superoxide dismutase³⁴ and reflects the expectation that the pseudo-first order approximation reports only the fastest part of the association reaction and neglects coupling of the association step with the preceding monomer folding reaction. The slow, τ_s, unfolding phase corresponds to the dimer dissociation reaction, and for unfolding above ∼2.8 M urea, the τ_i phase is dominated by the monomer unfolding reaction. The model suggests that observation of the τ_i phase in unfolding is possible even though the faster monomer unfolding follows the slow dimer dissociation. This counter-intuitive result is consistent with the small amplitude of this phase and was confirmed by independent kinetic simulations (O.B. and C.R.M., unpublished results). The deviations between the predicted microscopic rates and the observed τ_s relaxation times between 2.5 and 4 M urea result from the coupling of the monomer folding/unfolding and bimolecular association/dissociation kinetic steps in the transition region. This behavior is predicted by an eigenvalue analysis using these microscopic rates (Figure S4 in Supplementary Material).

The microscopic rate constants in the absence of urea, k and the urea dependence of the rate constants, m^‡, are provided in Table 1, along with the calculated thermodynamic parameters for the monomer folding reaction, the dimerization reaction and the global stability. At protein concentrations above 1 μM, the rate-limiting monomer folding reaction, k_f = 9.44×10⁻² s⁻¹, obscures the subsequent, faster subunit association reaction, k_a = 1.02×10⁶ M⁻¹ s⁻¹. The unfolding reaction is controlled by the dimer dissociation reaction above 4 M urea; at 0 M urea, k_d = 2.15×10⁻³ s⁻¹. The subsequent monomer unfolding reaction is about 10-fold faster at 4 M urea; at 0 M urea, k_u = 1.59×10^×2 s⁻¹. The dimerization reaction, 2M ⇆ N2, contributes −11.83 kcal (mol dimer)⁻¹ to the global stability (Table 1) and is equivalent to a 2.1 nM dissociation constant. The apparent monomer folding reaction, 2U ⇆ 2M, only contributes −2.10 kcal (mol dimer)⁻¹ to the global stability in the dimer reference frame. The apparent global stability of HIV-PR*,

$$\Delta {{\mathrm{G}}^{\mathrm{o}}}_{2\mathrm{U}∕{\mathrm{N}}_2}=\Delta {{\mathrm{G}}^{\mathrm{o}}}_{2\mathrm{M}∕{\mathrm{N}}_2}+2\Delta {{\mathrm{G}}^{\mathrm{o}}}_{\mathrm{U}∕\mathrm{M}}$$ (1)

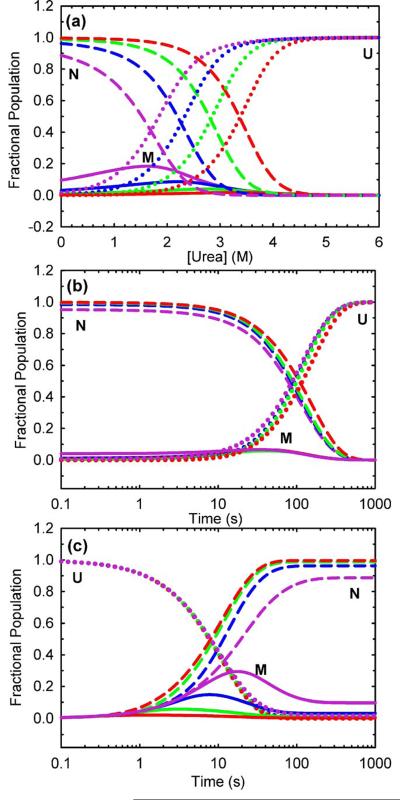
is −13.93 ± 0.08 kcal (mol dimer)⁻¹, within error of the stability directly determined by urea titration at equilibrium, −14.23 ± 0.23 kcal (mol dimer)⁻¹. These kinetic and thermodynamic parameters dictate very small populations of folded monomer at equilibrium (Figure 6a), during unfolding (Figure 6b) and during refolding (Figure 6c) at protein concentrations ranging from 100 nM to 100 μM. The small but systematic deviations observed for the 0.5 and 1.0 μM equilibrium data fit to a two-state model (Figure 3b) presumably reflect small populations of monomer at the lower protein concentrations (Figure 6a).

Table 1.

Microscopic rate constants and kinetic m^‡ values obtained from the global kinetic analysis of HIV-PR* at pH 6.0 and 25 °C.

HIV-PR*a
	Value	Errorf	Units
$\mathrm{U}\underset{k_u}{\overset{k_f}{\leftrightarrows }}\mathrm{M}$
kf	9.44 × 10−2	± 0.06 × 10−2 ± 0.40 × 10−2 g	s−1
m‡f	0.72	± 0.01	kcal (mol monomer)−1M−1
ku	1.59 × 10−2	± 0.09 × 10−2 ± 1.4 × 10−2 g	s−1
m‡u	−0.18	± 0.01	kcal (mol monomer)−1M−1
ΔG°(U/M)b	−1.05	± 0.04 ± 0.52 g	kcal (mol monomer)−1
m (U/M)c	0.89	± 0.02	kcal (mol monomer)−1M−1
$2\mathrm{M}\underset{k_d}{\overset{k_a}{\leftrightarrows }}{\mathrm{N}}_2$
ka	1.02 × 106	± 0.06 × 106 ± 0.50 × 106 g	M−1 s−1
ma‡	0.58	± 0.02	kcal (mol dimer)−1 M−1
kd	2.15 × 10−3	± 0.02 × 10−3 ± 0.05 × 10−3 g	s−1
md‡e	−0.14	± 0.01	kcal (mol dimer)−1 M−1
ΔG°(2M/N2)b	−11.83	± 0.04 ± 0.29 g	kcal (mol dimer)−1
m (2M/N2)c	0.72	± 0.02	kcal (mol dimer)−1 M−1
$2\mathrm{U}\underset{{k^{\ast }}_u}{\overset{{k^{\ast }}_f}{\leftrightarrows }}2\mathrm{M}\underset{k_d}{\overset{k_a}{\leftrightarrows }}{\mathrm{N}}_2$
ΔG°kin(2U/N2)d	−13.93	± 0.08 ± 1.08 g	kcal (mol dimer)−1
mkin(2U/N2)e	2.50	± 0.04	kcal (mol dimer)−1 M−1

^a96 fluorescence kinetic traces were globally fit to the model shown in Scheme 1, 2U ⇆ 2M ⇆ N₂. The unimolecular rate constants $k_f^{\ast }$ and $k_u^{\ast }$ in Scheme 1, expressed with respect to a dimeric reference state, are related to the unimolecular rate constants k_f and k_u in the monomer reference state in the following way: k_f=(k_f*)^½ and k_u=(k_u*)^½. The association and dissociation rate constants (k_a and k_d) are always reported with respect to a dimer reference state. Buffer conditions were 100 mM sodium phosphate, pH 6.0, and 0.2 mM EDTA at 25 °C. Protein concentrations ranged from 0.1-12 μM.

^bCalculated according to ΔG°_(U/M) = −RTlnK = −RTln(k_f/k_u) and ΔG°_(2M/N2) = −RTlnK = −RTln(k_a/k_d).

^cCalculated according to m^‡_(U/M) = | m^‡_f| + | m^‡_u| and m^‡_(2M/N2) = | m^‡_a| + | m^‡_d.|.

^dGlobal stability obtained from the kinetic data, calculated according to ΔG°_kin(2U/N2) = 2ΔG°_(U/M) + ΔG°_(2M/N2).

^em value obtained from the kinetic data, calculated according to m^‡_kin(2U/N2) = 2| m^‡_f | + 2| m^‡_u| + | m_a^‡| + | m_d^‡_d.|.

^fErrors are standard errors from the fit unless otherwise indicated.

^gErrors obtained at the 68% confidence interval from a rigorous error analysis.

Figure 6.

Predicted fractional populations of HIV-PR* folding species (a) at equilibrium and during kinetic (b) unfolding and (c) refolding reactions at final protein concentrations expressed in monomer units of 0.1 μM (violet), 1 μM (blue), 10 μM (green) and 100 μM (red). Populations of native species (-----), the monomeric intermediate (—), and the unfolded species (^…….) are indicated. The unfolding jumps in (b) were simulated from 0 to 6 M final urea concentration, and the refolding jumps in (c) were simulated from 6 to 0 M final urea concentrations.

An alternative model in which dimer association is rapid and precedes the dominant folding reaction was also tested. However, this gave a significantly poorer fit (Prob(χ₁²/χ₂², υ₁, υ₂) < 1×10⁻⁸) and was less successful at capturing the concentration dependence of the kinetics. The estimate of the global stability from the alternative model (ΔG^o_2U/N2 = −11.95 kcal (mol dimer)⁻¹) was also poorer than for Scheme 1. The excellent global fits using Scheme 1 at a range of protein and urea concentrations and agreement with equilibrium data are overwhelming evidence in support of a monomer-limited folding scenario as in Scheme 1 over a dimerization early model.

Folding of a monomeric variant of HIV-Protease

To confirm the energetics of the monomeric intermediate predicted from the global kinetic analysis and to probe the role of the fast, low-amplitude FL folding reaction excluded from this analysis, the thermodynamic and kinetic properties of the monomer folding reaction were studied using a construct with a C-terminal deletion (Δ96-99) introduced into the HIV-PR* background (mHIV-PR*, residues 1-95).¹⁷ Size exclusion chromatography (data not shown) confirms that mHIV-PR* does not self-associate at concentrations used for folding studies (<80 μM). The CD (Figure 2a) and FL (Figure 2b) spectra for mHIV-PR* demonstrate that it adopts a folded structure, in agreement with a previous NMR structural analysis.¹³

The equilibrium unfolding transition of mHIV-PR*, monitored by CD, did not yield a distinct native baseline, consistent with a marginally-stable monomeric form (Figure 7a). Attempts to stabilize the folded form and achieve a native baseline with the osmolyte, TMAO,^35,36 and with lower temperatures were not successful (data not shown). The absence of a native baseline was resolved by using the initial amplitudes from mHIV-PR* CD unfolding kinetics (see below) to estimate the native baseline at higher urea concentrations (Figure 7a). By linear extrapolation to lower urea concentrations, it was possible to obtain a robust fit of the monomer equilibrium unfolding data to the two-state model, U ⇆ M. The free energy of folding in the absence of denaturant in the monomer reference state is −1.35±0.05 kcal mol⁻¹, and the m value is 1.45±0.24 kcal mol⁻¹ M⁻¹ (Table S1, Supplementary Material). The stability and m value are comparable to but somewhat greater than the parameters for the monomer in the context of the dimer obtained from the global analysis, ΔG^o_U/M=1.05±0.04 kcal mol⁻¹ and 0.89±0.02 kcal (mol monomer)⁻¹ M⁻¹ (Table 1). This issue will be addressed below.

Figure 7.

Folding properties of mHIV-PR*. (a) Equilibrium unfolding transition of 10 μM mHIV-PR* monitored by CD at 230 nm (filled circles). Initial kinetic amplitudes for unfolding jumps (open squares) provided a native baseline by linear extrapolation. (b) Comparison of the mHIV-PR* chevron, by manual-mixing CD (circles) and stopped-flow FL (slow phase (squares) and fast phase (triangles)), with the HIV-PR* chevron shown as lines. Unfolding and refolding kinetics are represented with closed and open circles, respectively. Buffer conditions are described in the caption to Figure 2.

The role of a possible transient folding intermediate in mHIV-PR* was elucidated by kinetic CD and FL studies. Similar to HIV-PR*, only a single exponential phase was observed in either unfolding or refolding of mHIV-PR* by CD (Figure 7b). By contrast, stopped-flow FL kinetics displayed a slow and fast phase in both unfolding and refolding. These phases occur in the same time ranges and with the same relative amplitudes as the intermediate and fast phases observed with HIV-PR*, ∼4-5:1, demonstrating that the fast phase observed in the unfolding/refolding of dimeric protease occurs within each subunit.

The single CD unfolding phase for mHIV-PR* is accelerated by ∼3-fold at 4 M urea compared to the τ_i, M → U, phase in the HIV-PR* chevron (Figure 4 and Figure 7b), and the urea dependence of the mHIV-PR* unfolding reaction is within error of that for the M → U reaction in the HIV-PR* system. This equivalence demonstrates a comparable change in the solvent accessible surface area when the monomeric construct and the monomer in the context of the dimer access their respective transition states.³⁷ Intriguingly, the single CD refolding phase observed for mHIV-PR* is slowed and lacks the urea dependence observed for the U → M reaction for HIV-PR* (Figure 4). Apparently, the rate-limiting transition state for folding shifts to become more unfolded-like when the C-terminal four residues are deleted. The result is very surprising, because the C-terminal residues deleted in mHIV-PR* would not be expected to be involved in structure when the partner subunit is absent (Figure 1b).

The simplest mechanism that can account for these data involves an on-pathway intermediate, I, for the monomer folding reaction, U ⇆ I ⇆ M. Although the detectable CD signal change monitors the I ⇆ M step, the low signal/noise ratio of far-UV CD does not preclude small changes for the U ⇆ I step. The FL signal is clearly sensitive to both steps. The I→M step is rate-limiting for HIV-PR*, but the U→I step is rate-limiting for mHIV-PR*. The small but discernable differences in the thermodynamic properties of the stable monomer and the monomer in the context of the dimer (see above) may reflect the presence of a fragile, weakly-folded intermediate, I, whose stability is ≤ 0.30 kcal mol⁻¹, and whose m value is ≤ 0.56 kcal mol⁻¹ M⁻¹, relative to the U state. A possible molecular explanation for the change in rate-limiting step for the monomeric construct is provided in the Discussion.

Discussion

A comprehensive thermodynamic and kinetic analysis of the reversible folding reaction of HIV-PR*, combined with an independent analysis of a monomeric construct, has revealed the folding mechanism for HIV-PR* (Scheme 2).

Scheme 2.

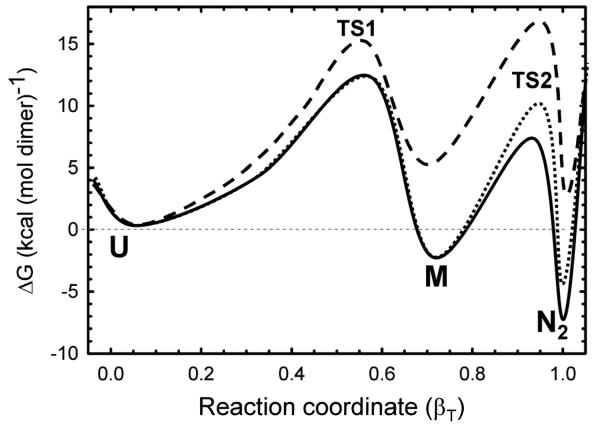
A reaction coordinate diagram illustrating the relative free energies of the three principal thermodynamic states and their intervening transition states at protein concentrations of 10 μM and 100 nM and in the absence of denaturant is shown in Figure 8. The reaction coordinate diagram at 4 M urea and 10 μM HIV-PR* concentration is also shown. The uncertainty in the thermodynamic and kinetic parameters for the I state precludes its inclusion in this diagram. The free energies of the U, M and N₂ thermodynamic states, the activation free energies of the intervening transition states and the m values associated with these parameters are shown in Table 1.

Figure 8.

Folding free energy surfaces for 10 μM (solid line) and 100 nM (dotted line) HIV-protease under native conditions (0 M urea) and for 10 μM (dashed line) HIV-PR* under unfolding conditions (4 M urea). The free energies were calculated for the 2U ⇆ 2M ⇆ N₂ model using a dimeric reference state and the parameters listed in Table 1. The activation free energies for the transition states, ΔG^o‡, were calculated from the rate constant, k, using the Kramers formalism, ΔG^o=−RTln(k/k_o), where R is the gas constant, T is the absolute temperature and k_o is the Kramers prefactor. The activation energy depends upon the estimate of the prefactor and is somewhat arbitrary. The Kramers prefactor value of 1×10⁸ s⁻¹ used here is considered to be a reasonable estimate.⁵⁴ The abscissa describes the reaction coordinate and is depicted as the Tanford β value, β_T. The abscissa is normalized to the total change in the m value for the folding reaction from 2U to N₂, 2.50 kcal (mol dimer)⁻¹ M⁻¹ (Table 1).

Note that the thermodynamic parameters for the 2U ⇆ 2M reaction are those extracted from the global analysis of the kinetic folding data shown in Table 1. Inclusion of the parameters for the U ⇆ I reaction, not incorporated in the global analysis, would engender small decreases in the free energies of the M state and the N₂ state, relative to the U state.

The reaction coordinate diagram highlights several interesting properties of the folding reaction. The dominant free-energy barrier under strongly-folding conditions (Figure 8, solid line) is TS1, indicating that folding of the monomer limits the formation of the native dimeric form at and above micromolar protein concentrations at low urea concentrations. At increasing denaturant concentrations (∼2 M urea and above; Figure 8, dashed line), under marginal folding conditions and unfolding conditions, the dominant free-energy barrier begins to switch to TS2 and folded monomer association in refolding and dimer dissociation in unfolding become rate-limiting. A switch in the dominant barrier from TS1 to TS2 also arises as the protein concentration is lowered into the nanomolar range (≤100 nM) (Figure 8, dotted line). The reaction coordinate also shows that the stability of the monomer is low, −1.05 kcal mol⁻¹, and only contributes marginally to that of the native dimer at the standard state (1 M), −14.23 kcal mol⁻¹ and at 10 μM, −7.46 kcal/mol⁻¹. The placement of the free-energy wells in Figure 8 along the Tanford β-value reaction coordinate derived from the kinetic m-values illustrates that approximately 70% of the buried surface area in the native protease is sequestered from solvent in the monomer folding reaction; the remaining 30% is buried upon formation of the dimer. As a consequence of these properties, the monomeric species is not highly populated during unfolding, refolding or at equilibrium during the urea-induced unfolding/refolding reaction at micromolar protein concentrations. At 10 μM protein concentration, the monomer comprises less than 4% of the population at equilibrium (Figure 6a) and less than 6% during refolding in the absence of denaturant (Figure 6c).

The removal of the final four residues to create the stable monomeric construct, mHIVPR*, switches the rate-limiting step in folding from the I → N to the U → I step (Scheme 2). A possible molecular explanation for this behavior can be found in the structure of the dimeric protease (Figure 1b). The proximal N- and C-terminal strands cannot pair in the fully-folded monomer because they are oriented in a parallel fashion with respect to each other. However, if both termini are in proximity and are flexible in the intermediate, I, they might be able to adopt the anti-parallel organization found between the N- and C-termini in the partner subunits in the native dimer. The deletion of the C-termini in mHIV-PR* would eliminate this source of stability in the monomeric folding intermediate, I, for the full-length chain. The resultant increase in free energy of the intermediate state and, presumably, its preceding transition state could serve to make the formation of the I state rate-limiting in the folding of mHIV-PR*. This hypothesis is consistent with the decrease in the urea dependence of the refolding reaction in mHIV-PR* (Figure 7b), denoting a more unfolded-like transition state. A similar response of the L97A variant of HIV-PR* (A. Kundu and C. R. Matthews, unpublished results), which would be expected to destabilize the putative pairing of the N- and C-terminal β-strands, supports this interpretation. A molecular dynamics simulation of a single subunit of HIV-PR³⁸ yielded a pair of populations, one with the anti-parallel pairing of the N- and C-terminal β-strands and another without the pairing. Perhaps these two conformations represent the I and M states in Scheme 2.

Comparisons with previous measurements of thermodynamic parameters

The stability of HIV-PR*, i.e., the free energy of folding for the 2U ⇆ N₂ reaction, reported in the present communication, −14.23 ± 0.23 kcal (mol dimer)⁻¹ at pH 6.0 and 25 °C compares very well with several previous measurements under similar conditions. Meek and his colleagues,¹⁹ using urea denaturation on the wild-type protease with Asp25, obtained a stability of −14.2 ± 1.4 kcal (mol dimer)⁻¹ at pH 6.0 and 25 °C. Freire and his colleagues²² performed a urea denaturation analysis of the active protease variant with D25 and Q7K, L33I and L63I to reduce self-proteolysis. The stability at pH 5.5 and 25 °C, −14.9 kcal (mol dimer)⁻¹ is also in very good agreement with present value. However, the possibility of compensating perturbations in the stability by the additional mutations remains to be investigated.

Zhang et al.³⁹ and, later, Darke et al.,²⁰ used ligand-induced dimerization assays to derive the free energy of the association reaction, 2M ⇆ N₂. These groups reported values of −12.0 kcal (mol dimer)⁻¹ at pH 5.0 and 37 °C and −12.0 kcal (mol dimer)⁻¹ at pH 5.5 and 37 °C, respectively. The corresponding K_d values are 3.6 ± 1.9 nM and 3.4 nM. Both of these reports are remarkably similar to the free energy change estimated from the global kinetic folding analysis at pH 6.0 and 25 °C, −11.83 ± 0.04 kcal (mol dimer)⁻¹ and a K_d of 2.0 nM. However, these three estimates disagree with the values obtained from an analytical ultracentrifugation (AUC) analysis.⁴⁰ The AUC results yielded a K_d of 5.8 μM for an active, autoproteolytic resistant HIV-1 protease (Q7K, D25, L33I and L63I) and 1.0 μM for an inactive variant (Q7K, D25N, L33I and L63I) at pH 7.0 and 4 °C, corresponding to free energies of dimerization of −6.6 and −7.6 kcal (mol dimer)⁻¹. Further, the micromolar K_d from the AUC study is not consistent with the results of size exclusion chromatography, which shows that HIV-PR* elutes as a dimer at low micromolar concentrations (A. Kundu and C. R. Matthews, unpublished data). It is possible that the low ionic strength of the buffer used in the AUC experiments, 20 mM sodium phosphate, and the higher pH, 7.0, could account for the discrepancy. It has been previously shown that the stability of HIV-PR is enhanced at higher salt concentrations⁴¹ and lower pH values.^20,21

The nanomolar K_d for HIV-PR* provides a pivot about which the monomer/dimer equilibrium shifts to modulate the proteolytic activity. Although the monomeric form would be favored at the initial stages of its self-cleavage from the Gag-Pol protein, the equilibrium would shift to favor the active dimeric form as the reaction proceeds and the concentration exceeds the nanomolar level. Eventually, self-proteolysis of the dimeric form would shift the equilibrium back to the monomeric form and, thereby, sharply reduce, if not eliminate, its enzymatic activity. As has been discussed previously,²⁰ the acquisition of activity and its subsequent loss as the concentration of the protease first increases and then decreases is an elegant example of Le Châtelier's Principle and the Law of Mass Action.⁴² Apparently, the sequence evolved so as to have this activity switch operate in the nanomolar range. If the initial mutations that lead to resistance have increased values for K_d, second-site replacements would presumably increase the free energy difference for the 2M ⇆ N₂ reaction and reestablish the nanomolar K_d.

The stability of mHIV-PR*, U ⇆ M, −1.05 kcal (mol monomer)⁻¹, is consistent with semi-quantitative estimates of stability derived from FL and NMR urea titrations on an N-terminal truncation monomer construct (residues 5-95).³³ Both Gō-model simulations and molecular dynamics simulations demonstrate the presence of stable monomeric forms of HIV-1 protease.²⁵ No other quantitative estimates of the stability of monomeric HIV-PR were found in the literature.

Implications of the folding free energy surface for HIV-PR* on the development of resistance to inhibitors

There are two striking features of the folding free energy surface of HIV-PR* that may enable the rapid development of resistance to inhibitors: the relatively weak subunit association reaction and the marginal stability of the folded monomeric forms. At 10 μM protein, the free energy of the association reaction is reduced from −11.83 kcal (mol dimer)⁻¹ (at the standard state of 1 M)) to a net of −4.83 kcal (mol dimer)⁻¹ (ΔΔG = +RT ln[protein]). The free energy of folding of the monomeric form, M, does not depend upon the protein concentration and remains at −1.05 kcal mol⁻¹ relative to the unfolded state, U. The relatively small free energy difference between the active dimeric form and the inactive monomeric form in the parent protein at physiological protein concentrations (nM to μM) means that mutations that reduce the affinity by even a few kcal (mol dimer)⁻¹ would significantly increase the populations of the inactive, monomeric protease. For example, if the dimerization free energy were reduced by 2.0 kcal (mol dimer)⁻¹ at 10 μM protein, the population of the monomeric form would increase 30-fold. From another perspective, the dimerization free energy may not be sufficient to override structural perturbations in the drug-resistant monomers and force them to adopt the structure of the drug-sensitive parent protein.

The marginal stability of the folded monomeric form, M, and the marginally-stable intermediate, I, might also enhance the opportunity for resistant variants to escape from inhibitor binding while maintaining activity. The fact that ∼10% of the population occupies the U state in equilibrium with the M state for the parent protein and the real possibility that mutations would be expected to selectively destabilize the more well-folded state, i.e., the M state, mean that protease variants have ready access to partially- or fully-unfolded states. Those states would have lower affinities for inhibitors, because they are less well-structured than the native state. However, they might still be capable of forming dimers and cleaving the Gag-Pol protein, because these marginally-stable forms could be induced to bind to their target sites. In an analogous way, natively-unfolded proteins only adopt defined structure when they bind to their target sequences.^43,44 Similar to HIV protease, natively-unfolded proteins often have multiple binding partners.^43,44 Although the initial resistance mutations might produce a protease with very poor catalytic properties, subsequent mutations could increase the stability of the monomers and/or the dimer complex so as to enhance catalysis. Thus, the conformational adaptability hypothesis^13,14 would find HIV-PR to be a receptive target for the concept that mutations can enhance access to conformers that retain enzymatic activity while reducing their affinity for the inhibitors.

Application of this HIV-PR folding analysis to drug-resistant HIV-1 protease variants will elucidate whether a mutation confers resistance by destabilizing the folded monomeric state or by weakening the mutual affinity of the subunits or a combination of both effects. For example, molecular dynamics simulations of HIV-1 protease variants with replacements distant from the active site have been shown to confer drug resistance by a hydrophobic sliding mechanism of the nonpolar side chains within each subunit.⁴⁵ Apparently, indirect effects of repacking distal buried side chains on the structure of the active site pocket enable resistance while maintaining proteolytic function. It will also be interesting to compare the folding free energy surfaces of drug resistant variants with those from replacements at residues that are strongly conserved (http://hivdb.stanford.edu).⁴⁶ The results may provide insights into the minimal physical properties of active dimeric protease and a rationale for the observation of variable and conserved residues in response to protease inhibitors.

Materials and Methods

Standard Buffers and Reagents

Lysis buffer contained 20 mM Tris hydrochloride, 1 mM sodium EDTA, pH 8.0. The purification buffer consisted of the lysis buffer with the addition of 7 M guanidine hydrochloride. The standard buffer for all folding experiments was 100 mM sodium phosphate, 0.2 mM EDTA, pH 6.0. Guanidine hydrochloride (98% pure), purchased from J. T. Baker Chemicals (Philipsburg, NJ), was used for purification, and G75 Sephadex, purchased from Amersham Biosciences (Uppsala, Sweden), was used as the matrix for the sizing column during purification. Ultrapure urea was purchased from MP Biomedical (Solon, OH). All other reagents were of standard molecular biology grade.

Protein expression and purification

A synthetic gene encoding for HIV-1 protease containing the mutations Q7K/D25N/C67A/C95A was the kind gift from Dr. Celia Schiffer at the University of Massachusetts Medical School. A double-stop codon was introduced to create the C-terminal deletion construct using the Stratagene Quick Change protocol. The vector pet11A was used for mutagenesis and maintenance of the gene in XL1 blue E. coli cells. DNA sequencing was performed at the University of California at Davis sequencing center. Protein was expressed using the E. coli pXC35 vector in the TAP 106 cell line, as previously described.⁴⁷

Inclusion bodies were purified from the cell lysate at 4 °C in standard lysis buffer following two rounds of sonication and washed in 2 M urea in the standard lysis buffer. The protein was unfolded from the inclusion bodies in purification buffer for one hour at 4 °C. Following overnight dialysis against the purification buffer at 4 °C, the protein was loaded onto a G75 Sephadex sizing column. Pure fractions, as determined by SDS-PAGE, were pooled and refolded by four rounds of dialysis against experimental buffer. Purified protein was then centrifuged and filtered to remove impure aggregates. Purity was assessed at > 98% by mass spectrometry. Protein was stored in experimental buffer at 4 °C.

Determination of Protein Concentration

The absorbance of tryptophan and tyrosine residues at 280 nm was monitored using an Aviv 140S UV-VIS spectrometer. The extinction coefficient of HIV-PR was determined using the method of Gill and von Hippel.⁴⁸ Protein was unfolded before measuring the absorbance so that all protein concentrations are expressed in terms of the monomer concentration. The protein concentration was then calculated by the absorbance at 280 nm using an extinction coefficient of 12700 M⁻¹cm⁻¹.

Equilibrium Studies

The protein was unfolded in incrementally increasing concentrations of urea in buffer to the same final protein concentration for each titration. Samples were equilibrated overnight at room temperature. Unfolding changes were monitored with both CD and FL at 25 °C, and the temperature was controlled with a Peltier controller. Each CD spectrum reflected the average of three spectra taken from 330 nm to 215 nm on a Jasco J810 CD spectrophotometer, with a 2.5 nm bandwidth, a scan rate of 20 nm (min)⁻¹, and an 8 s response time. FL emission spectra were taken on a Photon Technology International fluorimeter equipped with single-grating excitation and emission monochromators. The excitation wavelength was 295 nm, and emission was monitored from 300 to 500 nm.

Savuka, an in-house non-linear least-squares fitting software, was used to fit equilibrium unfolding data using a two-state dimeric thermodynamic model:^34,49,50

$$\begin{array}{cc}\hfill & {\mathrm{N}}_2\stackrel{K}{\leftrightarrows }2\mathrm{U}\hfill \\ \hfill F_{\mathit{app}}=& \frac{{(K^2+8K\left[P_{\mathit{tot}}\right])}^{1∕2}-K}{4\left[P_{\mathit{tot}}\right]}\hfill \\ \hfill \left[P_{\mathit{tot}}\right]=& 2\left[N_2\right]+\left[U\right]\hfill \end{array}$$ (2)

where F_app represents the apparent fraction of unfolded species and P_tot represents the total protein concentration in monomer units.

Global analysis of all wavelengths utilized singular value decomposition for data reduction as previously described.^31,51

Kinetic Studies

Manual-mix kinetic studies, with a dead-time of 5 s, were initiated by a 10-fold dilution into various final concentrations of urea with buffer and monitored via CD on a Jasco J810 CD spectrophotometer. Stopped-flow kinetic studies, with a dead-time of 5 ms, were initiated by a 6-fold or 10-fold dilution with urea or buffer using an Applied Photophysics Stopped-Flow Fluorimeter (model SX.18MV). Tryptophan fluorescence was detected with a 320 nm emission cut-off filter following excitation at 280 nm, and temperature was controlled at 25 °C using a recirculating water bath. To compensate for pressure-related instrumental artifacts associated with driving the syringes, the first 50 ms of each kinetic trace was deleted prior to analysis. All kinetic traces were fit to a constant plus a series of exponentials, A(t) = A(∞) + ΣΔA_iexp(−t/τ_i). Each τ_i was plotted as a function of urea concentration to provide a chevron analysis of the folding reaction.⁵²

Global Analysis Methods

Raw kinetic unfolding and refolding FL traces acquired at varying protein and urea concentration were globally fit to several different kinetic folding mechanisms using a Levenberg-Marquardt non-linear least squares fitting algorithm in an in-house fitting package, Savuka. The kinetic rate equations in each case were solved by numerical integration using a Runge-Kutta algorithm with adaptive step size.^49,53 For the three-state kinetic model (Scheme 1), the kinetic rate equations describing the concentration change of unfolded monomer (U), folded monomer (M) and folded dimer (N₂) with time were given by the following equations:

$$\begin{array}{cc}\hfill \frac{{\mathit{dc}}_U\left(t\right)}{\mathit{dt}}& =-k_f\cdot c_U\left(t\right)+k_u\cdot c_M\left(t\right)\hfill \\ \hfill \frac{{\mathit{dc}}_M\left(t\right)}{\mathit{dt}}& =-k_u\cdot c_M\left(t\right)-k_a\cdot c_M{\left(t\right)}^2+k_f\cdot c_U\left(t\right)+k_d\cdot c_{N_2}\left(t\right)\hfill \\ \hfill \frac{{\mathit{dc}}_{N_2}\left(t\right)}{\mathit{dt}}& =-k_d\cdot c_{N_2}\left(t\right)+k_a\cdot c_M{\left(t\right)}^2\hfill \end{array}$$ (3)

where the rate constants for the U ⇆ M kinetic step are written in terms of a monomer reference state and the rate constants for the association reaction, 2M ⇆ N₂, are written in terms of a dimeric reference state. The rate constants for the U ⇆ M kinetic step in Equation (3) are related to the rate constants in Scheme 1, written in the dimer reference state, by k_ij= (k_ij*)^1/2. The rate constant at any given urea concentration, k_ij, was expressed in terms of the rate in the absence of urea, k_ij0, and the m value:

$${\mathrm{k}}_{\mathrm{ij}}={\mathrm{k}}_{\mathrm{ij}0}\cdot {\mathrm{e}}^{-{\mathrm{m}}_{\mathrm{ij}}\left[\mathit{urea}\right]∕\mathrm{RT}}$$ (4)

The equilibrium free-energy at standard state conditions, i.e. in the absence of urea and 1 M reactants and products, between species i and j is obtained as:

$$\Delta G^o=-\mathit{RT}\ln \left(\frac{k_{\mathit{ij}}^o}{k_{\mathit{ji}}^o}\right)$$ (5)

The free-energy calculated in this manner using equations (3) and (5) yields the free-energy change of the unimolecular step, U ⇆ M, in the monomer reference state and the free-energy change for the bimolecular step, 2M ⇆ N₂, in the dimer reference state. The free-energy for the unimolecular steps calculated in the monomer reference state, ΔG^o,mono, can be converted to a dimeric reference state free-energy, ΔG^o,dimeric, by multiplying by two:

$$\Delta G^{o,\mathit{dimeric}}=2\Delta G^{o,\mathit{mono}}$$ (6)

For computational efficiency, kinetic traces comprising ∼1000 points were logarithmically averaged to yield ∼100 points evenly spaced in log-time and then fit simultaneously using an iterative procedure as previously described.³⁴ Adjustable global, i.e. linked, parameters in the Marquardt-Levenberg optimization consisted of the microscopic rate constants, k_ij^o, the kinetic m values, m_ij, and the Z values, a normalized measure of the extent to which the intermediate resembles the unfolded state, Z = (Y_I − Y_N2) /(Y_U − Y_N2). The spectroscopic signals of the native and unfolded state at each denaturant concentration were treated as local adjustable parameters. The protein concentration was held fixed at the experimentally measured value.

Each optimization began by solving for the equilibrium concentration of all species under the starting conditions and then correcting for the dilution ratio. For refolding traces the starting conditions were typically unfolding conditions and for unfolding traces the starting conditions were typically strongly folding conditions.

$$\begin{array}{cc}\hfill 0& =-k_f\cdot c_U\left(0\right)+k_u\cdot c_I\left(0\right)\hfill \\ \hfill 0& =-k_u\cdot c_I\left(0\right)-k_a\cdot c_M{\left(0\right)}^2+k_f\cdot c_U\left(0\right)+k_d\cdot c_N\left(0\right)\hfill \\ \hfill 0& =-k_d\cdot c_N\left(0\right)+k_a\cdot c_M{\left(0\right)}^2\hfill \end{array}$$ (7)

The solution of the kinetic rate equations, (3)-(4), proceeded from these initial conditions with the rate constants redefined according to the final denaturant concentration. This iterative procedure was repeated until the kinetic parameters were optimized to yield the best fit. The goodness of fit was evaluated by the randomness of the residuals and the reduced-χ².

A rigorous error analysis on the bimolecular rate constant and monomer unfolding rate constant was performed to check the robustness of the fit and to test for the existence of alternative minima.

Abbreviations

AIDS

acquired immunodeficiency syndrome

AUC

analytical ultracentrifugation

CD

circular dichroism

FL

fluorescence

HIV-1

human immunodeficiency virus, type 1

HIV-PR*

pseudo-wild-type HIV-1 protease, Q7K/D25N/C67A/C95A-HIV-1 protease, residues 1-99

mHIV-PR*

C-terminal deletion monomer construct of HIV-PR*, residues 1-95

MRE

mean residue ellipticity

TMAO

trimethylamine N-oxide

SF-FL

stopped-flow fluorescence