In the absence of writhe, DNA relieves torsional stress with localized, sequence-dependent structural failure to preserve B-form

Abstract

To understand how underwinding and overwinding the DNA helix affects its structure, we simulated 19 independent DNA systems with fixed degrees of twist using molecular dynamics in a system that does not allow writhe. Underwinding DNA induced spontaneous, sequence-dependent base flipping and local denaturation, while overwinding DNA induced the formation of Pauling-like DNA (P-DNA). The winding resulted in a bimodal state simultaneously including local structural failure and B-form DNA for both underwinding and extreme overwinding. Our simulations suggest that base flipping and local denaturation may provide a landscape influencing protein recognition of DNA sequence to affect, for examples, replication, transcription and recombination. Additionally, our findings help explain results from single-molecule experiments and demonstrate that elastic rod models are strictly valid on average only for unstressed or overwound DNA up to P-DNA formation. Finally, our data support a model in which base flipping can result from torsional stress.

INTRODUCTION

With forces in the tens of pN, DNA polymerases, RNA polymerases and helicases generate transient extremes of both underwound and overwound DNA (1–3). Segregation of the DNA during cell division also imparts forces on DNA (4). Because DNA is helical, these transient stresses are largely torsional (5,6). The DNA linking number, Lk, is the number of turns that one strand makes around the other (7,8). In the absence of broken strands, Lk is topologically invariant. The Lk of DNA with minimal torsional stress, Lk₀, is defined by

where N is the length of the helix in base pairs and h is the helical repeat. The exact value of h depends on the conditions (nucleotide sequence, temperature, ionic strength of the solvent, etc.) of the system and is commonly assumed to be between 10 and 11 bp. The specific linking difference,

is a length independent measure of the degree of positive or negative Lk. DNA is underwound for σ < 0 and overwound for σ > 0. Except perhaps in hyperthermophilic organisms (9), DNA is maintained homeostatically by topoisomerases in an underwound state in vivo (σ ≈ −0.06) (10,11), and this underwound state is a target of selection in evolving Escherichia coli populations (12).

Classically, isotropic elastic polymer models that assume constant persistence length, effective diameter and charge density, as well as a symmetric torsional potential energy function, have been used to study DNA structure and dynamics at the meso scale. In general, the results from these models agree with those of single-molecule experiments under small to moderate torsional deformations (13). At the same time, they fail to explain the single-molecule results for more underwound DNA and for overwound DNA under forces closer to those generated by polymerases (2). Because single-molecule experiments do not yield an atomistic view of DNA under torsion, and because there are no crystal structures of torsionally stressed DNA, the structure of DNA under these more biologically relevant conditions is unknown. Only recently has the study of torsionally stressed DNA become accessible to reliable computational methods (14–16).

In this article, we report base flipping, denaturation and Pauling-like DNA (P-DNA) formation caused by torsional stresses on DNA with sequence (TGTCCCTC)_3–5 in explicit aqueous saline solution by molecular dynamics (MD). We show that DNA under the mechanical strain of torsional stress does not always behave as an elastic rod, but has obvious non-linear elastic properties that may be of considerable importance in our understanding of biological phenomena. We show that dsDNA forms dramatic, localized defects to allow the rest of the helix to relax to normal B-DNA. Localized base flipping and denaturation might be expected to influence how proteins interact with DNA and provide an atomistic basis for how torsional stress may influence protein binding during such DNA processes as, e.g. DNA replication, transcription and recombination, and for the formation of ‘alternative’ DNA secondary structures (17,18). DNA overwinding and underwinding in cells may be either constrained, as we have modeled here, or not constrained. When DNA is not constrained, twisting is strongly coupled with writhing and bending, which we do not consider here.

MATERIALS AND METHODS

MD Simulations

Constant energy and volume (microcanonical) MD simulations in explicit aqueous saline solution on 19 systems were performed with specific linking differences −0.220 ≤ σ ≤ 0.391. Each simulation system contained at least three complete turns (1080°, Lk = 3) of a double-stranded DNA helix initially with a uniform twist angle between each base pair step. In the work of Guidice et al. (19), penalty functions were used to harmonically constrain twist (15) or to induce base pair flipping (19,20). These methods are useful, but would be problematic for our purposes because Lk must be held invariant or artifacts can result. We employed a technique for constraining Lk that avoids these problems, but also limits bending and forbids writhe. Each DNA helix extended from one end of the simulation volume to the opposite end where it continued through normal bonding attachments. Under this modified version of the usual periodic boundary conditions, the ends of each strand on one side of the volume were thus connected to the periodic images of the opposite ends producing a helix that is topologically circular, but infinite and so without curvature. This configuration of the DNA precludes writhing, so the simulations of various relative specific Lk differences show only the effects of twist, which was modulated by increasing N in underwound systems and decreasing N in overwound systems. Thus, Lk is invariant by design.

These simulations were designed to explore how torsional stress-induced twist, alone, can affect DNA structure on an atomistic scale. It is well-known that writhing is the preferred low-energy form of ΔLk for unconstrained polymers. When (or if) underwound and overwound DNA is not constrained by cellular forces or by packaging in the chromosome (for which the effect of ΔLk partition into Tw and Wr is unknown), then ΔLk may cause unconstrained DNA to writhe. It seems highly likely, however, that torsional stress will at least at times be limited to changes in twist. To fully understand the effect of ΔLk on biologically relevant DNA, simulations would have to include all possible DNA sequences, and account for all forces exerted upon the DNA by protein binding. This is not yet feasible. Therefore, as a step toward a fuller understanding of the relationship between ΔLk and DNA structure, we here start with the effects of DNA twist in the absence of writhe.

Initially, 21 DNA helices of varying σ generated by the program NAB (21) were ‘pre-salted’ by placing solvent ions in the helix grooves based upon actual ion positions relative to base pair steps that had been previously simulated for >20 ns (22). Pre-salting minimized the time required for equilibration because counterion convergence in MD simulations requires significantly more than the typical 1–2 ns of equilibration (23). TIP3P water molecules (24,25) filled the remaining space of each volume (5 nm × 5 nm by 0.34 nm depending on the number of base pairs). The net charge of the system was neutralized by Na⁺ and the bulk NaCl concentration was increased to 500 mM by randomly replacing the more distant water molecules with sodium and chlorine ions.

The energy of each system was minimized by steepest descent. During minimization, the RATTLE algorithm (26) failed to solve the bond constraints for the two most extreme cases (σ = −0.238 and 0.455), so they were dropped from the study. Minimization was followed by 1 ns of solvent equilibration with velocity reassignment to stabilize temperature. During equilibration, the volume of each system was re-sized to maintain a pressure near 1 atm. Production simulation occurred in the microcanonical ensemble at 300 K for 10 ns with 2 fs timesteps using extended system program (ESP) (22), an MD software program developed in the Pettitt laboratory and the CHARMM27 force field (25). The temperature was monitored and found to vary by less than ±1 K during the simulation, which is reasonable for a system of this size. ESP uses the velocity Verlet algorithm to integrate the equations of motion (27) and calculates long-range electrostatics using Ewald summation (28). CHARMM27 most accurately predicts the helical twist of DNA (29,30) and shows excellent agreement with experimental measurements of base flipping and the equilibrium between open and closed base pair states (20). Although the volume in a microcanonical ensemble is constant, the length of the DNA is not necessarily constrained as the helix is free to bow somewhat in order to compensate for any change in length that is conformationally induced. Indeed, minor bowing was observed in some underwound systems and in the P-DNA systems.

During production simulation, atomic coordinates were recorded at every 1 ps. These coordinates were analyzed with 3DNA (31) to determine base pairing and the lack thereof (local failure or denaturation), and to measure base pair step parameters, helical diameters and groove widths. These coordinates were also used to measure the distances between the sugar oxygens (O4*–O4*) in order to determine base flipping. According to the Horton criteria for base flipping (30), the O4*–O4* distance is ∼11.8 Å for a Watson–Crick base pair, 15.6 Å when one base is extruded by the helix by 180° and 18.8 Å when both bases are extruded.

To determine counterion distributions, the structure of the DNA at each time step was first aligned with the initial structure by minimizing the root mean square deviation (RMSD). Then the simulation volume was subdivided into voxels, and the counterions occupying each voxel were counted. To compare between systems, the counterion distributions were normalized by dividing the counts by the number of base pairs in the helix.

RESULTS

Rationale

Toward understanding how changes in DNA twist affect the structure of DNA at the atomic level, we took advantage of a previously studied double-stranded DNA sequence, TGTCCCTC, which had been equilibrated for >20 ns (22). Approximately four repeated copies of this sequence were in each of the B-form DNA systems studied here. Using periodic boundary conditions to connect the ends, the Lk was altered by adding base pairs to underwind the DNA and removing base pairs to overwind it relative to the relaxed structure. The specific linking differences and other details are given in Table 1. The movies for all simulations (S1 for the most underwound through S19 for the most overwound) are available as Supplementary Data at NAR online and at http://www.chem.uh.edu/faculty/pettitt/Research/.

Table 1.

Mean base pair step parameters and groove widths

Movie No.a	σ	No. of basesb	Shift, Å	Slide, Å	Rise, Å	Tilt, °	Roll, °	Twist, °	Minorc, Å	Majorc, Å
S1	–0.220	41	0.02 (0.09)d	–0.04 (0.15)	3.24 (0.08)	0.87 (0.64)	5.52 (1.09)	31.3 (2.2)	8.35 (0.84)	11.4 (1)
S2	–0.200	40	0.06 (0.12)	0.00 (0.17)	3.07 (0.13)	0.94 (0.98)	5.20 (1.39)	31.2 (2.2)	8.23 (0.60)	11.2 (0.8)
S3	–0.179	39	0.05 (0.09)	0.05 (0.13)	2.99 (0.13)	0.85 (1.05)	5.06 (1.38)	29.8 (1.4)	7.96 (0.66)	11 (0.8)
S4	–0.158	38	0.08 (0.08)	–0.08 (0.13)	3.17 (0.08)	0.81 (0.50)	4.83 (0.89)	32 (1.1)	7.73 (0.43)	11.1 (0.8)
S5	–0.135	37	0.05 (0.10)	–0.09 (0.15)	3.14 (0.13)	1.03 (1.10)	4.54 (1.34)	31 (1.2)	8.04 (0.47)	11.2 (0.8)
S6	–0.111	36	0.07 (0.09)	–0.16 (0.16)	3.34 (0.08)	0.88 (0.62)	5.62 (1.12)	32.8 (1.9)	8.33 (0.67)	11.6 (0.6)
S7	–0.086	35	0.03 (0.08)	–0.23 (0.13)	3.35 (0.07)	0.64 (0.63)	5.23 (0.93)	33.5 (1.1)	7.96 (0.33)	11.3 (0.6)
S8	–0.059	34	0.06 (0.07)	–0.12 (0.16)	3.35 (0.05)	0.80 (0.50)	4.68 (0.77)	34.8 (0.9)	7.66 (0.32)	10.9 (0.8)
S9	–0.030	33	0.04 (0.08)	–0.35 (0.23)	3.36 (0.13)	0.63 (0.53)	4.46 (0.86)	33.1 (0.8)	7.99 (0.38)	11.9 (1.3)
S10	0.000	32	0.04 (0.08)	–0.42 (0.10)	3.45 (0.04)	0.56 (0.54)	3.87 (0.68)	33.6 (0.4)	8.09 (0.30)	12.2 (0.4)
S11	0.032	31	0.06 (0.07)	–0.19 (0.10)	3.43 (0.04)	0.67 (0.51)	3.99 (0.72)	34.6 (0.4)	7.77 (0.28)	11.3 (0.3)
S12	0.067	30	0.06 (0.07)	0.00 (0.08)	3.38 (0.04)	0.61 (0.51)	4.07 (0.70)	35.9 (0.4)	7.46 (0.27)	10.4 (0.3)
S13	0.103	29	0.06 (0.06)	0.17 (0.07)	3.34 (0.04)	0.56 (0.49)	3.71 (0.70)	37.2 (0.4)	7.07 (0.24)	9.8 (0.3)
S14	0.143	28	0.04 (0.06)	0.41 (0.08)	3.31 (0.04)	0.59 (0.49)	2.73 (0.75)	38.5 (0.4)	6.52 (0.23)	9.2 (0.3)
S15	0.185	27	–0.03 (0.08)	0.83 (0.10)	3.36 (0.05)	0.02 (0.61)	0.39 (0.93)	39.7 (0.5)	6.05 (0.31)	9.7 (0.3)
S16	0.231	26	–0.07 (0.09)	1.24 (0.12)	3.42 (0.05)	–0.38 (0.72)	–2.09 (0.99)	41.5 (0.5)	5.17 (0.23)	10.3 (0.4)
S17	0.280	25	–0.21 (0.11)	1.66 (0.12)	3.50 (0.07)	–1.42 (0.87)	–5.01 (1.15)	42.7 (0.7)	4.46 (0.21)	11.3 (0.4)
S18	0.333	24	0.01 (0.09)	0.46 (0.29)	3.27 (0.07)	0.68 (0.95)	1.85 (2.11)	37.3 (1.1)	6.72 (0.57)	9.8 (0.4)
S19	0.391	23	–0.07 (0.17)	0.41 (0.29)	3.07 (0.28)	0.39 (1.30)	2.10 (2.61)	33 (2.4)	7.39 (1.13)	10.5 (0.8)

^aSimulations are available as Supplementary Data at NAR online and http://www.chem.uh.edu/faculty/pettitt/Research/.

^bSequence is (TGTCCCTC)₄ for the relaxed case, σ = 0.0, with the sequence extended or shortened to underwind or overwind, respectively.

^cMinor and major groove distances do not include the atomic radii of the phosphates (∼5.8 Å).

^dIn parentheses are shown the fluctuations as calculated by the standard deviation.

DNA twisting denatures DNA, flips bases and triggers P-DNA to preserve B-form

Representative structures (closest to the mean) for each system over the course of 10 ns simulations are shown (Figure 1A). In all of the underwound systems and also in the extremely overwound systems, DNA partitioned the twisting strain along its length into simultaneous distinct regions of normal B-DNA and regions of heteroclitic, or disrupted structure. The disrupted structure included local denaturation, base flipping and P-DNA, the latter of which is generally taken as a structure where the phosphodiester backbones are wound on the interior of the helix and the bases are splayed outwards into solvent (32,33). As a result of localized structural failure, at least 70% of an underwound helix remains canonically base paired. Overwound DNA, up to the P-DNA threshold, remains 100% base paired and is not denatured by torsional stress.

Figure 1.

Structures and time courses of twisted DNA. (A) Atomic structures of DNA as a function of underwinding or overwinding, σ, that have minimum RMSD from the average simulation structure. Regions of structural failure are rendered with sticks and regions of Watson–Crick base pairing are rendered with van der Waals spheres. The bases are colored: adenine, blue; thymine, purple; guanine, yellow; and cytosine, orange. Backbone atoms are in white. The σ = 0.0 (Lk₀) structure is a control showing that the simulation conditions, including the boundary, had no remarkable effect on the B-DNA structure. As an additional test of the boundary conditions, we translated the σ = −0.059 and σ = 0.391 systems through the periodic boundaries and were able to reproduce base flipping and P-DNA events, respectively. (B) Structural parameters (twist, roll, tilt, major groove, minor groove, rise, shift and slide) averaged over the sequence from snapshots taken every 100 ps over the total simulation time of 10 ns. The dashed lines are the values of a relaxed helix with the same sequence, as predicted by analysis of PDB structures (22).

Time courses of the base pair step angular parameters—tilt, roll and twist—distance parameters—slide, shift and roll—and the major and minor groove widths, as calculated by 3DNA (31), are shown (Figure 1B). Because these parameters are only germane for DNA that is base paired, Figure 1 shows how the ‘remaining’ B-DNA structure changed upon localized base flipping, denaturation and P-DNA formation. For each of the simulations, the parameters of the base paired regions were in good general agreement with previous X-ray and nuclear magnetic resonance (NMR) measurements (dashed lines) of relaxed B-DNA (34). General trends in these parameters over time and over σ (Table 1) were consistent with the well-known tilt-shift, twist-slide correlations and twist-roll, roll-slide anti-correlations (34).

Although the systems all started with a uniform distribution of twist, twist became non-uniform over the course of the simulations for all the underwound and for the most overwound systems. For all of the underwound helices, twist converged on the twist angle expected for relaxed B-DNA (dashed line) for most of the structure, indicating that the twist deficit resulting from underwinding was absorbed completely by the structural failure in the rest of the structure. In stark contrast, the twist angle for low to moderately overwound DNA (0.0 < σ ≤ 0.280) was constant along the length. When σ exceeded 0.28, P-DNA formed and the remaining DNA region converted to B-form, as in the underwound cases, on the twist angle expected of a relaxed B helix (dashed line). The convergence of the base pair step parameters to the values of relaxed B-form and their stability thereafter suggest that the structures have reached equilibrium, but it is not possible to be more definite about the structural equilibrium without allowing the simulations to run indefinitely, which was, unfortunately, not feasible.

The simulation of even the least underwound (σ = −0.03) helix showed facile base flipping and subsequent DNA relaxation (Movie S9). Base flipping occurred within the first nanosecond for all the underwound systems except for the σ = −0.03 helix. For that helix, base flipping occurred after 4 ns, and was stable for the rest of the simulation. In addition to the major and minor groove distances, the three geometric parameters most affected by base flipping were twist, rise and slide (Figure 1B). Before the base flipping event, for the σ = −0.03 helix, the DNA behaved much like an elastic rod, distributing an average twist of 32.7° over the length of the helix. Base flipping began when the intrinsic twist deficit became concentrated in a region of the fluctuating helix, simultaneously disrupting the hydrogen bonds of the second T–A pair and the adjacent G–C pair. Within 0.5 ns of this event, thymine flipped into the solution on the major groove side. Disruption of the hydrogen bonding for these two base pairs increased the local backbone flexibility, allowing it to absorb the twist deficit non-uniformly. Average slide was increased by 0.4 Å and average rise decreased by 0.15 Å. As a consequence, the remaining helical structure became very slightly overwound (34.8°) relative to the average twist of the σ = 0 helix (dashed line).

Up to the P-DNA threshold (σ = 0.333), we observed no failures in the helical structure of overwound DNA. At first glance, this threshold value might appear at odds with the P-DNA threshold values (σ ∼0.037) found in single molecule experiments (33,35). It is important, however, to consider the difference in lengths between the 20-50 kp DNA used in single molecule experiments and the 23–41 bp molecules used in the simulations here. The fraction of the helix that is P-DNA for any σ > 0 is σ/σ_P, where σ_P is the specific Lk of P-DNA (36). Estimates of σ_P from single molecule experiments range from two to three (33,36–38). If σ_P = 2, we would expect ∼17% of the σ = 0.333 helix and 20% of the σ = 0.391 helix to be P-DNA, which corresponds to 4 and 4.5 bp of P-DNA in our simulations. Indeed, we observed 4 and 5 bp of P-DNA in the σ = 0.333 and σ = 0.391 simulations, respectively. Given that the helical repeat for P-DNA when σ_P = 2 is ∼3.5 bp, it is unreasonable to expect P-DNA to occur for σ < 0.333 in such small systems. The results of our simulations, therefore, support the estimates of σ_P = 2 (36).

In the systems that formed P-DNA regions, the two phosphate backbones twisted tightly around each other, despite their negative charge, and the bases splayed outward. The B-DNA to P-DNA transition began soon after the beginning in the simulation of the σ = 0.391 helix (Movie S19) with the collapse of the minor groove in a 5-bp region resulting in an expansion of the major groove and the rupturing of the hydrogen bonds between the base pairs. As the bases flipped into the solvent, the phosphate backbones wrapped around each other, shifting the DNA strands by two bases relative to each other. Dramatic changes in the ionic atmosphere structure for this deformation are discussed below. Compensating structural change in the remaining DNA was evident as twist, roll, slide and shift rapidly converged on the average parameter values for the σ = 0 B-DNA helix. Because the transition between the DNA forms lasted for nearly the entire 10 ns of the simulation, we extended the simulation of the σ = −0.391 helix for an additional 5 ns and observed no additional change in the average structure compared with the structure at the end of the initial 10 ns. Thus, the P-DNA was stable and appeared to have reached equilibrium.

Base flipping and denaturation exhibited sequence dependence

Nucleic acid sequence strongly influenced the stability of the helical structure. We considered both base pairs and base steps in terms of local sequence. We found no obvious difference in the stability of T–A pairs versus C–G pairs under torsional stress despite the additional hydrogen bond. In contrast to DNA thermal melting where hydrogen bonding is the dominant interaction, base stacking interactions have a greater influence on helix stability under torsional stress, especially in the pyrimidine-rich sequences (TGTCCCTC)_3–5 used here (39,40). The sequence contains the CC, TC and GT base pair steps shown by NMR and MD simulations to be very rigid, and CT and TG steps, which are shown to be more flexible (34,41). As such, the first C–G base pair in the rigid cytosine triple was the least stable each time it occurred across all of the underwound structures. These C–G pairs in this sequence context were denatured 15.6% of the time. In contrast, the last T–A pair was the most stable in this context, denaturing only 3% of the time, again in accord with previous predictions (34,41).

Because σ was modulated in our simulations by adding or removing bases from the end of the sequence, the identity of the last base pair in our computational unit cell changes from system to system. This creates a subtle change in the sequence because the last base pair is covalently bonded to the image of the first base pair through our modified periodic boundary conditions. The two base pairs that cross the periodic boundary provided additional base steps to analyze. The link sequences were TT, CT, TT, CT, CT, CT, TT, GT and TT for each of the underwound systems from σ = −0.22 to −0.03. The stability of the link sequences was also consistent with previous predictions (34,41). The CT stacked links that occurred in the midst of the cytosine triplet (σ = −0.158 and −0.135) were relatively stable compared with other locations, and the positioning of a cytosine between two thymines, which was unstable in the other simulations, was the least stable as the link sequence as well.

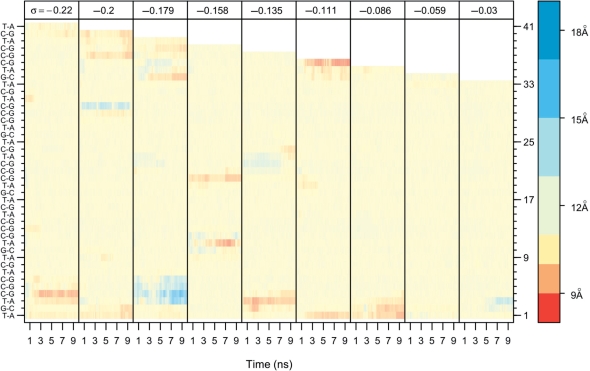
To further examine the role of sequence in base flipping and denaturation, we measured the distance between the sugar oxygens (O4*–O4*) for each base pair over time (Figure 2). This distance is ∼11.8 Å for Watson–Crick paired bases (neutral color). As a base flipped out of the helix into solution, the distance between the sugar oxygens increased, which is here shown as a blue gradient (Figure 2). When the O4*–O4* distance increased to 15.6 Å, one of the bases was flipped out of the helix by ∼180° (light blue), and at 18.8 Å, both bases have flipped out of the helix (dark blue) (42). Where consecutive base pairs have denatured, the concomitant absorption of the twist deficit caused the distance between the backbones to become compressed, which is shown in Figure 2 as a red gradient. When 0 ≤ σ ≤ 0.28, the systems did not denature or base flip, so their graphs are not shown. Nor are the graphs shown for P-DNA, where the distance between the sugar oxygens was small because the backbones wrapped around one another.

Figure 2.

Sequence-specific base flipping and denaturation as measured by the distance between the sugar oxygens (O4*) over time (total = 10 ns; sampling every 1 ps) and over σ. 11.8 Å (ecru) is the average distance for Watson–Crick base pairs. A distance of 15.6 Å (light blue) indicates that one base has flipped out, and 18.8 Å (dark blue) indicates that both bases have flipped out. In some cases, base pairs have denatured, but have not flipped out, and the twist deficit concentrated at the base pair compresses the distance between backbones (red). The white region at the top of the graph is a consequence of removing bases in order to modulate σ. Base pairs on the left are listed in sequence order starting from the bottom and numbered on the right axis.

It is immediately apparent by comparing each σ in Figure 2 that specific regions, and thus DNA sequences, of the torsionally stressed helices are more prone to base flipping and denaturation than others. As noted above, the first CG in the CG triplet and the preceding TA were the most frequently unpaired (Figure 2, blue and red), and the last TA was almost never unpaired. Importantly, the initial partitioning of the helix into the deformed and the B-form regions was not fixed over the course of the simulations. At the beginning of many of the simulations, the waves of conformational deformation appeared to sample multiple regions of the DNA for the suitability of structural deformation. As the simulations progressed, the twist deficit became concentrated in some of the deformed regions allowing other regions to re-form the B-DNA structure. For example, at the beginning of the σ = −0.22 simulation (Movie S1), there were deformations in at least four locations. As the simulation progressed, however, two of the deformations resolved themselves as the twist deficit was absorbed in the other two regions. The bottom region of base flipping (Figure 2, blue) evolved into a region of denaturation (Figure 2, red) at about the same time that the other two regions mended. Furthermore, some deformed regions appeared to migrate. In the σ = −0.135 simulation (Movie S5), a base flipped region at the end of the CG triplet in the middle of the helix slowly migrated away from the triplet. Because the last cytosine of the triplet was the most stable for all the simulations, it makes sense that it would mend itself at the expense of a less stable base pair. These small transient structural fluctuations, which had no significant effect on the average base pair step parameters, are additional evidence that the structures were equilibrated.

Electrostatic effects of torsional stress

The condensation of counterions in the grooves of the double helix decreases the helical repeat (increasing Lk₀, by definition) by screening the electrostatic repulsion between the negatively charged phosphates (43,44). In general, the higher the concentration of counterions, the lower the helical repeat. We addressed whether the converse relationship—the higher the helical repeat, the lower the counterion concentration—also holds. We hypothesized that increasing σ (in the absence of writhe) would increase local counterion concentrations.

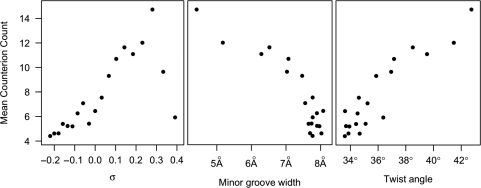
The mean counts of counterions within the major and minor grooves are shown in Figure 3. For overwound DNA, counterion concentrations increased (r = 0.955) with σ up to the P-DNA threshold. Beyond the P-DNA threshold, average counterion concentrations returned to levels typical of relaxed B-DNA. We attribute the increased counterion concentrations with DNA overwinding to the strong anti-correlation (r = −0.90) between counterion concentrations and the width of the minor groove (Figure 3). Increasing σ decreases the width of the minor groove, while simultaneously increasing the surface charge density of the DNA double helix. Hence, below the P-DNA threshold, the denser charge distribution of overwound DNA attracts greater numbers of counterions.

Figure 3.

Mean counterion count correlations with σ, minor groove width and twist angle. Counterions were counted by discretizing the simulation volume into 0.83 Å bins, then, for each time step, minimizing the RMSD of the DNA structure with the structure at the initial time step, and counting the counterion occupancy of each bin. The counterion counts were averaged over the number of base pairs in the helix. The distance across the minor groove between phosphates, the minor groove width, and the twist angle, the average angle of twist for each base pair step in a helix, were determined by 3DNA (31).

Underwinding DNA did not reduce average counterion concentrations to the same degree (r = 0.72) as overwinding increased it. Base flipping and denaturation allowed the majority of the helix to relax to B-form, so the charge density varied less for σ < 0 than for σ ≥ 0. Because the average twist angle for the underwound helices was approximately equal to that of the relaxed helix, counterion concentrations around underwound helices were similar to the concentration of counterions around the relaxed helix. The relaxation of the majority of the helix to B-form also explains why counterion concentrations were so strongly correlated (r = 0.92) with the average angle of twist between base pairs (Figure 3).

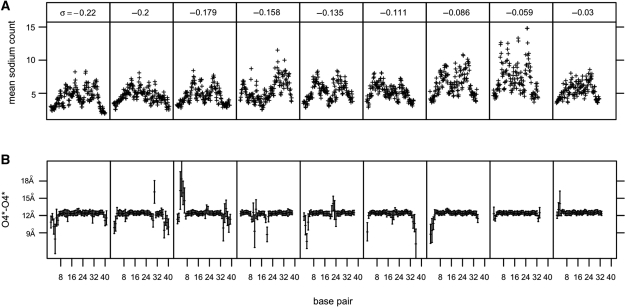
The trends described above reveal the relationship between counterion concentrations and σ on average. There was, however, notable variation in counterion concentrations in specific regions where the DNA structure failed. For underwound helices, lower concentrations of counterions were found where bases had flipped out or denatured. Mean sodium counts are shown compared with mean O4*–O4* distances for each base pair with standard deviations (Figure 4B). Bases that remained paired for the duration of the simulation showed little variance in the O4*–O4* distance, but those bases that experienced base flipping and denaturation exhibited large deviations from the mean. These deviations correspond to deficits in sodium ion counts. We attribute this effect to the concentration of twist deficit in areas of base flipping and denaturation that reduces the local density of negative charge by locally flattening and opening the helix, thereby requiring fewer counterions in the vicinity. The movement of extruded bases may also decrease counterion condensation by excluding counterions from the major and minor grooves. In P-DNA structures, counterions were interspersed with the flipped out bases and concentrated near the intertwined, negatively charged backbones. As a result, despite the extreme structural upheaval at the region of P-DNA, there was no discernable effect of P-DNA on the local counterion concentrations in comparison to the counterion concentrations surrounding the neighboring B-form regions.

Figure 4.

Relationship between mean sodium counts and structural failure. (A) Mean sodium counts in both the major and minor grooves as measured along the helical axis. Low counterion counts correspond to large deviations in average O4*–O4* distances with standard deviations for each base pair over σ (B).

DISCUSSION

Overall, our simulation findings can provide an atomistic picture for results from single molecule experiments (33,45,46), including the occurrence of Pauling-like DNA, and contradict the assumptions of globally isotropic elastic polymer models for underwound DNA. For underwound DNA, in general, twist is not uniformly distributed over the length of the helix; instead, underwound and overwound helices are distinctly asymmetric, and the so-called ‘S’ (overstretched) form of DNA, observed in single molecule experiments for underwound DNA (45), is likely explained by the appearance of regions of base flipped and denatured DNA.

The consistency among the 19 separate simulations and within the repeating sequences of each simulation, the agreement with previous computational and experimental results for DNA and the stability and reproducibility of the formed structures provide a measure of confidence in the data. Others have used MD simulations to look at the effects of underwinding on the structure of DNA (15,16,47,48), but none have looked at as comprehensive a range of σ as presented here and none utilized periodic boundary conditions. Kannan et al. (15) simulated twist in 12-bp DNA fragments and mapped the free energy curves of DNA twist deformations. They also found partitioning between regions of structural failure and B-DNA formation, but only at extreme (σ ≤ −0.25) levels of underwinding. While consistent with our results at extreme σ, the duration of their simulations was 1 ns, which we find is not enough time for the DNA structures to stabilize and equilibrate, even with our use of pre-equilibrated salt ions. Other simulations looked at 94-bp minicircles of DNA that were either relaxed or slightly positively supercoiled (16). Structural failure in these simulations was manifested as kinks, which likely resulted from the extremely short radius of curvature. While simulating 90 bp helices, Harris et al. (47) observed partial denaturation of underwound helices and kinking in overwound helices, which agree well with our results. Our simulations considered the effects of twist on largely unbent DNA by construction, which explains why we observed no kinks.

In order for writhe to be possible, sufficient numbers of counterions must be present in the intervening solvent to screen the electrostatic repulsion between two helical segments—given that writhe is not topologically forbidden as in the simulations here. Overwound DNA has a greater proclivity to writhe than underwound DNA (48). This result may be explained by the ability of overwound DNA to attract higher concentrations of counterions in the minor grooves. The effect of counterions on the interconversion between twist and writhe in supercoiled plasmids has been observed by electron cryo-microscopy, atomic force microscopy and implicit-solvent MD simulation (47,49–51). These studies all found that writhe is minimized in low salt concentrations and increases as the concentration of counterions increases. Hence, as the ionic strength of the solution increases, the positively charged counterions progressively screen more of the self-repulsion in the negatively charged DNA backbone. Our data show that the converse relationship—DNA twist, particularly positive twist, affects the local concentration of counterions—is also true.

Guidice et al. (32) used harmonic constraints to extrude bases from a pyrimidine-rich helix during MD simulations. They found that the free energy profile was quadratic for small angles of extrusion (between −20° and 25°), and increased roughly linearly as the angles widened. Flipping out a base in the quadratic region required 7–11 kcal/mol, and flipping out a base 100° required 13–23 kcal/mol. They also found that the major groove was more energetically favorable for purines (7–9 kcal/mol), but that pyrimidines were just as likely to flip into the major or minor grooves. By design their simulations did not account for changes in σ. We found no bases that spontaneously flipped into the major groove, but pyrimidines and purines equally flipped into the minor groove where the helix had flattened with twist deficit.

Roberts’ (52) prediction that base flipping is prevalent in DNA metabolism and likely an ‘ancient evolutionary discovery’, followed from the discovery of energy-free (with regards to the protein) base flipping in crystal structures of methyltransferases (53,54) and uracil–DNA glycosylases (55,56). In accord with Cheng and Roberts’ prediction (57), our results show that torsional stress is a potential source of the energy that extrudes bases from the helix. We note that NMR and simulation on unstressed double helices find rates for base flipping in the low millisecond regime (58,59). Our results were sufficiently short that no spontaneous flipping was observed for unstressed DNA in accord with those studies. Our study is not suitable for extracting rates for the stressed systems and so no other comparisons on rates are warranted. Our work implies that base flipping and denaturation that may occur during twisting processes where writhe is prevented may influence protein recognition, binding and action on DNA, as well as the formation of alternative secondary structures that are intermediates in DNA metabolism (17,18).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online and at www.chem.uh.edu/faculty/pettitt/DNAtwistmovies/.

FUNDING

Robert A. Welch Foundation (E-1028 to B.M.P); National Institutes of Health (R01GM066813 to B.M.P., R01AI054830 to L.Z.); Keck Center for Interdisciplinary Bioscience Training of the Gulf Coast Consortia (National Library of Medicine Grant No. 5T15LM07093 to G.L.R.).

Conflict of interest statement. None declared.