Uncertainty in Rank Estimation: Implications for Value-Added Modeling Accountability Systems

Abstract

Accountability for public education often requires estimating and ranking the quality of individual teachers or schools on the basis of student test scores. Although the properties of estimators of teacher-or-school effects are well established, less is known about the properties of rank estimators. We investigate performance of rank (percentile) estimators in a basic, two-stage hierarchical model capturing the essential features of the more complicated models that are commonly used to estimate effects. We use simulation to study mean squared error (MSE) performance of percentile estimates and to find the operating characteristics of decision rules based on estimated percentiles. Each depends on the signal-to-noise ratio (the ratio of the teacher or school variance component to the variance of the direct, teacher- or school-specific estimator) and only moderately on the number of teachers or schools. Results show that even when using optimal procedures, MSE is large for the commonly encountered variance ratios, with an unrealistically large ratio required for ideal performance. Percentile-specific MSE results reveal interesting interactions between variance ratios and estimators, especially for extreme percentiles, which are of considerable practical import. These interactions are apparent in the performance of decision rules for the identification of extreme percentiles, underscoring the statistical and practical complexity of the multiple-goal inferences faced in value-added modeling. Our results highlight the need to assess whether even optimal percentile estimators perform sufficiently well to be used in evaluating teachers or schools.

Accountability and Value-Added Modeling

School accountability is a national and state policy priority. The Senate, House of Representatives and over 40 state legislatures have passed bills or enacted laws to hold schools accountable for student outcomes. Accountability systems often involve ranking school districts, schools, and teachers. For example, Standard and Poor’s provides (at each state’s request) percentile rankings of all 501 Pennsylvania and 554 Michigan school districts, and evaluators in Dallas, Texas use relative performance metrics to assess teacher and school effectiveness (Webster & Mendro, 1997). Such comparisons may be used to sanction schools or teachers with low-ranking student outcomes and to provide monetary rewards for those with high-ranking student outcomes. In recent years, for example, California gave bonuses of up to $25,000 for teachers in schools with the highest ranking test-score gains (see http://www.cde.ca.gov/ope/awards/certstaff/).

Performance measures can be simple aggregates such as mean or median score, percentage of students exceeding a threshold, or year-to-year gains in scores at particular grades. More complex measures derive from value-added models that use longitudinal data on students and student background characteristics to determine school performance (Clotfelter & Ladd, 1996; North Carolina State Board of Education, 2000; Sanders, Saxton, & Horn, 1997; Webster, Mendro, Orsak, & Weerasinghe, 1998). Value-added models focus on growth in student achievement and produce estimates of the effects on growth attributable to individual teachers and schools rather than to other sources. The models are typically intricate, involving regression to adjust for differences in student and community characteristics (North Carolina State Board of Education, 2000; Meyer, 1997; Webster et al., 1998) and complex covariance matrices to account for multiple test scores from the same student and the nesting of students within classes and schools (Sanders et al., 1997; Webster et al., 1998).

Statistical Issues

Comparing schools and teachers requires simultaneous consideration of estimated values and their statistical uncertainties. For example, due to differential statistical stability, using hypothesis tests to identify poor performance can unfairly penalize teachers with relatively stable estimates, while direct use of estimates can unfairly penalize teachers with relatively unstable estimates. Gelman and Price (1999) and Shen and Louis (1998) formalize this competition and show that no single set of estimates or assessments can effectively address all goals. For example, teacher-specific maximum likelihood estimates (MLEs)¹, based on regression parameters and scores for only those students taught by that teacher, are valid for estimating teacher-specific performance. However, ranks derived from MLEs generally perform poorly. Ranks based on posterior means or Best Linear Unbiased Predictors (BLUPs) from a properly implemented Bayesian approach (Sanders et al., 1997; McClellan & Staiger, 1999; Kane & Staiger, 2001), while generally outperforming MLEs, also are not optimal. Procedures have been developed to address nonstandard inferences on random effects, using loss functions to structure histogram and rank estimates (Louis, 1984; Laird & Louis, 1989; Devine, Louis, & Halloran, 1994; Shen & Louis, 1998). The current study extends these analyses by using simulations to examine the performance of estimators optimized for estimating ranks (equivalently, percentiles) under squared error loss.

The remainder of the article is organized as follows. The next section outlines a two-stage Gaussian hierarchical model that is sufficiently general to capture the essential structure of more complicated value-added models. The two subsequent sections, Rank and Percentile Estimation and Performance Evaluation formalize the inferential framework for assessing rank estimation performance, defining the estimands, estimators and evaluation criteria. The Simulation Results section presents the results of the simulation study, considering global estimator performance, percentile-specific performance, and the operating characteristics of decision rules for identifying extreme percentiles. Finally, The Discussion section discusses the key results and their implications for inference in value added modeling.

Model Structure

Value-added models can be quite complicated, entailing a number of nested components such as students within classrooms, teachers within schools, schools within districts, etc. Therefore, hierarchical models (Bryk & Raudenbush, 1992) provide a natural and effective statistical framework in which to structure inferences. These models have been extensively studied and applied from both classical and Bayesian perspectives. We focus on the Bayesian perspective because it provides an integrated, coherent structure in which to evaluate ranking procedures. All inferences derive from the joint posterior distribution of the unknown parameters, with inferences guided by a loss function. See Carlin and Louis (2000) for details on Bayesian data analysis.

We obtain results on ranking performance for a standard two-level Gaussian-Gaussian, hierarchical model, which is sufficiently general to highlight the principal issues. For clarity, we present the model in terms of measurements at the teacher level, although the structure applies more broadly to measurements at greater levels of aggregation such as schools or districts. Let K be the number of teachers, and θ₁, …, θ_K denote the unknown teacher effects. For each teacher, we obtain a directly estimated effect Y_k (e.g., an MLE) with associated sampling variance ${\sigma }_k^2$. To focus on the fundamental issues, we restrict attention to the equal variance ( ${\sigma }_k^2\equiv {\sigma }^2$) case. The model we consider is

$${\theta }_1,\dots ,{\theta }_K\mid (\mu ,{\tau }^2)\mathit{iid}N(\mu ,{\tau }^2)$$ (1)

$$Y_k\mid {\theta }_k\mathit{ind}N({\theta }_k,{\sigma }^2),$$ (2)

where τ² is the “between-teacher” variance quantifying the degree of heterogeneity in the true teacher effects and σ² is the variance of the teacher-specific measurements Y_k. Note that σ² is not the variance of the observables nested within teacher (such as student test scores) which would commonly be termed the “within-teacher” variance. Rather, it reflects the sampling variability of the aggregate measurements at the teacher level. For example, in the simplest case where the variance of an individual student test score is γ² and Y_k is the mean test score for n students taught by teacher k, σ² = γ²/n.

We assume that (μ, τ², σ²) are known, so that the teacher effects have independent normal posterior distributions with means

$${\widehat{\theta }}_k^{pm}=(1-\rho )\mu +\rho Y_k,$$ (3)

and common variance ρσ², where ρ =τ²/(τ² + σ²). Performance of rank estimators does not depend on μ, so we set μ = 0 without loss of generality. Also, performance depends on τ and σ only through the ratio τ/σ. This introduces some indeterminacy; for example, τ/σ → 0 either because the teacher-specific variance is too large to yield information on the θs or because there is no variance among the θs (e.g., true teacher performance is identical). The true percentiles are ill-defined in the latter case, so we avoid this triviality by assuming nondegenerate, “standardized” teacher effects with τ = 1. Thus σ² should be interpreted as σ²/τ², the magnitude of the measurement error relative to the true heterogeneity among the teachers. Equivalently, performance depends only on the fraction of the total variance of the Y_k attributable to true differences among teachers, ρ = 1/(1 + σ²), which Bock, Wolfe, and Fisher (1996) call the “stability coefficient” for an estimated teacher effect. It ranges from 0 to 1, with larger values indicating more reliable inferences. We use ρ to index performance throughout the remainder of the article. Properties of the rank estimators also depend on the number of teachers K, but when ranks are converted to percentiles and K ≥ 20, this dependence is small and does not affect conclusions. Also, in practice it will be necessary to estimate μ and τ² as part of the overall analysis, but for large K our assumption that these hyperparameters are known has negligible influence on the evaluations.

This basic model captures the main features associated with ranking and can be used to evaluate more complicated models. In fact, the structure is relevant well beyond the context of value-added models to, for example, hierarchical Rasch models. The model requires values for the between-teacher variance, the direct teacher-specific estimates (e.g., MLEs) and the variances for these teacher-specific estimates. These estimates can be produced by a very complicated model with, for example, regression adjustments and multiple hierarchies, and can relate to single-year change scores, weighted combinations of such scores over years, or any other teacher-specific summary. The variances of these estimates can be similarly complicated, depending on the number of students, the degree of between-student variability, exam variance, and other factors as captured by a richly structured hierarchical model. However, as long as MLEs and associated variances are available, the sufficient statistics may be well approximated by a two-stage Gaussian model (in general with unequal σ_k). Within this framework the essential operating characteristics of inferential procedures can be evaluated efficiently and are representative of the characteristics of more complicated models. Of course, the model specified in Equations 1 and 2 assumes a common value of σ² for the teacher-specific variances. While this assumption does limit the suitability of the model as a proxy for more complicated value-added models, it does clearly communicate key results. The issues we identify carry over to the more general case.

Rank and Percentile Estimation

We begin by defining, for fixed values of the true teacher effects θ_k, the ranks

$$R_k=\text{rank}({\theta }_k)=\sum _{j=1}^K{I}_{\{{\theta }_k\ge {\theta }_j\}}.$$ (4)

Thus the smallest θ has rank 1. “Obvious” estimators for the R_k include the ranks of the observed data Y_k and the ranks of the posterior means. However, deriving an optimal estimator requires specifying a loss function. For overall performance we use summed squared error loss (SSEL) (Carlin & Louis, 2000), which for a generic collection of estimated ranks { $R_k^{\mathit{est}}$} is given by

$$\frac{1}{K}\sum _{k=1}^K{(R_k^{\mathit{est}}-R_k)}^2.$$ (5)

Under SSEL, in general the optimal ranks for the θ_k are neither the ranks of the observed data nor the ranks of the posterior means. Rather, the optimal ranks are the posterior mean ranks

$${\overline{R}}_k(\mathit{Y})=E[R_k\mid \mathit{Y}]=\sum _{j=1}^{K}Pr[{\theta }_k\ge {\theta }_j\mid \mathit{Y}].$$ (6)

Additional discussion and analytical results for these estimators, such as their covariance matrix, are provided by Laird and Louis (1989) and Shen and Louis (1998).

Unlike traditional ranks, the R̄_k are not restricted to take values in {1, …, K}. Rather, because they are shrunk toward the mid rank (K + 1)/2, they are not necessarily equally spaced and in general are not integers (Conlon & Louis, 1999). R̄ is not an “equal-shrinkage” estimator because even for fixed ρ, the amount of shrinkage varies with the true percentile and with the pattern (spacings) of the Y_k. This is in contrast to traditional effects estimators such as the posterior mean, whose degree of shrinkage does not depend on the true mean. Their shrinkage can be an attractive feature because ranks confined to the lattice may over-represent distance and under-represent uncertainty. In cases where the lattice ranks are required, we use

$${\widehat{R}}_k(\mathbf{Y})=\text{rank}[{\overline{R}}_k(\mathbf{Y})].$$ (7)

As shown by Shen and Louis (1998), in the equal variance case ( ${\sigma }_k^2\equiv {\sigma }^2$),

$${\widehat{R}}_k=\text{rank}(Y_k)=\text{rank}({\widehat{\theta }}_k^{pm}),$$ (8)

and so there is no issue as to what are the optimal (integer) ranks. However, in the unequal variance case, these three approaches can produce very different ranks, with the obvious estimators behaving poorly (Shen & Louis, 1998; Goldstein & Spiegelhalter, 1996; Morris & Christiansen, 1996). Thus, in general, one should use Equation 7 for integer ranks.

As K gets large, SSEL for the ranks gets large because the range of possibilities grows. Moreover, in practice the teacher percentiles (on the scale of 0 to 100) are more appropriate quantities to consider. We thus evaluate performance not for the R_k, but rather for the percentiles

$$P_k=100\times \frac{R_k}{K+1}.$$ (9)

The similarly transformed values of R̄_k(Y), denoted by P̄_k (Y), are the optimal estimators for the P_k with respect to SSEL. Also, we use P̂_k(Y)to denote the similarly transformed optimal integer ranks, which of course are no longer integers, but are constrained to the lattice 100k/(K + 1) for k = 1, …, K on which the P_k take values. All results discussed in the remainder of the article are for the percentiles P_k rather than the raw ranks.

Performance Evaluation

Our goal is to evaluate the performance of the percentile estimators P̄_k(Y) and P̂_k (Y) both averaged over all teachers and for teachers of a specific percentile. In both cases, we evaluate estimator performance by examining preposterior properties (i.e., average performance before either the θs or the Ys have been generated). The preposterior properties are the “classical” properties of the ranking estimator under repeated sampling from the model with fixed parameter ρ. Thus, although we use the Bayesian paradigm to motivate our ranking estimators, the properties evaluated are familiar to both the Bayesian and classical paradigms.

Aggregate Performance

For a general percentile estimator $P^{\mathit{est}}(\mathbf{Y})=[P_1^{\mathit{est}}(\mathbf{Y}),\dots ,P_K^{\mathit{est}}(\mathbf{Y})]$ of the percentiles P_k, we use MSE as our evaluation criterion, given by:

$$E\left[\frac{1}{K}\sum _{k=1}^K{(P_k^{\mathit{est}}(\mathbf{Y})-P_k)}^2\right]=\frac{1}{K}\sum _{k=1}^{K}E{[P_k^{\mathit{est}}(\mathbf{Y})-P_k]}^2,$$ (10)

where E averages over both θ and Y. We denote this aggregate MSE by MSE_P̄ for the estimators P̄_k and by MSE_P̂ for the estimators P̂_k, and we denote the root mean squared errors by RMSE_P̄ and RMSE_P̂. Because these quantities depend on both K and ρ, we make this dependence explicit with notation such as MSE_P̄(K, ρ) and MSE_P̂(K, ρ) when necessary. Note that because this criterion averages over all teachers, and for the basic model the θ_k are conditionally iid, MSE_P̂(K, ρ) or MSE_P̄(K, ρ) also apply to individual teachers (i.e., to θ_k for a fixed index k). However, they do not apply to “the largest θ”, “the smallest θ” or any other specific rank in the unobserved θ_k.

Percentile-Specific Performance

To evaluate performance for particular percentiles of the collection of θs, we need the following notation. Let 0 < p < 100 be the percentile of interest. For fixed K this value corresponds to one of the lattice percentiles 100k/(K + 1) for k = 1, …, K (i.e., it is one of the P_k). This distinction is unimportant as K gets large, but restricting p to take values on this grid simplifies presentation. Care must be taken to distinguish the teacher indices 1, …, K, which do not change from sample to sample, from the percentile indices which do change. Let Y^(p) denote the Y value generated by θ[_{p(K + 1)/100}], the p^th percentile of the θs, and let k_p be the coordinate index for Y^(p). That is Y^(p) = Y_{k p}. Note that Y ^(p) is not necessarily equal to Y_{[p (K + 1)/100]}, the p^th percentile of the Ys, and equivalently, k_p is not necessarily equal to p(K + 1)/100. Indeed, the true index of Y^(p) is unknown because all of the θs are unknown, but it is required to evaluate percentile-specific performance of ranking procedures.

For a general percentile estimator $P^{\mathit{est}}(\mathbf{Y})=[P_1^{\mathit{est}}(\mathbf{Y}),\dots ,P_K^{\mathit{est}}(\mathbf{Y})]$, we evaluate the MSE for estimating the percentile p by

$${\mathit{MSE}}_{\mathit{Pest}}(K,\rho ,p)=E\left[{(P_{k_p}^{\mathit{est}}-p)}^2\right],$$ (11)

where $P_{kp}^{\mathit{est}}$ is the percentile estimator for the teacher truly at the p^th percentile. We consider RMSE_P̄(K, ρ, p) and RMSE_P̂(K, ρ, p) in our evaluations.

Simulation Results

We used simulation to perform our evaluations because exact analytical results are not available outside of a small number of special cases (discussed later in this section), and only limited analytical approximations are available. In particular, we derived approximations to MSE_P̄(K, ρ) for any values of K and ρ as well as to MSE_P̂(K, ρ, p) for large K, the latter leading to an asymptotically exact expression for MSE_P̂(K, ρ) for large K. The simulation results agreed well with these analytical approximations; however, a complete and unified evaluation of the aggregate and percentile-specific performances of the different estimators required simulation.

All simulations were implemented on personal computers running Linux. We programmed two independent routines with identical function, one written in C and the other in R (Ihaka & Gentleman, 1996). The former was most efficient and used to produce all results presented here. The latter was used to verify these results, and in all cases the agreement was perfect. Both routines are available from the authors upon request.

We performed simulations for values of K equal to 20, 100 and 1,000. The case of K = 1,000 is virtually identical to those for larger K. For each value of K, we performed simulations for values of ρ from .05 to .95 in increments of .05, as well as .99. Some results for the limiting cases of ρ= 0 and ρ= 1 are available analytically and are provided as a basis of comparison. For each value of K and ρ, the simulations repeatedly generated the θ_k, Y_k, the resulting estimators of the percentiles, and their squared-error performance, both for particular percentiles and averaged across all percentiles. The K = 20 simulations used 100,000 iterations for each value of ρ, while 10,000 iterations were used for K = 100 and 5,000 for K = 1,000. The reduction of the number of iterations for large K reduced the computational burden of ranking and sorting such a large number of teacher effects for each iteration. Repeated experiments and an analysis of Monte Carlo standard errors indicated that the numbers of iterations were sufficient to characterize the results accurately. For example, the Monte Carlo standard errors of our estimates of MSE are less than 0.1% of the estimate for all values of ρ.

Aggregate Performance

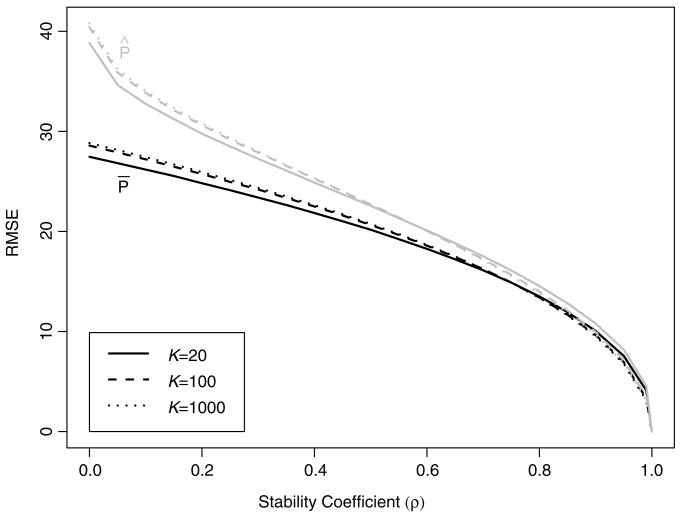
The most basic quantities to consider are the average performances RMSE_P̄(K, ρ) and RMSE_P̂(K, ρ) for different values of τ and K, summarized in Figure 1. Results for the limiting cases were obtained analytically. In the no-information case, since the teacher effects are a priori iid, the true value of P_k for a given teacher is distributed over repeated samples of the θs as a discrete uniform-random variable on 100k/(K + 1) for k =1, …, K. The mean of this distribution is 50 and the variance is (100)² (K − 1)/[12(K + 1)]. P_k completely shrinks to the mean in the no-information case, so that RMSE_P̄(K, 0) is simply the standard deviation. For large K, this value is approximately 29 as shown in the figure. On the other hand, P̂_k assigns percentiles uniformly across the range in the no-information case, so that the RMSE_P̂(K, 0) is $\sqrt{2}$ times the standard deviation, approximately 41 for large K. In the “complete- information” case where ρ =1, the data are perfectly informative about the θs and thereby about the true ranks, so the errors are zero. Values of RMSE_P̄(K, ρ) and RMSE_P̂(K, ρ) for all intermediate values of ρ were determined by simulation.

FIGURE 1.

RMSE_P̄(K, ρ) (black) and RMSE_P̂(K, ρ) (gray) as a function of the stability coefficient for different values of K.

Note that RMSE_P̂(K, ρ) ≥ RMSE_P̄(K, ρ) for every value of K and ρ, which follows from the optimality of R̄. The better performance of the optimal estimator is most pronounced for small values of the stability coefficient, with diminishing advantages as the stability coefficient increases. In all cases, the dependence on K is slight. The primary implication of Figure 1 is that even when using the optimal estimator under squared error loss, estimation of the percentiles is very difficult. Although the percentiles do not follow a Gaussian distribution, approximate 95%-confidence intervals for a randomly selected P_k would be 2 × 2 × RMSE_P̄(K, ρ) percentage points wide. Such intervals become shorter than the entire 0 to 100 range of percentiles only when ρ > 0.3, and more disturbingly, remain wide even when ρ becomes quite large (implying either extreme heterogeneity in the teachers or very informative data). For example, 95%-confidence intervals for the P_k do not become less than 25 percentage points wide until the stability coefficient exceeds .95. Thus, it is truly difficult to estimate percentiles, and one needs a rather gigantic teacher effect or rather miniscule variance in teacher-specific estimates to produce acceptable performance.

It is also interesting to consider the difficulty of estimating percentiles relative to the more traditional estimation of the θ_k effects themselves. Under squared error loss, the optimal effects estimators are the posterior means given in Equation 3, and the MSE for these estimators is the posterior variance ρσ². Note that as σ² → 0, the data become perfectly informative about the θ_k, no matter what the value of τ. However, performance in estimating percentiles depends only on the variance ratio (τ²/σ²), and setting τ² = 1 produces results that generalize to all τ² where the ratio remains constant. If a reduction in σ² is coupled with a corresponding reduction in τ², the performance for percentile estimation does not improve.

Moreover, the stability coefficient (times 100) represents the percentage reduction in the MSE for the estimating the θ_k produced by observing the Y_k, as (τ² − ρσ²)/τ² = ρ. The values presented in Figure 1 can be used to calculate the corresponding percentage reduction in MSE for estimating the P_k produced by observing the Y_k, given by [MSE_P̄(K, 0) − MSE_P̄(K, ρ)]/MSE_P̄(K, 0). It can be shown that the percentage reduction in MSE for the percentiles is bounded above by that for estimating the effects. The Y_k thus provide less information about the percentiles than they do about the effects themselves. However, the difference in reduction to MSE is quite small, always less than two percentage points.

Percentile-Specific Performance

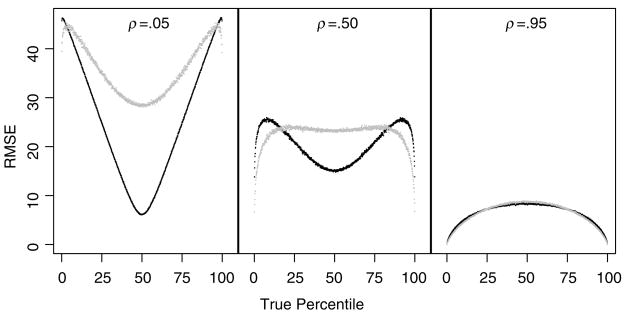
The aggregate properties of the percentile estimators, although informative about general performance, do not tell the more interesting story about their performance for specific θ percentiles. Indeed, for both estimators performance is highly dependent on the target percentile and on ρ. These comparisons are made in Figure 2, which provides percentile-specific RMSE performance (symmetric about the 50th percentile) for three different levels of the stability coefficient (.05, .50 and .95). For both estimators, overall performance tends to improve as the stability coefficient increases, with the estimators exhibiting nearly identical, effective behavior in the high-stability case. In less informative cases, although the optimal estimator has better average performance, it is dominated by P̂ for extreme percentiles. That is, although optimality implies that RMSE_P̂(K, ρ) ≥ RMSE_P̄(K, ρ), RMSE_P̂(K, ρ, p) can be substantially less than RMSE_P̄(K, ρ, p) depending on the values of p and ρ. The shrinkage of P̄ toward 50%, which is most pronounced when ρ is small, introduces large bias for extreme percentiles and is responsible for the poor performance of the estimator in these cases. On the other hand, P̂ “unshrinks” the optimal estimates back onto the percentile lattice by construction, which results in reduced error for extreme percentiles at the price of increased error for intermediate percentiles.

FIGURE 2.

Comparison of RMSE_P̄(1000, ρ, p) (black) and RMSE_P̂(1000, ρ, p) (gray) for specific percentiles and different values of the stability coefficient.

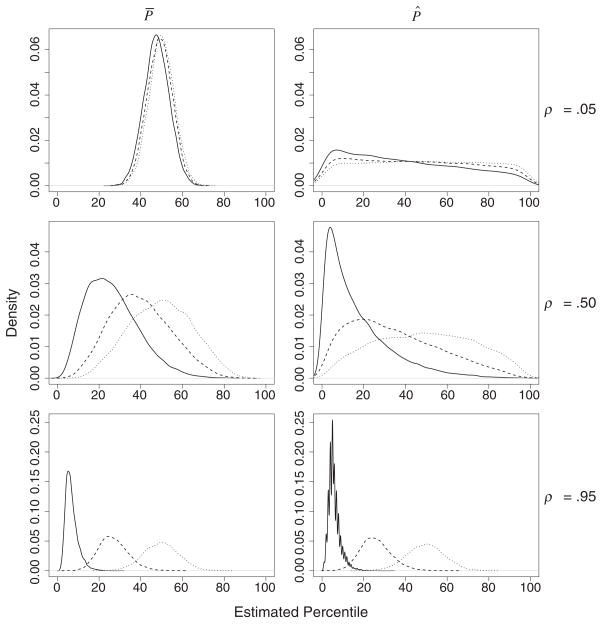
Figure 3 further illustrates the bias and variance trade-off between the two estimators. When the stability coefficient is small, the R̄ are tightly distributed around 50% for all true percentiles. Thus, by restrictive shrinkage, P̄ has little variance but bias grows as a function of the distance between p and 50. As the stability coefficient grows, the shrinkage is reduced and the variability of the estimator increases. Without shrinkage, the P̂ are much more variable, with nontrivial probability of taking values across the entire range when the stability coefficient is small. However, there is less bias in that the P̂ densities more quickly center around the true percentiles as the stability coefficient increases.

FIGURE 3.

Approximate large K sampling distributions of P̄ (left column) and P̂ (right column) for individuals truly at the 5th (solid), 25th (dashed) and 50th (dotted) percentiles. Rows correspond to stability coefficients of 0.05, 0.50 and 0.95.

Decision Rules Based on Percentile Range Membership

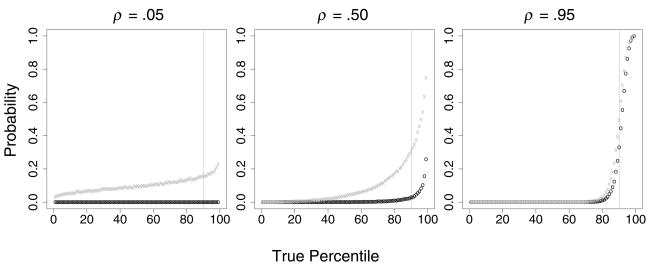
As discussed previously, a common goal of accountability programs is to identify the lowest and highest performing teachers or schools (e.g., the lowest and highest deciles) for remediation or reward. This task generally becomes easier as the stability coefficient increases, but at a rate that is discouragingly slow and also sensitive to which of P̄ or P̂ is used. Figure 4 shows the operating characteristics of two alternative decision rules for classifying teachers in the upper decile: (a) classify teachers as extreme if P̄ exceeds 90 or (b) classify teachers as extreme if P̂ exceeds 90. For each true percentile of the θs and for the stability coefficients of .05, .50 and .95, the figure displays the preposterior probability that each decision rule classifies individuals in the upper decile. Such a decision is incorrect for true percentiles in the range (0, 90) and is correct otherwise. Note that because of the symmetry, analogous results apply to the identification of teachers in the lower decile.

FIGURE 4.

Preposterior probabilities of P̄ (“o”) and P̂ (“x”) classifying individuals in the upper decile as a function of the true percentile.

Through conservative shrinkage, P̄ identifies teachers as extreme only when there is very strong evidence. This behavior maintains a low probability of incorrectly classifying teachers truly below the upper decile, but at the price of having a low probability of correctly identifying teachers truly in the upper decile. On the other hand, P̂ identifies extreme individuals regardless of the amount of information available in the data. This produces a greater probability of correctly classifying teachers in the upper decile, but also introduces a greater probability of misclassifying teachers in the remainder of the distribution. This can be extremely unreliable when the stability is small, as even the lowest performing teacher conceivably could be identified as being among the best. As the stability coefficient approaches zero, the probabilities for P̄ converge to zero for all percentiles, while those for P̂ converge to the a priori value of 0.1. The two decision rules converge to a common behavior as the stability coefficient increases to 1; however, they remain distinct for stability coefficients even as high as 0.95. Neither estimator achieves an acceptably low probability of misclassification until the stability coefficient is quite high.

Discussion

Our analysis provides important results on the feasibility of using value-added models as a mechanism for ranking teachers or schools. We conclude that, in general, estimating percentiles or ranks is quite difficult and substantial information is necessary for acceptable, aggregate performance. This information must manifest as either extreme heterogeneity among the teachers or very small sampling variance, producing high-stability coefficients. How large the stability coefficient must be to achieve the desired level of performance is of course subjective, but it is clear that estimators and decision rules are not truly reliable until the stability coefficient is near 1.

This goal is unlikely to be met, calling into question the advisability of using estimated ranks as a basis for policy decisions. For example, Bock et al. (1996) use data from 11 counties in Tennessee to estimate the teacher percentage of total variance in gain scores for fourth grade students. They assume teacher-specific effects estimated from 75 students — 25 students per class from three cohorts. The stability coefficient ranged between 0.47 and 0.51 for social studies and reading to slightly over 0.70 for language, math, and science. Even with these stability coefficients, the standard error of the optimal percentile estimator is approximately 16 percentage points for language, math, and science and approximately 21 percentage points for reading and social studies. Confidence intervals will cover nearly the entire percentile range.

Ranking schools may be equally difficult. Because schools have more students than classrooms, one might expect the school percentage of total variance to be larger than that of the teacher. However, using the Tennessee data, Bock et al. (1996) found that for two teachers with 25 students in each classroom and three cohorts used to estimate the school effects for a single grade, the school percentages of total variance were 47%, 67%, 65%, 69% and 62% for reading, language, math, science and social studies respectively. If we considered all five grades per school the percentages would be even lower. These low values are the result of small overall school effects relative to the variability produced by teachers. Estimated school-level ranks or percentiles will be highly unstable for school systems with similar variance components to those in Tennessee.

Estimating extremes presents additional statistical and practical complexities. The two, optimal percentile estimators trade off bias and variance in different ways, impacting both percentile-specific MSE performance and decision-rule operating characteristics. P̄ restricts the number of teachers found to be above or below an extreme, at the price of missing some who truly are extreme. P̂ behaves in the opposite manner, always finding teachers in the extremes, even if they are not. If policy makers intend to use estimated percentiles or ranks for accountability, it is advisable that the choice of estimator and related decision rules be guided by consideration of the losses incurred by these different kinds of errors. For example, if teachers identified as extreme are likely to face punitive sanctions or receive large monetary rewards (like the $25,000 bonus of California), then policy makers might find mis-classifying nonextreme teachers as relatively more costly and prefer to use decisions based on P̄. If teachers classified as low-performing will receive additional training, then policy makers might see missed training as costly and prefer using decision rules based on P̂.

Unfortunately, the results for the basic, two-stage model are in many ways “best-case.” Performance is evaluated under the assumption that the model is correct and that direct-estimate variability is constant over teachers or schools. In practice, these variances can be far from equal, inducing complicated performance. Of possibly greater importance, value-added models are subject to numerous potentially severe sources of bias, stemming from the nonrandom allocation of students to teachers and teachers to schools, systematic errors stemming from equating school or teacher “value-added” to the changes in test scores, and model misspecification. These influences further challenge the validity of rankings based on value-added models at the teacher and school levels.

Finally, our analyses based on the basic, two-stage model with a common sampling variance identify important properties, but more general scenarios warrant consideration. The most important generalization will be to study the unequal σ_k case. Performance will be very complicated, depending on the relation between true percentile and MLE variance. Another important generalization generates estimates using weighted square error loss, with deviations for extreme percentiles given greater weight (Stern & Cressie, 1999).

Biographies

J. R. LOCKWOOD is Associate Statistician, RAND, 201 N. Craig Street, Suite 202, Pittsburgh, PA 15213; lockwood@rand.org. He specializes in Bayesian statistics, MCMC methods, and environmental and education policy applications.

THOMAS A. LOUIS is Professor, Department of Biostatistics, Johns Hopkins University Bloomberg School of Public Health, 615 North Wolfe Street, Baltimore, MD 21205; tlouis@jhsph.edu. He specializes in environmental health and public policy, development of related statistical procedures, Bayesian models, analysis of longitudinally and spatially correlated data, small area estimation, analysis of observational studies and research synthesis.

DANIEL F. McCAFFREY is Statistician, RAND, 201 N. Craig Street, Suite 202, Pittsburgh, PA 15213; danielm@rand.org. He specializes variance estimation; hierarchical and mixed models, weighting missing data and imputation, performance assessment, validity of test scores and gains, teaching practices, student achievement, and school reform.