Summary
A frequent occurrence in medical research is that a patient is subject to different causes of failure, where each cause is known as a competing risk. The cumulative incidence curve is a proper summary curve, showing the cumulative failure rates over time due to a particular cause. A common question in medical research is to assess the covariate effects on a cumulative incidence function. The standard approach is to construct regression models for all cause-specific hazard rate functions and then model a covariate-adjusted cumulative incidence curve as a function of all cause-specific hazards for a given set of covariates. New methods have been proposed in recent years, emphasizing direct assessment of covariate effects on cumulative incidence function. Fine and Gray proposed modeling the effects of covariates on a subdistribution hazard function. A different approach is to directly model a covariate-adjusted cumulative incidence function, including a pseudovalue approach by Andersen and Klein and a direct binomial regression by Scheike, Zhang and Gerds. In this paper, we review the standard and new regression methods for modeling a cumulative incidence function, and give the sources of computer packages/programs that implement these regression models. A real bone marrow transplant data set is analyzed to illustrate various regression methods.
Keywords: binomial regression model, cause-specific hazard, competing risks data, cumulative incidence function, inverse weighting, pseudovalue, subdistribution hazard
1. Introduction
Problems in analyzing competing risks data often arise in biomedical researches, where each subject is at risk of failure from K different causes. When one event occurred, it precludes the occurrence of another event. For the competing risks data, one observes an on study time and a failure type indicator for each individual. In cancer studies, one common example of competing risks are disease relapse and death in remission. The cumulative incidence curve is the proper summary curve in analyzing the competing risks data. Unfortunately, it has been commonly seen in practice of using one minus Kaplan-Meier estimate for each competing cause. It overestimates the incidence rates of a particular cause in the presence of all other competing causes (see Klein et al. [1]). Recently, Klein and Moeschberger [2], Martinussen and Scheike [3], Pintilie [4], and Klein and Zhang [5] reviewed some basic statistical methods for analyzing the competing risks data.
In biomedical studies it is important to study the covariate effects on the cumulative incidence function (CIF) of a particular failure. The standard approach is to model cause-specific hazards for all causes. The Cox proportional hazards model [6] is the most commonly used regression model for all causes [7,8]. Shen and Cheng considered a special, additive risk model [I)] and Scheike and Zhang used a flexible Cox-Aalen model [10]. This approach is valid when all cause-specific hazards are modeled correctly. Since the cumulative incidence curve of a particular cause is a function of all cause-specific hazards, one problem is that it may be hard to evaluate the covariate effect on the cumulative incidence curve directly and it may be hard to identify which specific covariate has a time-varying effect on the CIF, where the covariate effect changes over time.
Recently, some new regression approaches have been considered and developed to model the CIF direcdy. The first approach is based on earlier work by Gray [ll] and Pepe [12] to directly model the subdistribution hazard function. Based on the subdistribution hazard function one can directly interpret the covariace effect on the cumulative incidence curve. Fine and Gray proposed a Cox-type proportional hazards model [13] and Sun et al. studied a more flexible and general model for the subdistribution hazard function [14]. The second approach to model the cumulative incidence curve directly is based on pseudovalues from a jackknife statistic constructed from the estimated CIF [15,16]. The final approach of directly modeling the CIF is based on binomial regression models using the inverse probability of censoring weighing technique. Scheike, Zhang and Gerds [17] considered a fully non-parametric regression model and a class of general semiparametric regression models, proposed score equations for the regression coefficient estimators, and derived its consistent variance estimators [17].
2. Cause-specific hazard approach
Let T1, …, TK be the potential unobservable failure times of total K type failures. For the competing risks data, we observe time to the first failure, T = min(T1, …, TK) and indicator the type of failure, ε = k, if T =Tk. For right censored competing risks data one observes the study time (failure time or censoring time) Xi = min(Ti, Ci) for each subject, where Ti and Ci are the failure time and censoring time for the ith individual, the event indicator Δi =I (Ti ≤ Ci), where I(.) is an indicator function, Δi =1 if {Ti ≤ Ci} and Δi =0 if {Ci <Ti}, and the cause of K type failures ε ∈ {1, …, K}, for i=1, …, n. For simplicity, we assume two competing risks (K=2). The summary curve of the cumulative incidence function (CIF) of cause 1 is the probability that an event of type 1 occurs at or before time t, F1(t) =P(T ≤ t, ε =1). The cause-specific hazard function of the kth type failure is defined as
| (1) |
It is the rate at which a specific cause of event is occurring at presence of other competing risks. The CIF of cause 1, F1(t) is a function of cause-specific hazard rates of both causes,
| (2) |
where is the cumulative cause-specific hazard function and . To estimate F1(t), let 0 =t0 < t1 < … <tD be the distinct event time points. At time ti, let and be the number of subjects failed of cause 1 and cause 2, respective, and let Yi be the number at risk prior to time ti. The non-parametric estimator of F̂1(t) is given by
| (3) |
where is the Nelson-Aalen [18, 19] estimator for the cumulative cause-specific hazard function and is the Kaplan-Meier [20] estimator for overall survival distribution. Based on martingale central limit theory [21, 22] the variance of F̂1(t) can be consistently estimated [22]. Note that one minus Kaplan-Meier estimator treating failure of other cause as censored observation, it estimates [1 − exp{−Λ1(t)}] which is the marginal probability in a counterfactual world where it is impossible to fail from other causes [1]. This quantity is hard to interpret and it overestimates the cumulative incidence rate of cause 1 when competing events are not independent [4]. However, it reduces to a cumulative incidence function estimator when there is a single type of failure.
In medical studies researchers need to compare the treatment effect of a particular failure for competing risks data. The weighted log-rank test, which compares the cause-specific hazard rates between groups, is most commonly used in analyzing time-to-event data. It is important to know that the log-rank test does not compare the CIF directly since the CIF is a function of both cause-specific hazard rates. Gray [11] proposed a weighted log-rank test testing the equivalence of the subdistribution hazard function between two treatment groups, where the subdistribution hazard function of cause 1 is given by (see Section 3 for detail). Since , the proposed test directly compares the CIFs between treatment groups [ll]. The CIF estimators and direct testing procedures are available in cmprsk and timereg R-packages created by Robert Gray [101] and Thomas Scheike [102], respectively.
Bone marrow transplant data: an example
For illustration purposes, we consider a data set of myelodysplasia (MDS) patients treated with HLA-identical sibling bone marrow transplantation (BMT). This is a Center for International Blood and Marrow Transplant Research (CIBMTR) study [23]. The study has two competing risks: treatment related death (TRM) defined as death in complete remission and relapse defined as recurrence of MDS. 408 patients with complete information were included in this example (161 patients died in complete remission and 87 patients relapsed).
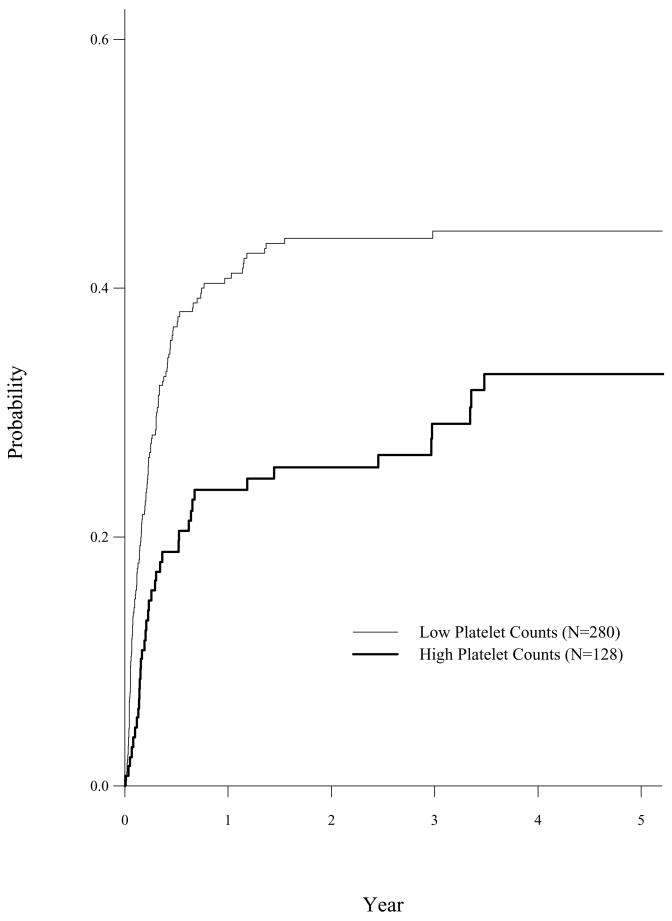
The CIBMTR study indicated that CIF of TRM were different for patients with low and high platelet counts (< 100×109/L (n=280) versus ≥ 100×109/L (n=128)). Table 1 shows the one minus Kaplan-Meier estimator treating relapse as censored event and the CIF estimator with p-value of Gray’s test using cuminc function of comprsk package for TRM by high and low platelet counts, respectively. It shows that (1 − Kaplan-Meier) estimator overestimates the CIF and Gray’s test indicates that patients with high platelet counts have a lower cumulative incidence rate of TRM. It is important to know that CIF is a proper summary statistic for the competing risks data and Gray’s test should be used if we are interested in comparing the difference of CIF between treatment groups.
Table 1.
One minus Kaplan-Meier estimator (SE), CIF estimator (SE) and Gray’s test for TRM by high and low platelet counts.
| 1 − Kaplan-Meier | CIF | ||||
|---|---|---|---|---|---|
| Time | Low | High | Low | High | P(Gray) |
| 1yr | 0.44 (0.03) | 0.25 (0.04) | 0.41 (0.03) | 0.24 (0.04) | 0.003 |
| 3yr | 0.50 (0.03) | 0.32 (0.05) | 0.45 (0.03) | 0.29 (0.04) | |
The plot.cuminc function of cmprsk package plots the estimated CIF by treatment groups and the output of cuminc function can be used to compute the pointwise confidence interval at a fixed time point. The CIF of TRM by platelet counts is given in Figure 1. Table 1 and Figure 1 showed that patients with high platelet counts (≥ 100×109/L) had a lower cumulative incidence rate of treatment related mortality than patients have low platelet counts.
Figure 1.
Cumulative Incidence of TRM by Patient Platelet Counts
Cox model for the cause-specific hazard function
For competing risks data researchers often want to examine and model the effects of covariates for a specific cause of failure. The standard approach is to model the cause-specific hazard functions for both causes [21]. Various models have been considered and adopted. First, Prentice et al [7] and Cheng, Fine and Wei [8] considered the commonly used Cox proportional hazards models for both causes,
| (4) |
where k(=1,2) represents the type of failure, λk0(t) is the baseline hazard function, Z is a p-dimensional vector of covariates, and βk is the vector of regression coefficients. Cox model can be fitted using standard survival analysis techniques with the modification that subjects failed from causes other than the cause of interest are treated as censored observations. Most statistical softwares, such as SAS, SPSS, and S-Plus, can be used to fit the cause-specific Cox proportional hazards model. Andersen et al. [21] study the estimator of the predicted CIF for a given set value of covariates, F1(t | z) =P(T ≤ t, ε =1 | z) and derived a variance estimator under the Markov model assumption. It is not clear how to construct the confidence band analytically based on the large sample properties. Cheng, Fine and Wei [8] suggested a plug-in estimator for F1(t | z) by
| (5) |
where Λ̂k0(t) is the estimator of the cumulative baseline hazard function , and derived a variance estimator for F̂1(t | z) [8, P227–228]. Without covariates this plug-in estimator (2.5) is asymptotically equivalent to the non-parametric estimator given in (2.3). Cheng, fine and Wei [8] also proposed to construct the confidence band for F1(t | z) over a given time period [t1, t2] based on a simulated method [8].
The predicted cumulative incidence probability is not a simple function of estimated parameters. It is not available currently in standard statistical packages. SAS macros for estimating the predicted cumulative incidence functions and its variance estimation based on a Cox regression model for the competing risks data has been developed by Rosthøj, Andersen and Abildstrom [24]. Two SAS marcos are available at [103]: cuminc computes the predicted CIF for both causes and cumincv computes the predicted CIF and its variance estimations.
Applied to example BMT data
We apply SAS macros to fit the BMT example data. Based on cause-specific hazard regression analysis, the early CIBMTR study [23] showed that two sets of different risk factors associated with TRM and relapse, respectively. Since the CIF of TRM is a function of cause-specific hazards of TRM and relapse. It is hard to identify which risk factors were significantly associated with the CIF of TRM. One approach is to include all risk factors for each cause of failure. For illustration purpose we fit same Cox model with covariates were significantly associated with TRM, i.e. age (continuous variable, standardized and centered at mean of 35 years old and ranged from 2 to 64 years old), platelet counts (1 for ≥ 100 ×109/L and 0 for < 100×109/L) and GVHD prophylaxis (1 for T-cell depletion BMT and 0 for Non-T-cell depletion BMT) for TRM and relapse. The SAS macro cumincv predicts the CIF for TRM and its variance estimation. It computes the predicted CIF of TRM for a 35 years old patient and received a Non-T-cell depleted marrow transplant for GVHD prophylaxis by low and high platelet counts (Table 2).
Table 2.
Fitting a Cox proportional hazards model, the predicted CIF (SE) of TRM for a 35 years old patient and received a Non-T-cell depleted marrow transplant for GVHD prophylaxis by low and high platelet counts.
| Time | Low Platelet Counts | High Platelet Counts |
|---|---|---|
| 1yr | 0.41 (0.03) | 0.28 (0.02) |
| 3yr | 0.46 (0.03) | 0.32 (0.02) |
Cox-Aalen model for the cause-specific hazard function
Shen and Cheng studied F1(t | z) based on a special additive model [9], which was first proposed by Lin and Ying for survival data [25]:
The Cox proportional hazards model and the Lin and Ying’s additive model do not allow the covariates to have time-varying effect.
As an alternative to the Cox model, Aalen proposed an additive hazards model [26]:,
| (6) |
These are two most commonly used regression models in survival analysis. Although the Cox model can be generalized to allow some covariates to have time-varying effects, but it is hard to estimate the fully nonparametric time-dependent regression coefficient functions. In practice, one may consider using a piecewise constant stepwise function to model the time-varying effect. One advantage of Aalen’s additive model is that it allows the covariates to have time-varying effects and that is easy to estimate. It is well known that additive model may not give monotone estimated survival probabilities and care needs to be considered when this happens [2]. Recently, Scheike and Zhang [10, 27] proposed a flexible additive-multiplicative model which combines the Cox proportional model and Aalen’s additive model (denoted as Cox-Aalen model),
| (7) |
where Xi is (p+1)-dimensional covariates with first element to be 1 for all subjects and Zi is q-dimensional covariates. Here, some covariates Xi have additive and time-varying effects, and other covariates, Zi have constant multiplicative effects. The proposed model reduces to a Cox model when Xi =1 and it leads to an Aalen’s additive model when Zi = 0. Scheike and Zhang [27] proposed some goodness of fit tests to determine which covariates to be included in additive part and multiplicative part of the mixed model, respectively. In practice, they suggested that the covariate could be included in the additive part of the model if it has a time-varying effect. Scheike and Zhang proposed asymptotically unbiased estimators for the regression coefficients and derived its variance estimators [27, P78–81]. When X is a vector of discrete covariates the mixed Cox-Aalen model leads to a stratified Cox model which is available in most statistical packages. The timereg package has a cox.aalen R-function which can be used to fit a general mixed Cox-Aalen model.
Scheike and Zhang studied the predicted cumulative incidence curve based on flexible Cox-Aalen model [10],
| (8) |
Where
and
We derived the variance estimator for F̂k(t | x, z,) and showed that proposed mixed Cox-Aalen model fits the data better than a standard Cox proportional hazards model when some covariates have time-varying effects.
Applied to example BMT data
Fitting a Cox model for the cause-specific hazard function, it assumes that all covariates have constant effects. The proportionality assumption can be tested by adding a time-dependent covariate which is available in most statistical packages. For the BMT data, the test gives a p-value of 0.04 for the covariate of platelet counts which indicates that there is evidence to suggest that patient platelet counts has a time-varying effect on the cause-specific hazard of TRM, and test indicates that proportionality assumption holds for relapse for all three covariates. We fit a mixed Cox-Aalen model for TRM where the platelet counts was included in the additive part of the model to facilitate the time-varying effect and fit a regular Cox model for relapse. Table 3 gives the predicted CIF of TRM at 1 and 3 years since transplant for a 35 years old patient and received a Non-T-cell depleted marrow transplant for GVHD prophylaxis by low and high platelet counts. Since Cox-Aalen model is a more flexible model allowing the platelet counts having time-varying effect, it should fit this BMT data better than the Cox proportional hazards model.
Table 3.
Fitting a mixed Cox-Aalen model, the predicted CIF (SE) of TRM for a 35 years old patient and received a Non-T-cell depleted marrow transplant for GVHD prophylaxis by low and high platelet counts.
| Time | Low Platelet Counts | High Platelet Counts |
|---|---|---|
| 1yr | 0.42 (0.03) | 0.26 (0.04) |
| 3yr | 0.46 (0.03) | 0.32 (0.05) |
Modeling the cumulative incidence function by cause-specific hazard functions approach is valid as long as the cause-specific hazards are correctly modeled for all causes. The Cox-Aalen model is a flexible model for this approach.
Subdistribution hazard approach
One approach of directly modeling the cumulative incidence function is based on Gray’s [11] subdistribution hazard technique, where the subdistribution hazard of cause 1 is given by:
| (9) |
There is a direct relationship between the cumulative incidence function and subdistribution hazard function:
| (10) |
one can interpret the covariate effect on the CIF directly. Fine and Gray proposed a Cox type proportional subdistribution hazards model [13]:
| (11) |
where is an unknown baseline subdistribution hazard function. Gray stated that is the hazard function for an improper random variable T* = T ×I(ε = 1) + ∞ × I(ε = 2). Thus, subjects failed from cause 2 should be considered at risk for all time. With complete data (no censoring), we set Ti = ∞ if ith individual failed from cause 2, then standard partial likelihood method can be applied and most standard statistical packages can be used to fit the Fine and Gray’s proportional subdistribution hazards model.
For right-censored incomplete competing risks data, Fine and Gray suggested using inverse probability of censoring weighting technique (IPCW) to fit the subdistribution hazards model and derived the variance estimators [13].
Recently, Gray developed a cmprsk R-library which is available to the public and its crr function can be used to fit the proportional subdistribution hazards model. The crr function allows the model to have time-dependent covariates, which can be used to test the proportionality by adding a time-dependent covariate: . The significant p-value of testing β2 = 0 indicates that the covariate Z has a time-varying effect on the cumulative incidence function of F1(t | Z). The predict.crr function computes and plot.predict.crr function plots the predicted cumulative incidence function for a given set of covariate values z. However, its variance estimates are not available in cmprsk R-package.
When some covariates have time-varying effects, similarly we can consider fitting a flexible Cox-Aalen subdistribution hazards model,
| (12) |
where x is (p+1)-dimensional covariates with first element to be 1 for all subjects and z is q-dimensional covariates.
Applied to example BMT data
The crr function has been applied to the BMT example data. The result shows a time-varying effect for the platelet counts (p=0.05). It indicates that the proportional subdistribution hazards model may not be the correct model for this data. When the proportional subdistribution hazards model does not fit the data well, Sun et al. considered an alternative flexible model [14]. Here, we fit a flexible Cox-Aalen subdistribution hazards model to the BMT data where platelet counts was included in the additive part of the model to facilitate its time-varying effect. The regression parameter estimators are β̂(Age) = 0.34, SE = 0.08, p <0.0001 and β̂(T-Dept) = − 0.61, SE = 0.27, p = 0.02. Due to the direct relationship between CIF and subdistribution hazard function, we can conclude that older patient had a higher incidence rate of TRM and T-cell depleted BMT for GVHD prophylaxis had a lower incidence rate of TRM. Based on Cox-Aalen subdistribution hazards model we can estimate the predicted CIF of TRM for a given set of covariate values.
Modeling CIF
Fine and Gray proposed to directly model the cumulative incidence function of a competing risks data by modeling the subdistribution hazard function [13]. Recently, some alternative new approaches have been proposed to model the cumulative incidence function directly by
| (13) |
where φ is a known link function. One approached is based on pseudo-value approach proposed by Andersen, Klein and Rosthøj [28] and another approached is based on binomial regression modeling studied by Scheike, Zhang and Gerds [17]. In this section, we introduce these approaches through the BMT example data.
Pseudovalue approach
Recently, Andersen, Klein and Rosthøj proposed a quite general technique to regression model for censored survival data [28]. This technique is based on the pseudo-value approach which has been applied to the competing risks data [15, 16]. Consider a prefixed grid of time points, t1, …, tM. In practice, it has been suggested using five to ten time points equally spaced on the event scale works well in most cases [15, 16] or some fixed time points which are interested to the researchers, such as one and three years after the treatment in BMT example data. At grid time point, tj, the cumulative incidence function can be estimated by a standard non-parametric estimator given in (2.3) based on the complete data set, F̂1(tj) and based on the sample of size n − 1 obtained by deleting the ith observation, . The pseudo-value of the ith subject at time tj is defined as
| (14) |
Let θij = F1(tj | Zi) be the conditional CIF which needs to be modeled. Klein and Andersen [14] considered to model θij by φ(θij) = αj +βTZi, where φ is a known link function, and suggested some common link functions such as logit link function of φ(θ) = log{θ/(1 − θ)} and the complementary log-log link function of φ(θ) = log{− log(1 − θ)}. The regression parameters, αj and β, can be estimated by solving a pseudo-score equation and its covariance matrix can be estimated by a sandwich variance estimator [15]. The complementary log-log link function leads to the proportional subdistribution hazards model proposed by Fine and Gray [13]. For the survival data, the logit link gives to a proportional odds model on the cumulative hazards model. Klein et al. [29] developed a SAS macro and an R functions to compute pseudo-values for right censored competing risks data [29], available at [104]. The SAS macro computes the pseudovalues for each subject at each grid time point. A SAS Proc GENMOD procedure can then be used to fit the regression model. Detailed examples on how to compute the pseudovalues and how to fit the regression model can be found at [104]. The SAS Proc GENMOD procedure reports the regression parameter estimate, standard error, 95% confidence interval and p-value of testing β =0. It also gives detailed R-codes for fitting the regression model using pseudo-value approach.
Applied to example BMT data
We now apply pseudo-value approach to the bone marrow transplant example data focusing on the competing risk of TRM. We pre-set a grid of 3 time points of {12, 36, 60}-months since transplant and fit the regression model with three variables: Z1=platelet counts (binary variable); Z2=patient age (continuous variable) and Z3=GVHD prophylaxis (binary variable). First, we fit a regression model, φ(θij) = αj + β1Zi1 + β2Zi2 + β3Zi3, with complementary log-log link function. The fitted model is equivalent to the Fine and Gray’s proportional subdistribution hazards model. Two approaches give similar results as expected (Model I of Table 4).
Table 4.
Regression analysis for TRM based on subdistribution hazard approach and pseudo-value approach for the proportional subdistribution hazards model (Model I) and mixed Cox-Aalen model (Model II).
| Subdistribution hazard | Pseudo-value | ||||
|---|---|---|---|---|---|
| Model | Variable | β̂(SE) | P | β̂(SE) | P |
| I | Platelet counts | −0.43 (0.18) | 0.02 | −0.41 (0.19) | 0.03 |
| Age | 0.34 (0.08) | < 0.0001 | 0.29 (0.08) | 0.0005 | |
| GVHD Prophylaxis | −0.60 (0.27) | 0.03 | −0.59 (0.29) | 0.04 | |
| II | Age | 0.34 (0.08) | < 0.0001 | 0.29 (0.08) | 0.0005 |
| GVHD Prophylaxis | −0.61 (0.27) | 0.02 | −0.59 (0.29) | 0.04 | |
Since patient platelet counts had a time-varying effect, we have considered a flexible Cox-Aalen subdistribution hazards model in Section 3. Here, we fit an equivalent model, φ(θij) = αj + β1jZi1 + β2Zi2 + β3Zi3, allowing platelet counts (Z1) having time-varying effect. Both approaches give quite close estimating results as well (Model II of Table 4).
Direct binomial modeling approach
Recently, Scheike, Zhang and Gerds proposed to directly model the cumulative incidence function through:
| (15) |
where φ(·) is a known link function, A(t) is an unspecified (p+1) dimensional regression coefficient functions and Z = (1, Z1, …, Zp). They proposed a regression analysis using the inverse probability of censoring weighted response. With log link function, φ(x) = log(1 − x) the proposed model leads to the Aalen’s generalized additive model. Note that this is a very general regression model allowing covariates to have time-varying effects. Some goodness-of-fit tests have been studied to test the time-varying effects; however in practice it is suffice to plot and visually examine the estimated regression function with the confidence bands. Scheike, Zhang and Gerds also studied a class of semiparametric models:
| (16) |
where g is a known function. With g(β, Z, t) = exp{βTZ} the multiplicative semiparametric model gives a Cox-Aalen model which includes the Cox model and Aalen’s additive model as special models. With g(β, Z, t) = βTZt the additive semiparametric model leads to a partially semiparametric additive model [30]. Scheike, Zhang and Gerds proposed score equations to estimate A(t) and β simultaneously and derived variance estimations for the estimated regression parameters and the predicted CIF for a given set of covariate values [17].
Applied to example BMT data
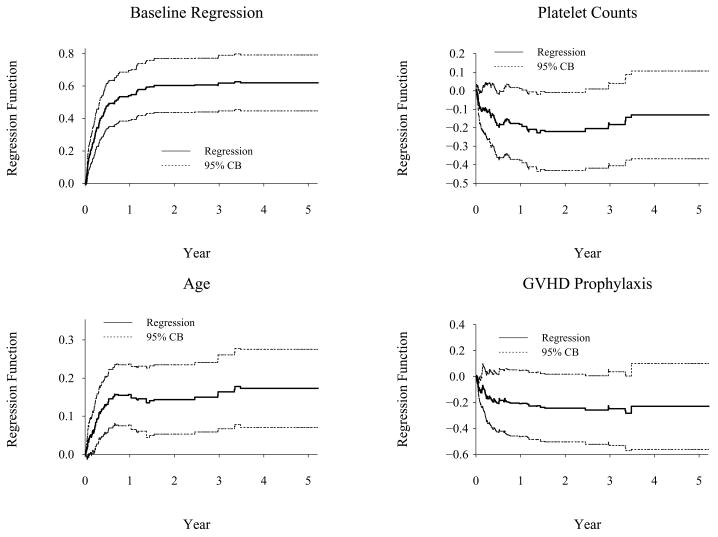
We now revisit the bone marrow transplant data using binomial modeling approach. These models can be fitted using the timereg package in version 1.0–5 and the comp.risk function which is available at http://staff.pubhealth.ku.dk/~ts/timereg.html. First, we fit a multiplicative parametric model, log{1 − F1(t | Z1, Z2, Z3)} = A0(t) exp{β1Z1 + β2Z2 +β3Z3}, where X1, X2, X3 are platelet counts, age and GVHD prophylaxis, respectively. This model is equivalent to the Fine and Gray’s proportional subdistribution hazards model. Both approaches give close estimating results (Model I of Table 5). To see if any covariate has a time-varying effect, we fit a fully nonparametric model with the log link function, log{1 − F1(t | X1, X2, X3)} =A0(t) + A1(t)X1 + A2(t)X2 + A3(t)X3. Figure 2 shows the estimated regression functions and their 95% confidence bands. The plots indicate that age had very strong time-varying effect, platelet counts had mild time-varying effect and the GVHD prophylaxis had a constant effect. It should be noted that effects of age are different with the subdistribution hazard approach and the binomial modeling approach. With the subdistribution hazard of TRM, age passes the proportionality test (p=0.86) and, in Section 4.1, we have modeled its effect as constant. With the binomial modeling approach, the plot in Figure 2 shows that age only had a significant effect on TRM within first 8 months of transplant and no effect thereafter.
Table 5.
Regression analysis for TRM based on subdistribution hazard approach and binomial modeling approach for the proportional subdistribution hazards model (Model I) and mixed Cox-Aalen model (Model II).
| Subdistribution hazard | Binomial modeling | ||||
|---|---|---|---|---|---|
| Model | Variable | β̂(SE) | P | β̂(SE) | P |
| I | Platelet counts | −0.43 (0.18) | 0.02 | −0.41 (0.19) | 0.03 |
| Age | 0.34 (0.08) | < 0.0001 | 0.29 (0.08) | 0.0005 | |
| GVHD Prophylaxis | −0.60 (0.27) | 0.03 | −0.59 (0.29) | 0.04 | |
| II | GVHD Prophylaxis | −0.63 (0.27) | 0.02 | −0.64 (0.29) | 0.03 |
Figure 2.
Cumulative Regression Function Estimation For TRM (Binomial Nonparametric Model)
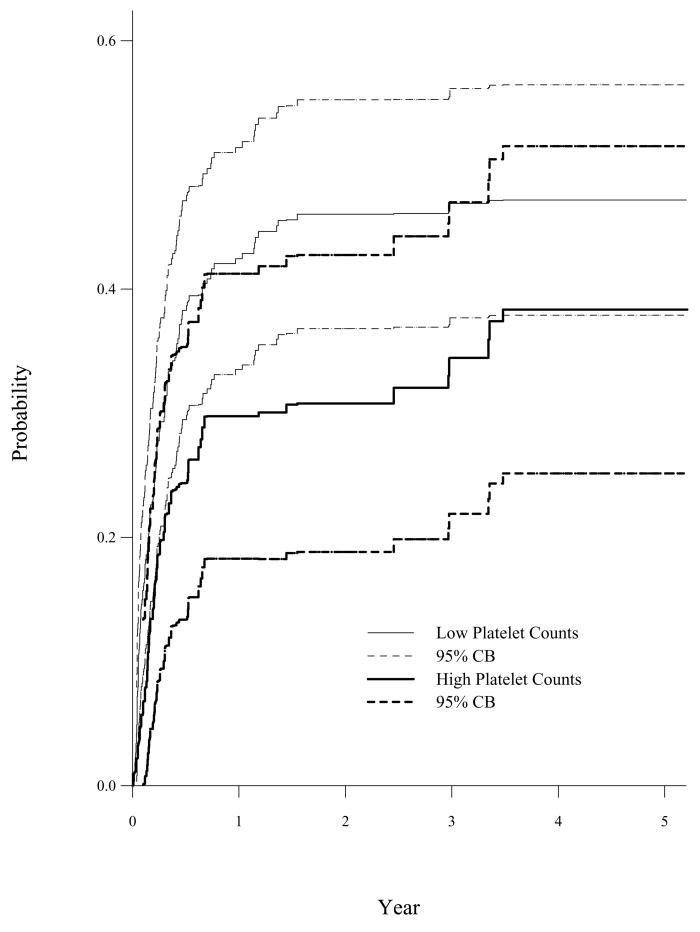
Finally, we fit a flexible model, log{1 − F1(t | X1, X2, X3)} ={A0(t) + A1(t)X1 + A2(t)X2}exp{βX3} to accommodate the time-varying effect. The estimated β̂(T-Dept) = −0.64, SE = 0.29, p = 0.03 is close to the estimated result based on subdistribution hazard approach (Model II of Table 5). The predicted cumulative incidence function of TRM for a 35 years old patient who received a non-T-cell depleted BMT for GVHD prophylaxis by low and high platelet counts are given in Figure 3. This flexible binomial Cox-Aalen model fits the BMT data well since it allows platelet counts and age to have time-varying effects.
Figure 3.
Predicted CIF of TRM for a 35 Years Old Patient with Non-T-Depleted BMT by Platelet Counts (Binomial Cox-Aalen Model)
5. Expert commentary
In biomedical studies one often needs to analyze censored competing risks data. The cumulative incidence curve of a particular cause of failure is a proper summary curve in analyzing the competing risks data and the Gray’s test should be considered if one interested in comparing the cumulative incidence functions between groups. Recently, new statistical methods have been developed to study and model the covariate effect on the CIF directly.
Five-year view
We reviewed standard nonparametric estimator for the cumulative incidence function based on cause-specific hazard function for all causes and reviewed some available statistic packages for estimating the cumulative incidence function. A common question in medical researches is to assess covariate effect on a cumulative incidence function. The standard approach is to construct regression models for all cause-specific hazard rate functions and then model a cumulative incidence curve as a function of all cause-specific hazards. This is valid as long as the cause-specific hazards are correctly modeled for all causes. Various new methods have been proposed in recent years, emphasizing on directly assessing covariate effect on a cumulative incidence function. For the new methods, estimation of a cumulative incidence function is constructed through modeling a subdistribution hazard function, pseudo-values from a jackknife statistics, or a binomial regression model. We reviewed the standard and new regression methods for modeling a cumulative incidence function, and give the sources of computer packages/programs that implement these regression models. In medical studies the predicted cumulative incidence probability of given set value of covariates often is important to the researchers.
These recently developed statistical methods and models have not been utilized frequently in many medical studies. These new statistical techniques are not available in most commonly used statistical packages, such as SAS, SPLUS and S-PLUS. In the next 5 years, more user friendly statistical programs need to be developed.
Key issues
Competing risks data often occurs in medical studies.
Cumulative incidence function is a proper summary statistics for analyzing competing risks data.
Cumulative incidence function is estimated by modeling the cause-specific hazard function of all causes.
Gray’s test compare the cumulative incidence function directly.
Modeling the covariate effect through modeling the cause-specific hazard function of all causes; modeling the subdistribution hazard function of a specific cause; modeling the cumulative incidence function directly using pseudo-value approach and direct binomial regression approach.
Acknowledgments
We thank the Center for International Blood and Marrow Transplant Research for providing us with the sample data.
Footnotes
Financial & competing interests disclosure
MJ Zhang and TH Scheike’s research ivas supported by a Grant (R01CA54706@12) from the National Cancer Institute. The authors have no other relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in tile manuscript apart, from those disclosed.
No writing assistance was utilized, in the production of this manuscript.
Contributor Information
Mei-Jie Zhang, Email: meijie@mcw.edu, Division of Biostatistics, Medical College of Wisconsin, 8701 Watertown Plank Road, Milwaukee, WI 53226, U.S.A. Tel: +1 414-456-8375; Fax: +1 414-456-6513.
Xu Zhang, Email: matxxz@langate.gsu.edu, Department of Mathematics and Statistics, Georgia State University, Atlanta, GA 30302, U.S.A. Tel: +1 404-413-6404; Fax: +1 404-413-6403.
Thomas H. Scheike, Email: ts@biostat.ku.dk, Department of Biostatistics, University of Copenhagen, Blegdamsvej 3, DK-2000, Denmark Tel: +45 353-27928; Fax: +45 353-27907
References
- 1.Klein JP, Rizzo JD, Zhang MJ, Keiding N. Statistical Methods for the Analysis and Presentation of the Results of Bone Marrow Transplants: Part I: Unadjusted Analysis. Bone Marrow Transplantation. 2001;28:909–915. doi: 10.1038/sj.bmt.1703260. [DOI] [PubMed] [Google Scholar]
- 2.Klein JP, Moeschberger ML. Survival Analysis: Techniques for Censored and Truncated Data. Springer; New York: 2003. [Google Scholar]
- 3.Martinussen T, Scheike TH. Regression Models for Survival Data. Springer; New York: 2006. Dynamic . [Google Scholar]
- 4.Pintilie M. Competing Risks: A Practical Perspective. John Wiley & Sons; New York: 2006. [Google Scholar]
- 5.Klein JP, Zhang MJ. Survival Analysis. Handbook of Statistics. 2007;27:281–317. [Google Scholar]
- 6.Cox DR. Regression Models and Life Tables (with Discussion) Journal of the Royal Statistical Society Series B. 1972;34:187–220. [Google Scholar]
- 7.Prentice RL, Kalbfleisch JD, Peterson AV, Flournoy N, Farewell VT, Breslow NE. The analysis of failure times in the presence of competing risks. Biometrics. 1978;34:541–554. [PubMed] [Google Scholar]
- 8.Cheng SC, Fine JP, Wei LJ. Prediction of Cumulative Incidence Function under the Proportional Hazards Model. Biometrics. 1998;54:219–228. [PubMed] [Google Scholar]
- 9.Shen Y, Cheng SC. Confidence Bands for Cumulative Incidence Curves under the Additive Risk Model. Biometrics. 1999;55:1093–1100. doi: 10.1111/j.0006-341x.1999.01093.x. [DOI] [PubMed] [Google Scholar]
- 10.Scheike TH, Zhang MJ. Extensions and Applications of the Cox-Aalen Survival Model. Biometrics. 2003;59:1036–1045. doi: 10.1111/j.0006-341x.2003.00119.x. [DOI] [PubMed] [Google Scholar]
- 11.Gray RJ. A Class of K-Sample Tests for Comparing the Cumulative Incidence of a Competing Risk. Annals of Statistics. 1988;16:1141–1154. [Google Scholar]
- 12.Pepe MS. Inference for Events with Dependent Risks in Multiple Endpoint Studies. Journal of the American Statistical Association. 1991;86:770–778. [Google Scholar]
- 13.Fine JP, Gray RJ. A Proportional Hazards Model for the Subdistribution of a Competing Risk. Journal of the American Statistical Association. 1999;94:496–509. [Google Scholar]
- 14.Sun LQ, Liu JX, Sun JG, Zhang MJ. Modelling the Subdistribution of a Competing Risk. Statistica Sinica. 2006;16(4):1367–1385. [Google Scholar]
- 15.Klein JP, Andersen PK. Regression Modeling of Competing Risks Data Based on Pseudovalues of the Cumulative Incidence Function. Biometrics. 2005;61:223–229. doi: 10.1111/j.0006-341X.2005.031209.x. [DOI] [PubMed] [Google Scholar]
- 16.Klein JP. Modelling Competing Risks in Cancer Studies. Statist in Medicine. 2006;25:1015–1034. doi: 10.1002/sim.2246. [DOI] [PubMed] [Google Scholar]
- 17.Scheike TH, Zhang MJ, Gerds TA. Predicting Cumulative Incidence Probability by Direct Binomial Regression. Biometrika. 2008:1–16. doi: 10.1093/biomet/ams096. [DOI] [Google Scholar]
- 18.Nelson W. Theory and Application of Hazard Plotting for Censored Failure Data. Technometrics. 1972;14:945–965. [Google Scholar]
- 19.Aalen OO. Nonparametric Inference for a Family of Counting Processes. Annals of Statistics. 1978;6:701–726. [Google Scholar]
- 20.Kaplan EL, Meier P. Non-parametric Estimation from Incomplete Observations. Journal of the American Statistical Association. 1958;53:457–481. [Google Scholar]
- 21.Andersen PK, Borgan Ø, Gill RD, Keiding N. Statistical Models Based on Counting Process. Springer; New York: 1993. [Google Scholar]
- 22.Lin DY. Non-parametric inference for cumulative incidence functions in competing risks studies. Statistics in Medicine. 1997;16:901–910. doi: 10.1002/(sici)1097-0258(19970430)16:8<901::aid-sim543>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 23.Sierra JP, Perez WS, Rozman WS, Carreras C, Klein JP, Rizzo JD, Davies JD, Lazarus SD, Bredeson CM, Marks DI, Canals C, Boogaerts MA, Goldman J, Champlin RE, Keating A, Weisdorf DJ, de Witte TM, Horowitz MM. Bone marrow transplantation from hla-identical siblings as treatment for myelodysplasia. Blood. 2002;100:1997–2004. [PubMed] [Google Scholar]
- 24.Rosthøj S, Andersen PK, Abildstrom SZ. SAS Macros for Estimation of the Cumulative Incidence Functions Based on a Cox Regression Model for Competing Risks Survival Data. Computer Programs and Methods in Biomedicine. 2004;74:69–75. doi: 10.1016/S0169-2607(03)00069-5. [DOI] [PubMed] [Google Scholar]
- 25.Lin DY, Ying Z. Semiparametric analysis of the additive risk model. Biometrika. 1994;81:61–71. [Google Scholar]
- 26.Aalen OO. A linear regression model for the analysis of life times. Statistics in Medicine. 1989;8:907–925. doi: 10.1002/sim.4780080803. [DOI] [PubMed] [Google Scholar]
- 27.Scheike TH, Zhang MJ. An additive-multiplicative Cox-Aalen regression model. Scandinavian Journal of Statistics. 2002;29:75–88. [Google Scholar]
- 28.Andersen PK, Klein JP, Rosthøj S. Generalized linear models for correlated pseudo-observations with applications to multi-state models. Biometrika. 2003;90:15–27. [Google Scholar]
- 29.Klein JP, Harhoff M, Andersen PK, Tarima S, Perme MP. SAS and R functions to compute pseudo-values for censored data regression. Computer Methods and Programs in Biomedicine. 2008;89:289–300. doi: 10.1016/j.cmpb.2007.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McKeage IW, Sasieni PD. A partly parametric additive risk model. Biometrika. 1994;81:501–514. [Google Scholar]
Websites
- 101.The cmprsk Package. 2008 February 16; www.cran.r-project.org/web/packages/cmprsk/cmprsk.pdf.
- 102.Scheike Thomas. Department of Biostatistics, University of Copenhagen; http://staff.pubhealth.ku.dk/-ts/timereg.html. [Google Scholar]
- 103.Biostatisitik Afdeling. www.biosiat.ku.dk/~pka.
- 104.Division of Biostatistics, Medical College of Wisconsin. www.biostat.mcw.edu.