Refining Homology Models by Combining Replica-Exchange Molecular Dynamics and Statistical Potentials

Abstract

A protocol is presented for the global refinement of homology models of proteins. It combines the advantages of temperature-based replica-exchange molecular dynamics (REMD) for conformational sampling and the use of statistical potentials for model selection. The protocol was tested using 21 models. Of these 14 were models of 10 small proteins for which high-resolution crystal structures were available, the remainder were targets of the recent CASPR exercise. It was found that REMD in combination with currently available force fields could sample near-native conformational states starting from high-quality homology models. Conformations in which the backbone RMSD of secondary structure elements (SSE-RMSD) was lower than the starting value by 0.5 to 1.0 Å were found for 15 out of the 21 cases (average 0.82 Å). Furthermore, when a simple scoring function consisting of two statistical potentials was used to rank the structures, one or more structures with SSE-RMSD of at least 0.2 Å lower than the starting value was found among the 5 best ranked structures in 11 out of the 21 cases. The average improvement in SSE-RMSD for the best models was 0.42 Å. However, none of the scoring functions tested identified the structures with the lowest SSE-RMSD as the best models although all identified the native conformation as the one with lowest energy. This suggests that while the proposed protocol proved effective for the refinement of high-quality models of small proteins scoring functions remain one of the major limiting factors in structure refinement. This and other aspects by which the methodology could be further improved are discussed.

INTRODUCTION

To understand the function of a protein at the atomic level the availability of an accurate three-dimensional model is essential. Where an experimentally determined structure is unavailable, structure prediction techniques can often provide sufficient information for many purposes. Despite the substantial progress in ab initio structure prediction,^1,2 homology modeling is still the most reliable and widely used approach to obtain high-quality structural models for a given target protein assuming that a suitable template structure can be identified by sequence similarity.^3–7 However, the extent to which current homology models can be used with confidence is unclear.⁶ This is in part due to alignment errors, but primarily due to the lack of effective methods that can be used to refine the structural models obtained.^8–10

Alignment quality has improved significantly over recent years with the introduction of the PSI-BLAST¹¹ technique and methods that combine profile-profile sequence comparisons^12–19 and structural information.^20–35 Nevertheless, problems associated with insertions, deletions and misalignments remain common especially when there is only a remote relationship between the query and the template sequence. These in turn lead to errors in the homology model, including errors in the packing of side chains, poorly defined conformations of loops, and distortions or shifts in secondary structure elements (SSEs). A number of recent studies began to address the alignment errors either by exploring alternative alignments^36–38 or by searching for reasonable conformations during the model building step.³⁹ In addition to errors stemming from the alignment procedure, there are also unavoidable errors in any homology model due to the fact that the query sequence and the template are by definition different. In principle, this means that all homology models must be refined. It appears optimal to divide the structure refinement process into two stages depending on the type of error to be addressed. First, local structural errors involving side chains, loops and SSEs are detected and removed while the overall structure of the backbone is kept fixed. Second, the protein backbone, which normally is taken directly from the template, is adjusted in an effort to improve the global fold.

Global structural refinement requires both an efficient means to sample conformational space and a means to accurately identify near-native structures.⁴⁰ While energy minimization (EM) has been used in a number of studies to optimize the initial model,^41–43 molecular dynamics (MD) simulation is the most commonly used sampling technique in refinement studies. In contrast a wide variety of different approaches have been used to attempt to select near-native conformations. For example, Lee et al⁴⁴ were able to select a near-native structure (1.8 Å Cα RMSD) from a MD-generated ensemble starting from a model of 2.8 Å RMSD with respect to the experimental structure using a MM-PBSA free energy function. Lu and Skolnick⁴⁵ used repeated cycles involving short MD simulations followed by scoring using a statistical potential to refine low-resolution ab initio models of 30 small proteins. Fan and Mark^46,47 studied the utility of extended MD simulations in water and a combination of MD together with a heuristic chaperon approach for the refinement of model structures generated using ROSETTA. Flohil et al⁴⁸ used a simple knowledge-based algorithm to select structures from a series of restrained MD simulations in an attempt to refine three homology models from CASP3. Krieger et al⁴⁹ optimized an all-atom force field that was used to refine 25 models which on average moved 0.1 Å closer to their native structures.

Despite occasional successes, the main conclusions that can be drawn from these studies are that 1) only conformations close to the initial structure are sampled using standard MD techniques (unless long time scales used) and that 2) the ability of the currently available scoring functions to distinguish near-native from compact non-native structures must be improved.⁴⁷ Most recently, Chen and Brooks⁵⁰ applied the replica-exchange molecular dynamics (REMD) technique with a generalized Born (GB) solvent model^51,52 to the refinement of 5 CASPR (the Continuous CASP Model Refinement Experiment) models. Alternative refinement procedures that do not depend on MD as the search engine have also been developed primarily in the context of ab initio structure prediction. Baker and co-workers² for example reported encouraging results for 5 of 16 small proteins using a refinement protocol in which multiple rounds of random torsion-angle perturbation and Monte Carlo (MC) relaxation were performed on low-resolution models built from a set of sequence homologues of the target protein using the standard fragment insertion approach from ROSETTA.⁵³ Another method based on fragment assembly and MC simulation is TASSER,⁵⁴ which has been applied to the refinement of NMR structures⁵⁵ and dimeric structural models.⁵⁶ Recently, these ab initio approaches have also been applied to the refinement of homology models. Misura et al⁵⁷ attempted to refine a series of homology models using a version of ROSETTA in combination with evolutionarily derived distance constraints. They found that in 22 out of 39 cases a model that is closer to the native structure than the template over the aligned regions could be found within the 10 lowest-energy models. However, this method was very computationally intensive with the refinement of one model requiring 90 CPU days. In addition to the approaches outlined above, a number of methods that employ statistical potentials or empirical scoring functions to select the near-native models from an ensemble of homology models have been developed.^{37,38,43,58,59}

In this article, we investigate the utility of a refinement protocol that combines replica-exchange molecular dynamics (REMD) as the primary sampling technique with series of different statistical potentials to select the best models. Temperature-based REMD has been shown to lead to enhanced sampling with respect to standard MD simulation techniques and has been extensively used in peptide folding simulations as well as for the refinement of NMR models.^60–64 In particular we have shown that the efficiency of temperature-based REMD results from a combination of enhanced sampling and conformational sorting among the temperature range.⁶⁵ Statistical potentials are widely used in various applications such as decoy discrimination,^66–69 model evaluation^70–74 and loop prediction.^75,76 In a previous study, we applied a recently developed statistical potential (DFIRE)⁶⁸ to the refinement of segments of proteins with considerable success.⁷⁷ The refinement protocol proposed in this study has been tested using models generated for 10 small proteins. In total 14 models were generated with duplicate models being generated for 4 of the 10 proteins. The backbone RMSD of SSEs (SSE-RMSD) for these models ranged from 1.76 to 2.73 Å. Another 7 models from the Continuous CASP Model Refinement Experiment (CASPR) were also included in the analysis. This extended the range of SSE-RMSD values to between 1.33 and 4.14 Å. Overall we find that REMD was the most effective of the range of sampling strategies investigated and that a simple combination of two statistical potentials appeared to be as accurate as two ROSETTA-based scoring functions.⁵³

MATERIALS AND METHODS

Test sets

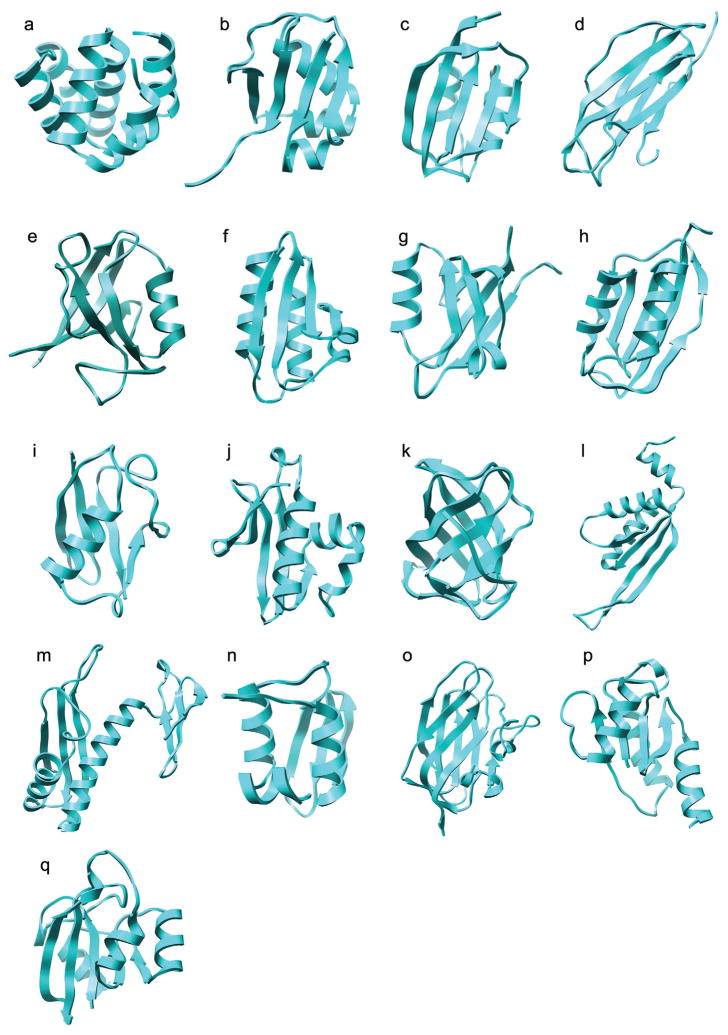
Two sets of models have been used to test the refinement protocol. The first set was specifically generated for this study in order to effectively test the refinement protocol. For these models it was required that a high-resolution crystal structure be available for the target structure, that a suitable template structure be available, that the proteins be of manageable size, and that the native structure is stable in the force field used. In order to generate these models the following five-step procedure was used. First, 68 proteins were selected from a database of 974 high-resolution (< 1.60 Å) crystal structures.⁷⁷ Proteins were selected if they had between 70 and 100 residues and there were no gaps or missing atoms in the structures. Second, a list of templates was identified for each protein and sequence alignments generated using HMAP,³² a fold-recognition method that combines sequence and secondary structure profiles. Third, a structural model was built for each template using Nest,⁷⁸ a model building program that combines rigid-body assembly and torsion-space optimization. Fourth, the models were compared to the corresponding experimental structures and only models for which the SSE-RMSD was in the range 1.0 to 3.0 Å were retained. After this stage only models for 17 proteins of the original 68 remained. Finally, a 5 ns MD simulation at 300K starting from the experimentally determined (native) structure was performed for each of these 17 proteins. The GROMACS package^79–81 was used to perform the MD simulations and the protocol is described in detail below in the section on “Conformational sampling”. Only models for those proteins for which the secondary structure elements were very stable in the simulations (SSE-RMSD < 1.5 Å) were retained (see Table I). For these 10 proteins the SSE-RMSD of the models ranged from 1.5 to 3.0 Å with respect to the native structure. For most proteins only one model was obtained, however, for four proteins 1cy5, 1mfg, 1r6j and 1wm3 two models were obtained giving 14 models in total. The second set of models against which the protocol was tested consisted of 7 CASPR targets obtained from http://predictioncenter.org/caspR. These proteins range in size from 70 to 138 residues. The coordinates for side chains not present in the crystal structures of the CASPR targets were generated using SCAP⁸² and gaps in the structure modelled using LOOPY.⁸³ Together, the two sets provided a total of 21 models for 17 proteins (Table I). As can be seen from Figure 1 these proteins have different topologies, secondary structure compositions and shapes. Only one protein, 1k5n, contained any disulfide bonds. In this case, the disulfide bond in the crystal structure was satisfied in the predicted model.

Table I.

Properties of the 17 Proteins Used to Test the Global Refinement Protocol

PDB	Cl	Description	Exp.	Resol.	Nres	SCOP	Ncharge
a. Small, globular protein data set
1cy5a	A	Apaf-1 caspase recruitment domain	X-ray	1.30	92	All α	−3
1fm0	D	Molybdopterin synthase subunit MoaD	X-ray	1.45	81	α + β	−7
1gxu	A	Hydrogenase maturation factor Hypf acylphosphatase-like domain	X-ray	1.27	88	α + β	−2
1k5n	B	beta-2-microglobulin, light chain	X-ray	1.09	100	All β	−1
1mfga	A	Erb-B2 interacting protein	X-ray	1.25	95	All β	−1
1opd	A	Histidine-containing protein	X-ray	1.50	85	α + β	−2
1r6ja	A	PDZ2 domain of syntenin	X-ray	0.73	82	All β	0
1urr	A	Drosophila melanogaster acylphosphatase	X-ray	1.50	97	α + β	6
1wm3a	A	Human SUMO-2 protein	X-ray	1.20	72	α + β	−1
1xmt	A	Putative acetyltransferase	X-ray	1.15	95	α + β	1
b. CASPR data set
1xe1	A	Hypothetical protein from Pyrococcus furiosus	X-ray	2.00	91	All β	3
1vm0	A	Hypothetical protein from Arabidopsis thaliana	X-ray	1.80	103	α + β	3
1vla	A	Hydroperoxide resistance protein OsmC	X-ray	1.80	138	α + β	0
1whz	A	Hypothetical protein from Thermus Thermophilus	X-ray	1.52	70	α + β	4
1tvg	A	Human PP25 gene product, HSPC034	X-ray	1.60	137	All β	−13
1xg8	A	Hypothetical protein from Staphylococcus aureus	X-ray	2.10	102	α/β	−7
1o13	A	Hypothetical NifB protein in FeMo-Co biosynthesis	X-ray	1.83	107	α/β	0

The items listed include the PDB entry name, chain identifier, description of the biological function and source of the protein, structure determination method, resolution in Å, total number of residues, SCOP secondary structure class and net charge at a pH of 7.0. For the CASPR target proteins, gaps in the crystal structure were completed using LOOPY and the coordinates of missing side chains generated using SCAP. The leader sequence was removed and selenomethionine (MSB) was changed to methionine (MET).

^aFor these proteins multiple starting models were tested in the refinement (see Table II).

Figure 1.

A cartoon representation of the crystal structures of the 17 proteins used to test the global refinement protocol. PDB entry names 1a. 1cy5; 1b. 1fm0; 1c. 1gxu; 1d. 1k5n; 1e. 1mfg; 1f. 1opd; 1g. 1r6j; 1h. 1urr; 1i. 1wm3; 1j. 1xmt; 1k. 1xe1; 1l. 1vm0; 1m. 1vla; 1n. 1whz; 1o. 1tvg; 1p. 1xg8; and 1q. 1o13.

Refinement Protocol

The refinement protocol consisted of three phases: 1) the identification and correction of local structural errors, 2) the sampling of conformational space around the original model using REMD (or other MD procedures), and 3) the selection of native-like structures using a variety of statistical potentials and scoring functions.

Local structural evaluation and correction

The purpose of this step was to identify and correct local structural errors that occurred in side chains, loops and SSEs. First, the local quality of the model was assessed using two statistical potentials and an empirical energy function each of which provide a normalized quality score per residue. These were the DFIRE potential,⁶⁸ an inverse Born radius (IBR)-based environmental potential (Zhu and Honig, in preparation) and a tabulated soft-core van der Waals potential.⁸⁴ The per-residue quality score was plotted against residue number and structural details were inspected visually for residues with scores above 2.0. Side chains, loops and segments deemed to be problematic were remodelled without reference to the native structure. Side chains were repacked using SCAP,⁸² loops remodelled using LOOPY⁸³ and alternative SSE conformations were generated using SegSam.⁷⁷ The local quality of the resulting structures was then revaluated to ensure an improvement in the quality of the model. Finally, the entire model structure was energy minimized (EM) using minimize.x within the TINKER package.⁸⁵ For this minimization an all-atom OPLS force field was used together with an implicit solvation model that combines mAGB model^86,87 and a surface term.⁸⁸

Conformational sampling

After local refinement, the 21 models were simulated using REMD in explicit water using a modified version of the GROMACS package.^79–81 In the REMD scheme,⁶¹ a number of independent simulations (replicas) are performed simultaneously at temperatures ranging from T₁ to T_M, where M is the number of replicas. At regular intervals, the temperatures of neighbouring replicas i and j are exchanged according to the following Metropolis criterion:

$$\text{acc}(\text{i}\to \text{j})=min(1,exp\{({\beta }_i-{\beta }_j)(E_i-E_j)\})$$ (1)

where β is the reciprocal temperature, 1/k_BT, with k_B the Boltzmann constant T, the temperature (K) and E is the potential energy of the system. By allowing replicas to explore a range of temperature space, REMD enables the system to cross energy barriers and access regions of conformational space that would be rarely sampled at standard temperatures.

The GROMOS96 43a1 force field^89,90 was used in all simulations. The protonation state of the ionizable amino acids was set appropriate for pH 7.0 assuming standard pK_as. No counter-ions were added to neutralize the system. Each model was solvated in a rhombic dodecahedron box using the SPC water model.⁹¹ The minimum distance between the solute and the wall of the unit cell was 10 Å. A twin-range method was used to calculate the non-bonded interactions. Interactions within the short-range cutoff of 9 Å were updated every step while interactions within the long-range cutoff (14 Å) were updated every 5 steps together with the pairlist. A reaction field correction⁹² was applied to the electrostatic interactions beyond 14 Å, using a dielectric constant for water of 78. Covalent bonds in the proteins were constrained using the LINCS algorithm⁹³ and the geometry of the water molecules was constrained using the SETTLE algorithm.⁹⁴ A time step of 2 fs was used. The protein-water system was first minimized using the steepest descent method and then equilibrated by performing a 100 ps MD simulation with positional restraints on the heavy atoms of the protein. The restrained MD simulations were performed at a constant temperature of 300 K and a constant pressure of 1 bar by coupling to an external heat and an isotropic pressure bath.⁹⁵ In the REMD simulations, the target temperatures for the replicas were determined between 280 and 320 K, using the method proposed by Garcia and Sanbonmatsu.⁶² For each protein model, the solvated system was equilibrated at five temperatures, T = 275, 287, 300, 312 and 325 K. The averaged energies E from the five simulations were fitted by a polynomial of T. Finally eq. 1 was solved iteratively between 280 and 320 K using P(exchange) ≈ 0.20. The 21 protein models with different numbers of replicas (Table III) were subjected to 5 ns REMD at constant (N, V, T) with exchanges attempted every 1 ps. Snapshots were stored every 2.5 ps, which led to a total of 2000 conformations per replica (temperature). The conformations corresponding to the 5 lowest temperatures (e.g. for 1fm0 T = 276.4, 279.5, 282.6, 285.7, 288.9; for 1vm0 T = 276.4, 278.0, 279.5, 281.1, 282.7) were subjected to further analysis.

Table III.

RMSD analysis of structures sampled by REMD simulation.^a

Models	No. Repli.	RMSDinit	RMSDminb	RMSDmax	RMSDave±std	Perc. (%)
a. Small, globular protein data set
1cy5_1	16	2.77	1.77	7.40	3.33 ± 0.97	34.1
1cy5_2	14	1.90	1.31	5.84	2.14 ± 0.33	17.7
1fm0	14	2.23	1.12	3.32	2.09 ± 0.38	63.8
1gxu	16	1.81	1.09	3.19	1.96 ± 0.32	28.9
1k5n	20	2.05	1.69	2.66	2.15 ± 0.15	29.7
1mfg_1	16	2.41	2.19	3.67	2.93 ± 0.25	3.0
1mfg_2	16	1.73	1.16	4.04	2.09 ± 0.48	20.6
1opd	16	3.22	2.32	5.32	3.43 ± 0.53	39.3
1r6j_1	14	2.15	1.07	4.51	2.68 ± 0.78	33.3
1r6j_2	14	1.77	1.32	3.40	2.17 ± 0.33	12.3
1urr	18	2.01	0.96	3.99	2.61 ± 0.69	21.0
1wm3_1	14	2.38	1.85	3.61	2.52 ± 0.22	24.6
1wm3_2	14	1.63	1.05	3.90	2.33 ± 0.48	7.5
1xmt	20	2.69	1.94	4.16	2.98 ± 0.38	22.1
b. CASPR data set
1xe1	16	1.26	0.94	3.04	1.56 ± 0.27	13.7
1vm0	26	3.00	2.50	9.20	4.03 ± 1.01	9.5
1vla	18	2.26	2.20	7.21	4.01 ± 0.82	0.0
1whz	16	1.69	0.75	3.82	1.98 ± 0.72	41.8
1tvg	20	4.29	3.15	6.27	4.48 ± 0.58	33.0
1xg8	18	4.68	3.88	8.65	6.03 ± 0.91	6.8
1o13	18	1.90	1.51	3.49	2.48 ± 0.38	5.3

The items listed include the model name, number of replicas used in REMD simulations, initial RMSD in the REMD simulation, minimum and maximum RMSD that can be found in the REMD simulation, average RMSD (and standard deviation), and the percentage of conformations that have lower RMSD than the starting structure.

^aRMSD here denotes the SSE-RMSD, the backbone RMSD of secondary structure elements. Only conformations sampled in the 5 REMD simulations with the lowest temperatures were used in the calculation of items listed in columns 3 to 6.

^bThe RMSD values that are at least 0.5 Å lower than the initial values are in bold.

Two additional sampling protocols based on conventional MD were also tested in addition to the REMD approach and served as controls. The first was a single long simulation 50 ns in length. The second was a series of short independent simulations (10×5 ns). The control simulations were performed at 300K using the same parameter settings as those used in the REMD simulations. Different initial velocities were, however, generated for each simulation.

Model selection using statistical potentials

The main scoring function used for model selection, RAPDF/HB, was a combination of two statistical potentials: a modified version of the RAPDF potential that uses the conditional probability reference state proposed by Samudrala et al⁶⁶ together with the distance binning procedure of DFIRE by Zhou et al,⁶⁸ and a modified version of the orientation-dependent hydrogen bonding potential of Kortemme et al.⁹⁶ Both RAPDF and DFIRE are atom-based, distance-dependent pairwise potentials that can be used to evaluate atom-atom interactions within a given protein structure. In our implementation of the hydrogen bonding potential, 13 hydrogen bonding patterns were explicitly defined according to the secondary structure type and location (backbone or side chain) of the donor and acceptor. A potential-of-mean-force (PMF) table was then derived for each of these patterns based on the statistics of a database of high-resolution crystal structures. Note, these statistical potentials do not distinguish between cysteines that are protonated and those that form disulfide bonds. The physical energy functions used in this study do distinguish between these two cases. The contributions of the two scores were combined using a scaling factor of 1.0 for the RAPDF score and a factor of 5.0 for the hydrogen bonding score. These weight factors were chosen so that the two terms made a comparable contribution to the final score. They were not optimized to give the best performance on this dataset.

Two alternative scoring functions were taken from the ROSETTA package and tested for comparison (http://depts.washington.edu/ventures/UW_Technology/Express_Licenses/Rosetta). The all-atom form of the ROSETTA scoring function⁵³ contains seven terms, including rama (Ramachandran torsion preferences), LJ (Lennard-Jones interactions), hb (hydrogen bonding), solv (solvation), pair (residue pair interactions such as electrostatics and disulfides), dun (rotamer self-energy) and ref (unfolded state reference energy). One of the functions tested was the default ROSETTA score containing all the energy terms as described by Kuhlman et al. (ROSETTA_soft).⁹⁷ In this function, the softened Lennard-Jones (LJ) potential option was used to compensate for the differences between the atom radii used in the MD simulations (GROMOS96 43a1) and those used in ROSETTA (CHARMM22⁹⁸). As an alternative, a subscore of the ROSETTA scoring function (“bk_tot” in the ROSETTA output) was used to evaluate the models (ROSETTA_sub). This function contains the same energy terms as in ROSETTA_soft except for the rama and ref terms. In addition, the normal as opposed to the softened LJ potential was used. The standard weighting factors were used for all terms in this function.

In the model selection, only conformations present in the 5 lowest temperatures (starting from ~280 K) of the REMD simulation were subjected to the model selection by the RAPDF/HB, ROSETTA_soft and ROSETTA_sub scores. The SSE-RMSD was used to evaluate the relative effectiveness of the three scores in selecting the most appropriate models. Note that the secondary structure elements were as defined as in the corresponding crystal structure.

RESULTS

Local structural evaluation and correction

In Table II the SSE-RMSD values and the percentage of problematic residues before and after local structure correction are listed. In general, local structure correction did not have a major effect on the SSE-RMSD (± 0.1 Å) but significantly reduced the percentage of residues with a quality score greater than 2.0. In cases where a high percentage of residues (> 30%) were problematic such as for 1opd, 1xmt, 1tvg and 1xg8, the SSE-RMSD of the model did increase after local structure correction and energy minimization. This reflects the low quality of the models and the difficulty of performing manual adjustments in such cases. For the models of 1gxu and 1whz, which had ~30% problematic residues, the SSE-RMSD was improved after model correction and minimization. These two models also show marked improvement after conformational sampling using REMD and model selection. In most cases the secondary structure elements were held fixed during the process of local structural correction. However, for the models 1opd and 1xg8, in which 61.18% and 83.33% of the residues were considered problematic, respectively, SegSam⁷⁷ was used to generate alternative conformations for those secondary structure elements that contained a high percentage of residues with quality scores > 2.0. Conformations with improved quality scores were selected but, as indicated by the SSE-RMSD values in Table II, such adjustments resulted in a deterioration of the model in a global sense.

Table II.

Structural properties of the 21 models used to test the global refinement protocol and the corresponding modeling information.

Model	Template	Exp.	Seq. ID	RMSD0a	Perc0b	PercSSE0c	Local refinementd	RMSD1a	Perc1b
a. Small, globular protein data set
1cy5_1	1c15	NMR	100	2.73	2.2	1.1	EM	2.77	0.0
1cy5_2	3ygs	X-ray	20	1.89	8.6	6.5	L, SC, EM	1.90	1.1
1fm0	1v8c	X-ray	26	2.19	29.6	18.5	L, SC, EM	2.23	3.7
1gxu	1ulr	X-ray	37	2.11	30.7	21.6	L, SC, EM	1.81	6.8
1k5n	1je6	X-ray	16	2.11	13.0	3.0	L, SC, EM	2.05	1.0
1mfg_1	1qav	X-ray	28	2.44	13.7	0.0	L, SC, EM	2.41	2.1
1mfg_2	1qlc	NMR	36	1.77	35.8	5.3	L, SC, EM	1.73	2.1
1opd	1k1c	NMR	42	2.57	61.2	43.5	L, SC, SG, EM	3.22	3.5
1r6j_1	1ry4	NMR	28	2.15	7.3	2.4	SC, EM	2.15	1.2
1r6j_2	1d5g	NMR	17	1.76	17.1	7.3	EM	1.77	1.2
1urr	1y9o	NMR	29	2.00	15.5	8.2	SC, EM	2.01	1.0
1wm3_1	1c3t	NMR	16	2.55	6.9	5.6	L, SC, EM	2.38	0.0
1wm3_2	1l7y	NMR	13	1.79	18.1	9.7	EM	1.63	0.0
1xmt	1r57	NMR	26	2.40	31.6	23.2	L, SC, EM	2.69	4.2
b. CASPR data set
1xe1	–	–	–	1.33	11.0	7.7	EM	1.26	5.5
1vm0	1h0x	X-ray	–	3.05	13.6	8.7	SC, EM	3.00	0.0
1vla	1ml8	X-ray	–	2.25	3.6	1.4	EM	2.26	5.8
1whz	–	–	–	1.75	31.4	10.0	SC, EM	1.69	2.9
1tvge	1jhj, 1eut, 1czs, 1kex, 1k12	X-ray	–	4.14	33.6	21.9	SC, EM	4.29	7.3
1xg8e	1h75, 1b4q, 1ego, 1eej	X-ray NMR	–	3.03	83.3	55.9	L, SC, SG, EM	4.68	10.8
1o13	1eo1	NMR	–	1.84	18.7	8.4	SC, EM	1.90	1.9

The items listed include the model name, PDB entry name of template(s), structure determination method for the template(s), sequence identity, SSE-RMSD and percentage of problematic residues before the local refinement, percentage of problematic SSE residues before the local refinement, modeling operations taken in the local refinement, SSE-RMSD and percentage of problematic residues after the local refinement and energy minimization. ‘–’ denotes that no information is available.

^aRMSD denotes SSE-RMSD, the backbone RMSD of the secondary structure elements.

^bPerc is the percentage of problematic residues with a score higher than 2.0 from any of the three scoring functions.

^cPerc_SSE0 is the percentage of problematic residues within SSEs with a score higher than 2.0 before the local refinement.

^dThe modeling operations include L, loop prediction; SC, side chain prediction; SG, generation of alternative conformations for the structural segments containing secondary structure elements. EM, energy minimization of the entire model structure.

^eFor these two CASPR targets the model was built using fragments of multiple templates.

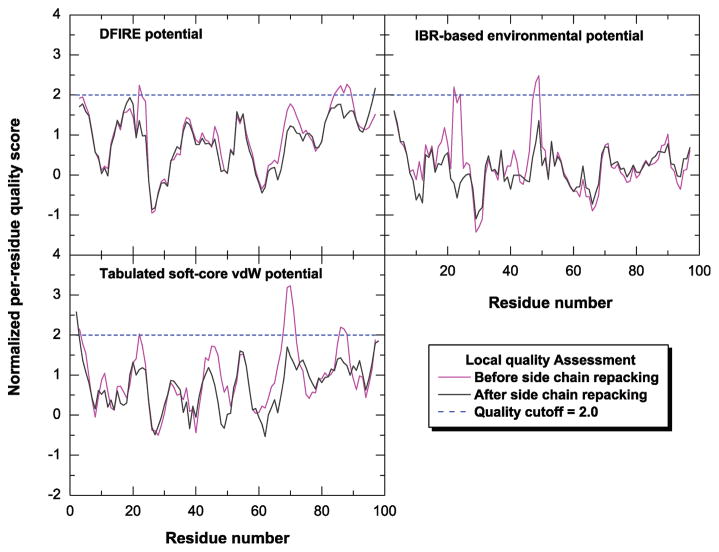
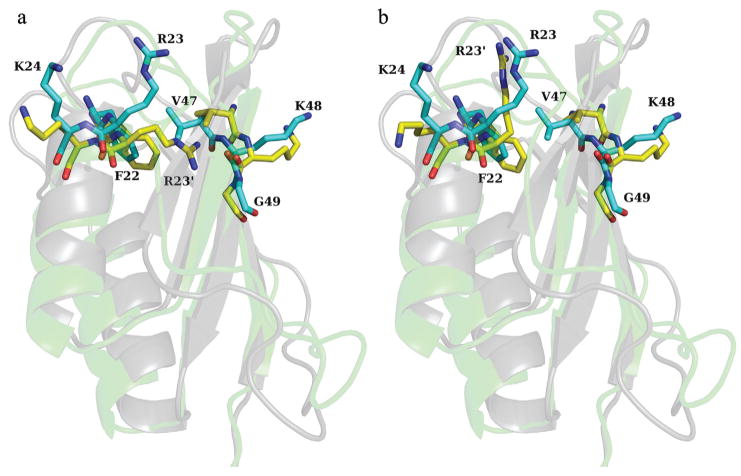
To illustrate how the local structural errors were identified and corrected the potential scores for the model of 1urr are plotted in Figure 2 before and after local structure correction. Two spatially related regions, residues 22 to 24 and residues 47 to 49, were considered problematic. As can be seen in Figure 3a residue R23 (charged) is buried within the protein in contact with two hydrophobic residues, F22 and V47. After repacking (Figure 2b), R23′ is exposed to water and is roughly in the same position and orientation as in the native conformation. In addition, there is a small rotation of the benzene ring of F22 resulting in the orientation of both F22 and V47 becoming more native-like. Another region, residues 67 to 70 is marked by high van der Waals scores but not recognized by the other two potentials, suggesting a simple violation in local geometry. Therefore, no reconstruction but only the minimization was performed which resulted in a large improvement in the van der Waals scores.

Figure 2.

The per-residue local quality score of the model for protein 1urr (PDB entry name) is plotted as a function of residue number. Three normalized, residue-based scoring functions are used in the local quality assessment including the DFIRE potential, inverse Born radius (IBR)-based environmental potential and tabulated soft-core van der Waals potential. The local quality scores before and after side chain repacking are shown in magenta and black, respectively. The dotted line in blue denotes the cutoff used for the local quality score, a value of 2.0.

Figure 3.

The superposition of the native structure for protein 1urr (PDB entry name) and the model structure before and after side chain repacking is shown in 2a and 2b, respectively. The residues 22 to 24 and 47 to 49 are represented as a stick model, while the protein body is represented as a cartoon model in shadow. In the stick model the carbon atoms of native structure are in yellow while the carbon atoms of model structure are in cyan. In the cartoon model the native structure is in gray while the model structure is in green. The residue name and residue number are only labeled for those of native structure except for R23, for which the corresponding residue in the model structure is labeled as R23′.

Conformational sampling with REMD

The main criterion used to evaluate the sampling efficiency was the SSE-RMSD with respect to the native structure (see Table III). For 15 out of the 21 cases investigated the lowest SSE-RMSD (RMSD_min) was more than 0.5 Å lower than that of the starting structure (RMSD_init). On average the improvement of SSE-RMSD was 0.82 Å. This suggests that REMD is an effective method to obtain near-native conformations. Conformations that were more than 0.2 Å closer to the native structure than the starting structure were found for all models except 1vla. The structure 1vla corresponds to the hydroperoxide resistance protein OsmC. OsmC is a domain-swapped dimer in which the two monomers are arranged head-to-head.^99–101 In the absence of the second monomer there is a significant change in the orientation of the N-terminal domain with respect to the large C-terminal domain.

The range of SSE-RMSD values observed as indicated by the difference between the values of RMSD_min and RMSD_max shows that a wide variety of conformational states were sampled in the REMD simulations. The percentage of conformations closer to the native state than the initial model varied greatly between the different models. In one case (1fm0) the majority of the conformations sampled (~64%) were closer to the native structure than the starting structure. However, on average only 22.3% of the conformations sampled had SSE-RMSD values lower than that of the starting structure. For 5 of the 21 cases less than 10% of the conformations sampled were closer to the native state than the original model.

Factors affecting REMD sampling

The model of 1mfg-1 was used to illustrate possible effects of the simulation protocol on the sampling efficiency. This model was selected because of its poor enrichment in lower SSE-RMSD conformations (3.0%). Three REMD protocols were tested. First, to determine the reproducibility of the results the simulations were rerun with different initial random atomic velocities. The temperature series were the same as in the original REMD simulation. In the second and third protocols, four additional replicas were used to either extend the range of temperature or reduce the temperature gap between replicas. The temperature series for these two protocols were derived using the same rules as for the standard protocol. The lowest SSE-RMSD found using the three protocols were 2.13, 2.16 and 2.03 Å, while the enrichment of lower SSE-RMSD conformations was 4.4, 7.1 and 8.0% respectively. The increase in the number of replicas appears to have had the greatest effect on sampling.

To illustrate possible effects of the initial conformation and the secondary structure composition of the protein on the extent of sampling in a REMD simulation, a series of simulations were performed starting from the native structures of three proteins, 1cy5, 1urr and 1k5n, using the same protocol that was used during the refinement of models. The three proteins simulated have distinct secondary structure compositions. As can be seen from Table I and Figure 1, 1cy5 is an all α protein, 1urr is an α+β protein and 1k5n is an all β protein. In addition, 1k5n has a disulfide bond that holds the two planar β-sheets tightly against each other. The mean SSE-RMSD values were 1.47, 0.94 and 0.84 Å, and the standard deviation of SSE-RMSD value was 0.69, 0.24 and 0.14 Å for 1cy5, 1urr and 1k5n, respectively. For 1cy5 and 1urr the range of conformations sampled is much smaller when starting from the native conformation than when starting from the model (see Table III). In the case of 1k5n, the sampling is clearly affected by the disulfide bond in both the native structure and the model. The effect of the secondary structure composition, if any, was small. The results suggest that on the time scale investigated the conformations sampled using REMD are largely determined by the initial conformation of the system.

Comparison of REMD and other MD-based protocols

The efficiency of two other MD sampling protocols was also investigated. The sampling protocols consisted of either a single long simulation or multiple short simulations. Table IV compares the results obtained using these approaches to those obtained using REMD with respect to two measures – the lowest SSE-RMSD and the enrichment of conformations with SSE-RMSD values lower than that of the original model. In the case of the single 50 ns simulation, the results were poor. Less than 2% of the conformations sampled had lower SSE-RMSD values than the initial model. Only in five cases 1gxu, 1mfg_2, 1r6j_2, 1wm3_2 and 1whz were a significant number of conformations with SSE-RMSD values lower than the original model sampled. Interestingly, in all of these five cases the starting SSE-RMSD was below 2.0 Å. Performing multiple short MD simulations was significantly better than a single long trajectory. In 14 of the 21 cases, the lowest SSE-RMSD found in the multiple simulations was more than 0.5 Å lower than the starting value and on average 17.1% of conformations sampled had a SSE-RMSD less than the starting model. A two-way analysis of variance (ANOVA) was used to examine if the differences in the results obtained using multiple MD and REMD were statistically significant. It was found that in terms of the lowest SSE-RMSD sampled the difference was not statistically significant (P=0.65). However, in terms of the enrichment, the probability of the results coming from the same distribution was only 5.0% (P=0.05) suggesting that REMD was still a more effective approach.

Table IV.

Comparison of three MD-based sampling protocols.^a

	REMD		50 ns MD		10×5 ns MD
Models	RMSDminb	Perc. (%)	RMSDminb	Perc. (%)	RMSDminb	Perc. (%)
a. Small, globular protein data set
1cy5_1	1.77	34.1	2.59	0.0	1.66	23.6
1cy5_2	1.31	17.7	1.90	0.0	1.60	3.8
1fm0	1.12	63.8	1.87	0.3	1.26	43.9
1gxu	1.09	28.9	1.10	49.6	1.14	26.2
1k5n	1.69	29.7	1.85	1.9	1.58	41.6
1mfg_1	2.19	3.0	2.29	0.1	2.15	2.0
1mfg_2	1.16	20.6	0.87	93.4	0.95	37.7
1opd	2.32	39.3	2.91	1.9	2.61	12.0
1r6j_1	1.07	33.3	2.15	0.0	1.48	11.5
1r6j_2	1.32	12.3	1.23	70.9	1.03	21.7
1urr	0.96	21.0	1.91	0.0	1.18	8.8
1wm3_1	1.85	24.6	2.00	18.0	1.47	20.8
1wm3_2	1.05	7.5	1.22	1.1	1.00	10.7
1xmt	1.94	22.1	2.48	0.0	1.87	9.9
b. CASPR data set
1xe1	0.94	13.7	1.05	0.7	0.96	11.8
1vm0	2.50	9.5	2.70	0.4	2.64	2.19
1vla	2.20	0.0	2.26	0.0	2.25	0.0
1whz	0.75	41.8	1.16	17.3	0.65	24.8
1tvg	3.15	33.0	3.83	1.5	3.38	21.1
1xg8	3.88	6.8	4.60	0.0	3.87	10.6
1o13	1.51	5.3	1.80	0.0	1.42	11.8

The items listed include the model name, minimum RMSD that can be found in the simulation and the percentage of conformations that have lower RMSD than the starting structure for three MD-based sampling protocols, which are REMD, a single 50ns MD simulation and ten 5ns MD simulations with different initial atomic velocities.

^aRMSD here denotes SSE-RMSD as in Table III. For the REMD protocol, only conformations sampled in the 5 REMD simulations with the lowest temperatures were used in the calculation of items listed in columns 2 and 3. For the other two MD-based protocols, all conformations sampled in the simulation(s) were used in the calculation of items listed in columns 4 to 7.

^bThe RMSD values that are at least 0.5 Å lower than the initial values are in bold.

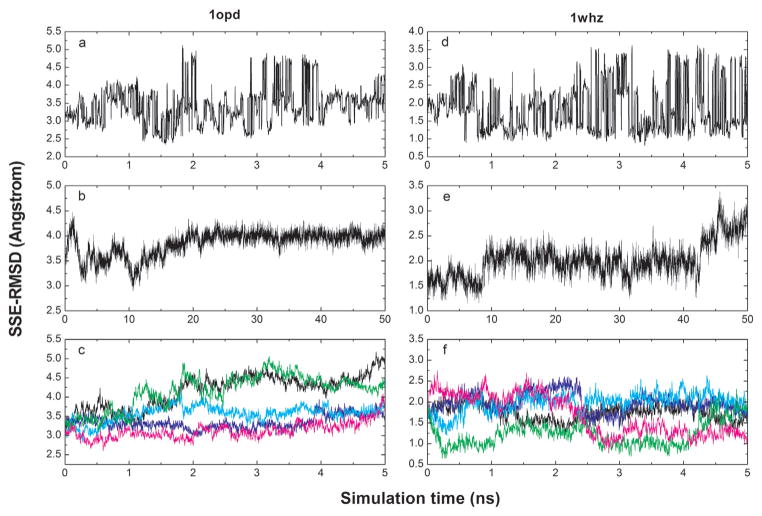
In Figure 4 the SSE-RMSD is plotted as a function of the simulation time for three MD-based sampling protocols. 1opd and 1whz were selected as illustrative examples because they differ markedly in the quality of the initial models. 1opd has relatively low quality with a SSE-RMSD value of 3.22 Å while 1whz is a near-native model with a SSE-RMSD of 1.69 Å. As can be seen from Figure 4, the three protocols exhibit very distinct patterns. The apparent discontinuities in the RMSD in the REMD trajectory (lowest temperature) correspond to exchanges of the replica (conformation) with the one present at the next higher temperature. In the case of 1opd, low-RMSD conformations (<2.5 Å) are only sampled between 1 and 2 ns. In the case of 1whz near-native conformations are sampled throughout the simulation. In addition to the frequent exchange of conformations, a slow increase of SSE-RMSD was observed for 1mfg_1, 1wm3_2, 1vla and 1xg8, for which the percentage of lower-RMSD conformations is below 10% (results not shown). In the single long MD simulation, conformations tended to drift away from sampling near-native states after a few to tens of nanoseconds. This was observed for all models except 1mfg_2. In this case the SSE-RMSD decreased significantly from 1.75 to 0.87 Å during the last 10 ns simulation. Using multiple short MD simulations the range of SSE-RMSD values explored was comparable to the REMD simulations. However, an ANOVA analysis suggested that statistically REMD was still better than multiple short MD simulations with respect to the enrichment in lower-RMSD conformations.

Figure 4.

A plot of the SSE-RMSD as a function of simulation time for the three MD-based sampling protocols and two models, 1opd and 1whz. The REMD trajectory at the lowest temperature is plotted in 4a and 4d, respectively. The single 50ns MD trajectory is plotted in 4b and 4e, respectively. The first five of the ten 5 ns MD trajectories are plotted in 4c and 4f, respectively.

Selection of the best models

Table V shows the SSE-RMSD of “the best model” ranked by different scoring functions. The best model was selected using the following procedure: First, the best scoring model in each of the 5 lowest-temperature REMD trajectories was determined. Then taking these five models the one with the lowest SSE-RMSD was selected as the best model. Using the combination of two statistical potentials (RAPDF/HB) 11 models were selected with a SSE-RMSD of at least 0.2 Å lower than the starting value. In addition less improvement (< 0.2 Å) was observed in 6 models. Using the ROSETTA_soft score, 7 models were selected with SSE-RMSD decreased by more than 0.2 Å and 6 models with less decrease of SSE-RMSD. ROSETTA_sub score yielded better results than ROSETTA_soft: 9 models were improved by at least 0.2 Å and 7 models by less than 0.2 Å. On average, the improvement of the SSE-RMSD with respect to the starting value was 0.21, 0.05 and 0.24 Å for RAPDF/HB, ROSETTA_soft and ROSETTA_sub, respectively. A two-way ANOVA test shows that the results from the three scores do not differ significantly (P=0.12). This suggests that a simple combination of two statistical potentials is as effective as the ROSETTA energy function in terms of model selection.

Table V.

RMSD of models selected by different scoring functions.^a

Models	RMSDinit	RMSDmin	RAPDF/HBb	ROSETTA_softb	ROSETTA_subb	RAPDF/HBEMc
a. Small, globular protein data set
1cy5_1	2.77	1.77	2.34 (5)	2.29	2.14	2.17
1cy5_2	1.90	1.31	1.51 (4)	1.39	1.64	1.44
1fm0	2.23	1.12	1.33 (5)	1.46	1.35	1.25
1gxu	1.81	1.09	1.31 (2)	1.59	1.45	1.29
1k5n	2.05	1.69	2.00 (1)	2.29	2.06	1.82
1mfg_1	2.41	2.19	2.90 (0)	2.67	2.31	2.53
1mfg_2	1.73	1.16	1.21 (5)	1.61	1.53	1.42
1opd	3.22	2.32	2.61 (2)	2.90	3.41	3.27
1r6j_1	2.15	1.07	1.83 (2)	2.08	1.24	1.33
1r6j_2	1.77	1.32	2.13 (0)	1.79	1.62	1.81
1urr	2.01	0.96	1.59 (1)	2.35	1.03	1.55
1wm3_1	2.38	1.85	2.20 (3)	2.26	2.26	2.30
1wm3_2	1.63	1.05	1.35 (1)	1.73	1.71	2.15
1xmt	2.69	1.94	3.20 (0)	3.18	2.52	2.91
b. CASPR data set
1xe1	1.26	0.94	1.05 (2)	1.17	1.17	0.87
1vm0	3.00	2.50	2.98 (1)	3.00	2.64	2.84
1vla	2.26	2.20	2.26 (0)	2.26	2.29	2.35
1whz	1.69	0.75	0.91 (5)	1.00	1.00	0.79
1tvg	4.29	3.15	4.38 (0)	3.48	4.21	4.09
1xg8	4.68	3.88	4.50 (2)	5.36	5.36	4.97
1o13	1.90	1.51	1.78 (2)	2.96	1.88	2.14

The items listed include the model name, initial RMSD in the REMD simulation, minimum RMSD can be found in the REMD simulation, RMSD of the best model ranked by RAPDF/HB score, two ROSETTA scores and RAPDF/HB score after energy minimization.

^aRMSD here denotes SSE-RMSD as in Table III. The RMSD values that are at least 0.2 Å lower than the initial values are in bold.

^bFor these three scoring functions, the best model was selected using the following procedure. First, the best scoring model in each of the 5 REMD trajectories at the lowest temperatures was determined by a given scoring function. Then taking these five models the one with the lowest SSE-RMSD was selected as the best model. Note that for the RAPDF/HB scoring function the number of models with lower SSE-RMSD than the initial values is listed in parentheses.

^cIn the RAPDF/HB_EM scoring scheme, the 100 top-scoring structures ranked by the RAPDF/HB function in each of 5 replica simulations used (a total of 500 structures) were subjected to energy minimization. The RAPDF/HB scores were then calculated for the minimized structures. The SSE-RMSD of the best model selected by the same procedure as described above is listed in the last column.

Based on the initial ranking generated using the RAPDF/HB function, the 100 top-scoring REMD snapshots for each of five replicas used (500 structures in total) were selected and subjected to the 1000 steps of energy minimization using L-BFGS truncated-Newton optimization algorithm in conjunction with the OPLS all-atom force field and mAGB/SA solvation model.^86,87 The minimized structures were re-ranked by the RAPDF/HB function. The SSE-RMSD of the best model selected by the same procedure as described above is listed for each model in Table V. Using the RAPDF/HB score in the final selection, the SSE-RMSD was improved for 14 models with respect to that before the minimization. However, the number of models that have at least 0.2 Å SSE-RMSD improvement remained the same, 11, after the minimization.

Correlation between scoring functions and SSE-RMSD

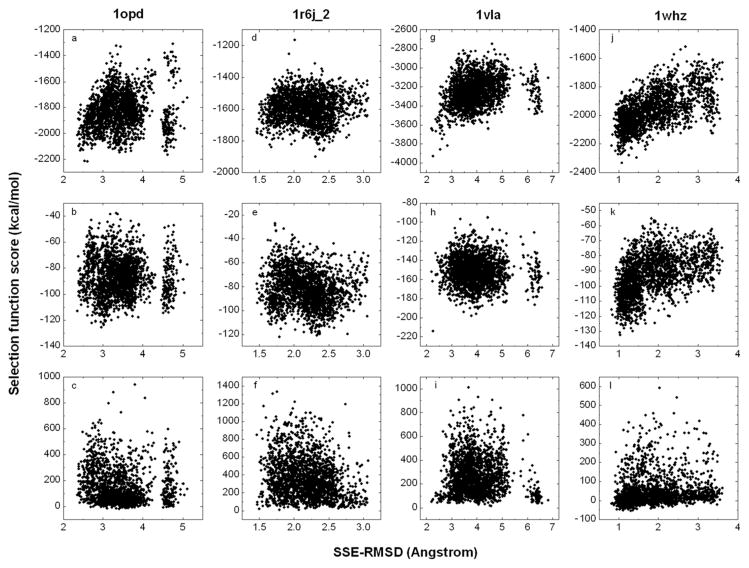
Figure 5 shows the RAPDF/HB, ROSETTA_soft and ROSETTA_sub scores plotted against the SSE-RMSD for the conformations taken from the REMD simulation at the lowest temperature investigated. Four models are presented to illustrate the types of correlation observed. Although the different scoring functions appear similarly effective for model selection, RAPDF/HB shows a better correlation with SSE-RMSD than do the two ROSETTA functions. Furthermore, the correlation shown by ROSETTA_soft appears better than ROSETTA_sub. In the case of 1opd (a low-quality model) the correlation is relatively poor for all scoring functions except RAPDF/HB. In the latter case a gap in the energy separates the two conformations with the lowest RMSD from the remainder. However, a number of high-RMSD conformations became energetically more favorable after energy minimization. This led to the selection of a structure with a SSE-RMSD of 3.27 Å using RAPDF/HB. In the case of 1mfg_1, 1r6j_1, 1r6j_2, 1xmt and 1tvg negative correlations between the energy and RMSD are observed. The case of 1r6j_2 is shown in Figure 5. Although it is unclear what causes the correlations to be negative, this problem certainly has affected the results of model selection (Table V). The case of 1vla deserves special mention as this protein was refined as a monomer but in fact forms a domain-swapped dimer. From Table IV it can be seen that using the three MD sampling protocols tested no conformations with lower SSE-RMSDs than the starting model were sampled. Nevertheless, from Figure 5 it can be seen that there is in fact a very weak correlation between the RAPDF/HB score and the SSE-RMSD (correlation coefficient 0.28). No correlation was found using the ROSETTA functions. The final example, 1whz, shows the highest correlation coefficient, 0.63, of all the models tested. From Table V it can be seen that after energy minimization there was a further improvement in the SSE-RMSD from 0.91 to 0.79 Å for this model. Positive correlations were observed for the majority of the models using the RAPDF/HB function. After 1whz the best correlation between the energy and the SSE-RMSD was observed for 1fm0, which also yielded the best sampling result in terms of percentage of low-RMSD conformations.

Figure 5.

The correlation of selection function score and SSE-RMSD for three scoring functions and four models, 1opd, 1r6j_2, 1vla and 1whz. The correlation of RAPDF/HB score and SSE-RMSD is plotted in 5a, 5d, 5g and 5j, respectively. The correlation of ROSETTA_soft score and SSE-RMSD is plotted in 5b, 5e, 5h and 5k, respectively. The correlation of ROSETTA_sub score and SSE-RMSD is plotted in 5c, 5f, 5i and 5l, respectively.

Scoring of the native conformations

As shown in Table III, for 15 out of the 21 models the lowest SSE-RMSD sampled by REMD is on average 0.82 Å lower than that of the starting structure. However, as shown in Table V the scoring functions investigated here had only very limited ability to identify conformations with the lowest SSE-RMSD values. This raises the question of whether these scoring functions could recognize the native structure. In order to address this issue, the RAPDF/HB score for native structure of each of the 17 proteins was calculated and compared to the score obtained for the REMD conformation that had the lowest SSE-RMSD and that had the lowest RAPDF/HB score (Table VI). In all cases the native structure had a significantly lower score than any of the structures sampled in the REMD simulations. This demonstrates that the RAPDF/HB score could in principle be used to identify near-native structures. However, the structures with the lowest SSE-RMSD values were not ranked as the most native-like structure by the potential. A similar analysis performed using the ROSETTA functions yielded similar results (data not shown). Statistical potentials such as RAPDF/HB and ROSETTA are derived from high-resolution crystal structures. These structures are often solved using data obtained at cryogenic temperatures. In addition the rotameric states of the side chains, bond angles and dihedral angles are usually constrained to ideal or equilibrium values. As a consequence, these potentials are weighted toward fine details of side chain packing and hydrogen bond geometries and perform less well when scoring conformations from molecular dynamics simulations which contain thermal noise and which should satisfy the experimental data only as an average over a representative ensemble. It should also be noted that in this work the analysis is based on conformations with low SSE-RMSD values whereas the scoring of the structures was based on the entire molecule. Thus while the secondary structure elements in the conformations selected were native-like, other regions of the protein may have transiently adopted less favorable conformations. There are other possibilities such as the native well on the conformational free energy landscape not being directly accessible from these particular near-native models. In this case the use of alternative sampling methods such as soft-core van der Waals potentials during the REMD simulations or Hamiltonian REMD^102–104 may be more effective than the temperature REMD alone.

Table VI.

RAPDF/HB scores of native structure and conformations sampled by REMD.

Models	Enative	Emin	Elrms
a. Small, globular protein data set
1cy5_1	−4054	−3124	−3055
1cy5_2	−4054	−3268	−2989
1fm0	−2848	−2307	−2130
1gxu	−3297	−2542	−2314
1k5n	−3084	−2319	−1982
1mfg_1	−2633	−2330	−1901
1mfg_2	−2633	−2294	−2002
1opd	−2850	−2216	−1970
1r6j_1	−2539	−2052	−1938
1r6j_2	−2539	−1902	−1666
1urr	−3156	−2529	−2074
1wm3_1	−2588	−2066	−1568
1wm3_2	−2588	−1963	−1746
1xmt	−3357	−2227	−1656
b. CASPR data set
1xe1	−2458	−1934	−1794
1vm0	−3642	−2874	−2514
1vla	−4843	−3930	−3639
1whz	−2894	−2333	−2056
1tvg	−3703	−2923	−2253
1xg8	−3122	−2084	−1670
1o13	−3740	−2771	−2264

The items listed include the model name, RAPDF/HB score of the native structure for this model, the lowest RAPDF/HB score of REMD-generated structure and RAPDF/HB score of the lowest SSE-RMSD structure sampled in the REMD simulation.

DISCUSSION

The questions that can be addressed using protein structure prediction techniques depend on the quality of predicted models.⁶ Although there has been significant progress in structure prediction techniques over the last decade, two crucial problems – structure refinement and model assessment have still not been solved. As mentioned above, it seems reasonable to partition the structure refinement process into two phases: local refinement which primarily involves the correction of errors in side chain packing or within loops and secondary structure elements (SSE) and global refinement which aims at resolving differences in the overall fold of the molecules. These two phases require different strategies and techniques and are normally performed sequentially.¹⁰⁵

The problem of detecting local structural errors was addressed more than a decade ago with statistical potentials such as Verify3D^70,71 and Prosa.^72,73 Since then, a number of statistical potentials have been developed to evaluate protein structures in atomic detail.^66–69,74 Recently machine-learning techniques have been used to combine various features such as structural properties¹⁰⁶ and statistical potentials¹⁰⁷ as input to predict local model quality. In the current work the local quality of the model was first assessed using three normalized, residue-based scoring functions, of which two are based on recently derived statistical potentials⁶⁸ (Zhu and Honig, in preparation). These three scoring functions used in combination appear to be sufficient to identify and address most of the local errors in the models tested. The local structural errors identified in the models were associated with the packing of side chains, loops and SSEs. The first two types of error could be readily corrected using existing methods.^82,83 The errors within SSEs were more difficult to address as changes in the secondary structure elements directly affected the global fold. In this work a combination of local sampling⁷⁷ with manual adjustment was used in an attempt to correct apparent errors in SSEs. In general these changes only lowered the overall quality of the model. This work together with other recent studies on the SSE refinement,^77,108,109 suggest that an automated procedure is preferable to manual adjustment during local structural refinement.

The global refinement of structural models of proteins remains a major challenge. Although progress has been marginal, a number of recent studies have attempted to address this problem using different approaches.^46,47,57,110 There are two fundamental challenges in global refinement: 1) efficiently sampling the available conformational space and 2) selecting near-native conformations. In this study temperature-based REMD^60,61 was the primary method used to sample the conformational space surrounding the initial model. REMD allows exchanges between systems simulated at a range of temperatures. In principle this enables the system to cross energy barriers that would not be possible to cross at lower temperatures. Of equal importance on short time scales, REMD acts to sort a range of independent simulations giving increased weight to low-energy conformations.⁶⁴ The sampling efficiency of REMD was compared to a single extended simulation and a series of short simulations of equivalent length. Although REMD performed best of the three strategies investigated it was only marginally more efficient than performing multiple short MD simulations. This suggests that on the time scale simulated the potential for REMD to enhance barrier crossings was not significant. One possibility to improve the sampling efficiency might be to include more high-temperature replicas, in this case however it is necessary to also include structural restraints to avoid complete unfolding as proposed by Chen and Brooks.⁵⁰ In their work, REMD simulations on a broader range of temperature (270 – 600K) were used together with dihedral and distance restraints to maintain the secondary structure elements and overall topology during the refinement. Another possibility may be to use models based on alternative sequence alignments generated from various procedures as replicas in the REMD simulation. REMD provides a general framework through which a range of alternative sampling approaches can be incorporated into refinement calculations,^111,112 however further studies are required to demonstrate that REMD truly enhances the sampling of native-like conformations given the limitations in the available force fields.^113,114

Even if near-native conformations can be sampled efficiently, the question of how to identify the near-native conformations from a large ensemble of low-energy alternatives remains. Scoring functions must be both fast and accurate. Thus while energy functions based on molecular mechanics force fields in combination with an implicit description of solvation effects might in principle be of sufficient accuracy to discriminate native from non-native conformations,¹¹⁵ such approaches require extensive optimization of protein structures prior to scoring, which is computationally expensive. Statistical potentials in contrast are fast and simple to implement but can be sensitive to slight deviations from ideal geometries. In this study we compared a combination of two statistical potentials (RAPDF/HB)^66,96 to alternative functions from ROSETTA. The use of RAPDF as the primary scoring function was based on the observation that RAPDF was more effective at discriminating native from non-native structures obtained from the MD simulations while DFIRE was more effective at discriminating between models generated in the course of structure prediction and modeling.^77,107,116 We believe this difference stems from the differences in their respective reference state, which relates to how a random distribution is defined in the derivation of the statistical potential. Our results also suggest that the selection function must be compatible with the sampling protocol in order to achieve the best performance. Incorporation of the hydrogen bonding potential was highly effective in improving the RMSD results. Together, the RAPDF and hydrogen bonding potentials constituted a simple but effective scoring function which could potentially be used as the basis to develop a more sophisticated scoring function. The results from the two ROSETTA functions examined are varied, ROSETTA_soft showed the better correlation between energy and RMSD but was less effective in selecting the conformations with the lowest RMSD. In this function, the rama term that accounts for the preference of backbone dihedrals and the softened LJ term that accounts for atomic clashes in modeling appeared to yield inappropriate rankings when applied to conformations generated using MD simulations.

Although each of the scoring functions could discriminate the native structure from alternative models, none of the scoring functions tested could reliably identify near-native structures sampled during the REMD simulations. One explanation for this could be the sensitivity of these potentials to thermal noise inherent in MD-generated structures. Another contributing factor could be that the scoring functions were applied to the whole structures while the structural comparisons were based on the SSE-RMSD which considers only a subset of backbone atoms. Intuitively a global quality measure that can take into account both backbone and side chain information¹¹⁷ may lead to better correlations, while the use of coarse-grained statistical potentials that simplify side chains¹¹⁸ may be an alternative approach. Independent of the scoring function, it is also possible to improve the model selection by using a structure-clustering algorithm, which has been found to be useful in a number of studies in ab initio structure prediction^119,120 and local structural refinement.⁷⁷ In our study, EM was found to improve the RMSD results for only 60% of the models. This might be due to the inconsistency of using a physical energy function to optimize the structures but a statistical potential to rank the minimized structures. The physical energy function used also contains an electrostatic solvation term^86,87 that will affect the structural packing of charged and polar residues during minimization. However, none of the statistical potentials used include such solvation effects explicitly.

In addition to conformational sampling and model selection, other factors may also play a role in structure refinement. One factor is whether the protein forms part of a larger complex. In this case, the model should be refined in the multimeric state. However, this can be extremely challenging and has yet to be properly addressed in structure prediction. Recently, Grimm et al reported a benchmark study of dimeric threading and structure refinement,⁵⁶ in which three model dimers under optimal conditions were refined. In each case the two models were connected by a 30-glycine linker so that methodology developed for single proteins (TASSER⁵⁴) could be applied. In our study, the refinement of the isolated monomer of 1vla, which in reality forms a domain-swapping dimer, was the only case in which conformations with lower SSE-RMSD values than the initial model were not sampled during the REMD simulations. Similarly, the scoring functions, which have been primarily developed for single isolated proteins may have to be re-evaluated for use with proteins removed from multimeric complexes. Another factor that affects refinement, in particular the selection step, is the overall quality of the model. In our study, the REMD protocol was an equally effective sampling protocol for both sets of models. In contrast the scoring functions appeared to perform better on the non-CASPR models, for which the structure was of higher quality. Overall the refinement of small, globular and near-native models was more successful than the refinement of irregularly shaped larger models with relatively low quality. This was particularly evident when the RAPDF/HB function was used for selection. The only two successful examples in the CASPR data set were 1xe1 and 1whz, which both are small, globular structures with low starting RMSD values.

In summary, we have presented a simple but effective strategy for refining homology models. A number of fundamental issues in structure refinement, such as conformational sampling and model selection, have been investigated by testing alternative methods on a data set of 21 models with various qualities. We believe that the experience gained from this study will greatly facilitate the design of more effective strategies for global refinement.