Abstract
How intracellular signals are propagated with the appropriate strength, duration and fidelity over time is poorly understood. To address these issues, intracellular signal transduction was studied both analytically and numerically using a simplified cascade model. The main observations can be summarized as follows: when the response kinetics is the Michaelis-Menten type, the signal strength will always reach the same magnitude as the cascade length increases, regardless of the type of stimulus applied (i.e., either continuous or unitary pulse). However, when the response kinetics is the Hill type (Hill coefficient >1), there exists a stimulation threshold. If the stimulus is below the threshold, the signal decays toward zero; in contrast, if the stimulus is above the threshold, the signal amplitude reaches a non-zero steady state. The time taken for the signal to proceed through the cascade increases as the half-maximum point, or Hill coefficient, increases, whereas the duration of the output signal at the end of the cascade decreases as the half-maximum point increases. In the presence of a positive feedback, the stimulation threshold increases; under these conditions, the feedback strength necessary for bistability changes (with power-law characteristics) inversely related to the length of the cascade. In the presence of a negative feedback, oscillations are induced when the Hill coefficient is greater than one and the cascade has more than two steps. Likewise, the feedback strength required to generate oscillations changes (again with power-law characteristics) inversely with the length of the cascade.
INTRODUCTION
Molecular networks are comprised of multiple signaling motifs that, when coupled together, engender distinct responses to external stimuli [1–4]. These responses have important but poorly understood temporal properties. For example, in many systems a short stimulus (i.e., a pulse) gives rise to a fleeting immediate response and a delayed onset response of prolonged [5–11] or even permanent [12–15] duration. Specific cases are illustrative: protection against heart or brain injury can be induced by a short stimulus that engenders both an early protective period that begins immediately and is short lived, and a delayed protective period that is substantially prolonged [5–7]. During the maturation of oocytes, progesterone stimulation causes an initial short period of maturation promoting factor expression and a second, sustained period of higher expression of the protein. This second increase in maturation promoting factor persists in a plateau phase until the cell is fertilized, at which point the factor levels begin to oscillate in a behavior that drives cell cycle progression [12–14]. Another important and interesting response is the so-called early long-term potentiation and late long-term potentiation in excitable cells in which a single stimulus causes short long-term potentiation which lasts a few hours, but multiple sequential stimuli induce long long-term potentiation which lasts more than 24 hours [16]. It has been hypothesized that post-translation modifications and gene transcription account for the immediate and delayed responses, respectively. However, the mechanisms for the length of delay, the duration of the response, and stimulation threshold are not well understood.
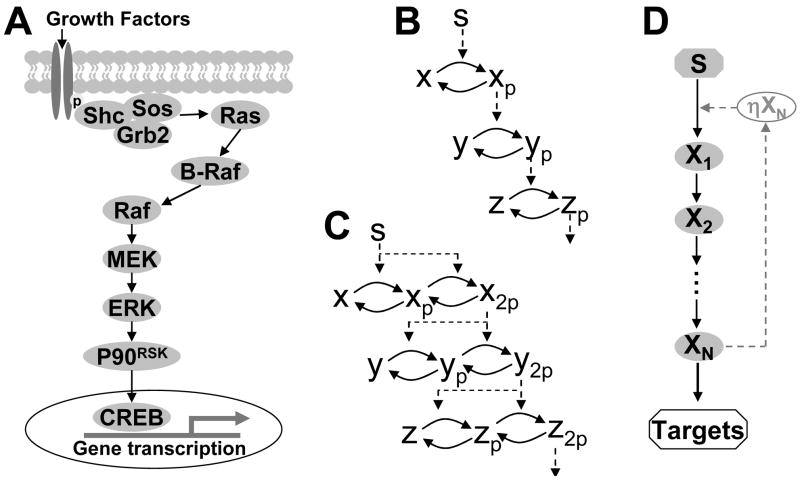
Signaling cascades, which are ubiquitous in biological systems, have been candidate models for the mechanisms of these biological response [17, 18]. It has been shown in experiments that a cascade can result in utrasensitive response [19, 20] as well as signal amplification [21]. Many mathematical modeling studies on signal transduction through cascades have been carried out, among which the mitogen-activated protein kinases (MAPK) (Fig. 1A) are the most well studied. Modeling studies of MAPK cascades have demonstrated their utility for ultra-sensitive responses [19–22] and have revealed that they produce bistability and limit cycle oscillations [23–26] under constant stimulation. In these modeling studies, either a cascade model with a single phosphorylation/dephosphorylation cycle in each step (Fig. 1B) or a cascade model with dual phosphorylation/dephosphorylation cycles in each step (Fig. 1C), was used. However, these behaviors are not unique to MAPK responses and can be observed in any signaling process involving several molecules. Signal transduction in cascades with arbitrary steps in response to a time-dependent stimulus has been investigated either numerically or analytically in recent studies [18, 21, 27–30]. Heinrich et al [27] and Chaves et al [28] investigated signal amplification and attenuation in a cascade of arbitrary length with the response kinetics of Fig. 1B. Sontag and Chaves [29] studied signal amplification as a general phenomenon in a class of nonlinear signaling pathways. These studies showed that depending on the reaction kinetics, a weak stimulus may be amplified into a stable signal in the cascade, or a strong stimulus may be damped gradually in the cascade and fail to propagate the signal to the target at the end of the cascade.
Figure 1.
Schematic plots of signaling cascades. A. An example of MAPK signaling cascades. B. A linear signaling cascade model. C. A dual phosphorylation/dephosphorylation model of signaling cascades, respectively. D. A simplified scheme for a signaling cascade with arbitrary cascade length N, as used in this study. The dashed line denotes a feedback loop with can be either positive or negative.
In this study, we used both numerical and analytical methods to investigate the signal transduction dynamics in a simplified model of signaling cascade of arbitrary length as shown in Fig. 1D. We studied the factors affecting the signal delay, the signal duration, and the stimulation threshold; we also studied the dynamics caused by positive and negative feedback loops. Our findings provide fundamental insights into distinct types of dynamical behavior engendered by variation in each of these three parameters (cascade length, kinetics and feedback) and provide rationale for why all three are varied in a signaling network to impart interesting biological responses.
MATHEMATICAL MODELING AND METHODS
The model in Fig. 1B has been used in several studies [26–30] to investigate signal transduction dynamics in the MAPK cascades. The differential equation for a protein in the cascade, e.g., for xp, is:
| (1) |
where we assume x + xp = 1 and a is the inactivation rate constant. The steady state response of xp to the stimulus S is the Michaelis-Menten type (or the Hill type with coefficient=1). The differential equation for yp (or zp) has the same form as Eq. 1, except S is substituted by xp (or yp). Models of Fig. 1C were also used, in which the proteins in the cascades are dually phosphorylated/dephosphorylated [20, 23]. In this case, the differential equations, e.g., for x2p and xp, are:
| (2) |
where x + xp + x2p = 1 and a is the dephosphorylation rate constant. If one assumes that the xp reaches its equilibrium state fast, then xp can be approximated as a function of x2p, from the second equation of Eq. 2, i.e., . Inserting this expression into the first equation, we have:
| (3) |
The differential equation for y2p (or z2p) has the same form as Eq. 3, except S is substituted by x2p (or y2p). As shown by Huang and Ferrell [20], the steady state response at each step of the cascade can be well approximated by a Hill function with coefficient β being greater than 1. When S is a constant, the steady state response of x2p is , and the solution of Eq. 3 is where is the time constant of phosphorylation (activation) or dephosphorylation (inactivation) of x2p. Eq. 3 can be expressed as dx2p/dt = [f(S) − x2p]/τ.
Although analytical treatment of Eq. 1 (or the signaling cascade model in Fig. 1B) can be carried out [27, 28], it becomes difficult (or almost impossible) to analytically treat Eq. 2 or Eq. 3 (or the signaling cascade model in Fig. 1C) since the differential equations are nonlinear. Based on the fact that the steady state response of the cascade in Fig. 1C can be well approximated by a Hill function [19, 20, 22], and to allow analytical treatment, we used, instead, a simplified general model (shown in Fig. 1D) and also assume the response of each step follows the Hill function with a response time constant τ. Then the differential equations are simplified to:
| (4) |
where N is the length of the cascade and X0 = S is the stimulus amplitude. S can be either a constant or a pulse with duration T0. Note that τ is not constant (see Eq. 3) but depends on the signal of the previous step, i.e., Xn−1(t). For simplicity and analytical treatment, we set τ to be constant in this study. For the same reason, we assume that all steps in the cascade are identical, i.e., Eq. 4 is a homogeneous cascade model. f(X) was chosen to be a Hill function:
| (5) |
The Hill coefficient β ≥ 1 was used in this study since higher Hill coefficients can be achieved in biological systems by multi-step phosphorylation [31–33] or other mechanisms [34–36] in each step of the cascade. We also studied the effects of positive and negative feedback loops (the dashed pathway in Fig. 1D); the modifications to Eq. 4 will be detailed in the corresponding sections below. The parameters used in this paper are α, β, τ, the feedback strength η, and the stimulus strength S and its duration T0. A constant stimulus is equivalent to T0 → ∞. The numerical results in this study were obtained by integrating Eq. 4 using a fourth-order Runge-Kutta method with a time step 0.01.
RESULTS
Signal transduction in a singling cascade in response to an external stimulus
A. Steady state response to a constant stimulus
Under a constant stimulus S, the steady state solution of Eq. 4 satisfies [we denote Xn as the steady state of Xn(t)]:
| (6) |
which is just an iterated map with X0 = S. When β = 1, an explicit solution of Eq. 6 can be obtained as:
| (7) |
When β > 1, we are unable to analytically solve Eq. 6 for arbitrary stimulus strength S. However, we can still determine whether a signal is amplified or attenuated through the signaling cascade by analyzing the steady states (or fixed points) of Eq. 6 and their stabilities. In other words, a fixed point of Eq. 6 corresponds to a constant signal in the signaling cascade, i.e., Xn = Xn−1 = ···= S. The steady state solution of Eq. 6 (denoted as Xs) can be solved from
| (8) |
which leads to
| (9) |
or
| (10) |
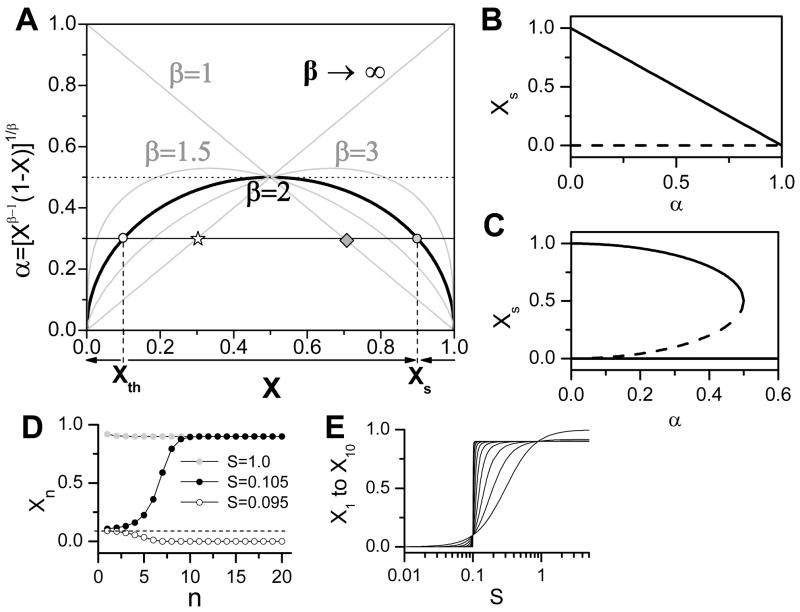
The solutions for Eq. 10 are not obvious, but since is a unimodal function when β >1, it can have either no solution or two solutions (see Fig. 2A for a graphical illustration). The two solutions degenerate into one solution Xc= (β − 1)/β at α = αc = (1 − 1/β)(β − 1)−1/β. For example (Fig. 2A), for β = 2, the two solutions are , and these two solutions degenerate into Xc = 0.5 at αc = 0.5. Therefore, for β >1, Eq. 8 has three solutions when α < αc and one solution (Xs = 0) when α >αc (Fig. 2B). A special case is when β = 1, Eq. 10 has only one solution which is Xs = 1 − α. Therefore, for β = 1, Eq. 8 has two solutions: Xs = 0 and Xs = 1 − α.
Figure 2.
Steady state responses to a constant stimulus in a cascade. A. Graphical determination of steady states of the equation α = [Xβ−1(1− X)]1/β for different β. The horizontal solid line is α = 0.3, which intersects with the β = 2 curve at Xth = 0.1 and Xs = 0.9. The dashed line is α=0.5, which is tangential to the β =2 curve at Xc=0.5. B. The two steady states of Eq. 6 versus α for β =1. C. The steady states of Eq. 6 versus α when β =2. D. The signal amplitude versus the cascade step number n for different S. α=0.3, β =2. E. Steady state response to S for X1 to X10. α=0.3, β =2 (the response becomes steeper from X1 to X10).
We then analyze the stability of the steady states by linearizing Eq. 6 around its fixed point, i.e.,
| (11) |
The steady state solution is stable when |λ| < 1, but unstable when |λ| >1. For β = 1, Xs = 0 is unstable since λ = 1/α >1, while Xs = 1 − α is stable since λ = α < 1. For β > 1, Xs = 0 is then stable since λ = 0 < 1. For the other two solutions, the eigenvalue can be obtained by inserting Eq. 10 into Eq. 11, which is:
| (12) |
Since when Xs = Xc = (β − 1)/β, λ = 1, then λ > 1 when Xs <Xc, and λ < 1 when Xs > Xc. Therefore, the larger of the two solutions of Eq. 10 is stable and the smaller is unstable (dashed line in Fig. 2B).
From the steady states and their stabilities, one can determine if a signal is amplified or attenuated through the cascade. For β = 1, the signal is amplified when S < 1 − α but attenuated when S >1 − α. In other words, for any stimulation strength, since Xs = 0 is unstable, the signal strength always approaches the stable steady state (1 − α) through the signaling cascade. For β > 1, if S is smaller than the unstable steady state (labeled as Xth in Fig. 2A), the signal will decay towards zero (Fig. 2D). If S is greater than Xth, then the signal will approach the stable steady state (Xs in Fig. 2A). Therefore, there is a stimulation threshold Xth for β >1 but not for β = 1. Note that in the case of β >1, when α >αc, the signal always decays, approaching zero, since there is only one steady state solution which is zero. In Fig. 2E, we plot Xn versus S, showing that Xn decreases as n increases when S < Xth, but Xn increase as n increases. In other words, as more steps are added to the cascade, the sensitivity increases, taking on more Boolean activation characteristics. This is similar to what is observed by increasing the Hill coefficient with other parameters constant; however, the latter allows for rapid activation whereas the former results in an activation delay. From a stress adaptation standpoint, this type of response provides clear benefits: small stimuli can induce responses due to high sensitivity but these responses are delayed in their onset. This allows the system to detect small stresses before they are of a deleterious magnitude and to mobilize appropriate long term response.
Response to a pulse stimulus
When the stimulus S is a pulse instead of a constant, the transduction of the signal is influenced by the duration T0 of the stimulus and the time constant τ of the cascade, in addition to α and β. When β = 1, since there is no stimulation threshold for strength and duration, any small stimulus can elicit a large output from the cascade following a given time (Fig. 3A), while a large stimulus elicits a large initial signal but then decays to a plateau level (Fig. 3B). When β >1 a stimulation threshold exists. Under these conditions, the output elicited by a sub-threshold stimulus decays toward zero (Fig. 3C), but a supra-threshold stimulus can give rise to a stable output from the cascade (Fig. 3D). Fig. 3E shows the critical parameter αc versus β for a signal elicited by a large stimulus (S=1) to transduce without decaying to zero in the cascade for T0 = 10 and τ = 5 (triangles), compared with that for a constant stimulus (line). For β >1, αc is smaller than that for the steady state, as expected. The critical stimulus strength Sc required for successful propagation through the cascade decays rapidly as the stimulus duration T0 increases (Fig. 3F), but increases rapidly as τ increases. Output from the cascade fails altogether when τ reaches a critical value (Fig. 3G). This behavior is akin to capacitance in the signaling system, where a small input builds up over time to ultimately reach a critical threshold.
Figure 3.
Response of the cascade to a pulse stimulus and the emergence of threshold. A. Xn (n=1 to 10) versus time for a weak stimulus (S=0.01, the thick gray line) for α=0.5 and β =1. B. Same as A but for S=1. C. Signal (X1 to X10) attenuation due to sub-threshold stimulus (S=0.15). α=0.3 and β =2. D. Signal amplification due to supra-threshold stimulus (S=0.16). α=0.3 and β =2. Note the different scales of y-axis in panels C and D. E. αc vs. β. The solid line is αc = (1 − 1/β)(β − 1)−1/β which is for the constant stimulus. Symbols are from numerical simulations of Eq. 1 for pulse stimulus with duration T0=10. S=1, and N=10 were used. F. The minimum T0 versus S necessary for a response to be generated through the system with α=0.3 and β =2. G. The maximum τ versus S to generate a response through the system with the parameters α=0.3, β =2, and T0=10. τ=5 was used for A–F.
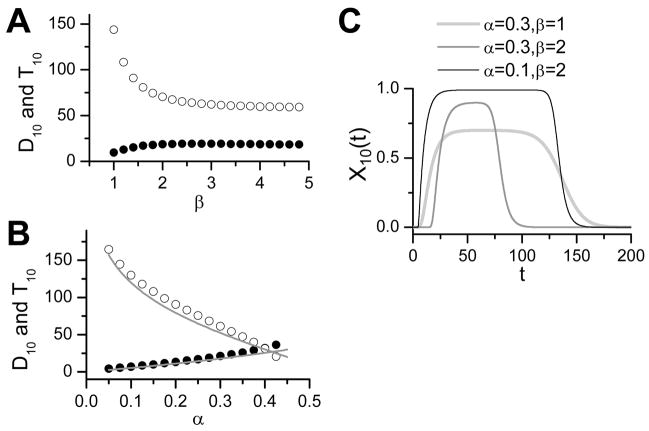
The delay and signal duration depend on α and β. Fig. 4A plots the delay (filled circles) and signal duration (open circles) versus β for X10 of the cascade, showing that, initially, as β increases, the delay time (D10) increases and the signal duration (T10) decreases; eventually, both saturate (interestingly, this occurs around the same point of half-maximum response, or β). Fig. 4B shows the delay and signal duration versus α for X10 of the cascade, the delay time increases and the signal duration decreases until signal transduction fails in the cascade. Fig. 4C shows some example traces of X10(t) for different combinations of α and β.
Figure 4.
Regulation of signal delay and duration. A. Signal delay of X10 (D10) and duration of X10 (T10) versus β for α=0.3. B. D10 and T10 versus α for β =2. Lines are the analytical results from Eq. 17. C. X10 versus time for different α and β. T0=10, τ=5, and N=10 were used.
Although an analytical solution cannot be easily be obtained due to the nonlinearity of f(X) in Eq. 4, one can derive approximate solutions under conditions of large β and a strong stimulus, since f(X) is very close to a step function when β is large. One can then solve Eq. 4 in three intervals by setting f(Xn−1) to be:
| (13) |
where Dn−1 is the activation delay of Xn−1, Tn is the signal duration of Xn, and μn−1 is the amplitude of Xn−1. See Fig. 5 for definitions of these quantities. The solution for Xn(t) in the three intervals can then be obtained as:
| (14) |
where . In Eq. 14, D0 = 0, μ0 = S, and T0 is the width of the stimulus. Dn and Tn are calculated by the following linear iterated equations:
| (15) |
Figure 5.
Schematic plot of the relation between Xn−1 (gray solid line), f(Xn−1) (black dashed line), and Xn (black solid line). Dn is defined as the duration between the time when the stimulus is given and the time when Xn increases to α at which f(Xn)=1/2. Tn is defined as the duration during which Xn> α.
The next task is to calculate ΔDn and ΔTn. We define ΔDn as the duration in which Xn grows from zero to α, and ΔTn + ΔDn as the duration in which Xn decays from μn to α (see Fig. 5). Using Eq. 14, one obtains:
| (16) |
At the limit of β → ∞, and τ → 0, then un → 1, and thus we obtain from Eqs. 15 and 16 the delay time in activation of Xn and its duration as:
| (17) |
In Fig. 4B, we also plot Dn and Tn versus α for β = 2 (lines) using Eq. 17 which agree well with the numerical results.
Effects of feedback loops on bistability and limit cycle oscillations
A. Positive feedback
In the case of positive feedback as illustrated in Fig. 1D, the differential equation for X1 in Eq. 4 was changed to:
| (18) |
and the other equations were kept unchanged. To understand how this positive feedback loop affects the dynamics of the system, the stability of the steady state is analyzed below. From Eqs. 4 and 18, one obtains the Jacobian for a steady state as:
| (19) |
where
| (20) |
and
| (21) |
The characteristic equation for the eigenvalues of the Jacobian is:
| (22) |
The solutions of Eq. 22 are:
| (23) |
where which is always positive since znn−1 and z1N are all positive. This indicates θ= π when N is odd and θ= 0 when N is even. The maximum eigenvalue is always a real number since and can be always satisfied in Eq. 23, i.e.,
| (24) |
Therefore, the steady state is stable when and unstable when ; the loss of stability occurs via a saddle-node bifurcation.
Michaelis-Menten response kinetics (β = 1)
When β = 1, the steady state can explicitly obtained. Based on Eq. 7, the steady state relation between XN and X1 is:
| (25) |
Inserting Eq. 25 into Eq. 18, the steady state solution for X1 satisfies:
| (26) |
The solutions of Eq. 26 are:
| (27) |
where A = (α + S)(1 − αN−1) + η(1 − α), B = S(1 − αN−1) + η(1 − α) − (α + S)(1 − α)αN−1, and C = S(1 − α)αN−1. Since A and C are positive for S > 0, only one of the two solutions is positive. In the special case of S = 0, the system has two nonnegative solutions, which are: X1 = 0 and . The nonzero solution exists only when η > αN. Since α < 1, a weaker feedback strength is needed for a larger N (i.e., a longer cascade) to maintain a nonzero signal amplitude when there is no stimulation.
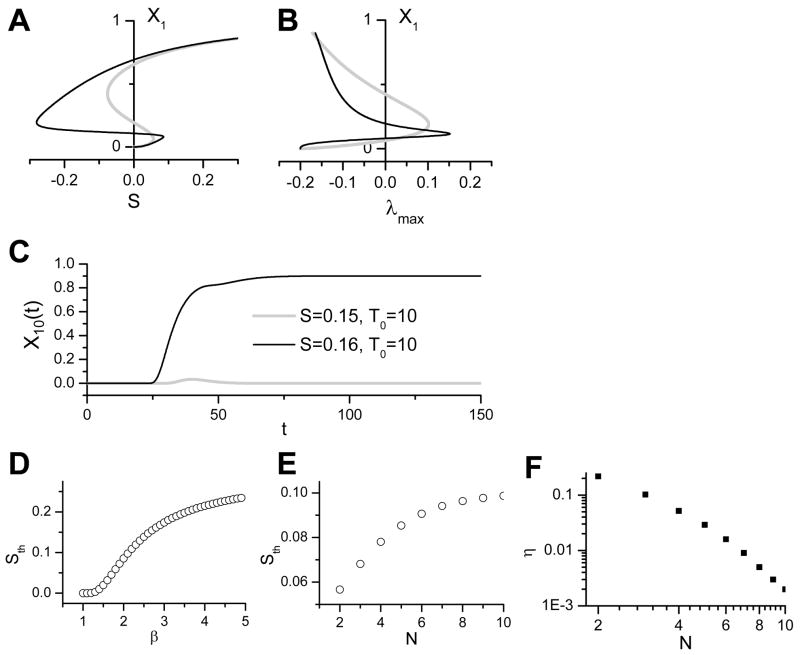
Fig. 6A shows the steady state of X1 for N = 2 (gray line) and N = 5 (black line) versus S while Fig. 6B shows the steady state X1 versus λmax calculated using Eq. 23. The negatively sloped region of the steady state solutions is unstable (the λmax > 0 region in Fig. 6B). Note that increasing the length also increases the magnitude of the hysteresis. Since the smaller solution only occurs in the negative S regime except when X1 = 0, it is not practically interesting since S cannot be negative. However, since X1 = 0 is unstable, any stimulation is sufficient to trigger a signal through the cascade (Fig. 6C). For obvious reasons this property is undesirable in a biological system because any external or internal noise would give rise to a sustained output.
Figure 6.
Effects of positive feedback in linear signal cascade modeled with Michaelis-Menten kinetics (β =1). α=0.3 and η=0.5. A. The steady state of X1 versus stimulus strength for N=2 (gray) and N=5 (black). B. The steady state of X1 versus the maximum eigenvalue λmax for the two cases in A. C. X10 versus time for a very weak (gray) and a strong stimulus (black). N=10.
Hill type response kinetics (β >1)
When β >1, we can numerically solve the steady state for different stimulus strength S, two examples of which are shown in Fig. 7A. The steady state X1 versus λmax calculated using Eq. 23 is shown in Fig. 7B. The positively sloped regions of the steady state solutions in Fig. 7A are stable (the λmax < 0 regions in Fig. 7B) and the negatively sloped region is unstable (the λmax > 0 region in Fig. 7B). Because a stimulation threshold exists, a sub-threshold stimulus is incapable of eliciting an output from the system, whereas a supra-threshold stimulus does induce signaling (Fig. 7C). The stimulation threshold increases as β increases (Fig. 7D), and also increases as the cascade length N increases (Fig. 7E). The feedback strength η that is needed for bistability to occur decreases close to power-law manner as N increases, as shown in a log-log plot (Fig. 7F). Thus, when positive feedback is present, longer cascades lower the threshold for the system to enter a bistable regime.
Figure 7.
Effects of positive feedback in nonlinear signal cascade modeled with Hill kinetics (β >1). A. The steady state of X1 versus stimulus strength for N=2 (gray) and N=5 (black). B. The steady state of X1 versus the maxiumu eigenvalue λmax for the two cases in A. C. X10 versus time for subthreshold (gray) and suprathreshold (black) stimulus. D. Stimulus threshold (Sth) versus β for α=0.3, η=0.5, and N=10. E. Sth versus N for α=0.3, η=0.5, and β =2. F. Minimum η required for bistability to occur versus cascade length N for α=0.3 and β =2.
B. Negative feedback
In the case of negative feedback as illustrated in Fig. 1D, the differential equation for X1 in Eq. 4 was changed to:
| (28) |
and the other equations were kept unchanged. The Jacobian is the same as the positive feedback case in Eq. 19 except that
| (29) |
The eigenvalue spectrum is thus the same as Eq. 23, except that , θ = π when N is even, and θ= 0 when N is odd. Since znn−1 is positive for all n and z1N is negative, then b is positive. When β = 1, no instability can occur. When β >1, instability occurs only when N > 2 since when N = 2 the two eigenvalues are . It is well known that a three-variable model is needed for negative feedback to cause limit cycle oscillations [37, 38], which is also the case for the model in this study. Figs. 8A and B show two bifurcation diagrams for N = 5 and N = 8 which show that the system underwent a Hopf bifurcation leading to limit cycle oscillations. Fig. 8C shows traces of Xn(t) during limit cycle oscillations. The minimum feedback strength needed for limit cycle oscillations to occur decreases as either the cascade length or β increases (Fig. 8D), but increases as α increases (Fig. 8E). In fact, the minimum feedback strength needed for oscillation decays as N increases, following a power-law relation (Fig. 8F). It is obvious that the period of limit cycle oscillations is longer for a longer cascade or a longer protein half-life τ. Because the feedback strength necessary for oscillations decreases as the length of the cascade increases, selection for longer cascades would decrease the overall flux through the system and fine tune the amplitude of transduced signal.
Figure 8.
Effects of negative feedback. A. Bifurcation diagram versus stimulus strength S showing the stable steady state of X1 (black circles), the unstable steady state of X1 (dashed line), and the maximum and minimum values of X1 during oscillations (open circles). α=0.3, β =2, and N=5. B. Same as A except N=8. C. X1 to X8 versus time showing oscillations. D. the critical feedback strength η versus β for different cascade length for α=0.3. E. The critical feedback strength η versus α for β =2 and N=5. F. Minimum η required for limit cycle oscillations to occur versus cascade length N for α=0.3 and β =2.
DISCUSSION
General properties governing how intracellular networks respond to external stimuli are incompletely understood. It is well established that virtually all cell types exhibit a range of responses following unitary or prolonged stimuli. That a response occurs (or does not occur) following stimulation of a cell is a fundamental property of how signaling networks support the internal functions of the cell and allow the cell to interface in a coherent manner with the extracellular environment. In this study, we used a simplified signaling cascade model to investigate the dynamics of signal transduction in response to external stimuli. Several biological implications can be drawn from this study as discussed below.
First, we showed that a stimulation threshold appeared when the response kinetics is Hill type with coefficient β >1. In this case, a stimulus that does not reach the threshold fails to generate a propagating signal and the output of the cascade decays toward zero. On the other hand, a stimulus above the threshold induces a non-zero amplitude signal through the cascade. However, it is not the case when the response kinetics is Michaelis-Menten type, i.e., any stimulus gives rise to an output from the cascade. This threshold may be responsible for the occurrence of the late long-term potentiation [16] and has been modeled previously [17]. It is noteworthy that previous studies have shown bistability caused by positive feedback acts as the dynamical mechanism underlying biological switches in many systems [14, 39–42]. The Hill type response is referred to as a graded response, however, even though the response kinetics is Hill type in each step, a switch-like (or binary) behavior can be achieved in a multi-step signaling cascade without a positive feedback as long as the Hill coefficient β >1, as shown by our analysis. Hysteresis and binary behaviors have been used in experiments as evidence of positive feedback-induced bistability; however, caution must be taken, because hysteresis and binary responses may also be observed in experimental measurements while the actual signaling network is simply a signaling cascade without positive feedback. This observation may occur due to the existence of stimulation threshold that engenders binary response behavior and memory over time (that is, the emergence of hysteresis in the system).
Secondly, an important function of stimulation threshold is to prevent sub-threshold environmental noise from eliciting an output from the cascade. However, once the external noise becomes supra-threshold, it can be further amplified by the cascade to be a robust signal. On the other hand, based on our stability analysis, the signal amplitude saturates in the cascade; therefore, once a signal is transducing in the cascade, the internal noise may be attenuated, as also shown previously [43].
Thirdly, we demonstrated that the delay time between stimulus and response and the duration of the response were both proportional to the product of the signaling cascade length and the half-life τ of the protein level or protein function/activity (Eq. 17). In biological systems, protein half-lives may vary from minutes to several hours [44]. Therefore, to maintain a 3 to 4 day signal duration, such as in cardiac or neural protection against injury [5–7], a signaling cascade with many steps is required. It should be noted that a long cascade can result in a very long (several days) signal duration which may be treated as a permanent signal experimentally due to relative short period of observation. For example, whether the maturation promoting factor levels during oocyte maturation is due to a strong positive feedback loop or a long signaling cascade remains unknown.
CONCLUSION AND OUTLOOK
We studied how parameters in a cascade affected the dynamical instabilities of the signaling system and showed that the likelihood of bistability and limit cycle oscillations increases greatly as the length of the cascade increases. This observation is attributable to the fact that the cascade results in a very steep response which is prone to dynamical instabilities. These studies provide novel analytical insights into how cells temporally regulate phenotype, and identify critical parameters within intracellular networks that govern rapid response and delayed onset signal transduction.
We used a homogeneous cascade model with a simplified kinetics, whereas in real systems, the behavior of the individual molecules participating in a cascade and the kinetics of the biochemical reactions may all differ. We set the time constant τ to be a fixed number, yet it changes during a chemical reaction cycle. Therefore, how these temporal and structural heterogeneities affect the dynamics of the signaling cascade needs to be further evaluated. It will be worthwhile to validate the theoretical insights in a specific biological signal transduction model that incorporates the realistic molecules and biochemical reactions. Nevertheless, the simple model used in the present study provides a basic theoretical understanding of the dynamics of biological signal transduction.
Acknowledgments
This study was supported by the NIH (HL087132, TMV) and the Laubisch Endowment at UCLA.
GLOSSARY
- Signal transduction
Signal transduction in biology is a process which propagates a stimulus to enact a cellular function. For example, nutrients or hormones can stimulate signaling transduction in the cell that activates genes, causes protein production, modulates metabolism or otherwise affects cell growth or survival
- Signaling cascade
A signaling cascade is a series of biochemical reactions in which the reaction products of one step catalyze, or serves as necessary reactants in, reactions in the next step
- Bistability
Bistabiliy means that a system can have two stable states of equilibrium under the same conditions. The system can reisde on either one of the two states depending on the initial condition of the system. Bistability is used to expain switch behaviors in biological systems [14, 40, 41, 45, 46]
- Limit cycle oscillations
Limit cycle oscillations are a temporal periodic solution of a nonlinear system. For a stable limit cycle, nearby states always approach this same oscillatory state asmptotically. Most known biochemical oscillations, such as circadian rhythms or cell division cycle, are limit cycle oscillations [47, 48]
References
- 1.Shen-Orr SS, Milo R, Mangan S, et al. Network motifs in the transcriptional regulation network of Escherichia coli. Nat Genet. 2002;31:64. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
- 2.Mangan S, Alon U. Structure and function of the feed-forward loop network motif. Proc Natl Acad Sci U S A. 2003;100:11980. doi: 10.1073/pnas.2133841100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ma’ayan A, Jenkins SL, Neves S, et al. Formation of regulatory patterns during signal propagation in a mammalian cellular network. Science. 2005;309:1078. doi: 10.1126/science.1108876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Behar M, Dohlman HG, Elston TC. Kinetic insulation as an effective mechanism for achieving pathway specificity in intracellular signaling networks. Proc Natl Acad Sci U S A. 2007;104:16146. doi: 10.1073/pnas.0703894104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yellon DM, Downey JM. Preconditioning the myocardium: from cellular physiology to clinical cardiology. Physiol Rev. 2003;83:1113. doi: 10.1152/physrev.00009.2003. [DOI] [PubMed] [Google Scholar]
- 6.Papadia S, Stevenson P, Hardingham NR, et al. Nuclear Ca2+ and the cAMP response element-binding protein family mediate a late phase of activity-dependent neuroprotection. J Neurosci. 2005;25:4279. doi: 10.1523/JNEUROSCI.5019-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bordet R, Deplanque D, Maboudou P, et al. Increase in endogenous brain superoxide dismutase as a potential mechanism of lipopolysaccharide-induced brain ischemic tolerance. J Cereb Blood Flow Metab. 2000;20:1190. doi: 10.1097/00004647-200008000-00004. [DOI] [PubMed] [Google Scholar]
- 8.Taylor DA, McGrath JL, O’Connor BJ, et al. Allergen-induced early and late asthmatic responses are not affected by inhibition of endogenous nitric oxide. Am J Respir Crit Care Med. 1998;158:99. doi: 10.1164/ajrccm.158.1.9709091. [DOI] [PubMed] [Google Scholar]
- 9.Dweik RA, Comhair SA, Gaston B, et al. NO chemical events in the human airway during the immediate and late antigen-induced asthmatic response. Proc Natl Acad Sci U S A. 2001;98:2622. doi: 10.1073/pnas.051629498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Su M, Young AJ, He C, et al. Biphasic response of the regional lymphatics in the normal lymphocyte transfer reaction. Transplantation. 2001;72:516. doi: 10.1097/00007890-200108150-00026. [DOI] [PubMed] [Google Scholar]
- 11.Hong SJ, Li H, Becker KG, et al. Identification and analysis of plasticity-induced late-response genes. Proc Natl Acad Sci U S A. 2004;101:2145. doi: 10.1073/pnas.0305170101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Murray AW, Solomon MJ, Kirschner MW. The role of cyclin synthesis and degradation in the control of maturation promoting factor activity. Nature. 1989;339:280. doi: 10.1038/339280a0. [DOI] [PubMed] [Google Scholar]
- 13.Ferrell JE., Jr Xenopus oocyte maturation: new lessons from a good egg. BioEssays. 1999;21:833. doi: 10.1002/(SICI)1521-1878(199910)21:10<833::AID-BIES5>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- 14.Xiong W, Ferrell JE., Jr A positive-feedback-based bistable ‘memory module’ that governs a cell fate decision. Nature. 2003;426:460. doi: 10.1038/nature02089. [DOI] [PubMed] [Google Scholar]
- 15.Fera E, O’Neil C, Lee W, et al. Fibroblast growth factor-2 and remodeled type I collagen control membrane protrusion in human vascular smooth muscle cells: biphasic activation of Rac1. J Biol Chem. 2004;279:35573. doi: 10.1074/jbc.M400711200. [DOI] [PubMed] [Google Scholar]
- 16.Kandel ER. The molecular biology of memory storage: a dialogue between genes and synapses. Science. 2001;294:1030. doi: 10.1126/science.1067020. [DOI] [PubMed] [Google Scholar]
- 17.Smolen P, Baxter DA, Byrne JH. A model of the roles of essential kinases in the induction and expression of late long-term potentiation. Biophys J. 2006;90:2760. doi: 10.1529/biophysj.105.072470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Han Z, Vondriska TM, Yang L, et al. Signal transduction network motifs and biological memory. J Theor Biol. 2007;246:755. doi: 10.1016/j.jtbi.2007.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ferrell JE., Jr Tripping the switch fantastic: how a protein kinase cascade can convert graded inputs into switch-like outputs. Trends Biochem Sci. 1996;21:460. doi: 10.1016/s0968-0004(96)20026-x. [DOI] [PubMed] [Google Scholar]
- 20.Huang CYF, Ferrell JE. Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc Natl Acad Sci USA. 1996;93:10078. doi: 10.1073/pnas.93.19.10078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hooshangi S, Thiberge S, Weiss R. Ultrasensitivity and noise propagation in a synthetic transcriptional cascade. PNAS. 2005;102:3581. doi: 10.1073/pnas.0408507102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ferrell JE., Jr How responses get more switch-like as you move down a protein kinase cascade. Trends Biochem Sci. 1997;22:288. doi: 10.1016/s0968-0004(97)82217-7. [DOI] [PubMed] [Google Scholar]
- 23.Kholodenko BN. Negative feedback and ultrasensitivity can bring about oscillations in the mitogen-activated protein kinase cascades. Eur J Biochem. 2000;267:1583. doi: 10.1046/j.1432-1327.2000.01197.x. [DOI] [PubMed] [Google Scholar]
- 24.Markevich NI, Hoek JB, Kholodenko BN. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J Cell Biol. 2004;164:353. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wang X, Hao N, Dohlman HG, et al. Bistability, stochasticity, and oscillations in the mitogen-activated protein kinase cascade. Biophys J. 2006;90:1961. doi: 10.1529/biophysj.105.073874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Behar M, Hao N, Dohlman HG, et al. Mathematical and computational analysis of adaptation via feedback inhibition in signal transduction pathways. Biophys J. 2007;93:806. doi: 10.1529/biophysj.107.107516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Heinrich R, Neel BG, Rapoport TA. Mathematical models of protein kinase signal transduction. Mol Cell. 2002;9:957. doi: 10.1016/s1097-2765(02)00528-2. [DOI] [PubMed] [Google Scholar]
- 28.Chaves M, Sontag ED, Dinerstein RJ. Optimal length and signal amplification in weakly activated signal transduction cascades. J Phys Chem B. 2004;108:15311. [Google Scholar]
- 29.Sontag E, Chaves M. Exact computation of amplification for a class of nonlinear systems arising from cellular signaling pathways. Automatica. 2006;42:1987. [Google Scholar]
- 30.Morishita Y, Kobayashi TJ, Aihara K. An optimal number of molecules for signal amplification and discrimination in a chemical cascade. Biophys J. 2006;91:2072. doi: 10.1529/biophysj.105.070797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nash P, Tang XJ, Orlicky S, et al. Multisite phosphorylation of a CDK inhibitor sets a threshold for the onset of DNA replication. Nature. 2001;414:514. doi: 10.1038/35107009. [DOI] [PubMed] [Google Scholar]
- 32.Deshaies RJ, Ferrell JE. Multisite phosphorylation and the countdown to S phase. Cell. 2001;107:819. doi: 10.1016/s0092-8674(01)00620-1. [DOI] [PubMed] [Google Scholar]
- 33.Qu Z, Weiss JN, MacLellan WR. Regulation of the mammalian cell cycle: a model of the G1-to-S transition. Am J Physiol Cell Physiol. 2003;284:C349. doi: 10.1152/ajpcell.00066.2002. [DOI] [PubMed] [Google Scholar]
- 34.Goldbeter A, Koshland DE., Jr An amplified sensitivity arising from covalent modification in biological systems. Proc Natl Acad Sci U S A. 1981;78:6840. doi: 10.1073/pnas.78.11.6840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Qian H. Amplifying signal transduction specificity without multiple phosphorylation. Biophys J. 2003;84:1410. doi: 10.1016/S0006-3495(03)74955-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Qian H. Phosphorylation energy hypothesis: open chemical systems and their biological functions. Annu Rev Phys Chem. 2007;58:113. doi: 10.1146/annurev.physchem.58.032806.104550. [DOI] [PubMed] [Google Scholar]
- 37.Goodwin B. An entrainment model for timed enzyme synthesis in bacteria. Nature. 1966;209:479. doi: 10.1038/209479a0. [DOI] [PubMed] [Google Scholar]
- 38.Bliss RD, Painter PR, Marr AG. Role of feedback inhibition in stabilizing the classical operon. J Theor Biol. 1982;97:177. doi: 10.1016/0022-5193(82)90098-4. [DOI] [PubMed] [Google Scholar]
- 39.Pomerening JR, Sontag ED, Ferrell JE., Jr Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat Cell Biol. 2003;5:346. doi: 10.1038/ncb954. [DOI] [PubMed] [Google Scholar]
- 40.Sha W, Moore J, Chen K, et al. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc Natl Acad Sci U S A. 2003;100:975. doi: 10.1073/pnas.0235349100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Becskei A, Seraphin B, Serrano L. Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion. EMBO J. 2001;20:2528. doi: 10.1093/emboj/20.10.2528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ozbudak EM, Thattai M, Lim HN, et al. Multistability in the lactose utilization network of Escherichia coli. Nature. 2004;427:737. doi: 10.1038/nature02298. [DOI] [PubMed] [Google Scholar]
- 43.Thattai M, van Oudenaarden A. Attenuation of noise in ultrasensitive signaling cascades. Biophys J. 2002;82:2943. doi: 10.1016/S0006-3495(02)75635-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Belle A, Tanay A, Bitincka L, et al. Quantification of protein half-lives in the budding yeast proteome. Proc Natl Acad Sci U S A. 2006;103:13004. doi: 10.1073/pnas.0605420103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 46.Qu Z, MacLellan WR, Weiss JN. Dynamics of the cell cycle--checkpoints, sizers and timers. Biophys J. 2003;85:3600. doi: 10.1016/S0006-3495(03)74778-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Novak B, Tyson JJ. Design principles of biochemical oscillators. Nat Rev Mol Cell Biol. 2008;9:981. doi: 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tsai TY, Choi YS, Ma W, et al. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science. 2008;321:126. doi: 10.1126/science.1156951. [DOI] [PMC free article] [PubMed] [Google Scholar]