Construction of a DNA Nano-Object Directly Demonstrates Computation

Abstract

We demonstrate a computing method in which a DNA nano-object representing the solution of a problem emerges as a result of self-assembly. We report an experiment in which three-vertex colorability for a 6-vertex graph with 9 edges is solved by constructing a DNA molecule representing the colored graph itself. Our findings show that computation based on “shape processing” is a viable alternative to symbol processing when computing by molecular self-assembly.

Natural processes from which three dimensional molecular structures emerge can be seen as "structural" computation in nature [1]; the folding of protein chains into their tertiary structures is a familiar example. By contrast, classical models of computing and information processing are based not on direct physico-chemcal processes, but rather on operations on sequences of symbols [2]; we are all familiar with the representation of variables by 0s and 1s in electronic computers. In traditional DNA-based computing, DNA sequences have been used to represent binary symbols and linear DNA sequences encoding vertices, edges and paths have been used to represent graphs to solve problems involving graphs; by performing parallel molecular operations with these molecules, answers have been extracted by employing protocols that entail a series of sequential screening operations [3–7]. Similarly, computational methods involving the self-assembly of DNA tiles into one-dimensional [8] or two-dimensional arrays [9] use the cohesive ends of the tiles to encode binary symbols. By contrast, stable branched DNA molecules [10] offer the opportunity to produce a molecular version of the graph structure, one that acts both as an information processing tool and as a solution to a computation. As abstract mathematical objects in electronic computers graphs are usually represented by their adjacency matrix, which indicates the connectivity of the vertices by the edges.

However, graphs are often drawn as diagrams, by indicating vertices as points in space and edges as arcs or curves connecting the vertices. It is well known that such graph representations can be embedded in 3-space, so that the curves representing the edges do not intersect except at the vertices. Our approach uses precisely such a spatial representation of the graph, thereby avoiding the encryption of its structure into a set of symbols that in turn correspond to DNA sequences. Here, we show that a system containing DNA molecules that can self-assemble into a nano-object, can be used in conjunction with enzymes that catalyze ligation and restriction reactions, to perform a computation. As an example, we have produced a molecular solution to an instance of a non-trivial [11] graph-theoretic problem by assembling a DNA nano-object with the connectivity of the actual graph.

Description of the method

A graph is a construct consisting of vertices connected by edges. The question of whether the vertices of a given graph can be rendered using three colors, such that edge-connected vertices are colored distinctly is called "the three-colorability problem". A general procedure for solution of this and other computational problems through self-assembly of complex molecular structures has been theoretically described in [13]. In this approach, each k-degree vertex in a given graph G is represented as a k-armed branched junction molecule with extended single stranded 5’ ends. We call these molecules vertex building blocks. These extensions are used to identify uniquely each edge that connects two adjacent vertices. The sequence of the single stranded extensions of the arms consists of three parts x, y, and z. The portions x and z uniquely specify the edge, whereas the sequence of the portion y specifies the color of the vertex. Therefore, all arms of a k-armed branched junction have identical middle y portions on the single stranded extensions of its arms indicating the color of the vertex. A vertex of degree 1 can be represented by a DNA hairpin.

For a given graph, if a vertex v is adjacent to a vertex w, the portions x and z of the single stranded extension on one of the arms of the molecule representing v are complementary to the portions x and z of the extension of one of the arms of the molecule representing w. If the middle portion y is also complementary, then this would indicate that the two vertices v and w are colored with the same color. The colors are encoded such that each color sequence contains a cleavage site for a restriction enzyme, such that when two arms of identically colored vertices are hybridized, they form a restriction site that can be cut by the appropriate enzyme. For three-colorability, three enzymes are needed, and therefore only three types of y portion codes are employed.

Each vertex is represented with three types of molecules corresponding to the three colors, each distinguished by the middle y portion of the single stranded extensions on the arms. Given the vertex building blocks for a given graph, the general algorithm for solving the three-colorability problem then consists of the following steps, regardless of the size of the graph: (a) anneal: allow for the sticky ends of the vertex building blocks to join and hybridize. (b) ligate: join the open nicks with a ligase, (c) cleave: destroy the molecular structures where vertices with the same color are joined by applying the three restriction enzymes that cut the hybridized y portions. (d) extract: if any graph structure of the size of the input graph remains, the graph is three colorable, otherwise it is not.

Experimental implementation

Here, we demonstrate the experimental implementation of the method. By employing molecular self-assembly of a nano-object representing the graph itself, we report a solution of the three-colorability problem for a graph of 6 vertices and 9 edges. As noted above, the approach inherently uses a constant number of steps, regardless of the size of the graph. The molecular structure corresponding to the graph encoding the solution of the problem was identified through its resistance to cleavage by restriction endonucleases. A linear molecule that traverses each edge of the graph at least once proved the formation of the structure. The molecule was identified by its length and confirmed through sequencing.

There are three logical steps involved in computing by DNA self-assembly: (i) encoding the problem in molecular components, (ii) creating possible solutions to the problem through assembling these components via cohesive non-bonded interactions, and (iii) extracting the answer from the assembled components; the last step often necessitates the ligation of key strands [3,9] and may entail the amplification of correct answers and/or the removal of incorrect answers[3,5].

Encoding

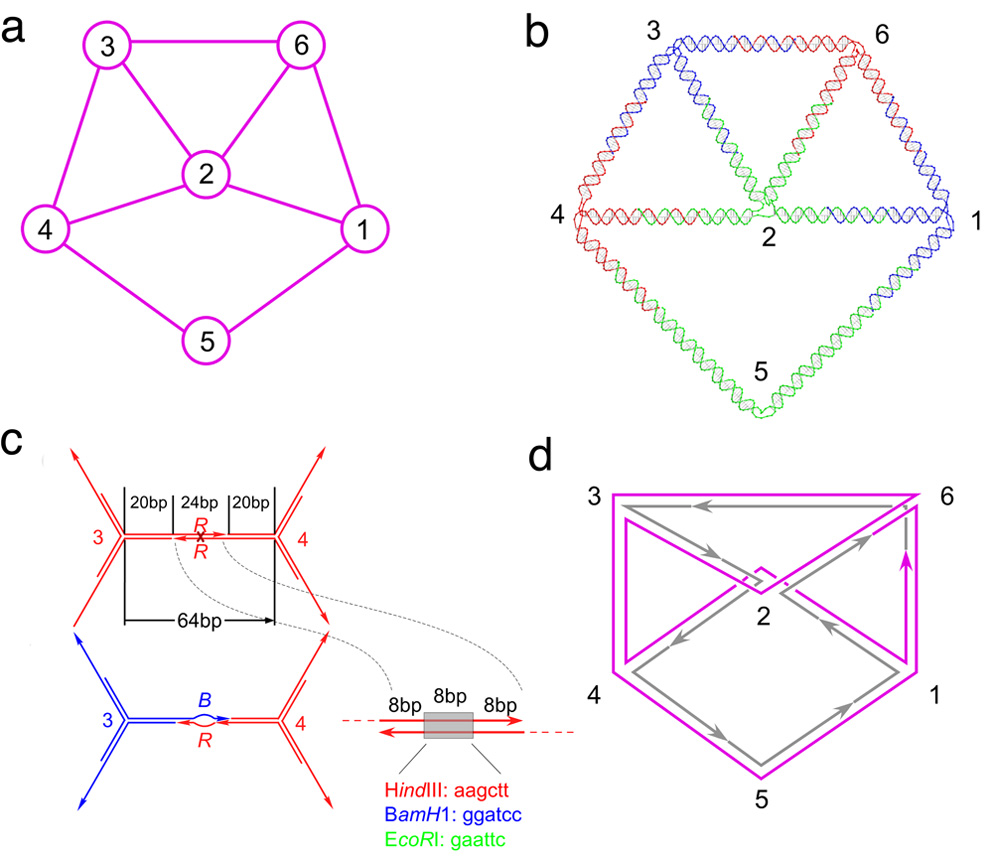
The graph used in the implementation is illustrated in Figure 1a.

Figure 1. Schematics Describing this Computational System and Experiments.

(a) The connectivity of the graph and the numbering of the vertices are shown. (b) A molecular representation of the graph. This drawing was created using the program GIDEON(17). The color assignments of the vertices and of the branched junction that flank them are indicated. The molecule shown is a cyclic single strand of DNA. (c) The structure of the sticky ends. A homochromic edge between vertices 3 and 4 is shown in red above a blue-red heterochromic edge. The homochromic edge contains a restriction site for Hind III in the middle of the sticky end, whereas the heterochromic edge has two distinct mismatched restriction sites indicated as a "bubble". The possible enzyme sites are shown color coded, as is the structure of the sticky ends. The portions of the sticky ends flanking the restriction sites (first 8 and last 8 nucleotides) contain vertex-edge specific sequences. (d) The structure of the reporter strand. The graph is shown in a representation with the helices unwound. Each edge has an integral number of helical turns. The reporter strand visiting every edge is illustrated in magenta. The strands that are not phosphorylated, and hence not ligated to the reporter strand, are illustrated as individual strands in gray. Arrows indicate the 3' ends of the strands.

It consists of six vertices 1,2,…,6, and edges {1,2}, {1,5}, {1,6}, {2,3}, {2,4}, {2.6}, {3,4], {3,6} and {4,5}. Vertex 2 is connected to its neighbors by four edges and therefore represented with 4-armed vertex building block molecule, vertex 5 is connected to its neighbors by two edges, represented with a 2-armed molecule, i.e., a duplex, and the other four vertices are connected to their neighbors by three edges, hence all are represented with 3-armed vertex building blocks. Figure 1b shows how we have encoded this graph in DNA; the edges are all double helical strands of DNA, the vertices correspond to the branch points of DNA branched junctions and the resulting structure (after hybridization) is a cyclic single strand traversing the graph twice. Comparison of Figures 1a and 1b shows that our encoding structurally corresponds to the chosen representation of the graph, where the helix axes correspond to its edges. All edges contain 64 nucleotide pairs except those connected to vertex 5, which contain 97 nucleotide pairs. Edges {5,1} and {5,4} were lengthened to avoid steric or electrostatic clashes with edges {2,1} and {2,4}, which would have occurred if they were all the same length. To allow flexibility of the junction molecules, each branch point is flanked by three unpaired thymidines in each strand, except for vertex 5, which has four. The length of the edges and the unpaired thymidines were chosen to minimize the strain of the structure once it is assembled, after a physical model of the molecule was examined. The investigations of a similar object representing the same graph structure showed existence of at least two topoisomers [14], and we expect that the structure presented here may not necessarily have only one topological embedding in space. The encoding of the graph structure is designed such that the final construct is obtained by hybridizing the 2-arm, 3-arm and 4-arm branched junctions through cohesive ends, thereby forming its edges.

The structure of the cohesive ends extending from each arm of the vertex building blocks consists of three portions x, y and z, as shown in Figure 1c. Their design enables assembly of the structure that represents the computation. Every cohesive (sticky) end is 24 nucleotides long. The outer parts of each cohesive end (portion x indicated through nucleotides 1–8 and portion z through nucleotides 17–24) are encrypted with vertex-edge specific sequences. The inner portion y (nucleotides 9–16) encodes the 'color' of the vertex which contains a restriction site. In our experiment a restriction site for HindIII represents the color red, a site for BamH1 represents the color blue and a site for EcoR1 represents the color green. The middle parts, portions y, of the sticky ends in all of the strands that make up a given junction molecule are identical, indicating the color of the vertex represented by the junction. In forming an edge, if sticky ends encoding the same color are hybridized, thereby joining two identically-colored vertices in violation of the colorability rule, the resulting edge becomes susceptible to digestion by the appropriate restriction enzyme. If an edge is formed joining differently colored vertices, the overlapping middle region of the sticky ends contains two different mispaired sites, and the resulting edge is immune to restriction.

Solving the problem

For each vertex, three copies of the corresponding vertex building blocks, one copy for each of the three colors, should be placed in a test tube. However, if the graph is three colorable, it is three colorable by any permutation of the colors. Hence, the generality of the problem is not lost by fixing two distinct colors for two adjacent vertices. In our experiment, the color for vertex 1 was fixed with blue by representing this vertex only with a ‘blue’ vertex building block in the reaction solution, and the color for vertex 2 was fixed to ‘green’. The encoding of the problem ensures that a single annealing step of hybridizing complementary sticky ends results in the desired graph structure. This step is followed by enzymatic restriction by the three chosen enzymes cleaving all edges that join identically-colored vertices. The solution of the problem is obtained as a molecule representing the graph structure with mis-paired portions along each edge. So as to identify the structure representing the solution, cohesive ends were sealed by DNA ligase. Ligation to form covalent species containing the solution is needed so that solutions can be identified. Non-covalent species are not necessarily stable, and can re-assort their components through processes that include strand invasion and branch migration.

Identifying the answer

Ideally, the ligase and the restriction enzymes would be mixed together in a one-pot reaction, from which cyclic single-stranded molecules traversing the whole graph structure twice (gray and magenta portion in Figure 1d) would emerge as the surviving product material [12– 14]. As a practical matter, the optimal temperatures for ligation and restriction are sufficiently different that the two reactions were performed in separate steps. In addition, enzymatic ligation concurrent with restriction might result in the unwanted rescue of some of the restricted fragments; high-yield non-enzymatic ligation that does not use restricted ends, such as 2’,2’ ligation[15], ultimately would be a more robust method to use in a one-pot reaction. Note that the surviving graph-traversing molecule contains mis-pairs in each edge. Thus, it does not correspond to the free energy minimum amongst the possible hydrogen-bonded self-assemblies of the vertex building blocks. The existence of this molecule provides a positive answer to the question of whether the given graph is 3-colorable.

Another practical limitation inherent to our demonstration is that ligation of synthetic DNA is not sufficiently robust to produce adequate quantities of a completely ligated cyclic molecule, a product that could be assayed either as exonuclease-resistant [13,14], or as a species that migrates off-diagonal on a 2D gel [14]. We have dealt with this issue here by limiting the ligation to a 'reporter' strand that traverses each edge at least once; the strand we have used for this work is shown in magenta in Figure 1d. Although not every DNA graph structure can be constructed as one cyclic molecule [12], every DNA graph structure can contain such a reporter strand that visits every edge at least once [16]. If a graph contains vertices of degree 1, the reporter strand needs to include both strands of the hairpin, as well as the loop.

Experimental results

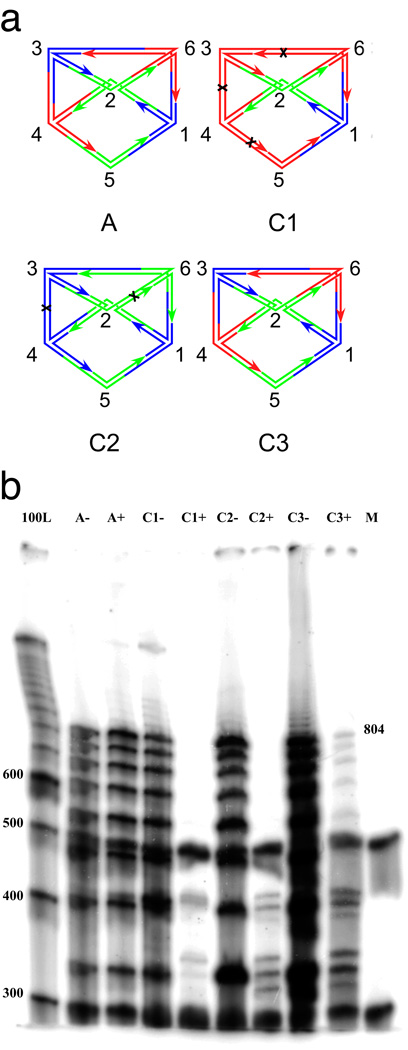
The results of the ligation and restriction experiments are shown in Figure 2. Four experiments are diagrammed in Figure 2a and the results are visible in Figure 2b. In the positive control experiment, the experiment labeled A, only the junctions corresponding to the correct solution are added to the ligation mixture. There is no apparent difference between the lanes containing restricted material (labeled A+) and unrestricted material (labeled A−) because there are no restriction sites in the assembled molecule in this case. As noted above, no generality is lost if we fix two adjacent vertices to different colors; we have fixed vertex 1 to be blue and vertex 2 to be green. The negative control experiments are labeled C1 and C2. In addition to the fixed vertices, the graph constructed in experiment C1 contains DNA for vertices 3–6 corresponding only to red coloring; the graph constructed in experiment C2 contains only blue and green vertices. The target species of reporter strand (804 nucleotides long) is destroyed by restriction in both experiments (lanes C1+ and C2+).

Figure 2. Denaturing gel electrophoresis.

(a) Schematic representations of the experiments reported here. The labels of the graphs correspond to the names of the experiments. Experiment A (for answer) contains only the branched junctions that produce the result. Experiment C1 (for one color) contains branched junctions corresponding to the two fixed vertices, vertex 1 (blue), vertex 2 (green) and all other vertices in red. Black crosses indicate the cleavage sites on the red edges. Experiment C2 (for two colors) contains branched junctions corresponding to all vertices in colors blue and green. The graph labeled C2 is only one possibility that can be assembled. Cleavage sites on homochromatic edges are indicated. Experiment C3 (for three colors) contains branched junctions corresponding to blue vertex 1, green vertex 2, and all colors for vertices 3–6. The correct undigested answer is shown. There are 81 (34) different molecules formed. Except for the answer illustrated, all other molecules contain at least one homochromatic edge and therefore are cleaved. (b) The gel showing the results of the experiments performed. From left to right, the lanes correspond to a 100 nucleotide marker, pairs of experiments containing the answer only (A), a one-color combination (C1), a two-color combination (C2) a three-color combination (C3) and a labeled marker (M) added in equal quantities to each experimental lane so that relative intensities of the lane's contents can be estimated; this prevents some lanes from being under-represented. Experiments after ligation but before enzyme restriction are indicated with a '−', and experiments after restriction are labeled with a '+'. The target reporter strand traverses every edge; seven edges once and two 64 bp edges twice. Its length, including the free thymidines is 804. Note that the target 804-mer reporter strand survives digestion in lane C3+, but not in lane C1+ nor in lane C2+.

Other than permutation of the colors, the graph in Figure 1a has only one solution for the 3-colorability problem. The actual computation is performed in experiment C3 where branched junctions of all colors for vertices 3–6 were added to the fixed-color vertices 1 and 2. By fixing colors for vertices 1 and 2, there is only one coloring of the graph solving this three-colorability problem, shown in Figure 2a (graph C3). Fixing these vertices eliminates five of the six solutions that are equivalent to the one we have obtained, thereby simplifying the analysis. We note that the generality of the solution is not reduced by fixing colors of two vertices, because solutions that differ by a permutation of the colors can be considered equivalent. Considering that the remaining four vertices can appear in any of the three colors, the solution represents 1/3⁴ (= 1/81, ~1.2%) of the ligated structures that form; this estimate is based on the assumption that all ligations are equally probable. This solution can be identified through the target 804-nucleotide reporter strand. In close agreement with the estimate of 1.2%, we find ~1.0% of the target strand material in lane C3- survives digestion, as seen in lane C3+. All other bands in the lane are the result of incomplete ligation. We point out that theoretically, no other graphs can be formed by the given building blocks except the graph itself and its dimers, trimers, etc. [13].

To prove that the target 804-nucleotide reporter strand traces the edges of the correctly colored graph, we amplified this molecule and sequenced it. The reporter strand contains the predicted sequence for the correct solution (see Supporting Material). Control PCR experiments testing for the presence of any edges flanked by vertices of the same color show that none are present if the DNA is produced by DNA polymerase from nucleoside triphosphates; synthetic DNA sometimes contains sufficient chemical errors to thwart complete digestion by the restriction endonucleases. We found it necessary to use triphosphate-based strands (produced enzymatically by DNA polymerase, rather than by organic synthesis) only on the edge connecting vertices 4 and 5, although it might in general be advisable to use DNA produced this way for all strands. The quantitative results of the control experiments are shown in the Supporting Information. The current experimental approach is not highly efficient, owing to technical issues; a discussion of the limits is included in the Supporting Information.

Concluding remarks

We have demonstrated that solving a graph theoretic problem can be performed by assembly of a DNA nano-object representing the graph structure itself. Thus, we have used self-assembly of a nanostructure, instead of binary or linear encodings for the graph or paths in the graph to solve a graph-theoretic problem. The problem chosen for this experiment falls in the class of well-known NP-complete problems. Although theoretically it can be shown that variety of other computational problems can be solved in this way [13,14], this method for solving hard computational problems would be difficult to scale experimentally. We estimate that under current experimental conditions the method would be limited to graphs with approximately 13 vertices and 28 edges as explained in the Supporting Information. However, the experiment shows clearly that an environment containing molecules prone to self-assemble via specific recognition rules can be seen to perform a computation when the appropriate components (enzymes here) are present to aid in the extracting the answer. Moreover, in principle, a complex shape, including sequences that mispair, results from the computation, and this shape actually represents the answer of the computation; experimental limitations here resulted in the production of the reporter strand. From all molecules that assemble into the graph structure, only the configuration with mis-pairing on each edge provides the answer to the problem and survives the digestion. Our findings confirm the notion that in information processing through molecular self-assembly, computation based on "shape processing" represents a viable alternative to computation based on symbol processing. Furthermore, if we consider that natural self-assembly processes that produce complex molecular shapes, associated with a selection process, perform computation, we are left with the question "What do they compute and does this computation confer a selective advantage?" [18]