New Insights into the Stratum Corneum Lipid Organization by X-Ray Diffraction Analysis

Abstract

The characteristic 13-nm lamellar phase that is formed by lipids in the outermost layer of the skin, the stratum corneum (SC), is very important for the barrier function of the skin. To gain more insight into the molecular organization of this lamellar phase, we performed small-angle x-ray diffraction (SAXD) using various lipid mixtures mimicking the lipid composition in SC. In the SAXD pattern of each mixture, at least seven diffraction orders were observed, attributed to the lamellar phase with a repeat distance ranging from 12.1 to 13.8 nm. Using the sampling method based on the variation in repeat distance, we selected phase angles for the first six diffraction orders. Using these phase angles for the lamellar phase, a high-resolution electron density distribution could be calculated. Subsequently, from SAXD patterns of isolated SC, the electron density distribution of the lamellar phase was also calculated and appeared to be very similar to that in the lipid mixtures. This demonstrates that the lipid mixtures serve as an excellent model for the lipid organization in SC, not only with respect to the repeat distance, but also in terms of the electron density distribution within the unit cell.

Introduction

The skin forms the interface between the human body and the environment. It protects our body against various biological and chemical hazards and from desiccation in a dry environment. The outermost layer of the skin, the stratum corneum (SC), forms the main barrier against diffusion of substances across the skin (1). This layer consists of overlapping flattened dead skin cells. Each cell is surrounded by lipids, which serve as the mortar between the cells. The lipids form multiple sheets of lamellae and are mainly composed of ceramides (CER), cholesterol (CHOL), and free fatty acids (FFA). These lipid classes are present in an approximately equimolar ratio (2). In the SC, the lipids form two lamellar phases with repeat distances of ∼6 and 13 nm, also referred to as the short periodicity phase and long periodicity phase (LPP), respectively. Furthermore, the orientation of the lipid lamellae is approximately parallel to the SC surface (3). Within the lipid lamellae, the lipids are organized predominantly in a crystalline lateral packing (4,5). The presence of oriented lipid lamellae as well as the crystalline packing is thought to contribute greatly to the barrier function of the SC.

Previous studies showed that mixtures prepared with either synthetic CER or native CER mixed with CHOL and with FFA mimic the SC lipid organization very closely (6–8). Although CER and CHOL play a prominent role in the formation of the two lamellar phases, the addition of FFA is crucial for the formation of the densely packed orthorhombic crystalline structure (6,9). Furthermore, the presence of CER1, an acyl CER with a linoleic acid linked to a very long ω-hydroxy fatty acid chain (see Fig. 1), is a prerequisite for the formation of the LPP (6,10,11).

Figure 1.

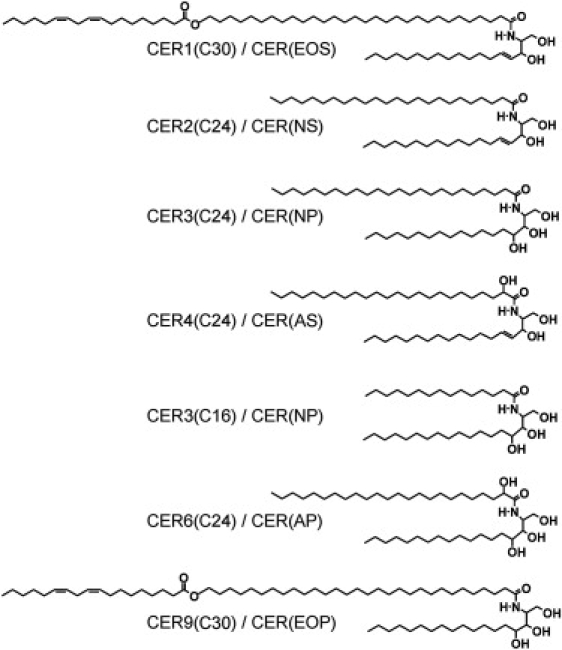
Molecular structure of the synthetic CER used in the lipid mixtures of Table 1. The nomenclature according to Motta et al. (40) is also provided.

Although over the years, a lot of information has been gathered on the SC lipid organization and the role the various lipid classes play in this organization (10–13), until now no high-resolution electron density profile of the LPP has been presented. In previous studies, several attempts have been made to determine an electron density profile of the LPP. White et al. performed the first calculations using a block-shaped electron density profile (14). Our group performed electron density calculations in which the electron density profiles were simulated by Gaussian curves (4,15). However, both studies suffered from the fact that no swelling of the lamellae was induced and therefore no unique electron density profile could be determined. More recently, McIntosh used a mixture of isolated pig CER, CHOL, and palmitic acid and performed x-ray diffraction studies (16). Although information was obtained on the distribution of CHOL in the repeating unit, due to the low resolution of the electron density profile the lipid organization in the repeating unit could not be unraveled. Therefore, the aim of this study is to obtain more detailed insights into the molecular organization of the LPP by analyzing a large number of x-ray diffraction curves obtained from SC lipid mixtures. In addition, the diffraction curves of SC isolated from pig skin, mouse skin, and in vitro cultured skin (that is, skin cultured from cells) were also analyzed for comparison. By using six reflection orders of the LPP, electron density profiles could be constructed with 1.1-nm resolution. By analyzing these high-resolution electron density profiles, novel insights on the location of CER1 in the repeating unit could be obtained.

Materials and Methods

Materials

Synthetic CER1(C30) (CER(EOS)); CER2(C24) (CER(NS)); CER3(C24) (CER(NP)); CER4(C24) (CER(AS)); CER3(C16) (CER(NP)); CER6(C24) (CER(AP)); and CER9(C30) (CER(EOP)) were generously provided by Cosmoferm (Delft, The Netherlands). The Palmitic acid (C16:0), stearic acid (C18:0), arachidic acid (C20:0), behenic acid (C22:0), tricosanoic acid (C23:0), lignoceric acid (C24:0), cerotic acid (C26:0), cholesterol, cholesterol sulfate, and acetate buffer salts were purchased from Sigma-Aldrich Chemie (Schnelldorf, Germany). All organic solvents used are of analytical grade and manufactured by Labscan (Dublin, Ireland). The water used is of Millipore quality (Billerica, MA).

Isolation of ceramides

Pig or human SC lipids were extracted from isolated SC using the method of Bligh and Dyer (17) and applied on silicagel as published previously (18). The lipid composition of the collected fractions was established by one-dimensional, high performance thin layer chromatography (19).

Preparation of the lipid mixtures

The isolated or synthetic CER, CHOL, and FFA were dissolved in chloroform/methanol (2:1 v/v). The solvents were mixed in appropriate ratios to achieve the required compositions. Approximately 1.5 mg of lipids in solution was sprayed as an unoriented glob of lipids of ∼1 mm high in the center of a mica strip of 10 × 2 mm using a Camag Linomat IV sample applicator (Muttenz, Switzerland). Only a very small area of ∼2 mm² is used to ensure a random orientation of the lamellae in the sample. Spraying was performed at a rate of 5 μL/min, under a gentle stream of nitrogen gas. Subsequently, each lipid sample was equilibrated at a temperature around the melting point of the lipid mixture, which was either 60 or 70°C, dependent on the composition. When preparing dry lipid mixtures, after 10 min of equilibration the sample is cooled down to room temperature. In the case of hydration (11 out of the 12 measured lipid mixtures, see Table 1), after 10 min of equilibration at elevated temperatures, acetate buffer (pH 5.0) was added to the sample before cooling down to room temperature and the sample is kept under buffer until measured. To homogenize the hydrated samples, five freeze-thawing cycles were carried out between −20°C and room temperature. Composition, equilibration temperature, and hydration method of all SC lipid models used for phase calculations are provided in Table 1. The exact composition and preparation method of the mixtures prepared from isolated pigCER were described previously (20). CerA designates a mixture of synthetic ceramides containing CER1, CER2, CER3, CER4, CER3(C16), and CER6 (see also Fig. 1) in a molar ratio of 15:51:16:4:9:5, which closely resembles the CER composition in pig SC (18). For the FFA mixture, the following composition was selected: C16:0, C18:0, C20:0, C22:0, C23:0, C24:0, and C26:0 at a molar ratio of 1.8:4.0:7.7:42.6:5.2:34.7:4.1, respectively. This chain length distribution is based on the FFA composition in SC (21).

Table 1.

Mixtures used for the determination of phase angles

Lipid mixture composition and molar ratios	Symbol in Figs. 3 and 4	Hydration	Eq. temp. (°C)	Repeat distance (nm)
CerA/Chol/FFA 1:1:1	○	pH 5	70	12.3
CerA/Chol/FFA 1:1:1	○	pH 5	70	12.4
CerA/Chol/FFA 1:1:1	○	pH 5	70	12.1
CerA/Chol/FFA: ChSO4 1:1:1:0.1	○	pH 5	70	12.4
PigCER/Chol/FFA 1:1:1	▵	No	60	12.8
PigCER/Chol/FFA 2:1:1∗	▵	pH 5	60	13.0
PigCER/Chol/FFA/ISIS 2:1:1:1∗	▵	pH 5	60	13.0
PigCER/Chol/FFA/IPIS 2:1:1:1∗	▵	pH 5	60	13.4
PigCER/Chol/FFA/GMIS 2:1:1:1∗	▵	pH 5	60	13.8
15% synthCER1 + HCER[2..9]/Chol/FFA 1:1:1	♢	pH 5	70	13.5
30% synthCER1 + HCER[2..9]/Chol/FFA 1:1:1	♢	pH 5	70	13.4
CerA/Chol/FFA 1:1:1†	>	pH 5	70	12.3

The three moisturizers used in these mixtures are isostearyl isostearate (ISIS), isopropyl isostearate (IPIS), and glycerol monoisostearate (GMIS). Cholesterol sulfate is abbreviated to ChSO₄; CER isolated from human SC is abbreviated to HCER; and CER isolated from pig SC is abbreviated to PigCER. CerA designates a mixture containing the first six synthetic CERs presented in Fig. 1.

^∗Published previously (20).

^†This sample has an adjusted CerA composition in which a part of the CER1 is replaced by CER9 (8.5% CER1, 6.5% CER9).

X-ray diffraction analysis

All samples were measured at the European Synchrotron Radiation Facility (ESRF) in Grenoble (France), at the small-angle x-ray diffraction (SAXD) beam line BM26b as described previously (8). Data acquisition was performed for a period of 10–15 min. From the scattering angle, the scattering vector (q) was calculated by q = 4πsinθ/λ, in which λ is the wavelength at the sample position and θ the scattering angle. One-dimensional intensity profiles were obtained by transformation of the two-dimensional SAXD pattern from Cartesian (x,y) to polar (ρ,ϕ) coordinates and subsequently, integration over ϕ from 60 to 120°. Although the integration was performed over a range of ϕ, the summed intensity over this angle was divided by the number of pixels present in the integration range. This method is similar to linear scan integration and therefore a correction factor proportional to h is required.

Peak intensities were calculated from the diffraction curve using a mathematical curve-fitting procedure. This fitting procedure can be described as follows: First a baseline is created that follows the decaying curve. Secondly, the peaks present in the SAXD pattern are fitted with Gaussian peak shapes by a least-squares approximation. When the peak in the SAXD pattern is composed of two overlapping reflections from different phases (for example, when a peak exhibits a shoulder), this peak is fitted by two Gaussians. The repeat distance (d) of the LPP and additional phases was determined from the position (q_h) of all nonoverlapping reflections attributed to the LPP or additional phase by d = 2πh/q_h. Vice versa, the position of an overlapping Gaussian was calculated from its lamellar repeat distance by q_h = 2πh/d (maximally three out of seven reflections for the LPP were overlapping in a mixture). For clarity, in the figure where a SAXD curve is displayed, the fitted Gaussian peaks are plotted together with the measured diffraction curve.

To compare the integrated peak intensities calculated from a SAXD curve originating from different samples (encompassing different signal strengths), a normalization method is required. Our normalization method is adapted from the method presented by Blaurock and Nelander (22). The normalization procedure can be described as follows: In a diffraction pattern, the intensity for each order, I(h), is divided by the total intensity over all orders (the sum of I(h) for h = 1 to n; see Eq. 1). In contrast to Blaurock and Nelander, we did not correct for the increase in bilayer repeat distance (D/D_min) due to the limited variation in repeat distance observed in the LPP. Subsequently, structure amplitudes were calculated from these normalized intensities after correction for the Lorentz factor (equal to h) and correction for the linear integration (also by a factor h) (see (23)), as

$$\left|F\left(h\right)\right|=\sqrt{I{\left(h\right)}_{\text{norm}}·h^2},\text{where}I{\left(h\right)}_{\text{norm}}=I\left(h\right)/\sum _{h=1}^{n}I\left(h\right)\text{.}$$ (1)

In this equation, |F(h)| is the structure amplitude corresponding to the normalized intensity I(h)_norm at diffraction order h, and n is the maximum number of orders included in the calculations.

Calculation of an electron density distribution

Sampling of the continuous Fourier transform is performed by plotting the structure amplitudes for all the sets of diffraction data, with each set containing a small variation in repeat distance. Up to six orders of diffraction are included in the calculations. In the procedure of selecting the correct phase for each diffraction order, Shannon's sampling theorem (24) is used to construct a continuous curve through one set of diffraction data. Shannon's equation as presented by Franks and Lieb (25) is rewritten as

$$F_{\text{cont}}\left(q\right)=\sum _{h=-n}^n\left|F\left(h\right)\right|·\varphi \left(h\right)·\sin \left(\frac{qd}{2}-\pi h\right)/\left(\frac{qd}{2}-\pi h\right)\text{.}$$ (2)

In this equation, ϕ(h) is the phase angle of diffraction order h. The unit cell of the LPP is centrosymmetric, as has clearly been shown by the broad-narrow-broad pattern of RuO₄ fixed lipids in SC, visualized in the electron microscope (16,26). Therefore, ϕ(h) is either 0 or 180°, and thus the sign of the structure factors is either plus or minus, respectively. The zero order structure factor F(0) is equal to the positive average electron density of the lamellae and is arbitrarily set to 1 to fit with the data. However, the value of F(0) does not play a role in the calculation of an electron density distribution other than creating an offset value.

With Eq. 2, a continuous function was calculated that fitted with one data set of structure factors calculated from the six diffraction peaks of a selected sample. As for each of the six structure factors of this data set, a plus or minus sign is possible, 64 phase combinations are possible, and therefore 64 continuous functions can be calculated. All these continuous functions were calculated and compared with the experimentally determined structure factors of the lipid mixtures presented in Table 1. For each of the 64 curves, the fit with experimental data is evaluated by the method of least squares, provided in

$$R^2=1-\left[\sum _{\text{i}}{\left(dat{a}_{\text{i}}-fi{t}_{\text{i}}\right)}^2/\sum _{\text{i}}{\left(dat{a}_{\text{i}}-\overline{data}\right)}^2\right]\text{.}$$ (3)

In this equation, data_i and fit_i represent, respectively, the i^th experimental value and the i^th fit value, and $\overline{data}$ represents the mean of all experimental values. Furthermore, a value of R² = 1 designates a perfect fit. The phase combination of the curve that most closely fitted with all the experimental data according to the method of least squares was selected as the correct set of phases.

Finally, with the correct phase set, together with a set of structure amplitudes obtained from a selected lipid mixture, an electron density profile ρ(x) for the LPP was calculated using (27)

$$\rho \left(x\right)=F\left(0\right)+2\sum _{h=1}^n\left|F\left(h\right)\right|·\varphi \left(h\right)·\cos \left(\frac{2\pi hx}{d}\right)\text{.}$$ (4)

In this equation, d is the repeat distance of the unit cell and x is the distance from the center of the unit cell.

Results

The SAXD pattern of a lipid mixture

An x-ray diffraction pattern of a lipid mixture composed of PigCER/CHOL/FFA in a 2:1:1 molar ratio (see Table 1) is provided in Fig. S1 (in the Supporting Material). The rings display a uniform density demonstrating the random orientation of the lipid lamellae. The integrated intensity of these rings over an angle of 60° is displayed in Fig. 2. In the diffraction pattern of this mixture, the seven diffraction orders of the LPP are well separated from the two diffraction peaks assigned to CHOL and to the short periodicity phase. The first six diffraction peaks of the LPP from this particular lipid mixture will be used for the calculation of an electron density profile, described below.

Figure 2.

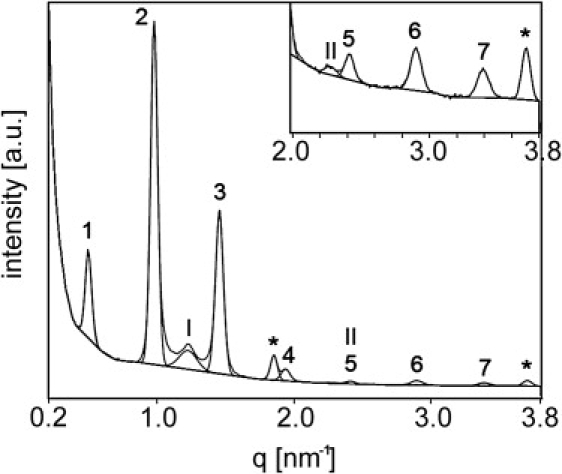
Result of the integration of the ring-shaped diffraction pattern of a lipid mixture with PigCER/CHOL/FFA in a 2:1:1 molar ratio over a 60° angle (see Fig. S1 in the Supporting Material). The Gaussian peaks that are fitted to the SAXD pattern are used to determine the peak areas. The diffraction peaks associated to the LPP are indicated by Arabic numbers. The other peaks that are present arise from a short lamellar phase (indicated by Roman numerals) and crystalline cholesterol (indicated by asterisks).

Determination of structure factors and solving of the phase problem

For a series of additional lipid mixtures listed in Table 1, small angle x-ray diffraction data are also collected. The data show that all these lipid mixtures form an LPP very similar in length to the LPP observed in SC. However, as shown in Table 1, the lipid mixtures exhibit a small variation in the repeat distance between 12.1 and 13.8 nm.

For each lipid mixture presented in Table 1, a set of structure amplitudes is calculated from the intensities of the various diffraction peaks using Eq. 1. In Fig. 3, the calculated structure amplitudes are plotted. Each group of structure amplitudes that belong to the same diffraction order (indicated by 1–6) is encircled in this figure. We took six orders of diffraction for the calculations as we noticed that by including the seventh order, there was overlap in the position of the structure amplitudes in reciprocal space. Probably this overlap is the result of the different compositions used in our study, because small changes in the unit cell structure are caused only by changes in the higher orders of diffraction. Therefore it is not clear whether there is a phase change between the Fourier transform of the sixth and seventh order. From Fig. 3 it is already obvious that the data points sample a continuous function. Each group of structure amplitudes in Fig. 3 (belonging to the same diffraction order) can have either a plus or a minus sign, as the unit cell of the LPP is considered to be centrosymmetric (26). When including six orders of diffraction in the calculations (encircled in Fig. 3), the number of possible phase combinations is 2⁶ = 64. To determine the correct phase combination, first a continuous line is fitted through the set of structure factors of the lipid mixture with PigCER/CHOL/FFA 2:1:1 using Shannon's theorem (see Eq. 2). Subsequently, based on the six structure amplitudes of the PigCER/CHOL/FFA 2:1:1 mixture, continuous Fourier functions were calculated for all 64 phase combinations. The correct phase solution is that particular combination of phases for which the continuous Fourier transform fits closely with the structure amplitudes, calculated from the diffraction patterns of the lipid mixtures listed in Table 1. The phase solution that resulted in the best fit of the calculated continuous Fourier transform with the experimental structure amplitudes is plotted in Fig. 4. This phase solution was selected as the best solution according to the method of least-squares (R² = 0.972). For orders 1–6, the phase solution resulted in the following combination of signs: − + + − − +. The second best solution with a slightly lower R² is the solution with the exact opposite sign combination of + − − + + −. As the sign combination − + + − − + resulted in the best fit, and is, in addition, in agreement with the sign combination for the first three orders reported by McIntosh using very similar lipid mixtures (16), we considered the − + + − − + sign combination as the correct phase combination. This phase combination will be used to calculate an electron density profile for the LPP.

Figure 3.

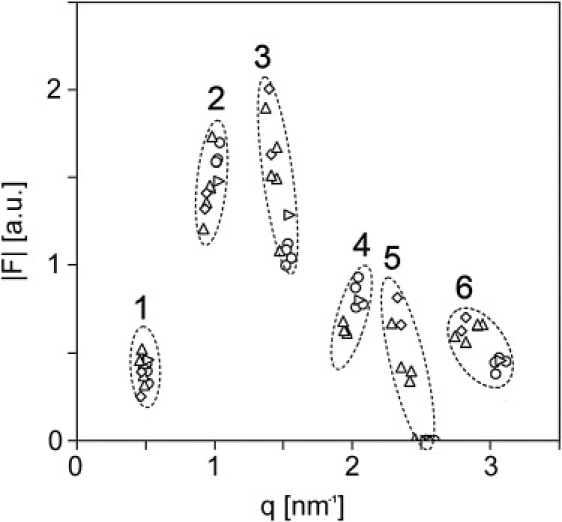
Plot of the structure amplitudes obtained from diffraction patterns of the lipid mixtures presented in Table 1. Encircled are the structure factors that belong to the same order of diffraction, indicated by numbers 1–6.

Figure 4.

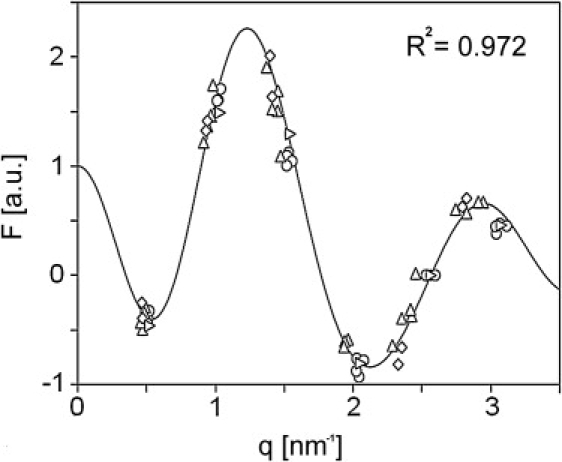
Plot of the continuous Fourier curve, calculated with one set of structure factors from the lipid mixture PigCER/CHOL/FFA in 2:1:1 ratio, is shown fitting through the structure factors of the remaining lipid mixtures in Table 1. The curve and structure factors are calculated using the phase solution, with respective phase signs for orders 1–6 being − + + − − +.

The electron density profile of the LPP

From the set of structure amplitudes obtained for the selected lipid mixture (PigCER/CHOL/FFA 2:1:1) together with the phase combination − + + − − +, the electron density profile is constructed using Eq. 4. This profile is plotted in Fig. 5. The maximum resolution of details in the profile (d/2h_max) is 1.1 nm. Within the repeating unit of the LPP (d = 13 nm), four regions with a high electron density are present. At the boundary of the unit cell, two high electron density regions are located at ∼−6.5 and +6.5 nm. In addition, closer to the center of the unit cell, two other narrow high electron density regions are located at −2.0 and +2.0 nm, with a very small submaximum at 0 nm in between. Model calculations of the electron density of the CER1 and CER2 headgroup relative to the electron density of the CER double alkyl chain (using atomic numbers, following the method of Franks (28)) revealed that the headgroups are ∼1.5 times more dense than the alkyl chains (data not shown). Thus, in general, the high electron density peaks correspond to the polar headgroups, whereas the lower electron density regions correspond to the hydrocarbon chains of the lipids. Therefore, the electron density profile of Fig. 5 results in a unit cell containing three lipid layers. One lipid layer is located in the center with a width of 4.0 nm and on each side of this central lipid layer two adjacent layers are located, both being 4.5 nm in width.

Figure 5.

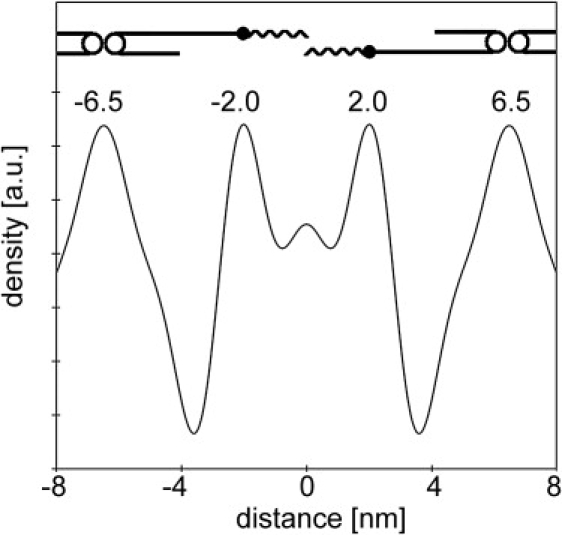
The calculated electron density profile for the LPP in the lipid mixture with PigCER/CHOL/FFA in 2:1:1 molar ratio. Also provided is a model showing the possible location of the CER1 molecule inside the unit cell.

The smallest detail in the electron density profile in Fig. 5 is located at the center of the unit cell; a small submaximum at 0 nm. As six orders have been used for the electron density calculation and the submaximum is not present in all calculated electron density profiles of the lipid mixtures used, this small submaximum is not considered as relevant.

X-ray diffraction profiles of intact SC

In previous studies, the similarity between the repeat distance of the LPP in the lipid model mixtures and in SC has been presented (11,16,18,29). With the new phase information for the structure factors and the related electron density profiles, the next question is whether the electron density profiles of the LPP in the lipid mixtures are also representative for the LPP in SC. This would demonstrate that the lamellar organization in lipid mixtures and in SC is similar, at a high level of detail. To determine this, accurate information about the peak intensities of the LPP in SC is required. This information is available for the LPP in mouse SC (15), in SC of cultured skin (i.e., skin generated from isolated skin cells; V. S. Thakoersing, M. Ponec, and J. A. Bouwstra, unpublished results) and in pig SC (18). Unfortunately, for SC from human skin, the diffraction peaks of the LPP are not available at a sufficient resolution. For SC isolated from human skin equivalents and from mouse skin, the peak intensities for, respectively, six and five diffraction orders of the LPP could be calculated directly from the corresponding diffraction curves using the Gaussian fitting procedure. However, in the case of pig SC, the diffraction peaks are very broad and overlapping (30). Therefore recrystallization of the lipids was required, providing much sharper peaks (18). With the peak intensities and the set of phase angles provided above, the structure factors were calculated. The structure factors for the SC are provided in Fig. 6 together with the previously obtained continuous Fourier function of the example lipid mixture PigCER/CHOL/FFA 2:1:1. It is striking that the six structure factors of the LPP detected in SC of cultured skin and the five structure factors in pig SC fit well with the continuous Fourier function. However, with respect to the five reflections in the diffraction curve of the mouse SC, the deviations are larger. The matching of the structure factors of the LPP in pig SC and in SC of cultured skin indicates that the electron density distribution in the model mixtures is very similar to that in SC. The partial correlating mouse SC structure factors, however, imply that the mouse SC and the model mixtures contain a somewhat different molecular structure for the LPP.

Figure 6.

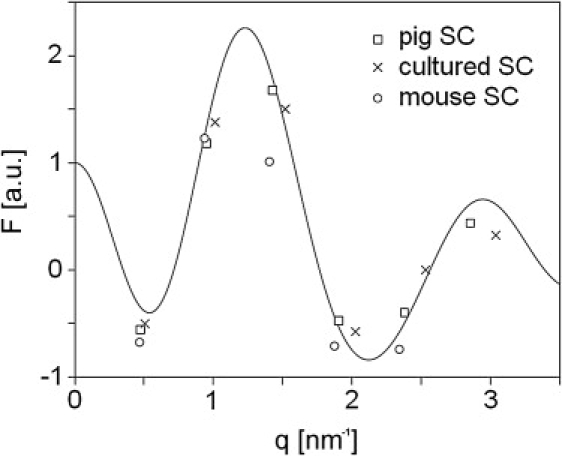
Cultured skin SC, mouse SC, and pig SC structure factors, plotted together with the continuous Fourier transform displayed in Fig. 4. The structure factors of cultured skin SC and pig SC fit nicely with the continuous Fourier transform, whereas the structure factors of mouse SC fit to a lesser extent.

Discussion

The high-resolution electron density profile presented in this article provides a more detailed insight into the molecular organization of the LPP. We combined the x-ray diffraction data of a large number of SC model mixtures in which the lipids form the LPP with a slight variation in repeat distance. With the intensities of six reflections we were able to select a set of phase angle combinations, namely − + + − − +. By combining the phase angles with the structure amplitudes of the six reflections attributed to the LPP, we calculated an electron density profile for the unit cell of the LPP. From the trend that the structure factors of all model mixtures sample the same function (see Figs. 3 and 4), it follows that a very similar electron density profile for the LPP is present in all mixtures, with slight variations due to the variation in the composition of the mixtures. This similarity in electron density profile for the model mixtures prepared with either synthetic CER or isolated CER, demonstrates a very similar molecular organization for the LPP in these mixtures. The similarity at this high level of detail is quite remarkable, as the fatty acid chain-length variation and the headgroup variation in the synthetic CER mixture is less abundant than in isolated CER mixtures. In the former, only acyl chains with a chain-length of 16, 24, and 30 carbon atoms are present, whereas in the latter there is a wide variation in acyl chain-length, ranging from ∼14 to 34 carbon atoms. Furthermore, as we included both dry and hydrated samples, this also suggests that the addition of a buffer at pH 5 does not dramatically change the electron density profile of the unit cell and therefore confirms that almost no swelling of the lamellae is induced, as observed previously (7,11,15).

We calculated the structure factors from reflections attributed to the LPP in SC isolated from pig, mouse, or cultured skin. The structure factors of the LPP in SC of pig and of cultured skin fitted well with the continuous Fourier transform obtained for the lipid mixtures, demonstrating that the electron density profile in the unit cell of the LPP in the mixtures is very similar to the profile of the LPP in SC of pig and cultured skin. Although the mouse SC exhibits a slightly different organization, the lipid mixtures serve as an excellent model for the lipid organization in SC of pig and cultured skin, not only with respect to the similarity in repeat distance of the LPP (11,16,18,29), but also in mimicking the molecular organization in the unit cell of the LPP. This is a big step forward toward unraveling the molecular organization of the LPP in SC.

Average electron density profiles for the LPP in the mixtures

Our method for determining the phase angles of the structure factors is slightly different from the swelling method that is commonly used. The swelling method is based on increasing a lamellar repeat distance by varying the hydration level of the lipid mixture (28,31,32). However, in previous studies it has been observed that at physiological conditions the repeat distance of the LPP in SC or in SC lipid models is almost insensitive to the level of hydration (7,11,15). Only when using a high pH value and/or a high cholesterol sulfate content, is it possible to induce swelling in the LPP (16). As we preferred to use lipid mixtures mimicking the physiological conditions as closely as possible, we utilized a variation in repeat distance for the LPP, observed in the SAXD patterns of mixtures with different lipid compositions (see Table 1). The small variation in repeat distance we observed (from 12.1 to 13.8 nm) is probably induced by either a variation in the average lipid chain-length in the different mixtures, or a variation in headgroup architecture. This implies that the structure factors in Fig. 4 sample an average continuous Fourier function, representative for the average electron density in the unit cell of the LPP in the lipid mixtures.

From electron density profile to molecular organization

The electron density profile in Fig. 5 exhibits four high electron density regions inside the unit cell; two electron density peaks are located at the border of the unit cell at ∼−6.5 and +6.5 nm, while two smaller high electron density peaks are located at −2.0 and +2.0 nm from the center of the unit cell. This suggests a unit cell with three lipid bilayers of 4.5, 4.0, and 4.5 nm in width.

The electron density profile in Fig. 5 is supported by several observations: The trilayer arrangement is in agreement with the broad-narrow-broad pattern observed in RuO₄ stained SC as explained by Madison et al. (33). Also, in a previous study, McIntosh used the swelling method to select a set of phase angles for the first three reflections of a mixture with pigCER/CHOL/palmitic acid 2:1:1 (16). His set of three phase angles corresponds to the first three we also selected (− + +).

When using the three signs and only the first three reflections obtained for our mixture, the calculated electron density profile is very similar to the electron density profile obtained by McIntosh. He concluded that only two asymmetric bilayer regions are present in the unit cell of the LPP with a water layer between the outer headgroups in the unit cell. The resolution of the electron density profile was 2 nm, while in our studies the resolution of the electron density profile increased to 1.1 nm. This higher resolution allowed us to determine the electron density peaks at a higher precision. The electron density region between −2.0 and +2.0 nm in our profile corresponds to the water region in the electron density profile of McIntosh. Although this region shows a medium electron density similarly as observed by McIntosh, this medium density level cannot be explained by a water layer for two reasons:

• 1.This electron density profile is also present in lipid mixtures prepared in the absence of a buffer (see Table 1, the equimolar pigCER/CHOL/FFA mixture).
• 2.Due to the similarities in the Fourier transform, the lipid organization in SC is very similar to that in the lipid mixtures. However, in SC, almost no swelling was observed after hydration at physiological conditions (11,15).

Constructing a molecular model for the LPP based on the density profile may provide more insight into the molecular organization of the LPP. Because CER1 is crucial for the formation of the LPP and forms the backbone of the molecular structure of the LPP (10,34), we will only focus on the location of CER1 in the unit cell of the LPP. Furthermore, in previous studies it has been reported that a fluid phase is present in the lipid model mixtures (6,35), which is correlated to the presence of the CER1 linoleate chain. Therefore, this fluid phase must also be accounted for in the molecular model for the LPP.

Possible location of CER1 in the unit cell

Firstly, due to the large width of the high electron density peaks located at the border of the unit cell, it is likely that two polar headgroups are located in these regions at ∼±6 and ±7 nm. The smaller width of the high electron density peaks at ∼−2.0 and +2.0 nm indicates that either a single headgroup or the ω-hydroxy ester bond of CER1 is present in this region. Secondly, the length of the acyl chain of CER1 in mixtures with isolated CER can range from 26 to 34 carbon atoms. Assuming a 0.127 nm increase in chain-length per C-C bond (36), the fully extended CER1 acyl chain-length is ∼3.8 ± 0.5 nm. This length fits into the 4.0 nm distance between the high density peaks at −6 nm and −2.0 nm. As the unit cell is centrosymmetric, two CER1 molecules are present in an opposed configuration in the unit cell. In this configuration, the CER1 headgroup is located at the peak positions of −6 or +6 nm and the linoleate tail is located in the central trough of the electron density profile between −2.0 and +2.0 nm. In this configuration, the CER1 linoleate tails are almost not interdigitating. In Fig. 5, a schematic representation is provided of the proposed location of CER1 in the unit cell. CER1 plays a prominent role in this molecular arrangement for the LPP as it forms the backbone of the molecular structure in this unit cell: in the absence of acyl CER, the LPP cannot be formed (6,10,11). Furthermore, in phospholipid bilayer systems, CHOL is known to have an affinity toward saturated hydrocarbon chains as compared to unsaturated chains (37–39). If this can be extrapolated to CER systems, in our model CHOL is expected to be located in the outer lipid layer regions and not in the central trough where the linoleate chains are present. Concerning the location of CER1 and the trilayer electron density profile, this model exhibits important aspects of the sandwich model published previously (34).

Conclusions

In this article, we determined a solution for the electron density distribution of the LPP with high resolution, showing the structure of the LPP in more detail. Furthermore, the electron density distribution in the LPP of the mixtures was found to closely resemble the density distribution in the LPP of isolated SC samples. This demonstrates that the molecular organization in the mixtures mimics the organization of the LPP in SC. Thus, the lipid mixtures serve as an excellent model for the lipid organization in SC. Finally, additional information must be obtained to select the phase angles for higher diffraction orders and to solve the molecular organization of the LPP in more detail. This will be the subject of future studies in our group.

Supporting Material

One figure is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01303-4.