A superior descriptor of random textures and its predictive capacity

Abstract

Two-phase random textures abound in a host of contexts, including porous and composite media, ecological structures, biological media, and astrophysical structures. Questions surrounding the spatial structure of such textures continue to pose many theoretical challenges. For example, can two-point correlation functions be identified that can be manageably measured and yet reflect nontrivial higher-order structural information about the textures? We present a solution to this question by probing the information content of the widest class of different types of two-point functions examined to date using inverse “reconstruction” techniques. This enables us to show that a superior descriptor is the two-point cluster function C₂(r), which is sensitive to topological connectedness information. We demonstrate the utility of C₂(r) by accurately reconstructing textures drawn from materials science, cosmology, and granular media, among other examples. Our work suggests a theoretical pathway to predict the bulk physical properties of random textures and that also has important ramifications for atomic and molecular systems.

Two-phase random textures are ubiquitous in nature and synthetic situations. Examples include heterogeneous materials (e.g., composites, porous media and colloids) (1, 2), geologic media (e.g., rock formations) (3), ecological structures (e.g., tree patterns in forests) (4), cosmological structures (e.g., galaxy distributions) (5, 6), and biological media (e.g., animal and plant tissue) (7). Over a broad range of length scales, two-phase random textures exhibit a rich variety of structures with varying degrees of disorder and complex bulk properties (8–10), and questions concerning their quantitative characterizations continue to present many fundamental and practical challenges.

It is well known that an infinite set of n -point correlation functions is generally required to completely statistically characterize such textures and their physical properties in the infinite-volume limit. A variety of different types of correlation functions arise in rigorous theories of structure/property relations (1). One such basic quantity is the standard n-point correlation function S_n(x₁, x₂, …, x_n), which gives the probability of finding n points at positions x₁, x₂, …, x_n all in one of the phases (1, 11). Because the information contained in such an infinite set of functions is generally unattainable in practice, a natural starting point is to characterize the structure and bulk properties of random textures by using lower-order versions. The two-point function S₂, which is experimentally accessible via scattering of radiation (12), provides information about the distribution of pair separations. The three-point function S₃ reveals information about how these pair separations involved in S₂ are linked into triangles. The four-point function S₄ controls the assembly of triangles into tetrahedra. A natural question is how much additional useful information do S₃ and S₄ contain over and above S₂? We will show that triangular and tetrahedral statistics do not significantly increase information content over and above pair statistics for textures possessing no long-range order.

Therefore, an outstanding problem in condensed matter theory is to identify other two-point correlation functions that can be both manageably measured and yet reflect nontrivial higher-order structural information about the textures. The aim of this article is to provide a solution to this problem using inverse techniques; specifically, “reconstruction” methods. The purpose of a reconstruction (construction) technique is to reconstruct (construct) realizations of two-phase random textures that match limited structural information on the textures in the form of lower-order correlation functions (1, 13), which are called the “target” functions. An effective reconstruction procedure enables one to generate accurate renditions of random textures at will (14–20), and subsequent analysis can be performed on the reconstruction to obtain desired macroscopic properties of the texture nondestructively (14, 18). Here, we use this inverse methodology to determine the amount of structural information that is embodied in a set of targeted correlation function by quantifying the extent to which the original structure can be accurately reconstructed by using those target functions. We quantify the accuracy of a reconstruction by measuring unconstrained (untargeted) correlation functions and comparing them with those of the original medium.

We adapt the inverse reconstruction method of Yeong and Torquato (13, 14) to show that a superior two-point signature of random textures is the two-point cluster function C₂(r) (21), which is sensitive to topological connectedness information. We demonstrate that C₂(r) contains not only appreciably more information than S₂, but more information than a variety of other “two-point” quantities, including the surface–surface correlation function F_ss, the surface–void correlation function F_sv, the pore-size function F, lineal-path function L, and the chord-length density function p (1). (All the aforementioned correlation functions are defined precisely below.) Such a comprehensive study that investigates and compares all of the aforementioned statistical descriptors via inverse techniques has heretofore not been undertaken. Our results have practical implications for materials science, liquid- and solid-state physics, biological systems, cosmology, hydrology, and ecology.

Definitions of the Two-Point Correlation Functions

In the theory of random media, a variety of different types of two-point correlation functions naturally arise (1). Here, we define seven different ones that will be employed in this article. Consider d-dimensional two-phase textures in which phase i has volume fraction ϕ_i (i = 1, 2) and is characterized by the indicator function

where V_i is the region occupied by phase i (equal to 1 or 2). Note that here “phase” is used in a general sense in that it can refer to a solid, liquid or even void. The standard two-point correlation function is defined as

where angular brackets denote an ensemble average. This function is the probability of finding two points x₁ and x₂ both in phase i. Henceforth, we will drop the superscript “i” and only consider the correlation functions for the phase of interest. For statistically homogeneous and isotropic microstructures, which is the focus of the rest of the article, two-point correlation functions will only depend on the distance r ≡ |x₁ − x₂| between the points and hence S₂(x₁, x₂) = S₂(r).

The surface–void F_sv and surface–surface F_ss correlation functions are respectively defined as

where M(x) = |▽I(x)| is the two-phase interface indicator function. By associating a finite thickness with the interface, F_sv and F_ss can be interpreted, respectively, as the the probability of finding x₁ in the “dilated” interface region and x₂ in the void phase and the probability of finding both x₁ and x₂ in the dilated interface region but in the limit that the thickness tends to zero (1).

The lineal-path function L(r) is the probability that an entire line of length r lies in the phase of interest, and thus contains a coarse level of connectedness information, albeit only along a lineal path (1, 22). The chord-length density function p(r) gives the probability associated with finding a “chord” of length r in the phase of interest and is directly proportional to the second derivative of L(r) (23). (Chords are the line segments between the intersections of an infinitely long line with the two-phase interface.) The pore-size function F(δ) is related to the probability that a sphere of radius r can lie entirely in the phase of interest (1) and therefore is the three-dimensional “spherical” version of the lineal measure L.

The two-point cluster function C₂(r) gives the probability of finding two points separated by a distance r in the same cluster of the phase of interest (21). Note that a cluster of a phase is any topologically connected subset of that phase. The two-point cluster function can be measured experimentally using any appropriate three-dimensional imaging technique (e.g., tomography, confocal microscopy and MRI) (1). The fact that C₂ contains intrinsic three-dimensional topological information is to be contrasted with S₂, which can be obtained from a planar cross-section of the texture. In general, C₂ is expected to embody a much greater level of three-dimensional connectedness information than either L or F, but the degree to which this is true has yet to be quantitatively demonstrated, which is one of the aims of this article.

Inverse Reconstruction Technique

The stochastic optimization reconstruction algorithm for digitized media formulated by Yeong and Torquato (13) is ideally suited to carry out the aforementioned analysis because it can incorporate different types of target statistical descriptors. This algorithm is both robust and simple to implement (15–20). In this method, one starts with an initial realization of a random medium and a set of target correlation functions f̂_n¹(R), f̂_n²(R), f̂_n³(R), …, which are obtained (i.e., measured) from the medium of interest. Here, f̂_n^α(R) is an n-point correlation function of type α, R ≡ r₁, r₂, … r_n, and r_i denotes the position vector of the ith point. The method proceeds to find a realization in which calculated correlation functions f_n¹(R), f_n²(R), f_n³(R), … best match the corresponding target functions. This is achieved by minimizing an “energy”

which is defined to be the sum of squared differences between the calculated and target functions, via a simulated annealing method in which a sequence of trial realizations is generated and accepted with the probability min {exp(−ΔE/T),1}, where ΔE is the energy difference between the new and old realizations and T is a fictitious temperature. The initially “high” temperature is lowered according to a prescribed annealing schedule until the energy of the system approaches its ground-state value within a very small tolerance level.

Degeneracy of Ground States Using S₂ Alone.

It is instructive to consider the energy defined by Eq. 4 when only the standard two-point correlation function S₂ is used. In this special instance, the energy is given by

where Ŝ₂ and S₂ are the two-point correlation functions of the target and reconstructed medium, respectively. We note that most previous reconstruction studies have only tried to match S₂. However, it is now well established that S₂(r) is not sufficient information to generally get an accurate rendition of the original microstructure (13–15, 19, 20). In other words, the ground states when only S₂ is incorporated in the energy (Eq. 5) are highly degenerate due to the nonuniqueness of the information content of this two-point function, which is clearly illustrated by the subsequent examples in the paper. The reader is also referred to supporting information (SI) Text, which provides a rigorous explanation for the degeneracy of the ground states for digitized representations of textures.

Insufficiency of Conventional Three-Point Information.

An obvious additional set of correlation functions that could be incorporated in the reconstruction is the higher-order versions of S₂, namely, S₃, S₄, etc. However, not only is the three-point correlation function S₃ more difficult to compute, it is not at all clear that its incorporation will result in appreciably better reconstructions because it only introduces local information about triangles when there is no long-range order, the most common occurrence. We can quantitatively verify the insufficiency of conventional triangular information by reconstructing a one-dimensional equilibrium distribution of equal-sized hard rods (24) using S₃ (see SI Text for technical details). Fig. 1 compares this reconstruction with those involving S₂ alone and a combination of S₂ and C₂. It is clear that the reconstruction using S₂ only results erroneously in a highly clustered “rod” phase. Although incorporating S₃ provides an improved reconstruction, it still contains large clusters and isolated rods that can be much smaller than actual rod size. On the other hand, the S₂–C₂ hybrid reconstruction produces the most accurate rendition of the target medium. Although this one-dimensional example is suggestive that C₂ contains nontrivial structural information in excess to what is contained in S₂, one must investigate this problem in higher dimensions, which presents algorithmic challenges, as we will describe in the next section.

Fig. 1.

Equilibrium hard rods. (A) Target: an equilibrium hard-rod system in which the equal-sized rods cover 50% of the space. Each rod in the system is 10 pixels in length. (B) S₂-alone reconstruction. (C) S₃ reconstruction. (D) S₂–C₂ hybrid reconstruction. For visualization purposes, the one-dimensional rod systems are artificially extended in the vertical direction.

Efficient Algorithmic Implementation of the General Problem

Here, we present a general methodology that enables one to efficiently incorporate a wide class of lower-order correlation functions in the Yeong–Torquato reconstruction procedure. The aforementioned probabilistic interpretations of the correlation functions enable us to develop a general sampling method for reconstruction of statistically homogeneous and isotropic digitized textures based on the “lattice-gas” formalism, which was introduced in ref. 20 and has been generalized here. In the generalized formalism, pixels with different values (occupying the lattice sites) correspond to distinct local states and pixels with the same value are considered to be “molecules” of the same “gas” species (20). The correlation functions of interest can be obtained by binning the separation distances between the selected pairs of molecules from particular species.

In the case of S₂, all molecules are of the same species. We denote the number of lattice-site separation distances of length r by N_S(r) and the number of molecule-pair separation distances of length r by N_P(r). Thus, the fraction of pair distances with both ends occupied by the phase of interest, i.e., the two-point correlation function, is given by S₂(r) = N_P(r)/N_S(r). To obtain C₂, one needs to partition the molecules into different subsets Γ_i (species) such that any two molecules of the same species are connected by a path composed of the same kind of molecules, i.e., molecules that form a cluster, which is identified using the “burning” algorithm (25). The number of pair distances of length r between the molecules within the same subset Γ_i is denoted by N_Pⁱ(r). The two-point cluster function is then given by C₂(r) = ∑_iN_Pⁱ(r)/N_S(r). The calculation of F_ss and F_sv requires partitioning the molecules into two subsets: the surface set κ_S containing only the molecules on the surfaces of the clusters and the volume set κ_V containing the rest. In a digitized medium, the interface necessarily has a small but finite thickness determined by the pixel size. Thus, the surface–surface and surface–void correlation functions can be regarded as probabilities that are given by F_ss = N^ss(r)/N_S(r) and F_sv = N^sv(r)/N_S(r), respectively; where N^ss(r) gives the number of distances between two surface molecules with length r and N^sv is the counterpart for pairs with one molecule on the surface and the other inside the cluster.

The lineal path function L can be obtained by computing the lengths of all digitized line segments (chords) composed of pixels of the phase of interest, and for each chord incrementing the counters associated with the distances equal to and less than that chord length (13, 14). The chord-length density function p can then be easily obtained by binning the chord lengths that are used to compute L (1). The pore-size function F can be computed by finding the minimal separation distances of pixels within the phase of interest to those at the two-phase interfaces. The minimal distances are then binned to obtained a probability distribution function, the complementary cumulative distribution function of which is F (3).

We have also devised methods to track clusters and surfaces that enable one to quickly compute the correlation functions of the new realization based on the old ones (see SI Text for technical details) and thus make the Yeong–Torquato reconstruction procedure much more efficient than methods that directly resample the correlation functions for each trial realization.

We have used this general procedure here to reconstruct a wide spectrum of random textures, including model microstructures, such as the cherry-pit model, equilibrium hard spheres, Debye random media and symmetric cell materials (1), as well as the digitized representations of sandstones (3), metal-ceramic composites (26), concrete microstructures (27), laser speckle patterns (20) and galaxy distributions. Using the aforementioned largest set of correlation functions utilized to date, our analysis reveals that the best reconstructions always incorporate the two-point cluster function C₂(r). In what follows, we will present specific results for only a subset of the correlation functions that we used, namely, various combinations of S₂, F_ss, F and C₂, for the nonpercolating phases of a concrete microstructure (27), a distribution of galaxies, and a three-dimensional hard-sphere packing.

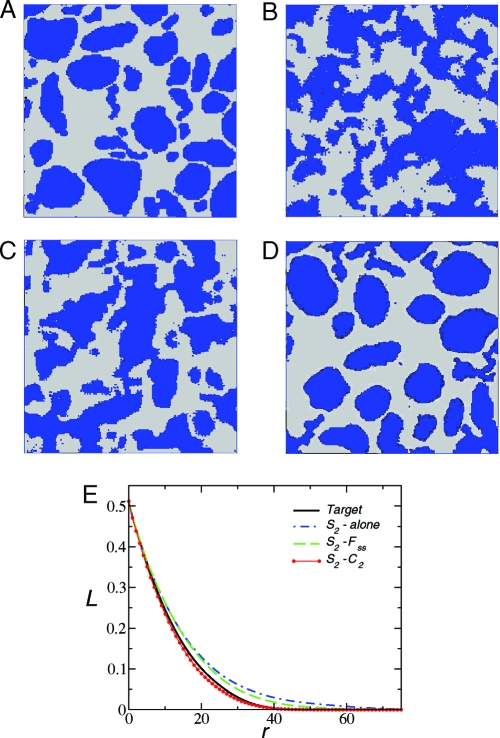
Concrete Microstructure.

The wide range of structural features in concrete, from nanometer-sized pores to centimeter-sized aggregates, makes it a wonderful example of a multi scale microstructure (28). Fig. 2A shows a binarized digitized image of a concrete sample cross-section. We have thresholded the original image so that the blue phase represents the stones and the lighter gray phase is the cement paste. The “stone” phase is characterized by a dense dispersion of “particles” of various sizes: a nontrivial situation to reconstruct. Using S₂ alone overestimates clustering in the system and indeed incorrectly yields a percolating particle phase. Thus, although S₂ of the reconstruction matches the target one with very small error (see Fig. S1), such information is insufficient to get a good reconstruction. Incorporating both S₂ and surface–surface function F_ss leads to a better rendition of the target system but the reconstruction still overestimates the degree of clustering. On the other hand, incorporating C₂ yields an excellent reconstruction in that the stone phase clearly appears as a particle dispersion with a size distribution that closely matches that of the target structure. As noted in the introduction, we can quantitatively test the accuracy of the reconstructions by measuring unconstrained correlation functions and comparing them with the corresponding quantities of the target system. Here, we choose to compute the unconstrained lineal-path function L. Fig. 2E reveals that the lineal-path function of the reconstruction that incorporates C₂ matches the target function L well and it clearly is appreciably more accurate than the other reconstructions.

Fig. 2.

Concrete microstructure. (A) Target system: a binarized image of a cross-section of concrete (27). The linear size of the digitized texture is N_L = 170 pixels. (B) S₂-alone reconstruction. (C) S₂–F_ss hybrid reconstruction. (D) S₂–C₂ hybrid reconstruction. All the reconstructions are associated with a final energy (error) E ≈ 10⁻⁸. (E) The unconstrained lineal-path function L of the reconstructions and the target image. Pixel size supplies the unit for the distance r.

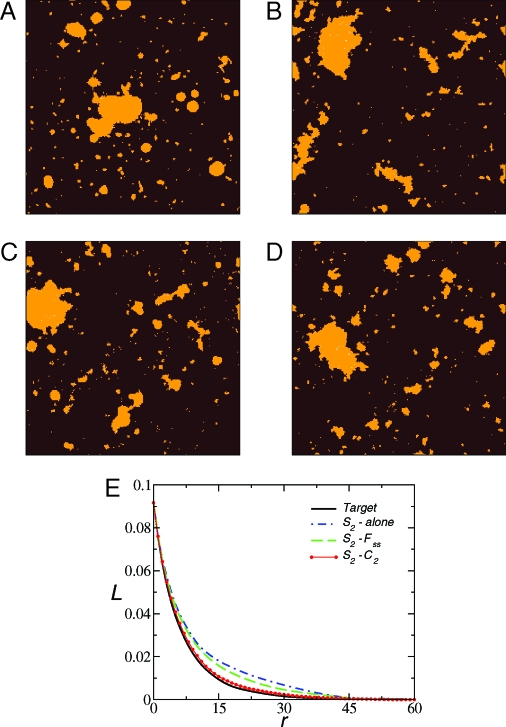
Galaxy Clusters.

Correlation functions have been used to understand the formation of galaxies and the large scale structures of the Universe (4, 5). Such characterizations are becoming increasingly important with the advent of high-quality surveys in cosmology. We suggest that the reconstruction procedure can provide an important tool in cosmological and astrophysical applications, especially in helping to determine the lower-order correlation functions that reflect a priori information about nontrivial structural features, such as multi scale clustering and filamentary structures in the Universe. Fig. 3A shows a binarized image of a portion of the Abell 1689 galaxy cluster. We have chosen the binarizing threshold such that the “galaxy” phase (bright spots in Fig. 3A) exhibits different sized clusters. As one can see, the “primary” (single largest) cluster in the target system has been reproduced by all the reconstructions. This is because the volume fraction of the “galaxy” phase is relatively small, whereas the target S₂ has a relatively long tail (see Fig. S2), which requires the clustering of a majority of galaxy phase. However, the “secondary” (smaller compact) clusters are significantly different for different reconstructions. The reconstruction using S₂ only produces large elongated secondary clusters. Incorporating F_ss enables one to obtain a better rendition; however, it still contains a few elongated secondary clusters. The incorporation of C₂ again provides the most accurate reconstruction. This is visually verified by examination of both the sizes and shapes of the primary and secondary clusters, and is quantitatively confirmed by the comparison of the unconstrained L of the reconstructed and target systems, as shown in Fig. 3E.

Fig. 3.

Galaxy clusters. (A) Target system: a portion of the Coma Cluster. The linear size of the digitized texture is N_L = 238 pixels. (B) S₂-alone reconstruction. (C) S₂–F_ss hybrid reconstruction. (D) S₂–C₂ hybrid reconstruction. All the reconstructions are associated with a final energy (error) E ≈ 10⁻⁸. (E) The unconstrained lineal-path function L of the reconstructed and target systems. Pixel size supplies the unit for the distance r.

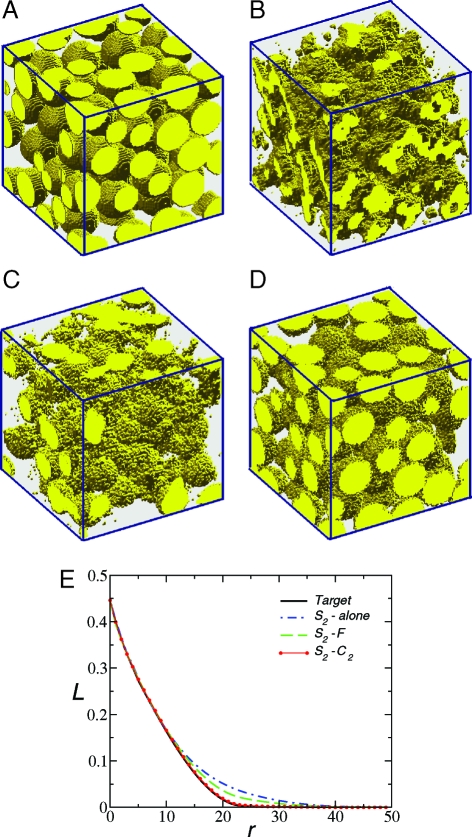
Sphere Packing.

As an application of our methodology to three dimensions, we have reconstructed a digitized realization of an equilibrium distribution of equal-sized hard spheres, as shown in Fig. 4A. This packing is generated using the standard Metropolis Monte Carlo technique for a canonical ensemble of hard spheres in a cubical box under periodic boundary conditions (1). A visual comparison of the hybrid reconstruction involving the two-point cluster function reveals that it accurately yields a dispersion of well-defined spherical inclusions of the same size, in contrast to the S₂ reconstruction, which again grossly overestimates clustering of the “sphere” phase. In contrast to the previous examples, here we incorporate the pore-size function F (not the surface correlation functions) in one of the reconstructions. Although the reconstruction incorporating F provides improvement over the rendition of the S₂-alone reconstruction, it is still inferior to the S₂–C₂ reconstruction in reproducing both the size and shape of the “sphere” phase. (The target and reconstructed correlation functions are shown in Fig. S3 and the SI Text.) The accuracy of the S₂–C₂ hybrid reconstruction can also be seen by comparing the unconstrained lineal-path function L of the target system with those of the reconstructed media (see Fig. 4E).

Fig. 4.

Sphere packing. (A) Target system: a digitized realization of a hard-sphere packing in which the spheres occupy 44.6% of space. The linear size of the digitized texture is N_L = 100 pixels. (B) S₂-alone reconstruction. (C) S₂–F reconstruction. (D) S₂–C₂ hybrid reconstruction. All the reconstructions are associated with a final energy (error) E ≈ 10⁻¹¹. (E) The (unconstrained) lineal-path function sampled from target and reconstructed realizations. Pixel size supplies the unit for the distance r.

Discussion

In summary, although it was known that the information content of the standard two-point function S₂ of a random texture is far from complete, we have demonstrated here that the next higher-order version S₃ generally does not contain appreciably greater information. The fact that this natural extension to incorporate higher-order S_n, which has been pursued in the last century in statistical mechanics, is not a fruitful path motivated us to inquire whether there exist sensitive two-point statistical descriptors that embody nontrivial structural information. We probed the information content of seven different types of two-point functions using inverse reconstruction methods. For all of the examples studied here, reconstructions that include the two-point cluster function C₂ were always found to be significantly more accurate than those involving any of the combinations of pairs of the other functions.

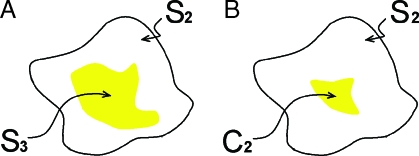
More precisely, the incorporation of C₂ significantly reduces the number of compatible microstructures as compared to the compatible microstructures consistent with the same three-point function S₃, which is schematically indicated in Fig. 5. The two-point cluster function is an especially sensitive structural signature when clustering and phase connectedness are present, the most difficult situations to treat. This can be seen from the reconstruction of the hard-rod system that incorporated C₂ (see Fig. 1). More importantly, we showed the utility of C₂(r) in higher dimensions by accurately reconstructing galaxy distributions, concrete microstructures and dense hard-sphere packings, among other examples.

Fig. 5.

The set of all microstructures associated with a particular S₂ is schematically shown as the region enclosed by the solid contour in A and B. The shaded region in A shows the set of all microstructures associated with the same S₂ and S₃. The shaded more restrictive region in B shows the set of all microstructures associated with the same S₂ and C₂.

Why is C₂(r) a superior two-point structural signature? To answer this question, it is useful to first compare it to S₂(r). The latter, unlike C₂(r), does not distinguish between events in which the end points of the line segment of length r fall in the same cluster of a particular phase and those that do not involve the same cluster of that phase (21). More precisely, C₂ is the “connectedness” contribution to the standard two-point correlation function, i.e.,

where D₂ measures the probability that the end points of a line segment of length r fall in different clusters of the phase of interest. Therefore, whereas S₂(r) is insensitive to clustering and percolation, C₂(r) becomes a progressively longer-ranged function as clusters grow in size such that its volume integral diverges at the percolation threshold (1, 21). By contrast, the quantities L, p, F, F_ss and F_sv are insensitive to crossing the percolation threshold. Indeed, for particle systems, one can show that C₂ is a functional of the infinite set of n-particle “connectedness” functions (21).

Thus, although C₂ is a “two-point” quantity, it actually embodies higher-order structural information in a way that makes it a highly sensitive statistical descriptor over and above S₂. This ability to “leapfrog” past the usual approach of incorporating additional information via higher-order versions of S₂ has important ramifications for new structure/property relation of random textures. Specifically, our work suggests that theories should be developed that relate the transport, mechanical, chemical and optical properties of random textures to functionals that incorporate C₂. It is clear that such theories would be highly predictive, because it is well established that the presence of clusters in textures can dramatically alter their macroscopic physical properties (1).

It should not go unnoticed that our work also has important implications for atomic and molecular systems where the analogous standard correlation functions that arise are the two-body correlation function g₂, three-body correlation function g₃, etc. (29–32) The three-body function g₃, for example, has been the focus of great attention, e.g., integral equations and approximations have been devised for g₃ (30–32). The spatial structure of disordered atomic or molecular systems may be regarded to be special cases of random textures. For example, the particles that comprise simple atomic systems are fully specified by their center-of-mass coordinates. These point distributions can be decorated in an infinite number of ways to produce random textures in the sense that we have defined them in this article. For example, one could circumscribe the points by spheres of size dictated by the physics of the problem (e.g., electron hopping distance). For such systems, our work suggests that the pair-connectedness function P₂ [i.e., the connectedness contribution to g₂ (1)] should contain far greater information than g₃ beyond that contained in g₂.