Lethal Mutagenesis in Viruses and Bacteria

Abstract

In this work we study how mutations that change physical properties of cell proteins (stability) affect population survival and growth. We present a model in which the genotype is presented as a set folding free energies of cell proteins. Mutations occur upon replication, so stabilities of some proteins in daughter cells differ from those in the parent cell by amounts deduced from the distribution of mutational effects on protein stability. The genotype–phenotype relationship posits that the cell's fitness (replication rate) is proportional to the concentration of its folded proteins and that unstable essential proteins result in lethality. Simulations reveal that lethal mutagenesis occurs at a mutation rate close to seven mutations in each replication of the genome for RNA viruses and at about half that rate for DNA-based organisms, in accord with earlier predictions from analytical theory and experimental results. This number appears somewhat dependent on the number of genes in the organisms and the organism's natural death rate. Further, our model reproduces the distribution of stabilities of natural proteins, in excellent agreement with experiments. We find that species with high mutation rates tend to have less stable proteins compared to species with low mutation rates.

MUTATION rates play an important role in the evolution and adaptation of bacteria and viruses. Considerable experimental evidence suggests that high mutation rates in RNA virus populations have powered their rapid evolution (Eggers and Tamm 1965; Domingo et al. 1978; de la Torre et al. 1990; Domingo 2000). However, artificially elevated mutation rates were shown to have deleterious effects on the fitness of RNA viruses and to eventually lead to extinction of the viral population beyond certain mutation rate thresholds (Loeb et al. 1999; Sierra et al. 2000; Pariente et al. 2001; Grande-Perez et al. 2002; Anderson et al. 2004; Freistadt et al. 2004; Bull et al. 2007; Graci et al. 2007, 2008; Zeldovich et al. 2007). This observation is called lethal mutagenesis for RNA viruses. Several authors proposed to use lethal mutagenesis to cure or control infection with RNA viruses, using certain mutagens (Anderson et al. 2004; Freistadt et al. 2004). The possibility of lethal mutagenesis in bacteria was also suggested and studied recently (Gessler 1995; Andre and Godelle 2006; Bull and Wilke 2008).

Previously, many attempts have been made, using population genetics, to theoretically describe the effect of mutation rates on the survival of a population (Muller 1964; Haigh 1978; Gessler 1995). The effect has frequently been described within the paradigm of Muller's ratchet (Muller 1964; Haigh 1978; Andersson and Hughes 1996), where the genome of an asexual organism accumulates stochastic deleterious mutations in an irreversible manner, leading to the systematic decrease in the fitness of the organism. The concept of Muller's ratchet applies to finite, asexual populations. It states that if back mutations cannot occur, eventually any finite asexual population will accumulate deleterious mutations and the mutation-free wild-type genotype would be lost. While such models provided some useful insights into the phenomenon of lethal mutagenesis, they often assume a single fitness peak and absence of back or compensating mutations and depend heavily on arbitrary parameters, such as selection coefficients or deleterious mutation rates. Such analyses therefore lack a more fundamental connection between the physical properties of the proteins within the organism, the metabolic network of the organism, and the feedback relationship between the mutation rate and organismal fitness.

In recent years, several theories of lethal mutagenesis have been proposed (Guo et al. 2004; Bull et al. 2007; Zeldovich et al. 2007; Bull and Wilke 2008). In a marked departure from earlier phenomenological approaches Zeldovich et al. (2007) suggested a model assuming that the loss of protein stability would lead to the loss of essential functions within the organism and therefore to a lethal phenotype. The evolution of a population in this model was mapped to a diffusion process in a multidimensional hypercube where each dimension represented stability of proteins encoded by an essential gene and adsorbing boundary conditions at ΔG=0 boundaries [where ΔG is the difference between free energy of the folded and unfolded proteins, which is the thermodynamic measure of protein stability (Zeldovich et al. 2007)] were imposed to account for the fact that loss of stability confers a lethal phenotype on an organism. This model differs from previous approaches in that, instead of depending on arbitrarily calibrated parameters such as selection coefficients or deleterious mutation rates, it is based only on the statistical distribution of proteins' folding free energy change after point mutations, which was directly derived from in vitro experiments. Furthermore, it predicts a lethal mutagenesis threshold that is consistent with experimental findings and discovers a deep relation between fundamental biophysical properties of proteins, the mutation rate, and organismal fitness.

However, despite these insights, the model proposed by Zeldovich et al. (2007) is based on a number of simplifying assumptions. First, it assumes a uniform mutation supply within the population, meaning that at any time, mutations could occur in any organism in the population with an equal and constant probability. However, in real biological systems mutations are coupled to replication. While the formalism developed by Zeldovich et al. (2007) allows one to consider the case when mutations are coupled to replication (see Methods in Zeldovich et al. 2007), this formalism gives numerically accurate predictions for the coupled mutation–replication only in the limit of low mutation rates. However, lethal mutagenesis occurs when the mutation rate is relatively high (approximately six mutations per genome per replication according to Crotty et al. 2001 and Zeldovich et al. 2007). Second, the model developed in Zeldovich et al. (2007) assumes a very simple “Θ-function-like” fitness landscape whereby fitness is the same for all protein stabilities as long as proteins are stable; i.e., it is flat for all ΔG<0. However, in reality as proteins become less stable they spend a greater fraction of time in the unfolded state, reducing therefore the effective concentration of functional proteins, which may affect fitness. Our study overcomes these limitations in a new computational model as outlined below.

If the organism has a conservative replication mechanism, as is the case for RNA viruses, then mutations would occur, with certain probabilities, only in the descendant copy, while the parent copy would remain unchanged (that may also be the case in organisms with double-stranded genomes, where the methylation mechanism keeps a master copy of the genome preserved). If the organism has semiconservative replication, as in bacteria and DNA viruses and double-stranded RNA viruses, then mutations could happen with certain probabilities in both daughter organisms.

Here we present a detailed study of the fitness effect of protein stability changing mutations, based on the coupled mutation–replication scenario and more explicit physical consideration of the effect of protein stability on fitness. Simulating evolution and population growth in this model, we observe lethal mutagenesis in conservative and semiconservative replicating populations. Further, we show how stationary distribution of protein stabilities (folding free energies) emerges and discuss the physical and evolutionary reasons for the observed moderate stability of proteins.

THE MODEL

In our model, we assume that the replication rate of an organism depends on the functionality of each of the proteins involved in the organismal replication process (below we call such proteins rate-determining proteins and genes encoding them rate-determining genes). Rate determining genes do not necessarily constitute the whole genome. Instead, it could be a small or a large subset of the genome, and the number may vary between species and strains (Nishikawa et al. 2008). However, an organism is able to replicate efficiently only when all of these proteins are able to function properly (Counago et al. 2006). Failure of a single rate-determining protein might result in the organism's dysfunction and hence reduce the organismal replication rate.

We also note that the subset of rate-determining genes may be smaller than the subset of essential genes. The difference between the two is that essential genes (i.e., the ones whose knockout causes a lethal phenotype) may not affect growth rate directly. In contrast, the supply of functional proteins that are encoded by rate-determining genes may affect critically the ability of a cell to replicate. An example of such proteins could be enzymes involved in nucleotide and amino acid metabolism, DNA polymerases, etc. Essential but not necessarily rate-determining proteins may be enzymes that are involved in metabolism of certain nutrients, proteins responsible for motility under certain conditions, etc.

Here we assume that the organism's replication rate is directly related to the copy numbers of rate-determining proteins in their folded, i.e., functional states. Protein domains are known to fold thermodynamically two-state (Privalov and Khechinashvili 1974; Privalov 1979; Shakhnovich and Finkelstein 1989), which means that only unfolded and folded forms of a protein domain can be present in an ensemble in significant quantities. The fraction of time a protein spends in its folded state is then given by

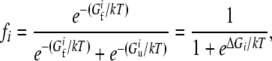(1)

where 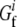and 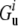are free energies of the folded and unfolded forms of protein i, respectively, and 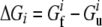is the difference between the two representing the stability of protein i. Factors f_i determine effective concentrations of functional rate-determining proteins in the organism. For simplicity, we assume that the proteins regulating organism replication are independent of each other; therefore, the percentage of folded proteins should be a function of only their stabilities 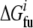and the environmental temperature.

The organismal fitness (growth rate in a fixed environment) is therefore determined by the percentage of properly folded rate-determining proteins in the organism. The replication rate for an organism with Γ different proteins controlling the replication process can be expressed as

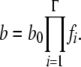(2)

Here, b₀ is the overall birth rate, a constant parameter that is determined by other organismal environmental factors such as temperature, acidity, or nutrition and by expression levels of all rate-determining genes (which are assumed constant in this model).

Equations 1 and 2 establish the fitness landscape in our model. The key aspect of the model is that it keeps track of the coarse-grained quantity of evolving proteins, their stability, rather than their exact sequences (Bloom et al. 2007; Zeldovich et al. 2007). In earlier work (Zeldovich et al. 2007) the fitness landscape had a strict step-function form where fitness (growth rate) was assumed to be constant when all essential proteins are stable (ΔG<0) and 0 when at least for one essential protein ΔG≥0. Here fitness depends on protein stability in a more continuous fashion because in addition to the “step-function” death condition of Zeldovich et al. (2007), in this model we assume the effect of copy number of folded proteins on fitness. However, the dependence of fitness on stability is still step-function-like whereby it is more pronounced at low stabilities and plateaus at moderate stability as suggested by the “Fermi-Dirac-like” function of Equation 1. According to Equation 1, as long as a rate-determining protein has folding free energy ΔG<−3 kcal/mol, then >99% of this protein's molecules are properly folded at room temperature, and therefore further stabilization of this protein would not bring too much additional growth rate. On the other hand, the effect of copy number of folded proteins on fitness does impose a strong limitation on less stable proteins. For example, if three rate-determining proteins each have stability around −1 kcal/mol, while all other proteins are more stable than −3 kcal/mol, then the overall fitness is decreased by 40% compared to another organism whose rate-determining proteins are all more stable than −3 kcal/mol.

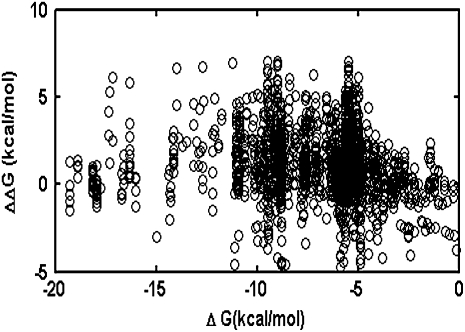
Mutations change folding free energy of proteins. The magnitude of the change is treated as stochastic in our model, whereas experimental evidence (Fersht 1999; Kumar et al. 2006; Zeldovich et al. 2007) has shown that statistically the impact of mutations on protein stability is biased toward the deleterious side. The statistics of changes of proteins' free energy after point mutations, ΔΔG, have been analyzed in Kumar et al. (2006) and Zeldovich et al. (2007). They are Gaussian-like with an average destabilizing effect of ∼1 kcal/mol and standard deviation of ∼1.7 kcal/mol. Several authors discussed the possibility that the distribution of ΔΔG itself could depend on the stability of the wild-type protein (DePristo et al. 2005; Bloom et al. 2006). To address this issue we considered the thermodynamic data on >2000 point mutations available in the database ProTherm (Kumar et al. 2006) and did not observe a pronounced statistical dependence of thermodynamic effect of mutations on stability of wild-type proteins (Figure 1).

Figure 1.—

Scatter plot of ΔΔG vs. the wild-type ΔG values taken from the ProTherm database. A total of 2188 data points of independent point mutation experiments were plotted. The dependence of ΔΔG on ΔG is weak (R = 0.11). The apparent narrowing of the distribution at low stabilities is due to the fact that mutations leading to ΔG>0 cannot be expressed.

The value of a fixed death rate can be highly species dependent. Although the possibility of bacteria aging has been explored, their natural death rate is small, and the aging process would take a long time (Menon et al. 2003; Stewart et al. 2005). However, for viral particles, because of various lytic and nonlytic immune responses (Wodarz et al. 2002), their death rate can vary from a small fraction to the majority of the viral population being eliminated at each replication cycle. Therefore, in the following discussion, we neglect natural death rate for bacteria and focus on the effect of death rate for viruses, in agreement with previous viral lethal mutagenesis models (Bull et al. 2007). Unlike bacteria viruses replicate in bursts, involving several generations. Here, for simplicity, and to better compare with bacterial lethal mutagenesis analysis, we introduce a coarse-grained (in time) description of viral replication that includes effective per generation average death rate parameter. For example, for a viral particle with burst size ∼1000 (occurring over log₂1000∼10 generations) and survival probability 10% after lysis, we assume that per generation death rate D ∼ 20% per generation. In other words, assuming the burst size is b, and survival probability after the burst is S, the per generation death rate parameter can be estimated as

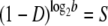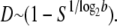This is a strong simplification that depends on the stability of various external biological factors. Nevertheless, assuming a constant death rate per unit time serves as a convenient parameter for comparing the lethal mutagenic processes across strains and species. The major assumptions of our model for different species are summarized in Table 1.

TABLE 1.

Assumptions about species replication in our model

	Duplication mechanism	Death rate	Rate-determining gene no.
Bacteria	Semiconservative, mutations could happen to both descendant copies	Negligible	Large (20 ∼ 300)
DNA virus	Semiconservative (mostly), mutations could happen to both descendant copies	Nonnegligible	Small (∼20)
RNA virus	Conservative (mostly), mutations happen to only one descendant copy, and a master genome is preserved	Nonnegligible	Small (∼20)

In addition to the replication and mutation factors, we also recognize from gene knockout experiments (Gerdes et al. 2003; Kobayashi et al. 2003) that the failure of any key protein to fold in a cell can be lethal to the organism. Therefore, we assume, as in Zeldovich et al. (2007), that loss of stability for any protein (in which case the folding free energy for this protein is >0) causes the death of an organism (i.e., confers the lethal phenotype). In our analysis this biological requirement is cast as a boundary condition:

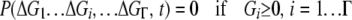(3)

(Zeldovich et al. 2007). Here P is the number of organisms in the population that have genotype 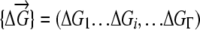at time t. We note that in our coarse-grained model, which does not explicitly treat protein sequences, the genotype of an organism is just the set of stabilities of its proteins.

The relation (3) indicates that there are no organisms in the population whose genomes encode unstable proteins [we focus here on viruses and bacteria that supposedly do not contain intrinsically disordered proteins (Xie et al. 2007)]. The biological motivation for this condition is that expression of unstable proteins not only deprives the organism of functional proteins but also may lead to their aggregation, causing the death of an organism (Drummond et al. 2005).

To summarize, we compare our model with several traditional population genetics models. Most population genetics models assume (explicitly or implicitly) a single fitness peak: the wild-type genotype (i.e., literally the genome sequence) is most fit while any mutation confers selective disadvantage. Due to the huge size of the sequence space, back mutations that restore the original wild-type genotype are not allowed. Compared to traditional population genetics models, our fitness–mutation feedback function is more complicated. A detailed comparison between this model and other population genetics models is given in Table 2. The key difference between them is that in our model the fitness landscape is considered in the coarse-grained space of protein stabilities rather than in the space of genomic sequences as in traditional approaches. The crucial point is that in our approach “back mutations” are the ones that restore (or improve) protein stability rather than the ones that restore the original genome sequences. For that reason beneficial mutations are quite frequent in our model and some form of equilibrium between beneficial and deleterious mutations establishes as can be seen below.

TABLE 2.

Similarities and differences between this model and traditional population genetics models

	Our model	Traditional models
Beneficial vs. deleterious mutation	Beneficial mutations and back mutations allowed	Mutations are deleterious, back mutations are not allowed
Relationship between mutation and fitness	Mutations decrease fitness on average, but beneficial and back mutations also exist	Mutations decrease fitness, wild types are the fittest
Dependence on genome size	Larger genomes lead to more rate-determining proteins, potentially increasing robustness	Independent of genome size
Selection criteria	All essential proteins must fold properly	Absent of deleterious mutations, or fewer than k mutations per organism
Generation time	Taken into consideration	Considered in some models, but not always considered

Simulation of evolution of populations:

On the basis of these principles, we simulate the evolution of populations for the cases of semiconservative and conservative replication. First, we prepare initial species with 100 identical organisms of the same genotype; initial stabilities of Γ-proteins in each organism have random values drawn from the analytical distribution of the functional form described in our previous work (Zeldovich et al. 2007). At each time step an organism can replicate with probability determined by the genotype-dependent replication rate parameter given by Equation 2. An organism is eliminated as soon as a mutation occurs that confers on any of its proteins a folding free energy value greater than zero.

Upon replication, mutations may happen in a descendant organism. Mutation in our model represents the change in stability of one or more proteins in the daughter organism compared with the parent organism; i.e., the genotype of the daughter organism can be presented as

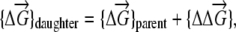where 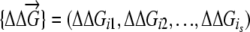describes changes of stabilities upon a replication event that resulted in s mutations in proteins 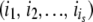. For semiconservative replication, mutations might occur in both the parent copy and the descendant copy. If it is conservative replication, mutations would then occur in the descendant copy only. We generate the number of mutations at each replication in a daughter organism, according to a Poisson distribution, and the parameter of the Poisson distribution is the average number of mutations per genome per replication, for this particular species. The mutation rate per gene is then 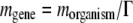. After selecting 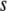—the total number of proteins to be mutated at a given replication event—we decide which proteins to mutate by selecting the set 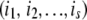at random. When mutation occurs, we alter the protein stability by an amount drawn from the Gaussian distribution with mean 1 kcal/mol and standard deviation 1.7 kcal/mol derived from the statistical analysis of experimental data on effects of point mutations on protein stability (Kumar et al. 2006; Zeldovich et al. 2007). The mutant daughter organism will therefore have an altered fitness value (derived from Equation 2), due to the changes in stability of some of its proteins.

For both bacteria and viruses, we impose an upper limit of population size of 5000 organisms by culling excess organisms at random. Throughout this study 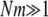for both bacteria and viruses, since we focus primarily on the high mutation rate regime where lethal mutagenesis may occur.

We set a constant death rate for viruses. At each generation, depending on the death rate, we randomly kill a certain fraction of new organisms. Thus population dynamics in our simulations essentially map into a peculiar 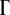-dimensional diffusion process with branching and growth with “position-dependent” (Equation 2) branching rate and with proper absorbing boundary conditions as explained above (Equation 3). We ran multiple independent simulations to eliminate the effect of genetic drift. During simulations, we let organisms evolve in a stable environment for ∼5000 generations, and we study the population dynamics and evolution of protein stabilities for a range of parameters.

RESULTS

Lethal mutagenesis with semiconservative replication (for bacteria and DNA viruses):

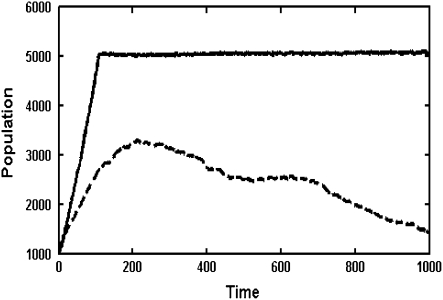
We define the lethal mutagenesis threshold as the minimum mutation rate that can result in a species with a sufficient initial large population to eventually go extinct. As shown in Figure 2 as well as in previous work (Zeldovich et al. 2007), as long as the mutation rate is smaller than some critical value, the population can sustain itself for a sufficiently long time. However, when the mutation rate exceeds a certain threshold, lethal mutagenesis occurs as can be seen in Figure 2.

Figure 2.—

Population dynamics with different mutation rates for a bacterium with 20 rate-determining proteins (dashed line, four mutations per replication; solid line, three mutations per replication).

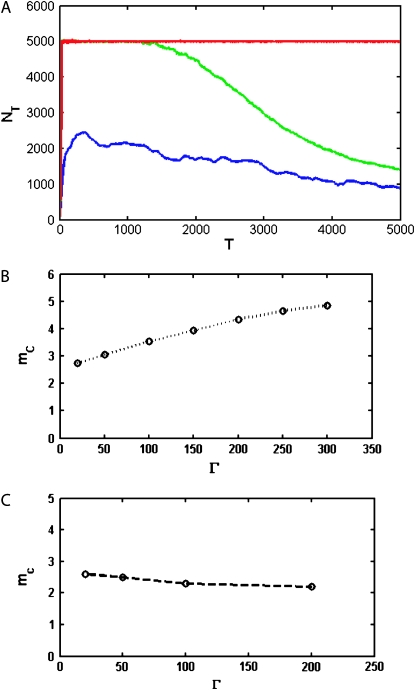
The effect of mutations on population dynamics depends on the number of rate-determining genes 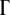as shown in Figure 3. The lethal mutagenesis threshold shown in Figure 3B is slightly different numerically from that predicted in the previous analytical model (around three mutations per genome per replication for semiconservative replication and around six for conservative replication for all genome sizes) (Zeldovich et al. 2007), and the reasons may be twofold. First, herein we consider the coupled replication–mutation scenario, in which mutations occur only during replication events. Second, we also consider a more realistic fitness landscape, in which the stabilities of proteins affect the organism replication rate; that is, all rate-determining proteins have certain influence on the rate of replication. The more properly folded copies of a protein there are in the organism, the faster the replication rate is and hence the higher the organism fitness. Hence there is a collective contribution term from all rate-determining genes in the organism. As shown in Figure 3A, at a fixed mutation rate of three mutations per genome per replication, the increase in the number of rate-determining genes results in a lower probability that the species will become extinct.

Figure 3.—

The effect of the number of rate-determining genes. (A) Population dynamics with different rate-determining genes, with the mutation rate fixed at three mutations per replication line (blue line, 10 proteins; green line, 50 proteins; red line, 100 proteins). When the number of rate-determining genes is low, the population becomes extinct very quickly, whereas when it is high, the population can have sustainable growth. (B) Lethal mutagenesis threshold 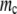as a function of Γ for semiconservative replication. As the number of rate-determining genes increases, the mutagenesis threshold grows as well. The threshold shows a tendency toward saturation with an increased number of rate-determining proteins. (C) Mutagenesis threshold 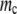as a function of the number of genes, in the control simulation whereby the replication rate is set to a constant independent of protein stabilities. Here the lethal mutagenesis threshold is roughly constant and ∼20% lower than the analytical prediction because of the coupled mutation–duplication effect in this simulation.

A possible reason for dependence of the lethal mutagenesis threshold on the number of genes 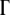in the present model is as follows. Prior to lethality, organisms enter the regime where one or several proteins are marginally stable, which causes considerable slowing down of their replication rate. Therefore, compared to a simple organism, a complicated organism with more rate-determining genes is more likely to enter the slowly replicating phase, and deleterious mutations that finally cause death will accumulate slower in time. Hence larger genome sizes lead to some increase of the lethal mutagenesis threshold.

To check this assertion, a control simulation was performed using the fitness landscape exactly as in Zeldovich et al. (2007), where replication rate is a constant as long as all proteins are at least marginally stable. In this case, the lethal mutagenesis threshold is a constant value of ∼2.5, essentially independent of the number of rate-determining genes (Figure 3C). This finding is consistent with that of Zeldovich et al. (2007), which also predicted that the lethal mutagenesis threshold (counted as number of mutations per genome per generation) is independent of the genome size for the flat fitness landscape at 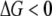. The reason for the slight numeric discrepancy of 20% between the analytical prediction and simulations is due to the effect of coupling of mutations and replications. Furthermore, as can be observed in Figure 3C, with the elimination of the slow replication regime (in the control simulation all viable organisms are always replicating with the same speed), the lethal mutagenesis threshold is significantly reduced as well. This is exactly because slowly replicating organisms make extinction less likely in a given finite amount of time.

Therefore, our results, as indicated in Figure 3, B and C, suggest that even under optimal growth conditions for bacteria, when the natural death rate is negligible, a certain lethal mutagenesis threshold still exists for the species. Moreover, our results shown in Figure 3B indicate that the lethal mutagenesis threshold increases and plateaus when the number of rate-determining genes increases.

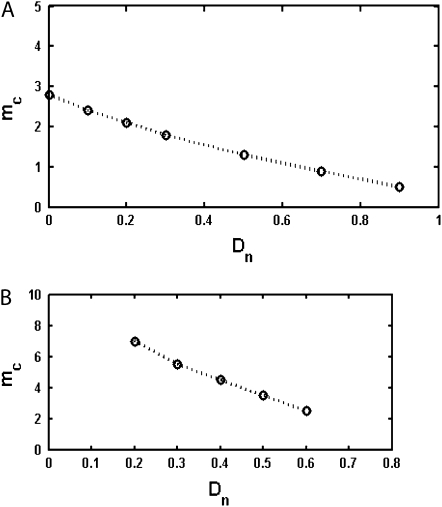
For semiconservatively replicating viruses we also consider a variable death rate that can range from 10% of the initial average population birth rate to 90% of the initial average population birth rate. As we can see in Figure 4A, in the presence of this finite death rate, the lethal mutagenesis threshold is significantly reduced. As the natural death rate increases from 10 to 90% of the replication rate, the lethal mutagenesis threshold for a population of organisms with 20 rate-determining genes decreases from 2.8 mutations per replication to ∼0.5 mutations per replication. (see Figure 4A).

Figure 4.—

(A) Lethal mutagenesis threshold 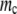as function of 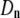, the natural death rate for DNA viruses. This simulation is performed for organisms with 20 rate-determining genes. The natural death rate is measured as a ratio probability of death of a progenitor at each replication event to the birth rate. (B) Lethal mutagenesis threshold as a function of the natural death rate for RNA viruses, with the number of rate-determining genes set at 20.

Lethal mutagenesis for conservative replication (for RNA viruses):

Some RNA viruses may replicate conservatively. In our numerical simulation, we use a simplified model for conservative replication whereby one master genome is preserved while the descendant genome might undergo certain mutations. Our results showed that in this case viruses can sustain higher mutation rates before reaching a lethal mutagenesis threshold compared to semiconservatively replicating organisms.

RNA viruses usually have small genomes; many of them contain around a dozen or so of proteins, and we therefore consider most RNA virus genes as rate determining (Sanjuan et al. 2004). Here we take their number as 20 and study the lethal mutagenesis threshold for conservatively replicating viruses as a function of viral natural death rate. As shown in Figure 4B, the threshold decreases quickly with the increase of natural death rate.

Our numerical simulation actually showed that under the same natural death rate and the same numbers of rate-determining genes, the conservative replication's lethal mutagenesis threshold would be ∼15% greater than twice lethal mutagenesis threshold for the semiconservatively replicating organisms. Therefore the coupled mutation–replication scenario affects conservative replication by shifting the lethal mutagenesis threshold slightly upward compared to the analytical prediction for the uncoupled case.

Distribution of protein stabilities in evolved populations:

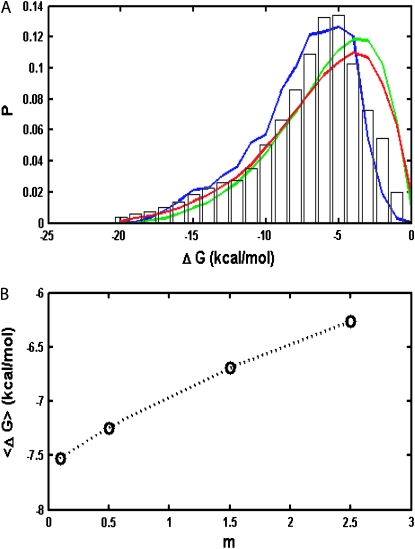
After evolving in a steady thermal environment for sufficient time, the distribution of protein stabilities within an organism reaches equilibrium, as shown in Figure 5A.

Figure 5.—

(A) Distribution of protein stabilities in bacterial species with high and low mutation rates. [Bars, experimental data compiled from the ProTherm database (Kumar et al. 2006); blue line, low mutation rate case, 0.1 mutation per genome per replication; green line, analytical model prediction from Zeldovich et al. (2007); red line, high mutation rate case, 2.5 mutations per genome per replication)]. The number of rate-determining genes is fixed at 20. (B) Stability of all proteins averaged over all organisms in a population vs. mutation rate in mutations per genome per replication.

An important new finding from our calculations is that the mutation rate significantly affects the stationary stability distributions for all proteins in a population. When the mutation rate is increased, more and more proteins become marginally stable. Moreover, as we can see from Figure 5A, at a low mutation rate, which is the case for most DNA-based organisms, protein stability distribution in our simulation agrees very well with the stability distribution of real proteins drawn from the experimental database, which is a considerable improvement compared with the previous analytical model (Zeldovich et al. 2007).

DISCUSSION

In this work, we systematically studied lethal mutagenesis for several biological systems and discussed the effect of various parameters, such as mutation rate, death rate, number of rate determining genes, and replication mechanisms, on the lethal mutagenesis threshold.

Our model is based on a minimal biologically reasonable assumption that the organismal replication rate is determined by the concentration of functional (i.e., correctly folded) rate-determining proteins and that loss of stability by any of these would result in a lethal phenotype. When all rate-determining proteins in the organism are stable and properly folded, the organismal replication rate is high, and the population growth is fast. However, deleterious or beneficial mutations may occur during the replication process. A deleterious mutation in our model is one that increases the folding free energy of a rate-determining protein, destabilizing it and decreasing the number of its properly folded copies in the organism, leading to a decrease of the replication rate. Furthermore, a deleterious mutation could also result in a protein having folding free energy greater than zero, which is lethal to the organism. In this case, the organism would not be able to survive and would eventually die.

Our results showed that the lethal mutagenesis threshold increases and plateaus with the number of rate-determining genes. On the other hand, the threshold could be made smaller with an increase in the natural death rate for the organism. Therefore, our work might potentially lead to a more directed search for bacterial lethal mutagenesis (Bull and Wilke 2008). Although previous lethal mutagenesis experiments have been more focused on RNA viruses, recently several experiments have also been carried out on bacterial systems with increased mutation rates (Sniegowski 1997). However, these bacteria usually exhibit unchanged fitness or some beneficial mutation traits, rather than decreased fitness, in the stable environment of the experimental setup. The advantageous effect of higher mutation rates that are still well below the lethal mutagenesis threshold was also found in recent ab initio microscopic simulations of model cells (Heo et al. 2009). This is because, although the elevations in the mutation rate in these systems are between 10- and 100-fold over their wild-type mutation rates (Sniegowski et al. 1997; Drake et al. 1998), they are still well below the lethal mutagenesis threshold and therefore could lead to fixation of beneficial mutations by hitchhiking instead of extinction.

However, lethal mutagenesis is still potentially achievable in bacteria. In our model, we observed that the lethal mutagenesis threshold could be reduced by choosing a bacterium species with fewer numbers of rate-determining genes, in an environment with a nonnegligible natural death rate. For example, for a bacterium or DNA virus species with 20 rate-determining genes and a death rate of 20% of the initial replication rate, the lethal mutagenesis threshold is ∼2.1 mutations per genome per replication. Even though this number is still above the current level of the observable bacterial mutation rate, exploring bacteria's lethal mutagenesis in various experimental settings can still lead to basic insights about mutation, replication rate, and organismal fitness and therefore may be well worth the effort.

We also separately considered lethal mutagenesis in DNA-based organisms and RNA-based organisms. Our results showed that given the same natural death rate, organisms with conservative replication mechanisms, such as RNA viruses, could tolerate a higher mutation load than DNA-based organisms with a semiconservative replication mechanism, in accord with the prediction of the analytical theory (Zeldovich et al. 2007). Experimentally, ribavirin is the drug commonly considered as a candidate for causing lethal mutagenesis in RNA viruses (Crotty et al. 2002; Freistadt et al. 2004). Many experiments have focused on introducing ribavirin to retroviruses such as human immunodeficiency virus, hepatitis C, and the vesicular stomatitis virus (VSV), etc. This often leads to an increased mutation rate and possibly to the lethal mutagenesis of such viruses. As shown by Crotty et al. (2001), a population of polioviruses can become 90% extinct at exactly 6 mutations per genome per replication, while the normal mutation rate for this virus is ∼1 mutation per genome per replication. This is in agreement with our prediction of ∼6.2 mutations per genome per replication for RNA viruses with 15 proteins controlling the replication rate and a natural death rate of 25% of the wild type's replication rate.

In recent years, many studies of lethal mutagenesis were based on the original model of Muller's ratchet (Haigh 1978; Gessler 1995; Rouzine et al. 2008). Although these models provided many useful insights on various aspects of adaptation and mutation, our model is different in that we link the fundamental genotypic property—protein stability—with the phenotype and do not employ the selection coefficient and other a priori unknown parameters. Here we infer fitness directly from the stabilities of rate-determining proteins of the organism and relate the death phenotype to the loss of structure (and therefore function) of key proteins.

Recently Bull et al. proposed a model of lethal mutagenesis of bacteria and viruses (Bull et al. 2007; Bull and Wilke 2008). In their model, the extinction threshold for bacteria is 0.69 deleterious mutations per genome per replication, and the threshold for viruses is different from ours, too. A possible reason for such a difference is that they considered only deleterious mutations, whereas we considered all mutations affecting protein stability, which may be beneficial, deleterious, or neutral. In our model, a beneficial mutation makes a rate-determining protein more stable, providing more copies of properly functioning proteins in the cell. Beneficial mutations constitute a significant fraction among all point mutations in our model, and therefore it is very important to take them into consideration. The beneficially mutated strains will then have a higher replication rate and be farther from the “death boundary” and therefore produce more offspring. Meanwhile, we also allow mutations occurring in different proteins to interfere with each other through their cumulative effect on fitness (Equation 2), and the dynamics of multiple mutations are taken into account. However, it is worthwhile to compare our prediction of ∼3 mutations per organism per duplication for a semiconservative mechanism with that of Bull et al.'s prediction of 0.69 deleterious mutations per organism per duplication. Note that in the fitness landscape model employed here, the probability to have a deleterious mutation (the one that has 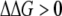) among all possible mutations is ∼71%. Given this condition, 3 mutations per organism per replication roughly correspond to 2 deleterious mutations per organism per replication. Moreover, considering the effect of back mutations and the ability for beneficial mutations to increase fitness in our model, the effective “rate-decreasing” mutation number should be even <2 here. We thus note that our result is slightly different from that of Bull et al., but the two numbers are of the same order of magnitude.

The major conceptual difference between our model and several models rooted in formal population genetics including Muller's ratchet and the recent studies of Bull and coauthors (Bull et al. 2007; Bull and Wilke 2008) is that in our model the main cause of lethal mutagenesis is in actual mutation-induced death events: Cells or viruses can literally die when they acquire lethal mutations that make one of their proteins unstable. In contrast, in other models the lethal mutagenesis occurs when the replication rate falls below a certain threshold. For that reason one should not expect the results from the two approaches to exactly match each other.

The effect of protein stability on phenotype was considered in our earlier analytical theory (Zeldovich et al. 2007). To make the model tractable we did not consider the coupled mutation–replication process there. Although this approximation works well at low mutation rates, it becomes less quantitatively accurate at high mutation rates. While the analytical theory in Zeldovich et al. (2007) provided a qualitatively correct estimate for the lethal mutagenesis threshold, our present study shows that these estimates may be 15–20% off more accurate numbers based on simulations of coupled replication–mutation events and a more realistic fitness landscape given by Equation 2. Thus a coupled mutation–replication model is essential for a more accurate estimate of the lethal mutagenesis threshold, which occurs at high mutation rates per replication where the analytical approximation of Zeldovich et al. (2007) remains qualitatively but not quantitatively correct.

Many earlier experimental works (Crotty et al. 2001; Anderson et al. 2004) associated the lethal mutagenesis in RNA viruses with “error catastrophe” predicted by Eigen and co-workers for the quasispecies model (Eigen et al. 1989). According to this model at high mutation rates the population loses fitness by delocalizing in sequence space (Eigen et al. 1989). However, it was argued in Zeldovich et al. (2007) and demonstrated in Heo et al. (2009) that error catastrophe in the quasispecies model is a consequence of a highly unrealistic single fitness peak assumption. On the other hand close agreement between lethal mutagenesis thresholds predicted here and in the observed one (Crotty et al. 2002) makes it highly plausible that the physical cause of lethal mutagenesis is the persistent loss of stability of one or more essential proteins at higher mutation rates.

Another important result of our model is prediction of distribution of stabilities of proteins in evolved populations, without adjustable parameters and in almost perfect agreement with the experiment (see Figure 5A). Analytical theory predicted the distribution of stabilities, which was in good but not perfect agreement with reality. In particular, the peak of the predicted distribution was shifted toward lower stabilities compared to the experiment, and analytical distribution overall predicted a greater number of marginally stable proteins than observed in the experiment. There could be three possible reasons for the discrepancy between analytical results and the experiment: (1) bias in the ProTherm database reflecting overall difficulties of the experimental study of marginally stable proteins, (2) that the assumption of the analytical theory that evolutionary processes had reached steady state may not be fully justified, and (3) that the step- function-like fitness landscape used in the analytical theory is too oversimplified by not taking into account the gradual loss of fitness as proteins become marginally stable. The present study indicates that reason 3 is correct for the discrepancy between analytical prediction and the experiment. When we took into account that low-stability proteins essentially lead to lower fitness due to a smaller fraction of folded (and therefore functional) essential proteins, the agreement between predicted and observed distribution of stabilities very much improved without introducing additional adjustable parameters. Apparently lower fitness at a larger proportion of marginally stable proteins gives rise to additional pressure leading to the shift of the distribution toward somewhat more stable proteins.

Our study, as well as previous analytical work, provides a realistic explanation for the observation that most proteins are not exceedingly stable—indeed the distribution of protein stabilities peaks around −5 kcal/mol (see Figure 5A). Several authors attributed such moderate stability to the functional requirement of flexibility that calls for lower stability of a protein. An observation that stabilities of natural proteins are not too high was suggested as evidence for the coupling between function and stability (DePristo et al. 2005). However, the problem with this argument is that it is based on the assumption that any observed behavior of proteins has adaptive causes. As noted in our earlier work (Zeldovich et al. 2007) as well as in work by others (Taverna and Goldstein 2002; Bloom et al. 2007; Bloom and Arnold 2009), the observed range stabilities of natural proteins can be explained without assuming a selective advantage of any particular value of stability.

Experiments show that increasing stability by site-directed mutagenesis does not affect the biological function of a protein. A number of earlier works that seemed to suggest otherwise have been sometimes seriously misinterpreted. In most of these earlier studies (see, e.g., Shoichet et al. 1995 and Beadle and Shoichet 2002), only active site residues were mutated and indeed loss of activity accompanied by some stabilization of the protein was observed for several mutations. However, this result suggests only that carving an active site (often enriched with polar and/or charged amino acids) on a surface of an enzyme may indeed destabilize the protein. However, to prove that limited stability of a protein is a prerequisite of its function, one has to study the functional effect of stabilizing mutations outside the active site and show that these also lead to loss of function. These experiments are necessary to separate the indirect effect of mutations on function through stability alteration from a direct effect on function due to mutations in the active site. When a protein was mutated outside the active site, the increase of stability did not result in a loss of activity (Bloom et al. 2006). Our study provides another piece of evidence for independence of stability and activity of proteins, by accurately predicting the distribution of protein stabilities without assuming any relation between the two.

Taverna and Goldstein (2002) argued that protein stability is not too high for an entropic (in sequence space) reason: that there are many more sequences corresponding to proteins of low to moderate stability than to more stable ones. A similar observation was made by Bloom et al. (2007) in their study of neutral evolution of protein stability. While this argument is certainly a correct one, it does not explain why the distribution of protein stabilities has a well-defined peak around −5 kcal/mol rather than being shifted toward less stable proteins whose sequences represent an overwhelming majority. Our study answers this question by showing that the distribution of protein stabilities is established as a compromise between two opposing factors: (a) physical factors that favor less stable proteins for entropic (in sequence space) reasons outlined in Taverna and Goldstein (2002) and (b) population genetics pressure that favors more stable proteins by eliminating from populations organisms that carry marginally stable proteins. The organisms whose genotypes encode more marginally stable proteins become eliminated from populations for two reasons: (1) their fitness is lower because the fraction of folded proteins is diminished and, more importantly, (2) their fitness is lower because organisms with less stable proteins are closer to the death boundary; i.e., they leave less viable progeny.

A new insight coming from this study is the dependence of stability of proteins in a population of organisms on mutation rates. Our simulations predict that species with higher mutation rates (such as RNA viruses) should have less stable proteins than their lower mutations rates counterparts. The underlying reason for this finding is that mutations that destabilize proteins are deleterious in our model. At low mutation rates purifying selection dominates and organisms carrying destabilizing mutations are purged from the population—hence the distribution of protein stabilities is shifted toward more stable proteins. As mutation rates get higher the supply of deleterious mutations increases and purifying selection is no longer capable of purging all mutants from the population—hence the distribution shifts toward less stable proteins. The observed dependence of protein stability on mutation rate m arises only in the regime 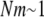; otherwise purifying selection is able to purge any destabilizing mutant from the population. Further, we note that this effect is due to continuous dependence of fitness on protein stability (i.e., inhomogeneous generation time) as given by Equations 1 and 2. In our earlier study with the step-function fitness landscape where mutations are neutral as long as 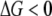, the long-time distribution of protein stability was independent of mutation rates (Zeldovich et al. 2007). Our results can also be contrasted with earlier studies of mutational robustness, which predicted that higher mutation rates would lead to emergence of more robust proteins (Bornberg-Bauer and Chan 1999; van Nimwegen et al. 1999). In these studies strictly neutral mutations were considered while in our model strictly neutral mutations do not exist as there is a direct relation between protein stability and fitness.

A recent study by Tawfik and coauthors provides some support to our prediction, showing that the attributes of protein stability such as contact density are significantly different in proteins of RNA viruses than in those of DNA-based organisms (Tokuriki et al. 2009). However, as suggestive as it is, the work of Tawfik et al. (Tokuriki et al. 2009) is not a proof of lower stability of RNA viral proteins: a much more comprehensive analysis based on throughput measurements of protein stabilities in several organisms is required to confirm or disprove this prediction.

Finally, we note that our model of lethal mutagenesis is minimalist in that it did not account for various important biological processes, such as gene recombination, Darwinian selection due to competition for limited resources, or interaction between an organism and external factors. For example, ribavirin has been demonstrated to have at least three activities in vivo or in cell culture, including inhibition of cell replication, immunomodulatory effects, and incorporation as a mutagenic nucleoside by the viral RNA polymerase (Crotty et al. 2002). Therefore, further efforts and extensions, such as more explicit consideration of protein function, protein–protein interactions, or the structure–function relationship, would also be valuable to the understanding of lethal mutagenesis in bacteria and viruses.