DEFORMATION-DEPENDENT ENZYME MECHANOKINETIC CLEAVAGE OF TYPE I COLLAGEN

Abstract

Collagen is a key structural protein in the extracellular matrix of many tissues. It provides biological tissues with tensile mechanical strength and is enzymatically cleaved by a class of matrix metalloproteinases (MMPs) known as collagenases. Collagen enzymatic kinetics has been well characterized in solubilized, gel and reconstituted forms. However limited information exists on enzyme degradation of structurally intact collagen fibers and, more important, on the effect of mechanical deformation on collagen cleavage. We studied the degradation of native rat tail tendon fibers by collagenase after the fibers were mechanically elongated to strains of ε = 1-10%. After the fibers were elongated and the stress allowed to relax, the fiber was immersed in Clostridium histolyticum collagenase and the decrease in stress (σ) monitored as a means of calculating the rate of enzyme cleavage of the fiber. An enzyme mechanokinetic (EMK) relaxation function T_E(ε) in sec^-1 was calculated from the linear stress-time response during fiber cleavage, where T_E(ε) corresponds to the zero-order Michaelis-Menten enzyme-substrate kinetic response. The EMK relaxation function T_E(ε) was found to decrease with applied strain at a rate of ~9% per percent strain, with complete inhibition of collagen cleavage predicted to occur at a strain of ~11%. However, comparison of the EMK response (T_E vs ε) to collagen’s stress-strain response (σ vs ε) suggested the possibility of three different EMK responses; (1) constant T_E(ε) within the toe region (ε<3%), (2) a rapid decrease (~50%) at the transition of the toe-to-heel region (ε≅3%) followed by (3) a constant value throughout the heel (ε=3 to 5%) and linear (ε=5 to 10%) regions. This observation suggests that the mechanism for the strain-dependent inhibition of enzyme cleavage of the collagen triple helix may be by a conformational change in the triple helix since the decrease in T_E(ε) appeared concomitant with stretching of the collagen molecule.

Introduction

Collagen degradation is a mechanism for extracellular matrix (ECM) remodeling and maintenance, and in response to trauma, disease and inflammation. Collagenases-1, 2 and 3 are the primary enzymes that act to degrade interstitial collagens (types I, II and III) in humans and animals. These collagenases are part of a larger family of enzymes (matrix metalloproteinases or MMPs) characterized by a zinc dependency for catalytic activity [1]. MMPs are secreted by the cell as inert zymogens in response to the cell being activated by inflammatory cytokines, such as growth factors (interleukin-1) [2] and mechanical loads [3]. In order for collagen cleavage to occur, the collagenase (MMPs-1, 8 and 13, respectively) gains access to the collagen triple helix by binding to the enzyme’s attachment domain along the α-chains, followed by separation (unwinding) of the α-chains to expose the cleavage site, and then cleavage of the α-chain by the enzyme’s catalytic domain [1,4]. Collagenases contain two protein domains joined by a linker (hinge), a hemopexin C domain to which the collagen molecule attaches, and a catalytic domain responsible for the α-chain cleavage [1,4]. MMP-1, 8 and 13 will cleave all three α-chains of interstitial collagens by a single scission at a specific site, located 3/4 from the N terminal and 1/4 from the C terminal, which is characterized by a Gly⁷⁷⁵-Ile⁷⁷⁶ or Gly⁷⁷⁵-Leu⁷⁷⁶ peptide bond, resulting in two fragments of the collagen molecule [1]. Following this initial cleavage other MMPs (mainly gelatinases and stromelysins) can collectively further degrade the collagen fragments. However, the mechanism of the initial cleavage of the collagen molecule must originate with collagenase binding, triple helix unfolding and ¾-¼ scissoring.

Like mammalian collagenases, Clostridium histolyticum collagenase (CHC or bacterial collagenase) is both Zn²⁺ and Ca²⁺ dependent. However, it differs from mammalian collagenases in that it can cleave collagen at multiple sites [5,6]. The bacterial collagenases are a group of highly related metalloproteinases that yield several subdivisions of distinct collagenases, Classes 1 and 2. Lin et al. [7] demonstrated through SDS-PAGE analysis that purified CHC consists of two independent but comparable collagenases, type-β and type-δ collagenases. Class 1 enzymes initially cleave collagen near the periphery of the triple helix domain, while class 2 enzymes cleave near the interior, fragmenting the collagen into nine segments [5].

Our focus in this study was on collagenases and fibrillar type collagens. We are particularly interested in the ability of collagenases to cleave fibrillar collagens of the musculoskeletal system (ligaments, tendons, cartilage, meniscus). Diarthrodial joints are subjected to a lifetime of mechanical loading. One mechanism associated with the initiation of collagen degradation is cleavage of the collagen network in the extracellular matrix by collagenases, primarily MMP-1 and 13 [3,8]. Mechanical factors are important when considering rates and mechanisms of enzymatic activity, and how a mechanical deformation of the substrate, enzyme or both (i.e., the mechano-chemical interaction [11,12]) will effect the enzymatic activity is applicable to many tissues and enzymes. We refer to this physical mechanism as Enzyme MechanoKinetics (EMK). In our study we utilized rat tail tendon to model the collagen-enzyme mechanokinetic interactions. The linear orientation of type I collagen in rat tail tendon allows us to easily extract collagen fibers and uniaxially deform these fibers in tension while exposing them to enzymatic degradation.

The phenomenon of deformation-dependent cleavage of collagen by bacterial collagenase was previously reported in three earlier studies. Using a thin collagen tape formed from reconstituted bovine tendon (1.3 mm × 12 cm × 32 um thick), Huang and Yannas [11] found that increasing tensile strain up to 4% (grip-to-grip) resulted in a decrease in the rate of enzymatic degradation, while strains above this (to 7%) caused an increase in the rate. They speculated that these phenomena were a result of restricted enzyme transport to the cleavage site and the opening of new cleavage sites, respectively. However, the potentially disrupted and unknown structural organization of reconstituted collagen limits the interpretation of their results on effect of axial strain on the interaction between the collagen molecule and collagenase. Nabeshima et al. [12] applied a single uniaxial tensile strain of 4% (grip-to-grip) to intact rabbit patellar tendon, and after 20 hours of incubation with enzyme found that the tendon’s tensile failure strength was significantly greater compared to the tensile strength of similarly incubated unloaded tendon. They reported that mass transport of the enzyme into the tendon was not responsible for this difference, and attributed the inhibition in enzyme cleavage of the tendon to several possible mechanisms associated with altered collagenase-matrix interaction, including stretching of the triple helix and local pH changes from redistribution of free water. More recent, Ruberti and Hallab [13] uniaxially loaded (1-2 N) strips of bovine cornea (3 mm × 20 mm × 0.8 mm thick) in Clostridiopeptidase A for 120 hours and reported a loss in collagen birefringence only in the collagen fibers that were not aligned to the tensile load. The authors attributed this result to a “strain-stabilization” mechanism making enzyme binding and cleavage more difficult, though tissue strains were not reported.

Unfortunately the use of reconstituted, unorganized and gross collagen specimens, and imprecise and indirect measures of collagen strain and degradation, makes interpretation of these results difficult when trying to determine the mechanisms of enzyme-substrate interaction. Our study was designed to avoid these shortcomings by using a single collagen fiber (rat tail tendon) in its native state, measuring the applied strain directly on the fiber (longitudinal and transverse), measuring the degradation of single fibers both mechanically and optically. We utilized a similar mechanochemical model as Huang and Yannas [11] to test whether uniaxial tensile deformation of type I collagen would result in a change in the collagen-enzyme cleavage process. We also chose to use Clostridium histolyticum collagenase as opposed to mammalian collagenase because CHC is readily available, inexpensive, and biochemically active at room temperature [14], the latter critical to our mechanochemical testing system. We hypothesized that a mechanically applied elongation of the rat tail tendon fiber would result in inhibition of the enzymatic degradation, and that the inhibition would be proportional to the amount of fiber elongation. To test this hypothesis we stretched (loaded) rat tail tendon fibers to different strain levels, immerse the fibers in bacterial collagenase, and measured the rate of enzyme cleavage by measuring the decrease in fiber load. We found that as the strain applied to the collagen fibers increased, the rate of enzyme degradation was significantly reduced, though not completely inhibited.

Materials and Methods

Chemicals

Dulbecco’s phosphate buffered saline (PBS) with calcium (CaCl₂, 0.133 mg/ml) and magnesium (MgCl₂, 0.1 mg/ml), Dimethylmethylene blue (DMMB) and Dimethylaminobenzaldehyde (DMAB) reagents were obtained from Sigma-Aldrich (St. Louis, MO). Type II bacterial collagenase (Clostridium histolyticum, ≥125 units/mg dry weight) was obtained from Worthington Biochemical Corporation (#CLS-2, Lakewood, New Jersey). All other reagents were obtained from Sigma-Aldrich and were reagent grade unless otherwise noted.

Rat Tail Tendons

In accordance with institutional animal care and use procedures, type I collagen fibers from the tails of three six-month old Lewis rats, euthanized for other unrelated studies, were used in this investigation. Using a sterile scalpel blade the tail was sectioned between the coccygeal vertebrae at the base and distal tip of the tail for a total length of approximately 150 mm. The tail was removed immediately after euthanasia and placed in a -20° C storage freezer. Upon freeze-thaw (~60 minutes at room temperature 23-25° C) type I collagen fibers (i.e. fascicle of diameter ~300 um) were teased from the tail, sectioned into 70 mm length specimens, and soaked in 15 ml 1x PBS. The fibers were divided into four groups: (1) water, collagen and proteoglycan contents (n=12), (2) mechanical testing (n=6), (3) osmotic stress effect (n=4) and (4) EMK testing (n=24).

Collagen-to-Enzyme Ratio

An estimate for total number of collagen molecules (substrate concentration [S]) in the collagen fiber was calculated using the surface area of the tendon fiber exposed to the aqueous environment, divided by the approximate collagen molecule size, assuming complete packing. The enzyme concentration [E] was derived from the total collagenase weight, divided by the approximate molecular weight of a bacterial collagenase enzyme suspended uniformly in a fixed volume. We modeled the collagenase-collagen interaction as a solid two-dimensional sheet of collagen substrate contacted by a single layer of collagenase in suspension. Since the reaction of interest, [E][S], is restricted to a two-dimensional area, we approximated a volume per molecule of collagenase enzyme in uniform suspension and then calculated a face surface area by considering the volume as a cube. It is important to note that these simplifications in this model include no consideration of potential noncollagenous substrates at the surface of the fibril (e.g., proteoglycan), possible steric hindrance between the collagen and collagenase molecules, and as stated above, assuming a uniform suspension. Using the molecular weight for Rattus norvegicus (rat) collagen obtained from the National Center for Biotechnology Information (http://rsbweb.nih.gov/ij) protein database and for bacterial collagenase of 116 kDa [6,15], we estimated the maximum substrate-to-enzyme concentration ratio [S]:[E] >100:1. Thus the collagen fiber cleavage could be assumed to follow a zero order kinetic reaction during the early collagenase degradation phase [16].

Water, Proteoglycan and Collagen Contents

Tendon fibers (n=12) were incubated in buffered saline for 1 hr, weighed (wet) on a microbalance (25 Electrobalance, Cerritos, CA), lyophilized overnight for 24 hrs, and weighed (dry). The fiber water content (% wet weight) was calculated from the wet and dry weights. Dehydrated samples were then solubilized with papain, and aliquots taken for further analysis of collagen and proteoglycan content.

The collagen content of the tendon fibers was assayed by determination of hydroxyproline content. Hydroxyproline was measured by chromophore formation with 4-Dimethylaminobenzaldehyde (DMAB) against standards and reported as a percent of fiber dry weight (DW) (modified from Woessner [17] and Edwards and O’Brien [18]. The solubilized samples were hydrolyzed under acidic conditions at 110 °C for 3 hours, oxidized with Chloramine-T, and then exposed to DMAB dissolved in 1-propanol and perchloric acid (Baker, Phillipsburg, NJ) at 65 °C. Chromophore absorption was then measured with a spectrophotometer (340 ATTC, Tecan US, Chapel Hill, NC) at 550 nm and compared to a standard curve of pure hydroxyproline.

Proteoglycan content was assayed by determination of the glycosaminoglycan (GAG) content. GAG was measured colorimetrically by reaction with 1,9-Dimethylmethylene blue (DMMB) dye and reported as a percent of fiber dry weight (modified from Farndale et al. [19,20]). Solubilized samples were diluted with distilled water, exposed to DMMB dye, absorbance measured at 540 nm, and compared against a standard curve of chondroitin-4-sulfate.

Mechanical Test System

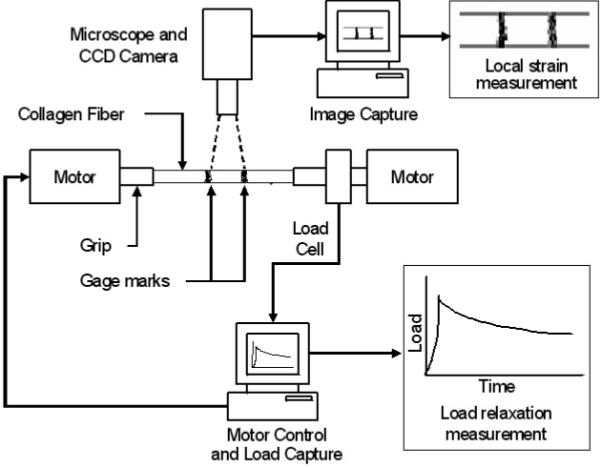
All mechanical and chemical testing procedures were performed at room temperature (23-25° C). A novel Collagen Enzyme MechanoKinetic Automated Test System (CEMKATS) was developed to elongate the type I collagen fiber (mechanical-elongation phase) and measure the change in load (1) after the elongation was applied (mechanical-relaxation phase), and (2) after the fiber was submerged in enzyme (enzyme-cleavage phase). The CEMKATS (Fig. 1) consisted of two stepper motors (range = 12.5 mm, resolution = 2 um) (StepperMike, Oriel, Stratford, CT) aligned axially on linear stages (Parker Hannifin, Cleveland, OH), positioned approximately 15 cm apart, which were mounted onto an optical vibration isolation table (Newport, Stratford, CT) (Fig. 1). The motors were connected to a stepper controller (Oriel, Stratford, CT) interfaced to a personal computer (Pentium 4, Gateway, Irvine, CA) via an RS-232 terminal data link. LabView software (National Instruments, Austin, TX) was used to drive each stepper motor in full-step mode (2 um/step) at a maximum velocity 1 mm/s. Both motors were programmed to operate simultaneously to elongate the collagen fiber at a constant 2 mm/s.

Figure 1.

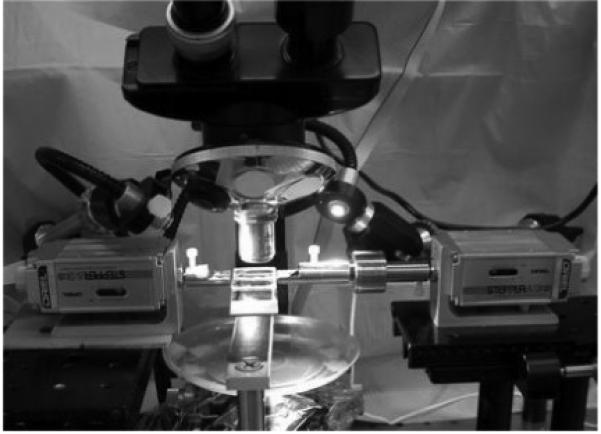
a. The collagen enzyme mechanokinetic automated test system (CEMKATS) used to mechanically stretch the collagen fiber between grips attached to two stepper motors. The load applied to the fiber is monitored using a 250 gram load cell attached to the right grip while images the fiber’s elongation and diameter are recorded using a digital camera (not shown) attached to a microscope. Two personal computers (not shown) were used to simultaneously control the motors and record the load and camera images.

b. The collagen fiber is affixed to the test grips by gluing the fiber within a groove and hole and then positioning the fiber within a 1 mm wide by 25 mm long channel. PBS is slowly dripped into the channel during the fiber elongation and load relaxation phases, and then replaced with bacterial collagenase during the enzyme mechanokinetic cleavage phase.

c. Schematic diagram of the collagen enzyme mechanokinetic automated test system (CEMKATS) used to mechanically stretch the collagen fiber and measure the resulting fiber load and elongation during the elongation, relaxation and enzyme cleavage phases. The fiber is stretched using two stepper motors and the load is continuously recorded using a load cell. The fiber elongation (gage marks) and diameter are recorded using a digital camera attached to a microscope. The stepper motors and recording transducers are interfaced to two personal computers for continuous and simultaneous control and data recording, respectively.

Custom-made grips to hold the ends of the collagen fiber were attached to each stepper motor (Fig. 1b). Each grip consisted of a flat surface with a ~0.5 mm deep V-groove extending to a small hole. One of the grips was attached to a 250-gram load cell (resolution = 0.24 mg, Sensotec Model 31, Honeywell, Columbus, OH) which was interfaced with the computer via a signal conditioner (Sensotec Model GM) and data acquisition board (National Instruments). At the time of testing, the grip ends were positioned ~27 mm apart, the ends of the collagen fiber (wet) placed into the groove and through the hole, and the fiber secured in the groove and hole using ethyl cyanoacrylate glue (Elmer’s, Columbus, OH). Using the motors, the fiber was slowly tensed to ~1-2 gms and then unloaded to remove any slack in the fiber. Measurement of the initial grip-to-grip fiber length, L_o, was made using a Vernier caliper (L_o~25-27 mm), and this length used to determine the amount of fiber elongation, δL, required to achieve the desired fiber strain, E_o (=ΔL /L_o). The fiber was then suspended into a 1 mm wide by 25 mm long channel containing PBS at room temperature. A continuous PBS drip (~1 drop/s) was applied to the fiber through a syringe needle positioned near the end of the channel such that the fiber remained hydrated (immersed) throughout the duration of the load-relaxation phase of the test (Fig. 1b).

In this test configuration, about ~1 mm of the fiber length was exposed to the air between the ends of each grip and the channel. The portion of the collagen fiber exposed to air (~8% of the fiber) will shrink and stiffen as it dries and could possibly effect the final strain applied to the fiber within the channel at the end of the mechanical-relaxation phase (1-8 hrs). To correct for possible drying artifacts when using the grip-to-grip length to calculate the fiber strain, two black gage marks (~ 0.2 mm thick, inkjet printer ink) were placed approximately 2-5 mm apart in the center of the fiber, equidistant from each of the grips, and digitally imaged through a light microscope (Wild, Heerbrugg, Switzerland) using a CCD camera (DMCIe, Polaroid, Waltham, MA) (Figs. 1b and 2). The camera was interfaced to a second computer, where it recorded time-captured images of the gage marks and the fiber’s diameter during the test (Fig. 2). Images were recorded at four time points: (1) pre-strain t_o, (2) post-strain t_p, (3) post-stress (load) relaxation t_r, and (4) post-enzyme cleavage t_e (Figs. 2 and 3). The post-strain and post-stress relaxation images were analyzed using NIH Image J software (www.nih.gov/nih-image) to measure the distance (resolution ~1 um) between the center of the gage marks and outer edges of the fiber’s diameter, and these used to calculate the axial and radial strains within the fiber at t_p and t_r, respectively. The fiber’s axial strain ε_l was calculated from the change in distance δl between the gage marks, ε_l = δl/l_o, and the radial strain ε_d calculated from the change in fiber diameter δd, ε_r = δd/d_o, where l_o and d_o are the pre-strain distance and diameter, respectively. The fiber stress, σ, was calculated from the load, F, and fiber cross-sectional area, A, where σ = F/A in N/m² (Pascal, Pa), assuming the fiber cross-section was circular [21].

Figure 2.

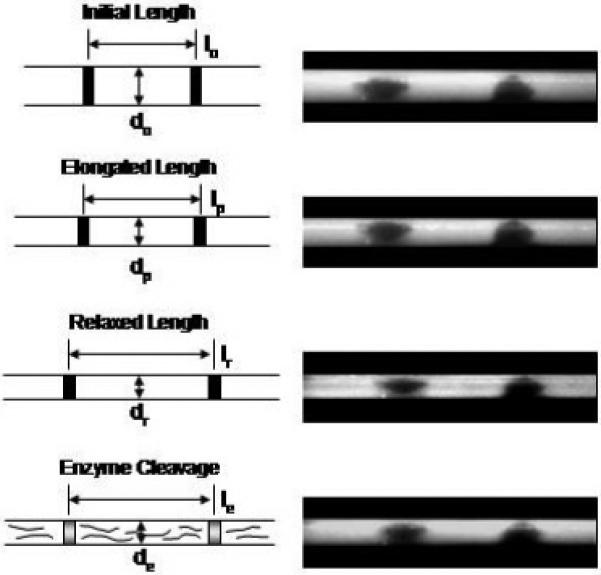
The local fiber axial strain (change in distance between gage marks) and radial strain (change in diameter) at the center of the fiber were recorded using a microscope and digital camera image capture at (a) time t=0, unstrained initial lengths l_o and d_o, (b) time=t_p, at the end of the elongation phase at peak stress, l_p and d_p, (c) time=t_r, after mechanical stress relaxation, l_r and d_r, and (d) time=t_e, after collagenase cleavage, l_e and d_e. The initial, elongation and relaxation lengths (a, b and c, respectively) were used to determine the fiber’s axial and radial strains. Fiber images (right) are for an initial 3% grip-to-grip strain.

Figure 3.

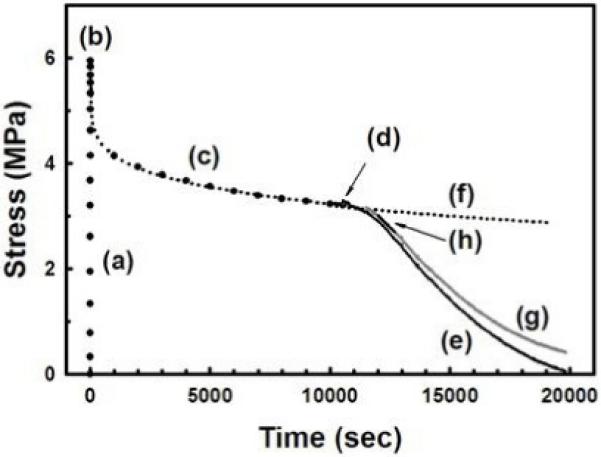
Typical mechanical-elongation (a), mechanical stress-relaxation (c) and enzyme-cleavage (e) responses for the rat tail tendon fibers subjected to a constant applied strain (3%) and degradation by bacterial collagenase, respectively. The peak stress occurs at the end of the mechanical -elongation phase (b). Immediately after the fiber is exposed to the collagenase (d) there is a small transient increase in fiber stress due to the osmotic stress. The mechanical stress-relaxation response (c) was curve-fit using Eq. 1 (dotted line) and extended beyond (d) to predict the continued mechanical stress-relaxation (f). This was used to correct the enzyme-cleavage response (g). The linear portion of the corrected enzyme-cleavage response (h) was used to calculate the EMK relaxation function. For clarity the data shown in (a), (e) and (g) is plotted at 1 second intervals and in (c) at every 100 seconds.

Mechanical-Relaxation Tests

Preliminary mechanical tests were performed to determine the time required for stress-relaxation (load equilibrium) after the application of the applied strain E_o. Collagen fibers were strained to 2% or 4% (grip-to-grip, 2 mm/s) in PBS (pH=7.2) and the strain held constant while monitoring the decrease in stress (load) as a function of time (1 Hz sampling frequency) until a equilibrium-relaxation stress, σ_r, was reached at t_r (Fig. 3). The mechanical stress-relaxation response σ_m(t) was analyzed using a three-parameter power function of time [22], given by

$${\sigma }_{\mathrm{m}}\left(\mathrm{t}\right)={\sigma }_{\mathrm{p}}-\alpha {\mathrm{t}}^{\beta }$$ (1)

where σ_p is the time-independent peak stress at the end of the mechanical-elongation phase at time t_p, t the time, α and β are relaxation constants, and the stresses σ_m(t) and σ_p are calculated using the pre-strain fiber cross-sectional diameter D_o and area A_o. The relaxation constants α and β can be easily determined for each fiber from the least-squares best-fit of Eq. 1 to the experimental data.

Effect of fiber strain on collagen cleavage

Fibers (n=24) were stretched to 1%, 2%, 3% or 4% in PBS (pH=7.2), allowed to reach stress equilibrium (σ_p→σ_r), and 1% bacterial collagenase (10 mg/ml) in PBS (pH=7.2) added to the entire channel (~1 sec). The enzyme-cleavage phase was continuously monitored by recording the decrease in the fiber’s enzyme-cleavage stress, σ_e(t), as the collagen in the fiber was cleaved by the bacterial collagenase (Fig. 3). The fiber stress σ_e(t) was calculated from the load and A_o and monitored until σ_e(t)→0.

In some cases, the fiber’s mechanical-relaxation stress σ_m(t) did not reach equilibrium before the enzyme was introduced. Thus, equation (1) was used to calculate (predict) the mechanical stress-relaxation σ_m*(t) occurring during the enzyme-degradation phase (Fig. 3). The decrease in fiber stress only due to enzyme cleavage of the fiber, σ_e*(t), was calculated from the measured enzyme-degradation stress, σ_e(t), by removing the mechanical-stress relaxation occurring after the enzyme was introduced at time t_r, such that

$${{\sigma }_{\mathrm{e}}}^{\ast }\left(\mathrm{t}\right)={\sigma }_{\mathrm{e}}\left(\mathrm{t}\right)+{\sigma }_{\mathrm{r}}-{{\sigma }_{\mathrm{m}}}^{\ast }\left(\mathrm{t}\right)$$ (2)

for t≥t_r (Fig. 5).

Figure 5.

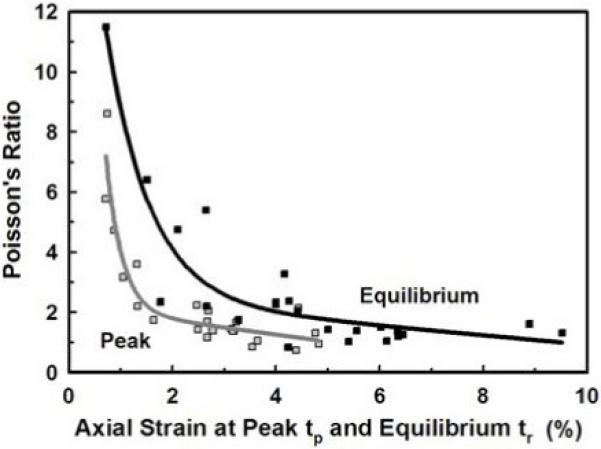
The Poisson’s ratio (ε_d/ε_l) at the end of the mechanical-elongation (peak ) and mechanical stress-relaxation (equilibrium ■) phases decreased with increasing axial strain (ε_l) at the peak and equilibrium times, t_p and t_r, respectively. For both phases the data fit best to an exponential-linear model. Note that the greatest decrease in the Poisson’s ratio occurs for ε_l(t_r)≤3%.

According to the Michaelis-Menten model for simple steady-state enzyme-substrate kinetics, the rate of enzyme degradation of collagen will be linear (0^th order) with respect to time under the condition that [S]>>[E] (concentration of substrate>>enzyme). Thus, we defined the slope of the linear (initial) portion of the enzyme-cleavage response (σ_e*(t) versus time) to be the EMK relaxation function T_E(ε) in sec^-1, given by

$${\mathrm{T}}_{\mathrm{E}}\left(\epsilon \right)=[\mathrm{d}{\sigma }_{\mathrm{e}}\ast \left(\mathrm{t}\right)∕\mathrm{dt}]∕{\sigma }_{\mathrm{r}}$$ (3)

where the rate of change in σ_e*(t) has been normalized to the equilibrium-relaxation stress σ_r at time t_r. The EMK relaxation function T_E(ε) is a measure of the collagenolytic activity for fiber degradation, which is assumed to start on the outside of the fiber as this layer is most accessible, and dependent on the applied strain ε (axial and radial). The EMK relaxation function was determined for each fiber from the best-fit straight line to the initial portion of the enzyme-cleavage phase after osmotic stress relaxation (Fig. 3).

Effect of Osmotic Stress

Solvents such as water that are capable of forming intra-molecular hydrogen-bonds with the triple helices will cause the collagen fibers to swell, whereas solvents containing large molecules (e.g. C. histolyticum collagenase, 116 kDa [6]) will draw water out of the triple helices [23]. As a result of the interaction of water and solutes with the collagen molecule, a significant intramolecular hydration force is possible if the fiber is subjected to an osmotic stress. This hydration force could effect the axial load while the fiber is held at a constant elongation. To evaluate the affect of an osmotic stress on the fiber when the collagenase is introduced into the channel, separate tests were performed using dextran (MW=79.4 kDa) and inactivated bacterial collagenase. In the former, stress-relaxation tests were performed on fibers stretched to 2% or 4% strain in PBS containing Ca²⁺ (pH=7.2). Once stress equilibrium was reached, dextran (10 mg/ml) in PBS solution was added to the channel and the change in the stress σ_m was monitored until stress equilibrium was again reached. In the latter case, tests were performed in which the collagenase activity was inhibited by omitting the Ca²⁺ from the PBS (CHC is Ca²⁺ dependent). Similar to the dextran tests, stress-relaxation tests were first performed in Ca²⁺ and Mg²⁺ free PBS, then bacterial collagenase (10 mg/ml in Ca²⁺ and Mg²⁺ free PBS) was added once stress equilibrium was reached, and σ_m(t) again monitored until stress equilibrium was again reached.

Statistical Data Analysis

The parameters α, β and T_E(ε) were calculated from the experimental data for the mechanical-relaxation and enzyme-cleavage phases using best-fit linear least-squares regression analysis (Systat Software, Richmond, CA) to equations (1) and (3), respectively. Means ± standard deviations were calculated for all measured parameters unless indicated otherwise. Statistical significance was determined using ANOVA and the two-tailed Student’s t-test at the α=0.05 level. Multiple linear regression analysis of the collagenolytic activity, T_E(ε), was performed to determine its dependency on the axial and radial strains, fiber diameter, and the peak and equilibrium relaxation stresses [24,25].

Results

Water, Proteoglycan and Collagen Contents

Analyses were performed on individual tendon fibers (N=12) to determine the water content (free water per fiber wet weight) and the amounts of proteoglycan (GAG per dry weight) and collagen (hydroxyproline per dry weight). Water content of the tendon fibers was 65.2% ± 1.8%. GAG content was 0.28% ± 0.07% per dry weight, in agreement with the 0.24% reported by others [26]. The GAGs are located on the proteoglycan monomer (aggrecan) which contains approximately 93% GAGs (87% chondroitin sulfate and 6% keratan sulfate) and 7% protein. Thus the amount of proteoglycan was approximately 0.49% per dry weight and 0.17% per wet weight, similar to previously reported values for tendon [27]. Hydroxyproline content was 8.5% ± 0.5% per dry weight, in agreement with 8.2% reported by Marsolais et al. [28] and 8.9% reported by Scott et al. [29]. If the content of hydroxyproline is assumed to be 12.5% by weight of collagen [18], the collagen content was approximately 68% and 24% of the fiber’s dry and wet weights, respectively.

Stress-Relaxation Tests

Preliminary mechanical stress-relaxation tests were performed on collagen fibers to determine the time required to reach stress equilibrium prior to the introduction of the bacterial collagenase. Typical stress-time responses were observed for all fibers, with a rapid rise in stress during the mechanical-elongation phase followed by a slow decrease in stress once the grip-to-grip elongation ceased (mechanical-relaxation phase) (Fig. 3). Fibers were strained to 2% or 4% (E_o, n=3 each) based on their initial fiber grip-to-grip lengths (L_o = 25.3 ± 0.5 mm). However, the actual axial strain measured directly on the fiber at the end of the elongation phase, ε_l(t_p), was 2.09 ± 0.06% and 4.55 ± 0.26%, respectively. The corresponding peak stresses σ_p were 5.8 ± 2.3 MPa and 15.2 ± 11.2 MPa, and these decreased by 67% and 91% at equilibrium. The stress-relaxation response σ_m(t) was fit to the three-parameter power function (Eq. 1) yielding α and β values of 1.271 ± 0.589 MPa and 0.138 ± 0.024 for the 2% applied strain, respectively, and 0.641 ± 0.252 MPa and 0.292 ± 0.106 for the 4% strain. Finally, the fibers reached stress equilibrium in 1.6 ± 1.3 hrs and 4.7 ± 1.8 hrs, respectively, determined when the load-relaxation rate was <1 mg/sec or ~0.001% σ_p/sec.

For the enzyme studies collagen fibers were stretched to 1%, 2%, 3% or 4% axial (grip-to-grip) strain and allowed to reach stress equilibrium (t_r~2-4 hrs, mean 3.3 ± 0.9 hrs, Table 1) before the introduction of the collagenase. Twenty-four fibers were tested, with initial diameters D_o of 324 ± 86 um (range 177-582 μm) and grip-to-grip lengths L_o of 25.3 ± 0.6 mm (Table 1). The stress-relaxation response for all twenty-four samples was similar to those reported above. Values for the fiber peak and equilibrium stresses and strains, time to reach mechanical equilibrium, and the relaxation constants α and β are given in Table 1 for each applied strain E_o. The fiber peak axial strain ε_l(t_p) ranged from 0.7% to 4.8% while the peak radial strain ε_d(t_p) were significantly greater, ranging from 2.9% to 9.5% (Fig. 4). At stress equilibrium the axial and radial strains increased to approximately twice that of their peak values, increasing by 1.71±0.37 and 2.04±0.63, respectively, even though the grip-to-grip strain was held constant (Table 1, Fig. 4). The increase in strain may be from drying of the exposed fiber ends or uneven fibril elongations, though the exact mechanism for this was not determined (see Discussion).

Table 1. Mechanical and Enzyme Mechanokinetic Stress Relaxation Parameters^*.

Applied Strain (grip-to-grip), Eo,%	1%	2%	3%	4%
Fiber Diameter, do, um	324 ± 67	303 ± 65	380 ± 139	304 ± 68
Mechanical Stress Relaxation
Peak Axial Strain, ε1(tp), %	1.01 ± 0.27	2.49 ± .39	3.25 ± 0.16	4.38 ± 0.42
Equilibrium Axial Strain, ε1(tr), %	1.90 ± 0.74	4.54 ± 0.91	5.13 ± 1.16	6.86 ± 1.98
Peak Radial Strain, εr(tp), %	4.3 ± 1.24	4.15 ± 1.1	4.34 ± 0.85	5.16 ± 2.39
Equilibrium Radial Strain, εr(tr), %	8.72 ± 3.53	7.43 ± 1.62	9.94 ± 2.2	8.93 ± 3.95
Peak Stress, σp, MPa	3.96 ± 1.89	8.40 ± 2.73	6.04 ± 3.86	14.55 ± 8.96
Equilibrium Stress, σr, MPa	1.51 ± 1.39	2.76 ± 1.32	1.59 ± 1.69	1.17 ± 0.56
Mechanical Equilibrium Time, tr, hrs	2.1 ± 0.9	3.1 ± 1.1	3.9 ± 1.2	4.2 ± 1.5
Relaxation constant, α ,MPa	0.44 ± 0.32	1.22 ± 0.66	0.90 ± 0.95	2.34 ± 2.86
Relaxation constant, β	0.21 ± 0.05	0.16 ± 0.04	0.18 ± 0.09	0.21 ± 0.08
EMK Stress Relaxation
Osmotic Equilibrium Time, min	5.2 ± 5.0	17.2 ± 8.9	3.9 ± 4.1	17.4 ± 22.2
Zero Order Time, min	8.4 ± 3.3	16.8 ± 5.7	27.9 ± 16.1	18.9 ± 18.9
Relaxation Function, TE(ε1), 10-4 sec-1	2.49 ± 0.89	1.40 ± 0.49	1.07 ± 0.33	0.72 ± 0.33

^*Means ± standard deviation; n = 6, 7, 5 and 6 fibers for 1%, 2%, 3% and 4% strain, respectively

Figure 4.

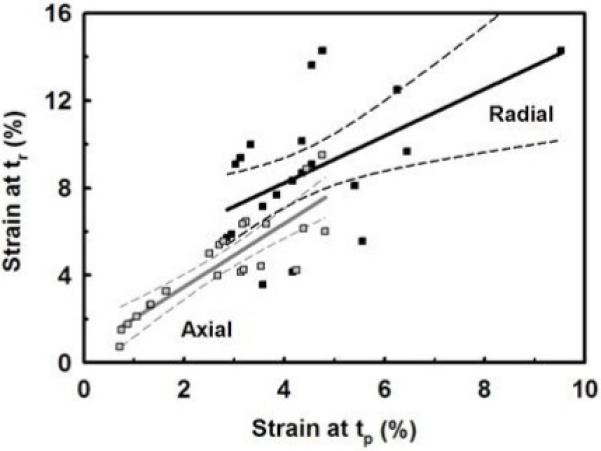
Plot of the fiber’s axial (ε_l ) and radial (ε_d ■) strains at the end of the mechanical-elongation (t_p) and mechanical stress-relaxation (t_r) phases. The radial strain was always greater then the axial strain at both times. After mechanical stress-relaxation both strains increased significantly. The best-fit linear model ± 95% confidence interval is shown.

We also found that the radial strain was almost twice that of the axial strain at both times. The Poisson’s ratio (ν = ε_l/ε_d = radial strain/axial strain) at stress equilibrium ν(t_r) was linearly correlated (equal) to the Poisson’s ratio at the peak stress ν(t_p) (ν(t_r)/ν(t_p) = 0.972±0.852, r=0.758). The mean peak and equilibrium Poisson’s ratios were ν(t_p) = 2.23±1.83 and ν(t_r) = 2.64±2.41, respectively, which were not statistically different (p>0.05, pooled mean ν = 2.43±2.16, n=48), again indicating equivalence at both times. These values for collagen fibers are similar to those for whole tendon [30] and indicate that interstitial fluid (water) is being exuded as the fiber is elongated. When the Poisson’s ratio was plotted against the axial strain at the peak and equilibrium stresses (times t_p and t_r, respectively, Fig. 5), it was found that the Poisson’s ratio decreased rapidly for small axial strains (~2% for peak and ~4% for equilibrium), and then remained relatively constant for higher axial strains. The data fit best to an exponential-linear model (r=0.945) as shown in Figure 5. This model indicates that when initially loaded the fiber’s diameter rapidly decreases as the fiber begins to elongate (exponential decay) but with increasing load and axial strain it becomes more difficult to decrease the fiber’s diameter (linear decay).

Finally, analysis of the peak and equilibrium stresses as a function of their respective peak and equilibrium strains found that the peak stress increased linearly with peak strain (slope=0.28±0.41 MPa/mm/mm, p<0.004) while the equilibrium stress was independent of the equilibrium strain (mean=1.8±1.4 MPa, p>0.5) (Fig. 6). The decrease in the peak stress with stress relaxation (peak/equilibrium=7.3±7.1) was significantly greater then the increase in the peak strain with stress relaxation (equilibrium/peak=1.7±0.08), suggesting these are independent phenomena.

Figure 6.

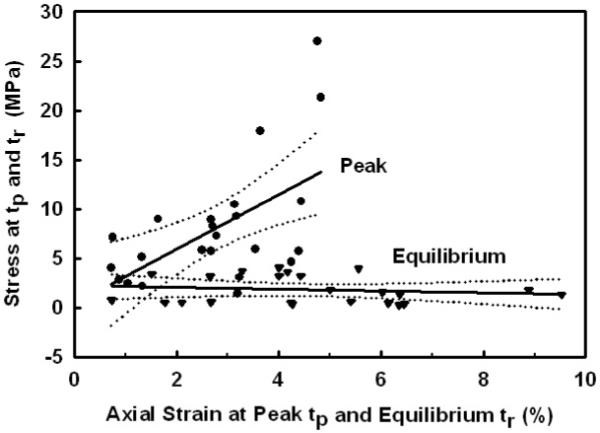
The peak stress at the end of the mechanical-elongation phase (peak ■) time t_p, increased linearly with increasing axial peak strain. However, the equilibrium stress at the end of the stress-relaxation phase (equilibrium ▼) at time t_r, was independent of the equilibrium stress. Note that after stress-relaxation the equilibrium strains increased by 1.71±0.37 as shown in Fig. 4.

Effect of Osmotic Stress

When a collagen molecule is exposed to a large non-penetrating molecule, such as dextran (79 kDa) and bacterial collagenase (68-130 kDa) [5], an osmotic stress is generated between the external solution containing the molecule and the collagen’s intramolecular space. This osmotic stress has been shown to change the triple-helical spacing between the individual α chains [23,31]. To evaluate how an osmotic stress would effect the equilibrium stress σ_r (magnitude and time), dextran or inactive bacterial collagenase in PBS solution was introduced into the bath channel after stress equilibrium was reached in fibers strained to 2% or 4%, the later inactivated by the absence of Ca⁺² from the PBS. For fibers strained to 2%, the dextran and collagenase caused an immediate increase (0.6% and 1.5%, respectively) in the axial stress σ_m and then a return (decrease) to the initial equilibrium stress over a period of several minutes. Fibers stretched to 4% had no change in their equilibrium stress following introduction of the dextran or collagenase. For both strains and molecules, the equilibrium stress did not change for an additional 45 minute period, indicating the absence of any longer-term osmotic effect and verifying the collagenase inactivity.

Enzyme Mechanokinetic Tests

After the fibers were elongated and allowed to reach stress equilibrium, 1% bacterial collagenase was added to the bath channel and the stress continuously monitored. As the collagenase cleaved the collagen molecules, the decrease in the fiber’s enzyme-cleavage stress, σ_e(t), was recorded until σ_e(t)=0. The EMK relaxation function T_E(ε), Eq. (3), was calculated from the slope of a best-fit straight line to the experimental data for σ_e*(t) versus time by least-squares regression analysis (Fig. 3). Only the initial linear portion of the response (zero order) was used, and to avoid any osmotic effects the zero order response interval (pooled mean = 17.5 ± 12.7 min) was always taken after osmotic stress equilibrium (11.5 ± 12.8 min) was reached (Table 1). Mean values for T_E(ε) at each applied strain E_o are given in Table 1. Overall there was a 73% decrease in enzymatic activity (T_E) as the strain increased from 1% to 4%. When T_E(ε) was plotted versus the fiber’s axial peak and equilibrium strains (Fig. 7), T_E(ε) was found to linearly decrease with increasing axial strain at a rate of 17.0% and 9.2% per percent strain, respectively. By extending the regression line to both axes, predictions for an undeformed fiber at zero strain gave T_E(0) = 2.70 ± 1.48 ×10^-4 s^-1 and 2.49 ± 1.17 ×10^-4 s^-1, respectively, which were not statistically different (pooled mean = 2.60 ± 1.35 ×10^-4 s^-1, p>0.05), while complete inhibition with T_E(ε)=0 would occur at an axial strain of ε_l = 5.9% and 10.9%, respectively.

Figure 7.

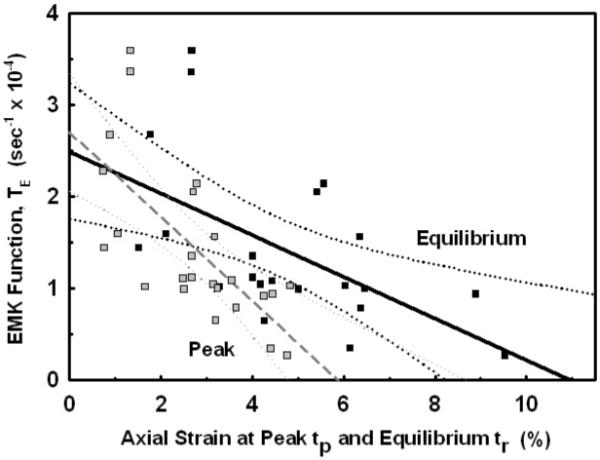
The Enzyme MechanoKinetic (EMK) relaxation function T_E(ε_l) is plotted as a function of the axial strain at the end of the mechanical-elongation () and mechanical stress-relaxation (■) phasesε_l(t_p) and ε_l(t_r), respectively. A best-fit linear model ± 95% confidence interval is shown for the peak (--) and equilibrium (—). Note that a sharp transition in T_E(ε_l) appears to occurred at ε_l≃3%.

Separate verification of enzyme cleavage was observed visually as the fiber’s diameter continuously decreased during the degradation process. The strain-induced inhibition was also confirmed by monitoring the fiber’s diameter at the end of the enzyme-cleavage phase (σ_e(t)=0), where the final diameter decreased by 8.4% ± 8.2%, 4.0% ± 2.2%, 1.3 ± 1.8% and 1.3% ± 2.0% for each applied strain of 1%, 2%, 3% and 4%, respectively.

Multiple linear regression analysis was performed to determine what, if any, independent parameters might influence the decrease in T_E(ε). The variables most likely to influence the retardation of collagenolytic activity are the fiber’s axial and radial strains at the peak elongation,ε_l(t_p) and ε_d(t_p), and at stress equilibrium, ε_l(t_r) and ε_d(t_r), the stress at the peak and equilibrium, σ_p and σ_r, respectively, and possibly the fiber’s diameter at the beginning and end of the mechanical-relaxation phase. A stepwise multiple linear regression was performed using all the data for each fiber to determine which independent parameters of fiber geometry and mechanical response had a statistically significant effect on T_E(ε). Of all the independent variables, the axial strain at peak and equilibrium accounted for 48% and 33% of the decrease in T_E(ε), respectively, while only 2-3% of the variation could be accounted for when including ε_d(t_p)_, ε_d(t_r) and σ_p in the analysis. The other independent parameters, geometric or mechanical, had no effect on the change in the rate of enzyme cleavage of the collagen fibers.

Discussion

The major finding of this study was that mechanical deformation of type I collagen fibers caused by an axial strain (elongation) applied to the fiber will result in a significant decrease in the rate of collagen degradation by bacterial collagenase. Our findings are in agreement with previously published reports [11,12,13] that a tensile strain applied to type I collagen was able to reduce the rate of collagen cleavage by bacterial collagenase. From our statistical analyses it is evident that the axial strain had the largest influence (~33-48%) on decreasing the collagenolytic activity as compared to fiber stress and radial strain. We termed this mechanically-induced substrate-enzyme interaction the Enzyme MechanoKinetic (EMK) effect. While the exact mechanism of action is unknown, the phenomenon documented herein suggests that it is the mechanical deformation of the collagen fiber, at the microstructural level, that is the primary factor responsible for the inhibition in bacterial collagenase cleavage of the collagen molecule. However, as discussed below further investigations will be necessary to determine the exact mechanism for this change in the mechano-chemical kinetic interaction.

Monomeric type I collagen is composed of two α(1) chains and one α(2) chain. Cleavage by mammalian collagenases occurs by triple helicase activity at a specific cleavage site, the mechanism of which has been well characterized [1,4]. Mammalian collagenase attaches to a binding region located along the collagen molecule, initiating the loosening of the triple helix and exposure of the ¾-¼-cleavage site, followed by a scissoring across the three chains by the collagenase catalytic domain. It is important to note that mammalian collagenase cannot immediately cleave collagen but must first attach via its haemopexin-like C-terminal domain (CTD) to a substrate-binding site (exosite) located toward the N-terminus of the collagen substrate. A protein linker in the collagenase, that connects the CTD to the catalytic domain, together with the catalytic domain was hypothesized to perturb or unwind the catalytic active site on the triple helix enabling α-chain cleavage (termed helicase activity) [1,4,32], and later verified that the linker destabilized the secondary structure of the collagen at the cleavage site allowing cleavage of the α chains [33].

With this in mind, bacterium Clostridium histolyticum collagenases (CHC), of which bacterial collagenase is classified, is able to cleave collagen at numerous sites, all of which are distinct from the mammalian cleavage site but require a similar type of enzyme-substrate interaction. French et al. [34,35] suggested that the CHC hyperreactive sites are dependent upon site-specific localized conformations and amino acid sequences. Along the collagen molecule repeats of the Gly-Pro-Hyp amino acid sequence are believed to account for the rigid and tightly wound sections that may hinder bacterial collagenase accessibility, while areas void of this sequence were common among the classified hyperreative sites [34-36]. Although it is unclear whether or not triple helicase activity is observed with CHC, the substrate-binding site S3a and S3b (mammalian exosite attachment equivalent) and segmental structure S2 (mammalian linker domain equivalent) motif is conserved for both bacterial and mammalian collagenase [6]. Our results for bacterial collagenase and type I collagen suggest that elongation of the collagen molecule may (1) change (increase) the distance between the enzyme-substrate binding site and the substrate catalytic domain, preventing the segmental structure from reaching the active domain (discussed above), (2) elicit a strain-induced conformational change in the structure of the collagen molecule (triple helices) creating a chemical-thermal instability at the hyperreactive binding sites, or (3) elicit a strain-induced conformational change in the structure of the collagen molecule and rearranging the constituent components (e.g., minor collagens, proteoglycans and other glycosaminoglycan containing proteins) to inhibit access to the hyperreactive sites and thus retarding degradation.

Collagen molecules bind uniaxially via N to C terminal connections. However, these layers of adjacent collagen molecules are then connected to subsequent layers located above and below by hydrogen N-H and O-H bonds [37,38]. Due to the self assembly nature of collagen, there appears to be a long range attraction which prevents molecules from coming too far apart and which induces the self assembly where hydrogen water bridges surrounding the molecule act as specific recognition sites for attracting other collagen molecules [39,40]. More important, however, is that an exponential increase in the interaction energy (forces between triple helices) occurs as the α-chain separation distance decreases [23,31]. Heightened hydration interaction forces are observed nearing the last 10-20 angstroms of α-chain separation (osmotic stress as high as 1000 MPa have been measured). Kuznetsova et al. [23] proposed that this increased interaction force is due to the energy required to rearrange the hydrogen bonding network near the molecular surfaces of macromolecules, such as might occur as the collagen molecule’s diameter is reduced as the molecule is stretched in response to an axial tensile load. Alterations in the ionic strength will also effect electrostatic interactions (<1 MPa at 15-60 Å). When the collagen molecules come into close proximity the van der Waals forces (<1 MPa at 10-25Å separation) result in an attraction or repulsion dynamic. Thus, a high concentration of repulsion ionic character will position the molecules further away from neighboring molecules creating a greater separation distance and ultimately a larger diameter. Conversely, attractive ionic character would link the molecules with a greater affinity, resulting in smaller diameters.

In our study both osmotically generated fiber stress and strain would factor in some of these responses, however from our results the osmotic effects observed in the fiber equilibrated within 20 minutes of exposure to dextran and bacterial collagenase. In contrast, the initial elongation (mechanical-elongation phase, Fig. 2) reduces the separation distance between the collagen fibers by ε_d(t_p) followed by a further reduction in separation to ε_d(t_f) as the axial strain increases during stress relaxation (mechanical-relaxation phase) (Figs. 2 and 4). As the fiber diameter decreases there will be a local dehydration of the fiber as the fiber and α-chain separation distances decrease, resulting in a concomitant increase in the triple-helical hydration force [31,39,40,41]. We hypothesize that the exponential increase in the hydration force probably accounts for the nonlinear decrease in the fiber’s diameter (Poisson’s ratio) observed with increasing axial strain (Fig. 5). Furthermore, the close proximity of the collagen fibers after the strain is applied creates a repulsive energetically unfavorable atmosphere that may prohibit the enzyme from accessing the catalytic domain. As the fiber strain increased this effect presumably becomes more pronounced and the rate of enzyme degradation is reduced. However, these hypotheses will need verification before an exact mechanism can be determined.

One limitation in this study was the use of bacterial collagenase in a non-temperature controlled system. Although bacterial collagenase is active at room temperature between a pH of 7-9, these conditions do not reflect physiological conditions. However this should not effect our general findings. In addition our study was focused on the effect of the mechanical deformation of the collagen fiber to inhibit the fiber’s degradation by collagenase, and not on the actual mechanism responsible for the inhibition. In general the degradation rate of any substrate by an enzyme is governed by the enzyme-substrate attachment (reversible binding rate) as well as the enzyme’s ability to scissor the substrate (irreversible cleavage rate), both of which can be affected by the deformation of the substrate and the enzyme. In particular, increases in the elongation of the collagen molecule would induce a conformational change within the α-chains of the triple helix, causing a change in the molecule shape and thereby altering the collagen-collagenase attachment or cleavage sites, or both, to thus inhibit enzymatic degradation. Since only the overall degradation rate was measured in this study we cannot distinguish the mode of inhibition. In addition bacterial collagenase cleaves collagen at more sites then does mammalian collagenase, which scissors only at the 3/4-1/4 cleavage site. We don’t expect mammalian collagenase to produce different results relative to the inhibition as the use of bacterial collagenase is a worse-case treatment due to its aggressive nature. However future testing will have to be performed using mammalian collagenase to fully delineate the exact mechanisms involved relative to human pathology.

Another over simplification in this study was the measure of collagen fiber strain rather then molecule strain. We assumed that the axial strain ε_l measured from the gage marks placed on the outer diameter of the fiber at the center of the fiber’s length to effectively be the local strain along and within the entire collagen fiber (fibril and molecule). However, this must be best viewed as an approximation since the exact relationship between fiber, fibril and molecule strains are as yet unknown. Conflicting findings have been reported as to whether all the fibrils within the fiber are elongated simultaneously or sequentially (e.g., inner→outer or outer→inner fibril straightening) [43,44]. Furthermore, some drying of the fiber ends exposed to the air outside the fluid channel may have taken place as we found a two-fold increase in the peak axial and radial strains in the center of the fiber after stress-relaxation (1.71±0.37 and 2.04±0.63, respectively). Using the average initial grip-to-grip distance of 25.6 mm and channel length of 25 mm, the calculated air-exposed portion of the fiber ends after grip-to-grip elongations of 1-4% would be approximately 2-5%, respectively. If the exposed ends dried and contracted by ~65% (water content), then the equilibrium strain could have increased by an additional ~1-3% and could account for the approximate doubling of the axial and radial strains at the center of the fiber. However independent testing (data not shown) of unloaded fibers allowed to fully dry found less then a 1% decrease in the fiber’s length. The exact mechanism responsible for the increase in the equilibrium stain will require further investigation.

It has been previously shown that the stress-strain response of rat tail tendon (i.e., collagen fascicle as used in the study) can be divided into three distinct segments, the toe, heel and linear regions, Fig. 8a [42,43]. At small strains (≤2-3%) the toe region corresponds to a straightening of the collagen crimp in the collagen fascicle (fiber/fibril), while the heel region (~3-5%) is believed due to straightening of kinks in the gap region of the collagen fibril, possibly associated with other molecules present in the fibril structure (e.g., minor collagens, GAGs or fibronectin) [45]. In the linear region (~5-10%) stretching of the intermolecular cross-links and triple-helix occurs, probably in that order as the stiffness of the triple-helix is several orders of magnitude greater then that of the cross-links. However in our study we found that after stress-relaxation the fiber’s equilibrium stress was strain-independent, the peak stress decreasing by ~86% to ~1.8 MPa for peak strains ranging from 1 to 5%. This result, taken together with the observed increase in fiber strain at equilibrium (δε_l(t_r)~2-fold) suggests the presence of an intrinsic viscoelastic component within the extracellular solid matrix, probably at the microstructural level and possibly due to intermolecular slippage. There is evidence in the literature for a thermodynamically conserved (reversible) molecular micro-unfolding of the collagen triple-helix when the fibril is stretched (wormlike chain model), which may be due to the unwinding or separation of the polypeptide chains [46,47]. While we do not know the mechanism for the strain-independent decrease in the peak stress, this could explain some of the variability in the EMK response if not all of the collagen molecules within the fiber are elongated uniformity.

Figure 8.

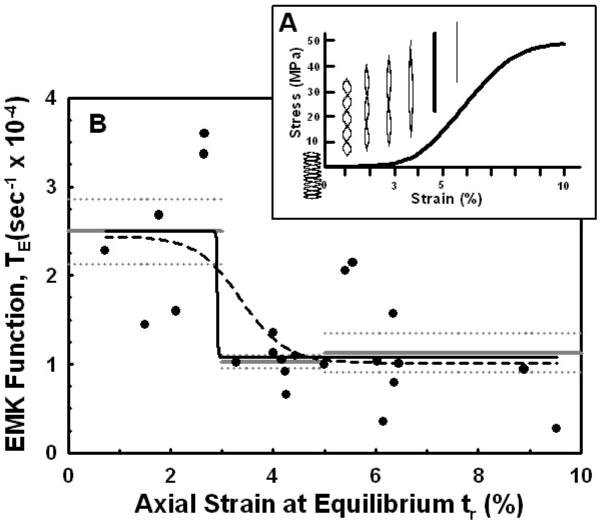
Nonlinear curve fits to the Enzyme MechanoKinetic (EMK) relaxation function T_E(ε_l) as a function of the axial strain ε_l(t_r) after mechanical stress-relaxation. (A) Schematic representation of fiber elongation in the toe (ε_l=0-3%), heel (3-5%) and linear (>5%) regions of the stress-strain response. In the toe region the fiber crimp pattern straightens, followed by stretching of the fiber in the heel and linear regions. Adapted from [42,43]. (B) Best-fit four-parameter logistic models are shown with variable slope (dashed black line) and constant slope (solid black line). The mean ± standard error of the mean for T_E(ε_l) in each region are also shown (gray, solid and dotted, respectively). Note that the transition in T_E(ε_l) occurs for ε_l=2.9-3.4%.

In our study the axial strains within the fiber at the end of the mechanical-relaxation phase ε_l(t_r) ranged from 1-10% (Fig. 4), which spans all three regions of the stress-strain response and is significantly greater than used in all previous studies [11,12,13]. Thus based on the axial strains at the end of the mechanical-relaxation phase, when the collagenase was introduced, the measured EMK response in our study incorporated all three structural mechanisms involved in fiber elongation (crimps, kinks, cross-links and triple helix). As can be seen in Figure 8b for T_E(ε) vs ε_l(t_r), the least inhibition of collagenase cleavage occurred in the toe region where for ε_l(t_r)≤3% the mean T_E(ε) = 2.50±0.89 ×10^-4 s^-1 (n=6). After the toe region there is a significant transition to increased inhibition (decrease in T_E) in the heel region (ε_l(t_r) = 3-5%, T_E(ε) = 1.03±0.20 ×10^-4 s^-1, n = 8) and linear region (ε_l(t_r) = 5-10%, T_E(ε) = 1.13±0.67 ×10^-4 s^-1, n=9), where both regions were not significantly different (p>0.6; ε_l(t_r)>3-10%, pooled mean T_E(ε)=1.08±0.53×10^-4 s^-1, n=17).

To further analyze the nonlinear characteristic of the T_E(ε) vs ε_l(t_r) response, a four-parameter logistic function (i.e., a sigmoidal dose-response) was fit to the data in Figure 8b, given by

$${\mathrm{T}}_{\mathrm{E}}\left({\epsilon }_1\right)={\mathrm{T}}_{\mathrm{Emin}}+({\mathrm{T}}_{\mathrm{Emax}}-{\mathrm{T}}_{\mathrm{Emin}})∕(1+{10}^{(\epsilon 1-\epsilon \mathrm{o})\mathrm{B}})$$ (4)

where T_Emax=T_E(0), T_Emax=T_E(∞), T_E(ε_o)=½(T_Emin+T_Emax), and the transition slope B≥1. Shown in Fig. 8b is equation (4) fit to the data for B=1 (no slope), yielding T_Emax=2.44×10^-4 s^-1, T_Emin=1.08×10^-4 s^-1, B=1/%, and ε_o=3.4%, and for a variable slope, yielding T_Emax=2.49×10^-4 s^-1, T_Emin=1.08×10^-4 s^-1, B=61.3/%, and ε_o=2.9%. Note that T_Emax and T_Emin for both cases are equivalent to the means for T_E(ε) in the toe region and heel/linear regions, respectively, and the strain at the transition between T_Emax and T_Emin, ε_o=2.9-3.4%, is similar to the transition strain between the toe and heel regions (~3%).

From our results we can speculate on one possible mechanism for the enzyme inhibition indicated by the discontinuity in the EMK Funtion T_E indicated in Fig. 8, that is, we hypothesize a three-domain model. The above results, taken together with the rapid decrease in the fiber’s diameter in the toe region (Poisson’s ratio, Fig. 5), suggests that straightening the crimp in the collagen fiber is insufficient to inhibit enzyme cleavage of the collagen molecule. On the contrary, it suggests that a conformation change in the triple helix is necessary for inhibition. We hypothesize this can occur by two concurrent mechanisms as the collagen fiber is mechanically loaded, (1) intermolecular triple-helix forces (causing tensile axial strain) as the macromolecular forces are transferred to the α-chains of the triple helix through the intermolecular kinks and cross-links between the triple helices, and (2) intramolecular triple-helix forces (causing compressive radial strain) as the fiber’s cross-sectional area (diameter) decreases generating increased intramolecular hydration forces. Our data suggests that both these mechanisms would begin in the heel region, after the collagen crimp is straightened, and transition rapidly as the collagen triple helix is deformed.

As stated earlier only ~50% of the reduction in the EMK cleavage of the collagen fiber was attributed to known parameters of which the axial strain accounted for ~48%. While the remaining ~50% is currently unknown we presume that the inconsistency between the fiber and molecule axial strains may account for some of this discrepancy. Specifically if every collagen triple-helix molecule within the fiber was not stretched to the same applied strain, as would be expected when the fiber elongation was performed via grip-to-grip attachments, then molecules that were not fully strained would effect the accuracy of the strain-dependent rate of degradation. Those molecules not strained or strained to less then the assumed strain would be cleaved as if unloaded or at a different (faster) degradation rate, respectively. Expanding on this concept, if an axial strain >3% is necessary to alter the collagen molecule’s cleavage/multiple hyperreactive sites, that is its molecular conformation, and if triple helix cleavage would be completely inhibited in molecules subjected to an axial strain >3%, as we are hypothesizing, then the results found in this study would reflect only those collagen molecules not strained >3%. From this perspective, the reduced rate of degradation for strains ≤3% could be a result of the time required for enzymes to attach to the exosites and cleave the collagen molecule while enzymes attaching to the exosites of those molecules that were strained >3% would not reach the catalytic domain (degradation inhibition).

Other factors in addition to axial strain that might influence the degradation rate of intact solid collagenous structures (fibers) include mass transport (diffusion) of the enzyme into the fibril, steric hindrance of the large enzyme molecules within the fibril, local osmotic and pH effects, and the relative concentrations and interactions of minor collagens (e.g., IX and XI) and glycoproteins (aggrecan, biglycan, decorin) [16,45]. Enzyme exclusion from the intermolecular space might occur as the fiber is strained but only if the enzyme had free unrestricted access to the space in the unloaded state. Enzyme diffusion and steric hindrance was included in an analytical model of enzyme degradation (erosion) of collagen fibrils by Tzafriri et al. [16], where the enzyme was excluded from penetrating the fibril and enzyme binding and cleavage could only occur on the fibril surface. They reported that when [S]≫[E] a 0^th order linear Michaelis-Menten response occurred in the first hour of degradation, independent of enzyme transport (the time scale for enzyme absorption and diffusion was ~1 min and ~2 min, respectively). As collagen cleavage reached the substrate-depleted condition [S]≪[E] and the individual enzyme molecules now compete for the hyperreactive sites, the degradation followed a 1^st order nonlinear response. In our experimental design [S]≫[E], and the EMK relaxation function T_E(ε) was calculated only during the linear portion of the enzyme-cleavage phase (~8-28 min, Table 1), after any enzyme-substrate osmotic effect had occurred (4-17 min, Table 1). Under these conditions and the assumptions used by Tzafriri et al. [16], enzyme transport would have a small effect on T_E(ε). While restricted enzyme transport due to fiber strain can not be completely ruled out, especially as the fibers used in this study were large (diameter > 300 um), we believe our results indicate that a strain-dependent conformational change in the collagen molecule was the mechanism responsible for the inhibition of collagen cleavage by bacterial collagenase.

Conclusions

At present, the effect of strain on the rate of enzyme degradation in an individual collagen molecule (triple-helix) is unknown. It may be that higher strains than applied in this study (>10%) are necessary to completely inhibit fiber cleavage, or that strains nearing fiber failure (~11-15%) may promote enzyme degradation as microfailure begins to occur. However, comparison of the EMK response (T_E vs ε) to collagen’s stress-strain response (σ vs ε) appeared to indicate the possibility of three different EMK responses as a function of increasing strain; (1) constant T_E(ε)=2.50±0.89 ×10^-4 s^-1 within the toe region (ε<3%) where straightening of the crimps in the collagen fibrils occurs, (2) an instantaneous decrease (~50%) in T_E(ε) at the end of the toe region (ε≅3%), and (3) constant T_E(ε)=1.08±0.53×10^-4 s^-1 throughout the heel (ε=3 to 5%) and linear (ε=5 to 10%) regions where stretching (deformation) of the collagen triple helix is observed. Using a wider spectrum of strains and different experimental methods may better clarify the molecular mechanisms responsible for these phenomena.

Finally, there exists a novel relationship between enzyme activity and mechanical disturbance in collagen that surpasses the previously held method of mere enzyme-substrate complex formation. Further understanding of factors such as physiological temperature, fibril versus molecule strains, increasing the elongation to approach fibril failure, exosite and catalytic site distances, and the unfolding patterns of collagen constituents (e.g., proteoglycan) are all valid studies that would aid in developing the underlying molecular basis to describe how and why the rate of collagenolytic activity decreases as the strain increases. These capabilities will be critical in future studies to determine whether non-collagen matrix structural components, steric hindrance and/or attachment site inaccessibility are contributing to the enzyme mechanokinetic effect reported herein.